Modeling nonlinear stress-strain model for sulfate dry-wet cycle erosion of concrete: considerations for the initial compaction stage

Abstract

Sulfate dry-wet cycle erosion significantly affects the mechanical properties of concrete. Investigating the uniaxial compressive stress-strain relationship under these conditions is essential for developing accurate constitutive models. This study analyzes the uniaxial stress-strain curves of concrete subjected to dry-wet cycles in 5% and 15% sulfate solutions. The results show that the initial compaction phase in the stress-strain relationship is particularly pronounced under increasing sulfate concentrations and cycle counts. The concrete experiences an extended compaction phase, which accounts for up to 35.71% of the total strain process. This finding challenge traditional constitutive models, which struggle to accurately describe this phase. To address this issue, the study develops a nonlinear stress-strain model for concrete, incorporating the initial damage caused by sulfate dry-wet cycle erosion, based on Weibull statistical damage mechanics principles. The research indicates that the effects of sulfate concentration and cycle count are predominantly reflected in the pronounced nonlinearity of the skeleton strain function’s opening size (a) and shape characteristics (b), modeled using a fourth-degree polynomial. The model demonstrates an excellent fit to experimental data with an R² value of 0.99989, showing that the proposed nonlinear stress-strain relationship effectively captures the uniaxial mechanical behavior of concrete under sulfate dry-wet cycle erosion and provides a robust framework for developing constitutive models in such environments.

Introduction

Concrete, as a common building material, is widely used in various engineering fields. With the implementation of the Western Development Strategy, a large number of concrete structures such as railway piers are being constructed in the central and western regions of China. In the southwestern region, when building underground projects like highways and railway tunnels, in addition to being subjected to external loads, they also face the erosion effects of substances such as sulfates. Research has been conducted to determine how concrete structural performance is affected by acid rain of varying concentrations¹. Many concrete structures are damaged due to the corrosion caused by sulfates in acid rain, thereby severely compromising the safety of engineering structures^2,3. Through long-term research conducted by foreign scholars, it has been found that sulfate erosion significantly impacts concrete. Liu et al.⁴. studied the effects of erosion type, erosion age, and sulfate solution concentration on the compressive strength of concrete; they established that there is a Pearson IV function relationship between the compressive strength of concrete and the sulfate solution, and that the main type of erosion affecting the concrete is chemical erosion. Chen, Yuan, and others^5,6 investigated the impact of different mineral admixtures on the resistance of concrete to cyclic sulfate exposure. They found that the degree of deterioration of concrete varied depending on the mixture added under cyclic sulfate environments. Furthermore, they observed that the performance of concrete under cyclic sulfate exposure evolves in two stages: an improvement stage and a deterioration stage. Zhang et al.⁷.investigated the corrosion behavior of ordinary concrete and improved concrete with different admixtures under dry-wet cycling conditions. They conducted tests on the compressive strength and splitting tensile strength of the concrete. The study revealed that the concrete strength initially increases during the early stages of corrosion but gradually decreases later on. Based on the experimental results, they predicted the service life of modified concrete under sulfate corrosion. Xu et al.⁸. used phosphor gypsum-based cold-bonded fine aggregate to replace natural sand in the preparation of high-sulfate cement concrete. They studied its compressive strength, splitting tensile strength, flexural strength, and stress-strain curves, concluding that using alternative materials such as phosphor gypsum-based cold-bonded fine aggregate under high sulfate conditions is highly reliable. Concrete carbonation accelerates the corrosion process within its internal structure. Kumar et al.⁹. proposed an adaptive neuro-fuzzy inference system based on machine learning to predict the degree of concrete carbonation, which is simpler and more cost-effective compared to existing models. The influence of sulfate erosion on concrete performance extends far beyond that. Among them, the stress-strain curve of concrete under uniaxial compression contains important mechanical performance indicators. Therefore, establishing the constitutive relationship of concrete under compression during sulfate erosion is of great significance for studying the effects of sulfate erosion on concrete.

Scholars have conducted extensive research on constitutive relationships. Hu, Feng, and others^10,11have established a mathematical model for the constitutive relationship of plastic concrete under triaxial compressive stress. Based on uniaxial compression tests and triaxial tests, they investigated the constitutive behavior of plastic concrete. They found that the strength of plastic concrete increases with increasing confining pressure. Additionally, they observed that the compressive strength of rubberized concrete decreases with an increase in rubber particle content. However, the deformability of the concrete increases with an increase in rubber particle concentration. These findings highlight the complex interplay between the composition and mechanical properties of plastic and rubberized concrete under different stress conditions. Deng, Wang, Zhao, and others^12,13,14 designed a significant number of recycled aggregate concrete specimens and obtained important data such as stress-strain curves through experiments. From the perspective of constitutive relationships, they studied the influence of the classification of recycled coarse aggregates on the mechanical properties of recycled aggregate concrete. Karimi et al.¹⁵developed an anisotropic non-linear viscoelastic constitutive model that is sensitive to tension compression stress patterns by extending Schapery’s model. Yang et al.¹⁶ conducted uniaxial compression tests on wet concrete and developed a segmented damage constitutive model. Xie et al.¹⁷, based on the conversion law of bond strength on the bond-interface of reinforced concrete, established a mesoscale mechanical model using spring-friction elements. Bai et al.¹⁸developed a constitutive model for concrete under extreme dynamic loads using micromechanics of damage, the Duvaut-Lions formula, and elastoplastic theory. Wen et al.¹⁹ considered the effects of cracks during the compression process of rocks and established a constitutive model for rocks. Zhou et al.²⁰ developed a damage constitutive model for cyclic loading and considered the influence of temperature variations on the model. Yang et al.²¹. studied ultra-high-performance concrete subjected to wet-dry cycles with four different sulfate concentrations, analyzing the uniaxial compressive strength and energy evolution of the specimens after the test. They identified the characteristic stress points of ultra-high-performance concrete under sulfate attack during the uniaxial compression process. Liu et al.²²., considering the crack closure effect under compressive stress, investigated the damage evolution process under sulfate erosion and developed an improved fully coupled non-local dynamic model.

Research significance

Current research on concrete constitutive relationships primarily focuses on the effects of different stress paths, loading methods, and the impact of various materials on concrete strength. However, studies on concrete constitutive relationships under sulfate cyclic erosion are relatively scarce. Scholars have a clear understanding of the mechanisms of sulfate and hydrochloric acid erosion^23,24,25,26, although most research has been centered on changes in various indicators after erosion. Some studies have also examined the uniaxial compressive stress-strain relationship of concrete subjected to sulfate erosion, recognizing that this relationship reflects the deformation characteristics and failure process of concrete at different stress stages, and includes crucial mechanical indicators. It is a fundamental constitutive relationship, and sulfate erosion inevitably alters the stress-strain curve. Several studies have explored various aspects such as the basic functional forms of the stress-strain relationship, the effects of different acidic solutions on the curve, the impact of wet-dry cycling simulating seawater erosion on the curve, CT imaging observations, and changes in curves for different aggregate concretes^{27,28,29,30,31,32}. Research indicates that sulfate erosion significantly affects the microstructure and compressive strength of concrete, particularly due to changes in pore structure caused by sulfate reaction products, leading to increased porosity and a more pronounced effect on the initial densification stage³³. However, few studies have specifically considered the changes in the pore densification stage of the stress-strain relationship during uniaxial compression due to sulfate erosion. This paper particularly addresses the significant impact of sulfate erosion on the pore densification stage of the concrete stress-strain curve, describes the evolution of skeleton strain under different concentrations and erosion durations, and establishes a constitutive relationship for sulfate-eroded concrete based on Weibull probability damage statistical theory. This study can provide theoretical references for related engineering problems and support future research on more complex constitutive relationships of concrete under sulfate erosion.

Experiment

Concrete specimen fabrication

The trial was conducted using P.O 42.5 cement, and the admixture selected was Class F Class II fly ash sourced from Chongqing Huaidian Trade Co. Polycarboxylic acid-based high-performance water reducing agent was used as a water reducing agent, with a water reduction rate of ≥ 25.0%. The concrete mix proportions used in the experiment are shown in Table 1. According to the actual situation, the specimens were prepared using the method of dry mixing followed by wet mixing with a mixer, totaling 4 min. The specimen dimensions are 100 mm × 100 mm × 100 mm, and the concrete strength is C60 (as shown in Fig. 1). After demolding, the specimens were placed in a standard curing room at a temperature of (20 ± 2) ℃ and a relative humidity of more than 95% for a period of 28 days.

Fig. 1

The fabrication of concrete specimens.

Table 1 Mixture of high strength concrete unit: (kg·m^− 3)

Experimental design

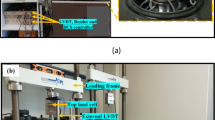
The sulfate dry-wet cycle test is conducted in accordance with the standard GB/T 50,082—2009, titled 《Standard Test Methods for Long-Term Performance and Durability of Ordinary Concrete》. The concrete was immersed in 5% and 15% sodium sulfate solution for 14 h, then removed and air-dried for 2 h, followed by drying in an 80 °C oven for 6 h. The dried concrete was then cooled in the laboratory for 2 h until it reached room temperature, completing one cycle of wet-dry exposure. After 0, 7, 14, 21, 42, and 63 cycles of erosion, concrete specimens were removed and subjected to uniaxial compression tests using a computer-controlled pressure testing machine produced by Shanghai Hualong Testing Instrument Co., Ltd. (as shown in Fig. 2). This machine has a maximum load capacity of 2000 kN and can be used for testing the mechanical properties of various composite materials such as concrete, including tensile, compression, tearing, bending, and other tests.

Fig. 2

The computer-controlled pressure testing machine.

Experimental results and analysis

Using a computer-controlled pressure testing machine, uniaxial compression tests were conducted on concrete specimens subjected to sulfate dry-wet cycle erosion. Stress-strain data of concrete under different sulfate concentrations and different numbers of dry-wet cycles were obtained and plotted.

Fig. 3

The experimental stress-strain results. (a) 5% sulfate solution (b) 15% sulfate solution.

Fig. 4

Comparison between the calculated results from other literature and experimental curves.

As shown in the Fig. 3, under the erosion effect of sulfate at different concentrations and cycle numbers, the stress-strain trends are basically consistent. The initial densification stage during the concrete failure process is clearly visible. When the number of cycles is 7 and 14, the difference between the curves is minimal. Compared with the uneroded specimens, the slope of the stress-strain curve increases, and the peak point of the curve shifts to the left and increases. This is because with the erosion of sulfates, new minerals gradually form inside the concrete, filling the internal voids of the concrete specimens. As a result, the stress required for the concrete specimens at the same strain increases, and the peak stress also increases. In concrete treated with 5% sodium sulfate solution, the slope and peak stress of the stress-strain curve are maximum at 21 cycles. When the number of cycles exceeds 42, the curves shift to the right, and both the peak stress and the slope decrease significantly. This is because in the later stage of erosion, microcracks develop inside the concrete, increasing its porosity.

The stress-strain curve of concrete subjected to 15% sulfate concentration and 63 cycles is compared with stress-strain curves calculated by models from other literature^34,35,36. As shown in the Fig. 4, it is apparent that due to the models not considering the influence of the initial densification stage, their curves poorly fit the experimental curves in the initial densification and elastic stages. The subsequent discussion will consider the impact of the initial densification stage on the stress-strain curve and study the constitutive relationship of concrete under sulfate erosion.

Concrete constitutive relationship based on weibull probability

Determination of damage variables

Initial damage of concrete

Sulfate attacks can alter the porosity of concrete, either increasing or decreasing it, consequently impacting the initial damage. In this paper, we choose the elastic modulus definition method³⁷, which now has a fairly complete theoretical basis, to define the initial damage of eroded concrete with the initial damage equation D₀ as:

$${D_0}=1 - \frac{{{E_{\text{t}}}}}{{{E_0}}}$$

(1)

where E_t is the modulus of elasticity of concrete after erosion, and in E₀ is the modulus of elasticity of uneroded concrete.

Based on the experimental data, a plot illustrating the relationship between the number of dry and wet cycles of sulfate and the initial damage of concrete is presented in Fig. 5.

Fig. 5

Relationship between initial damage and days of sulfate drying and wetting cycle.

When the initial damage is negative, it signifies a beneficial impact of sulfates on concrete. When the initial damage is positive, it indicates the adverse effect of sulfates on concrete. From Fig. 5, it is evident that as the sulfate concentration increases, the initial damage to the concrete also increases. The initial damage variables caused by sulfate on concrete under the erosion effect of a 5% sulfate solution are all negative. This implies that the impact of sulfate on concrete is detrimental, indicating a negative effect until approximately 63 wet and dry cycles. However, as the number of days of wet and dry cycles increased, the influence of sulfate on concrete exhibited a pattern where the enhancement effect initially increased and then subsequently decreased. At 42 cycles, the enhancement effect of sulfate on the initial damage of concrete was most pronounced, resulting in the concrete’s initial damage reaching its lowest value of -0.521. When the concentration of the sulfate solution was 15%, the initial damage of the concrete initially decreased and then increased with an increasing number of wet and dry cycles. Specifically, at 7, 14, and 21 cycles, the initial damage values were negative. Among these, the 14th cycle had the smallest initial damage value of -0.0947. However, after 42 and 63 cycles of wet and dry cycles, the initial damage of the concrete transformed into positive values, clearly indicating the negative effect of sulfate on the initial damage of the concrete. The phenomenon is due to the strengthening of the physical and chemical effects of sulfate on concrete as the number of wet and dry cycles increases. When the number of cycles is small, the internal pores of the concrete are filled with minerals, leading to reduced initial damage and indicating a positive effect of sulfate. However, as the number of cycles increases, microcracks form within the concrete, resulting in larger initial damage and continuing to demonstrate the positive effect of sulfate on the initial damage of concrete. The harmful impact of sulfate on the initial damage of concrete. As the concentration of sulfate increases, the rate of mineral crystallization also increases, leading to a quicker transition from positive to negative effects. Consequently, an inflection point is observed at a sulfate concentration of 15% earlier in the process. Under the influence of high concentrations of sulfate erosion, the recrystallization of gypsum in concrete leads to greater damage compared to the damage caused by calcium alumina at low concentrations. This high concentration of sulfate erosion generates an increased number of microcracks in the concrete, surpassing the damage caused by low concentration erosion. Consequently, when the number of wet and dry cycles is low, concrete eroded by high concentrations of sulfate exhibits a negative effect on the initial damage of the concrete.

A nonlinear fit to the initial damage variable curve in Fig. 5 yields an expression for the initial damage of concrete under sulfate attack as a function of the number of dry and wet cycles days, along with the corresponding parameters, listed in Table 2:

$$D_{0} = An^{4} + Bn^{3} + Cn^{2} + Dn + E'$$

(2)

Table 2 Expression parameters of initial damage variables.

Mechanical damage during uniaxial compression process

Concrete, as a heterogeneous material, often exhibits randomness in mechanics, and the damage generated during its compression process is also randomly distributed. Some scholars have combined the damage parameter with the Weibull statistical distribution to derive the evolution equation of concrete under uniaxial compression³⁸. This paper, based on the principles of statistical damage mechanics, approximates concrete under uniaxial compression as composed of countless small units. The damage factor can be expressed as the ratio of failed small units to the total number of small units.

Assuming that the strain and unit strength of concrete under compression follow a Weibull probability distribution, the expression for the Weibull probability density function is as follows:

$$p(F)=\frac{k}{m}{(\frac{\varepsilon }{m})^{k - 1}} \cdot \exp [ - {(\frac{\varepsilon }{m})^k}]$$

(3)

where m and k are the Weibull distribution parameters. Let N_D represent the number of microelements that undergo deformation damage in concrete, and N represent the total number of microelements. In this context, the relationship between these two variables can be expressed as follows:

$${N_{\text{D}}}=N\int {p(F)d(F)}$$

(4)

$${N_{\text{D}}}= - N\exp [{( - \frac{F}{m})^k}]+N$$

(5)

Under the assumption that the unit strength of concrete follows a Weibull probability distribution, the microelements in the concrete gradually undergo damage during the compression process. Therefore, the damage variable of concrete during the compression process can be defined as D_ε:

$${D_{\text{\varvec{\upvarepsilon}}}}=\frac{{{N_{\text{D}}}}}{N}=1 - \exp [{( - \frac{\varepsilon }{m})^k}]$$

(6)

The total damage variable²⁸, D, during the compression of concrete undergoing wet and dry cycles of sulfate can be expressed as:

$$D={D_0}+{D_{\text{\varvec{\upvarepsilon}}}} - {D_0}{D_{\text{\varvec{\upvarepsilon}}}}$$

(7)

Assuming that the Weibull distribution parameters m and k have a functional relationship with the number of days of dry and wet cycles of sulfate, and substituting Eq. (1) and Eq. (6) into Eq. (7) yields the equation for the damage variables of concrete under the action of sulfate erosion during uniaxial compression:

$$D=1 - \frac{{{E_{\text{t}}}}}{{{E_0}}}\exp [ - {(\frac{\varepsilon }{{{m_{(n)}}}})^{{k_{(n)}}}}]$$

(8)

Determination of Skeleton strain

Sulfate erosion has a pronounced impact on the porosity of concrete³⁹. The initial porosity of concrete prior to compression is a key factor contributing to nonlinearity during the pore compaction phase. Consequently, it is crucial to carefully examine the influence of the number of wet and dry cycles as well as the concentration of sulfate on the pore compaction stage when studying the effect of sulfate erosion on the stress-strain curve of concrete and its intrinsic relationship. The total strain ε experienced by concrete during compression can be categorized into two components⁴⁰: skeletal strain ε_s and pore strain ε_v. The skeletal strain ε_s refers to the deformation produced by the applied force on the concrete skeleton. In this particular paper, it is presumed that the skeletal strain is elastic, implying that it follows Hooke’s Law and exhibits a linear relationship with the applied stress. Indeed, the pore strain ε_v corresponds to the plastic deformation caused by the expulsion of air from the pores within the concrete under pressure. The relationship between the skeletal strain ε_s and the pore strain ε_v can be expressed as follows:

$$\varepsilon ={\varepsilon _{\text{s}}}+{\varepsilon _{\text{v}}}$$

(9)

Based on the given assumptions regarding the skeleton strain, it is understood that there exists a relationship between the skeleton strain ε_s and the modulus of elasticity E. Therefore, the skeleton strain can be mathematically expressed as follows:

$${\varepsilon _{\text{s}}}=\frac{\sigma }{E}$$

(10)

The expression for the skeleton strain with strain was obtained using origin software as:

$${\varepsilon _{\text{s}}}=a{\varepsilon ^b}(\varepsilon \leqslant {\varepsilon _{\text{A}}})$$

(11)

where parameter a represents the size of the skeleton strain curve opening and b is the curve shape parameter.

Assuming that void strain ceases to grow once the concrete internal voids are fully closed, the skeletal strain can be represented using a segmented function. In the case of uniaxial compression of concrete, the expression for skeletal strain is as follows:

$${\varepsilon _{\text{s}}}=\left\{ \begin{gathered} {a_{(n)}}{\varepsilon ^{{b_{(n)}}}}{\text{ }}(\varepsilon \leqslant {\varepsilon _{\text{A}}}) \hfill \\ \varepsilon - {\varepsilon _{{\text{A}}(n)}}+\frac{{{\sigma _{{\text{A}}(n)}}}}{{{E_{(n)}}}}{\text{ }}(\varepsilon >{\varepsilon _{\text{A}}}) \hfill \\ \end{gathered} \right.$$

(12)

Table 3 Values of a and b for different cycle Times.

The values of ‘a’ and ‘b’ in the pore compacting stage were determined by fitting the experimental data, as presented in Table 3.

As depicted in Table 3, it is evident that sulfate erosion significantly impacts the ‘a’ and ‘b’ values within the skeletal strain equation. In the absence of concrete erosion, both skeletal strain and total strain exhibit characteristics of quadratic functions, which aligns with the current findings⁴¹. However, with an increase in the number of wet and dry cycles, there was observed a fluctuating pattern in both the number of functions and the image opening. Specifically, they initially decreased, then increased, and finally decreased again. Notably, for a sulfate concentration of 5%, the values of ‘a’ and ‘b’ were found to be the smallest for 7 dry and wet cycles, measuring 13.089 and 1.658, respectively. When the number of cycles increased to 42, the values of ‘a’ and ‘b’ reached their highest values, measuring 79.432 and 2.137, respectively. Conversely, for 7 dry and wet cycles, the values of ‘a’ and ‘b’ were found to be the smallest, measuring 20.658 and 1.739, respectively, when the sulfate concentration was elevated to 15%. Furthermore, for 21 cycles, the largest values of ‘a’ and ‘b’ were observed, measuring 77.784 and 2.040, respectively. The change in the number of functions and image openings can be attributed to the chemical reaction between sulfate and the hydration products of concrete during 7 dry and wet cycles. This reaction leads to the formation of newborn minerals that occupy the pores within the concrete³⁹. These newborn minerals contribute to the load-bearing capacity of the compressed concrete, similar to the function of the concrete skeleton. As a result, the skeletal strain of the concrete becomes relatively larger, leading to smaller values for the number of functions (b) and the opening parameter (a) compared to concrete affected by erosion. However, as the number of wet and dry cycles increases, the concrete undergoes changes in both dry and water-saturated states. It is worth noting that calcium alumina and gypsum, present in the concrete, have a certain degree of water absorption and swelling⁴². During the wet and dry cycles, the newborn minerals continuously undergo dehydration, shrinkage, water absorption, and swelling processes. The combined effect of water absorption-induced crystal swelling and crystallization-induced swelling generates swelling forces within the concrete. These forces exert pressure on the internal structure of the concrete, leading to the development of microcracks⁴³. The presence of microcracks in the concrete significantly contributes to the generation of pore strain during the compression process. These microcracks result in a reduced percentage of skeletal strain in the concrete. As a consequence, the values of the skeletal strain functions (b) and the opening parameter (a) gradually increase. As the number of wet and dry cycles continues to increase, the ongoing development of microcracks provides space for the regrowth of minerals. The pores within these microcracks gradually get filled with newborn minerals. When the concrete is subjected to pressure, these newborn minerals once again start to bear a portion of the load, causing the skeletal strain values to increase once more. Consequently, the values of the opening parameter (a) and the number of skeletal strain functions (b) begin to decrease gradually. The trends of the ‘a’ and ‘b’ values for varying sulfate concentrations and different numbers of wet and dry cycles are depicted in Fig. 6.

Fig. 6

Relationship between skeleton strain evolution equation parameters and dry wet cycle days of sulfate. (a) Change of a value with the number of sulfate dry and wet cycles, (b) Change of b value with the number of sulfate dry and wet cycles.

With an increase in sulfate concentration, the inflection points of the ‘a’ and ‘b’ values progressively shift to earlier stages. The variation in sulfate concentrations and the distinct products generated by chemical reactions account for this phenomenon. With an increase in sulfate concentration, the erosion products undergo a gradual transformation from calcium aluminate to gypsum³⁹. At a sulfate erosion level of 15%, the microcracks within the concrete predominantly result from the recrystallization of gypsum, which exhibits significantly greater water absorption and swelling compared to calcium aluminate. As a result, the concrete experiences the development of microcracks within a shorter duration of wet and dry cycles, leading to an earlier occurrence of the turning point for the skeletal strain parameter. With an increased number of wet and dry cycles, the higher concentration of sulfate leads to variances in water absorption and swelling of reaction products. Consequently, a greater number of microcracks and larger gaps are induced. During the compression process, the pore strain increases while the skeletal strain decreases relatively. Therefore, when the number of wet and dry cycles surpasses a certain threshold, the skeletal strain function parameter of concrete eroded by high-concentration sulfate solution becomes lower than that of concrete eroded by low-concentration sulfate. It appears that in Fig. 6, the trend of variation for the ‘a’ and ‘b’ values is similar for the same concentration. By conducting non-linear fitting of the ‘a’ and ‘b’ values with respect to different sulfate concentrations and various dry and wet cycle durations, an equation for the fitting is obtained as represented in Eq. (13), the parameter values in Eq. (13) with different sulfate concentrations are listed in Table 4.

Table 4 Table of f (x) parameter values.

$$f(x)={A_1}{x^4}+{A_2}{x^3}+{A_3}{x^2}+{A_4}x+{A_5}$$

(13)

Establishment of the Model

The preceding discussion explored the damage variables and skeleton strains of concrete under uniaxial compression. Establishing a constitutive model considering the effect of sulfate cyclic erosion during the initial densification stage requires incorporating Weibull statistical distribution and damage variables. Additionally, the concrete strain values are replaced by skeleton strains, as follows:

$$\sigma ={E_0}(1 - D)\varepsilon$$

(14)

Substituting Eq. (8) into Eq. (14), we obtain:

$$\sigma ={E_{\text{t}}}\varepsilon \exp [ - {(\frac{\varepsilon }{{{m_{(n)}}}})^{{k_{(n)}}}}]$$

(15)

Taking into account the influence of sulfate on the pore compaction stage of concrete, Eq. (15)⁴¹is modified by replacing ε with the skeletal strain ε_s from "Concrete specimen fabrication. Therefore, we obtain:

$$\sigma ={E_{\text{t}}}{\varepsilon _{\text{s}}}\exp [ - {(\frac{{{\varepsilon _{\text{s}}}}}{{{m_{(n)}}}})^{{k_{(n)}}}}]$$

(16)

Based on the characteristics of the stress-strain curve, the following geometric boundary conditions are adopted to derive the concrete equation: σ = σ_pk,ε = ε_spk.

,ε = ε_spk, and d_σ/d_ε=0:

$${m_{(n)}}=\frac{{{\varepsilon _{{\text{spk}}}}}}{{{{\frac{1}{{{k_{(n)}}}}}^{(\frac{1}{{k(n)}})}}}}$$

(17)

$${k_{(n)}}=\frac{1}{{\ln (\frac{{{E_{\text{t}}}{\varepsilon _{{\text{spk}}}}}}{{{\sigma _{{\text{pk}}}}}})}}$$

(18)

$${E_{\text{t}}}=(1 - {D_0}){E_0}$$

(19)

Here, ε_spk represents the peak skeleton strain, while σ_pk indicates the peak stress. Substituting Eqs. (12), (17), (18), and (19) back into Eq. (14) simplifies the expression to:

$$\sigma =\left\{ \begin{gathered} (1 - {D_0}){E_0}{a_{(n)}}{\varepsilon ^{{b_{(n)}}}}\exp \left[ { - {{\left( {\frac{{{a_{(n)}}{\varepsilon ^{{b_{(n)}}}}}}{{{m_{(n)}}}}} \right)}^{{k_{(n)}}}}} \right]{\text{ }}(\varepsilon \leqslant {\varepsilon _{\text{A}}}) \hfill \\ (1 - {D_0}){E_0}\left( {\varepsilon - {\varepsilon _{{\text{A}}(n)}}+\frac{{{\sigma _{{\text{A}}(n)}}}}{{(1 - {D_0}){E_0}}}} \right)\exp \left[ { - {{\left( {\frac{{\varepsilon - {\varepsilon _{{\text{A}}(n)}}+\frac{{{\sigma _{{\text{A}}(n)}}}}{{(1 - D){E_0}}}}}{{{m_{(n)}}}}} \right)}^{{k_{(n)}}}}} \right]{\text{ }}(\varepsilon >{\varepsilon _{\text{A}}}) \hfill \\ \end{gathered} \right.$$

(20)

Model validation and discussion

The comparison results between the theoretical values calculated using Eq. (20) for the uniaxial compressive principal structure relationship of concrete under different sulfate concentrations and numbers of wet and dry cycles, and the stress-strain curve values obtained from the tests, are illustrated in Fig. 7. As depicted in Fig. 7, it can be observed that the theoretical calculations align well with the experimental results of the uniaxial stress-strain curves of concrete under various sulfate concentrations and numbers of wet and dry cycles. Figure 8 presents the plotted comparison between the curves from the literature^34,35,36, the test curves, and the curves obtained in this study.

Fig. 7

Comparison between the calculation results of the model built in this paper and the test curve. (a) 5% sulfate solution (b) 15% sulfate solution.

Fig. 8

Comparison between model calculation results and test curves.

Fig. 9

Comparison of model calculation results with experimental curves from other literature.

From Fig. 7, it can be observed that the point plot based on Eq. 20 shows a high degree of fitting with the experimental data. Except for a few points at 21 and 42 cycles that slightly deviate from the experimental curve, all other points calculated using the formula lie on the experimental curve, indicating a very high degree of fitting between the point plot based on Eq. 20 and the experimental data.

From Fig. 8, it is clear that the curve obtained from the constitutive relationship in this study, with R² = 0.99989, is closest to 1 and has an RMSE smaller than that of curves from other literature, demonstrating that the model prediction from this study is more accurate.

Figure 9 shows a comparison of experimental data from other researchers⁴⁴ with various models. From the figure, it can be seen that the model curve from this study, with R² = 0.9956 and RMSE = 2.331, is similar to the curve from that literature, which has R² = 0.9960 and RMSE = 2.323. However, the figure clearly shows that the model from this study provides better predictions during the initial compaction stage. The constitutive models in other literature did not consider the effect of initial pore compaction on the curve, resulting in significant deviations from the experimental curve during the pore compaction and yielding stages. Compared to the fitted curves in the literature, the curve obtained from the constitutive relationship proposed in this study, which considers the effect of sulfate on the initial pores of concrete, shows better consistency with the experimentally obtained stress-strain curve.

Conclusion

• (1) Under the influence of different sulfate concentrations and cycle counts, the uniaxial compressive stress-strain behavior of concrete follows a consistent trend, with a distinct compaction phase in the initial stage. Sulfates react with concrete components, degrading its effective ingredients and increasing porosity, making the initial compaction phase more pronounced. When the cycle count is below 42, the curve’s peak shifts leftward and increases due to the formation of new minerals filling micro-cracks in the concrete. Once the cycle count exceeds 42, micro-crack development in the later erosion stages loosens the structure, causing a rightward curve shift and a significant decrease in both peak stress and slope. At 42 cycles, the concrete’s initial damage reaches its lowest value of -0.521. This occurs because sulfate reactions form new minerals that fill micro-cracks, temporarily enhancing the concrete’s density and strength, resulting in negative initial damage.

• (2) The effects of sulfate concentration and cycle count are primarily reflected in the pronounced nonlinearity of the skeleton strain function’s opening size (a) and shape characteristics (b). For sulfate solutions of varying concentrations, both a and b initially decrease, then increase, and finally decrease again as the wet-dry cycle count rises. Higher sulfate concentrations lead to increased values of a and b, with minimum values of 13.089 and 1.658 for lower concentrations, and 20.658 and 1.739 for higher concentrations.

• (3) This study develops a uniaxial nonlinear stress-strain model for concrete subjected to sulfate erosion and wet-dry cycles. The model achieves a high goodness-of-fit with experimental results (R² = 0.99989), effectively capturing the uniaxial mechanical properties of concrete under sulfate wet-dry erosion condition. These findings offer valuable insights for developing constitutive models for concrete subjected to sulfate erosion and wet-dry cycles.