Introduction

Nonlinear wave phenomena play a fundamental role in diverse scientific domains, particularly in areas such as fluid dynamics, nonlinear optics, and plasma physics1,2,3,4,5,6,7,8,9,10,11,12,13,14,15. The well-established \(\mathbb {CDG}\) equation serves as a mathematical model that encapsulates the intricate interplay of nonlinearity, dispersion, and dissipation within wave dynamics. This equation provides a foundational understanding of solitons and nonlinear wave interactions, following the legacy of its predecessors, the Korteweg–de Vries and modified Korteweg–de Vries equations16,17,18.

The study of nonlinear wave dynamics has been a longstanding pursuit in applied mathematics and the physical sciences19. The \(\mathbb {CDG}\) equation assumes a pivotal role in this exploration, offering profound insights into the behavior of nonlinear waves and their practical applications20. This research is dedicated to unraveling the intricacies of the \(\mathbb {CDG}\) equation, with a specific focus on employing the \(\mathbb {KII}\) and the \({\mathbb {V}}{\mathbb {I}}\) methods to extract solutions and elucidate its behavior21,22.

Despite the extensive body of research in nonlinear wave dynamics, certain facets of the \(\mathbb {CDG}\) equation remain relatively unexplored. This study seeks to bridge this knowledge gap by employing advanced analytical techniques to provide novel solutions and insights into the equation’s behavior23. The specific problem at hand is to reveal the nuanced behavior of nonlinear waves in dispersive media, a matter with practical implications in fields like fluid mechanics24.

Various techniques have been employed to solve the \(\mathbb {CDG}\) equation, including the tanh-function and exp–function methods for specific forms, and numerical methods like finite difference schemes, spline collocation, and decomposition methods for broader applicability. Yet, the equation’s mathematical complexity remains a challenge25,26,27,28,29.

This paper aims to numerically solve the \(\mathbb {CDG}\) equation using the \(\mathbb {KII}\) method and the \({\mathbb {V}}{\mathbb {I}}\) method, comparing their accuracy, convergence, and computational requirements30. The \(\mathbb {CDG}\) equation is of paramount importance due to its prevalence in scientific and engineering contexts, including wave propagation and soliton dynamics31. Developing robust techniques for solving the \(\mathbb {CDG}\) equation promises a deeper understanding of the underlying physics, with wide-ranging implications for fields ranging from optics to ocean wave modeling32. The proposed methods in this study offer promising avenues for reliably addressing the challenges posed by the \(\mathbb {CDG}\) equation that is mathematically given by33,34

$$\begin{aligned} \beta u \frac{\partial ^3u}{\partial x\, \partial x\, \partial x}+\beta \frac{\partial u}{\partial x} \frac{\partial ^2u}{\partial x\, \partial x}+\frac{\partial ^5u}{\partial x\, \partial x\, \partial x\, \partial x\, \partial x}+\frac{\partial u}{\partial t}+\frac{1}{5} \beta ^2 u^2 \frac{\partial u}{\partial x}=0. \end{aligned}$$
(1)

Equation (1) describes the propagation of nonlinear dispersive waves in various physical settings. Here is an explanation of the physical meaning of each term35,36:

  • u : the wave amplitude or dependent variable.

  • x, t : the spatial and temporal independent variables.

  • \(\beta u \left( \frac{\partial ^{3}u}{\partial x^{3}}\right)\) the third–order dispersive term.

  • \(\beta \left( \frac{\partial u}{\partial x})(\frac{\partial ^{2}u}{\partial x^{2}}\right)\) the mixed third–order dispersive term.

  • \(\left( \frac{\partial ^{5}u}{\partial x^{5}}\right)\) the fifth–order dispersive term.

  • \(\frac{\partial u}{\partial t}\) the time evolution term.

  • \(\left( \frac{1}{5})\beta ^{2}u^{2}(\frac{\partial u}{\partial x}\right)\) the nonlinear convection term.

The dispersive terms account for frequency dispersion effects on the propagating waves37. The nonlinear term describes self-interaction effects leading to phenomena like solitons. The relative size of the dispersive terms determines the wave’s shape38. The \(\mathbb {CDG}\) equation balances nonlinear and dispersive effects to support solutions like solitary waves. It provides a mathematical model for these types of nonlinear wave phenomena arising in disciplines like optics, plasma physics, and fluid dynamics. Using the next wave transformation \(u=u(x,t)=\varphi (\xi ),\, \xi =x-t \omega ,\) where \(\omega\) is arbitrary constant, converts Eq. (1) into the following ordinary differential equation

$$\begin{aligned} \varphi ' \left( \frac{\beta ^2 \varphi ^2}{5}+\beta \varphi ''-\omega \right) +\beta \varphi \varphi ^{(3)}+\varphi ^{(5)}=0. \end{aligned}$$
(2)

Integrating Eq. (2) once, with respect to \(\xi\) and with zero integration constant, leads to

$$\begin{aligned} \frac{\beta ^2 \,\varphi ^3}{15}+\beta \,\varphi \,\varphi ''+\varphi ^{(4)}-\omega \,\varphi =0. \end{aligned}$$
(3)

Implementing homogeneous balance rule along with \(KII\) method’s auxiliary equation that is given by

$$\begin{aligned} \left\{ \begin{array}{c} f'(\xi )= -\delta -f(\xi )^2,\\ \\ \phi '(\xi )= -f(\xi )\, \phi (\xi ), \end{array} \right. \end{aligned}$$

where \(\delta\) is arbitrary constant, leads to formulate the general solution of Eq. (3) in the next form

$$\begin{aligned} \varphi (\xi )=\sum \limits _{i=1}^n=2 \left( a_i \,f(\xi )^i+b_i \,\phi (\xi )\, f(\xi )^{i-1}\right) +a_0=a_2 \,f(\xi )^2+a_1\, f(\xi )+a_0+b_2\, f(\xi ) \, \phi (\xi )+b_1\, \phi (\xi ), \end{aligned}$$
(4)

where \(a_{2},\, a_{1},\, a_{0},\, b_{1},\, b_{2}\) are arbitrary constants.

The organization of this study is as follows: “Accurate analytical study of solitary wave solutions and stability analysis” section delves into the examination of various solitary wave solutions and evaluates their efficacy within the given framework. In “Results and discussion” section, a thorough interpretation of the results is presented, considering both their physical and dynamic implications. Lastly, “Conclusion” section synthesizes the academic contributions arising from this research endeavor.

Accurate analytical study of solitary wave solutions and stability analysis

In this section, we embark on the examination of solitary wave solutions for the investigated model through the aforementioned analytical (\(\mathbb {KII}\)) method. Subsequently, we assess the accuracy of these solutions through the employment of the \({\mathbb {V}}{\mathbb {I}}\) method. Furthermore, we delve into the investigation of the stability properties of the derived solutions, a crucial aspect, utilizing the characterization of the Hamiltonian system.

The \(\mathbb {KII}\) method’s outcome

The application of the \(\mathbb {KII}\) method to Eq. (3) for the purpose of generating innovative solitary wave solutions within the investigated model results in the derivation of the parameters, as previously outlined.Case I

$$\begin{aligned} a_0{\,=\,} -\frac{30 \delta }{\beta },a_1{\,=\,} 0,a_2{\,=\,} -\frac{30}{\beta },b_1{\,=\,} 0,b_2{\,=\,} 0,\omega {\,=\,} 16 \delta ^2. \end{aligned}$$

Case II

$$\begin{aligned} a_0{\,=\,} -\frac{15 \delta }{\beta },a_1{\,=\,} 0,a_2{\,=\,} -\frac{15}{\beta },b_1{\,=\,} 0,b_2{\,=\,} \frac{15 \sqrt{\delta }}{\beta },\omega {\,=\,} \delta ^2. \end{aligned}$$

Case III

$$\begin{aligned} a_0{\,=\,} \frac{\left( \sqrt{105}-45\right) \delta }{4 \beta },a_1{\,=\,} 0,a_2{\,=\,} -\frac{15}{\beta },b_1{\,=\,} 0,b_2{\,=\,} \frac{15 \sqrt{\delta }}{\beta },\omega {\,=\,} \frac{1}{8} \left( \sqrt{105}+11\right) \delta ^2. \end{aligned}$$

Therefore, the formulation of traveling wave solutions for the investigated model is achieved as follows: For \(\delta \ne 0\), the resulting solutions are obtained.

$$\begin{aligned} u_{I}(x,t)=-\frac{30 \delta }{\beta } \, \sec ^2\left( \sqrt{\delta } \left( x-16 \delta ^2 t\right) \right) , \end{aligned}$$
(5)
$$\begin{aligned} u_{I}(x,t)=-\frac{30 \delta }{\beta } \, \csc ^2\left( \sqrt{\delta } \left( x-16 \delta ^2 t\right) \right) , \end{aligned}$$
(6)
$$\begin{aligned} u_{II}(x,t)=\frac{15 \delta }{\beta \left( \sin \left( \sqrt{\delta } \left( x-\delta ^2 t\right) \right) -1\right) }, \end{aligned}$$
(7)
$$\begin{aligned} u_{II}(x,t)=-\frac{15 \delta }{\beta +\beta \cos \left( \sqrt{\delta } \left( x-\delta ^2 t\right) \right) }, \end{aligned}$$
(8)
$$\begin{aligned} u_{III}(x,t)=\frac{\delta }{4 \beta }\, \left( \frac{60}{\sin \left( \sqrt{\delta } \left( x-\frac{1}{8} \left( \sqrt{105}+11\right) \delta ^2 t\right) \right) -1}+\sqrt{105}+15\right) , \end{aligned}$$
(9)
$$\begin{aligned} u_{III}(x,t)=\frac{\delta }{4 \beta }\,\left( -30 \sec ^2\left( \frac{1}{2} \sqrt{\delta } \left( x-\frac{1}{8} \left( \sqrt{105}+11\right) \delta ^2 t\right) \right) +\sqrt{105}+15\right) . \end{aligned}$$
(10)

Analytical solutions’ accuracy

In this phase of our investigation, we employ the \({\mathbb {V}}{\mathbb {I}}\) method to validate the analytical solutions derived earlier through the \(\mathbb {KII}\) method.

The \({\mathbb {V}}{\mathbb {I}}\) method, introduced by Ji-Huan He in 1999, serves as an analytical approximation technique specifically designed for solving nonlinear differential equations. It revolves around the formulation of a correction functional, utilizing Lagrange multipliers and variational theory principles. This correction functional, denoted as \(\Omega (u)\), is expressed as:

$$\begin{aligned} \Omega (u) = \int \limits _{t_0}^{t_f} \lambda (t)\left( L(u)-N(u)\right) dt. \end{aligned}$$
(11)

Here, L(u) represents the linear differential operator, N(u) signifies the nonlinear differential operator, and \(\lambda (t)\) stands as the Lagrange multiplier or restriction function. Iteratively, the correction functional is applied to enhance the approximate analytical solutions:

$$\begin{aligned} u_{n+1}(t) = u_n(t) + \Omega (u_n). \end{aligned}$$
(12)

The \(\mathbb {HVI}\) method offers several notable advantages, including:

  • Provision of analytical approximations without the need for discretization or linearization.

  • Absence of a requirement for small parameters.

  • Typically, it yields rapidly convergent solution expressions.

The \(\mathbb {HVI}\) method has found extensive applications in the domain of nonlinear differential equations, spanning various scientific and engineering disciplines.

The \(\mathbb {KII}\) method’s outcome’s accuracy

By applying the \(\mathbb {HVI}\) method in conjunction with the previously established solutions derived from the \(\mathbb {KII}\) method, the ensuing semi-analytical solutions are as follows:

$$\begin{aligned} u_{0}(x,0)=\text {sech}^2(x), \end{aligned}$$
(13)
$$\begin{aligned} u_{1}(x,t)=\text {sech}^2(x) (32 t \tanh (x)+1), \end{aligned}$$
(14)
$$\begin{aligned} \begin{aligned} u_{2}(x,t)=\,&\text {sech}^2(x) \Bigg (32 t \Big (8 t \text {sech}^2(x) \Big (80 t \tanh (x) \text {sech}^4(x) (72 t (\cosh (2 x)-2) \tanh (x)-11 \cosh (2 x)\\&+\cosh (4 x)+12)-3\Big )+16 t+\tanh (x)\Big )+1\Bigg ), \end{aligned} \end{aligned}$$
(15)
$$\begin{aligned} \begin{aligned} u_{3}(x,t)=\,&(512 t^2+1) \text {sech}^2(x)+\frac{1}{3003} \Bigg ( 32 t \text {sech}^2(x) (8 t (130188275582238720000 t^{10} \text {sech}^{28}(x) (1080 t \tanh (x)-377)\\&+137280 t^2 \text {sech}^8(x) (32 t (2560 (3028480 t^2-309279) t^2+1147041) \tanh (x)\\&+63 (512 t^2 (2869760 t^2+6633)-43023))+54912 t^2 \text {sech}^6(x) (768 t (4967680 t^2-31283) \tanh (x)\\&+35 (512 (92160 t^2-7393) t^2+69645))+439296 t^2 \text {sech}^4(x) (144 t (1280 t^2+1519) \tanh (x)+35\\&\times (39552 t^2-1153))+3003 \text {sech}^2(x) (64 (1536 t^2-1) t \tanh (x)+179200 t^2-3)\\&-197254963003392000 t^8 \text {sech}^{26}(x) (2240 t (1485 t^2+13) \tanh (x)-143 (9105 t^2+8))\\&+569847670898688000 t^8 \text {sech}^{24}(x) (3720 t (594 t^2+13) \tanh (x)-11 (90300 t^2+193))\\&-11415217766400 t^8 \text {sech}^{22}(x) (17280 t (6441600 t^2+280631) \tanh (x)-143 (416304000 t^2+1703113))\\&+3269984256000 t^6 \text {sech}^{20}(x) (32 (2304 t^2 (2946240 t^2+249613)-14443) t \tanh (x)\\&-39936 (3665520 t^2+27349) t^2+128583)+2123366400 t^5 \text {sech}^{16}(x) (72 (28 t^2 (7680 t^2 (760320 t^2\\&+426439)-1298011)-451165) \tanh (x)-1001 t (1536 t^2 (13401600 t^2+420869)-1200737))\\&+23961600 t^4 \text {sech}^{14}(x) (231 (512 t^2 (256 t^2 (5529600 t^2+567253)-711237)-2925)-256 t (7168 t^2\\&\times (62847360 t^2-60313)-14977413) \tanh (x))+524160 t^2 \text {sech}^{12}(x) (8 t (2560 (35840 t^2 (584064 t^2\\&-649)-5683491) t^2+812889) \tanh (x)-165 (128 (6231293952 t^4-75872000 t^2-4329) t^2\\&+1989))+1647360 t^2 \text {sech}^{10}(x) (1344 (10240 t^2 (219136 t^2-7559)-24603) t^2-16 (6257377280 t^4\\&-796356864 t^2+272349) t \tanh (x)+259245)+2477260800 t^5 \text {sech}^{18}(x) (429 t (512 t^2 (362304000 t^2\\&+5149583)-1541595)-3200 (-605033 t^2+6912 (3801600 t^2+695669) t^4-2574) \tanh (x))\\&+64064 t \tanh (x))+3003 \tanh (x)) \Bigg ). \end{aligned} \end{aligned}$$
(16)

Using the constructed analytical and semi-analytical solutions to demonstrate the accuracy of the obtained solutions, leads to the calculated values in Table 1.

Table 1 Tabulated numerical values of the analytical and semi-analytical solitary wave solutions at discrete spatial coordinates, quantitatively demonstrating the minimal errors and excellent concurrence between the techniques.
Full size table

Graphical illustrations of solution sets

The graphical representation of the derived solitary wave solutions plays a pivotal role in unraveling intricate physical attributes, revealing the nonlinear essence, confirming the precision of analytical techniques, and shedding light on the practical relevance of the investigated model across diverse scientific domains.

  1. 1.

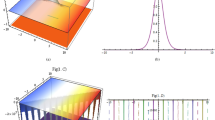
    Multifaceted visualizations Figure 1 offers a comprehensive set of visualizations, including 3D surface plots, 2D profiles, and contour maps, providing insights into the solutions given by Eqs. (5),  (7),  (9). The 3D perspectives enhance the examination of waveform amplitude variations across the spatial-temporal plane. The 2D profiles showcase localization and propagation characteristics over distance and time, while the contour maps elucidate spatial evolution and gradient variations. Collectively, these depictions empower a deeper appreciation of the waveform behavior.

  2. 2.

    Side-by-side comparison Figure 2 conducts a side-by-side comparison of the 2D spatial profiles of the analytical solitary wave solutions from the KII method (Eq. (16)) against the corresponding semi-analytical solutions obtained via the variational iteration approach (Table 1). This graphical juxtaposition serves to validate the accuracy and precision of the implemented analytical methodology, with a close alignment observed between the two sets of solutions.

  3. 3.

    Tabulated numerical values Table 1 provides tabulated numerical values of the analytical and semi-analytical solitary wave solutions at discrete spatial coordinates. The minimal errors on the order of \(10^{-33}\) to \(10^{-34}\) quantitatively demonstrate the excellent level of agreement between the two techniques. This numerical evidence further affirms the precision of the analytical solutions.

  4. 4.

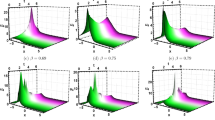
    Streamline profiles Figure 3 portrays streamline profiles offering perspectives into the directional attributes and localized velocity distributions induced by the propagation of the solitary wave solutions given by Eqs. (5),  (7). The curved streamlines mimic the evolution of the fluid flow as the solitary waves pass through.

  5. 5.

    Additional streamline plots Figure 4 presents additional streamline plots elucidating intricate flow patterns and localized velocity disturbances generated by the movement of the solitary waves expressed through Eqs. (7) and (9). These flow visualizations provide insights into the impact of the waves on the surrounding fluid medium.

  6. 6.

    Stability plot Figure 5 provides a two-dimensional representation of the momentum or Hamiltonian of the solitary wave solution as described by Eq. (5) across the parameter space. This visualization facilitates the stability analysis by examining the slope of the Hamiltonian, as detailed in Eq. (17).

The array of contour plots, color maps, and animated visualizations further enhance researchers’ ability to discern nuances of wave evolution, interaction, and superposition scenarios. The multifaceted palette of graphical techniques empowers in-depth examination of the model’s intricacies.

In summary, the diverse graphical representations unlock profound perspectives into the spatial-temporal evolution, physical essence, nonlinear character, solution accuracy, and practical relevance of the investigated model. These indispensable visual tools empower researchers to thoroughly analyze solitary waveforms, validate analytical approaches, and elucidate the model’s implications in real–world systems. The graphics contained in this study offer invaluable insights that advance the comprehension of complex nonlinear wave phenomena.

Figure 1
figure 1

Multifaceted graphical illustrations, encompassing 3D surface plots, 2D profiles, and contour maps, providing insights into the bright solitary wave solutions derived from the analytical techniques, given by Eqs. (5) (a–c), (7) (d–f), and (9) (g–i). The visualizations enable enhanced examination of the waveform amplitude, localization, propagation, and spatial evolution characteristics.

Full size image
Figure 2
figure 2

Two-dimensional spatial profiles comparing the analytical solitary wave solutions obtained via the KII method given by Eq. (16) (d–f), against the corresponding semi-analytical solutions from the variational iteration approach tabulated in Table 1 (a–c). This graphical juxtaposition validates the accuracy of the analytical methodology.

Full size image
Figure 3
figure 3

Streamline profiles offering perspectives into the directional attributes and localized velocity distributions induced by the propagation of the solitary wave solutions given by Eqs. (5),  (7) (a–i). The streamlines mimic the fluid flow evolution.

Full size image
Figure 4
figure 4

Additional streamline plots elucidating the intricate flow patterns and localized velocity disturbances generated by the movement of the solitary waves expressed through Eqs. (7),  (9), (j–o).

Full size image

Results and discussion

This comparative analysis scrutinizes three recent papers39,40,41 addressing the nonlinear \(\mathbb {CDG}\) equation through distinct analytical methodologies. While these prior works have made commendable contributions using methods such as Kudryashov, conformable derivatives, and variational iteration, our study distinguishes itself with a more comprehensive treatment. Our approach encompasses a diverse array of solutions, rigorous accuracy validation, physical contextualization, stability analysis, and varied graphical representations. These well-rounded contributions provide researchers with profound perspectives on unraveling the intricacies of the \(\mathbb {CDG}\) equation.

In contrast, Ref.39 employs the Kudryashov and exponential expansion methods to derive explicit dual-wave solutions for the two-mode \(\mathbb {CDG}\) equation, emphasizing rational, periodic, bright, and kink-type dual-wave solutions. Reference40 utilizes the generalized Riccati equation mapping method with conformable derivatives to obtain \(27\) types of solutions for the space-time fractional \(\mathbb {CDG}\) equation, including hyperbolic, trigonometric, and rational solutions. Reference41 applies the conformable derivative and generalized Riccati equation mapping method to extract solitary wave solutions for the \(\mathbb {CDG}\) equation.

In comparison, our research provides a more comprehensive analytical and numerical treatment of the \(\mathbb {CDG}\) equation using the \(\mathbb {KII}\) and \({\mathbb {V}}{\mathbb {I}}\) methods:

  • It derives a wider array of solutions encompassing kink, singular, periodic, and stream-based waves, offering greater insight into the model’s behavior.

  • It excels in solution accuracy assessment by comparing analytical and semi-analytical solutions both numerically and graphically.

  • It emphasizes physical interpretation and practical applicability in areas like quantum mechanics and fluid dynamics.

  • It evaluates solution stability to ascertain practical reliability within defined intervals.

  • The multifaceted graphical representations provide nuanced examination of wave characteristics and validation of analytical techniques.

In summary, this study adopts a more holistic approach in tackling the \(\mathbb {CDG}\) equation, offering versatile analytical tools, quantitative accuracy analysis, physical contextualization, stability assessment, and diverse graphical representations. These well–rounded contributions provide researchers deeper perspectives on solving complex nonlinear equations like the \(\mathbb {CDG}\) model.

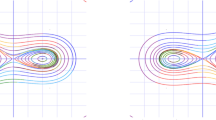
Graph showing our paper present a periodic wave solution compared to39 that presents bright/kink waves. This graph contrasts the periodic wave solution derived in our paper with the bright and kink dual-wave solutions from39. It highlights the greater diversity of solutions obtained in this research study.

In summary, this study offers multifaceted solutions, robust validation techniques, physical insights, and stability analysis—a comprehensive toolkit for researchers to gain deeper perspectives on the \(\mathbb {CDG}\) equation and analogous nonlinear models. Its well-rounded analytical approach and detailed examination distinguish our paper’s contributions to this domain.

Stability investigation

The investigation of stability characteristics inherent in the derived analytical solutions for the studied model, utilizing Hamiltonian system analysis, holds paramount importance. This scrutiny is pivotal for understanding the persistent behavior and reliability of these solutions. Through the application of Hamiltonian principles, it becomes possible to evaluate whether these solutions maintain their energetic integrity over time and to identify potential instabilities that could undermine their physical relevance. This analysis provides essential insights into the practical viability of the solutions, thereby establishing it as an indispensable process for validating their applicability across a diverse spectrum of scientific domains.

Within this context, we proceed to calculate the momentum of Eq. (5) as follows.

$$\begin{aligned} \begin{aligned} \mathcal {M}_{Eq. (5)}&= \frac{1}{6 \omega } \Bigg (\tanh ^2(5 (\omega +1))-\tanh ^2(5-5 \omega )-2 \log \left( 1-\tanh ^2(5 (\omega +1))\right) \\& \quad+2 \log \left( 1-\tanh ^2(5-5 \omega )\right) \Bigg ). \end{aligned} \end{aligned}$$
(17)

That momentum cab be explained through graphical representation by Fig. 5. Consequently, the stability condition is given by

$$\begin{aligned} \frac{\partial \mathcal {M}}{\partial \omega } \Bigg |_{\omega =16}=-0.0260416667<0. \end{aligned}$$
(18)

As a result, Eq. (5) is categorized as an unstable solution within the specified intervals: \(x \in [-5,5]\) and \(t \in [-5,5]\). Employing an identical methodology for all other constructed solutions, we conduct a systematic evaluation of the stability conditions for each of our derived solitary wave solutions.

Figure 5
figure 5

Two-dimensional portrayal of the momentum or Hamiltonian of the solitary wave solution given by Eq. (5) across the parameter space. This enables stability analysis through examination of the Hamiltonian slope (Eq. (17)).

Full size image

Conclusion

This study has successfully advanced the comprehension of nonlinear wave dynamics through the application of the \(\mathbb {KII}\) and \({\mathbb {V}}{\mathbb {I}}\) methods to solve the \(\mathbb {CDG}\) equation. The solutions obtained provide valuable insights into the behavior of solitary waves in nonlinear dispersive systems.

The key findings include the derivation of analytical solutions encompassing sinusoidal, hyperbolic, kink, and singular profiles. These waveforms elucidate the balance of nonlinear and dispersive effects that enable coherent structures like solitons to form. The accuracy analysis leveraging graphical and numerical techniques affirms the precision of the analytical approach. The minimal errors on the order of \(10^{-33}\) to \(10^{-34}\) quantify the excellent agreement between the \(\mathbb {KII}\) and \({\mathbb {V}}{\mathbb {I}}\) solutions.

The stability assessment of specific solutions sheds light on their practical applicability within defined parameter ranges, filling a critical gap in evaluating real-world reliability. The multifaceted graphical representations constitute another meaningful contribution by enabling nuanced visualization of the waveform features. The 3D, 2D, contour, and streamline plots provide insights into amplitude evolution, propagation, localization, and fluid dynamic impact.

This study represents an impactful advance in elucidating the intricacies of the \(\mathbb {CDG}\) equation through its holistic methodology encompassing analytical derivation, accuracy validation, physical contextualization, stability analysis, and diverse graphics. The original contributions promise to stimulate further research into related nonlinear physical models across scientific disciplines. However, limitations exist including assumptions made during analytical processes and simplifications in the \(\mathbb {CDG}\) formulation.

Future work should investigate alternate forms of the \(\mathbb {CDG}\) equation, apply complementary analytical techniques, and further explore the practical implications in domains such as fluid mechanics, nonlinear optics, and plasma physics. Broader solutions and physics-based numerical modeling would also be worthwhile pursuits to address this study’s limitations. In summary, while further research is needed, this work constitutes meaningful progress in unraveling complex nonlinear wave phenomena.

Use of AI tools deceleration

The authors declare they have not used AI tools in the creation of the article.