Efficient and secure service function chain deployment method for delay optimization in air traffic information network

Abstract

The air traffic information network is fundamental for ensuring the efficient and safe operation of flights. However, with the increasing demands of air traffic services, the rigidity of the traditional air traffic information network has become increasingly pronounced. Network function virtualization (NFV) technology presents an effective solution to address this issue. Within the NFV environment, the deployment of service function chains (SFC) forms the basis for achieving end-to-end air traffic services. This paper addresses the low delay and high security requirements inherent in air traffic services and proposes an efficient and secure SFC deployment for delay optimization (ESSFCD-DO) method. Primarily, the paper conducts a theoretical analysis of SFC deployment, and derives four key principles related to SFC delay, security, and resource cost. Subsequently, based on these principles, the ESSFCD-DO method is developed, which encompasses the virtual network function (VNF) aggregation algorithm for security and resources cost optimization (VNFAA-SRCO), the VNF deployment algorithm based on topology aware (VNFD-TA), and the algorithm for deploying virtual links based on k-shortest path. Experimental results demonstrate that, in comparison to other SFC deployment methods within this domain, ESSFCD-DO achieves significant optimizations in terms of end-to-end delay of SFC and long-term revenue-cost ratio, while ensuring security and service request acceptance rate.

Introduction

The air traffic information network is a comprehensive information network integrating communication, navigation, surveillance, and air traffic control (ATC), which forms the foundation for ensuring efficient and safe flight operations¹. Traditional air traffic information networks are characterized by network functionalities based on proprietary hardware, resulting in a closed network architecture tightly coupling software network functionalities with hardware physical platforms². This closed network architecture has led to numerous issues, such as substantial expenses for network upgrades and replacement³, poor manageability⁴, and limited scalability⁵. With the recent surge in flight volumes, the interactions within the air traffic information network have become increasingly frequent, consequently highlighting the drawbacks of the inflexible nature of the traditional air traffic information network⁶.

Network function virtualization (NFV) technology represents one of the vital next-generation technologies for addressing the rigidity issues of traditional air traffic information networks. NFV achieves flexible deployment of network functions⁸, decouples software network functionalities from hardware physical platforms, separates the development cycles of software and hardware⁹, and enables dynamic expansion of network functions¹⁰. Utilizing NFV technology, network functions can be treated as ordinary software, deployed at any location within the network as required, without the need for additional hardware installation. This significantly reduces operating costs while enhancing the flexibility of business deployments.

In an NFV-based air traffic information network, air traffic services are realized through service function chains (SFC)¹¹. SFC is a chain of virtual network functions¹² that must be deployed in the physical network to achieve end-to-end services¹³. Within the same physical network, the deployment method of SFC determines its deployment cost, service quality, and security performance¹⁴. Given the characteristics of air traffic services that require low delay and high security¹⁵, this paper conducts research on the deployment methods of SFC within the air traffic information network, proposing an efficient and secure SFC deployment for delay optimization (ESSFCD-DO) method.

This paper makes the following primary contributions:

• ·Theoretical analysis of security, end-to-end delay, and resource cost in the process of SFC deployment, leading to the summarization of four principles governing the SFC deployment process.

• ·Proposal of a VNF aggregation algorithm for security and resources cost optimization (VNFAA-SRCO) aimed at enhancing the security of SFC while reducing resource costs.

• ·Proposal of a VNF deployment algorithm based on topology aware (VNFD-TA) focused on optimizing end-to-end delay for SFC.

The remainder of this paper is organized as follows: “Related work” reviews related works. “System architecture and models” describes the process of SFC deployment in the air traffic information network. “SFC deployment analysis” provides a theoretical analysis of the SFC deployment process. “SFC deployment method design” introduces the proposed SFC deployment methods. “Performance evaluation and analysis” evaluates the performance of the proposed SFC deployment methods through simulation experiments. Finally, “Conclusion” summarizes the work and provides an outlook for future research.

Related work

The deployment of SFC serves as the foundation for realizing end-to-end services within NFV environments, making SFC deployment matters a continuous focal point within academic research. This section provides an overview and analysis of related works based on the classification of optimization objectives during the SFC deployment process.

Works^{16,17,18,19,20} have studied optimization issues related to delay within SFC deployments. Literature¹⁶ initially demonstrated that SFC deployment presents an NP-hard problem and subsequently proposed a joint SFC deployment and resource management scheme based on game theory methods to address SFC deployment concerns within heterogeneous edge environments. Literature¹⁷, focusing on the integrated space-air-ground network, presented a delay-aware SFC mapping method (SFCD-TDM) based on delay prediction, selecting the path with the lowest delay for SFC mapping. Literature¹⁸ partitioned SFC request flows into multiple sub-flows to consider parallel transmission. To meet delay requirements for parallel SFC, this work first utilized simulated annealing algorithms to find suitable physical nodes for VNF deployment and then employed a quantum genetic algorithm to address the link mapping problem. Literature¹⁹ modeled the SFC deployment problem as an integer linear programming model aimed at ensuring SFC delay requirements while minimizing network resource consumption. It designed a two-stage optimization solution to resolve this issue, with the first stage involving mapping the SFC to servers and the second stage optimizing and adjusting VNF deployment positions to achieve delay and resource consumption optimization. Literature²⁰ modeled the SFC deployment problem as an integer linear programming problem and introduced a heuristic hop-by-hop bandwidth allocation and SFC deployment algorithm to tackle this problem. Although this type of SFC deployment method can achieve considerable delay optimization in its corresponding environment, it does not consider the security issues faced by SFC.

Works^{21,22,23,24,25,26} investigated security optimization problems within SFC deployments. Literature²¹ introduced the secure service level agreement (SSLA) into SFC deployments to counteract attacks. This work initially employed linear programming to formulate SSLA-guaranteed SFC deployment problems and subsequently proposed a maximum security SFC deployment algorithm (SFCD-MS) to maximize the security of SFC deployments. Literature²² presented a security and delay-optimized SFC deployment method based on the Viterbi algorithm, considering security requirement levels and transmission delay. Literature²³ designed a credibility-based SFC deployment strategy to reduce the risk of software vulnerabilities leading to failures in VNF node operations. This work established a hierarchical credibility assessment model to select VNF nodes based on user credibility. Literature²⁴ introduced a risk-aware SFC deployment method using long short-term memory (LSTM) networks to predict potential attacks and then utilized deep Q-network based on the prediction results to complete SFC deployment. literature²⁵ presents a security deployment method for load balancing of service function chains. This method aggregates VNFs based on security constraints and functional exclusion constraints, and then employs the Viterbi algorithm to simultaneously deploy VNFs and virtual links. This type of SFC deployment method focuses on optimizing the security of SFC, so it cannot well balance resource cost and performance such as quality of service (QoS). Literature²⁶ combined the reasoning capabilities of a malicious behavior knowledge base to achieve dynamic SFC deployment and dynamic configuration of secure VNFs. This method fed information generated from secure services back to the knowledge base. Through knowledge base analysis, it generated business function chain paths and secure business configuration strategies, dynamically distributing these strategies to secure business functions. In response to the increasing security demands of network services,

Works^{27,28,29,30,31} delved into cost optimization issues within SFC deployments. Literature²⁷ described the SFC deployment problem in edge computing as an integer linear programming model with the objective of minimizing deployment costs and introduced a resource-aware deployment algorithm to address this issue. Literature²⁸ utilized deep reinforcement learning to solve the SFC deployment problem, considering resource constraints required by SFC and dynamic distribution of VNFs, effectively optimizing service costs and quality. Literature²⁹ established a joint optimization problem model for SFC deployment and computational resource allocation aiming to minimize both SFC deployment costs and end-to-end business delay. It proposed a multi-agent deep deterministic policy gradient algorithm to solve the model. Literature³⁰ first introduced a coupled bandwidth resource allocation (CBRA) model for multiple SFC resource sharing and then established an integer linear programming problem based on the CBRA model to minimize resource occupation, providing an SFC deployment algorithm which realized joint resource allocation for multiple SFCs. Literature³¹ studied parallelized SFC deployment problems in data center networks from the perspectives of reliability assurance and resource optimization. This work enhanced SFC reliability through backup mechanisms and optimized link resource consumption through parallelized SFC deployment. This type of SFC deployment method can usually optimize deployment cost while considering other aspects of SFC performance, but the deployment environment considered is all homogeneous networks. The air traffic information network is a heterogeneous network that includes ground servers and wireless access points, airplane platforms, and space-based satellite platforms. Therefore, this type of SFC deployment method is difficult to directly apply in the air traffic information network.

System architecture and models

This section begins with a description of the deployment issues pertaining to SFC within the air traffic information network. Subsequently, it establishes a physical network model for the air traffic information network as well as an SFC deployment model. Lastly, it presents an overview of evaluation criteria for SFC deployment methods.

Problem formulation

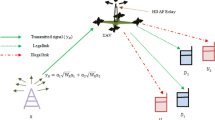
Figure 1 illustrates the transmission process of air traffic information in the NFV environment. The air traffic information network constitutes a complex space-air-ground integrated network, integrating satellite platforms, flights, ground infrastructure, and air traffic service providers. The space network consists of satellite platforms, the air network includes in-flight flights, and the ground network comprises various general servers, wireless access points, and air traffic service providers. Taking the process of providing meteorological information services for flights as an example, after meteorological centers collect meteorological data through meteorological sensors, weather satellites, weather radars, and other equipment, the data needs to undergo network function processing such as data fusion, data encryption, and network acceleration before it can be directly used by flights. In the NFV environment, these network functions can be flexibly deployed as VNFs to general-purpose physical platforms (satellite platforms or server platforms) without relying on proprietary hardware. Different VNFs are arranged in a sequential order to form a set of chained structures, known as SFC. The deployment of SFC at the physical network facilitates air traffic services, with the VNFs of SFC deployed to general-purpose physical platforms occupying their computing, storage, and forwarding resources, while the virtual links connecting VNFs are deployed onto physical links, occupying the bandwidth resources of the physical links.

Figure 1 illustrates the deployment scenarios of SFC1 (red dashed arrows) and SFC2 (purple dashed arrows). SFC1 is utilized for transmitting air traffic meteorological data, with the source endpoint being the meteorological center and the destination endpoint being flight 4. The three VNFs constituting SFC1 represent data fusion, data encryption, and network acceleration, and are deployed on servers 1, 4, and 8, respectively. SFC2, used for transmitting air traffic surveillance data, has its source endpoint at the surveillance center and the destination endpoint at flight 3. The four VNFs comprising SFC2 represent data compression, data encryption, load balancing, and QoS monitoring, and are deployed on servers 7, 2, satellite platform 6, and satellite platform 5, respectively.

During the SFC deployment process, each VNF can be deployed to any physical platform that meets resource constraints, and each virtual link can be deployed to any physical path between the two endpoints of the VNFs, provided it satisfies bandwidth constraints. Thus, the deployment methods for SFC are diverse. Each deployment method may result in different resource expenditures, end-to-end delay, security, and other performance characteristics. Therefore, focusing on the low-delay and high-security requirements of air traffic information transmission, this paper proposes an efficient and secure SFC deployment for delay optimization method. Since the premise of SFC security is that each instantiated VNF can operate securely, and the necessary condition for secure instantiation of VNFs is the secure operation of both the software VNFs and the physical resource platforms that support their operation, this paper considers reducing the number of physical resource platforms for VNF deployment to mitigate the risk of SFC cyberattacks. The advantage of this security reinforcement approach is the enhancement of SFC security without the need to introduce new redundant protective resources.

Fig. 1

SFC deployment scenario in the air traffic information network.

Network model

The paper abstracts the physical network in the air traffic information network as a weighted undirected graph G = (N, E), where N (n ∈ N represents physical node) denotes the physical node set, including the general server set N_s (n_s ∈ N_s denotes server), the satellite platform set N_a (n_a ∈ N_a denotes satellite platform), the wireless access point or switch set N_c (n_c ∈ N_c denotes wireless access point or switch), the set of flight N_f (n_f ∈ N_f denotes flight), and the ground service provider set N_p (n_p ∈ N_p denotes service provider). General servers and satellite platforms can be used to instantiate VNFs, while wireless access points or switches solely provide access and switching functions. Flights and ground service providers act as the source or destination endpoints of the SFC. The remaining available computational resources, storage resources, and forwarding resources of server n_s (n_s ∈ N_s) are denoted as Com(n_s), Sto(n_s), and For(n_s) respectively, with a delay of d(n_s) after VNF instantiation and a security of s(n_s) indicating the ability of server n_s to operate normally under a cyberattack, with values ranging between (0, 1). Similarly, the remaining available computational resources, storage resources, and forwarding resources of satellite platform n_a (n_a ∈ N_a) are denoted as Com(n_a), Sto(n_a), and For(n_a) respectively, with a delay of d(n_a) after VNF instantiation and a security of s(n_a) indicating the ability of satellite platform n_a to operate normally under a cyberattack, with values ranging between (0, 1). For convenience, let the set φ = {Com, Sto, For} denote the set of resource types, where k ∈ φ represents any one of the resources—computational, storage, or forwarding. E represents the set of physical links, and the remaining available bandwidth and delay of a physical link e (e ∈ E) are denoted as b(e) and d(e) respectively. The wired link is e_w, and the wireless link is e_l.

The SFC is represented as f = {I,O,D_max,S_min,T,V,L}, where I represents the source endpoint, O represents the destination endpoint, D_max represents the end-to-end delay upper limit, S_min represents the security lower limit, T represents the lifetime, V represents the set of VNFs composing the SFC, and L represents the set of virtual links connecting the VNFs. SFCs providing different services have different S_min. Table 1 categorizes the relevant services and their S_min in different areas of civil aircraft avionics networks. The S_min required for services in the Aircraft Control Domain (ACD) is the highest. Following that are the services in the Airline Information Services Domain (AISD). Lastly, the relevant services in the Passenger Information & Entertainment Services Domain (PIESD) are considered.

Table 1 The relevant services and their S_min in different areas of civil aircraft avionics networks.

The set V={v₁,v₂,…,v_|V|} includes v_i (i = 1,2,…,|V|, where |V| represents the number of elements in set V), representing the VNF at the i-th position in the SFC, with computational resource requirements Com(v_i), storage resource requirements Sto(v_i), forwarding resource requirements For(v_i), a bandwidth variation factor η(v_i), and a security s(v_i). The bandwidth variation factor η(v_i) is defined as the ratio of the data outbound bandwidth to the data inbound bandwidth for v_i. For VNFs such as firewalls, data decryption, and data compression, the bandwidth variation factor is less than 1, while for VNFs such as data encryption and data decompression, the factor is greater than 1. For VNFs like network address translation and QoS monitors, the bandwidth variation factor is approximately equal to 1. The security s(v_i) represents the ability of the virtual machine (VM) where v_i resides to operate normally under a cyberattack, influenced by factors such as the version of the VM and the number of vulnerabilities, indicating the security capability of the VNF and taking on values within the range of (0, 1). The set L={l₀,l₁,l₂,…,l_|V|} includes l_i (i = 1,2,…,|V|-1) representing the virtual link between v_i and v_i+1. Specifically, l₀ represents the virtual link between the source endpoint I and v₁, and l_|V| represents the virtual link between v_|V| and the destination endpoint O. The bandwidth requirement of l_i is denoted as b(l_i), satisfying the relationship as shown in Eq. (1).

$$b\left( {{l_i}} \right)=b\left( {{l_0}} \right)\prod\limits_{{j=1}}^{i} {\eta \left( {{v_j}} \right)}$$

(1)

The binary variable x_ij indicates whether v_i is deployed on server node n_j (x_ij=1 indicates v_i is deployed on server node n_j, x_ij = 0 indicates v_i is not deployed on server node n_j). The binary variable y_ij indicates whether v_i is deployed on satellite platform node n_j (y_ij=1 indicates v_i is deployed on satellite platform node n_j, y_ij=0 indicates v_i is not deployed on satellite platform node n_j). T0he binary variable z_ij indicates whether l_i passes through physical link e_j after being deployed to the physical network (z_ij=1 indicates l_i passes through physical link e_j after being deployed to the physical network, z_ij=0 indicates l_i does not pass through physical link e_j after being deployed to the physical network). Therefore, the following constraints need to be satisfied after the SFC is deployed to the physical network:

$$\sum\limits_{{{n_j} \in {N_s} \cup {N_a}}} {{x_{ij}}} +{y_{ij}}=1$$

(2)

$$\sum\limits_{{{e_j} \in E}} {{z_{ij}}} \geqslant 1$$

(3)

$$\sum\limits_{{{v_i} \in V}} {{x_{ij}}k\left( {{v_i}} \right)} \leqslant k\left( {{n_j}} \right)$$

(4)

$$\sum\limits_{{{v_i} \in V}} {{y_{ij}}k\left( {{v_i}} \right)} \leqslant k\left( {{n_j}} \right)$$

(5)

$$\sum\limits_{{{l_i} \in L}} {{z_{ij}}b\left( {{l_i}} \right)} \leqslant b\left( {{e_j}} \right)$$

(6)

$$\sum\limits_{{{v_i} \in V}} {\sum\limits_{{{n_j} \in {N_s} \cup {N_a}}} {\left( {{x_{ij}}+{y_{ij}}} \right)d\left( {{n_j}} \right)} } +\sum\limits_{{{l_i} \in L}} {\sum\limits_{{{e_j} \in E}} {{z_{ij}}d\left( {{e_j}} \right)} } \leqslant {D_{\hbox{max} }}$$

(7)

$$\prod\limits_{{{v_i} \in V}} {\prod\limits_{{{n_j} \in {N^f}}} {s\left( {{v_i}} \right)s\left( {{n_j}} \right)} } \geqslant {S_{\hbox{min} }}$$

(8)

Table 2 Summary of notations.

Where Eq. (2) ensures that each VNF can be deployed in the physical network and only on one physical node (server node or satellite platform node). Equation (3) ensures that each virtual link can be deployed in the physical network and can be deployed on multiple physical links. Equations (4) and (5) ensure that each type of resource requirement for VNF does not exceed the remaining resources of the deployed physical node. Equation (6) ensures that the bandwidth requirement of the virtual link does not exceed the remaining bandwidth of the deployed physical link. Equation (7) ensures that the delay of SFC does not exceed the end-to-end delay upper limit. The first term on the left-hand side of the inequality represents the delay generated by nodes, primarily including processing delay and transmission experiments. The second term represents the delay generated by the link, including propagation delay. Equation (8) ensures that the security of SFC must be greater than the security lower limit, where N^f represents the set of physical nodes where VNFs in SFC f are deployed. In order to improve the readability of the paper, the main notations and their descriptions are shown in Table 2.

Evaluation metrics

The evaluation metrics for the deployment of SFC in this paper encompass the SFC deployment success rate, average end-to-end delay, long-term revenue-cost ratio, and average security.

·The service request acceptance rate, denoted as ω_accept, is defined by Eq. (9), where NUM_suc(T) represents the number of successfully deployed SFCs within time interval T, and NUM_v(T) represents the total SFC requests arrived within the same time interval.

$${\omega _{accept}}=\mathop {\lim }\limits_{{T \to +\infty }} \frac{{NU{M_{suc}}\left( T \right)}}{{NU{M_v}\left( T \right)}}$$

(9)

·The calculation of the average end-to-end delay, D_ave, is determined by Eqs. (10) and (11). The end-to-end delay, D_g, for the g-th SFC is calculated as per Eq. (10).

$${D_g}=\sum\limits_{{{v_i} \in V}} {\sum\limits_{{{n_j} \in {N_s} \cup {N_a}}} {\left( {{x_{ij}}+{y_{ij}}} \right)d\left( {{n_j}} \right)} } +\sum\limits_{{{l_i} \in L}} {\sum\limits_{{{e_j} \in {E_s}}} {{z_{ij}}d\left( {{e_j}} \right)} }$$

(10)

$${D_{ave}}={{\sum\limits_{{g=1}}^{{NU{M_{suc}}}} {{D_g}} } \mathord{\left/ {\vphantom {{\sum\limits_{{g=1}}^{{NU{M_{suc}}}} {{D_g}} } {NU{M_{suc}}}}} \right. \kern-0pt} {NU{M_{suc}}}}$$

(11)

·The calculation of the long-term revenue-cost ratio is specified by Eqs. (12), (13), and (14). At time t, the revenue of successfully deploying an SFC is articulated in Eq. (12), while the resource cost incurred by the physical network is expressed in Eq. (13). Here, α and β represent the respective proportions of node and link resources, both of which are assumed to be 1 in this paper.

$$Re\left( {t,f} \right)=\alpha \sum\limits_{{{v_i} \in V}} {\sum\limits_{{k \in \varphi }} {k\left( {{v_i}} \right)} } +\beta \sum\limits_{{{l_i} \in L}} {b\left( {{l_i}} \right)}$$

(12)

$$Co\left( {t,f} \right)=\alpha \sum\limits_{{{v_i} \in V}} {\sum\limits_{{k \in \varphi }} {k\left( {{v_i}} \right)} } +\beta \sum\limits_{{{l_i} \in L}} {hop\left( {{l_i}} \right)b\left( {{l_i}} \right)}$$

(13)

$${{Re} \mathord{\left/ {\vphantom {{Re} {Co}}} \right. \kern-0pt} {Co}}=\mathop {\lim }\limits_{{T \to +\infty }} {{\sum\limits_{{t=0}}^{T} {Re\left( {t,f} \right)} } \mathord{\left/ {\vphantom {{\sum\limits_{{t=0}}^{T} {Re\left( {t,f} \right)} } {\sum\limits_{{t=0}}^{T} {Co\left( {t,f} \right)} }}} \right. \kern-0pt} {\sum\limits_{{t=0}}^{T} {Co\left( {t,f} \right)} }}$$

(14)

·The method for calculating the average security is outlined in Eqs. (15) and (16), where N^f represents the set of physical nodes where VNFs in SFC f are deployed.

$${s_g}=\prod\limits_{{{v_i} \in V}} {\prod\limits_{{{n_j} \in {N^f}}} {s\left( {{v_i}} \right)s\left( {{n_j}} \right)} }$$

(15)

$${s_{ave}}={{\sum\limits_{{g=1}}^{{NU{M_{suc}}}} {s\left( {{f_g}} \right)} } \mathord{\left/ {\vphantom {{\sum\limits_{{g=1}}^{{NU{M_{suc}}}} {s\left( {{f_g}} \right)} } {NU{M_{suc}}}}} \right. \kern-0pt} {NU{M_{suc}}}}$$

(16)

SFC deployment analysis

In order to facilitate representation and comprehension, this section analyzes and summarizes the principles of SFC deployment using server networks as a representative. As the various resource attributes of satellite platform nodes are similar to those of server nodes, the summarized principles are applicable to the entire air traffic information network.

Security analysis

As cyberattacks typically target physical node platforms and VM, this paper assumes that all physical links are secure. Consequently, the security of the SFC is only related to the deployment method of VNFs. Considering the three VNF deployment scenarios illustrated in Fig. 2, where Fig. 2a represents VNFs deployed across different servers, Fig. 2b represents the partial deployment of VNFs on the same server, and Fig. 2c represents all VNFs deployed on the same server.

Fig. 2

Different VNF deployment scenarios.

The necessary and sufficient condition for SFC security is that each instantiated VNF is secure. The necessary and sufficient condition for the security of an instantiated VNF is that the VNF is secure and the server hosting it is also secure. Assuming the likelihood of each server and each VNF being attacked are independent of each other, in deployment scenario 1 in Fig. 2, the probabilities of instantiated VNF1, instantiated VNF2, and instantiated VNF3 being secure are s(v₁)s(n₁), s(v₂)s(n₂), s(v₃)s(n₃), then the security of the SFC is given by:

$${s_1}\left( f \right)=s\left( {{v_1}} \right)s\left( {{n_1}} \right)s\left( {{v_2}} \right)s\left( {{n_2}} \right)s\left( {{v_3}} \right)s\left( {{n_3}} \right)$$

(15)

In deployment scenario 2 in Fig. 2, since VNF1 and VNF2 are deployed on server 2 simultaneously, the possibility of instantiating VNF1 and instantiating VNF2 simultaneously securely is s(v₁)s(v₂)s(n₂), then the security of the SFC is:

$${s_2}\left( f \right)=s\left( {{v_1}} \right)s\left( {{v_2}} \right)s\left( {{n_2}} \right)s\left( {{v_3}} \right)s\left( {{n_3}} \right)$$

(16)

In deployment scheme 3 in Fig. 2, since VNF1, VNF2, and VNF3 are deployed on server 2 simultaneously, the possibility of of instantiating VNF1, VNF2, and VNF3 simultaneously securely is s(v₁)s(v₂)s(v₃)s(n₂), then the security of SFC is as follows:

$${s_3}\left( f \right)=s\left( {{v_1}} \right)s\left( {{v_2}} \right)s\left( {{v_3}} \right)s\left( {{n_2}} \right)$$

(17)

Due to 0 < s(n₁) < 1 and 0 < s(n₃) < 1, it follows that s₁(f ) < s₂(f ) < s₃(f ).

Principle 1: Reducing the number of physical nodes for SFC deployment can enhance the security of the SFC.

Delay analysis

Considering the three different SFC deployment scenarios illustrated in Fig. 3, in scenario depicted in Fig. 3a, the path of SFC deployment to the physical network is source endpoint I → server1 → server 2 → server 5 → server 3 → server 4 → destination endpoint O, resulting in a path length of 6. In the scenario shown in Fig. 3b, the SFC deployment to the physical network follows a path that is source endpoint I → server 1 → server 2 → server 5 → server 4 → destination endpoint O, resulting in a path length of 5. In the scenario illustrated in Fig. 3c, the SFC deployment to the physical network follows a path that is source endpoint I → server 1 → server 2 → server 4 → destination endpoint O, resulting in a path length of 4.

Fig. 3

Different SFC deployment scenarios.

Assuming the delay of all servers is d(n) and that of all physical links is d(e), in deployment scenario 1 in Fig. 3, the end-to-end delay of the SFC is:

$$\begin{gathered} {D_1}\left( f \right)=d\left( {{n_1}} \right)+d\left( {{n_2}} \right)+d\left( {{n_3}} \right)+d\left( {{e_{I,1}}} \right)+d\left( {{e_{1,2}}} \right) \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} +d\left( {{e_{2,5}}} \right)+d\left( {{e_{5,3}}} \right)+d\left( {{e_{3,4}}} \right)+d\left( {{e_{4,O}}} \right) \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} =3d\left( n \right)+6d\left( e \right) \hfill \\ \end{gathered}$$

(18)

In deployment scenario 2 in Fig. 3, the end-to-end delay of the SFC is:

$$\begin{gathered} {D_2}\left( f \right)=d\left( {{n_1}} \right)+d\left( {{n_2}} \right)+d\left( {{n_5}} \right)+d\left( {{e_{I,1}}} \right)+d\left( {{e_{1,2}}} \right) \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} +d\left( {{e_{2,5}}} \right)+d\left( {{e_{5,4}}} \right)+d\left( {{e_{4,O}}} \right) \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} =3d\left( n \right)+5d\left( e \right) \hfill \\ \end{gathered}$$

(19)

In deployment scenario 3 in Fig. 3, the end-to-end delay of the SFC is:

$$\begin{gathered} {D_3}\left( f \right)=d\left( {{n_1}} \right)+d\left( {{n_2}} \right)+d\left( {{n_4}} \right)+d\left( {{e_{I,1}}} \right) \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} +d\left( {{e_{1,2}}} \right)+d\left( {{e_{2,4}}} \right)+d\left( {{e_{4,O}}} \right) \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} =3d\left( n \right)+4d\left( e \right) \hfill \\ \end{gathered}$$

(20)

Due to d(e) > 0, it follows that D₁(f ) > D₂(f ) > D₃(f ).

Principle 2: Reducing the length of the SFC deployment path can decrease the delay of the SFC.

Resource cost analysis

Consider the four distinct SFC deployment scenarios illustrated in Fig. 4, comprising a composition of four VNFs, where the bandwidth variation factors of VNF1, VNF2, and VNF4 exceed 1, while that of VNF3 is less than 1. In scenario 1 as depicted in Fig. 4a, VNFs are deployed on servers 1, 5, 2, and 4, with the SFC deployment path as follows: source endpoint I → server 1→ server 5 → server 2 → server 5 → server 4 → destination endpoint O. Scenario 2 shown in Fig. 4b swaps the deployment locations of VNF2 and VNF3 compared to scenario 1, altering the SFC deployment path to source endpoint I → server 2 → server 5 → server 4 → destination endpoint O, thereby avoiding data flow back and forth between servers 5 and 2, consequently reducing the SFC deployment path length. In scenario 3 depicted in Fig. 4c, compared to scenario 2, the VNF3 with a bandwidth variation factor less than 1 is co-located with the preceding VNF2 on the same server, without altering the SFC deployment path. Scenario 4 shown in Fig. 4d, compared to scenario 2, the VNF3 with a bandwidth variation factor less than 1 is co-located with the succeeding VNF4 on the same server, without altering the SFC deployment path.

The resource cost of the physical network in scenario 1 of Fig. 4 is:

$$\begin{gathered} C{o_1}\left( f \right)=\sum\limits_{{k \in \varphi }} {k\left( {{v_1}} \right)} +\sum\limits_{{k \in \varphi }} {k\left( {{v_2}} \right)} +\sum\limits_{{k \in \varphi }} {k\left( {{v_3}} \right)} +\sum\limits_{{k \in \varphi }} {k\left( {{v_4}} \right)} +b\left( {{l_0}} \right)+2b\left( {{l_1}} \right)+b\left( {{l_2}} \right)+b\left( {{l_3}} \right)+b\left( {{l_4}} \right) \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} =\sum\limits_{{k \in \varphi }} {k\left( {{v_1}} \right)} +\sum\limits_{{k \in \varphi }} {k\left( {{v_2}} \right)} +\sum\limits_{{k \in \varphi }} {k\left( {{v_3}} \right)} +\sum\limits_{{k \in \varphi }} {k\left( {{v_4}} \right)} +b\left( {{l_0}} \right)+2\eta \left( {{v_1}} \right)b\left( {{l_0}} \right)+\eta \left( {{v_1}} \right)\eta \left( {{v_2}} \right)b\left( {{l_0}} \right) \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} +\eta \left( {{v_1}} \right)\eta \left( {{v_2}} \right)\eta \left( {{v_3}} \right)b\left( {{l_0}} \right)+\eta \left( {{v_1}} \right)\eta \left( {{v_2}} \right)\eta \left( {{v_3}} \right)\eta \left( {{v_4}} \right)b\left( {{l_0}} \right) \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} =\sum\limits_{{k \in \varphi }} {k\left( {{v_1}} \right)} +\sum\limits_{{k \in \varphi }} {k\left( {{v_2}} \right)} +\sum\limits_{{k \in \varphi }} {k\left( {{v_3}} \right)} +\sum\limits_{{k \in \varphi }} {k\left( {{v_4}} \right)} \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} +\left[ {1+2\eta \left( {{v_1}} \right)+\eta \left( {{v_1}} \right)\eta \left( {{v_2}} \right)+\eta \left( {{v_1}} \right)\eta \left( {{v_2}} \right)\eta \left( {{v_3}} \right)+\eta \left( {{v_1}} \right)\eta \left( {{v_2}} \right)\eta \left( {{v_3}} \right)\eta \left( {{v_4}} \right)} \right]b\left( {{l_0}} \right) \hfill \\ \end{gathered}$$

(21)

Fig. 4

Different SFC deployment scenarios.

The resource cost of the physical network in scenario 2 of Fig. 4 is:

$$\begin{gathered} C{o_2}\left( f \right)=\sum\limits_{{k \in \varphi }} {k\left( {{v_1}} \right)} +\sum\limits_{{k \in \varphi }} {k\left( {{v_2}} \right)} +\sum\limits_{{k \in \varphi }} {k\left( {{v_3}} \right)} +\sum\limits_{{k \in \varphi }} {k\left( {{v_4}} \right)} +b\left( {{l_0}} \right)+b\left( {{l_1}} \right)+b\left( {{l_2}} \right)+b\left( {{l_3}} \right)+b\left( {{l_4}} \right) \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} =\sum\limits_{{k \in \varphi }} {k\left( {{v_1}} \right)} +\sum\limits_{{k \in \varphi }} {k\left( {{v_2}} \right)} +\sum\limits_{{k \in \varphi }} {k\left( {{v_3}} \right)} +\sum\limits_{{k \in \varphi }} {k\left( {{v_4}} \right)} +b\left( {{l_0}} \right)+\eta \left( {{v_1}} \right)b\left( {{l_0}} \right)+\eta \left( {{v_1}} \right)\eta \left( {{v_2}} \right)b\left( {{l_0}} \right) \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} +\eta \left( {{v_1}} \right)\eta \left( {{v_2}} \right)\eta \left( {{v_3}} \right)b\left( {{l_0}} \right)+\eta \left( {{v_1}} \right)\eta \left( {{v_2}} \right)\eta \left( {{v_3}} \right)\eta \left( {{v_4}} \right)b\left( {{l_0}} \right) \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} =\sum\limits_{{k \in \varphi }} {k\left( {{v_1}} \right)} +\sum\limits_{{k \in \varphi }} {k\left( {{v_2}} \right)} +\sum\limits_{{k \in \varphi }} {k\left( {{v_3}} \right)} +\sum\limits_{{k \in \varphi }} {k\left( {{v_4}} \right)} \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} +\left[ {1+\eta \left( {{v_1}} \right)+\eta \left( {{v_1}} \right)\eta \left( {{v_2}} \right)+\eta \left( {{v_1}} \right)\eta \left( {{v_2}} \right)\eta \left( {{v_3}} \right)+\eta \left( {{v_1}} \right)\eta \left( {{v_2}} \right)\eta \left( {{v_3}} \right)\eta \left( {{v_4}} \right)} \right]b\left( {{l_0}} \right) \hfill \\ \end{gathered}$$

(22)

The resource cost of the physical network in scenario 3 of Fig. 4 is:

$$\begin{gathered} C{o_3}\left( f \right)=\sum\limits_{{k \in \varphi }} {k\left( {{v_1}} \right)} +\sum\limits_{{k \in \varphi }} {k\left( {{v_2}} \right)} +\sum\limits_{{k \in \varphi }} {k\left( {{v_3}} \right)} +\sum\limits_{{k \in \varphi }} {k\left( {{v_4}} \right)} +b\left( {{l_0}} \right)+b\left( {{l_1}} \right)+2b\left( {{l_3}} \right)+b\left( {{l_4}} \right) \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} =\sum\limits_{{k \in \varphi }} {k\left( {{v_1}} \right)} +\sum\limits_{{k \in \varphi }} {k\left( {{v_2}} \right)} +\sum\limits_{{k \in \varphi }} {k\left( {{v_3}} \right)} +\sum\limits_{{k \in \varphi }} {k\left( {{v_4}} \right)} +b\left( {{l_0}} \right)+\eta \left( {{v_1}} \right)b\left( {{l_0}} \right) \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} +2\eta \left( {{v_1}} \right)\eta \left( {{v_2}} \right)\eta \left( {{v_3}} \right)b\left( {{l_0}} \right)+\eta \left( {{v_1}} \right)\eta \left( {{v_2}} \right)\eta \left( {{v_3}} \right)\eta \left( {{v_4}} \right)b\left( {{l_0}} \right) \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} =\sum\limits_{{k \in \varphi }} {k\left( {{v_1}} \right)} +\sum\limits_{{k \in \varphi }} {k\left( {{v_2}} \right)} +\sum\limits_{{k \in \varphi }} {k\left( {{v_3}} \right)} +\sum\limits_{{k \in \varphi }} {k\left( {{v_4}} \right)} \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} +\left[ {1+\eta \left( {{v_1}} \right)+2\eta \left( {{v_1}} \right)\eta \left( {{v_2}} \right)\eta \left( {{v_3}} \right)+\eta \left( {{v_1}} \right)\eta \left( {{v_2}} \right)\eta \left( {{v_3}} \right)\eta \left( {{v_4}} \right)} \right]b\left( {{l_0}} \right) \hfill \\ \end{gathered}$$

(23)

The resource cost of the physical network in scenario 4 of Fig. 4 is:

$$\begin{gathered} C{o_4}\left( f \right)=\sum\limits_{{k \in \varphi }} {k\left( {{v_1}} \right)} +\sum\limits_{{k \in \varphi }} {k\left( {{v_2}} \right)} +\sum\limits_{{k \in \varphi }} {k\left( {{v_3}} \right)} +\sum\limits_{{k \in \varphi }} {k\left( {{v_4}} \right)} +b\left( {{l_0}} \right)+b\left( {{l_1}} \right)+2b\left( {{l_2}} \right)+b\left( {{l_4}} \right) \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} =\sum\limits_{{k \in \varphi }} {k\left( {{v_1}} \right)} +\sum\limits_{{k \in \varphi }} {k\left( {{v_2}} \right)} +\sum\limits_{{k \in \varphi }} {k\left( {{v_3}} \right)} +\sum\limits_{{k \in \varphi }} {k\left( {{v_4}} \right)} +b\left( {{l_0}} \right)+\eta \left( {{v_1}} \right)b\left( {{l_0}} \right) \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} +2\eta \left( {{v_1}} \right)\eta \left( {{v_2}} \right)b\left( {{l_0}} \right)+\eta \left( {{v_1}} \right)\eta \left( {{v_2}} \right)\eta \left( {{v_3}} \right)\eta \left( {{v_4}} \right)b\left( {{l_0}} \right) \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} =\sum\limits_{{k \in \varphi }} {k\left( {{v_1}} \right)} +\sum\limits_{{k \in \varphi }} {k\left( {{v_2}} \right)} +\sum\limits_{{k \in \varphi }} {k\left( {{v_3}} \right)} +\sum\limits_{{k \in \varphi }} {k\left( {{v_4}} \right)} \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} +\left[ {1+\eta \left( {{v_1}} \right)+2\eta \left( {{v_1}} \right)\eta \left( {{v_2}} \right)+\eta \left( {{v_1}} \right)\eta \left( {{v_2}} \right)\eta \left( {{v_3}} \right)\eta \left( {{v_4}} \right)} \right]b\left( {{l_0}} \right) \hfill \\ \end{gathered}$$

(24)

Since η(v₁) > 0, Co₁(f ) > Co₂(f ). Since 0 < η(v₃) < 1, Co₃(f ) < Co₂(f ), and Co₄(f ) > Co₂(f ).

Principle 3: Reducing the SFC deployment path length can lower the resource cost of the physical network.

Principle 4: Co-locating VNFs with bandwidth variation factors less than 1 together with their preceding VNF decreases the resource cost of the physical network.

SFC deployment method design

The proposed efficient and secure SFC deployment for delay optimization (ESSFCD-DO) in this paper comprises three main components: VNF aggregation, VNF deployment, and virtual link deployment. Initially, guided by Principles 1 and 4, VNFs with a bandwidth variation factor less than 1 are aggregated with the VNF preceding them. Subsequently, the aggregated VNFs are deployed onto the same physical node, resulting in a reduction in the number of physical nodes required for SFC deployment. This step achieves the dual purpose of optimizing SFC security and physical network resource costs. Following this, in accordance with Principles 2 and 3, the aggregated VNFs are sequentially deployed onto the shortest path between the source and destination endpoints which satisfy the resource requirements, optimizing SFC delay. Finally, based on the VNF deployment positions, the virtual link deployment is achieved using the k-shortest path algorithm.

VNF aggregation algorithm for security and resource cost optimization

As per Principle 1, deploying multiple VNFs onto the same physical node enhances SFC security. Moreover, in line with Principle 4, deploying VNFs with a bandwidth variation factor less than 1 together with their preceding VNFs reduces the resource cost of physical network. Hence, this paper presents the VNF aggregation algorithm for security and resource cost optimization (VNFAA-SRCO). The core idea of VNFAA-SRCO is to aggregate VNFs with a bandwidth variation factor less than 1 with their preceding VNFs and deploy the aggregated VNFs onto the same physical node. Figure 5 illustrates the VNF aggregation scenario using VNFAA-SRCO.

Fig. 5

VNF aggregation scenario using VNFAA-SRCO.

Figure 5 illustrates the aggregation process of 3 SFCs using the VNFAA-SRCO algorithm. Each SFC has an initial bandwidth requirement of 10Mbps and consists of 4 VNFs, each with bandwidth variation factors denoted as η(v₁), η(v₂), η(v₃), η(v₄). The bandwidth requirement of each virtual link can be calculated using Eq. (1), and the results are annotated above the virtual links. We take SFC1 as an example to analyze the aggregation process of VNFs. VNF v₂ has a bandwidth variation factor less than 1, so VNFAA-SRCO aggregates it with v₁ positioned before it. Similarly, VNF v₃ with a bandwidth variation factor less than 1 is aggregated with v₂, which has already been aggregated with v1, resulting in the aggregation of v₁, v₂, and v₃. The aggregated v₁, v₂, and v₃ in SFC1 will be deployed on the same server, making the virtual links with bandwidth requirements of 12Mbps and 10.8Mbps the internal links of the server, eliminating the need to deploy them on physical links. The aggregation process for SFC2 and SFC3 is similar. The specific algorithm steps for VNFAA-SRCO are detailed in Table 3. The resource requirements of the aggregated VNF are the sum of the resource requirements of the individual VNFs before aggregation, and the bandwidth variation factor is the product of the bandwidth variation factors of the individual VNFs before aggregation. The algorithm VNFAA-SRCO only traverses all the VNFs in the SFC once, therefore the complexity of VNFAA-SRCO is O(|V|), where |V| is the number of VNFs in the SFC.

Table 3 Specific algorithm steps for VNFAA-SRCO.This picture is too blurry. It is recommended to embed the original table or increase the pixels of the picture.

VNF deployment algorithm based on topology aware

Based on the findings of Principles 2 and 3, it is evident that reducing the path length of SFC deployment can effectively decrease the end-to-end delay and resource cost of the SFC. Therefore, this paper introduces the design of a VNF deployment algorithm based on topology awareness (VNFDA-TA). The central idea of VNFDA-TA is to deploy VNFs along the shortest path between the source and destination endpoints which satisfy the resource requirements, while imposing constraints to prevent data flows from traversing back and forth between physical nodes. The specific procedure of VNFDA-TA is delineated in Table 4, in which hop(A, B) indicates the shortest hop between node A and node B.

The first phase of VNFDA-TA involves the deployment of the first VNF V_sum(1) (Lines 1–8). When deploying V_sum(1), the algorithm initially filters a set of physical nodes that satisfy the resource requirements of V_sum(1), Φ₁, from the physical nodes. Subsequently, from Φ₁, a subset of nodes, Φ₂, with the smallest hop(I,n_s) is selected. Finally, V_sum(1) is deployed on the node from Φ₂ with the highest security.

Table 4 Specific algorithm steps for VNFDA-TA.This picture is too blurry. It is recommended to embed the original table or increase the pixels of the picture.

The second phase of VNFDA-TA involves the deployment of subsequent VNFs in V_sum (Lines 9–19). When deploying VNF V_sum(i) (2 ≤ i≤|V_sum|), the algorithm similarly filters a set of physical nodes that satisfy the resource requirements of V_sum(i), Φ₁, from the physical network, and removes nodes that have already been utilized in the current SFC to create a set of nodes, Φ₂. Then, from Φ₂, a subset of nodes, Φ₃, with the smallest hop(VNF_Dep (i-1),n_s) + hop(n_s,O) is selected, aiming to position the VNF along the shortest path between the source and destination endpoints. Following this, a set of nodes, Φ₄, is chosen from Φ₃ satisfying hop(n_s,O) ≤ hop(VNF_Dep(i-1),O), constraining the data flow from oscillating during service. Eventually, VNF V_sum(i) is deployed on a node with the highest security from Φ₄.

The third phase of VNFDA-TA involves a security verification of the SFC post VNF deployment (Lines 20–25). If the security of the SFC is greater than the security lower limit S_min, the deployment result is output; otherwise, the deployment fails.

When deploying VNFs, the VNFDA-TA first traverses all VNFs in the SFC and then traverses all physical nodes for each VNF. Therefore, the algorithm complexity is O(|V|•|N|), where |N| indicates the number of physical nodes.

Virtual link deployment

When deploying virtual links, the first step involves removing physical links within the network that do not meet the bandwidth requirements. Subsequently, the k-shortest path algorithm is utilized to deploy the virtual link onto the shortest path between the nodes where the two end VNFs are deployed. Finally, the end-to-end delay of the SFC is computed to determine if it is greater than the end-to-end delay upper limit, D_max. If it is, the deployment fails; otherwise, the result of the SFC deployment is output.

Performance evaluation and analysis

This section conducts performance evaluations of the proposed SFC deployment method (ESSFCD-DO) in this paper through 2 sets of simulation experiments. The first set of experiments is used to evaluate the performance of ESSFCD-DO at different SFC arrival rates, while the second set of experiments compares the performance of ESSFCD-DO with other SFC deployment methods, including SFCD-TDM¹⁷, SFCD-MS²¹, and SASFC²⁵ proposed by other scholars in this field. In order to fully demonstrate the advantages of the proposed VNFAA-SRCO, a control algorithm SFCD-TA is also set up in the experimental section of this paper. This algorithm, apart from not using VNFAA-SRCO for VNF aggregation, keeps all other steps consistent with ESSFCD-DO. The evaluation metrics for SFC deployment methods in this paper include service request acceptance rate, average end-to-end delay, long-term average revenue-cost ratio, and average security. To reduce the randomness of the experiments, each set of experiments is conducted 10 times, and the average is taken as the final experimental result.

Experimental setup

The network topologies, German50 and Cost266, from the SNDlib³² are respectively simulated to represent medium-sized and small-sized distributed air traffic information networks. As depicted in Fig. 6, the network topology of German50 comprises 50 nodes and 88 links, while Cost266 consists of 37 nodes and 57 links.

Fig. 6

Experimental network topology. (a) Network topology of German50, (b) Network topology of Cost266.

In the experimental network topology, 70% of the nodes are randomly selected as server nodes, 10% as wireless access points or switch nodes, and 20% as satellite platform nodes. Links connected to satellite platforms are wireless, while others are wired. The simulation time is set to 50,000 units, with each time unit representing 1 s. SFC requests follow a Poisson distribution with parameter λ, and the survival time follows a negative exponential distribution with µ = 1000. The parameters for the air traffic information network and SFC requests are detailed in Table 5, in which U represent uniform distribution. Considering that satellite platforms operate in space with relatively lower power consumption than ground servers, and are difficult to install large network security components, we set its total resources to be less than those of the servers, the delay to be greater than that of the servers, and the security to be lower than that of the servers. Furthermore, since the channel capacity of wireless links is lower than that of wired links, we set the bandwidth of wireless links to be less than that of wired links and the delay to be greater than that of wired links.

Table 5 Experimental parameter setting.

Performance of ESSFCD-DO at different SFC arrival rates

The first group of experiments utilized the German50 network topology, with SFC arrival rates set to λ = 1/20, λ = 1/15, λ = 1/10, and λ = 1/5, to investigate the performance of ESSFCD-DO under different SFC arrival rates, as shown in Fig. 7. Figure 7a presents the experimental results of service request acceptance rate, indicating that the service request acceptance rate of ESSFCD-DO consistently remains above 0.93, attributed to the aggregation of VNFs and the reduction of SFC deployment path lengths, thereby better fulfilling security and latency requirements. Figure 7b illustrates the experimental results of average end-to-end delay of SFC, showing that the average end-to-end delay of ESSFCD-DO consistently remains below 60 ms after stabilization. This is achieved by utilizing the VNFDA-TA algorithm to deploy VNFs on the shortest path possible between the source endpoint and destination endpoint, thereby shortening the SFC deployment path length. Figure 7c shows the experimental results of the long-term average revenue-cost ratio. It can be observed that the long-term average revenue-cost ratio of ESSFCD-DO remains above 0.94 after stabilization. This is because ESSFCD-DO aggregates VNFs based on the bandwidth variation factor using the VNFAA-SRCO algorithm, reducing the bandwidth resources occupied by large-bandwidth virtual links on physical links. Additionally, the VNFDA-TA algorithm shortens the deployment path length of SFC, further reducing the use of bandwidth resources. Figure 7d presents the experimental results of the average security of SFC. It is evident that the average security of SFC in ESSFCD-DO remains above 0.915 after stabilization. This is because ESSFCD-DO reduces the number of deployed physical nodes by aggregating VNFs, thereby reducing the security threat risk faced by SFC.

Fig. 7

Performance of ESSFCD-DO at different SFC arrival rates. (a) Service request acceptance rate, (b) Average end-to-end delay of the SFC, (c) Long-term average revenue-cost ratio, (d) Average security of the SFC.

Performance comparison of ESSFCD-DO with other SFC deployment methods

In the second group of experiments, the German50 and Cost266 network topologies are respectively used, with the SFC arrival rate set to λ = 1/20, to investigate the performance differences between ESSFCD-DO and other SFC deployment methods. Experimental results are shown in Figs. 8, 9, 10 and 11.

Figure 8 shows the experimental results of service request acceptance rates for different SFC deployment methods, where Fig. 8a presents the results in the German50 network, and Fig. 8b shows the results in the Cost266 network. It can be observed that the service request acceptance rate of SFCD-MS reaches around 0.98 in both the German50 and Cost266 networks. The service request acceptance rate of ESSFCD-DO reaches around 0.95 in both the German50 and Cost266 networks. The service request acceptance rate of SASFC is around 0.92 in the German50 network and around 0.87 in the Cost266 network. SFCD-TO achieves a service request acceptance rate of around 0.86 in the German50 network and around 0.89 in the Cost266 network. The service request acceptance rate of SFCD-TDM is around 0.81 in the German50 network and around 0.85 in the Cost266 network. Comparing the experimental results of the five methods, it is found that the service request acceptance rate of ESSFCD-DO is second only to SFCD-MS and superior to the other three methods. This is because ESSFCD-DO aggregates VNFs before SFC deployment using the ESSFCD-DO algorithm, effectively enhancing the security of the SFC. Furthermore, during the SFC deployment process, VNFDA-TA is utilized to deploy VNFs on the physical nodes with the highest security on the shortest path between the source and destination endpoints, thereby optimizing the security and delay of the SFC. This makes it easier for the deployed SFC to meet security and delay requirements, leading to a higher service request acceptance rate compared to the other three methods. However, the constraints set by VNFDA-TA are more stringent than those of SFCD-MS, making it more challenging to find physical nodes that meet the constraints for VNF deployment, resulting in a lower service request acceptance rate compared to SFCD-MS.

Fig. 8

Results of service request acceptance rates. (a) German50 network, (b) Cost266 network.

Figure 9 shows the experimental results of the average end-to-end delay of different SFC deployment methods, where Fig. 9a presents the results in the German50 network, and Fig. 9b presents the results in the Cost266 network. It can be observed that the average end-to-end delay of ESSFCD-DO reaches about 60 ms in the German50 network and about 54 ms in the Cost266 network. The average end-to-end delay of SFCD-TO is around 67 ms in the German50 network and around 61 ms in the Cost266 network. The average end-to-end delay of SFCD-TDM is approximately 85 ms in the German50 network and about 78 ms in the Cost266 network. The average end-to-end delay of SASFC is around 99ms in the German50 network and around 86ms in the Cost266 network. The average end-to-end delay of SFCD-MS is about 99ms in the German50 network and about 89ms in the Cost266 network. Comparing the experimental results of the five methods, it can be seen that the proposed ESSFCD-DO method for SFC has a better average end-to-end delay than the other four methods. This is because ESSFCD-DO, on one hand, reduces the physical node count for VNF deployment by VNF aggregation, indirectly shortening the SFC deployment path length. Moreover, by using the VNFDA-TA algorithm, it deploys VNFs on the shortest path possible between the source and destination endpoints, further shortening the SFC deployment path length.

Fig. 9

Results of average end-to-end delay of SFC for different methods. (a) German50 network, (b) Cost266 network.

Figure 10 shows the experimental results of the long-term average revenue-cost ratio for different SFC deployment methods. Among them, Fig. 10(a) shows the experimental results in the German50 network, and Fig. 10(b) shows the experimental results in the Cost266 network. It can be observed that the long-term average revenue-cost ratio of ESSFCD-DO reaches around 0.99 in the German50 network and around 1.06 in the Cost266 network. The long-term average revenue-cost ratio of SFCD-TO reaches around 0.72 in the German50 network and around 0.79 in the Cost266 network. The long-term revenue-cost ratio of SFCD-TDM reaches around 0.44 in the German50 network and around 0.5 in the Cost266 network. The long-term average revenue-cost ratio of SFCD-MS and SASFC is approximately the same, reaching around 0.34 in the German50 network and around 0.4 in the Cost266 network. Comparing the experimental results of the five methods, it is evident that the long-term average revenue-cost ratio of the proposed ESSFCD-DO is superior to the other four methods. This is because ESSFCD-DO aggregates VNFs based on the bandwidth variation factor, reducing the bandwidth resources occupied by high-bandwidth virtual links in the physical network; furthermore, ESSFCD-DO further reduces resource costs by shortening the length of SFC deployment paths.

Fig. 10

Results of long-term average revenue-cost ratio for different methods. (a) German50 network, (b) Cost266 network.

Figure 11 shows the experimental results of the average security of different methods, where Fig. 11a presents the results in the German50 network, and Fig. 11b presents the results in the Cost266 network. It can be observed that the average security of SFCD-MS reaches around 0.937 in the German50 network and around 0.936 in the Cost266 network. The average security of ESSFCD-DO is approximately 0.918 in the German50 network and around 0.92 in the Cost266 network. The average security of SASFC is about 0.91 in the German50 network and around 0.9 in the Cost266 network. The average security of SFCD-TO reaches approximately 0.906 in the German50 network and around 0.905 in the Cost266 network. The average security of SFCD-TDM is about 0.9 in the German50 network and approximately 0.898 in the Cost266 network. Comparing the experimental results of the five methods, it can be seen that the average security of ESSFCD-DO is only second to SFCD-MS and better than the other three methods. This is because ESSFCD-DO reduces the number of physical nodes for VNF deployment through VNF aggregation and selects physically nodes with high security using VNFDA-TA to deploy aggregated VNFs, thus outperforming the other three methods in SFC average security. VNFDA-TA aims at comprehensive optimization of security and delay, while SFCD-MS aims at security optimization only, so ESSFCD-DO is inferior to SFCD-MS in SFC average security.

Fig. 11

Results of average security of SFC for different methods. (a) German50 network, (b) Cost266 network.

Conclusion

This paper addresses the SFC deployment issues within the NFV environment for air traffic information networks, proposing a method named efficient and secure service function chain deployment for delay optimization (ESSFCD-DO). This method encompasses a VNF aggregation algorithm for security and resource cost optimization (VNFAA-SRCO) and a VNF deployment algorithm based on topology aware (VNFDA-TA). In VNFAA-SRCO, VNFs are aggregated based on the bandwidth variation factor of each, thereby enhancing SFC security while reducing resource cost on the physical network. In VNFDA-TA, topology awareness is employed to deploy each aggregated VNF onto nodes along the shortest paths meeting resource requirements, thus optimizing SFC delay. Experimental results show that the ESSFCD-DO method proposed in this paper, compared to three other methods in the field, achieves significant optimization in balancing SFC security and service request acceptance rate, as well as in average end-to-end delay and long-term revenue cost ratio. However, due to the ESSFCD-DO method requiring aggregation of VNFs based on bandwidth variation factors before SFC deployment, the aggregated VNFs will be bundled together and deployed on the same physical node, thus reducing the flexibility of VNF deployment.

The roadmap of the new generation of aviation broadband communication technology of Civil Aviation of China clearly establishes the 5G application ecosystem of civil aviation in an all-round way, making the future new generation of aviation broadband communication technology based on 5G become the core technology to promote the digital transformation of civil aviation industry and enable “smart civil aviation”. The roadmap clearly states that NFV is one of the key supporting technologies to realize “smart civil aviation”. The ESSFCD-DO method proposed in this paper can realize the efficient deployment of SFC in the air traffic information network based on NFV network architecture, and reduce the service delay and resource cost. The challenges of deploying SFC in an air traffic information network using the ESSFCD-DO approach may include:

• (1) Security issues: Introducing NFV technology into the air traffic information network may increase the system’s attack surface. Traditional dedicated devices’ functions transition to software running on general-purpose servers, making both the software VNFs and the physical servers vulnerable to cyberattacks. While the ESSFCD-DO method can reduce the number of servers for SFC deployment and thus to some extent lower the risk of SFC failure due to cyberattacks, it may not be sufficient for air traffic control systems with high security requirements. Further research is needed to develop protective mechanisms for SFC.

• (2) Management and Operational Complexity Issues: The air traffic information network is a complex integrated IoT system involving space, air, and ground components like satellites, flights, servers, ATS providers, etc. Integrating NFV technology into this network will increase system complexity, necessitating enhanced management and operational mechanisms to monitor and maintain VNFs to ensure the system runs smoothly.

In the next step, we will conduct research on the protection mechanism and anomaly detection mechanism of SFC. For the research on the SFC protection mechanism, we plan to integrate honeypot technology and VNF shared backup solutions to achieve comprehensive optimization of SFC resource cost and security. For the research on the SFC anomaly detection mechanism, we plan to combine machine learning to achieve fast and accurate detection of security threats faced by SFC. Furthermore, traditional NFV technologies have been extensively researched in terrestrial cloud environments. However, the air traffic information network constitutes a complex integrated network combining space, air, and ground elements. There are still many gaps in the specifications of the space/air networks in the NFV environment. In the next step, we will leverage our expertise in air traffic control to further refine asset inventory and attack modeling research on space/air networks in the NFV environment, continuing to empower the advancement of “smart civil aviation” with cutting-edge networking technologies.