Study on wind load characteristics of gable roof under tornado

Abstract

This research simulates the behavior of a tornado on a double-slope roof using the Ward tornado generator and the $SS{T_{k - \omega }}$ turbulence model. The effects of different ground roughness, slope angle, and wind field position on the tornado load characteristics of gable roofs were studied. The tornado-generating device established the tornado field under various working conditions, and the simulation results were compared with the experimental data to verify the reliability of the simulation results. The wind pressure distribution of gable roofs with four different slope angles was analyzed to find the most unfavorable roof condition of the tornado field. The gable roof’s aerodynamic and wind pressure characteristics at various places in the tornado field were explored by comparing the wind pressure coefficients at five distinct positions on smooth and rough ground. The lift-drag and wind pressure coefficients of five kinds of ground roughness were calculated to determine the influence of different ground roughness on the aerodynamic force and partial pressure distribution of the gable roof. The ground roughness reduces the vortex ratio because the ground roughness reduces the maximum tangential wind speed and the radius of the vortex core. Therefore, the gable roof’s suction increases as the updraft increases.

Introduction

The tornado is an intense vortex of the three-dimensional flow field, which belongs to the extreme airflow and is harmful to the safety of buildings and people’s lives and property. Tornadoes are produced by thunderstorm clouds composed of air, water vapor, and ice crystals at high temperatures and pressure. Tornadoes will arise as thunderstorm clouds intensify, as they are also characterized by powerful airflow and a high concentration of static electricity. The tornado is a three-dimensional funnel-shaped vortex, entirely different from the linear boundary layer wind field. The wind pressure, speed, and vorticity caused by the tornado differ from those caused by the linear wind. Tornado damage to gable roofs is typical in rural areas because low-rise dwellings predominate there, and tornadoes frequently strike isolated rural areas. Therefore, it is necessary to study the double slope roof under the action of a tornado. It references low-rise building structure wind resistance by examining the relationship between tornado wind field and low-rise building structure.

The wind load characteristics of low-rise buildings in tornado wind fields were significantly influenced by wind pressure and average aerodynamic forces. The dynamic pressure characteristics were strongly influenced by the location of the tornado and differ significantly from those under straight-line wind conditions. The pressure properties were largely influenced by the pressure decrease brought on by the vortex. The pressure magnitude in the area of strong flow separation and the overall pressure distribution on the building surface were both impacted by the vortex translation velocity. The pressure caused by a tornado was typically 13% higher than the pressure caused by a straight line of wind^1,2,3. Volume-averaged velocity was proposed by Liu et al.⁴ who discovered that it was the connection between tornadoes and linear wind-induced mean force. Buildings in tornadoes react similarly to those in wind tunnels when the volume-averaged velocity was in the same direction, air pressure caused by the tornado being removed. A tornado-like vortex had low pressure at its center, as demonstrated by Hu et al.⁵. The strongest force generated by the tornado-like vortex was lifting forces, which were experienced by the building when it was at the center of the vortex. The surrounding wake flow pattern and the wind loads operating on the building model were significantly influenced by the building orientation angle connected to the tornado-like vortex.

The tornado-induced wind loads were greatly influenced by tornado factors like swirl ratio, translational velocity, and the distance between the building and the tornado’s mean path. The drag force increased with the speed of translation. The magnitude and direction of the forces rapidly altered as the tornado core approached the building. Greater and distributed local inspiratory forces were exerted on the building envelope. The building’s face perpendicular to the tangential flow experienced lower pressures than the other faces when it was situated close to the vortex core boundary^6,7,8,9. The wind pressure distribution and magnitude around the building model were closely correlated with the distance between the tornado vortex and the building model, according to Cao et al.¹⁰. The local pressure on the building surface, especially on the roof, was significantly related to the roof angle. According to research by Razavi et al.¹¹, a vortex’s peak load factor and peak ground pressure drop increased as the swirl ratio decreased. The peak roof rumble of buildings located on the mean tornado path was 6–19% smaller in the low vortex tornado case.

The effect of changing building opening types on the tornado vortex causes changes in internal pressures and local net roof winds in low-rise buildings. Wang et al.¹² found that when the opening ratio increased to 8%, the average pressure coefficient of the tornado core decreased. The lift on the top plate may change from top to bottom depending on the opening ratio and opening position. The building model with an opening ratio of 0.1% that was placed inside the vortex core had a minimum peak local net roof wind force that was 1.4 times greater than the building model with an opening ratio of 3.9%, according to Rajasekharan et al.¹³. Low-rise building tornado structures were more affected by roof geometry. Flat-roofed structures demonstrated the largest overall uplift, overall shear, local uplift, and bending moment, according to research by Razavi et al.¹⁴. Buildings with flat roofs experience local shear that was equivalent to or greater than their overall shear. Hipped roofs had higher shear resistance, whereas pitched roofs had superior rumbling resistance. Peak loads varied with eave height, roof pitch, aspect ratio, plan area, and other geometries, according to Case et al.¹⁵.

The literature mentioned above examines low-rise building roof geometry, different types of openings, the spacing between buildings, and the typical course of tornadoes. However, there are few studies on the wind pressure coefficient, average aerodynamic force, and unfavorable position of the gable roof with different ground roughness. The existing literature^16,17 shows that the ground roughness has a great influence on the core radius and the maximum tangential wind speed of the tornado field, thus affecting the wind load characteristics of the gable roof in the wind field. This work used numerical CFD simulation to apply the SST$k - \omega$ shear stress transport turbulence model. The influence of ground roughness on wind pressure coefficient, aerodynamic force, wind speed and vorticity of gable roof is explored in detail, and the influence of ground roughness on wind pressure and mechanical properties of gable roof is clarified, in this paper. In addition, the location of the most unfavorable wind pressure and the most unfavorable aerodynamic characteristics of the gable roof and the vorticity development around the gable building are shown, which provides a reference for the anti-tornado of the gable roof structure.

Numerical model and verification

Continuity equation and turbulence model

The following are the governing equations in the Cartesian coordinate system, assuming that the air is an incompressible fluid and that the dynamic viscosity is constant:

$$\frac{{\partial {U_i}}}{{\partial {x_i}}}=0$$

(1)

$$\rho \frac{{\partial {U_i}}}{{\partial t}}+\rho {U_j}\frac{{\partial {U_i}}}{{\partial {x_j}}}= - \frac{{\partial P}}{{\partial {x_i}}}+\frac{\partial }{{\partial {x_j}}}\left. {\left( {\mu \frac{{\partial {U_i}}}{{\partial {x_j}}} - \rho \overline {{{u_i}{u_j}}} } \right.} \right)$$

(2)

The average velocity vector is denoted by U_i, whereas the fluctuating velocity vector is represented by u_i. The coordinate vectors are x_i and x_j, and the Reynolds stress tensor is denoted by u_iu_j. The time is t, the air density is $\rho$ and P is the average pressure.

There is no energy conservation equation in this work since the tornado wind field does not take the heat diffusion issue into account. Turbulent flows are characterized by high complexity, non-stationarity, and irregular rotation. The fluid’s temperature, pressure, and velocity are also constantly changing in space and time. The shear stress transport ${\text{SS}}{{\text{T}}_{k - \omega }}$ turbulence model is used in this study to account for flow separation brought on by inverse pressure gradients¹⁸. The benefits of both the near-wall region and the distant field model calculations are combined in this way. The turbulent kinetic energy and dissipation rate equations for the turbulence model are as follows:

$$\frac{\partial }{{\partial t}}(\rho k)+\frac{\partial }{{\partial {x_i}}}(\rho k{u_i})=\frac{\partial }{{\partial {x_j}}}({\Gamma _k}\frac{{\partial k}}{{\partial {x_j}}})+{G_k} - {Y_k}+{S_k}$$

(3)

$$\frac{\partial }{{\partial t}}\left( {\rho \;\omega } \right)+\frac{\partial }{{\partial {x_i}}}\left( {\rho \;\omega {u_i}} \right)=\frac{\partial }{{\partial {x_j}}}\left( {{\Gamma _\omega }\frac{{\partial \omega }}{{\partial {x_j}}}} \right)+{G_\omega } - {Y_\omega }+{D_\omega }+{S_\omega }$$

(4)

Where k is the turbulent kinetic energy and $\omega$ is the dissipation rate. x_i and y_i are coordinate vectors and time is t. The air density is $\rho$ value is 1.225 kg/m³.Where${G_{\text{k}}}$and${G_\omega }$are the mean velocity gradients generated by k and ω, respectively. Valid diffusion terms for k and ω are ${\Gamma _{\text{k}}}$and ${\Gamma _\omega }$, respectively.${Y_k}$ and${Y_\omega }$ are the diffusion terms of k and ω, respectively. ${D_\omega }$is the orthogonal divergence term. What is more, ${S_{\text{k}}}$ and ${S_\omega }$ are user-defined terms.

Tornado generation device and model building

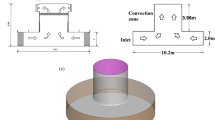
The Texas Tech Ward-type^19,20 tornado generator used in this paper is referred to as VorTECH^21,22,23. The simulator features a 2 m high input zone, an upper 4 m diameter airflow ascent hole, and a bottom convergence zone measuring 10.2 m in diameter. Figure 1 gives the dimensional drawing of the tornado generator. The boundary conditions, solution parameters and tornado numerical model parameters are given in Tables 1 and 2, respectively.

Fig. 1

Dimensional drawing of the tornado generator. (a) VorTECH Model Dimensions, (b) Tornado generating device.

Table 1 Boundary conditions and solving parameter.

Table 2 Parameters for numerical tornado simulator.

The formulas of radial Reynolds number, tangential velocity and radial velocity are as follows:

$${R_{{\text{er}}}}=\frac{Q}{{2\pi V}}$$

(5)

$${V_{\text{r}}}={U_1}{\left( {\frac{Z}{{{Z_1}}}} \right)^{\frac{1}{{\text{n}}}}}$$

(6)

$${V_{\text{t}}}= - {V_{\text{r}}}\tan \theta$$

(7)

$$\tan \theta =\frac{{2S{H_{{0}}}}}{{{R_{{0}}}}}$$

(8)

The apparatus utilized in this study has a 42.92 m³/s volume flow, which is equal to the inlet height’s Q flow²⁴. V is the kinematic viscosity of air, and the value is 1.5 × 10⁻⁵m²/s. The Reynolds number R_er = 4.56 × 10⁵ is obtained by calculation. Davies-Jones et al.²⁵, Jischke et al.²⁶ and Church et al.²⁷ found that the influence of the tornado generating device on the tornado is negligible, when the radial Reynolds number R_er≧10⁵. Where ${V_{\text{r}}}$ and ${V_{\text{t}}}$ are the radial and tangential velocities, respectively, and n is taken as 7^16,28. The radial velocities at the reference height are represented by the letters${Z_1}$and${U_1}$, respectively. Wall, for which K_s = 0, is the Standard wall function formulation. The inflow angle’s magnitude is represented by$\theta$, and the swirl ratio is represented by s^11,29. The tornado generating device’s in-flow height and out-flow region radius, respectively, are ${H_{\text{o}}}$ and ${R_{\text{o}}}$. The value of ${U_1}$was fixed to 0.39 m/s by comparing the velocity profile at the entrance to Tang’s experimental findings³⁰, where the wind field swirl ratio was determined to be s = 0.18. The SIMPLE semi-implicit algorithm is chosen for the calculation, and the accuracy of the second-order windward calculation is higher than that of the first-order. It can reduce the first-order data diffusion bias, so the second-order windward calculation is chosen.

The average structural force caused by the tornado was split into three categories: the impact force, the force caused by the tornado’s direct action on the structure, and the force associated with the pressure drop caused by the tornado³¹. The average lift and drag coefficient can better see the roof force and the equation is given as follows^24,32,33. The dimensionless wind pressure coefficient^4,10,11C_p is introduced in order to more accurately express the wind pressure distribution law of double-sloped roofs, and its expression is as follows:

$${C_{\text{p}}}=\frac{{P - {P_{{\text{ref}}}}}}{{0.5\rho V_{{{\text{tmax}}}}^{{\text{2}}}}}$$

(9)

$${{\text{C}}_{Fp,i}}{\text{=}}\frac{{{{\text{F}}_{p,i}}}}{{{1 \mathord{\left/ {\vphantom {1 {2{\text{\varvec{\uprho}V}}_{{tmax}}^{2}{{\text{A}}_i}}}} \right. \kern-0pt} {2{\text{\varvec{\uprho}V}}_{{tmax}}^{2}{{\text{A}}_i}}}}}$$

(10)

$${{\text{C}}_{Fw,i}}{\text{=}}\frac{{{{\text{F}}_{w,i}}}}{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}{\text{\varvec{\uprho}V}}_{{tmax}}^{2}{{\text{A}}_i}}}$$

(11)

Where P is model surface wind pressure. ${P_{{\text{ref}}}}$ is the reference static pressure, The reference pressure is the static pressure at the inlet boundary of the computational domain. The air density is $\rho$, and the maximum tangential wind speed of the model height of the empty tornado generating device without building model is ${{\text{V}}_{{\text{t}}\hbox{max} }}$^10,37. Table 3 shows the maximum tangential velocity of the wind field under different swirl ratios. The typical lift and drag coefficients are ${{\text{C}}_{Fp,i}}$ and ${{\text{C}}_{Fw,i}}$.${{\text{F}}_{pi}}$ and ${{\text{F}}_{w,i}}$ are the average lift forces. ${{\text{A}}_i}$indicates the projected area of the building model in the corresponding direction.

Table 3 The maximum tangential wind speed of the wind field under different vortex ratios.

Tornado wind field analysis and reliability verification

Near-ground buildings are more susceptible to the tangential velocity of a tornado. The Rankine model³⁴ and experiment data^24,30,35are used in this work to fit the numerical simulation results and verify the correctness of the numerical simulation method. The height of the entry area is z. The radial distributions of tangential velocity, radial velocity, dissipation rate and turbulent intensity are shown in Fig. 2. The tangential velocity away from the core grows quickly with the radius direction, as can be observed from the radial distribution of tangential velocity. The tangential velocity increases to the maximum value at the core radius. The tangential velocity exhibits a ‘nose shape’ as it slowly drops along the radius outside the vortex core radius. The simulation results in this paper are consistent with the experimental and Rankine model curves, which verify the reliability of the simulation results. The vertical profile of radial wind speed obtained from the results of this paper is consistent with the overall trend of the experiment and the Spencer tornado, but there is a slight deviation. The deviation is caused by different near-surface roughness and different pressure drop. The turbulent kinetic energy is greatest in the tornado wind field’s core radius, as can be observed from the radial distribution of the dissipation rate. The turbulent kinetic energy in the core area increases steadily with the increase of the height of the inlet area, which makes the fluid movement in the core area unstable and more prone to vortex. It can be seen from Fig. 2d that the turbulence intensity changes sharply in the core area and decreases slightly in the core. As it moves away from the core and close to the inlet area, the turbulence intensity gradually decreases and then stabilizes.

Fig. 2

Radial distribution of tangential velocity, radial velocity, turbulent kinetic energy and turbulent intensity. (a) Tangential velocity, (b) radial velocity, (c) turbulent kinetic energy, (d) turbulent intensity.

Simulation results and analysis

Grid division and result verification

The wind pressure on the building surface is greatly influenced by the interaction between the wind field and the building structure during a static tornado. The verification of the model in the core position of the wind field is shown in Fig. 3. The low-rise building has a scale ratio of 1:100^7,36. The size of the building model is 0.1 m x 0.05 m x 0.05 m, and the wind pressure coefficient of the building center line AB is taken. Table 4 shows the different meshes and their sizes considered in the mesh convergence study. This study uses an unstructured grid division to better illustrate the low-rise gable roof’s specific features and intricate structure. The five-layer boundary layer spreads outward at a ratio of 1.1, and the near-surface and low-rise building surfaces meshed together. There are 281.87 million grids with a minimum size of 0.01 m and a maximum length of 0.2 m. Figure 4 shows the grid division of the tornado-generating device and low-rise building model. The results of this study are compared with the simulation results of Verma³⁷ and the experimental results of TTU³⁸ when the swirl ratio is 0.83.

The results of Mesh-C with mesh refinement are similar to the experimental data, but Mesh-A and Mesh-B diverge from them. The findings of Mesh-D are nearly identical to those of Mesh-C after the mesh refining, and the difference is negligible. It can be seen that Mesh-C belongs to critical meshing. The difference in simulation results from Mesh-C to Mesh-D is less than 3%, and all of them are within the range of literature results. The following mesh system in this work refers to Mesh-C in the scenario of guaranteeing computation accuracy while taking cost and efficiency into consideration. The general pattern of the study findings presented in this work agrees with the outcomes of the experiments. The negative pressure of the top surface of the building is slightly larger than the experimental value, mainly due to the different roughness of the ground. However, the inaccuracy is within the acceptable range of the literature, according to the simulation results of Verma³⁷. It shows that the results of this study are accurate and reliable.

The interaction between tornado wind fields and low-rise buildings is investigated by moving the gable roof model into different wind field positions and analyzing its wind pressure coefficient, wind speed, and vorticity. The maximum core radius of the tornado wind field with varying ratios of vortex is shown in Table 5. The location and size of the double slope building in the wind field are shown in Fig. 5. The length of the gable roof is 0.105 m, the width is 0.07 m, and the height is 0.07 m. A 1:100 scale model was established without considering the coupling between the building and the wind field^7,36.

Table 4 Different grids considered for mesh convergence study with their mesh sizes.

Table 5 Parameters of tornado wind field.

Fig. 3

The model is located at the core of the wind field to verify. (a) the building model is located in the wind field position and the model expansion diagram, (b) the comparison of the wind pressure coefficient of the model located at the core of the wind field.

Fig. 4

Grid division of tornado generating device and low-rise building model.

Fig. 5

The double-slope building is located in the wind field position and the building model size. (a) The double slope building size, (b) The double slope building monitoring point layout, (c) The location and expansion diagram of the wind field.

Comparison of wind pressure coefficients of double-slope buildings with different slope angles

This study compares a double-sloped roof at the core radius to a core double-sloped roof to examine how the wind field of a tornado affects the wind pressure distribution of a double-sloped roof. The wind pressure distribution on smooth ground roofs is investigated in this study, given the 15°, 30°, 45°, and 60° slope angle wind field situations to identify the most adverse conditions for roofs. The wind field presents the maximum tangential velocity at the core radius, with a maximum core radius of 0.2 m. The wind pressure coefficients of the roof at the core and core radius locations are shown in Fig. 6.

The most significant negative pressure on the roof progressively rises as the slope angle increases when a double-slope building is situated in the center of the wind field. The double-slope building causes more significant damage to the high-altitude airflow of the tornado wind field as the breaking angle and roof height increase. There is obvious airflow separation on the leeward side of the corner of the side wall. There is a significant negative pressure at the airflow separation, where the separation bubble generates discrete vortices and reverse pressure gradients. It is evident that the low-rise double-slope building’s near-ground side wall corner is prone to damage, which the structural design should take into account. The corner airflow separation near the ground is small, and the wind pressure change of the entire double-slope building is minimal when the slope angle is 45°. Thus, the structural design should take precedence.

The side wall a is positive pressure when the double-slope building is situated at the wind field’s maximum core radius. The maximum negative pressure is seen at the intersection of Windward A and the side wall A when the gable roof’s slope angle is 15°. The double-slope building’s ridge experiences the highest negative pressure at a slope angle 30°, and the negative wind pressure coefficient falls to − 2. The roof is easily damaged at the above two maximum negative pressures, caused by the development of a vortex formed by airflow separation. The height of the tornado center and the vortex are proportional to the slope angle of the roof, which also affects the damage degree of the roof to the tornado center and the floating degree of the roof in the wind. Figure 7 shows the wind pressure coefficient around the double-slope low-rise building at the maximum core radius. The far-from-core end of the double-slope building exhibits a significant negative pressure and reverse pressure gradient when the gable roof’s slope angles are 15° and 30°. The near-core end of the double-slope building displays a significant reverse pressure gradient and negative pressure gradient at 45° and 60° slope angles because of the tornado vortex’s influence on the rise in building height and slope angle. This means that because of the weak negative pressure and surrounding vortex of the 15° slope roof, it should be recommended to improve the protection at the near-ground corner and roof ridge in the low double slope at the maximum core radius.

Fig. 6

Wind pressure coefficient of roof. (a,c,e,g) are slope angles 15°, 30°, 45°, 60° at the core position respectively. (b,d,f,h) are 15°, 30°, 45°, 60° slope angles at the maximum core radius, respectively.

Fig. 7

Wind pressure coefficient of the wind field around the pitched roof at the core radius. (a) 15° slope angle, (b) 30° slope angle, (c) 45° slope angle, (d) 60° slope angle.

Wind pressure coefficient of smooth ground in different locations

The locations of the double-sloped roofs in the wind field have varied wind pressure distributions. The double-sloped roof was put at r = 0R_max, r = 0.5R_max, r = 1.0R_max, r = 1.5R_max, and r = 2.0R_max in order to examine the wind pressure distribution of the roof at various points in the tornado wind field. The analysis is carried out for a double-sloped roof with a slope angle of 60° and a swirl ratio of 0.18 smooth ground. Figure 8 shows the wind pressure coefficient of smooth ground at different locations. The wind pressure on the double-sloped roof, which is situated at the center of the wind field, is entirely negative, with a wind pressure coefficient of -2.0. The wind pressure coefficient contour expands outward in concentric circles with expanding radii, and the wind field is totally covered by a single huge vortex. The highest negative pressure coefficient at the roof peaks at -1.9 when r = 0.5R_max. The primary vortex is destroyed and split into two vortices when the minimum negative pressure at the corner of the windward side farthest from the vortex core reaches − 0.55. The main wind vortex is destroyed by the roof when r = 1.0R_max and two tiny vortices are created on the near core and side of the roof. The windward side, distant from the vortex core, has the highest positive pressure, with a value of 0.4. The two vortices on the leeward side intersect at this point when the negative pressure reaches its maximum value of -1.6. The wind pressure coefficient progressively changes from − 1.2 at the leeward side corner at the center of the roof to -0.4 at the center and then gradually rises to 0.4 at the far-center roof corner. The wind pressure is more steady, and the wind field only contains the core vortex when r = 1.5R_max. The subsidiary vortex near the roof also vanishes. Because the roofs are far from the core vortex, the wind field has less of an impact on the rooftops when r = 2.0R_max, which results in all roofs having positive pressure. The magnitude and distribution of the wind pressure surrounding a structure are dependent on the distance from the primary vortex, which is located in the core radius roof and alternates between positive and negative pressure, with a significant floating wind pressure coefficient in the least favorable conditions.

Fig. 8

Wind pressure coefficient of smooth ground at different locations. (a) r = 0R_max, (b) r = 0.5R_max, (c) r = 1.0R_max, (d) r = 1.5R_max, and (e) r = 2.0R_max.

The typical position and turbulence characteristics of double-sloped roofs are observed in order to study the surface wind pressure distribution law more thoroughly. Turbulent energy is the energy generated by the irregular motion of fluid in fluid motion, which plays a vital role in the stability of fluid motion and energy conversion. Turbulent dissipation rate can reflect the flow characteristics and structural changes of the fluid. Therefore, studying turbulent kinetic energy and turbulent dissipation rate of double-sloped roofs is of practical importance. The wind pressure and turbulence characteristics of the roof measurement points located at different locations of the wind field are shown in Fig. 9. The wind pressure of Windward A and Leeward B is similar, and the variance is modest when r = 0R_max, as shown in Fig. 9a. There was a noticeable difference in roof wind pressure at the ridge of the double-sloped roof. The likelihood of the Windward Being harmed increases when r = 1.0R_max, when the positive pressure is on the Windward, And the negative pressure is on the leeward side. Turbulence intensity describes the degree of wind speed changing with time and space, reflects the relative intensity of fluctuating wind speed, and is also the essential characteristic quantity to describe the characteristics of atmospheric turbulence. The leeward side of the double-sloped roof’s turbulent kinetic energy is shown in Fig. 9b to rapidly decrease after a progressive increase as it goes away from the core within the core radius. The roof is outside the core radius, and the turbulent kinetic energy on the leeward side is relatively stable and less variable. The turbulent kinetic energy of the roof at the ridge is the smallest and gradually increases as it approaches the corner of the roof. The fluid energy loss is mainly due to the flow separation occurring at the corner of the airflow roof, resulting in irregular flow such as vortex and eddy. The double-sloped roof’s turbulent dissipation rate varies greatly, as seen in Fig. 9c. The roof’s turbulent dissipation rate is lowest when r = 2.0R_max. The turbulent dissipation rate of the roof is the largest when r = 0.5R_max. The turbulent dissipation rate of the windward side is greater than that of the leeward side, and the turbulent heat transfer on the windward side is increasing, causing more severe energy loss.

Fig. 9

Wind pressure and turbulence characteristics of roof measurement points located at different locations of the wind field. (a) Wind pressure coefficient, (b) turbulent kinetic energy, (c) turbulent dissipation rate.

Figure 10 shows the distribution of the mean aerodynamic coefficient of the roof at different locations. The double-sloped roof moves away from the core, as can be seen in Fig. 10a, and this causes the mean lift of Windward A within the core radius to rise quickly. The mean lift of Windward A increases slowly outside the core radius. The mean lift coefficient of windward B increases slowly within the core radius and then decreases gradually. Outside the core radius, the mean lift decreases rapidly. Figure 10b shows that the drag coefficients of Windward A and Leeward B are lower. This is mainly because the tornado wind field is primarily an updraft in the low swirl ratio condition, and the roofs have a lift. The mean wind pressures of Windward A and Leeward B are similar when the roofs are in the core position and are under more vital suction forces, as seen in Fig. 10c. The roof is within the core radius, and the negative pressure decreases rapidly as it moves away from the core location. The wind pressure increases gradually and slowly when the roof is outside the core radius. The positive and negative wind pressure difference between the Windward A and B roofs reaches its maximum at 1.65 due to the strong influence of tangential wind speed at r = 1.0R_max. The roof is particularly susceptible to damage between positive and negative pressure at this transition point. The tornado has less of an effect on the wind field on Windward A and Leeward B when the values are more similar when r = 2.0R_max and the roofs are under positive pressure.

Fig. 10

Mean aerodynamic coefficients of double-sloped roofs at different locations of wind farms. (a) Mean lift coefficient, (b) mean drag coefficient (c) wind pressure coefficient.

Wind pressure coefficient of rough ground in different locations

The wind pressure coefficient diagrams of double-sloped roofs on rough and open terrain at different locations are given in Fig. 11. Four vortices are created at each of the roof’s four corners when r = 0R_max. Smooth ground double slope roof is covered by a core vortex, and the extreme value of the negative wind pressure coefficient of rough ground is 0.5 smaller than that of smooth ground. The roof spans more vortex nuclei, the radius of the vortex nucleus decreases, and the swirl ratio is mostly reduced by the roughness of the ground. Three vortices are produced at the windward side’s near-center corner and the leeward corner of the double-sloped roof when r = 0.5R_max. The primary barriers to airflow from corner houses include airflow separation and vortex development, as well as the emergence of significant inverse pressure gradients. The rough ground roof on the tornado wind field damage is more than smooth ground two vortexes. The maximum positive pressure, which peaks at -2.5 when r = 1.0R_max, is found on the leeward side close to the middle of the ridge. The negative and positive pressures are in the shape of fish scales decreasing towards the middle, respectively. The windward side has a positive pressure coefficient of 0.5 when r = 1.5R_max, and the leeward side has a negative pressure coefficient of 0.5. The wind pressure coefficient is 1.0, the positive pressure on the windward side rises, and the wind pressure on the leeward side remains constant and unchanging when r  = 2.0R_max.

Fig. 11

Wind pressure coefficient of rough ground at different locations. (a) r = 0R_max, (b) r = 0.5R_max, (c) r = 1.0R_max, (d) r = 1.5R_max, and (e) r = 2.0R_max.

The mean aerodynamic coefficients of roofs at different locations of the wind field are given in Fig. 13. When compared to smooth ground, rugged and open terrain exhibit a consistent general trend in the mean lift coefficient, as seen in Fig. 12a. The mean resistance rises rapidly as the roof moves from the core, as seen in Fig. 12b. The roof is most vulnerable to damage when the maximum mean resistance is attained, or r = 1.0R_max. The roof is outside the core radius, the drag force on the roof decreases gradually, and the Windward A decreases the most. The double-sloped roof’s mean lift and resistance are lower when r = 2.0R_max, and the wind field has less impact on the roof since it is farther from the wind field’s center. According to Fig. 12c, the wind pressure on Windward A and Leeward B is comparable when r = 0R_max because the ground’s roughness causes the vortex nucleus radius to decrease. This also lessens the effect of the swirl ratio by lowering the tornado’s wind field’s swirl ratio. The mean wind pressure dramatically shifts from mean negative pressure to mean zero pressure and then gradually back up to mean positive pressure when r > 1.0R_max. There is an imbalance in the forces operating on the roof due to the pressure differential between Windward A and Leeward B being at its maximum at r = 1.0R_max, which makes the roof structure more susceptible to harm.

Fig. 12

Mean aerodynamic coefficients of the roof at different positions in the wind field. (a) Mean lift coefficient, (b) mean drag coefficient, (c) wind pressure coefficient.

Wind pressure coefficient for different ground roughness

The ground roughness was realized using equal sand roughness to investigate the impact of ground roughness on the double-sloped roof at the maximum core radius point in the wind field. The ground roughness was fitted by setting at the bottom of the tornado simulator, Blocken based on the atmospheric boundary layer (ABL) logarithmic law and the logarithmic law of the wall function first order continuum^39,40. This is achieved with a sand roughness height K_s, and a roughness constant C_s value of K_s = 20y₀ and C_s = 0.5. In the lower grassy plain case, y₀ = 0.03 m, then K_s = 0.6. The length of aerodynamic roughness is y₀. For rough open terrain y₀ = 0.1 m, then K_s = 2. In very rugged terrain, y₀ = 0.5 m, then K_s = 10. For the urban center y₀ = 2.0 m, then K_s = 40. The wind pressure coefficients for different ground roughness at the core radius are shown in Fig. 13. The maximum negative pressure of the double-sloped roof gradually increases as the rough height of the ground increases. The smooth ground roof’s maximum negative wind pressure coefficient is − 1.76. The maximum negative pressure on the lower grass-covered plain roof appears on the back of the windward side with a wind pressure coefficient value of − 1.5. Rough open terrain double-sloped roofs have a peak negative pressure of − 2.5. The maximum negative pressure on the roof of very rugged terrain occurs on the leeward side with a value of − 2.75. The peak negative pressure on the roof of the city center is − 3.25, mainly due to the ground roughness reducing the swirl ratio and decreasing the vortex nucleus radius. The simulation results are the same as the conclusions of Natarajan⁴⁰ and Sabareesh⁴¹ in the study. The disruption of the double-sloped roof to the tornado’s vortex core increases as the vortex nucleus’ radius diminishes, and as a result, the wind pressure coefficient floats higher. The maximal negative pressure on the roof increases with increasing roughness height and decreases in vortex nucleus radius and radius.

The roof’s wind pressure distribution falls from the most significant negative pressure in the middle of the leeward side to the minimum negative pressure in the corner. Then, gradually increase the positive pressure towards the windward away from the central roof angle until it increases to the maximum positive pressure. There is a significant inverse pressure gradient due to the airflow being divided and a vortex being generated due to the roof corner’s obstruction of the wind. The roof of the smooth ground develops two little vortices on the leeward and near-center sides. The vortex range on the near-center side of the roof from the lower grass cover plain to the urban center steadily shrinks until it vanishes as the rough height rises. The maximum positive pressure decreases with increasing roughness height. The maximum positive pressure on the lower grass-covered plains and very rough terrain roofs is located at the corner of the roof, away from the core. Positive and negative pressure differences are more likely to cause damage to the roof on the leeward side of the structure than on the windward side. Sabareesh⁸ obtained the same results in the study of surface roughness.

Fig. 13

Wind pressure coefficients for different ground roughness at the core radius. (a) Smooth floor, (b) Lower grass-covered plains, (c) Rough open terrain, (d) Very rugged terrain, (e) Urban centers.

The wind pressure and turbulence characteristics at measurement places of roofs with varying ground roughness are shown in Fig. 14 in order to examine the impact of ground roughness on the roof surface. The wind pressure on the Leeward B rises, then decreases as the roughness height increases, as seen in Fig. 14a. The wind pressure value line is equally consistent at high roughness heights. The turbulent kinetic energy is lower and nearly zero on the leeward side, as shown in smooth ground in Fig. 14b. The turbulent kinetic energy at the leeward side increases as the roughness height increases. The values of turbulent kinetic energy are similar for higher roughness heights. The turbulent kinetic energy of Windward A fluctuates more with the rise in rough height; the turbulent kinetic energy first decreases at K_s = 0.6 and then increases rapidly. Higher roughness values have similar turbulent kinetic energy values, which hold for each roughness height at the corner of the roof. The airflow in the roof is unstable, creating an unstable vortex and an irregular vortex flow on the windward side, which leads to a waste of fluid energy. The turbulent dissipation rate oscillates in Fig. 14c. The turbulent dissipation rate on the leeward side reaches its maximum with an increase in roughness height K_s = 0.6 and then steadily declines. Violent oscillations occur at the ridge of the double-sloped roof due to the airflow around the diagonal area of the roof, generating vortices and a large consumption of kinetic energy of the fluid. The general trend of the turbulent dissipation rate is growing on the Windward As it gets closer to the diagonal region of the roof.

Fig. 14

Wind pressure and turbulence characteristics of roof measurement points with different ground roughness. (a) Wind pressure coefficient, (b) turbulent kinetic energy, (c) turbulent dissipation rate.

The mean aerodynamic coefficients for roofs with different ground roughness are shown in Fig. 15. The mean lift on the Leeward B initially declines and then gradually increases, as shown in Fig. 15a. At the same time, the lift on the Windward A progressively increases as the ground roughness increases. The lifting force of double-sloped roofs is gradually smooth and does not vary significantly at higher rough heights. The lift force floats more when the height is low and rough. The mean resistance of Windward A proliferates at low rough heights, as can be observed in Fig. 15b. The mean drag and lift vary gradually at greater roughness heights, but only slightly, while the mean drag of windward B progressively increases. The main reason for this is that the roughness of the ground reduces the vortex nucleus radius, which reduces the swirl ratio, increases the updraft, and lifts the roof. The Windward A roof’s mean negative pressure steadily rises, as shown in Fig. 15c; as the roughness of the ground decreases, the vortex nucleus radius, the tangential wind speed drops, and the negative pressure region expands. The average resistance of Windward A proliferates at low rough heights, but the average resistance of Windward B increases gradually. The average resistance and lift force vary gradually and smoothly at increasing rough heights. The mean wind pressure of windward B is negative, with rough heights of 0 to 0.6. Once the rough height reaches 40, the mean wind pressure stabilizes and remains unchanged. The mean wind pressure initially declines, then steadily increases at rough heights of 0.6 to 2. The roughness height rises to a more significant value, and the ground roughness has less effect on the wind field and double-sloped roof¹⁶. The mean wind pressure on the windward side drops off at lower roughness heights, while the mean wind pressure on the leeward side first rises and then falls.

Fig. 15

Mean aerodynamic coefficients of roofs with different ground roughness. (a) Mean lift coefficient, (b) mean drag coefficient, (c) wind pressure coefficient.

Cloud map and traces around the building

This article chooses the swirl ratio of 0.2, horizontal height 0.02 m, and smooth ground to explore the flow field and wind velocity over the double-sloped roof. Figures 16 and 17 show the velocity clouds and traces of the roof located in the core and core radius. The roof is situated in the core, and the airflow is bypassed and separated due to the blockage of wind load by the angles around the roof. A vortex is formed on the leeward side, showing an inverse wind pressure gradient. There are more vortices as the slope angle increases. The number of vortexes increased from one at a slope angle 30° to three at 45°. From 45° to 60°, the number of vortices remains the same, but the range of vortices becomes larger.

When the slope angle of a double-sloped roof at its largest core radius is 30°, the roof angles block airflow, which leads to flow separation. Two small vortices are formed on the side located near the core, and a sizeable inverse pressure gradient appears in the wake below. Flow separation and vortices can be seen on the leeward and near-core sides of the roof when the slope angle is 45°. Columnar vortices arise along the flow separation line when the entering flow is perpendicular to the flow separation line. Only the near-core side of the roof develops a vortex when the slope angle is 60°. The vortex range and quantity increase as the angle of the roof slope increases. The most significant core radius of the roof is directly exposed to the wind load effect, where the surrounding wind speed is more substantial and violent, and the number of vortices is more critical, making the roof more susceptible to damage.

Fig. 16

The roof is located in the core velocity cloud map and trace map. (a) 30° slope angle, (b) 45° slope angle, (c) 60° slope angle.

Fig. 17

The roof is located in the core radius velocity cloud map and trace map. (a) 30° slope angle, (b) 45° slope angle, (c) 60° slope angle.

Vortex volume

This technique, which employs the new omega vortex identification method, is threshold-independent and can detect both powerful and weak vortices⁴². The ratio of the vorticity in the vortex core to the total vorticity is represented by Ω, which is based on splitting the vorticity into the vortex component and the non-vortex part. The location where the threshold Ω is more significant than 0.52 is the vortex. A rough open terrain (K_s=2.0) was selected to analyze the vorticity of a low-rise building at different locations in the tornado wind field. The vorticity of wind fields on smooth and rough ground is given in Figs. 18 and 19.

Vorticity entirely encloses the low-rise building when r = 0R_max and the ground is smooth. The side of the gable roof of the low-rise building is exposed because the radius of the vortex core decreases on uneven ground. The vortex nucleus radius of smooth ground is more significant than that of rough ground, mainly because the ground roughness reduces the wind field swirl ratio and, thus, the vortex nucleus radius. The tornado vortex core sustains more damage the farther the roof is from the tornado center. The roof’s region on smooth ground away from the core starts to be exposed at r = 0.5R_max when the vortex on the roof begins to detach from the central vortex. Roof vortices on rough ground are exposed in more parts, and vortices on the sides start to exist independently of the central vortex. The core vortex and the vortex of the double-sloped roof are connected by several vortex lines at r = 1.0R_max, and the independent attached roof’s vortex starts to form close to the central vortex. The tiny vortex of the double-sloped roof that connects to the core vortex breaks because of the distance between the low-rise building and the central vortex when r = 1.5R_max. The roof surface of rough open terrain has formed an independent branch vortex, circling upward to connect with the main vortex, and the windward side of the double-sloped roof has a tiny vortex when r = 2.0R_max. There is a large amount of vortex on the leeward and near-core sides, mainly due to the flow separation and vortex of airflow on the back and sides of the roof. Two distinct vortices emerge from the leeward side of the roof while on the smooth surface, rotating upward to join the central vortex, and two other vortices with upward extensions split off. The windward side of the roof only generates vortices in volume at the corner and side intersections with r ≥ 1.0R_max, whereas the leeward side generates a significant amount of vortices. The side of the vortex near the core forms a wave-like raised vortex, which tends to join with the central vortex. The roughness of the ground reduces the radius of the vortex nucleus, and the vortex is a little finer. The smooth ground vortex is thicker and closer to the building, thus forming more branch vortices or vortices that have just broken off.

Fig. 18

Smooth ground wind field vorticity (a) r = 0R_max, (b) r = 0.5R_max, (c) r = 1.0R_max, (d) r = 1.5R_max, and (e) r = 2.0R_max

Fig. 19

Vorticity of rough ground wind field (Ks = 2.0) (a) r = 0R_max, (b) r = 0.5R_max, (c) r = 1.0R_max, (d) r = 1.5R_max, and (e) r = 2.0R_max

Conclusions

The numerical simulations for low-rise buildings located in various wind fields and on multiple landforms are done in this article. The wind pressure coefficients, wind speed trace maps, and vorticity of the windward and leeward sides of the roof were examined based on various slope angles and ground roughness. The vortex development process around the gable roof and the aerodynamic characteristics of the structure are clarified, and the analysis of the wind speed effect and pressure drop effect under the action of tornado is realized, which provides a reference for the scale simulation of structural tornado wind load and the analysis of ground roughness, in this paper. The following conclusions were obtained:

(1) There is a clear airflow separation on the leeward side of the side wall corner when the double-slope building is at the center of the wind field. This is where a significant negative pressure is seen since the separating bubble creates a distinct vortex and reverse pressure gradient. This is a damage-prone area for the roof, which the structural designer should take into account. The structural design should take precedence when the slope angle is 45° because this will result in the most minor overall wind pressure change in a double-slope building. The primary vortex is disrupted, and flow separation and a vortex at the ridge occur when the double-slope building reaches the maximum core radius of the wind field. This causes the maximum negative pressure to appear on the leeward side near the ridge. The vortex and its center height grow as the roof slope angle increases, and the roof’s damage to the vortex gets worse.

(2) The turbulent kinetic energy gradually increases as it approaches the corner of the roof. Fluid power is lost due to irregular flow, such as vortex and eddy flow, which is produced as the flow separation occurs at the airflow roof’s corner. The roof resistance coefficient is small, mainly due to the low swirl ratio; the tornado wind field is mostly updraft, and the double-sloped roof shows the lift.

(3) The average lift values are more significant and less variable at higher rough heights. The lift force of the double-sloped roof increases mainly because the ground roughness reduces the vortex nucleus radius, which lowers the swirl ratio, thus increasing the updraft. The lift force of B on the leeward side is far greater than that of A on the roof, which can be damaged more quickly. Airflow in the roof is unstable, causing vortices and irregular vortex flow, which leads to a loss of fluid energy on the windward side’s increased rough height and turbulent kinetic energy.

(4) The corner of the roof around which the wind load is blocked, the airflow around which the movement and separation are caused, and the roof itself. Vortexes are formed on the leeward side, showing an inverse wind pressure gradient, with an increase in slope angle and an increase in the number of vortices. The slope angle increases, the vortex range expands, and the number of vortices reduces at the radius of the roof’s core. The roof is directly impacted by wind loads, and the wind speed around it is more significant and varies more drastically, making the roof more vulnerable to damage.