Introduction

The rapid adoption of renewable power sources (RPSs) reflects a global commitment to curb the detrimental effects of conventional energy production. Among these RPSs, wind energy stands out as a compelling means to combat the far-reaching consequences of global warming. Its effectiveness in reducing greenhouse gas emissions and promoting environmental sustainability has cemented its status as a prominent contender for replacing traditional fossil-based energy resources1. In this context, wind energy generation has emerged as a pivotal solution in the quest for sustainable and eco-friendly power generation. Wind turbines, standing tall on our landscapes with their iconic rotating blades, represent an embodiment of this transition towards cleaner energy sources. These technical wonders combine human ingenuity with the forces of nature to create a complex mechanism that transforms wind energy from kinetic energy into a useful energy source.

The most widely utilized wind generators for power generation are based on the variable-speed DFIG system due to its benefits in terms of cost, efficiency, size, wide operating range (hyper- and hypo-synchronization), and low noise in quadrature operation. As a result, they harvest higher electrical energy than fixed-speed wind generators2.

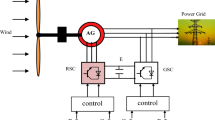
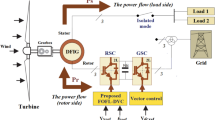
The two primary parts of DFIG are the rotor and the stator, just like conventional electric machines. DFIG generators’ stator windings directly link to the electrical grid. While the grid is coupled to the rotor windings via two bidirectional power converters known as the Rotor-Side Converter (RSC) and the Grid-Side Converter (GSC), respectively. The rotor windings are notable for this connection. DFIGs are preferred in modern WTSs because of their unique architecture, allowing for precise control and optimal electrical power. These power converters are essential for transferring electricity from the grid to the rotor and enabling two-way power flow. Typically, the RSC, as outlined in reference3, controls the integration of both active and reactive power to the electrical network. Simultaneously, the GSC ensures unity power factor (PF) function and regulates the DC-bus voltage. It is worth noting that the RSC is around 30% the size of the DFIG’s nominal power capacity and can independently regulate active and reactive powers4. As a result, we can generate electricity at the voltage and frequency levels stipulated by the utility grid, regardless of changes in the rotational velocity of the DFIG’s rotor5. The effectiveness and dependability of DFIG-based wind turbine generators depend heavily on this degree of control and flexibility. Maximum Power Point Tracking (MPPT), often known as maximizing power extraction from wind energy, is a primary goal in the normal functioning of wind turbine systems6,7,8. This work utilized an MPPT-based on optimal tip speed ratio (OPTSR) method to determine the required active power value.

Many research studies have been conducted in wind generator control to improve the quality of the power generated by DFIG and reduce variations in current and active power9,10,11. However, synthesizing these control strategies from the linear model of wind generators leads to performance degradation, particularly when faced with a real wind profile12. It is due to the strong nonlinearity of the wind generators. Therefore, the influence of disturbances on the system in general is not considered with sufficient accuracy. Consequently, this type of control cannot be utilized to maintain high tracking performance in the existence of external disturbances.

Among these control strategies, Direct Torque Control (DTC), Direct Power Control (DPC), Scalar Control (V/Hz), and Direct Vector Control (DVC) are the most reliable and stable methods. Our focus in this study is on using and assessing the DVC technique, which provides increased control accuracy and dependability for DFIG-based Wind Turbine Systems. Thus, the main purpose of our investigation is to create and implement a new regulator specifically designed for the DVC approach, using flux and voltage vectors within the (d-q) reference frame. One benefit of this control technique is that it may be applied to separately manage the reactive and active power in a DFIG-based WTS. Generally, PI regulators have been extensively utilized in this control system to manage the different parts of rotating currents and, consequently, the active and reactive power. Although PI regulators are widely used, there are still issues in implementing the DVC strategy for DFIG-based WTS. These issues include slow dynamic response and unfavorable ripples in active power, which are related to the limitations of the PI regulator, as mentioned in the reference13. In addition, the coefficients of the PI regulator have a major impact on the dynamic behavior of the DFIG-based WTS managed by the DVC method. So, it is essential to properly adjust the parameters of the PI regulator at various operating points and wind speeds. In other words, if the operating point changes, the PI regulator cannot adjust its fixed parameters, which greatly affects the efficiency and regulation of both active and reactive power14. Many different kinds of regulators have been designed to overcome this dilemma, including hysteresis, sliding mode, predictive, and synergetic regulators15,16,17,18. These regulators produced admirable outcomes, particularly in terms of quick dynamic reactions. However, when they develop more expertise and take some time to adjust, they still require strong talents to change their settings. It should be emphasized that all previous experiments utilized DFIG at modest power levels between 1 and 50 kW.

FO computation utilizes the order of real numbers for differentiation and integration instead of integers, allowing it to precisely define the dynamics of a system19,20,21. Because of its great degree of flexibility and straightforward design, the FO-PID controller has become more popular over the previous ten years for a variety of manufacturing control systems. Compared to a PID regulator, a FO-PID regulator offers more robustness and improved closed-loop performance. Despite being a generalization of conventional PID regulators, FO-PID regulators are frequently utilized in PIλDµ style, where the FO of the integral is indicated by λ, while µ represents the FO of the derivative22,23,24. These extra degrees of freedom offer more flexibility in adjusting the dynamic features of the system22,23,24. The use of the FO-PID controller in various WTSs is demonstrated in25,26,27,28. However, the use of FO-PID controllers in DFIG-based WTS is still not effective enough regardless of the encouraging outcomes attained by these regulators in the research above, due to their complicated nonlinear configurations and FO-PID parameters adjustment29. According to recent research, a more flexible control structure can be achieved by combining the FO-PID control and the fuzzy logic control30,31,32. Consequently, combining fuzzy and FO-PID controllers is advised to enhance the functionality of DFIG-based WTS. As a result, the two controllers combine to form the FOFPID controller. One of the most interesting solutions for managing delayed nonlinear processes and open-loop unsteady systems with time delay is the FOFPID regulator33.

Combining these two types of controllers has produced several advantages, such as the capacity to modify controller gains without being aware of the precise system model, quick response times with enhanced regulator adaptability, and the capacity to handle significant disturbances like parameter changes and RPSs variations34. Additionally, it’s important to remember that the FOFPID regulator has been seen in different settings in recent research. These configurations involve a parallel arrangement of Fuzzy FO-PI and Fuzzy FO-PD controllers, as demonstrated in research35 using the FO fuzzy PI + PD controller, in reference36 using the FO fuzzy P + ID controller, and in reference37 using the FO fuzzy PI + D regulator. Moreover, the reference38 has examined the FO fuzzy PD controller with a focus on digital execution and robustness assessments.

The current study presents the FOFPID control structure. This regulator is suitable for the control problems in which the plant deals with hard external disturbances and model uncertainties. Fractional calculus and type-1 fuzzy sets are the core parts of the designed FOFPID regulator, which provide robust control performance. In addition, type-1 fuzzy sets in the structure of the suggested regulator reduce computational efforts and the number of tuning parameters. Accordingly, the regulator can easily implemented and tuned.

In the field of controller optimization, an enhanced FOFPID controller has been presented using the Ant-Lion Optimizer (ALO), as detailed in article39, specifically for applications requiring Buck converters. Furthermore, the literature has a variety of combination and cascade structures designed for the use of the FOFPID regulator40. These varied setups and optimization strategies demonstrate the FOFPID regulator’s versatility and adaptability in tackling various control difficulties across domains. However, a careful tuning approach is required for many coefficients, especially for FOFPID regulator. Consequently, selecting an optimization method for the FOFPID regulator presents several difficulties. Numerous optimization methods, including neural network optimizer (NNO), colony optimizer (ACO), particle swarm optimizer (PSO), genetic algorithm (GA), Salp swarm algorithm (SSA), and grey wolf optimizer (GWO), have been effectively utilized to enhance the dynamic reaction of industrial systems by selecting the most appropriate coefficients for the FOFPID regulator41,42,43,44,45,46,47,48. Likewise, the coefficients of the FOFPID regulator were adjusted by the Differential Evolutionary Optimizer (DEO) technique48. However, the aforementioned optimization methods have some shortcomings, including long calculation times, poor convergence, poor accuracy, saturation, difficult parameter configuration, and absence of adaptability. Consequently, these characteristics have prompted the implementation of the SSO method to deal with a range of technical applications in different domains, involving a design of FO-Fuzzy controller49, machine vision50, control of micro-grids51, traffic control52, and protection against islanding53. To overcome shortcomings of the aforementioned optimization techniques, we use the SSO developed by Erik Cuevas in our evolutionary optimization method. SSO It is a new generation of population-based meta-heuristic technique that is inspired by the actions of social spiders, where they work together to construct webs and exchange positional information. SSO operates through a community of spiders looking for the best way to solve a certain problem. The study49 has demonstrated that SSO performs noticeably better than current optimization methods. This study aims to completely and directly adjust the DFIG’s reactive and active power by developing, analyzing, and evaluating the effectiveness of a FOFPID controller using an innovative algorithm that uses the SSO method. Hence, to decrease the integral time absolute error of the DFIG current, the SSO technique identifies the gains of the considered FOFPID controller. In this work, the SSO method has been selected because of its efficient exploration strategy, simplicity, flexibility, and adaptability, which makes it an excellent choice for optimizing parameters of complex control such as FOFPID regulators. As far as we know, the FOFPID controller based on an SSO approach has yet to be used to regulate DFIG-based WTS.

Accordingly, the FOFPID controller is a new controller, which is implemented for the first time in the control of DFIG-based WTS. In this work, the FOFPID controller is designed to improve the advantages and effectiveness of traditional direct vector control (DVC) for DFIGs, where an improved SSO optimization algorithm is used in parallel to control the performance of active and reactive power. Thus, in this study, we concentrated on the internal current control loop to ensure the desired performance could be attained.

Research gap

  • There is a wide scope of improvement in the DFIG-based WTS active and reactive power by exploring system behaviour and control techniques via simulation studies.

  • There is a need to develop robust control algorithms by considering the realistic DFIG based WTS model and parametric variations that will help in improving the stability problems.

  • There is a need to expand the use of FOFPID regulators with a greater degree of flexibility in the control of DFIG-based WTS.

  • There is a possibility to exploit the SSO approach to properly adjust the FOFPID regulator gains.

Motivation and contribution

The control of overall DFIG-based WTS for efficient and stable operation is a research area that poses theoretical problems and practical significance, with distinct technological concerns such as interactions, environmental uncertainties, stability, non-linearity, etc. To fulfill the above-mentioned goals, suitable control technique should be developed to deal with these challenges. Amongst the many regulators suggested in the literature, FOFPID is the one that is most frequently utilized. Due to a variety of FOFPID regulator gains, the SSO method is employed to obtain the best results and the most effective solutions. Many researchers have suggested the SSO to optimize the regulator gains, though it takes more time and becomes stagnant while searching for the global optimum. The SSO is utilized in the study since the FOFPID regulator optimization has not been investigated extensively.

The important contributions of this article are as follows:

  • To exploit and establish the appropriateness of FOFPID regulator for active and reactive power regulation in a DFIG-based WTS.

  • To construct and evaluate SSO-aided FOFPID regulator to increase the performance of active and reactive power regulation in DFIG-based WTS.

  • To determine the efficiency of the FOFPID regulator under challenging conditions, including wind speed changes, parameter uncertainties, and active power adjustments.

  • The simulation results generated using FOFPID will be compared with a standard PID regulator employing the SSO method and a Fuzzy regulator to evaluate system performance.

Below is a summary of the significant improvements that this research can provide in the field of wind energy systems and their integration into the power grid:

  • Improving the performance of DFIG-based WECS under variable wind conditions;

  • Enhancing power generation by reducing power ripple rates;

  • Improving the quality of injected currents into the power grid, with a THD target of less than 5% according to IEEE standards;

  • Increasing the durability of wind energy systems.

The remaining part of this article has six parts. Part 2 discusses the DFIG-based WTS, and Part 3 presents its DVC. Part 4 describes the recommended FOFPID regulator. Part 5 explains the SSO method. Part 6 comprehensively describes the simulation experiments and their results, incorporating a comparison with a PI controller and a Fuzzy controller. Part 7 concludes with some observations and comments on the dynamic behavior of the considered FOFPID controller.

Structure of DFIG-based WTS

Figure 1 illustrates the detailed configuration that was used for this work. In this structure, the stator windings of DFIG are directly coupled to the three-phase electric grid, whereas the rotor windings are coupled to the main mover by an AC-DC-AC converter6. The AC-DC-AC converter provides three-phase rotor excitation power with adjustable frequency, phase, and magnitude and guarantees that the slip power can flow on both sides.

Fig. 1
figure 1

Structure of DFIG-based WTS.

Full size image

DVC technique of the DFIG-based WTS

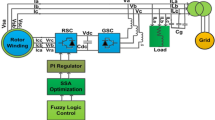
The DVC technique of the DFIG-based WTS is implemented in a dq rotating reference frame aligned with d axis of stator voltage vector Vs of the DFIG system54,55. Using the Park transformation, all three-phase values were transferred to two constant values in the dq reference frame. To calculate the transformation angle for Park transformation from abc to dq orientation, the rotor position estimation algorithm is utilized. The rotor current for each rotor current element (d-q) can be controlled using a PI controller. Idr*and Iqr* values can be calculated through the external loops. The inner loop is responsible for regulating rotor currents, while the external loop is solely responsible for handling the stator’s reactive and active power. In summary, the entire control arrangement of a DFIG-based WTS is displayed in Fig. 2. The MPPT controller, the Idr and Iqr control, and Ps and Qs regulators are all included in this integrated control system.

Fig. 2
figure 2

Architecture of the WTS control strategy based on DFIG.

Full size image

Suggested FOFPID controller

This part describes the application of a FOFPID regulator to efficiently and robustly regulate a DFIG-based WTS instead of a PI controller, which is applied to the internal current loop.

Fractional calculus (FCs)

FCs is a generalized form of differentiation and integration that uses non-integer orders for the main function aDbµ. Where a and b represent the highest and lowest bounds of the function aDbµ, and µ denotes the integration or differentiationorder22,23. aDbµ refers to the fractional derivative as well as the fractional integral simultaneously. It has the following definition:

$$_{a}D_{b}^{a}\left\{ {\begin{array}{*{20}{c}} {} \\ {\begin{array}{*{20}{c}} {\frac{{{d^\mu }}}{{d{t^\mu }}}~~~~~~~~~~~~~~~R\left( \mu \right)>0} \\ {1~~~~~~~~~~~~~~~~~~~R\left( \mu \right)=0} \\ {\mathop \smallint \limits_{a}^{b} {{\left( {dt} \right)}^\mu }~~~~~~R\left( \mu \right)<0} \end{array}} \end{array}} \right.$$
(1)

Using the differ-integral of Riemann Liouville, the designed control technique is implemented as defined in the Eq. 2:

$$_{a}D_{b}^{a}f\left( t \right)=\frac{1}{{\Gamma \left( {m - a} \right)}}\frac{{{d^m}}}{{d{t^m}}}\mathop \smallint \limits_{a}^{b} \frac{{f\left( \tau \right)}}{{{{\left( {t - \tau } \right)}^{a+1 - m}}}}d\tau$$
(2)

Where f(t) denotes the utilized function, m is the integer part of a, and Γ is Euler’s gamma function of x.

$$\Gamma \left( x \right)=\mathop \smallint \limits_{0}^{\infty } {e^{ - t}}{t^{x - 1}}dt$$
(3)

This study uses the CRONE support package to implement the fractional operators42.The range of frequencies was taken [0.01, 100] rad/s, which was chosen by trial and error. The FO factors in the considered regulator are calculated by applying a modified 5-order Oustaloup filter to find a balance between accuracy and simplicity in the calculations.

FO-based PID (FOPID) controller

A more general variant of the integer-order PID regulator is the FOPID regulator. This indicates that it looks like a PID regulator when projected from point to plane. Also, because of its regulator coefficients and integral and derivative orders, it can offer an additional degree of flexibility42. The transfer function Gc(s) for this kind of controller can be defined mathematically using the following formula:

$${G_c}\left( s \right)=\frac{{U\left( s \right)}}{{E\left( s \right)}}={K_p}+{K_i}{s^{ - \lambda }}+{K_d}{s^\mu }$$
(4)

Where Kp, Kd, and Ki are the derivative, proportional, and integral factors of the FOPID regulator, λ denotes the fractional factor of integral parts, and µ indicates the fractional factor of derivative parts. The graphical representation provided in Fig. 3 illustrates the orders of the PID and FOPID controllers. The vertical axis describes the differentiator’s order (µ). Variations in the horizontal axis might occur in the integrator’s order (λ).

Fig. 3
figure 3

Description of FOPID controller.

Full size image

Construction of the FOFPID regulator

Fuzzy control system (FCS) uses realistic nonlinear concepts to produce human-like thinking and manipulate the process effectively rather than relying on complex mathematical design. Recent studies have demonstrated that adding an FCS to the FO calculus for integration and differentiation enhances the degrees of freedom and gives some extra adaptability to the design of classical FCS-based PID regulators33. The FOFPID regulator has seen significant structural growth in the last several years. In the suggested structure, the derivative order rate of the error at the input to the FCS is replaced by its FO part (Dµ) with an integrator and a summation unit at the FCS output to deliver the whole controller output, as it is displayed in Fig. 4. According to prior uses, this specific controller structure has proven to be the most effective among the FO-Fuzzy architectures33.

Fig. 4
figure 4

Architecture of the recommended FOFPID regulator.

Full size image

The DFIG transfer function can be expressed by Eq. 5:

$$G\left( s \right)=\frac{1}{{\sigma {L_s}s+{R_r}}}$$
(5)

The output of the proposed FOFPID controller in the temporal domain is as follows:

\(\:{U}_{FO\:Fuzzy\:PD+I}\left(t\right)={U}_{FO\:Fuzzy\:PD}\left(t\right).{K}_{u}+{U}_{FOI}\left(t\right).{K}_{u}={K}_{u}.\left[f\left({K}_{p}e,{K}_{d}{D}^{\mu\:}e\:\right)+{K}_{i}Ie\right]\)(6)(21)

In the novel form of FOFPID controller, the order (µ) along with the gains (Ki, Kp, Kd, Ku) are the optimization parameters that require adjustment via the SSO method. The suggested FOFPID controller (see Table 1) utilizes a two-dimensional linear rule base that considers the fuzzy output, the fractional rate of error, and the error. This rule base employs Mamdani-type inferencing and works in conjunction with traditional triangle membership functions MFs (see Fig. 5).Triangular shaped MFs are used in FCS because of their simplicity, inexpensiveness, fewer memory requirement and improved output56.

Table 1 Rule bases of the FOFPID controller to be adjusted.
Full size table
Fig. 5
figure 5

MFs for inputs/output of FCS.

Full size image

The formulation of the fuzzy IF-THEN rules for the FOFPID regulator is adapted from reference57:

\({{\varvec{R}}^{({\varvec{l}})}}:\,\text{I}\text{F}\,E \text{i}\text{s}\,A_{1}^{l}\,\text{a}\text{n}\text{d}\,DE\,\text{i}\text{s}\,A_{2}^{l}\,\text{T}\text{H}\text{E}\text{N}\,y\,\text{i}\text{s}\,B_{1}^{l}\)

Where Ali(i = 1, 2) and Bl1 indicate the linguistic variables of the inputs and output of the FCS, the variable l = 1,…, m denotes the number of the fuzzy IF-THEN rules. For each input and output variable, seven triangular MFs are utilized, resulting in (7 × 7) rules as presented in Table 1. Negative Large, Negative Medium, Negative Small, Zero, Positive Small, Positive Medium, and Positive Large are represented by the linguistic variables NL, NM, NS, ZR, PS, PM, and PL in Fig. 5. As a result of the facts in Table 1, the primary rule may be represented by:

IFDE is equal to ZR and E is equal to NL, THENν must be NL.

According to this rule, we can conclude that the control strategy as if the error derivate is “Zero” and the error is “Negative Large”. Hence, the output will also be “Negative Large.” The Fuzzy output’s crisp value is calculated by defuzzification’s center of gravity (CG) procedure. To improve the complete closed-loop performance of a DFIG-based WTS. This work focuses on adjusting the scaling factors (SFs) of the FCS and other design parameters of FOFPID regulator, while maintaining the rule base and the form of MFs unmodified58.

SSO algorithm for FOFPID regulator

The SSO is a metaheuristic technique that simulates the reciprocal activities of social spiders suggested by Cuevas et al.49. He considered the characteristics of social spider groups and their collaborative activities when creating this interesting technique. Due to its inherent adaptive exploitation and exploration capabilities, SSO outperforms metaheuristic methods like Bat, GA, PSO, and BFOA. Nowadays, the SSO algorithm is being utilized to resolve several complicated optimization problems49,50,51,52,53. An SSO mainly consists of two essential search agents: social spiders and communal web. Males and females make up the social spider community. In SSO algorithm, individual solutions represent the search space, each corresponding to a spider’s position inside a community web. Each spider is assigned a weight based on the solution’s fitness value, which the social spider represents.

First, a population is created as part of the SSO method, abbreviated as S, with N spider locations (solutions). The community has two types of individuals: males mi and females fi. The total number of female spiders Nf is randomly chosen around 85% of the whole population N. Hence, to find Nf and Nm, we use Eqs. 7 and 8:

$${N_f}=floor\left[ {\left( {0.9 - rand\left( {0.1} \right)0.0.25} \right)N} \right]$$
(7)
$${N_m}=N - {N_f}$$
(8)

Where rand represents a random value between [0, 1] and floor (.) converts a real value to an integer value. Accordingly, N components constitute the complete community S, which is then separated into F and M subgroups. The subgroup F contains a set of female spiders F = {f1; f2; …; fNf}, whereas M assembles the male spiders M= {m1; m2; …; mNm}, where S= {s1; s2; …; sN}, such that S= {s1 = f1; s2 = f2; …; sNf=fNf, sNf+1=m1, sNf +2= m2, …;sN= mNm}.

Utilizing the following formula, the location of the female spider fi is arbitrarily initialized from the lower starting position (pjlow) and the upper starting position (pjhigh):

$$f_{{i,~j}}^{0}=p_{j}^{{low}}+rand\left( {0.1} \right).\left( {p_{j}^{{high}} - p_{j}^{{low}}} \right)$$
(9)

i=1,2,…,Nf; j=1,2,…,n.

Though the location of the male spider miis decided randomly by Eq. 9:

$$m_{{k,~j}}^{0}=p_{j}^{{low}}+rand\left( {0.1} \right).\left( {p_{j}^{{high}} - p_{j}^{{low}}} \right)$$
(10)

K=1,2,…,Nm’j=1,2,…,n.

Where 0 represents the starting population, whereas j, i, and k are the distinct indices. The operation rand (0, 1) provided a random value between 0 and 1. fi,jis the jth variable of the ith female spider location. The weight of each spider in the suggested SSO method denotes the quality of the solution corresponding to the spider (i) in the community (S). It is possible to express each spider’s weight using the following equation:

$${\omega _i}=\frac{{J\left( {{s_i}} \right) - wors{t_s}}}{{bes{t_s} - wors{t_s}}}$$
(11)

Where J(si) is the cost function derived from the evaluation of the spider position si, Eq. (11) is utilized to calculate the worst and best quantities by taking into consideration the following restricted optimization problem:

\($$ best_{s} = \mathop {\min }\limits_{{k\hat{I}\left\{ {1,...,N} \right\}}} J(s_{k} ){\mkern 1mu} {\mkern 1mu} and{\mkern 1mu} worst_{s} = \mathop {\max }\limits_{{k\hat{I}\left\{ {1,...,N} \right\}}} J(s_{k} )\)(12)

Through the shared network, colony members may communicate with one another. Small vibrations are used to carry the information, which is required for the population of spiders to be organized collectively. The weight and distance of the spider that created the vibrations impact them. Equation 12 gives the vibrations felt by the particular member i from member j:

$${V_i}{b_{i,j}}={\omega _j}.{e^{ - d_{{i,j}}^{2}}}$$
(13)

Where the di, j is the Euclidean distance between the member i and j, such that \({d_{i,j}}=\left\| {{s_i} - {s_j}} \right\|\).

In the SSO method, there are different kinds of vibrations (see Fig. 6):

1. VibrationsVibci; Given that the member c(sc) is the closest member to individual i(si) and hence has the largest weight, the information (vibration) communicated between them can be described as follows:

$${V_i}b{c_i}={\omega _c}.{e^{ - d_{{i,c}}^{2}}}{V_i}b{c_i}={\omega _c}.{e^{ - d_{{i,c}}^{2}}}$$
(14)

2. VibrationsVibbi; The information transferred between the best member b(sb) and the individual i(si) of the whole group S can be represented by:

$${V_i}b{b_i}={\omega _b}.{e^{ - d_{{i,b}}^{2}}}$$
(15)

3. VibrationsVibfi; The individual i(si) and the closest female f(sf) have an information exchange that can be expressed as follows:

$${V_i}b{f_i}={\omega _f}.{e^{ - d_{{i,f}}^{2}}}$$
(16)
Fig. 6
figure 6

Vibration models in the SSO approach: (a) Vibci, (b) Vibbi and (c) Vibfi.

Full size image

The female members change their places in the following manner at every cycle k:

$$f_{i}^{{k+1}}=\left\{ {\begin{array}{*{20}{c}} {f_{i}^{k}+\rho .{V_i}b{c_i}\left( {{s_c} - f_{i}^{k}} \right)+\tau .{V_i}b{b_i}\left( {{s_b} - f_{i}^{k}} \right)+\delta \left( {rand - 0.5} \right)~with~probability~PF~~~~~~~~} \\ {f_{i}^{k} - \rho .{V_i}b{c_i}\left( {{s_c} - f_{i}^{k}} \right) - \tau .{V_i}b{b_i}\left( {{s_b} - f_{i}^{k}} \right)+\delta \left( {rand - 0.5} \right)~with~probability~1 - PF} \end{array}} \right.$$
(17)

Where ρ, τ, δ and rand are random numbers in [0, 1], while PF denotes the probability threshold. The male spiders are classified as either dominant (D) or non-dominant (ND) male members and arranged in decreasing order according to their weight value; the members whose weight \(\:{\omega\:}_{{N}_{f+m}}\)is located in the middle is considered the median male members. The male members swap their position at every cycle k in the following manner:

$$m_{i}^{{k+1}}=\left\{ {\begin{array}{*{20}{c}} {m_{i}^{k}+\rho .{V_i}b{f_i}\left( {{s_f} - m_{i}^{k}} \right)\delta \left( {rand - 0.5} \right);~if~{\omega _{{N_{f+i}}}}>{\omega _{{N_{f+m}}}}} \\ {m_{i}^{k}+\rho \left( {\frac{{\mathop \sum \nolimits_{{h=1}}^{{{N_m}}} m_{h}^{k}{\omega _{{N_{f+i}}}}}}{{\mathop \sum \nolimits_{{h=1}}^{{{N_m}}} {\omega _{{N_{f+h}}}}}} - m_{i}^{k}} \right);~~~if~{\omega _{{N_{f+i}}}} \leqslant ~{\omega _{{N_{f+m~~~~~~~~~~~~~~~~~~~}}}}} \end{array}} \right.$$
(18)

Where the member denotes the female member who is closest to the male member i.

Upon updating both male and female members, the final operator describes the coupling process, in which only dominant male members will cooperate with female members inside the mating radius, which is calculated as follows:

$$r=\frac{{\mathop \sum \nolimits_{{j=1}}^{n} \left( {p_{j}^{{high}} - p_{j}^{{low}}} \right)}}{{2.n}}$$
(19)

Where n denotes the problem’s dimension, Pjhigh and Pjlow are the higher and lower limits for the selected dimension. Obviously, the spider with the most weight has the highest impact on the new product. The influence probability Psi of each individual is calculated using the SSO technique in the following manner:

$$P{s_i}=\frac{{{\omega _i}}}{{\sum\nolimits_{{j \in {T^k}}} {{\omega _j}} }}$$
(20)

Where Tk represents the set of individuals involved in the mating process and j∈Tk.

The SSO algorithm

To implement the SSO technique, the following steps are required, which summarize the preceding equations of the SSO approach:

Step (1) The SSO process starts by setting the total number of solutions N in the community size S, the limit of PF and the total number of iterations itr.

Step (2) Nf and Nm is determined by Eq. 6 Eq. 7.

Step (3) Commence the population setup for both males and females within the solutions, and determine the mating radius.

Step (4) The subsequent procedure continues until the termination requirements are met.

Step (5) Each solution in the population is assessed by computing the weight of each spider in S as in Eq. (10).

Step (6) Spiders should be moved by the female cooperative operator in Eq. 16.

Step (7) The male cooperative operator in Eq. 17 should be used to move the male spiders.

Step (8) Execute the mating procedure as specified in Eq. 18.

Step (8.1) Increase the number of iterations.

Step (8.2) Generate the optimal solution.

Step.9. Finish the procedure if the stop requirement is met; otherwise, return to Step 3.

Figure 7 displays the schematic diagram of the SSO algorithm.

Fig. 7
figure 7

Schematic diagram of the suggested SSO method.

Full size image

Cost function for tuning the optimal regulator parameters

In order to determine the optimal five parameters for the FOFPID regulator by SSO and minimize the given cost function (J) as described in Eq. 20, a constrained optimization problem is formulated. The present work uses ITAE as a cost function to analyze the effectiveness of the FOFPID current controller, which can be described as follows:

$$ITEA=\mathop \smallint \limits_{0}^{{{T_{sim}}}} t\left| {\Delta I\left( t \right)} \right|dt$$
(21)

Where:

\(\Delta I\left( t \right)={I^*} - {I_{actual}}\)

The term ΔI(t) in Eq. 20 refers to the deviations in the rotor currents (ΔIdr, ΔIqr),respectively, or the difference between the required and actual rotor currents. Tsim represents the duration of the simulation. As a result, the problem is stated as:

$$~J\left( {\mu ,~{K_p},~{K_d},~{K_i},~{K_u}} \right)=ITEA$$
(22)

The limits imposed on the regulator’s parameters are known as constraints. Thus, the minimization of the cost function is subjected to Eq. 22:

$$\left\{ {\begin{array}{*{20}{c}} {{\mu _{min}} \leqslant \mu \leqslant {\mu _{max}}} \\ {{K_{p\_min}} \leqslant {K_p} \leqslant {K_{p\_max}}} \\ {{K_{i\_min}} \leqslant {K_i} \leqslant {K_{i\_max}}} \\ {{K_{d\_min}} \leqslant {K_d} \leqslant {K_{d\_max}}} \\ {{K_{u\_min}} \leqslant {K_u} \leqslant {K_{u\_max}}} \end{array}} \right.$$
(23)

Where max and min represent the maximum and minimum limits of each gain in the recommended FOFPID controller. In the considered design method, Kp_min, Kd_min, Ki_min and Ku_min are set to Zero, whereas, Kp_max, Kd_max, Ki_max and Ku_max are set to 20. The chosen values for µmin and µmax are 0 and 1.

The same regulator is utilized for both active and reactive power regulation to simplify and reduce the suggested FOFPID regulator’s installation cost. The SSO computed the optimized gain values for the recommended FOFPID regulator and the standard PI regulator and presented them in Table 2.

Table 2 Best gain values obtained by a SSO strategy.
Full size table

Figure 8 illustrates the best ITAE objective function for 250 iterations using two optimized regulators. It can be observed that the optimized FOFPID regulator provides the lowest fitness function value of 0.00011.These results clearly show that the optimized FOFPID regulator performs well in both steady state and dynamic modes.

Fig. 8
figure 8

The best ITAE value for 250 iterations.

Full size image

Algorithms such as BAT59, PSO60, ACO43, and BFO61 were also applied to identify the optimal FOFPID regulator gains that provide the minimum ITAE value. The optimal values ​​found by each optimization method are provided in detail in Table 3.

Table 3 Optimum gains of suggested FOFPID regulator.
Full size table

These optimal values ​​are necessary to compare the success of the suggested SSO method with other optimization methods and its effectiveness in determining the gains of the FOFPID regulator. Based on the data presented in Table 3, the smallest ITAE value was obtained using the suggested SSO method and was recorded as 0.00011. Whereas, the PSO method produced the highest ITAE score of 582.48. The rest of the optimization methods gave results that fall between these two extremes.

Figure 9 displays and compares the performance of the suggested SSO method with other optimization techniques. This graphic gives useful insights not only into the effectiveness of the SSO method but also into its benefits and problems. These findings can be used as a key benchmark for increasing the performance of control systems and choosing the correct optimization method.

Fig. 9
figure 9

Convergence profiles of BAT, PSO, ACO, and BFO methods using FOFPID regulator.

Full size image

Simulation evaluations

Following simulation experiments, the aptitude and flexibility of the recommended FOFPID controller were evaluated. This section further compares the FOFPID controller to a standard PI controller. The Matlab/Simulink™ programming environment was used to run numerical simulations of a grid-connected DFIG-based WTS. Three scenarios were used to evaluate controller performance. In the first case, the regulator’s responsiveness to variations in active power was evaluated. The second scenario then tested the regulator’s performance in the context of varying wind speeds. Finally, the third scenario employed sensitivity evaluation to evaluate the effectiveness of the suggested regulator against variation in DFIG parameters. Note that the DFIG studied in this work has a nominal power of 2 MW. Table 4 describes the DFIG settings that were used in the simulation framework.

Table 4 Specifications of the 2 MW DFIG utilized in simulation55.
Full size table

Case 1: change in stator active power and its impact

The first test conducted to compare the recommended FOFPID, PI regulator and fuzzy controller is the reference tracking by applying the stator active power steps to the DFIG system, and at the same time the stator reactive power was fixed at zero value to obtain the unity PF on the network side. The DFIG parameters were adjusted according to their nominal values, and the control strategy was applied with the same optimal values as those determined in the previous section. The values for active power fluctuations given in the DFIG for this case are as follows: -1 MW when t is less than 3 s and − 1.32 MW when t is greater than 3 s and less than 6 s. Figure 10 illustrates the outcomes derived from this particular case. Figure 11 displays that the adjusted FOFPID regulator offers more stable active power compared with the adjusted PI and Fuzzy regulator when the DFIG experiences a variation in the active power. Furthermore, compared to the PI and fuzzy regulator, the DFIG active power stabilizes significantly faster with the FOFPID controller and flawlessly follows its reference value. The dynamic behaviors observed in the DFIG with respect to variations in stator active power are briefly summarized in Table 5. Specific performance measurements, such as rising time (tr), maximum overshoot (Mo), steady-state error (es), and settling time (ts) are used to describe these results. Notably, the outcomes display that the Fuzzy regulator and the adjusted FOFPID controller both attain the lowest values for all the above-mentioned measures. Based on the features of tr, Mo, es and ts, it is obvious that the suggested FOFPID regulator has significantly improved the active power responses of the stator compared to the adjusted PI and Fuzzy regulator.

Fig. 10
figure 10

DFIG active power.

Full size image
Fig. 11
figure 11

Zoom of DFIG active power.

Full size image
Table 5 Responses of the PI, FO FOFPID and fuzzy controllers.
Full size table

Case 2: step variations in wind velocity and its impact

In this particular case, the DFIG performs flawlessly, assuming nominal parameter values without any disturbances or external variations. In this article, the active power reference signal for DFIG is generated using a wind turbine system (WTS) and MPPT system. Figure 12 depicts a fast change in wind speed, rising from 8 m per second to 10 m per second and then decreasing from 10 m per second to 8 m per second. This wind velocity profile clearly distinguishes the sub-synchronous and upper-synchronous operational modes. In Fig. 13 (a–b), we present the responses of key variables, including rotor speed (in radians per second), stator active power (in watts), rotor currents (in amperes), and stator currents (in amperes), as dictated by the utilization of the adjusted FOFPID controller, the adjusted PI controller, and the Fuzzy regulator, respectively. The ideal rotor speeds for achieving the appropriate DFIG active power levels are shown in Fig. 13 (a–b) as 1250 and 1550 revolutions per minute (RPM), respectively. When applying the adjusted FOFPID controller, the reported findings for the DFIG’s active power show a remarkable level of precision in monitoring their reference signals, closely followed by the Fuzzy regulator. Moreover, in comparison to the outcomes of the adjusted PI and fuzzy regulator, the adjusted FOFPID controller effectively lowers ripple content. For the three regulators, the rotor currents (iqr) completely follow their references values (Fig. 13.c). But the improved FOFPID regulator presents superior characteristics in terms of tr, ts and es compared to the adjusted PI and Fuzzy regulators. Figure 13.d illustrates the stator current for the DFIG related to the wind speed.

Likewise, Fig. 14 exhibits the THD evaluations of stator current for the three regulation situations, the recommended regulator (Fig. 14.a), conventional PI regulator (Fig. 14.b) and Fuzzy regulator (Fig. 14.c). These findings show that the THD analysis of stator current for the adjusted FOFPID controller is 0.59%, compared to 0.83% for the Fuzzy controller. Therefore, the adjusted FOFPID controller can offer a higher current quality than Fuzzy and conventional PI methods. This adjusted FOFPID controller reduced the THD of stator current by approximately 28.96%.

Fig. 12
figure 12

Wind speed.

Full size image
Fig. 13
figure 13

Simulation outcomes: (a) rotor velocity (rad/s), (b) active power (W), (c) rotor currents Iqr(A), (d) stator current (A).

Full size image
Fig. 14
figure 14figure 14

THD evaluations: (a) recommended FOFPID controller, (b) the adjusted PI controller, (c) the Fuzzy controller.

Full size image

Case 3: effect of random wind velocity

The system under evaluation is put through a scenario with unpredictable wind velocity circumstances in Scenario 3. Figure 15 illustrates the wind velocity profile used in these simulation experiments. The performance characteristics of the mechanical rotor speed, stator active power, active rotor current (Iqr), and three-phase rotor currents are each illustrated in Fig. 16. These performance findings are assessed for three separate situations, each utilizing a different control strategy: the adjusted PI, the adjusted FOFPID, and the Fuzzy controller. We examine the rotational speed tracking performance in Fig. 16.a. Notably, the optimized PI regulator displays a slower reaction and a rather significant tracking inaccuracy. While tracking the appropriate rotational velocity, the adjusted FOFPID regulator exhibits practically flawless behaviour.

Figure 16.b depicts the stator active power response. A comparison of the adjusted FOFPID regulator, the adjusted PI regulator, and the Fuzzy regulator demonstrates that the adjusted FOFPID controller achieves the stator active power tracking objectives satisfactorily. Figure 16.c illustrates an investigation into active rotor current regulation. The findings unequivocally demonstrate that the responses of the Fuzzy and optimized PI regulators oscillate, departing from the required active rotor current. Thus, it can be concluded that the proposed FOFPID controller exhibits excellent performance and resilience in the face of unpredictable wind velocity situations.

Fig. 15
figure 15

Wind speed.

Full size image
Fig. 16
figure 16

Simulation outcomes: (a) rotor velocity (rad/s), (b) active power (W), (c) active currents Iqr(A), (d) rotor current (A).

Full size image

Case 4: impact of perturbations in parameters

For case 4, we modify the DFIG parameters to demonstrate the effectiveness of the adjusted FOFPID controller and to compare its behaviour with the adjusted PI controller and Fuzzy regulator. Between the interval 3s and 6s, the resistance of the stator of the DFIG has grown by 150% of its initial value, while the DFIG runs at a constant wind speed of 8 m/s. As shown in Fig. 17, the adjusted FOFPID controller significantly reduced the active power oscillations of the stator, demonstrating that the suggested regulator is more flexible than the adjusted PI and Fuzzy regulators. Compared with the adjusted PI controller and the fuzzy controller, the adjusted FOFPID controller successfully minimizes the active power oscillations in respectable proportions, with rates of 99.80%, 92.15%, and 95.68% for each controller. Figure 18 depicts the THD of stator current utilizing the adjusted FOFPID (Fig. 18.a), the adjusted PI controller (Fig. 18.b), and the Fuzzy controller (Fig. 18.c) after changing the DFIG parameters. Considering these outcomes, the adjusted FOFPID regulator provided a THD of 1.23%, lower than 1.38% of the Fuzzy regulator. In comparison, the adjusted PI regulator yielded a THD of 4.72%. Obviously, the adjusted FOFPID controller guarantees current THD reduction, with an enhanced proportion of 26.05%.

Fig. 17
figure 17

Stator active power (W).

Full size image
Fig. 18
figure 18

Simulation outcomes: (a) the recommended FOFPID controller, (b) the adjusted PI controller, (C) Fuzzy controller.

Full size image

In addition to the THD, it might be more interesting to compute the Weighted Total Harmonic Distortion (WTHD). This would offer a more realistic evaluation of the harmonic distortion impacts. The average WTHD comparison results are presented in Fig. 19. The modulation index range has been selected between 0.55 and 0.85 for a better examination. It can be seen from Fig. 19 that the suggested FOFPID regulator delivers smaller WTHD than the other two regulators. For example, at the modulation index 0.7, the WTHD is 0.052%, 0.044% and 0.042% for optimal PI regulator, Fuzzy regulator and suggested FOFPID regulator, respectively.

Fig. 19
figure 19

Average WTHD comparison results of three regulators.

Full size image

Comparison with similar control schemes utilized in DFIG-based WTS

A comparison can be made between the suggested FOFPID regulator and other well-known control strategies described in the literature, including Synergetic Control (SC62), Hybrid SMC-SC63 algorithm, Model Predictive Control (MPC64) and Multilayer Perceptron (MLP65) control in terms of implementation simplicity, robustness, durability, reliance on mathematical models, speed of response, computational burden, and power quality. Table 6 summarizes a comparative study between the suggested FOFPID regulator and the various strategies currently known to control DFIG-based WTS. It is worth mentioning that the proposed FOFPID regulator is among the best and most robust, with very fast dynamic response when compared to many other regulators such as SC, hybrid SMC-SC, MPC, and MLP. However, there are some shortcomings regarding the proposed FOFPID regulator, such as practical implementation and computational complexity. Hence, we can conclude that the suggested FOFPID regulator has the characteristics that make it one of the best suitable solutions to regulate DFIG-based WTS in the future.

Table 6 A comparative study between the suggested FOFPID regulator and various published regulators.
Full size table

Conclusion

In order to improve the current responsiveness of linked DFIG inside WTS, this study provided a novel method for designing and fine-tuning a fuzzy PDI controller. The SSO approach was utilized to calculate the best controller coefficients of the recommended FOFPID regulator. In addition, under many uncertainties, such as a 150% change in stator resistor, stator active power disturbances, and wind speed variations, the resilience of the adjusted FOFPID controller was assessed. Across all evaluated scenarios, the simulation outcomes consistently display that the adjusted FOFPID controller beats both the adjusted PI controller and the Fuzzy regulator. In particular, it produces better stator current responses and efficiently reduces power variances. The THD in the stator current is also decreased due to the use of the adjusted FOFPID regulator, enhancing the overall quality of the electricity network. Notably, the recommended FOFPID regulator shows potential for use in WTSs, providing an essential direction for future study. Transition from simulation to real implementation by performing trials in a laboratory or on a small-scale DFIG-based wind turbine system. It will assist in validating the FOFPID regulator’s real-world applicability and performance. Work with wind energy sector partners to conduct field tests on larger-scale wind turbine systems. Field-testing enables the regulator’s performance to be assessed under a variety of operating settings and assists in identifying any difficulties unique to realistic deployments. Investigating cutting-edge optimization strategies to dynamically adjust the regulator’s gains in response to shifting operating conditions, such as adaptive optimization approaches, enforcement learning methods, or evolutionary methods, is recommended. Use the FOFPID regulator to conduct a thorough study of the environmental effects of DFIG-based WTSs, taking into account lifecycle analyses, carbon footprint analytics, and sustainable wind farm development.