Introduction

Microstructures on elastic beds are used in various applications, including MEMS devices, flexible electronics, biomechanics, soft robotics, microfluidics, energy harvesting, acoustic metamaterials, and microscale sensors and actuators. These structures are crucial for sensing applications, flexible electronics, tissue engineering, soft robotics, lab-on-a-chip devices, energy harvesting, noise reduction, sound insulation, and acoustic signal manipulation. The interaction between microstructures and elastic supports influences device performance, and researchers and engineers explore different materials, fabrication techniques, and modeling methods to address specific challenges in each application. A multidisciplinary approach is required to understand and optimize the performance of these structures1,2,3,4,5.

The Rayleigh-Ritz method was first used for the mathematical modeling of micro-structures with rigid boundaries by Cheng and Nicolas6,7. This method could perfectly calculate natural frequencies, nevertheless, Ilanko and Dickinson8 indicated that by using the negative stiffness the estimated values have less accuracy. Yarovaya9 used the Winkler model to estimate the foundation force of the elastic bed. In this work, the Cauchy relation was used to calculate the strain and also, and Hooke’s law was reliable for the strain and stress. In this way, the displacement of the circular plate can be achieved. Bahr et al.10 investigated the behavior of a micro-structure in a fluidized bed. They concluded that the mechanical properties of the silicon granules, which are used in the fluidized bed, are critical in the applied technique for the construction of the fluidized bed.

Bauer et al.11 considered the dynamic behavior of an elastic-micropillar array sensor under fluctuating wall stress. In their study, the pillars are assumed to be uniform, homogenous, and circular beams, Also, the Stokes fluid theory is applied to model the external drag force. They assumed that the total nonlinearity is less than 1%, and they indicated that the application of the pillars is mainly influenced by the density of the pillars to air. Wang et al.12 fabricated a microstructure based on PDMS (Polydimethylsiloxane) micropillars to study the transient behavior of the microstructure. This microstructure could measure the force of about 2 µN. In their setup, they used the linear elastic model to predict the dynamic response of the pillars.

The Finite Element Galerkin method is an efficient tool for solving nonlinear equations13,14,15,16. Kubba et al.17 designed a micro capacitive pressure sensor and also they studied the effect of the pressure and temperature on the behavior of the sensor using the Finite Element method. Jindal et al.18 performed a simulation using MATLAB to forecast the dynamic performance of the sensor. They introduced a new design parameter which gives a good hint to design the sensor before the fabrication. A fast response to dynamic interaction sensor is presented by Gui et al.19. In this study, they used graphene and porous nylon networks in the sensor gap and the results indicate that, in this way, the sensitivity of the sensor is grown. A flexible bed using ionic liquid is modeled by Qing et al.20. They could increase the sensitivity of the sensor compared to the traditional one. PDMS hydrogel has a great impact on the dynamic performance of circular plates. Ahamed et al.21 used flexible PDMS hydrogel in the capacitive pressure sensors and finally, they concluded that at lower pressures this type of material can increase the sensitivity and dynamic response of the circular plate. Also, textile is used as the elastic bed to model the human motion monitoring sensor22. The using of the textile as the elastic bed can reduce the recovery time of the plate to 7ms. The composite material is used in the modeling of the structure of the circular plate by Lu et al.23 and they could increase the sensitivity and the dynamic response to 400%. Fathalilou et al.24 introduced a nonlinear model that predicts the effect of the dielectricity of the material on the dynamic response of the pressure sensor. In this work, Hfo2 has been used as a soft material to enhance the dynamic response of the sensor. Ghanbari and Rezazadeh25 modeled the dynamic behavior of the circular plate that uses silicon oil as the elastic bed. In this way, the dynamic behavior of the membrane is modified compared to the traditional one.

There are a lot of mathematical linear and nonlinear models to simulate the dynamic response of soft materials. Rotanova et al.26 used Hooke’s theory to model the hyperelastic material behavior. They drew the strain-stress diagram for this material and observed that the diagram shows 50–150% elongation for different cases. Rausch et al.27 applied the Ogden model to study the dynamic behavior of soft tissue using the Finite Element method. The mentioned model is one of the popular models to study the behavior of soft materials. Xiao et al.28 developed the Arruda-Boyce model to predict the dynamic response of the large elastic soft material. They found that for this kind of material, the mentioned model has good agreement with the experimental data. Yeoh model is one of the effective models to simulate the behavior of soft materials. Eldeeb and Shabana29 compared the Neo-Hookean, Mooney Rivlin, and Yeoh Models to soft materials oscillations and as a result, the Neo-Hookean model has an efficient answer compared to others.

The PDMS micropillar arrays are a new and efficient design to fabricate highly sensitive sensors and elastic beds of isolators due to their good dynamic response30. Zhou et al.31 designed and fabricated a structure that used the PDMS micropillar array coupled with the micromagnetic field as an elastic bed. This type of structure showed good performance in the body of the sensors. Also, the micropillar array has been used as a structure that can recognize cellular deformation, migration, and adhesion to diagnose diseases in biomedical applications32. In the new applications of capacitive sensors, the micropillar array can increase the sensitivity and improve the dynamic response of the sensor against excitement. Wen et al.33 proposed a human health monitoring sensor that uses an interlocked micropillar array. This new structure could reduce the dynamic response time to 56 ms and relaxation time to 140 ms. Also, this structure could improve the low detection limit to 15 Pa.

As it is clear, the PDMS micropillar array structure has a great impact on the designing of the new health monitoring sensors and elastic beds in the micro isolators. However, there are a few works that concentrate on this matter. Thus, the mathematical modeling of the static and dynamic behavior and the frequency response of the circular plate coupled with the PDMS micropillar structures would be very useful in the designing of very high-performance sensors and elastic beds. As no work recently focused on this subject, in the present work, a circular plate that is attached to the PDMS micropillar is proposed. Different types of PDMS with various mechanical properties are examined and the static and dynamic behavior and frequency responses of the system are extracted and compared to each other using the Galerkin method. In addition, as discussed before, as the Neo-Hookean model has good capability in the prediction of the elastic behavior of the soft materials, this method is employed more over considering the Inertial Effects in this study. In this way, the best state of the structure and mechanical properties can be selected for the design of the sensors and elastic bed.

Mathematical modeling

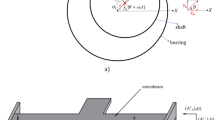
The 3D sight of the capacitive pressure sensor with flexible and fixed microplates which uses the porous polymer as a dielectric is presented in Fig. 1.

Fig. 1
figure 1

The 3D model of the annular electrically actuated circular microplate using a porous polymer as the dielectric (a) and configuration of micropillar array on the fixed plate (b).

Full size image

The strains in the radial and peripheral directions that cause the circular plate’s transversal and radial displacements can be used with nonlinear strains in axisymmetric terms13. :

$$\varepsilon _{\varrho } = \frac{{\partial {\mathcal{U}}}}{{\partial \varrho }} + \frac{1}{2}\left( {\frac{{\partial {\mathcal{W}}}}{{\partial \varrho }}} \right)^{2} - \zeta \frac{{\partial ^{2} {\mathcal{W}}}}{{\partial \varrho ^{2} }}$$
(1)
$$\varepsilon _{\vartheta } = \frac{{\mathcal{U}}}{\varrho } - \frac{\zeta }{\varrho }\left( {\frac{{\partial {\mathcal{W}}}}{{\partial \varrho }}} \right)$$
(2)

\(\:\mathcal{U}\) and \(\:\mathcal{W}\) represent the motion in the r and z directions successively. Hence, \(\:\varrho\:\) and \(\:\zeta\:\) affirm the radial and axial circumstances.

The stress-strain correlation using Hooke’s theory can be achieved in Eqs. 3 and 4:

$$\sigma _{\varrho } = \frac{E}{{1 - v^{2} }}\left\{ {\left[ {\frac{{\partial {\mathcal{U}}}}{{\partial \varrho }} + \frac{1}{2}\left( {\frac{{\partial {\mathcal{W}}}}{{\partial \varrho }}} \right)^{2} + v\frac{{\mathcal{U}}}{\varrho }} \right] - \zeta \left( {\frac{{\partial ^{2} {\mathcal{W}}}}{{\partial \varrho ^{2} }} + \frac{v}{\varrho }\left( {\frac{{\partial {\mathcal{W}}}}{{\partial \varrho }}} \right)} \right)} \right\}$$
(3)
$$\sigma _{\vartheta } = \frac{E}{{1 - v^{2} }}\left\{ {\left[ {v\left( {\frac{{\partial {\mathcal{U}}}}{{\partial \varrho }} + \frac{1}{2}\left( {\frac{{\partial {\mathcal{W}}}}{{\partial \varrho }}} \right)^{2} } \right) + \frac{{\mathcal{U}}}{\varrho }} \right] - \zeta \left( {v\frac{{\partial ^{2} {\mathcal{W}}}}{{\partial \varrho ^{2} }} + \frac{1}{\varrho }\left( {\frac{{\partial {\mathcal{W}}}}{{\partial \varrho }}} \right)} \right)} \right\}$$
(4)

The module of elasticity and Poisson’s ratio of the circular plate are indicated by E and ν in order.

The radial and tangential forces acting on the circular plate in terms of transversal and radial motions of the plate can be achieved by integrating the stresses over the respective direction as Eqs. 5 and 6.

$$N_{\varrho } = \frac{{Eh}}{{1 - v^{2} }}\left[ {\frac{{\partial {\mathcal{U}}}}{{\partial \varrho }} + \frac{1}{2}\left( {\frac{{\partial {\mathcal{W}}}}{{\partial \varrho }}} \right)^{2} + v\frac{u}{\varrho }} \right]$$
(5)
$$N_{\vartheta } = \frac{{Eh}}{{1 - v^{2} }}\left[ {v\left[ {\frac{{\partial {\mathcal{U}}}}{{\partial \varrho }} + \frac{1}{2}\left( {\frac{{\partial {\mathcal{W}}}}{{\partial \varrho }}} \right)^{2} } \right] + \frac{{u_{M} }}{\varrho }} \right]$$
(6)

In Eqs. 5 and 6, \(\:h\) denotes the thickness of the circular plate. The radial and transversal displacements can be obtained by considering the electrostatic force, according to the second law of Newton as Eqs. 7 and 8.

$$- \frac{1}{\varrho }\left[ {\frac{\partial }{{\partial \varrho }}\left( {\varrho N_{\varrho } } \right) - N_{\vartheta } } \right] + \rho h\frac{{\partial ^{2} {\mathcal{U}}}}{{\partial t^{2} }} + C_{2} \frac{{\partial {\mathcal{U}}}}{{\partial t}} = 0$$
(7)
$$\nabla ^{2} \left( {D\nabla ^{2} {\mathcal{W}}} \right) - \frac{1}{\varrho }\left[ {\frac{\partial }{{\partial \varrho }}\left( {\varrho N_{\varrho } \frac{{\partial {\mathcal{W}}}}{{\partial \varrho }}} \right)} \right] + \left( {\rho h} \right)\frac{{\partial ^{2} {\mathcal{W}}}}{{\partial t^{2} }} + C_{1} \frac{{\partial {\mathcal{W}}}}{{\partial t}} + P_{p} - P\left( {\varrho ,t} \right) = 0$$
(8)

where \(\:{C}_{1}\) and \(\:{C}_{2}\) are equivalent damping ratios. There are some studies with experimental data for plates without micropillars, which establish the quality factor and facilitate the calculation of the damping ratio range for the plate34,35,36. Additionally, there are experimental studies for PDMS, such as37,38, which assist in the approximation of damping coefficients. \(\:D=\frac{E{h}^{3}}{12(1-{\nu\:}^{2})}\) is the bending rigidity of the membrane, \(\:{P}_{p}\) is a distributed pressure due to the compression of the Micro-pillar array between both plates, \(\:P(\varrho\:,t)\) is the exerted peripheral pressure.

In the present work, It is assumed that the edge of the circular plate is clamped, thus, the boundary conditions can be represented as Eq. 9.

$${\mathcal{W}}\left( {R,t} \right) = 0;\quad \left. {\frac{{\partial {\mathcal{W}}\left( {\varrho ,t} \right)}}{{\partial \varrho }}} \right|_{{\varrho = R}} = 0;$$
(9)

The transversal or out-plane stiffness of the plate is small enough compared to the in-plane stiffness, so the natural frequencies of transversal vibration modes of the circular plate are smaller than those of radial vibrations. Consequently, the displacement in the radial direction can be safely neglected in low-frequency actuation of the plate. Therefore, regarding the clamped boundaries of the circular plate, averaging radial forces, and taking into account mid-plane stretching, the nonlinear equation of the flexural displacement can be achieved as Eq. 1013,38.

$$f_{1} \left( {{\mathcal{W}},P_{p} ,P\left( {\varrho ,t} \right)~} \right) = \nabla ^{2} \left( {D\nabla ^{2} {\mathcal{W}}} \right) - \frac{{Eh}}{{1 - \upsilon ^{2} }}\left( {\frac{1}{{2R}}\mathop \int \limits_{0}^{R} \left( {\frac{{\partial {\mathcal{W}}}}{{\partial \varrho }}} \right)^{2} d\varrho } \right)\nabla ^{2} {\mathcal{W}} + \left( {\rho h} \right)\frac{{\partial ^{2} {\mathcal{W}}}}{{\partial t^{2} }} + c\frac{{\partial {\mathcal{W}}}}{{\partial t}} + P_{p} - P\left( {\varrho ,t} \right) = 0$$
(10)

If the axisymmetric condition is the ruler, the relations of \(\:{\nabla\:}^{2}\) and \(\:{\nabla\:}^{4}\) can be presented in Eq. 11 form.

$$\nabla ^{2} = \frac{{\partial ^{2} }}{{\partial \varrho ^{2} }} + \frac{1}{\varrho }\frac{\partial }{{\partial \varrho }},\;\nabla ^{4} = \frac{{\partial ^{4} }}{{\partial \varrho ^{4} }} + \frac{2}{\varrho }\frac{{\partial ^{3} }}{{\partial \varrho ^{3} }} - \frac{1}{{\varrho ^{2} }}\frac{{\partial ^{2} }}{{\partial \varrho ^{2} }} + \frac{1}{{\varrho ^{3} }}\frac{\partial }{{\partial \varrho }}$$
(11)

The radial tension in the mid-plane of the plate regarding the restrained boundaries of the plate is given in Eq. 10 as the second term in the form of an integral, which makes averaging radial tension over the radial coordinate. It can be neglected in the small displacements and should be significant in the large motions39.

Utilizing the incompressible Neo-Hookean model for micropillars subjected to uniaxial loading

In the context of large deformations, the deformation gradient tensor is a better choice than the strain tensor. The deformation gradient tensor provides a more accurate representation of how a material body has deformed from its initial configuration to its current state, especially when dealing with significant changes in shape, size, and rotation.

The deformation gradient tensor (\(\:\mathbb{F}\)) relates the initial and current configurations of material points and encompasses both the linear changes in shape (strain) and the rotation of the material. It is given by the formula13:

$$\begin{gathered} {{\mathbb{F}}_{ij}}=\frac{{\partial {\xi _i}}}{{\partial {\chi _j}}}={\delta _{ij}}+\frac{{\partial {u_i}}}{{\partial {\chi _j}}} \hfill \\ {\mathbb{F}}={\text{I}}+\nabla u \hfill \\ \end{gathered}$$
(12)

where \(\:{\xi\:}_{i}\) represents the current coordinates of a material point in the deformed configuration and \(\:{\chi\:}_{j}\)represents the initial coordinates of the same material point in the undeformed configuration and \(\:{u}_{i}\) is the displacement vector component.

The Cauchy-Green or stretch tensor (\(\:\mathbb{C}\)) is an important concept in continuum mechanics, especially when dealing with deformation analysis. It quantifies how material elements change in length due to deformation while disregarding any accompanying rotations. In three dimensions, the stretch or right Cauchy-Green tensor can be defined as13:

$${\mathbb{C}}={{\mathbb{F}}^T}{\mathbb{F}}={\left( {{\text{I}}+\nabla u} \right)^T}\left( {{\text{I}}+\nabla u} \right)=I+\left( {\nabla u} \right)+{\left( {\nabla u} \right)^T}+\left( {\nabla u} \right){\left( {\nabla u} \right)^T}$$
(13)

The principal stretches (\(\:{\psi\:}_{1}\), \(\:{\psi\:}_{2}\), and \(\:{\psi\:}_{3}\)) are the eigenvalues of the stretch tensor (\(\:{\mathbb{C}}_{ij}\)). They represent the magnitudes of the deformation along the principal material directions. In the context of linear elasticity and small strains, the principal stretches can be determined by diagonalizing the stretch tensor13:

$$U_{{ij}} = R_{{ik}} \Lambda _{{kl}} R_{{lj}}$$
(14)

where \(\:{R}_{ij}\) is the rotation tensor that diagonalizes \(\:{U}_{ij}\). It consists of the eigenvectors of \(\:{\mathbb{C}}_{ij}\) as columns. \(\:{{\Lambda\:}}_{kl}\)is a diagonal matrix with the principal stretches \(\:{\psi\:}_{1}\), \(\:{\psi\:}_{2}\), and \(\:{\psi\:}_{3}\) as its diagonal entries. So, the principal stretches can be obtained from the eigenvalues of the stretch or Cauchy-Green tensor.

The strain energy density function \(\:\mathbb{W}\) in a neo-Hookean material model can be expressed in terms of the principal stretches (\(\:{\psi\:}_{1}\), \(\:{\psi\:}_{2}\), and \(\:{\psi\:}_{3}\)) as follows13,28,29:

$${\mathbb{W}}={{\mathbb{C}}_1}\left( {I - 3 - 2\ln \left( J \right)} \right) - {{\mathbb{D}}_1}{\left( {J - 1} \right)^2}$$
(15)

Es is the young modulus of the micropillars. Thus,

$$I={\left( {{\psi _1}} \right)^2}+{\left( {{\psi _2}} \right)^2}+{\left( {{\psi _3}} \right)^2};J={\text{det}}\left( {\mathbb{F}} \right)$$
(16)

In the context of an incompressible polymeric material, the third invariant of the deformation tensor, which indicates changes in volume, is equal to 1.

$$J={\psi _1}{\psi _2}{\psi _3}=1$$
(17)

the strain energy density \({\mathbb{W}}\) assumes the following simplified form:

$${\mathbb{W}}={{\mathbb{C}}_1}\left( {I - 3} \right)$$
(18)

In the present scenario, given the small cross-sectional dimensions of the micropillars, it is reasonable to consider them as being subjected to uniaxial loading conditions, which is a valid assumption in this context.

$${\sigma _3} \ne 0;~~{\sigma _2}={\sigma _1}=0$$
(19)

It should be noted that the use of continuous polymer support would result in the material experiencing more complex stress states, which are not adequately captured by the current model. Consequently, the model used in the current analysis is specifically tailored to the discrete nature of micropillars and cannot be extended to continuous polymer systems without significant modifications. Under uniaxial extension or compression considering \(\:{\psi\:}_{3}\)= \(\:\psi\:\) as follows28, leads to the following:

$${\psi _1}{\psi _2}=\frac{1}{\psi };~~{\psi _1}={\psi _2}=\frac{1}{{\sqrt \psi }}$$
(20)

The Cauchy stress differences for an incompressible hyper-elastic material can be expressed in terms of the principal stretches as follows:

$${\sigma _3} - {\sigma _1}={\psi _3}\frac{{\partial {\mathbb{W}}}}{{\partial {\lambda _3}}} - {\psi _1}\frac{{\partial {\mathbb{W}}}}{{\partial {\lambda _1}}}=2{{\mathbb{C}}_1}\left( {\psi _{3}^{2} - \psi _{1}^{2}} \right)~$$
(21)

For the uniaxial case, Eq. (22) takes the following form

$${\sigma _3}={\sigma _\zeta }=2{{\mathbb{C}}_1}\left( {{\psi ^2} - \frac{1}{\psi }} \right)=2{{\mathbb{C}}_1}\left( {\frac{{{\psi ^3} - 1}}{\psi }} \right)$$
(22)

Writing principle stretch value in terms of deformation gradient will result in the following:

$$\psi ={\psi _3}={\psi _\zeta }=\frac{{\partial {w_p}}}{{\partial \zeta }}+1$$
(23)

The equation of motion for the ith micropillar is based on Newton’s second law:

$$\frac{{\partial {\sigma _\zeta }}}{{\partial \zeta }}=\rho \frac{{{\partial ^2}w_{p}^{{\left( i \right)}}}}{{\partial {t^2}}}$$
(24)

Taking into account equations (22), and (23), the nonlinear dynamic equation of motion for a micropillar is as follows:

$${f_2}\left( {w_{p}^{{\left( i \right)}}\left( {\zeta ,t} \right)} \right)=2{{\mathbb{C}}_1}\left[ {3\left( {\frac{{{\partial ^2}w_{p}^{{\left( i \right)}}}}{{\partial {\zeta ^2}}}} \right){{\left( {\frac{{\partial w_{p}^{{\left( i \right)}}}}{{\partial \zeta }}+1} \right)}^2}\left( {\frac{{\partial w_{p}^{{\left( i \right)}}}}{{\partial \zeta }}+1} \right) - \frac{{{\partial ^2}w_{p}^{{\left( i \right)}}}}{{\partial {\zeta ^2}}}\left( {{{\left( {\frac{{\partial w_{p}^{{\left( i \right)}}}}{{\partial \zeta }}+1} \right)}^3} - 1} \right)} \right] - {\rho _p}\left( {\frac{{{\partial ^2}w_{p}^{{\left( i \right)}}}}{{\partial {t^2}}}} \right){\left( {\frac{{\partial w_{p}^{{\left( i \right)}}}}{{\partial \zeta }}+1} \right)^2}=0$$
(25)

Since the tip of the micropillars should follow the movement and the end of the columns are fixed, the boundary conditions governing the movement of the micropillars are as follows:

$$F_{p}^{{\left( i \right)}} = 2A_{p} \mathbb{C}_{1} \left. {\left[ {\frac{{\left( {\frac{{\partial w_{p}^{{\left( i \right)}} }}{{\partial z}} + 1} \right)^{3} - 1}}{{\left( {\frac{{\partial w_{p}^{{\left( i \right)}} }}{{\partial \zeta }} + 1} \right)}}} \right]} \right|_{{\zeta = 0}}$$
(26)

The force applied to the plate by the ith micropillar is calculated from Eq. (22), taking into account the cross-sectional area of the micropillar.

$$F_{p}^{{\left( i \right)}}=2{A_p}{{\mathbb{C}}_1}{\left. {\left[ {\frac{{{{\left( {\frac{{\partial w_{p}^{{\left( i \right)}}}}{{\partial z}}+1} \right)}^3} - 1}}{{\left( {\frac{{\partial w_{p}^{{\left( i \right)}}}}{{\partial \zeta }}+1} \right)}}} \right]} \right|_{\zeta =0}}$$
(27)

It should be noted that, as shown in Fig. 1, the microplate sits on an array of micropillars, and therefore several discrete forces are applied to the microplate depending on the location of each micropillar. However, due to the significant number of micropillars, it becomes reasonable to treat the array as a continuous polymer support beneath the plate. Consequently, by defining a density number for the micropillars as \(\:{n}_{p}=\frac{{N}_{p}}{A}\), the deformation of the micropillar can be characterized by Eq. (25) from which the superscript (i) is removed.

$$f_{2} \left( {w_{p} \left( {\varrho ,\zeta ,t} \right)} \right) = 2{\mathbb{C}}_{1} \left( {\frac{{\partial ^{2} w_{p} }}{{\partial \zeta ^{2} }}} \right)\left[ {2\left( {\frac{{\partial w_{p} }}{{\partial \zeta }} + 1} \right)^{3} + 1} \right] - \rho _{p} \left( {\frac{{\partial ^{2} w_{p} }}{{\partial t^{2} }}} \right)\left( {\frac{{\partial w_{p} }}{{\partial \zeta }} + 1} \right)^{2} = 0$$
(28)

where \(\:A\) represents the total surface area of the microplate and Np is the total number of micropillars. Therefore, the corresponding boundary conditions will take the following form.

$$w_{p} \left( {\varrho ,0,t} \right) = {\mathcal{W}}\left( {\varrho ,t} \right);~~w_{p} \left( {\varrho ,h_{p} ,t} \right) = 0$$
(29)

To homogenize the boundary conditions for the motion of the micropillars, we assume that their comparison can be expressed as the sum of two functions.

$$w_{p} \left( {{\varrho },0,t} \right) = {\mathcal{W}}\left( {{\varrho },t} \right)\left( {1 - \frac{\zeta }{{h_{p} }}} \right) + \mathcalligra{w}({\varrho },\zeta ,t)$$
(30)

By substituting Eq. (30) into Eq. (28) and keeping only nonlinear terms of order 3 or lower, the equation takes the following form. It is worth noting that while neglecting the nonlinear terms may seem to simplify the analysis to that of a purely elastic bed, similar to a Winkler foundation, it is important to note that this approach goes beyond that. This analysis not only considers the stiffness of the bed, but also its inertia and damping effects. This comprehensive treatment allows for a more accurate representation of the dynamic behavior of the system, especially under high-frequency excitations where these factors significantly influence the response.

$$\begin{gathered} f_{2} \left( {{\mathcal{W}}\left( {\varrho ,t} \right),\mathcalligra{w}\left( {\varrho ,\zeta ,t} \right)} \right) = 2{\mathbb{C}}_{1} \left( {\frac{{\partial ^{2} \mathcalligra{w}}}{{\partial \zeta ^{2} }}} \right)\left[ {3 + 6\left( {\frac{{\partial \mathcalligra{w}}}{{\partial \zeta }} - \frac{{\mathcal{W}}}{{h_{p} }}} \right) + 6\left( {\frac{{\partial \mathcalligra{w}}}{{\partial \zeta }}} \right)^{2} - 12\frac{{\partial \mathcalligra{w}}}{{\partial \zeta }}\left( {\frac{{\mathcal{W}}}{{h_{p} }}} \right) + 6\left( {\frac{{\mathcal{W}}}{{h_{p} }}} \right)^{2} } \right] \hfill \\ \quad - \rho _{p} \left[ {\frac{{\partial ^{2} \mathcalligra{w}}}{{\partial t^{2} }} + \left( {1 - \frac{\zeta }{{h_{p} }}} \right)\frac{{\partial ^{2} {\mathcal{W}}}}{{\partial t^{2} }}} \right]\left[ {1 + 2\left( {\frac{{\partial \mathcalligra{w}}}{{\partial \zeta }} - \frac{{\mathcal{W}}}{{h_{p} }}} \right) + \left( {\frac{{\partial \mathcalligra{w}}}{{\partial \zeta }}} \right)^{2} - 2\frac{{\partial \mathcalligra{w}}}{{\partial \zeta }}\left( {\frac{{\mathcal{W}}}{{h_{p} }}} \right) + \left( {\frac{{\mathcal{W}}}{{h_{p} }}} \right)^{2} } \right] = 0 \hfill \\ \end{gathered}$$
(31)

As observed, when nonlinear terms are ignored, the dynamic motion equation of pillars can be simplified to the conventional linear longitudinal motion equation. The distributed force or pressure that the micropillars apply to the plate per unit area can be calculated.

$$P_{P} \left[ {\mathcalligra{w}\left( {\varrho ,0,t} \right),{\mathcal{W}}\left( {\varrho ,t} \right)} \right] = 2n_{p} A_{p} {\mathbb{C}}_{1} \left. {\left[ {\frac{{\left( {\frac{{\partial \mathcalligra{w}}}{{\partial \zeta }} - \frac{{\mathcal{W}}}{{h_{p} }} + 1} \right)^{3} - 1}}{{\left( {\frac{{\partial \mathcalligra{w}}}{{\partial \zeta }} - \frac{{\mathcal{W}}}{{h_{p} }} + 1} \right)}}} \right]} \right|_{{\zeta = 0}}$$
(32)

Where \(\:{A}_{p}\) is the area of a single pillar. It is important to note that including the relationship (34) in Eq. (10) introduces an additional nonlinearity, which significantly complicates the equation. Therefore, as the method used is numerical and includes both spatial and temporal coordinates, this added complexity can be treated as a known forcing term. The magnitudes of force term can be obtained from the last time-step and it can be updated via integration overall the solution domain in each step. The model with more elastic constants is a good choice for a wider range of materials, as it can better align with experimental data. The Money-Rivlin model is suitable for PDMS40. For the present case, the micropillars with small cross-section dimensions can be considered under uniaxial loading conditions. Thus, The Mooney-Rivlin model reduces to the Neo-Hookean model. The Neo-Hookean model is the most commonly used elasticity model for hydrogels, as it is the simplest constitutive model for describing the nonlinear elastic behavior of materials.

It is crucial to address the asymmetry of hydrogels and elastomeric materials in tension and compression. This is due to the intrinsic nonlinearity and material behavior of hyperelastic materials, which may result in discrepancies in the mechanical response between tension and compression. However, the present study employs a primary static compression loading condition and a dynamic loading about a static equilibrium condition, which is typically smaller than the static one due to the specific application of the stated problem under examination. Therefore, this study focuses on the compression behavior of the columns. Furthermore, this model accurately reflects the material’s compression response.

Numerical solution

To get a reliable solution to the equations, one notable approach is the Galerkin weighted residual method, which is equivalent to the principle of virtual work33,41. To solve Eqs. 10 and 22, it is assumed that the solution of these equations can be presented as Eqs. 33 and 34 respectively. The shape functions are \(\:{\varphi\:}_{n}\left(\varrho\:\right)\), \(\:{\psi\:}_{m}\left(\zeta\:\right)\).

These functions adhere to the boundary conditions and are applied to unknown time-dependent functions (\({\mathcalligra{a}_n}\left( t \right)\) and \({\mathcalligra{b}_{nm}}\left( t \right)\)) in a series form33:

$${\mathcal{W}}\left( {\varrho ,t} \right) = \mathop \sum \limits_{{n = 1}}^{\infty } \mathcalligra{a}_{n} \left( t \right)\phi _{n} \left( \varrho \right)$$
(33)
$$\mathcalligra{w}\left( {{\varrho },\zeta ,t} \right) = \sum\limits_{{n = 1}}^{\infty } {\sum\limits_{{m = 1}}^{\infty } {\mathcalligra{b}_{{nm}} \left( t \right)\phi _{n} \left({\varrho } \right)\psi _{m} \left( \zeta \right)} }$$
(34)

The unlimited series presented in Eqs. 33 and 34 can be truncated to the finite series (Eqs. 35 and 36).

$${\mathcal{W}}^{N} \left( {\varrho ,t} \right) = \mathop \sum \limits_{{n = 1}}^{N} \mathcalligra{a}_{n} \left( t \right)\phi _{n} \left( \varrho \right)$$
(35)
$$\mathcalligra{w}^{{NM}} \left( {\varrho ,\zeta ,t} \right) = \mathop \sum \limits_{{n = 1}}^{N} \mathop \sum \limits_{{m = 1}}^{M} \mathcalligra{b}_{{nm}} \left( t \right)\phi _{n} \left( \varrho \right)\psi _{m} \left( \zeta \right)$$
(36)

After substituting Eqs. 35 and 36 into Eqs. 10 and 22, the errors of the solution can be introduced as δ1 and δ2, according to Eqs. 37 and 38.

$$f_{1} \left[ {{\mathcal{W}}^{N} \left( {{\varrho },t} \right),\mathcalligra{w}^{{NM}} \left( {{\varrho },\zeta ,t} \right),P_{p} \left( {w^{N} \left( {{\varrho },t} \right),\mathcalligra{w}^{{NM}} \left( {{\varrho },\zeta ,t} \right)} \right),P\left( {{\varrho },t} \right)} \right] = \delta _{1}$$
(37)
$$f_{2} \left( {{\mathcal{W}}^{N} \left( {\varrho ,t} \right),\mathcalligra{w}^{{NM}} \left( {\varrho ,\zeta ,t} \right)} \right) = \delta _{2}$$
(38)

Equations 37 and 38 can be expanded to Eqs. 39 and 40 form respectively.

$$\begin{gathered} f_{1} \left( {{\mathcal{W}}^{N} \left( {\varrho ,t} \right),\mathcalligra{w}^{{NM}} \left( {\varrho ,\zeta ,t} \right),P_{p} \left( {{\mathcal{W}}^{N} \left( {\varrho ,t} \right),\mathcalligra{w}^{{NM}} \left( {\varrho ,\zeta ,t} \right)} \right),P\left( {\varrho ,t} \right)} \right) = D\mathop \sum \limits_{{n = 1}}^{N} \varrho ^{3} \mathcalligra{a}_{n} \left( t \right)\phi ^{{\left( 4 \right)}} _{n} \left( \varrho \right) + 2D\mathop \sum \limits_{{n = 1}}^{N} \varrho ^{2} \mathcalligra{a}_{n} \left( t \right)\phi ^{\prime\prime\prime}_{n} \left( \varrho \right) \hfill \\ \quad - D\mathop \sum \limits_{{n = 1}}^{N} \varrho {a}_{n} \left( t \right)\phi ^{\prime\prime}_{n} \left( \varrho \right) + D\mathop \sum \limits_{{n = 1}}^{N} \mathcalligra{a}_{n} \left( t \right)\phi ^{\prime}_{n} \left( \varrho \right) + \frac{{Eh}}{{2R\left( {1 - \nu ^{2} } \right)}}\mathop \sum \limits_{{m = 1}}^{N} \mathop \sum \limits_{{s = 1}}^{N} \mathop \sum \limits_{{n = 1}}^{N} \left\{ {\mathcalligra{a}_{m} \mathcalligra{a}_{s} \mathcalligra{a}_{n} \left( {\phi ^{\prime\prime}_{n} \left( \varrho \right) + \frac{1}{\varrho }\phi ^{\prime}_{n} \left( \varrho \right)} \right)} \right\} \hfill \\ \quad \mathop \int \limits_{0}^{R} \left( {\phi ^{\prime}_{s} \left( \varrho \right)\phi ^{\prime}_{m} \left( \varrho \right)} \right)d\varrho + \rho h\mathop \sum \limits_{{n = 1}}^{N} \ddot{\mathcalligra{a}}_{n} \left( t \right)\phi _{n} \left( \varrho \right) + c\mathop \sum \limits_{{n = 1}}^{N} \dot{\mathcalligra{a}}_{n} \left( t \right)\phi _{n} \left( \varrho \right) + P_{p} \left( {{\mathcal{W}}^{N} \left( {\varrho ,t} \right),\mathcalligra{w}^{{NM}} \left( {\varrho ,\zeta ,t} \right)} \right) + P\left( {\varrho ,t} \right) = \delta _{1} \hfill \\ \end{gathered}$$
(39)
$$\begin{gathered} f_{2} \left( {{\mathcal{W}}^{N} \left( {\varrho ,t} \right),\mathcalligra{w}^{{NM}} \left( {\varrho ,\zeta ,t} \right)} \right) = 2{\mathbb{C}}_{1} \left( {\mathop \sum \limits_{{n = 1}}^{N} \mathop \sum \limits_{{m = 1}}^{M} \mathcalligra{b}_{{nm}} \left( t \right)\phi _{n} \left( \varrho \right)\psi _{m}^{{''}} \left( \zeta \right)} \right)\left[ {3 + 6\left( {\mathop \sum \limits_{{f = 1}}^{N} \mathop \sum \limits_{{p = 1}}^{M} \mathcalligra{b}_{{fp}} \left( t \right)\phi _{f} \left( \varrho \right)\psi _{p}^{'} \left( \zeta \right) - \frac{1}{{h_{p} }}\mathop \sum \limits_{{i = 1}}^{N} \mathcalligra{a}_{i} \left( t \right)\phi _{i} \left( \varrho \right)} \right)} \right. \hfill \\ \quad + 6\mathop \sum \limits_{{f = 1}}^{N} \mathop \sum \limits_{{p = 1}}^{M} \mathop \sum \limits_{{s = 1}}^{N} \mathop \sum \limits_{{k = 1}}^{M} \mathcalligra{b}_{{fp}} \left( t \right)\mathcalligra{b}_{{nm}} \left( t \right)\phi _{f} \left( \varrho \right)\psi _{p}^{'} \left( \zeta \right)\phi _{s} \left( \varrho \right)\psi _{k}^{'} \left( \zeta \right) - 12\left( {\mathop \sum \limits_{{f = 1}}^{N} \mathop \sum \limits_{{p = 1}}^{M} \mathcalligra{b}_{{fp}} \left( t \right)\phi _{f} \left( \varrho \right)\psi _{p}^{'} \left( \zeta \right)} \right) \hfill \\ \left. {\mathop {\quad \sum }\limits_{{i = 1}}^{N} \mathcalligra{a}_{i} \left( t \right)\phi _{i} \left( \varrho \right) + \frac{6}{{h_{p} }}\mathop \sum \limits_{{i = 1}}^{N} \mathop \sum \limits_{{j = 1}}^{N} \mathcalligra{a}_{i} \left( t \right)\phi _{i} \left( \varrho \right)\mathcalligra{a}_{j} \left( t \right)\phi _{j} \left( \varrho \right)} \right] - \rho _{p} \left[ {\mathop \sum \limits_{{n = 1}}^{N} \mathop \sum \limits_{{m = 1}}^{M} \ddot{\mathcalligra{b}}_{nm} \left( t \right)\phi _{n} \left( \varrho \right)\psi _{m} \left( \zeta \right) + \left( {1 - \frac{\zeta }{{h_{p} }}} \right)\mathop \sum \limits_{{i = 1}}^{N} \ddot{\mathcalligra{a}}_{i} \left( t \right)\phi _{i} \left( \varrho \right)} \right] \hfill \\ \quad \left[ {1 + 2\left( {\mathop \sum \limits_{{f = 1}}^{N} \mathop \sum \limits_{{p = 1}}^{M} \mathcalligra{b}_{{fp}} \left( t \right)\phi _{f} \left( \varrho \right)\psi _{p}^{'} \left( \zeta \right) - \frac{1}{{h_{p} }}\mathop \sum \limits_{{i = 1}}^{N} \mathcalligra{a}_{i} \left( t \right)\phi _{i} \left( \varrho \right)} \right)} \right. + \mathop \sum \limits_{{f = 1}}^{N} \mathop \sum \limits_{{p = 1}}^{M} \mathop \sum \limits_{{s = 1}}^{N} \mathop \sum \limits_{{k = 1}}^{M} \mathcalligra{b}_{{fp}} \left( t \right)\mathcalligra{b}_{{nm}} \left( t \right)\phi _{f} \left( \varrho \right)\psi _{p}^{'} \left( \zeta \right)\phi _{s} \left( \varrho \right)\psi _{k}^{'} \left( \zeta \right) \hfill \\ \quad - 2\left( {\mathop \sum \limits_{{f = 1}}^{N} \mathop \sum \limits_{{p = 1}}^{M} \mathcalligra{b}_{{fp}} \left( t \right)\phi _{f} \left( \varrho \right)\psi _{p}^{'} \left( \zeta \right)} \right)\mathop \sum \limits_{{i = 1}}^{N} \mathcalligra{b}_{i} \left( t \right)\phi _{i} \left( \varrho \right)\left. { + \frac{1}{{h_{p} }}\mathop \sum \limits_{{i = 1}}^{N} \mathop \sum \limits_{{j = 1}}^{N} \mathcalligra{a}_{i} \left( t \right)\phi _{i} \left( \varrho \right)\mathcalligra{a}_{j} \left( t \right)\phi _{j} \left( \varrho \right)} \right] = \delta _{2} \hfill \\ \end{gathered}$$
(40)

The solutions that are given above don’t satisfy the displacement equations. To solve this problem, a weighted averaged integral should be applied to equations, in this way, the errors will be equal to zero33,41. Consequently, the system has balance from the energy viewpoint.

$$\mathop \int \limits_{0}^{R} f_{1} \left[ {w^{N} \left( {\varrho ,t} \right),u^{{NM}} \left( {\varrho ,\zeta ,t} \right),P_{p} \left( {w^{N} \left( {\varrho ,t} \right),u^{{NM}} \left( {\varrho ,\zeta ,t} \right)} \right),P\left( {\varrho ,t} \right)} \right]\varphi _{j} \left( \varrho \right)d\varrho = 0\;\;j = 1, \ldots ,N$$
(41)
$$\mathop \int \limits_{0}^{{h_{p} }} \mathop \int \limits_{0}^{R} f_{2} \left( {w^{N} \left( {\varrho ,t} \right),u^{{NM}} \left( {\varrho ,\zeta ,t} \right)} \right)\phi _{i} \left( \varrho \right)\psi _{j} \left( \zeta \right)d\varrho d\zeta = 0,\;\;i = 1, \ldots ,N,\;\;j = 1, \ldots ,M$$
(42)

It should be noted that the \({{\mathbb{C}}_1}\) can be assumed as, where Ep is the Young’s modulus of pillar:

$${{\mathbb{C}}_1}=\left( {\frac{1}{6}} \right) \cdot {E_p}$$
(43)

Balancing the energy of the system yields a set of \(\:N+\:N\times\:M\) time-dependent ordinary differential equations (ODEs). Solving the equations indicated above, specify the coefficient as the dependent on time. More information on the static analysis and dynamic analysis solution of equations and the frequency response analysis can be found in38,39.

The exerted pressure is assumed that have a static term moreover a dynamic term, in which the dynamic term fluctuates around the static point. Thus, the exerted pressure can be found in the form of Eq. 44.

$$P\left( {\varrho ,t} \right) = P_{0} + P_{d} \left( {\varrho ,t} \right),~~P_{d} \left( {\varrho ,t} \right) = P_{d} \left( {\varrho ,t + T} \right)$$
(44)

Note that pressure dynamic fluctuations in real applications are not limited to a single harmonic pressure. Instead, they can follow a periodic pattern and be presented as a sum of harmonic series with different frequencies through a Fourier transform.

$$P_{d} \left( {\varrho ,t} \right) = \mathop \sum \limits_{{n = 1}}^{\infty } {{\Theta }}_{n} \sin \left( {n{{\Omega }}t} \right)$$
(45)

Typically, the first terms of a series may hold significant value while the subsequent terms can be disregarded. Note that the applied pressure Fourier transform has some frequency contents. However, the system will have a periodic steady-state solution. If there are two or more fluctuation sources in the sensor or problem, and both are periodic but have no common divisor for the periods, the system solution will be in the form of a quasi-periodic solution. Our study is currently limited to the periodic case, although the applied method can be easily applied to the quasi-periodic case by defining multidimensional time variables.

For convenience, the undefined coefficients \({\mathcalligra{a}_n}\left( t \right)\), and \({\mathcalligra{b}_{nm}}\left( t \right)\) can be represented as an (N + M)-dimensional vector.

$$\vec{\mathbb{Q}}\left( t \right) = \left\{ {\begin{array}{*{20}c} {\mathcalligra{a}_{1} \mathcalligra{a}_{2} \mathcalligra{a}_{3} \ldots \mathcalligra{a}_{{N}} \mathcalligra{b}_{{11}} \mathcalligra{b}_{{12}} \mathcalligra{b}_{{13}} \ldots \mathcalligra{b}_{{1N}} \ldots \mathcalligra{b}_{{M1}} \mathcalligra{b}_{{M2}} \mathcalligra{b}_{{M3}} \ldots \mathcalligra{b}_{{MN}}} \\ \end{array} } \right\}^{T}$$
(46)

Equations (41) and (42) can be amalgamated and expressed as:

$$f\left( {\vec{\mathbb{Q}}\left( t \right)} \right) = 0$$
(47)

To examine the frequency response of the system of nonlinear coupled equations, the solution to Eq. (47) can be expressed as a series of sine and cosine functions.

$$\begin{gathered} \vec{\mathbb{Q}}^{{\left( i \right)}} \left( t \right) = \left\{ {\Phi _{0}^{{\left( i \right)}} + \mathop \sum \limits_{{j = 1}}^{S} \left( {\Phi _{j}^{{\left( i \right)}} \cos \left( {j\Omega t} \right) + \Psi _{j}^{{\left( i \right)}} \sin \left( {j\Omega t} \right)} \right)} \right\},\;\;i = 1, \ldots ,\left( {N + M} \right) \hfill \\ A_{j}^{{\left( i \right)}} = \sqrt {\left( {\Phi _{j}^{{\left( i \right)}} } \right)^{2} + \left( {\Psi _{j}^{{\left( i \right)}} } \right)^{2} } \hfill \\ \end{gathered}$$
(48)

Here, \({\text{A}}_{j}^{{\left( i \right)}}\) represents the dimensionless amplitude of the frequency response at the jth harmonic. Substitution solution (46) into Eqs. (41) and (42) leads to the errors as:

$$f\left( {\vec{\mathbb{Q}}^{{\left( i \right)}} \left( t \right)} \right) = \varepsilon ^{{\left( i \right)}} \left( t \right),~~i = 1, \ldots ,\left( {N + M} \right)$$
(49)

When implementing a weak integrally satisfying method, the weighted residual or energy function (denoted as \(\:{\overrightarrow{{\Lambda\:}}}^{\left(i\right)}\)), can be expressed using the following equation at a given initial guess for the coefficients:

$$\vec{\Lambda }^{{\left( i \right)}} = \mathop \int \limits_{0}^{{\frac{{2\pi }}{\Omega }}} \varepsilon ^{{\left( i \right)}} \left( t \right)\vec{w}_{k} \left( t \right)dt,~~k = 0,1,~2,~3,~ \ldots 2s$$
(50)

where \({\vec {w}_k}\left( \tau \right)\) is the weight function, which can be defined as:

$$\vec{w}_{k} \left( t \right) = \left\{ {1,~\sin \left( {k\Omega t} \right),~\cos \left( {k\Omega t} \right)} \right\},~~~k = 1,~2,~3,~ \ldots ,s$$
(51)

The vector of unknown coefficients for a given actuation frequency \(\Omega\) can be defined as:

$$\vec{Y}^{{\left( i \right)}} = \left\{ {\Phi _{0}^{{\left( i \right)}} ,\Phi _{1}^{{\left( i \right)}} \ldots \Phi _{s}^{{\left( i \right)}} ,\Psi _{1}^{{\left( i \right)}} \ldots \Psi _{s}^{{\left( i \right)}} } \right\}^{T} ,$$
(52)

Consequently when the actuation frequency increases to a new value \(\:{\Omega\:}+\varDelta\:{\Omega\:}\) the vector of unknown coefficients will be as \(\:{\overrightarrow{Y}}^{\left(i\right)}+\varDelta\:{\overrightarrow{Y}}^{\left(i\right)}\). The implicit ARC length method is a numerical technique designed to solve nonlinear equations. It has also been successfully used in nonlinear frequency response analysis. This method is particularly useful when dealing with phenomena such as bifurcation, jumps, subharmonic isolas, and snapback behavior. This method accurately traces the frequency response curve without considering the incremental step frequency as a fixed value. Instead, it gradually increases from zero to a desired value with dynamic increments based on the behavior of the frequency response curve and the unknown amplitude values. Because the implicit ARC Length method considers the frequency increment as an unknown value, an additional equation must be defined. This equation, commonly referred to as the ARC length equation, is defined as follows, which is a constraint equation that makes conventional methods such as the Newton-Raphson method converge in softening, hardening, or limit points.

$$\mathbb{R}\left( {\Delta \vec{Y}^{{\left( i \right)}} ,\Delta \Omega } \right) = \left( {\Delta \vec{Y}^{{\left( i \right)}} } \right)^{T} \left( {\Delta \vec{Y}^{{\left( i \right)}} } \right) + \sigma ^{2} \left( {\Delta \Omega } \right)^{2} - \left( {\Delta S} \right)^{2}$$
(53)

where \(\:\sigma\:\) is a scaling factor. Since the implicit ARC Length method is iterative, assuming that the amplitude and frequency increments \(\:\varDelta\:{\overrightarrow{Y}}^{\left(i\right)}\) and \(\:\varDelta\:{\Omega\:}\) satisfy the ARC Lenght Eq. (53), it is possible to obtain a simplified linearized version of this constraint equation, adopting the idea of Riks and Wempner (1971) for (i + 1)th iteration, i.e42.

$$\mathbb{R}\left( {\Delta \vec{Y}^{{\left( i \right)}} ,\Delta \Omega } \right) = ~\left( {\Delta \vec{Y}^{{\left( i \right)}} } \right)^{T} \left( {\delta \vec{Y}^{{\left( i \right)}} } \right) + \sigma ^{2} \Delta \Omega \delta \Omega$$
(54)

For convenience, we combine the energy function (Eq. 50) with the ARC length constraint (Eq. 54) and call it the cost function. The value of the cost function at (n + 1)th iteration can be written in terms of its value at the nth iteration using the Taylor expansion series as follows:

$$\left\{ {\begin{array}{*{20}c} {\vec{\Lambda }^{{\left( i \right)}} } \\ \mathbb{R} \\ \end{array} } \right\}_{{n + 1}} = \left\{ {\begin{array}{*{20}c} {\vec{\Lambda }^{{\left( i \right)}} } \\ \mathbb{R} \\ \end{array} } \right\}_{n} + \left[ {\left. {\left[ {\begin{array}{*{20}c} {\frac{{\partial \vec{\Lambda }^{{\left( i \right)}} }}{{\partial \vec{Y}^{{\left( i \right)}} }}} & {\frac{{\partial \vec{\Lambda }^{{\left( i \right)}} }}{{\partial \Omega }}} \\ {\Delta \vec{Y}^{{\left( i \right)}} } & {\sigma ^{2} \Delta \Omega } \\ \end{array} } \right]} \right|_{{\left( {\begin{array}{*{20}c} {\vec{Y}^{{\left( i \right)}} = \left( {\vec{Y}^{{\left( i \right)}} + \Delta \vec{Y}} \right)_{n} } \\ {\Omega = \Omega _{n} } \\ \end{array} } \right)}} } \right]\left\{ {\begin{array}{*{20}c} {\delta \vec{Y}^{{\left( i \right)}} } \\ {\delta \Omega } \\ \end{array} } \right\}$$
(55)

Given that the desired value of the cost function is zero, the values of the unknown coefficient variations can be determined as:

$$\left\{ {\begin{array}{*{20}c} {\delta \vec{Y}^{{\left( i \right)}} } \\ {\delta \Omega } \\ \end{array} } \right\} = - \left[ {\left. {\left[ {\begin{array}{*{20}c} {\frac{{\partial \vec{\Lambda }^{{\left( i \right)}} }}{{\partial \vec{Y}^{{\left( i \right)}} }}} & {\frac{{\partial \vec{\Lambda }^{{\left( i \right)}} }}{{\partial \Omega }}} \\ {\Delta \vec{Y}^{{\left( i \right)}} } & {\sigma ^{2} \Delta \Omega } \\ \end{array} } \right]} \right|_{{\left( {\begin{array}{*{20}c} {\vec{Y}^{{\left( i \right)}} = \left( {\vec{Y}^{{\left( i \right)}} + \Delta \vec{Y}} \right)_{n} } \\ {\Omega = \Omega _{n} } \\ \end{array} } \right)}} } \right]^{{ - 1}} ~\left\{ {\begin{array}{*{20}c} {\vec{\Lambda }^{{\left( i \right)}} } \\ \mathbb{R} \\ \end{array} } \right\}_{n} ,$$
(56)

Consequently, the updated value for amplitude and frequency increments will be as follows

$$\left\{ {\begin{array}{*{20}c} {\Delta \vec{Y}^{{\left( i \right)}} } \\ {\Delta \Omega } \\ \end{array} } \right\}_{{n + 1}} = ~\left\{ {\begin{array}{*{20}c} {\Delta \vec{Y}^{{\left( i \right)}} } \\ {\Delta \Omega } \\ \end{array} } \right\}_{n} + \left\{ {\begin{array}{*{20}c} {\delta \vec{Y}^{{\left( i \right)}} } \\ {\delta \Omega } \\ \end{array} } \right\}$$
(57)

The process continues until acceptable results are obtained that satisfy both the energy balance equation and the ARC length equation to a specified level of accuracy.

Solution verification

To achieve an efficient approximation of the solution in a weak formulation for a differential equation, it is important to ensure that the shape functions align with the boundary requirements of the problem, are linearly independent, and satisfy the completeness condition. Additionally, it would be beneficial to select shape functions that promote convergence with a low number of shape functions. The shape functions utilized in this procedure are provided below, and they satisfy all the aforementioned requirements30.

$$\phi _{n} \left( \varrho \right) = 1 + \cos \left( {\frac{{\left( {2n - 1} \right)\pi \cdot \varrho }}{R}} \right)$$
(58)
$$\psi _{n} \left( \zeta \right) = \sin \left( {\frac{{n\pi \zeta }}{{h_{f} }}} \right)$$
(59)

To validate the solution procedure, the Finite Element (FE) based (COMSOL Multiphysics 6.1 software) is utilized. For the initial model, the micropillar effects in the bottom of the flexible silicon are neglected and only air is considered in the gap between the flexible and fixed plate. As can be seen in Fig. 2a, the developed model and the results extracted from the FE software are a very good accordance. In this case, the pressure load exerted on the top surface of the flexible plate is increased gradually, and the silicon membrane displacement is achieved according to the pressure load. Figure 2b indicates the contour of the displacement of the flexible plate for the case without a micropillar array. The structured grid is employed in COMSOL to perform the solution. Since the numerical works need the grid check study, Fig. 2c exhibits the grid independence check results. As can be seen, the displacement of the center of the silicon plate is considered for studying the grid size. After assuming a 200,000 number for grids, the solution will be independent of the grid size. Figure 2d represents the flowchart of the solution procedure.

Fig. 2
figure 2

Validation of the results for the case without micropillars array, Maximum displacement of the silicon plate (a), Countour of the displacement of the flexible plate (b), Plate center displacement for different grid sizes (c), Flow chart of the solution procedure (d).

Full size image

As in the present work the array of the Micropillars (depicted in Fig. 1) assumed between the flexible and fixed plates as an elastic bed, the results of the present work are compared to the extracted results from the COMSOL. There is a very good agreement between the results (Fig. 3a). Figure 3b indicates the contour of the displacement of the flexible plate for the case with a micropillar array. The properties and the geometrical configuration of the micropillars are presented as case 1 in Table 1. The main advantage of the current method to the COMSOL is the low calculation time. In the COMSOL software, since it uses a large grid, for each case, for a Quad-core intel CPU, it takes about 30 min to converge the solution. However, for this method, the same calculation in higher precision is less than a minute.

Fig. 3
figure 3

Validation of the results for the case with micropillars array, Maximum displacement of the silicon flexible plate (a), Countour of the displacement of the flexible plate (b).

Full size image

Results and discussions

In the present section, the array of micropillars on the fixed plates is assumed as an elastic bed for the flexible plate. The micropillars are made from PDMS hydrogel30 and cover half of the area (They have been placed one in between) of the fixed plate. Four different types of PDMS are considered for the materials of the micropillars, as cases 1 to 4, in the present study. The geometrical configuration and physical properties of the different types of PDMS that have been considered for the materials of the micropillars and plates are presented in Table 1.

Table 1 Geometrical and physical properties of the case studies.
Full size table

Static analysis

Figure 4a and d demonstrate the maximum displacement of the circular plate versus the external pressure load. Increasing the pressure load causes the displacement of the circular flexible plate. The maximum displacement of the plate takes place at the center of the plate. Maximum values of Young’s modulus lead to maximum resistance of the plate against the deflection. Thus, case 4, as it has the maximum value of Young’s modulus, could tolerate the maximum magnitudes of the external pressure. Case 1 has a high sensitivity against the pressure. The external pressure is assumed to be less than 70% of the buckling of the pillars. In this range of the pressure load, before buckling, the displacement of the circular plate shows a semi-linear behavior against the exerted pressure load due to the low displacement of the micropillars. As can be expected, the high values of Young’s modulus of the pillars, in the same geometrical configurations, empower the ability of the circular plate to tolerate the higher values of the external forces. For a high-pressure load that affects the elastic bed, the structure of case 4 can be applied in the system. However, for the highly sensitive devices, according to the field of application, each design of cases 1 to 3 can be used.

Fig. 4
figure 4

Displacement of the circular plate vs. external pressure load.

Full size image

Overall, the incorporation of micropillars introduces a novel parallel stiffness to the system, which effectively reduces the overall deflection and influences the sensitivity of the plate to external pressure or force. However, when these structures are used as capacitive structures as sensors or as micro-actuators, the use of micropillars offers significant advantages, particularly in enhancing the electrostatic force due to the high dielectric constant of the materials employed. The increased dielectric constant in the micropillars amplifies the electrostatic force, which is a critical factor in improving the device’s overall sensitivity. Furthermore, the further enhancement of this effect by incorporating specific nanoparticles into the micropillars will increase the dielectric constant even more. While the elastic bed does contribute to the system’s stiffness, it is clear that it also plays a role in enhancing the electrostatic interactions and, consequently, the sensitivity.

Transient analysis

In the event of a Transinet input, a transient analysis is necessary to ascertain the dynamic behavior of the system. Hilbert expansion is used to discretize the system in a spatial domain30. Also, time integration is applied to the equation over the domain30. The equations, as discussed before, have nonlinear terms. For each time integration step, the nonlinear values are assumed to be known from the previous step and new values are achieved from the solution. For each case, constant external pressure is applied to watch the transient behavior, overshoot, and settling time. The solution of the extracted nonlinear ordinary differential equations has been performed using the 4th -order Runge-Kutta method30. It should be noted that for each case, the magnitude of pressure does not exceed 60% of the buckling pressure, thus the values of the pressure are 8 kPa, 16 kPa, 45 kPa, and 50 MPa for cases 1 to 4 respectively. The time step for the solution of the Runge-Kutta method should be at least 5 times smaller than the natural frequency of the plate. Thus, in the present study, it is assumed that 10− 8. Figure 5a and d indicate the transient behavior of cases 1 to 4 against constant external pressure load. Small values of the overshoot and settling time in the MEMS systems increase the precision of the device and the stability. So, case 4 reached the steady condition in the lesser time (less than 0.1 µs) while it has a big value of the overshoot at the beginning. Case 2 has the lowest overshoot and a fast response compared to the other cases due to the good damping effect of it. However, the worst transient response is for case 3 which has several oscillations to get the steady condition. In many medical uses sensors and MEMS devices elastic bed’s fast response to the steady-state condition and low values of the overshoot are so important. In case 3, the spring effect of the system could overcome the damping effects of the system and as a result, the system shows some oscillations at the first steps of the solution to get the steady condition.

Fig. 5
figure 5

Displacement of the circular plate due to constant external pressure vs. time.

Full size image

Frequency response analysis

As mentioned above, the Frequency Response Analysis can be performed by assuming an external force (here external pressure load) that has a fixed value term plus a fluctuating term (sinusoidal) (indicated in Eq. 56). To get the frequency response, the values of the ω are varied from 0 to the higher values (nominal infinite values) to capture the amplitude of the system oscillations, and the behavior of the system is considered. For each frequency, an amplitude can be achieved and the aim of the frequency analysis is the study of the system behavior in each frequency and capture the resonance frequencies of a system. In Fig. 6a and d, the frequency response of each case is demonstrated for cases 1 to 4 respectively. It should be mentioned that the analysis has been performed for two different magnitudes of the pressure load, and the plate displacement amplitude for each case is extracted from the solution.

Fig. 6
figure 6

Frequency response analysis of cases.

Full size image

From Fig. 4, it can be understood that increasing the magnitude of the external pressure didn’t change the values of the resonance frequency while increasing the amplitude. Also, as is expected, the system is softened by enhancing the pressure load, however, in case 4, it caused a nonlinear behavior and after the resonance frequency, the system showed hardening. Another main achievement of the frequency analysis is that by increasing Young’s modulus and hardening the micropillar materials, the magnitudes of the resonance frequency are also grown. It can be seen that case 1 which has the lowest Young’s modulus has also a low resonance frequency (about 0.7 MHz) and case 4 has the maximum value (60 MHz). In some medical applications, like Capacitive Micromachined Ultrasonic Transducers (CMUTs), higher frequency resonances are necessary to design high-performance devices. In this application, the resonance frequency must be greater than 10 MHz. Therefore, the structure of case 4 can be useful in such kinds of applications. However, in highly sensitive measuring devices like heart rate capturing devices, lower values of the frequency resonance are needed. In case 4, it is obvious that increasing the pressure leads to the system hardening due to higher values of Young’s modulus. It can be concluded that case 3 is the best option to use in the CMUT devices. However, in the frequency response of cases 1 to 4, there is no secondary resonance in the curve. Secondary resonances don’t have an important role in the elastic bed devices in MEMS applications. But, in CMUTs, the appearance of the secondary resonances can help to capture more clear and more precise images.

Effects of the geometrical configuration

In the present part, the effects of the changing of the geometrical configuration are investigated on the performance and the response of the circular plate. Table 2 presents the configuration of the circular plate and micropillar array.

Table 2 Geometrical and physical properties.
Full size table

Static analysis

The maximum displacement of the flexible circular plate and the maximum tolerable external load are highly dependent on the mechanical properties of both plate and micropillars and their geometrical configuration. In the present case, a low Young’s modulus PDMS is used in the micropillars, and the height of the pillars is increased. however, increasing the thickness of the circular plate leads to enhancement of the maximum tolerable external pressure load. Figure 7 indicates the maximum displacement of the circular plate vs. external pressure. The maximum pressure is kept at less than 70% of the buckling load.

Fig. 7
figure 7

Maximum static displacement of the circular plate vs. pressure load.

Full size image

Transient analysis

As mentioned before, the transient analysis is one of the main steps in the designing of elastic micro-beds. The dynamic time-dependent response of the system is shown in Fig. 8. As is clear the fast response and small value of the overshoot in these systems is associated with the geometrical configuration and the mechanical properties.

Fig. 8
figure 8

Transient behavior against the pressure.

Full size image

In the present case, increasing the thickness of the circular plate couldn’t overcome the soft PDMS materials, and the height of the Pillars. Therefore, due to low damping effects, it takes more than 4 µs for the oscillation to be damped. The overshoot from the stable point is also higher in this case due to the high spring effect of the pillars. So, in some highly accurate applications, it is recommended to use high Young’s modulus materials and lesser height for pillars.

Frequency response analysis

The frequency response analysis of this case has been depicted in Fig. 9 for various exerted pressure. In this case, as is clear, using soft material with low Young’s modulus and high height, while increasing the circular plate thickness, could increase the resonance frequency of this case. However, in this case, increasing the frequency of the external fluctuating term of the pressure caused the system hardening and high nonlinear behavior of the system. As is expected, the increasing external pressure augmented the amplitude of the displacement of the plate while enhancing the nonlinear behavior of the plate response.

Fig. 9
figure 9

Frequency response analysis.

Full size image

Conclusion

In the present study, an array of micropillars made of PDMS polymers is considered an elastic bed between two microcircular fixed and flexible plates. The Neo-Hookean model is used to extract the governing equations, and the solution method is based on Galerkin-based discretization in both spatial and temporal domains. The following results are obtained. Using the energy balance principle and a Fourier transform to expand the steady-state solution, frequency response analysis is performed using a continuation-based approach.

The unknown coefficients of the expansion series are computed by a physically gradient descent-based learning strategy. In addition, a dynamic step size approach for frequency increments is chosen and implemented using the ARC length method to efficiently follow the solution path. The following results are deduced from this study:

  • Increasing Young’s modulus of the micropillar materials, in the same geometrical configurations of both pillars and circular plates, leads to the enhancement of the maximum tolerable external pressure load by the circular plate before buckling. So, case 4, which has the highest Young’s modulus, can withstand again higher pressures.

  • Mechanical properties of the Micropillars affect the transient response of the system. Young’s modulus of about 710 kPa (case 2) has the maximum damping effect and small overshoot which can be used in highly precise sensors. On the other hand, case 4 which has the biggest Young’s modulus has a fast transient response while having a big overshoot.

  • Frequency response analysis of all cases has a nonlinear behavior in the resonance frequency. Increasing the pressure load enhances the displacement amplitude of all cases. In cases 1 to 3, increasing the fluctuating term of the pressure softened the system and the pick tends to the right-hand side. In case 4, augmentation of the pressure load from a specified limit caused the system to harden.

  • In cases 1 to 4, the high damping effects of the system caused the system not to have secondary resonances.

  • Increasing the thickness of the circular plate enhances the maximum tolerable pressure load while increasing the settling time in the dynamic response.

  • Soften the micropillar material and increasing the height caused to appearance of the secondary resonance in the frequency response. Also, increasing the thickness of the plate leads to the system hardening in the frequency response.

As a prospective research project, one avenue for further investigation would be to enhance the configuration of the pillar and the array with tilted micropillars when the micropillars are subjected to a combination of compression and bending. This approach could result in a considerable reduction in the equivalent stiffness.