Introduction

The stability of high rock slopes in expressway widening projects is influenced not only by geological conditions, rainfall, and seismic events, but more significantly by engineering activities. Given that traffic is not halted during the widening process, ensuring stability during excavation becomes crucial, presenting a complex challenge in the realm of multi-parameter geotechnical engineering1,2,3,4. During the expressway widening, secondary excavation and unloading of slopes is required, as well as the removal of their original supporting structures, leading to the redistribution of slope stresses; if not handled properly, slope instability failure is highly probable5,6. Therefore, thorough investigation of slope stability and reliability based slope stability analysis during both construction and long-term operation is imperative7,8,9. Implementing effective slope supporting and reinforcing measures is crucial to safeguarding slope safety and stability in expressway widening projects.

Anchor bolt reinforcement, achieved by applying prestress to establish a stress compression zone within its zone of influence, plays a crucial role in controlling the deformation of rock masses on slopes to ensure safety and stability10,11. Significant research has been conducted on the stability of slopes reinforced with prestressed bolts. In a FLAC3D numerical analysis, Li Jian12 argued that reinforcing a high and steep slope with prestressed bolts does not enhance the shear strength of the potential sliding surface. Instead, the primary function of this reinforcement method is to restrict the displacement of the potential sliding mass within the slope. Based on the conventional Newmark method, Jia Zhibo13 explored the stability of prestressed bolt-reinforced slope under seismic action through the pseudo-dynamic calculation. Bai Haifeng14 investigated the preferable slope strengthening mechanism of prestressed anchor cable under strong earthquake by FLAC3D. Wang Zhide15 studied the effects of prestressed anchor cable length, spacing and angle on the rock slope stability, and proposed parameter optimization on that basis. Utilizing the field pull-out test data, Gong Xiaonan16 built a mechanical model for force transfer mechanism of tension-type prestressed anchor cables through double strata. Ren Xingyun17 completed the preliminary design of anchor cable based on engineering experience, and quantitatively optimized the cable arrangement parameters for rectangular roadway roofs. A Cailong18 introduced an innovative method for calculating the direction angle of prestressed anchor cables, accounting for slope and sliding surface inclinations. Additionally, new materials such as basalt fiber bolts and NFR (Negative Poisson Ratio) prestressed bolts are increasingly used in slope reinforcement, prompting further studies on the anchoring mechanisms of these materials19,20.

In summary, the existing methods for enhancing slope stability using prestressed bolts are primarily assessed through numerical analysis based on the principles of slope deformation. However, due to the lack of updated anchoring design specifications, the current guidelines only outline the permissible range for anchoring angle design in support structures, omitting specific provisions for designs informed by the mechanical properties of the structures and the distribution of anchor bolts along the depth of anchoring21,22,23,24,25,26. This study initially scrutinized the characteristics of slope deformation during excavation and the distribution of axial forces in the supporting structure of an expressway widening project. Subsequently, by exploring various anchoring angle scenarios, the study determined the optimal anchoring angle for prestressed bolt-reinforced slopes by considering a blend of slope deformation characteristics and the maximum axial force acting on the supporting structure. Lastly, leveraging the mechanical attributes of prestressed bolt structures, the study enhanced the computational formula for the optimal anchoring angle of bolt-reinforced slopes, aiming to provide valuable insights for prestressed bolt construction in expressway widening projects.

Design of centrifugal model test

Model design

The TLJ-3 geotechnical centrifuge at Chang’an University, with a maximum capacity of 60 g·t, was utilized for the experiments. The setup included a rotating device, a model casing measuring 700 mm × 360 mm × 500 mm, an acquisition system, a transmission system, and a processing system. The configuration of the test equipment is illustrated in Fig. 1.

Figure 1
figure 1

TLJ-3 centrifuge in Chang’an University.

Full size image

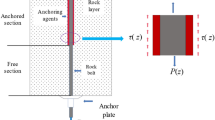
A high bedding rock slope (K593 + 260–K593 + 555) from the Beijing–Shanghai Expressway Widening Project (Laiwu-Linyi section) was chosen as the prototype slope for the centrifugal model test. The existing slope was 40.7 m high and 20 m long, with a class I/II slope rate of 1:0.75, a class III/IV slope rate of 1:1, a downdip stratum inclination of 10°, bolt diameter of 32 mm and an anchoring angle of 20°. From top to bottom, the stratum lithology was heavily weathered limestone and moderately weathered limestone. After comprehensively considering factors like the size of model casing and boundary conditions, the similarity ratio n of centrifugal model test was set to 1:100.based on dimensional analysis, the similarity relationship of each parameter is shown in Table 1. Given the stratigraphic complexity of the prototype slope, the geometric dimensions of the test slope were determined according to the similarity ratio relationship. The profile of the slope utilized in the centrifugal model test is illustrated in Fig. 2.

Table 1 Correspondence between physical quantities of archetypal-centrifugal model.
Full size table
Figure 2
figure 2

Profile of excavation slope in centrifugal model test (unit: mm).

Full size image

Test materials

Anchor bolt material

Taking into consideration the similarity ratio, the elastic modulus of copper was set to 70 GPa, with good ductility. Pure copper strips measuring 5.0 mm in width and 0.8 mm in thickness were used, as depicted in Fig. 3(a). To mimic the grouting body, the entire length of the prestressed bolt was coated with epoxy resin, with a 10 cm long anchorage section. The prestress of the bolt was controlled using a customized prestress application device27, as demonstrated in Fig. 3(b).

Figure 3
figure 3

Schematic diagram of prestress bolt device. (a) Prestressed anchor bolts material. (b) Prestress application device.

Full size image

Slope material

Due to the model size and experimental operability constraints, epoxy resin was used to simulate the grouting material. During the test, the physical and mechanical parameters of the model soil sample should be identical to those of the actual soil sample. Considering that the shear strengths of heavily and moderately weathered limestone were relatively low in the field geological exploration data, and that limestone was preliminarily simulated according to a proportion of m (gypsum): m (barite powder): m (cement): m (water) = 1:0.6:4:0.2, the strength parameters of simulated limestone differed insignificantly from those of dynamically compacted soils. To ensure the continuous repeatability of the test, the model soil was obtained by dynamic compaction of soils with different water contents, which was used to simulate heavily and moderately weathered limestone.

Through such geotechnical tests as water content test, consolidation test and direct shear test, the values of model soil mechanical indices, including density ρ, water content w, compression modulus Es, cohesion c and internal friction angle φ, were respectively obtained, as listed in Table 2.

Table 2 Mechanical parameters of slope rock in centrifugal test.
Full size table

Layout of testing components

Deformation of anchor bolt was measured by attaching strain gauge onto the bolt surface, and the bolt axial force was inversely calculated by the amount of deformation. Miniature earth pressure cells were used to measure the earth pressure in the slope during the excavation, while a laser rangefinder was utilized in the centrifuge to measure the horizontal displacement at the top of the slope. Figures 4 and 5 present various testing components and their planar layout.

Figure 4
figure 4

Testing components. (a) Strain gauge. (b) Miniature Earth pressure cell. (c) Laser rangefinder.

Full size image
Figure 5
figure 5

Layout of testing components (unit: mm).

Full size image

Test schemes and procedure

Test schemes

Different anchoring angle conditions for the centrifugal model test of prestressed bolt are detailed in Table 3.

Table 3 Prestressed bolt centrifugal test schemes.
Full size table

Test procedure

  1. 1.

    Preparation. Contour lines were delineated on the side walls of the model casing, including the primary excavation line, the secondary excavation line and the layered filling line, as shown in Fig. 6 (a).

  2. 2.

    Layered filling. In order to achieve a 10° inclination for the potential sliding surface of slope, one side of the model casing bottom was raised (15 cm) to ensure that the angle between the casing and the ground was 10°. According to the size of slope model and the degree of compaction, a total of 11 layers were filled, and the thickness of each paving was 4 cm, as shown in Fig. 6 (b).

  3. 3.

    Embedding of testing components. After filling a certain number of layers (5, 7 and 9), horizontal and vertical earth pressure cells were embedded, and a 6-mm square steel model was placed with a protractor while reserving the bolt holes, as illustrated in Fig. 6 (c).

  4. 4.

    Primary excavation E0. The initial slope was formed according to the contour line on the glass plates of model casing side walls, and the excavation was completed one time without consuming excessively long time. After slope cutting, the epoxy-coated anchor bolt attached with a strain gauge was placed into the holes, and then prestress was applied, as depicted in Fig. 6 (d).

  5. 5.

    Secondary excavation. A graded excavation process (E1→E2→E3→E4) was executed. Following each phase of excavation, the centrifuge was activated to monitor the displacement of the slope top and the axial force on the anchor bolts. Figure 6 (d) showcases the centrifugal acceleration duration curves post various excavation stages.

  6. 6.

    Centrifuge activation and test data collection. After completion of bolt support, the centrifuge was initiated, and the centrifugal acceleration was slowly increased from 0 g to 100 g and maintained for 5 min, after which it was gradually decreased from 100 g to 0 g.

Figure 6
figure 6

Test flow chart. a. Contour line delineat. b. Layered filling. c. Testing component embedding. d. Slope excavation.

Full size image

Analysis of test results

Horizontal displacement at slope top

The excavation process during the test followed the principle of graded excavation from top to bottom: Class IV slope excavation E1 – Class III slope excavation E2 – Class II slope excavation E3 – Class I slope excavation E4. Figure 7 illustrates the response law of horizontal displacements at the lower slope top in various construction stages.

Figure 7
figure 7

Curves of cumulative horizontal displacement at slope top for different anchoring angles. (a) Cumulative horizontal displacements at slope top under different anchoring angles in various excavation stages. (b) Incremental horizontal displacements at slope top under different anchoring angles in various excavation stages. (c) Variations of cumulative horizontal displacement at slope top with the anchoring angle.

Full size image

It is evident from Fig. 7 (a)–(b) that during graded excavation of the slope, the cumulative horizontal displacements at the slope top all increased nonlinearly for different anchoring angles. The increase in cumulative displacement at slope top during the primary excavation E0 was up to 2.0 mm, while was less than 1.0 mm during the secondary excavation, indicating more obvious increase in the displacement during the primary excavation than that during the secondary excavation. In the secondary excavation stage of slope top E1, the horizontal displacement at slope top increased the most, which was attributable to the destabilization of originally stable slope resulting from the excavation disturbance. In the secondary excavation stage of slope foot E4, the horizontal displacement at slope top increased significantly, mainly due to the reduced stability caused by the removal of the key anti-sliding block at the base of the slope.

Figure 7 (c) illustrates the variation in horizontal displacements at the slope top in relation to the anchoring angle (10°–60°). The results show a trend where the displacements initially decrease and then increase as the anchoring angle varies, indicating the presence of an optimal anchoring angle. For anchoring angles of 10°–20°, there were minimal cumulative displacements (all approximately 2 mm), accompanied by small increases in the cumulative horizontal displacement at the slope top. This can be attributed to the small included angle between the bolt and rock stratum, as well as the limited effective anchoring length at lower anchoring angles. Increasing the anchoring angle appropriately can extend the effective anchoring length, thereby enhancing slope stability. In the case of anchoring angles ranging from 20°–30°, there was a gradual but slight increase in cumulative horizontal displacements at the slope top. Subsequently, for anchoring angles of 30°–60°, these displacements experienced a significant increase, reaching a maximum cumulative displacement of over 3 mm at anchoring angles of 45°–60°. This notable increase can be attributed to the excessive anchoring angle leading to a gradual reduction in the effective support length of the prestressed bolt, thereby weakening its reinforcement effect and consequently undermining slope stability.

In summary, during various stages of excavation, the cumulative horizontal displacements at the slope top exhibited a nonlinear increasing trend. At anchoring angles of 10°–30°, the displacements were all less than 1 mm during the primary excavation, while during the Class IV and III slope excavation, the displacements changed significantly. When the anchoring angles were 30°–45°, the increases in horizontal displacements at slope top were large, leading to weakened reinforcement effect of the bolt. At anchoring angles of 45°–60°, the cumulative horizontal displacements at slope top all exceeded 3 mm, and the changes in displacement were significant, indicating that the reinforcement effect was insignificant when the anchoring angle was larger than 45°. Thus, it is recommended that the anchoring angle of prestressed bolt in the project should not exceed 45°, consistent with the slope anchoring angle range of 15°–45° stipulated in the Design Code for Highway Landslide Control.

Distribution of anchor bolt axial forces

The axial forces at different positions of prototype prestressed bolt were calculated from the strain gauge readings at various sections of model bolt by Eq. (1):

$$N={\text{n}}{\varepsilon _i}EA$$
(1)

where E represents the elastic modulus of bolt (GPa); A represents the sectional area of bolt (mm2); εi denotes the strain of each section; n is the similarity ratio.

The distribution of prestressed anchor bolt axial forces along the depth direction, at various anchoring angles, was obtained by extracting the axial forces at different measuring points, as displayed in Fig. 8a and e.

Figure 8
figure 8

Distributions of anchor bolt axial forces at different anchoring angles. (a) 10°. (b) 20°. (c) 30°. (d) 45°. (e) 60°.

Full size image

As is clear from Fig. 8, the axial force in the free section of the anchor bolt basically remained unchanged at about 100 kN, which was in tension. The axial force in the anchorage section of the anchor bolt decreased along the anchoring depth towards the bottom. With the progress of excavation, the axial force in the free section decreased gradually, the peak axial force near the weak plane decreased significantly, and the axial force in the free section also presented a monotonic decreasing trend. At anchoring angles of 10°–60°, the peak axial forces after the excavation of the slope foot were 60.5%, 62.45%, 56.10%, 50.13% and 41.20% of the pre-excavation peak values, respectively, indicating a great loss in the original bolt stress after the slope excavation and stabilization. The attenuation amplitude of bolt first increases and then decreases, and when the bolt angle exceeds 20°, the prestress attenuation amplitude of bolt increases significantly with the increase of anchoring angle, indicating that there is an optimal anchoring angle.

Combining Fig. 8 (a)–8 (e), it could be found that the anchoring angle of bolt significantly impacted the amplitude of prestressed bolt prestress attenuation, while having an insignificant impact on the pattern of axial force distribution in the anchorage section. The greatest axial force attenuation in the anchorage section was observed when the anchoring angle range was 45°–60°.

The distribution of earth pressure in slope

To analyze the slope stability in the expressway widening project before excavation, a centrifuge was used to gradually increase the centrifugal acceleration of the slope until reaching instability failure. Eight stages of acceleration (20–40 g–60–80 g–100–120 g–130–140 g) were set up. In the first six stages, the centrifugal acceleration was increased at a rate of 20 g/stage. Thereafter, the acceleration was increased at a rate of 10 g/stage. Each stage was stabilized for 3 min. Figure 9 depicts the earth pressure variations with time. The time-varying curves of earth pressure at different positions of the slope top, mid-slope and slope foot are presented in Fig. 10 at an anchoring angle of 10°.

Figure 9
figure 9

Time change curve of earth pressure under different accelerations.

Full size image
Figure 10
figure 10

Variation law of earth pressure in slope. (a) Earth pressure variations with anchoring angle (100 g). (b) Earth pressure variations with anchoring angle (140 g).

Full size image

Analysis of Fig. 9 reveals that the earth pressure remained constant during uniform rotation with accelerations ranging from 0 to 120 g, signifying a state of stability in the slope throughout the centrifugal acceleration process. Subsequently, as the acceleration increased to 140 g, there was a gradual rise in earth pressures at the top, mid-slope, and foot of the slope. However, with acceleration exceeding 140 g, a slight decrease in earth pressure at these locations was observed, indicating a developing trend of deformation and sliding in the slope. Notably, the increase in earth pressure at the slope’s crest was less rapid compared to that at the mid-slope and slope foot, pointing towards a continuous rise in the sliding force and a clear trend towards sliding.

According to Fig. 10, for slopes reinforced with prestressed bolt at different anchoring angles, the earth pressure intensity rankings were earth pressure at slope foot > earth pressure at mid-slope > earth pressure at slope top. This was because the overlying soil load borne by the slope foot was greater than that at the mid-slope and slope top. As the anchoring angle increased, the earth pressures at different positions on the slope initially increased and then decreased. Particularly, the earth pressures sustained by the slopes with anchoring angles between 45° and 60° were lower than those at the same positions with anchoring angles between 10° and 30°. This difference was attributed to the slopes with anchoring angles of 45°–60° exhibiting a tendency towards sliding deformation towards the free face, resulting in reduced earth pressure and indicating the presence of an optimal anchoring angle.

Evaluation of reinforcement effect

As suggested by the horizontal displacement of slope and the distribution of prestressed bolt axial forces in various excavation stages, the slope stability was influenced by the anchoring angle. To further evaluate the slope reinforcement effect at different anchoring angles after excavation, the maximum axial forces of prestressed bolt at different anchoring angles were selected to establish the relationship curves between axial force and acceleration, as displayed in Fig. 11.

Figure 11
figure 11

Curves of axial force of anchor bolt at weak surface against acceleration with different anchoring angles. (a) Anchoring angle of 10°. (b) Anchoring angle of 20°. (c) Anchoring angle of 30°. (d) Anchoring angle of 45°. (e) Anchoring angle of 45°.

Full size image

As indicated by the relationship between the prestressed bolt axial force and acceleration at various anchoring angles shown in Fig. 11 (a)–(e), a slow increase point A, a steep increase point B and a flatten out point C were present in the maximum axial force–acceleration curves, according to which the curves could be divided into four stages. All of these curves presented a variation pattern of “slow increase – uniform increase – steep increase – basic stabilization”.

In Fig. 11 (a), the maximum axial force of prestressed bolt increased slowly at centrifugal accelerations of 0–80 g, while increased at a constant rate within 80–100 g, indicating that the anchoring force gradually exerted its reinforcement effect. A sharp increase in maximum axial force was noted within 80–120 g, suggesting that the slope began to gradually lose stability. When the acceleration was up to 140 g, the axial force reached the ultimate load (100 kN) of bolt, resulting in the instability failure of slope. The centrifugal acceleration at that time was the critical acceleration αr for slope failure. Suggestively, the bolt was in the working state during stage AB, in the limit state at points B, C, and after point C, the slope underwent instability failure. Hence, the maximum axial force–centrifugal acceleration could characterize the progressive failure process of the slope. Similarly, the accelerations of slope instability failure under different anchoring angles could be derived. Specifically, the critical centrifugal accelerations for slope instability were 130 g, 140 g, 140 g, 120 g and 120 g, respectively, when the anchoring angles were 10°, 20°, 30°, 45° and 60°.

A proportional relationship existed between the slope stability and the centrifugal acceleration25. The maximum critical acceleration occurred at anchoring angles ranging from 20° to 30°. This indicates that at anchoring angles conducive to heightened slope instability failure, the slope exhibited the highest stability and the most effective reinforcement. In conclusion, an optimal anchoring angle was identified for prestressed bolt-reinforced slopes.

Conclusions

Five centrifugal model tests were conducted to investigate the mechanical properties of prestressed bolts during the entire slope excavation process. The test analyzed the supporting structure at five varying anchoring angles to examine the distribution pattern of axial force in prestressed bolts and the horizontal displacement characteristics at the top of the slope. The study also evaluated the effectiveness of slope reinforcement, leading to the following conclusions:

  1. 1)

    The cumulative horizontal displacement at the slope’s peak demonstrates a nonlinear increasing trend, with significant variations in displacement increments during different excavation stages. Minor increases occur during soil mass excavation at the upper part of the slope, while rapid escalation is observed during the excavation of the slope foot. It is suggested that graded excavation should be adopted for the secondary excavation of slope engineering. Moreover, it is recommended to appropriately reduce the rate of excavation when working on the top and foot of the slope .

  2. 2)

    The axial force of the bolt in the anchorage section follows an attenuating distribution curve along the anchoring depth. As excavation progresses, the prestress in the anchorage section gradually decreases, leading to a notable reduction in peak axial force near the weak plane. Moreover, the axial force distribution in the free section of the bolt exhibits a monotonically decreasing pattern.

  3. 3)

    The angle of anchorage significantly influences the magnitude of bolt prestress attenuation but shows little impact on the axial force distribution in the anchorage section. Notably, at anchoring angles between 45° and 60°, there is a pronounced attenuation in the bolt’s axial force within the anchorage Sect. 

  4. 4)

    The maximum axial force–acceleration curves of the bolt reveal three distinct feature points: a slow increase at point A, a steep rise at point B, and a plateau at point C, displaying a progression of “slow increase – uniform increase – steep increase – basic stabilization.” During stages AB, the bolt operates, reaching a limit state at points B and C. Beyond point C, the slope experiences instability failure, marking a critical point in the slope’s progressive failure process.