Introduction

With the rapid developments of big data, computing power and algorithms, artificial intelligence has entered a new development trend in recent years. The evolution of artificial intelligence has greatly advanced the development of the computing science. Deep learning technology is constantly developing and improving, which in turn enables the computer to handle highly complex tasks such as image recognition, speech recognition and text analysis. Deep learning demonstrates significant values in many fields, such as multilayer perceptron applied in nuclear binding energy predictions1, convolutional neural network applied in image recognition2, generative adversarial network applied to synthetic financial scenarios generation3.

Partial differential equation (PDE), with integer-order or fractional derivatives, is an important branch of mathematics, which is involved in many disciplines, such as quantum mechanics and fluid mechanics in physics, heat conduction and structural mechanics in engineering, neuronal activity and cancer cell growth in medical science, option pricing and risk valuation in economics. With the development of integer-order calculus, fractional calculus went through several stages of decline and has developed rapidly. Compared to integer-order calculus, fractional calculus can characterize complex evolutionary processes with time span and spatial domain value correlation. With the need for theoretical and applied researches, the definitions and property theorems of fractional calculus are constantly developing and improving. The classical definitions contain fractal derivative4, conformable fractional derivative5, Riemann-Liouville fractional derivative6, Caputo fractional derivative7, Caputo-Fabrizio fractional derivative8, Atangana-Baleanu fractional derivative9, and so on. At present, many integer-order derivative models have been transformed into fractional derivative models, and the analytical and numerical methods originally used to solve integer-order equations have been developed to deal with fractional differential equations. The continuous updating of models and the continuous improvement of algorithms are the focus of researches in various disciplines.

With the in-depth research of machine learning, the physics-informed neural networks (PINNs) were put forward by Raissi et al10.. The algorithm combines PDE’s physical constraints with the neural networks, and then provides a new way to solve PDE more efficiently and accurately. Specifically, they constructed residual terms for the PDE, initial conditions and boundary conditions in partial differential models, then added the constructed loss terms to the loss function of neural network, finally approximated solutions by continuously optimizing the parameters of the neural networks. The PINNs algorithm can be well applied to various types of equations and obtain high precision solutions11,12,13,14. Recently, scholars have made some improvements based on the PINNs and proposed many new methods, such as nPINNs15, ModalPINNs16, PPINNs17, MO-PINNs18, B-PINNs19etc. However, these methods are mainly used to deal with a kind of PDEs with known free boundary conditions. Wang and Perdikaris20, based on PINNs, proposed a neural network algorithm to solve PDE with unknown free boundary.

The solutions of PDE with unknown free boundary are the most difficult and complicated, because such PDE often does not have explicit solutions. The free boundary problems widely exist in research fields such as physics and finance. In the study of American options, we can regard American options as a kind of PDEs with unknown free boundaries. American options are exercised at any time before the expiration date, while European options only are exercised when they expire. It is precisely because of the flexibility of American options in exercising that American options are favored by investors. Investors can choose whether to exercise or not according to the true market situation, so investors can better avoid the risks in market, which proves that American options can better realize hedging, thereby increase investors’ returns. At present, scholars’ researches on American options mainly focus on numerical methods such as finite difference method21, binomial trees method22, Monte Carlo simulations method23, finite element method24and so on. These traditional numerical methods have their own advantages, but also face some disadvantages. For example, when dealing with high-dimensional data, traditional numerical methods will encounter the problem of the curse of dimensionality, which may make the problems difficult to solve. The neural networks can be well applied to high-dimensional data, but for now, using the neural network methods to analyze American option pricing from the perspective of PDE is still in a development stage. Louskos25used the PINN algorithm proposed by Raissi to study American call option from the perspective of Black-Scholes equaiton. Nwankow et al26. designed DNN to analyze American put option pricing together with the front-fixing transformation. Gatta et al27. studied American options based on PINN algorithmic, the trick is to perform more training steps of the solution network against a single step of free boundary at each epoch. Started from the perspective of the Black-Schoels equation, scholars employed the neural networks to analyze the pricing of American put option and validated the proposed algorithm by numerical simulation methods.

The work explores the effectiveness of neural network algorithms and fractional calculus in the pricing problem of American options. Through introducing the solution assumption and the data enhancement layer, the combined physics-informed neural network is designed for the free boundary problems of the generalized Black-Schoels equations with Caputo, Caputo-Fabrizio and Atangana-Baleanu-Caputo fractional derivatives. The transfer learning is applied to the algorithm proposed in the work to predict the true market. Real market simulation demonstrates the effectiveness of the proposed algorithm, which makes up for the lack of analysis of real market data in relevant literature on American option pricing.

Neural network algorithm

The section designs the combined PINN for the free boundary problem of American put option and introduces the transfer learning method.

Combined physics-informed neural network

The classical American put option pricing model is based on the integer-order Black-Scholes equation. American put option price of the work is proposed to meet the space-time fractional Black-Scholes models, which adopts the nonlocal fractional derivatives to displace integer derivative of the classical equation. Fractional derivative model is the promotion and unification of the classical model, which better characterizes the fractal structure of the market.

$$\begin{aligned} & _{C/CF/ABC}D^{\alpha }_t V+rS _{C/CF/ABC}D^{\beta }_S V+\frac{1}{2}\sigma ^2S^2 _{C/CF/ABC}D^{2\beta }_{SS} V=rV,~~B(t)<S<+\infty ,~~0\le t<T, \nonumber \\ & V(S,T)=(K-S)^+,~~~~B(T)<S<+\infty ,\nonumber \\ & V(B(t),t)=K-B(t),~~~0\le t<T, \nonumber \\ & D_S V(B(t),t)=-1,~~~0\le t<T, \nonumber \\ & \lim _{S\rightarrow +\infty }V(S,t)=0,~~~0\le t<T, \nonumber \\ & B(T)=K. \end{aligned}$$
(1)

Where V is American put option price, which depends on the underlying asset price S and the time t. \(\sigma ,~r,~K,~T\) respectively denote the volatility, the risk-free interest rate, the exercise price and the expiration time. B(t) is an unknown free boundary. The orders \(\alpha ,~\beta\) belong to (0.1]. If \(\alpha =\beta =1\), the generalized model (1) reduces to the classical Black-Scholes model28,29. If \(0<\alpha ,~\beta <1\), \(_C D\) , \(_{CF} D\) and \(_{ABC} D\) represent the following Caputo, Caputo-Fabrizio and Atangana-Baleanu-Caputo fractional derivatives. The definitions of these three derivatives are based on the integro-differential operator, which have the global correlation performance and better reflect the historical dependence process of the system function development.

Definition 2.1

7 Caputo fractional derivative of the function \(\zeta (z)\) of order \(0<\vartheta <1\) with \(a\ge 0\) is expressed by

$$\begin{aligned} _{C}D^{\vartheta }\zeta (z)=\frac{1}{\Gamma (1-\vartheta )}[\int ^z_a\frac{\dot{\zeta }(\xi )}{(z-\xi )^{\vartheta }}d\xi ]. \end{aligned}$$
(2)

Definition 2.2

8 Caputo-Fabrizio fractional derivative of the function \(\zeta (z)\) of order \(0<\vartheta <1\) with \(a\ge 0\) is defined as

$$\begin{aligned} _{CF}D^{\vartheta }\zeta (z)=\frac{M(\vartheta )}{1-\vartheta }[\int ^z_a \dot{\zeta }(\xi )\exp (-\frac{\vartheta }{1-\vartheta }(z-\xi ))d\xi ]. \end{aligned}$$
(3)

Where \(M(\vartheta )\) is a normalization function and satisfies \(M(0)=M(1)=1\).

Definition 2.3

9 Atangana-Baleanu-Caputo fractional derivative of the function \(\zeta (z)\) of order \(0<\vartheta <1\) with \(a\ge 0\) is expressed as

$$\begin{aligned} _{ABC}D^{\vartheta }\zeta (z)=\frac{AB(\vartheta )}{1-\vartheta }[\int ^z_a \dot{\zeta }(\xi )E_\vartheta (-\frac{\vartheta }{1-\vartheta }(z-\xi )^\vartheta )d\xi ]. \end{aligned}$$
(4)

Where \(E_\vartheta\) denotes the generalized Mittag-Leffler function and \(AB(\vartheta )\) is a normalization function satisfying \(AB(0)=AB(1)=1\).

Fractional dynamic systems, as an important branch in modern control system theory, provide a more sophisticated and complex system description tool for us with their unique fractional derivative characteristics. However, this also brings corresponding challenges, namely how to ensure the existence, uniqueness, and stability of these systems. The analysis of existence, uniqueness, and stability of fractional dynamic systems is a complex and important task. Through in-depth study of the theory and application of fractional calculus, we can better understand the characteristics of these systems and provide strong support for the analysis and design of actual systems. The fractional partial differential systems under \(\psi\)-Hilfer fractional derivative30and Caputo gH-differentiability31are studied. Derakhshan32 discussed the existence, uniqueness and Ulam-Hyers stability of the definite problem of the equation with Caputo time-fractional derivatives of variable order before giving numerical approximate solutions. On the basis that the the models satisfy well-posedness in conformity to the above literatures, the work adopts the neural network algorithm to compute optimized series solutions of fractional derivative option pricing models. In deep learning, with the increase of the number of iterations, the value of the model’s loss function gradually decreases and stabilizes. This means that the model is constantly learning the patterns and features in the data and gradually optimizing its internal parameters to achieve better prediction results.

For the convenience of solving and promoting precision, V(S, t) is assumed to have the following structure,

$$\begin{aligned} & \bar{V}(S,t)=\eta _0+\sum _{i=1}^\infty \frac{\eta _{i1}}{i!}(\eta _{i2}S+\eta _{i3}t)^i. \end{aligned}$$
(5)

In terms of the designed model architecture, the work introduces the enhancement layer to expand the coordinate dimension of the training data in the combined PINN.

$$\begin{aligned} (S,t)\rightarrow \{\textrm{a}(S,t),~(S,t),~\textrm{b}(S,t)\}. \end{aligned}$$
(6)

Where \(0<a<1\) and \(b>1\) are constant parameters.

Specifically, the following two deep neural networks are employed to approximate the parameters of Eq.(4) and the free boundary,

$$\begin{aligned} NN_1(S,t,\theta )=[\eta _0,\cdots ,\eta _{i1},\eta _{i2},\eta _{i3},\cdots ]^T,~~NN_2(t,\beta )\approx B(t). \end{aligned}$$
(7)

Where \(NN_1\) is used to predict the optimized parameters of the expression (5), \(NN_2\) denotes the prediction of the unknown free boundary B(t). \(\theta\) and \(\beta\) are the parameters of the neural network. From the form of the construction solution, we can see that the expansion order increases at every time, three parameters will be added to the construction solution.

The loss functions can be constructed on the basis of Eq.(1),

$$\begin{aligned} & MSE_{FBSE}=\frac{1}{N_{FBSE}}\sum ^{N_{FBSE}}_{i=1}| _{C/CF/ABC}D^{\alpha }_t\bar{V}+rS _{C/CF/ABC}D^{\beta }_S \bar{V}+\frac{1}{2}\sigma ^2S^2 _{C/CF/ABC}D^{2\beta }_{SS} \bar{V}-r\bar{V}|^2,\nonumber \\ & MSE_{t=T}=\frac{1}{N_T}\sum ^{N_T}_{i=1}|\bar{V}(S,T,\theta )-(K-S)^+|^2,\nonumber \\ & MSE_{S=B}=\frac{1}{N_B}\sum ^{N_B}_{i=1}|\bar{V}(NN_2(t,\beta ),t,\theta )-K+NN_2(t,\beta )|^2,\nonumber \\ & MSE_{B^{'}}=\frac{1}{N_{B^{'}}}\sum ^{N_{B^{'}}}_{i=1}|D_S \bar{V}(NN_2(t,\beta ),t,\theta )+1|^2,\nonumber \\ & MSE_{S=S_{max}}=\frac{1}{N_{S_{max}}}\sum ^{N_{S_{max}}}_{i=1}|\bar{V}(S_{max},t,\theta )|^2,\nonumber \\ & MSE_{B_T}=\frac{1}{N_{B_T}}\sum ^{N_{B_T}}_{i=1}|NN_2(T,\beta )-K|^2. \end{aligned}$$
(8)

Among them, \(MSE_{FBSE}\) represents the residual function of the space-time fractional Black-Scholes equations. \(MSE_{t=T}\), \(MSE_{S=B}\), \(MSE_{B^{'}}\), \(MSE_{S=S_{max}}\), \(MSE_{B_T}\) denote the losses of the terminal condition and the boundary conditions satisfied by American put option. \(N_{FBSE},~N_T,~N_B,~N_{B^{'}},~N_{S_{max}},~N_{B_T}\) represent the corresponding batch sizes.

The parameters in the two sets of neural networks can be estimated by minimizing the loss functions. The total loss function is defined as follows,

$$\begin{aligned} & \mathcal {L}(\theta ,\beta )=\lambda _{FBSE}MSE_{FBSE}+\lambda _{t=T}MSE_{t=T}+\lambda _{S=B}MSE_{S=B}+\lambda _{B^{'}}MSE_{B^{'}}+\lambda _{S=S_{max}}MSE_{S=S_{max}}+\lambda _{B_T}MSE_{B_T}. \end{aligned}$$
(9)

Where \(\lambda _{FBSE},~\lambda _{t=T},~\lambda _{S=B},~\lambda _{B^{'}},~\lambda _{S=S_{max}},~\lambda _{B_T}\) represent the weight coefficients of various losses.

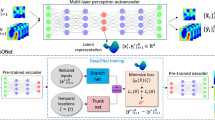
The structural diagram of the combined PINN is given in Fig.1.

Fig. 1
figure 1

The combined PINN.

Full size image

It is needed to point that the pricing strategy of the integer-order Black-Scholes model can be implemented without the solution assumption (5) and the designed enhancement layer (6). In such situation, the idea of Wang and Perdikaris20 was extended directly to solve the free boundary problem of integer-order Black-Scholes equation. In the subsequent market application, comparative analysis will be conducted on the two pricing results. From the comparison results, the concise transformation form (5) and (6) can achieve optimized results. The effect of the strategy is particularly significant in solving the space-time fractional derivative models.

Transfer learning

Transfer learning is a method in the field of machine learning and it aims to apply what has been learned in one task or domain to another related task or domain. The transfer learning method can lower the training time of the models, reduce the demand of the models for the amount of data and polish up the performance of the models.

At present, transfer learning has been applied in many fields and achieved remarkable success. Swietojanski et al33. gave the application of transfer learning method in speech recognition, such as fine-tuning on the pre-trained deep neural network to adapt to specific accents, noise environments and other application scenarios to improve the model in speech recognition performance. Taylor and Stone34gave the application of transfer learning method in reinforcement learning. Chicco et al35. found that the gene function in the existing biological database is incomplete and bimolecular experiments are slow and expensive to improve the database, so they used the method of transfer learning to extract the feature of other biological databases, then applied to the target biological system to improve the prediction performance.

In reality, we often encounter the problems that true market data is scarce, difficult or expensive to obtain. However, in the case of small amount of data, it may lead to poor learning effect of the neural network models or lead to over-fitting of the models, which in turn leads to poor generalization of the models on the test set. The work introduces the transfer learning method into American put option, aiming to enable the neural network models to be trained on a larger data set and enhance the generalization performance of the models on true market data.

Grid sampling

From the perspective of PDE, we need to establish a discrete domain to price American put option using the combined PINN. Commonly used grid generation methods include uniform grid, equispaced grid, Latin hypercube sampling, and so on. Pricing analysis of American options by generating a grid is also used in the finite difference method. Kwok et al36. gave an equispaced grid,

$$\begin{aligned} \Delta y=1.5\sigma \sqrt{t},~~\Delta t=\frac{T}{N}. \end{aligned}$$
(10)

Where \(\Delta y\) and \(\Delta t\) denote the lengths of the segmented intervals on the space dimension and the time dimension. In the finite difference method, we often need to pay attention to the generation method of the grid points, because it will affect the accuracy of the final solution, which to a certain extent has caused the limitations of the method.

Using neural network algorithm to solve American option, Nwankwo et al26. used the stretched grid method to generate data points for model training. Namely

$$\begin{aligned} y_{stretched}=y^{\sqrt{p}}_{uniform},~~t_{stretched}=t^{p}_{uniform},~p>1. \end{aligned}$$
(11)

In these papers, the authors emphasize that the methods of the grid sampling will affect the final accuracy. The work uses the above two grids and the most common uniform grid to generate the same amount of data for training and prediction, and compares American put option prices predicted by the combined PINN. The three types of grid sampling are drawn in Fig.2.

Fig. 2
figure 2

Three types of grid sampling.

Full size image
Fig. 3
figure 3

The prediction accuracy and convergence of the combined PINN.

Full size image

The experimental results are shown in Fig.3. Fig.3(a) shows the price predictions of the combined PINN for American put option in three different grid distributions. From Fig.3(a), we can see that although the grids are generated in different ways, the final prediction results are almost consistent. It is worth mentioning that, in order to further show that the algorithm proposed in the work not only solves the limitation of the grid generation, but also guarantees the prediction accuracy, we deliberately introduce the traditional binomial tree method. American put option prices predicted by the binomial tree method are taken as labels and the results from the combined PINN under uniform grid, stretched grid and equispaced grid are compared. It can also be seen from the figures that the grid generation methods don’t affect the final prediction accuracy. Fig.3(b) shows the convergence of the model under different grids during the training process. What needs to be explained is that the number of iterations of the stretched grid method is 60,000 epochs in the actual experimental process, while the uniform grid and the equispaced grid are iterated 40,000 epochs. Here, in order to compare the convergence of the three grids, we only select the loss during the first 40,000 epochs under the stretched grid method. It can be seen that the convergence speeds of the uniform grid and the equispaced grid are faster than that of the stretched grid method. For simplicity, the uniform grid is adopted to generate our training data in the following experiments.

So far, we have proved the generality and flexibility of our algorithm in grid sampling through numerical experiments, and this generality will not affect the prediction accuracy of the model to a certain extent. This also shows that our algorithm extends the grid sampling to a more general situation, and solves the limitation of some neural network algorithms that have strong restrictions on the grid sampling.

Application analysis of the real market

The section includes two aspects: firstly, comparative analysis between the work algorithm and the direct application of Wang’s neural network is made based on the classical model under \(\alpha =\beta =1\); secondly, the neural network algorithms for Caputo, Caputo-Fabrizio and Atangana-Baleanu-Caputo fractional derivative models are carried out and analyzed.

Plastic option (04/09/2022-01/10/2023) is taken as an example, whose subject code is L2302. The exercise price is 10,000 RMB and a total of 191 transaction data have been obtained, which come from the Wind database. All the work is carried out on M1 chip MacBook Air. The open source Pytorch tool is employed to build the combined neural network framework proposed in the work. The model training is carried out on the CPU. All experiments use min-batch, which reduce the training time of the system. The parameters are supposed as \(T=1\), \(K=10\), \(S_{max}=50\), \(r=0.035\), \(\sigma =0.20\). Numpy linspace function is used to evenly generate 100 points on [0, T] and 10,000 points on \([0,S_{max}]\). Numpy meshgrid function is taken to construct a uniform grid and generate training data.

Comparative analysis under the classical Black-Scholes model

The specific design of the combined PINN is as follows. In the first group of neural networks, the number of input layer’s neurons is 2, representing S and t. The numbers of hidden layers and hidden units are 10 and 100. Here we construct the fourth-order approximate solution, so the number of the output layer’s neurons is 13. In the second group of neural networks, the number of input layer neurons is 1, representing t. The numbers of hidden layers, hidden units and output layer’s neuron are 10, 100 and 1. Using the Adam optimizer to optimize the parameters in two sets of neural networks, the purpose is to share some parameters between the two sets of neural networks. Without loss of generality, we take \(a=0.2\) and \(b=1.1\) in the data enhancement layer.

In the training process of the combined PINN, the learning rate is 0.0001, the number of epochs is 40000, and the batch size is 100. In particular, it is pointed out that triple batch size is used in the \(N_{FBSE}\). The mean squared error loss function and Tanh activation function are adopted to perform optimization calculations.

Fig. 4
figure 4

Price predictions and relative errors under integer-order derivative.

Full size image

Based on the transfer learning method, the prediction results of the combined PINN for American put option in the true market are drawn in Fig.4(a), together with the results from Wang’s approach20. Application of Wang’s approach into American put option can adopt the same procedures as the combined PINN without solution assumption (5) and (6). It can be seen that the work’s combined PINN pricing strategy has reached a certain level of good results in predicting the prices of American put option in the true market. The corresponding prediction errors are drawn in Fig.4(b).

In order to more intuitively compare the prediction errors of the two methods on the true market, we subtract the predicted errors of Wang’s method from the predicted errors of the combined PINN, and visualize the results shown in Fig.5. Points above the red line represent values greater than zero and points below the red line represent values less than zero. From the points distribution in Fig.5, it is obvious that the combined PINN has a relatively low prediction error.

Fig. 5
figure 5

Visualization of prediction errors.

Full size image

Experiment results under the space-time fractional Black-Scholes models

In the wake of the study of the model (1) with \(\alpha =1,\beta =1\), the section shifts the research on the pricing of American options to the fractal market, with a focus on explaining the pricing results under the definitions of fractional derivatives. Fractional derivatives have characteristics such as non-locality and long-range correlation, making them more suitable for describing special physical phenomena such as non-stationary, nonlinear, and memory effects.

Under Caputo fractional derivative (2), the calculation results of fractional derivatives of \(\bar{V}\) with fourth-order expression are

$$\begin{aligned} & _{C}D^{\alpha }_t \bar{V}=(\eta _{11}\eta _{13}+\eta _{21}\eta _{22}\eta _{23}S+\frac{\eta _{31}\eta ^2_{32}\eta _{33}}{2}S^2+\frac{\eta _{41}\eta ^3_{42}\eta _{43}}{6} S^3)\frac{t^{1-\alpha }}{\Gamma (2-\alpha )}+(\eta _{21}\eta ^2_{23}+\eta _{31}\eta _{32}\eta ^2_{33}S\nonumber \\ & ~~~~~~~~~~~~~~~+\frac{\eta _{41}\eta ^2_{42}\eta ^2_{43}}{2}S^2)\frac{t^{2-\alpha }}{\Gamma (3-\alpha )}+(\eta _{31}\eta ^3_{33}+\eta _{41}\eta _{42}\eta ^3_{43} S)\frac{t^{3-\alpha }}{\Gamma (4-\alpha )}+\eta _{41}\eta ^4_{23}\frac{t^{4-\alpha }}{\Gamma (5-\alpha )},\nonumber \\ & _{C}D^{\beta }_S \bar{V} =(\eta _{11}\eta _{12}+\eta _{21}\eta _{22}\eta _{23}t+\frac{\eta _{31}\eta _{32}\eta ^2_{33}}{2}t^2+\frac{\eta _{41}\eta _{42}\eta ^3_{43}}{6} t^3)\frac{S^{1-\beta }}{\Gamma (2-\beta )}+(\eta _{21}\eta ^2_{22}+\eta _{31}\eta ^2_{32}\eta _{33}t\nonumber \\ & ~~~~~~~~~~~~~~~+\frac{\eta _{41}\eta ^2_{42}\eta ^2_{43}}{2}t^2)\frac{S^{2-\beta }}{\Gamma (3-\beta )}+(\eta _{31}\eta ^3_{32} +\eta _{41}\eta ^3_{42}\eta _{43}t)\frac{S^{3-\beta }}{\Gamma (4-\beta )}+\eta _{41}\eta ^4_{42}\frac{S^{4-\beta }}{\Gamma (5-\beta )},\nonumber \\ & _{C}D^{2\beta }_{SS} \bar{V} =(\eta _{11}\eta _{12}+\eta _{21}\eta _{22}\eta _{23}t+\frac{\eta _{31}\eta _{32}\eta ^2_{33}}{2}t^2+\frac{\eta _{41}\eta _{42}\eta ^3_{43}}{6} t^3)\frac{S^{1-2\beta }}{\Gamma (2-2\beta )}+(\eta _{21}\eta ^2_{22}+\eta _{31}\eta ^2_{32}\eta _{33}t\nonumber \\ & ~~~~~~~~~~~~~~~+\frac{\eta _{41}\eta ^2_{42}\eta ^2_{43}}{2}t^2)\frac{S^{2-2\beta }}{\Gamma (3-2\beta )}+(\eta _{31}\eta ^3_{32}+\eta _{41}\eta ^3_{42}\eta _{43} t)\frac{S^{3-2\beta }}{\Gamma (4-2\beta )}+\eta _{41}\eta ^4_{42}\frac{S^{4-2\beta }}{\Gamma (5-2\beta )}. \end{aligned}$$
(12)

Based on the above operations, following the design of the combined PINN given in Section 4.1, the number of epochs is extended to 60,000. In particular, we use 5 times batch size in the training of \(N_{FBSE}\) with space-time Caputo fractional derivative, the purpose is to obtain better prediction accuracy.

Fig. 6
figure 6

Price predictions and relative errors under Caputo fractional derivative.

Full size image

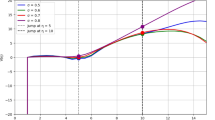
The price predictions of American put options based on the space-time fractional model are drawn in Fig.6. We can see that under Caputo fractional derivatives, the combined PINN with solution assumption based on the transfer learning algorithm has achieved good prediction results. But it is worth mentioning that Caputo fractional derivative model is more complex than integer-order model and it takes longer time to train. Fig.6 shows the numerical fittings under different fractional derivatives. From that, the orders of fractional derivative do not affect the trend of the graph. Empirical researches have found that the choice of fractional derivative order has little impact on predicting price trends. However, under different orders, there are deviations in the numerical values, which can be understood as small differences of price fluctuations in different fractional dimensional spaces. And under Caputo fractional derivatives, the results obtained when taking the fractional values of \(\alpha\) and \(\beta\) are very good.

By replacing the kernel \((z-\xi )^{-\vartheta }\) and \(\frac{1}{\Gamma (1-\vartheta )}\) of Eq.(2) with the function \(\exp (-\frac{\vartheta }{1-\vartheta }(z-\xi ))\) and \(\frac{M(\vartheta )}{1-\vartheta }\), Caputo and Fabrizio8 gave the new fractional derivative (3) without singular kernel, which are more suitable for characterizing some behaviors in materials with huge heterogeneities and different scale structures. Under Caputo-Fabrizio fractional derivative (3) and \(M(\vartheta )=1\), fractional derivatives of \(\bar{V}\) with the third-order expression are

$$\begin{aligned} & _{CF}D^{\alpha }_{t} \bar{V} =-\frac{1}{\alpha }(\eta _{11}\eta _{13}+\eta _{21}\eta _{22}\eta _{23}S+\frac{\eta _{31}\eta ^2_{32}\eta _{33}}{2}S^2) [\exp (\frac{\alpha t}{\alpha -1})-1]-\frac{2}{\alpha ^2}(\eta _{21}\eta ^2_{23}+\eta _{31}\eta _{32}\eta ^2_{33}S) [(\exp (\frac{\alpha t}{\alpha -1})-1)\nonumber \\ & ~~~~~~~~~~~~~~~~~\times (\alpha -1)-\alpha t]-\frac{3}{2\alpha ^3}\eta _{31}\eta ^3_{33} [2\exp (\frac{\alpha t}{\alpha -1})(\alpha -1)^2-\alpha ^2(t^2+2t+2) +2t\alpha +4\alpha +2],\nonumber \\ & _{CF}D^{\beta }_{S} \bar{V } =-\frac{1}{\beta }(\eta _{11}\eta _{12}+\eta _{21}\eta _{22}\eta _{23}t+\frac{\eta _{31}\eta _{32}\eta ^2_{33}}{2}t^2) [\exp (\frac{\beta S}{\beta -1})-1]-\frac{2}{\beta ^2}(\eta _{21}\eta ^2_{22}+\eta _{31}\eta ^2_{32}\eta _{33}t) [(\exp (\frac{\beta S}{\beta -1})-1)\nonumber \\ & ~~~~~~~~~~~~~~~~~\times (\beta -1)-\beta t]-\frac{3}{2\beta ^3}\eta _{31}\eta ^3_{32} [2\exp (\frac{\beta S}{\beta -1})(\beta -1)^2-\beta ^2(S^2+2S+2) +2S\beta +4\beta +2],\nonumber \\ & _{CF}D^{2\beta }_{SS} \bar{V} =\frac{1}{(\beta -1)^2}(\eta _{11}\eta _{12}+\eta _{21}\eta _{22}\eta _{23}t+\frac{\eta _{31}\eta _{32}\eta ^2_{33}}{2}t^2) S\exp (\frac{\beta S}{(\beta -1)})+\frac{2}{\beta ^2(\beta -1)}(\eta _{21}\eta ^2_{22}+\eta _{31}\eta ^2_{32} \eta _{33}t)\nonumber \\ & ~~~~~~~~~~~~~~~~~\times [\exp (\frac{\beta S}{(\beta -1)})(S\beta -\beta +1)+\beta +1] +\frac{3}{\beta ^3}\eta _{31}\eta ^3_{32}[\exp (\frac{\beta S}{(\beta -1)})(S\beta -2\beta +2) +S\beta +2\beta -2]. \end{aligned}$$
(13)

Employing the solving strategy of Caputo fractional derivative model, the number of epochs is 80,000. 6 times batch size is used in the training of \(N_{FBSE}\) under Caputo-Fabrizio fractional derivative. The space-time fractional Black-Scholes model is numerically solved by the combined PINN together with the above equalities (13). Using the same set of sample data, the price predictions of American put option are drawn in Fig.7. From error floating range, it can be seen that Caputo-Fabrizio derivative can well describe the behavior of option prices changing over the time and the underlying asset price. Similarly, Fig.7 displays the influence of the order of fractional derivative on the pricing results under the sense of Caputo-Fabrizio derivative. By comparing the solution curves and error curves under that \(\alpha ,~\beta\) take integer values and different fractional values, it can be found that taking fractional values at most time points yields better prediction results. This indicates that the presented fractional derivative model (1) includes the classical model and has certain advantages.

Fig. 7
figure 7

Price predictions and relative errors under Caputo-Fabrizio fractional derivative.

Full size image

Based on the definition of Caputo and Fabrizio8, Atangana and Baleanu9 introduced the generalized Mittag-Leffler function \(E_\vartheta (z)=\sum ^\infty _{k=0}\frac{z^{k}}{\Gamma (\vartheta k+1)}\) to presented fractional duratives with non-local kernel under Caputo and Riemann-Liouville senses. The work adopts Atangana-Baleanu fractional derivative (4) in Caputo case to study the effectiveness of neural network algorithms. Under \(AB(\vartheta )=1\), fractional derivatives of \(\bar{V}\) with the third-order expression are

$$\begin{aligned} & _{ABC}D^{\alpha }_{t} \bar{V} =\frac{1}{1-\alpha }(\eta _{11}\eta _{13}+\eta _{21}\eta _{22}\eta _{23}S+\frac{\eta _{31}\eta ^2_{32}\eta _{33}}{2}S^2) [t-\frac{\alpha }{(1-\alpha )\Gamma (\alpha +2)}t^{\alpha +1}]+\frac{1}{1-\alpha }(\eta _{21}\eta ^2_{23}+\eta _{31}\eta _{32}\eta ^2_{33}S) \nonumber \\ & ~~~~~~~~~~~~~~~~~~~\times [\frac{t^2}{2}-\frac{\alpha }{(1-\alpha )\Gamma (\beta +3)}t^{\alpha +2}]+\frac{1}{(1-\alpha )}\frac{\eta _{31}\eta ^3_{33}}{2} [\frac{t^3}{3}-\frac{\alpha }{(1-\alpha )\Gamma (\beta +4)}t^{\alpha +3}],\nonumber \\ & _{ABC}D^{\beta }_{S} \bar{V}=\frac{1}{1-\beta }(\eta _{11}\eta _{12}+\eta _{21}\eta _{22}\eta _{23}t+\frac{\eta _{31}\eta _{32}\eta ^2_{33}}{2}t^2) [S-\frac{\beta }{(1-\beta )\Gamma (\beta +2)}S^{\beta +1}]+\frac{1}{1-\beta }(\eta _{21}\eta ^2_{22}+\eta _{31}\eta ^2_{32}\eta _{33}t) \nonumber \\ & ~~~~~~~~~~~~~~~~~~~\times [\frac{S^2}{2}-\frac{\beta }{(1-\beta )\Gamma (\beta +3)}S^{\beta +2}]+\frac{1}{(1-\beta )}\frac{\eta _{31}\eta ^3_{32}}{2} [\frac{S^3}{3}-\frac{\beta }{(1-\beta )\Gamma (\beta +4)}S^{\beta +3}],\nonumber \\ & _{ABC}D^{2\beta }_{SS} \bar{V} =(\eta _{11}\eta _{12}+\eta _{21}\eta _{22}\eta _{23}t+\frac{\eta _{31}\eta _{32}\eta ^2_{33}}{2}t^2) [S-\frac{2\beta }{(1-\beta )\Gamma (\beta +2)}S^{\beta +1}+\frac{\beta ^2}{(1-\beta )^2\Gamma (\beta +1)\Gamma (\beta +2)}S^{2\beta +1} \nonumber \\ & ~~~~~~~~~~~~~~~~~~~\times hyper((-\beta ,\beta +1),(\beta +2),1)]+(\eta _{21}\eta ^2_{22}+\eta _{31}\eta ^2_{32} \eta _{33}t)[\frac{1}{2}S^2-\frac{2\beta }{(1-\beta )\Gamma (\beta +3)}S^{\beta +2}\nonumber \\ & ~~~~~~~~~~~~~~~~~~~+\frac{\beta ^2}{(1-\beta )^2\Gamma (\beta +1)\Gamma (\beta +3)}S^{2\beta +2}hyper((-\beta ,\beta +2),(\beta +3),1)]+\frac{\eta _{31}\eta ^3_{32}}{2}[\frac{1}{3}S^3-\frac{2\beta }{(1-\beta )\Gamma (\beta +4)}S^{\beta +3}\nonumber \\ & ~~~~~~~~~~~~~~~~~~~+\frac{\beta ^2}{(1-\beta )^2\Gamma (\beta +1)\Gamma (\beta +4)}S^{2\beta +3}hyper((-\beta ,\beta +3),(\beta +4),1)]. \end{aligned}$$
(14)

Where hyper denotes Hypergeometric functions which can be given by the following power series.

If \(c\ne 0,-1,-2,\cdots\) and \(|z|<1\), then

$$\begin{aligned} hyper((a,b),c,z)=\sum ^\infty _{n=0}\frac{a^{(n)}b^{(n)}}{c^{(n)}}\frac{z^n}{n!}. \end{aligned}$$
(15)

Where \(x^{(n)}\) is the Pochhammer symbol, and

$$\begin{aligned} x^{(n)}= \left\{ \begin{aligned}&1,~~n=0, \\&x(x+1)\cdots (x+n-1),~~n>0. \end{aligned} \right. \end{aligned}$$
(16)

When a or b is 0 or a negative integer, the series only has finite terms. For complex numbers z that satisfy \(|z|\ge 1\), hypergeometric functions can be obtained by analytically extending the function defined within the unit circle along any path that avoids fulcrums 0 and 1.

When selecting consistent data for network design, Fig.8 draws the price predictions of American put option under Atangana-Baleanu-Caputo fractional derivative (4). It should be noted that the existence of hypergeometric functions leads to the complexity of neural network implementation when a specific fractional derivative definition is adopted. This is because the nature and structure of the hypergeometric function are relatively complex, making it difficult to apply directly to the framework of neural networks. To overcome this difficulty, we have chosen a strategy of abandoning the exact form of the function and instead using its approximation. By utilizing the continuous optimization process of the neural network model, a numerical method is used to find an optimal approximation result.

Fig. 8
figure 8

Price predictions and relative errors under Atangana-Baleanu-Caputo fractional derivative.

Full size image

Simulation of optimal exercise boundary

Optimal exercise boundary is the difficulty and critical point of American option pricing. Due to its existence, it is hard to find analytical pricing formula, especially for fractional derivative models. Fig.9 presents the simulation diagrams of the optimal exercise boundary under the three types of Black-Scholes models. From this, it can be seen that the trend of the optimal exercise boundary under the integer-order model is consistent with those under the space-time fractional models with Caputo, Caputo-Fabrizio and Atangana-Baleanu-Caputo fractional derivatives.

It must be said that the work focuses on the space-time fractional Black-Scholes equations, so the values of the free boundary and American put option prices interact with each other, which also means that the better of the models fits the true market price, the more accurate of the optimal exercise boundary will be. Since the combined PINN algorithm is adopted to derive approximations to the solutions of Eq.(1), there will always exist prediction errors. Meanwhile, both the randomness of training data selection and the number of the batch size will lead to errors in the predictions of option prices in true market. In addition, the complexity of defining fractional derivatives can lead to errors in approximate calculations. In order to better fit the price of the true market and more accurately simulate the optimal exercise boundary, we can choose to increase the batch size of \(N_{FBSE}\). The purpose of the work is to improve the prediction accuracy of the option prices, so that a more accurate optimal exercise boundary can be simulated.

Fig. 9
figure 9

Optimal exercise boundary.

Full size image

Discussions

The work proposes the combined PINN to price American put option based on the fractional Black-Scholes model through defining the solution assumption and the loss function, adding data enhancement layer and introducing the transfer learning. To deepen further researches on the relevant theories, the existing problems and some gains are worthy to be presented and discussed.

Neural network is an effective algorithm for solving the free boundary problems of PDE. The free boundary not only exists in financial problems, but also has lots of corresponding problems in physical mechanics. Therefore, exploring the free boundary problems has theoretical significance and practical value. The work presents the combined PINN to deal with the free boundary problem of American put option together with real market data, and introduces the solution assumption (5). As mentioned in Section 4.1, the concise transformation can improve accuracy to a certain extent compared with the direct application of Wang’s method. The effect of the assumption is particularly significant in solving space-time fractional derivative model. So the approach suggests that we may introduce some transformation forms in the execution of neural network algorithms, such as linear structure, exponential structure, etc.

The work twins neural network and fractional calculus together to deal with the free boundary problem of American put option. Caputo fractional derivative is an extension of Gr\(\ddot{u}\)nwald-Letnikov’s definition. With Caputo fractional derivative, many models in physics, medicine and economics have been extended and solved. Removing singular kernel, Caputo-Fabrizio and Atangana-Baleanu fractional derivatives have been proposed and rapidly gained widespread applications. The work adopts the two non-local definitions to characterize the price path of American put option in fractal market. The empirical analyses tell us that the combination of neural network and fractional calculus has strong executions and prediction capabilities. In addition to the definitions adopted in the work, we can choose Riemann-Liouville fractional derivative, and so on.

Due to the relatively short lifespan of option data in the mainland Chinese market, the work introduces the transfer learning method to predict the prices of American put option in the true market, which improves the accuracy and accelerates the prediction speed. The transfer learning method proposed in the work can be extended to the related researches on financial derivatives.

Conclusions and prospects

After conducting an in-depth study on the use of fractional derivative models and neural networks to solve the American put option pricing problem, future work will focus on several aspects to further promote theoretical researches and practical applications in this field.

Firstly, future researches will aim to improve the predictive accuracy and stability of the fractional derivative models. As financial markets become increasingly complex and volatile, there is a higher demand for the accuracy and robustness of option pricing models. Therefore, we will enhance the predictive capabilities of the models by optimizing neural network structures, adjusting the orders of fractional derivatives, and introducing more market characteristic variables.

Secondly, we plan to extend the models to a broader range of option types and market environments. While current research focuses primarily on American options, we will explore the pricing of other types of options such as European options and Asian options. At the same time, we will also consider applying the models to different financial markets such as the foreign exchange market and bond market to test the universality and adaptability of the models.

Furthermore, with the rapid development of artificial intelligence technology, we will explore the application of more advanced machine learning algorithms and deep learning frameworks to option pricing problems. For example, we can use reinforcement learning algorithms to simulate investor trading behavior, thereby more accurately predicting changes in option prices. At the same time, we will also pay attention to the application potential of new neural network structures such as convolutional neural networks and generative adversarial networks in the field of option pricing.

Finally, we will also focus on the real-time nature and online learning ability of option pricing models. In the actual financial market, market environment and investor behavior are constantly changing, so option pricing models need to have the ability to update and learn online in real time. In the future, we will study how to integrate the model with real-time data streams to achieve dynamic prediction and risk management of option prices.

In summary, future work will focus on improving model prediction accuracy, expanding application scope, introducing advanced algorithms, and enhancing real-time capabilities to promote continuous development and innovation in the field of option pricing.