Optimization of carbon emission in an integrated machine-piece scheduling and vehicle routing problem and its solution using MOPSO and NSGAII metaheuristic algorithms

Abstract

The growth of the global economy is accompanied by significant energy consumption, and greenhouse gas emissions create various problems such as global warming and environmental degradation. To protect the environment, governments are seeking to reduce carbon emissions. Production systems that operate solely based on economic factors in the workshop only consider problems such as production speed, cost, and processing time. Two aspects can be effective in saving energy and reducing emissions at the production planning level: using routing to find the shortest path for collecting workpieces to the workshop, and turning off machines with long idle times and restarting them at the appropriate time. If the workshop production problem is combined with vehicle routing, a new problem arises. According to the research conducted so far, an integrated mathematical model for production routing has not been designed in a situation where the routing is before the production workshop. In this research, this bi-objective model is introduced, and it is solved using the augmented epsilon-constraint (AEC) method. The proposed mixed-integer linear programming model of this research includes three dimensions: environmental, social (customer satisfaction), and economic simultaneously. Given the high complexity of the mathematical model, MATLAB software and MOPSO and NSGA-II algorithms were used to solve it at higher dimensions. Seven evaluation criteria were used to compare the two proposed algorithms, and the results show that the MOPSO algorithm performs better. The findings suggest that minimizing pollution may involve sacrificing on-time delivery to customers. Consequently, decision-makers must carefully weigh the trade-off between reducing environmental impact and maintaining satisfactory delivery performance, ultimately deciding on an acceptable pollution level.

Introduction

In recent decades, globalization has forced supply chains to expand beyond national borders, leading to intense competition in markets¹. To meet the growing expectations of customers, companies realize that they must increasingly rely on an effective supply chain². An inefficient supply chain can lead to high costs and loss of competitiveness³. Integrated production and distribution planning is a key aspect of supply chain management that significantly contributes to lowering transportation costs and boosting customer satisfaction⁴. This is achieved by optimizing resource allocation, ensuring timely delivery, streamlining production processes, and promoting environmentally friendly practices. These benefits enable businesses to maintain a competitive edge and meet customer expectations in an ever-evolving market⁵. Quantitative approaches to integrating production and distribution planning have received attention from researchers and companies in recent years. They can significantly improve the performance and sustainability of the supply chain⁶.

The integration of production and distribution processes is critical for supply chain management, both at tactical and operational levels. This integration ensures efficient resource allocation, streamlines operations, and enhances overall supply chain performance⁷. As early as the late 20th century, the need for simultaneous scheduling of production and outbound distribution emerged, prompting numerous advancements in this domain. Substantial savings have been reported in the literature as a result of integrating these two key activities⁸.

Tactical planning typically addresses medium-term production-distribution coordination, focusing on lot-sizing, resource allocation, and inventory management, as well as product distribution to customers. This integrated approach proves essential for optimizing supply chain efficiency and ensuring that resources are effectively utilized to meet customer demands⁹. In conclusion, the need for integrated production and distribution scheduling has been recognized for decades, and the benefits of such an approach are well-documented. By carefully coordinating these two fundamental supply chain processes, businesses can achieve significant savings and enhance their overall operational performance. In the realm of supply chain optimization, addressing routing and scheduling decisions in an integrated manner holds significant potential for improving efficiency and reducing costs. Two primary methods have emerged for tackling these interconnected challenges: the route-then-schedule and schedule-then-route approaches. This article delves into the intricacies of these strategies and examines the benefits of a hybrid model that combines their strengths. The route-then-schedule approach involves first determining optimal transportation routes before scheduling production activities^{1,2,3,4,5,6,7,8,9,10}.

This method prioritizes the efficient movement of goods between locations, ensuring timely deliveries and reducing transportation costs. Once the routing decisions are made, production schedules are adjusted to meet the logistical demands. Conversely, the schedule-then-route approach begins with optimizing production schedules and subsequently plans the transportation routes based on the established production plan¹¹. By initially focusing on scheduling, this method seeks to maximize production efficiency and minimize production costs, while still considering the implications for the distribution stage. Despite their individual advantages, both approaches have inherent limitations when applied independently. A hybrid model that thoughtfully integrates routing and scheduling decisions can overcome these drawbacks, offering a more holistic view of the supply chain. This hybrid approach considers both production and distribution stages simultaneously, enabling better-informed decisions that optimize the entire supply chain from end to end¹².

In this article, we provide a comprehensive exploration of routing and scheduling integration strategies within the context of supply chain optimization. Through an in-depth analysis of the route-then-schedule and schedule-then-route approaches and an examination of the potential benefits of their hybridization, we aim to contribute valuable insights for researchers and practitioners seeking to enhance the efficiency and sustainability of their supply chain operations. Moving forward, we will delineate the specific objectives and key contributions of this research, highlighting the novel aspects of our approach to addressing the identified challenges in the realm of supply chain optimization. An industrial company whose activity is focused on piece scheduling and processing generally deals with piece processing in such a way that after job delivery, the company has the necessary profit to continue its activities and has enough time to distribute it to the final customer. This has led to the machine (for piece processing) being kept on until the last piece is processed.

During the operation period, the machine is either in a processing or idle state. This problem not only increases the production of pollutants by the machine but also affects the production cost, as the fuel price to keep the machine running is very expensive. Therefore, if the carbon emissions during the idle period are greater than restarting the machine, the machine can be turned off. This switching operation is an effective method for saving energy. This problem leads to a specific delay in the completion time of processing. Piece processing may be completed late, and some pieces may even fail to be delivered on time. However, if the pieces are better planned to be available to the machine for piece processing, this machine shutdown and idle time can be compensated to avoid any damage to the distribution planning, so that the pieces are processed and delivered to customers on time. The vehicle routing problem (finding the shortest distance travelled by vehicles) enables the collection of pieces before the workshop and their delivery to the workshop in a shorter time through optimized transportation and routing. The machine’s access time for piece processing will certainly improve in a situation where pieces are transferred to the workshop without routing planning compared to a situation where they are transferred with routing planning. Here, the combination of the vehicle routing problem and workshop scheduling is very useful.

Integrated production and distribution planning (literature review)

The vehicle routing problem with a heterogeneous fleet is another form of the vehicle routing problem, which was introduced by Golden et al. in 1984, where vehicles have different fixed and variable costs⁷. The objective function of this problem usually includes distance, cost, and the number of vehicles. A very important and practical type of these problems is the vehicle routing problem with time windows. Solomon in 1986 first introduced the vehicle routing problem with time windows, where service to each customer must be provided within a specified time interval⁸. Green routing models with the goal of determining the optimal route to minimize environmental pollutants have been introduced in the literature since 2006. Today, with the increase in vehicles for goods distribution and the increase in road construction activities, humans, intentionally or unintentionally, are recognized as a major threat to the environment.

Armentan et al. (2011) introduced a multi-layer supply chain model that incorporated suppliers, various products, multi-period inventory, and distribution planning to minimize inventory and production costs⁹. Bilgen and Çelebi (2013) tackled the short-term production and distribution planning problem in the dairy industry by developing a mixed-integer linear programming model that accounted for real-world factors such as sequence-dependent setup times, machine speeds, overtime, and batch size constraints¹⁰. In 2019, Mehranfar et al. investigated production and distribution network design problems in the context of carbon emission policies, employing a new hybrid whale optimization algorithm for their mixed-integer nonlinear programming model¹¹. Kumar et al. (2020) conducted a systematic literature review of quantitative approaches for integrating production and distribution planning in supply chains, presenting a classification framework with eight dimensions¹². Aktas and Temiz (2020) explored a production and distribution problem with economic and environmental impacts, modeling a multi-product, multi-echelon production and distribution network with various transportation alternatives¹³. Lastly, Kazemi et al. (2021) examined integrated production and distribution scheduling in a workshop with unrelated parallel machines in the production line, aiming to minimize total tardiness and delivery costs¹⁴.

Wu et al. in 2022 studied a production and distribution problem with limited capacity, where location, production, and distribution decisions are strongly related and are considered simultaneously in the optimal decision-making. They proposed a metaheuristic algorithm based on unsupervised learning¹⁵. Parvizinejad and Golzadeh in 2022 presented the vendor-managed inventory problem in the production and distribution supply chain based on a scenario. The main objective is to maximize the producer’s profit in a three-tier supply chain network consisting of various strategic and tactical decisions under uncertain conditions¹⁶. Rabbani et al. in 2022 presented an integrated production and distribution model by combining Stackelberg competition and make-to-order production systems in different periods¹⁷. Ben Abid et al. in 2022 addressed a bi-objective tactical integrated production and distribution planning problem for a multi-echelon, multi-site, multi-product, and multi-period supply chain network. The proposed model considers a multi-modal transportation network of sea and air to increase the responsiveness and flexibility of distribution planning¹⁸. Lin et al. in 2023 created a mixed-integer linear programming model for eco-friendly production and distribution planning for a manufacturer in a two-channel multi-layer supply chain. This problem has been solved using a non-dominated sorting genetic algorithm and an improved lion pride optimization algorithm¹⁹.

Bektas and Laporte in 2011 discussed the dependence of vehicle emissions on speed and the amount of cargo carried by the vehicle in their paper²⁰. Kırlik et al. in 2012 presented the single-machine scheduling problem to minimize the total weighted tardiness in the presence of sequence-dependent setup times and used metaheuristic algorithms to solve it²¹. Fister et al. in 2013 developed the firefly algorithm to solve scheduling problems²². Marichelvam et al. in 2014, considering that scheduling problems are NP-hard, developed a discrete metaheuristic algorithm for this domain²³. Xu et al. in 2014 provided a systematic comparison of hybrid evolutionary algorithms (HEAs), which independently use six combinations of three crossover operators and two population update strategies to solve the single-machine scheduling problem with setup times²⁴. Pusavec et al. in 2015 presented a paper in two general sections, methods and a case study, to achieve sustainable production at the level of machining technology. To address these problems, the paper presented sustainable production through alternative machining technologies, i.e., machining assisted by high-pressure and cryogenic jets, which have a high potential for cost reduction and improved competitiveness by reducing resource consumption and, consequently, less waste generation²⁵.

Song and Huo in 2016 presented a permutation flow shop scheduling (PFS) problem with the objectives of minimizing total carbon emissions and makespan. To solve this multi-objective optimization problem, they first investigated the structural properties of non-dominated solutions. Inspired by these properties, they developed an extended National Endowment for the Humanities (NEH) energy-saving method²⁶. Chao Lu et al. in 2017 studied the permutation flow shop scheduling problem where energy-saving and energy storage are considered important problems. After presenting the mathematical model, they used a hybrid multi-objective backtracking search algorithm (HMOBSA) to solve it²⁷. Moons et al. in 2017 provided a review paper on integrated production scheduling and vehicle routing. They pointed out that considering production and routing separately does not lead to overall optimal solutions, and considering these two problems simultaneously and solving the integrated problem leads to a 5–20% improvement²⁸.

Eshtehadi et al. in 2017 presented a robust model for the green transportation problem where demand and travel time are uncertain. Three types of robustness techniques were also proposed and modeled, which produced suitable solutions and resulted in a slight increase in the objective function. These objective functions are minimizing fuel consumption and carbon dioxide emissions²⁹. Piroozfard et al. in 2018 presented a paper on scheduling that addressed environmental problems, with the objective function of simultaneously minimizing total tardiness and the amount of carbon emissions. In fact, with these objective functions, they discussed sustainability in their model. They also improved the multi-objective genetic algorithm and used it to solve their model³⁰. Van Fan et al. in 2018 in a review paper discussed sustainability problems, addressing greenhouse gases and climate change. They actually studied the importance of considering air pollutants in optimization problems and evaluating air pollution-related constraints, particularly in the transportation sector³¹.

Kargari Esfand Abad et al. in 2018 worked on a vehicle routing model for pickup and delivery, where they considered environmental pollution in the cross-docking system. The activities considered in this system include loading, sorting, and unloading ship cargo. The sustainability discussion in this paper is related to fuel consumption³². Qamhan et al. in 2019 presented an Evolutionary Discrete Firefly Algorithm (EDFA) to solve the real-world production system problem. Scheduling a set of jobs on a single machine considering non-zero release dates, sequence-dependent setup times, and periodic maintenance with the objective of minimizing the maximum completion time³³. Nguyen et al. in 2022 presented a mixed-integer linear programming model for drone routing with the goal of minimizing costs, which are incurred by a transportation fleet consisting of trucks and drones³⁴. Marampoutsas et al. in 2022 presented an integer linear programming model for vehicle routing to collect glass bottles³⁵.

Heidari et al. in 2022 in their paper presented a mixed-integer programming model for open and closed-loop green location routing. Their two-level model consists of factories, warehouses, and customers, aiming to minimize costs and carbon dioxide emissions³⁶. Wang et al. in 2022 presented a paper to minimize carbon dioxide emissions, which is achieved through the concept of multi-depot instead of single-depot, which can reduce carbon dioxide emissions by up to 37.6%. They developed a branch-and-price algorithm to solve the model, and sensitivity analyses showed that factors such as vehicle speed, customer demand, and service time also affect the amount of carbon dioxide emissions³⁷.

Peng et al. in 2024 introduced a mathematical model that effectively combines production, inventory, and distribution routing decisions to optimize supply chain operations³⁸. Komijani et al. in 2024 proposed a green closed-loop supply chain planning model that holistically integrates primary and secondary product-related decisions, fostering sustainability in manufacturing processes³⁹. Farghadani-Chaharsooghi and Karimi in 2023 developed a mixed-integer linear programming model that incorporates various real-world constraints, such as outsourcing, lateral transfers, backorders, lost sales, and time windows, to enhance production routing problem solutions⁴⁰. Manousakis et al. devised a fundamental production routing problem (PRP) model focused on generating repeatable cyclical production and delivery schedules to streamline operations⁴¹. Vadseth et al. in 2023 examined the multi-vehicle production routing problem, emphasizing the importance of simultaneous decision-making in production, inventory, and routing for optimal results⁴². Farghadani-Chaharsooghi et al. in 2022 devised a novel framework that integrates inventory, production, distribution, routing, and workforce planning decisions, promoting a comprehensive approach to supply chain management⁴³. Majidi et al. in 2022 presented a multi-objective integrated sustainable model that combines pricing, manufacturing, labor, and routing aspects for perishable products, ensuring efficient and environmentally friendly practices⁴⁴. Li, Z., et al. (2024), The authors propose a LiDAR-OpenStreetMap matching method for vehicle global position initialization based on boundary directional feature extraction. This method demonstrates high robustness and effectiveness in urban environments⁴⁵. Liu, K., et al. (2024), This study investigates the use of image transformation for partial discharge source identification in vehicle cable terminals of high-speed trains. The authors’ approach improves both PD location accuracy and data reliability compared to existing methods⁴⁶. Zhou, Z., et al. (2021), This paper presents a short-term lateral behavior reasoning method for target vehicles, considering driver preview characteristics. Their approach outperforms current methods in terms of accuracy and stability⁴⁷. Liu, X., et al. (2021), The authors develop a trajectory prediction model for preceding target vehicles based on a lane crossing and final points generation model, considering driving styles. This model exhibits better performance in complex traffic scenarios⁴⁸. Chen et al. (2022), The paper proposes a disparity-based multiscale fusion network for transportation detection, demonstrating improved performance compared to existing methods⁴⁹. Chen et al. (2023), In this study, the authors propose a joint scene flow estimation and moving object segmentation method for rotational LiDAR data. Their approach shows higher accuracy in both tasks compared to current methods⁵⁰. Chen et al. (2022), The authors provide a comprehensive review of vision-based traffic semantic understanding in intelligent transportation systems. This review highlights current trends and potential directions in the field⁵¹.

Necessity of the research

One of the important and necessary problems for today’s manufacturing and distribution companies is the problem of customer satisfaction, one of the components of which is on-time delivery. In addition, to compete in global markets, reducing emissions, which is one of the principles of sustainability, must be observed. In this research, to reduce the time of the final piece reaching the customers, the combination of routing and scheduling is examined, where scheduling is performed after routing. The routing problem ensures that the time from supply to the workshop is minimized, and this problem has a significant impact given the minimum access time to the pieces throughout the planning.

The distinguishing feature of this research from other studies is that only routing has been considered, but in some studies, both routing and scheduling have been performed, but in a way that the pieces are first completed in the workshop (pieces scheduling) and then routing is performed to send the pieces to the customers. The existing research gap, as mentioned earlier, is that in the integrated routing and scheduling problems, the piece access time through vehicle routing has not been considered; this means that routing is considered first (collecting pieces for the workshop by vehicles and minimizing the access time to the pieces through routing) and then scheduling, which is the subject of this research.

Problem statement and mathematical model

Today, problems such as cost reduction, tardiness reduction, profit increase, customer satisfaction increase, and the like are considered important objectives in vehicle routing and workshop scheduling problems. In this problem, attention has been paid to another aspect of the objectives, which are the environmental objectives that have been of great concern to producers and researchers due to the strict regulations imposed by international organizations and governments. The objective of this study is to develop a solution that minimizes carbon emissions from two sources: vehicle fuel consumption during the routing process and workshop machinery usage in scheduling. By addressing both aspects, we aim to contribute to a more sustainable and environmentally friendly approach to supply chain management. On the other hand, the importance of considering the scheduling and routing problems simultaneously has been proven in recent years. This research also examines both problems simultaneously in a way that routing is performed first and then scheduling, as routing before the workshop has not been considered before. The importance of the problem is that the piece arrival time to the workshop is very important; if the access time to the pieces is high, routing can be used to reduce the piece arrival time to the workshop and ultimately reduce the piece arrival time to the customer. The mathematical model of the problem is presented below. The problem assumptions are as follows:

• Each piece enters at different times and cannot be processed before its arrival time.

• The arrival time of the pieces to the workshop is calculated from the pre-production routing (the arrival time of the vehicles to the workshop).

• Piece processing times are deterministic.

• Piece processing cannot be interrupted once started.

• A vehicle must start from the factory, travel along the planned route, and return to the factory.

• The loading time of the pieces is considered in this research.

• The production system is a workshop and a single machine.

This research considers an integrated distribution (from supplier to workshop) with transportation vehicles and a production (piece processing) system. A distribution and processing plan is created to achieve goals such as minimizing carbon emissions and costs. Each workpiece arrives at different times and cannot be processed before its arrival time. A workpiece cannot be processed until the previously arrived piece is processed. Once the processing of a workpiece has started, it cannot be interrupted. Each workpiece must be ready before its processing (delivery) deadline. It is assumed that the weight, processing time, arrival time, and delivery time are known before the planning. It is assumed that there are sufficient vehicles for transportation, moving at a constant speed. A vehicle must depart from the factory, move along the planned route, and return to the factory. In fact, a closed-loop routing is performed (i.e., it is assumed that the workshop has its vehicles and does not rent them). For further explanation, refer to Fig. 1.

Fig. 1

Integrated representation of scheduling and routing problem³.

In Fig. 1, vehicle $\:{V}_{1}$ carries pieces $\:\left\{1-4-5-3\right\}$, and vehicle $\:{V}_{2}$ carries pieces $\:\left\{6-9-2-8-7\right\}$ to the workshop; as a result, the access time to the piece in the case without routing will be less, and then the processing will be performed on the pieces in the workshop. In this research, in addition to scheduling and routing, emissions are examined in both the routing and workshop sections. In the scheduling piece, problems related to machine maintenance and repair are also considered.

The objective of this problem is to reduce carbon emissions from vehicle fuel in the routing piece and also reduce these emissions from the workshop machinery in the scheduling piece. On the other hand, the importance of considering the scheduling and routing problems simultaneously has been proven in recent years. This research also examines both problems simultaneously in a situation where routing is performed first and then scheduling, as routing before the workshop has not been studied before. In this research, the primary focus is on the significance of the arrival time of pieces at the workshop. If the access time for pieces is prolonged, routing can play a crucial role in minimizing delays. By optimizing routing, the time it takes for pieces to reach the workshop can be significantly reduced, ultimately leading to improved delivery times for customers.

Indices
$\:N=\left\{\text{0,1},\text{2,3}\dots\:N\right\}$	In the integrated problem, $\:N∕0$ is the symbol of all customers as well as all parts. It is noteworthy that 0 is the symbol of the virtual work piece and also the symbol of the depot in the routing problem
$\:p=\left\{\text{1,2},3\dots\:P\right\}$	position index of the workpiece in the sequence
$\:k=\left\{\text{1,2},3\dots\:V\right\}\:$	vehicle index, $\:k\in\:V$
Parameters
$\:{W}_{k}$: unladen vehicle weight$\:\:k$	$\:{Q}_{k}$: maximum load of vehicle $\:k$
$\:{TP}_{i}$: workpiece processing time$\:\:i$	$\:v$: speed of travel of a vehicle.
$\:{D}_{ij}$: travel distance on the arc$\:\:(i,j)$	$\:{W}_{i}$: weight of the workpiece$\:\:i$
$\:{\text{T}}^{off}$: the duration of turning off the machine	$\:{\text{T}}^{on}$: duration of turning on the machine
$\:{\text{E}}^{off}$: power consumption, turn off the machine	$\:{\text{E}}^{on}$: power consumption to turn on the machine
$\:{\text{E}}^{P}$: amount of power when the machine processes a work piece.	$\:{\text{E}}^{I}$: amount of power when the machine is idle.
$\:{\text{R}}^{g}$: diesel carbon conversion factor	$\:{\text{R}}^{e}$: electricity carbon conversion factor
$\:{\lambda\:}_{k}$: constant fuel consumption of the vehicle $\:k$	$\:{\lambda\:}_{ij}$: fixed fuel consumption$\:\:(i.j)\:\left(mile\right)$
$\:{p}_{i}$: demand to pick up the piece $\:i$	$\:{G}_{ijk}$: vehicle fuel consumption k in the arc of the path$\:\:(i.j)$
$\:M$: time for maintenance and repairs	$\:{\:S}_{ij}$: setup time for job $\:i$ after job $\:j$
$\:A$: a big number	$\:NT:\:$fixed time between maintenance and repairs
$\:{G}_{sum}$: fuel consumption to collect all workpieces	$\:{E}_{sum}:\:$power consumption for processing all workpieces
$\:{\text{T}}^{r}:\:$breakeven duration, that is, the least duration required for a restarting operation and the amount of time for which a restarting operation, rather than running the machine at idle, is favorable	$\:{C}_{sum}:\:$total carbon emissions for processing all workpieces
$\:\delta\:$: late fees	$\:{d}_{i}$: time to deliver for piece $\:i$
Decision variables
$\:{x}_{ji}^{{\prime\:}}$: It is one if workpiece $\:j$ is processed before $\:i$ and zero otherwise.	$\:{x}_{ijk}$: If we go from node $\:i$ to node $\:j$ with vehicle $\:k$, it is one and otherwise it is zero.
$\:{y}_{ip}:$ If the work piece$\:\:i$ If it is placed in the $\:p$-th place of the sequence, it is one and otherwise it is zero.	$\:{Z}_{ik}:$ one if piece $\:i$ is carried by machine $\:k$ and zero otherwise.
$\:{N}_{p}:$ If the maintenance and repairs are done immediately before the work piece that is in position $\:p$, it is one and otherwise it is zero.	$\:{z}_{i}:\:$one if the machine is idle before processing workpiece $\:i$, and zero if the machine is idle.
$\:{TS}_{p}$: time to start processing the workpiece of position $\:p$th	$\:{Tt}_{ki}$: time when the $\:k$th truck arrives at node $\:i$
$\:{TF}_{p}:$ end time of the processing of the workpiece of position pth	$\:{Tar}_{k}:\:$time when the $\:k$th truck arrives at the factory
$\:{C}_{p}$: life of the machine immediately after the processing of the workpiece of the position $\:p$th	$\:{l}_{ij}:$ vehicle load in the arc of the track $\:(i,j)$
$\:{ST}_{jip}$: decision variable that is equal to $\:{S}_{ij}$ if workpiece $\:j$ is processed in position $\:p$ and zero otherwise.	$\:{TA}_{i}$: time when workpiece $\:i$ arrives at the factory (access time in scheduling)
$\:{y}_{ij}:\:$ number of pieces taken from the customer	$\:{F}_{i}$: time to complete the work is $\:i$th
$\:{zv}_{i}:$ decision variable for linearization

Constraints and objective functions.

In instances where the time interval between two consecutive workpieces is greater than the restart duration, and the power consumption during the idle period exceeds that of restarting the machine, switching off the machine can effectively minimize carbon emissions. Following the approaches of²⁷, a breakeven duration can be determined using Eq. (1):

$$\:{\text{T}}^{r}=max\left\{\frac{{\text{E}}^{on}+{\text{E}}^{off}}{{\text{E}}^{I}},\:{\text{T}}^{on}+{\text{T}}^{off}\right\}\:$$

(1)

Therefore, the total electricity consumption for production is expressed as Eq. (2):

$$\:{E}_{sum}=\sum\:_{i=1}^{n}{\text{E}}^{P}{TP}_{i}+\sum\:_{i=1}^{n}({\text{E}}^{on}+{\text{E}}^{off}){z}_{i}+\sum\:_{i=1}^{n}{\text{E}}^{I}({TS}_{i}-{TS}_{i-1}-{TP}_{i-1})\times\:\left(1-{z}_{i}\right)$$

(2)

The third part of this objective function is non-linear, which is linearized using constraints (4) and (5) according to Eq. (3):

$\:{zv}_{i}$: decision variable for linearization

$$\:\sum\:_{i=1}^{n}{\text{E}}^{I}\left({TS}_{i}-{TS}_{i-1}-{TP}_{i-1}\right)\times\:\left(1-{z}_{i}\right)\:\:\:\:\:\:\:\:\:\:⟹\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\sum\:_{i=1}^{n}{zv}_{i}$$

(3)

$$\:{zv}_{i}\ge\:{\text{E}}^{I}\:\left({TS}_{i}-{TS}_{i-1}-{TP}_{i-1}\right)-M\times\:{z}_{i}\:\:\:\:\:\:\forall\:\:\:\:\:\:i>1$$

(4)

$$\:{zv}_{i}\le\:{\text{E}}^{I}\:\left({TS}_{i}-{TS}_{i-1}-{TP}_{i-1}\right)+M\times\:{z}_{i}\:\:\:\:\:\:\:\:\forall\:\:\:\:\:\:i>1$$

(5)

where Eqs. (6) and (7) hold:

$$\:{z}_{1}=1$$

(6)

$$\:{z}_{i}=\left\{\begin{array}{cc}0&\:{TS}_{i}-{TS}_{i-1}-{TP}_{i-1}\le\:\:{\text{T}}^{r}\\\:1&\:otherwise\end{array}\right.\:\:\forall\:\:\:i=\text{2,3},\:\dots\:,\text{n}$$

(7)

Equation (2) consists of three components: the first term represents the power consumption during the machine’s processing state, while the second and third terms denote the power consumption during the restarting and idle states, respectively. Equation (6) outlines the conditions for the machine’s initial activation and final deactivation. Lastly, Eq. (7) determines the machine’s operational state options.

Fuel consumption is related to vehicle type, driving speed, vehicle weight, load, and distance. Based on the Bektas and Laporte⁴² paper, the fuel consumption of vehicle $\:k$ on arc $\:(i,j)$ is expressed as (8):

$$\:{G}_{ijk}=\left({\lambda\:}_{ij}\left({W}_{k}+{l}_{ij}\right)+{\lambda\:}_{k}{v}^{2}\right)$$

(8)

Fuel consumption for collecting all workpieces is given in Eqs. (9) and (10):

$$\:{G}_{sum}=\sum\:_{i=0}^{n}\sum\:_{j=0}^{n}\sum\:_{k=1}^{m}{G}_{ijk}{x}_{ijk}$$

(9)

Finally, the total carbon emissions for collecting and processing all workpieces is equal to Eq. (10):

$$\:{C}_{sum}={\text{R}}^{e}{E}_{sum}+{\text{R}}^{g}{G}_{sum}$$

(10)

The final problem is as described in (11):

$$\:{Min\:\:\:C}_{sum}$$

(11)

$$\: min \, \, \sum\:_{i}\left[{d}_{i}-{F}_{i}\right]\times\:\delta\:$$

(12)

Equation (12) expresses the objective function of the problem, which is to minimize the total carbon emissions for collecting and processing orders, and the second objective is to reduce the delivery time to the customer.

The constraints of the routing problem are as follows:

$$\:S.To:\sum\:_{i=1}^{n}{x}_{0ik}\le\:1\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\forall\:\:k=\text{1,2},\:\dots\:,m$$

(13)

Equation (13) shows that each vehicle can leave the factory at most once.

$$\:\sum\:_{i=1}^{n}{x}_{i0k}\le\:1\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\forall\:\:k=\text{1,2},\:\dots\:,m$$

(14)

Equation (14) states that each vehicle can return to the factory at most once.

$$\:\sum\:_{j=1}^{n}\sum\:_{k=1}^{m}{x}_{ijk}=1\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\forall\:\:i=\text{1,2},\dots\:,n,\:i\ne\:j$$

(15)

$$\:\sum\:_{i=1}^{n}{x}_{ii{\prime\:}k}-\sum\:_{j=1}^{n}{x}_{{i}^{{\prime\:}}jk}\:=0\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\forall\:\:{i}^{{\prime\:}}=1,\:\dots\:,n,\:k=1.\:\dots\:.m$$

(16)

$$\:\sum\:_{i\in\:N}{y}_{ji}-\sum\:_{i\in\:N}{y}_{ij}={p}_{j}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\forall\:\:j\in\:c$$

(17)

$$\:\sum\:_{i=1}^{n}\sum\:_{j=0}^{n}{{W}_{i}x}_{ijk}\le\:{Q}_{k}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\forall\:\:k=\text{1,2},\dots\:,m$$

(18)

$$\:\sum\:_{j=1}^{n}{x}_{ijk}\ge\:{z}_{ik}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\forall\:\:i=1,\:\dots\:,n\:,\:k=1,\dots\:,m$$

(19)

$$\:\sum\:_{k=1}^{m}{z}_{ik}=1\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\forall\:\:i=\text{1,2},\dots\:,n$$

(20)

$$\:{y}_{ij}\le\:{Q}_{k}\:\times\:{x}_{ijk}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\forall\:\:i,j\in\:\mathbb{N},\mathbb{\:}k=1,\dots\:,\:m$$

(21)

Constraint (15) states that each node must be visited only once. Equation (16) shows that if we enter a node, we must exit it. Constraint (17) limits the number of vehicles used. Constraint (18) states that the total load of each vehicle must not exceed the vehicle capacity. Constraints (19) to (21) assign the workpieces to the vehicles.

$$\:\sum\:_{i=0}^{n}{l}_{i{i}^{{\prime\:}}}-\sum\:_{j=0}^{n}{l}_{{i}^{{\prime\:}}j}={W}_{{i}^{{\prime\:}}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\forall\:\:{i}^{{\prime\:}}=\text{1,2},\dots\:,n$$

(22)

$$\:\sum\:_{k=1}^{m}{({Q}_{k}-{W}_{i})x}_{ijk}\ge\:{l}_{ij}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\forall\:\:i\:,j=1,\:\dots\:,n$$

(23)

$$\:\sum\:_{k=1}^{m}{{W}_{j}x}_{ijk}\le\:{l}_{ij}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\forall\:\:i\:,j=1,\:\dots\:,n$$

(24)

Constraints (22) to (24) represent flow protection and truckload limitation. Constraint (22) calculates the load of the device in each arch and constraints (23) and (24) state that if a load passes through an arch, it is conditional on the use of that arch.

$$\:{{Tt}_{kj}\ge\:{Tt}_{ki}+{D}_{ij}-A(1-x}_{ijk}),\:\:\:\forall\:\:i=0,\:\dots\:,n\:,\:\:j=1,\:\dots\:,\:n,k=1,\:\dots\:,\:m$$

(25)

$$\:{{Tt}_{kj}\le\:{Tt}_{ki}+{D}_{ij}+A(1-x}_{ijk}),\:\:\forall\:\:i=0,\:\dots\:,n\:,\:\:j=1,\:\dots\:,\:n\:,k=1,\:\dots\:,m\:$$

(26)

$$\:{{Tar}_{k}\ge\:{Tt}_{ki}+{D}_{i0}-A(1-x}_{i0k})\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\forall\:\:i=1,\:\dots\:,n,\:\:\:k=1,\dots\:,\:m$$

(27)

$$\:{{Tar}_{k}\le\:{Tt}_{ki}+{D}_{i0}+A(1-x}_{i0k})\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\forall\:\:i=1,\:\dots\:,n,\:\:\:k=1,\:\dots\:,\:m$$

(28)

Constraints (25) to (28) calculate the time the vehicles arrive at the factory.

The limitations of the scheduling problem are as follows:

$$\:\sum\:_{j=0,j\ne\:i}^{n}{x}_{ji}^{{\prime\:}}=1\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\forall\:\:i=1,\:\dots\:,n$$

(29)

$$\:\sum\:_{i=1,j\ne\:i}^{n}{x}_{ji}^{{\prime\:}}\le\:1\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\forall\:\:j=1,\:\dots\:,\:n$$

(30)

$$\:\sum\:_{i=1}^{n}{x}_{0i}^{{\prime\:}}=1\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\forall\:\:i=1,\:\dots\:,\:n$$

(31)

$$\:\sum\:_{p=1}^{n}{y}_{ip}=1\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\forall\:\:i=1,\:\dots\:,\:n$$

(32)

$$\:\sum\:_{i=1}^{n}{y}_{ip}=1\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\forall\:\:p=1,\dots\:,\:n$$

(33)

$$\:{y}_{ip}+{y}_{jp+1}\le\:2{x}_{ij}^{{\prime\:}}-A\left({y}_{ip}+{y}_{jp+1}-2\right),\:\:\forall\:\:i,j=1.\:\dots\:.\:n,\:\:\:\:\forall\:\:p=1.\:\dots\:.\:n-1$$

(34)

$$\:{y}_{i1}=\:{x}_{0i}^{{\prime\:}},\:\:\:\forall\:\:i=1,\dots\:,n$$

(35)

$$\:{ST}_{jip}=\:{S}_{ji}{x}_{ji}^{{\prime\:}}+A\left({y}_{jp-1}+{y}_{ip}-2\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\forall\:\:i,j,p=1,\:\dots\:,\:n$$

(36)

$$\:{TS}_{j}\ge\:M{{z}^{{\prime\:}}}_{i}+NT\sum\:_{i=1}^{j}{{z}^{{\prime\:}}}_{i}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\forall\:\:j=1,\:\dots\:,n$$

(37)

$$\:{TS}_{p}+\:\sum\:_{i=1}^{n}({TP}_{i}{y}_{ip}+\sum\:_{j=1}^{n}{ST}_{jip})\:\le\:\:{TF}_{p}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\forall\:\:p=1,\dots\:,n$$

(38)

Constraint (29) shows that each job has only one job before it in the sequence, and the first job in the sequence is considered a dummy job ($\:j=0$). Equation (30) states that the maximum number of jobs after a job in the sequence is not greater than one. Due to the fact that there is no job after the last job, the equality does not hold. Constraint (31) places the dummy job as the first job in the sequence. Constraint (32) shows that each job has only one position in the sequence. Constraint (33) shows that each position in the sequence is occupied by only one job. Constraints (34) and (35) ensure the sequence order of the jobs using two decision variables $\:{x}_{ij}^{{\prime\:}}$ and $\:{y}_{ip}$. For example, if job $\:i$ is in position $\:k$ ($\:{y}_{ip}=1$) and job $\:j$ is also before job i ($\:{x}_{ji}^{{\prime\:}}=1$), then job $\:j$ will be in position $\:k-1$. Constraint (36) calculates the setup time of each job based on its position and the previous job. Equation (37) states that the processing of a job cannot start during maintenance and repair activities. Constraint (38) shows that the processing of a job does not start until the previous job is processed.

$$\:{TS}_{1}+\:\sum\:_{i=1}^{n}({TP}_{i}+{S}_{0i})\:{y}_{i1}\le\:\:{TF}_{1}$$

(39)

$$\:\sum\:_{i=1}^{n}({TA}_{i}+{TP}_{i}+{S}_{0i})\:{y}_{i1}\le\:{C}_{1}$$

(40)

$$\:{TF}_{p}-NT\sum\:_{i=1}^{p}{{z}^{{\prime\:}}}_{i}={C}_{p\:}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\forall\:\:p=1,\:\dots\:,n$$

(41)

$$\:{C}_{p}\le\:NT\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\forall\:\:p=1,\:\dots\:,n$$

(42)

$$\:\sum\:_{i=1}^{n}{TA}_{i}{y}_{ip}-\:{TS}_{p}\:\le\:0\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\forall\:\:p=1,\:\dots\:,n$$

(43)

$$\:{C}_{max}\ge\:\:{TF}_{i}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\forall\:\:i=1,\dots\:,n$$

(44)

Constraint (39) calculates the start and completion times of the jobs. Equation (40) calculates the machine processing lifetime after processing the first job. Equation (41) calculates the machine lifetime after processing each job. Constraint (42) ensures that the machine processing lifetime is greater than the time required between two maintenance and repair activities. Constraint (43) shows that processing does not start until the job is available. Equation (44) states that the completion time of the last job is greater than or equal to the completion time of each job.

Solving multi-objective optimization models

Various approaches have been proposed to solve multi-objective decision-making/optimization (MODM) problems. To solve a MODM problem using the AEC method, has been developed the planning model (45) where $\:{s}_{i}$ are non-negative variables for the deficit, and $\:{\varphi\:}_{i}$ is a parameter for normalizing the value of the first objective function relative to objective $\:i$, $\:{\varphi\:}_{i}=\frac{R\left({f}_{1}\right)}{R\left({f}_{i}\right)}$. Given that the mathematical model of this research falls into the category of models with high complexity, the GAMS software will not be able to solve the model on a large scale and can only solve the model on a small scale. As a result, another software must be selected for the solution, in this case, MATLAB software. For this purpose, first, a heuristic approach is used to create a solution for the problem, and the best solution is selected from the created solutions. The necessary information for solving the mathematical model in MATLAB using the MOPSO and NSGA-II algorithms is presented below³⁶.

$$\:\begin{array}{c}Min\:\:{f}_{1}\left(x\right)-\sum\:_{i=2}^{n}{{\varphi\:}_{i}s}_{i}\\\:{f}_{i}\left(x\right)+{s}_{i}={e}_{i}\:i=\text{2,3},.,n\\\:x\in\:X\\\:{s}_{i}\ge\:0\end{array}$$

(45)

Non-dominated sorting genetic algorithm (NSGA-II)

The genetic algorithm is one of the metaheuristic algorithms for solving the problem. This algorithm uses the principles of Darwin’s natural selection to find the optimal formula or solution for predicting and adapting patterns. The Non-dominated Sorting Genetic Algorithm (NSGA) was proposed by Deb et al.¹. In this algorithm, two important operators are added to the single-objective genetic algorithm, which transforms it into a multi-objective algorithm. This algorithm is based on the sorting of non-dominated solutions along with crossover and mutation operators³⁶.

Multi-objective particle swarm optimization (MOPSO)

The Multi-Objective Particle Swarm Optimization (MOPSO) algorithm was presented by Coello et al., which is used to solve multi-objective problems². In fact, this algorithm is an extension of the Particle Swarm Optimization (PSO) algorithm. In the MOPSO algorithm, a concept called an archive or repository is added. The archive or repository refers to the non-dominated population found, which is maintained separately from the main population, and in other words, the repository members provide an approximate Pareto front. In the NSGA-II algorithm, there is no concept of an archive, and the best solutions are maintained within the main population. The way of representing the solutions in this algorithm is similar to the NSGA-II algorithm, with the difference that in this algorithm, the term “particle” is used instead of “chromosome”.

Solution representation

Recognizing that both vehicle routing and scheduling are individually classified as NP-hard problems^{1,2,3,4,5,6,7,8,9,10,36}, it follows that their combined mathematical model will also exhibit NP-hard characteristics. Consequently, the utilization of meta-heuristic algorithms is necessary to effectively solve the integrated problem. As mentioned in the previous section, in this research, metaheuristic algorithms and MATLAB software have been used, but first, the way to reach a feasible solution in MATLAB should be presented. In this research, to achieve an initial solution, two solution representations are used, where the first solution representation is for determining the visit sequence and assigning customers to vehicles, and the second solution representation is for determining the job sequence.

Solution representation for determining the visit sequence and assigning customers to vehicles

For this purpose, a random vector of numbers between 0 and 1 is created with a dimension of I, where I is the number of customers. Then, the resulting vector is multiplied by V (the number of vehicles) and rounded up. In this way, the assignment of customers to vehicles is obtained. To determine the sequence of customers for each vehicle, the random numbers between 0 and 1 in the initial vector are sorted in ascending order, and the customers will be visited according to this sorting.

For example, if we have 5 customers and 2 vehicles, a random vector can be as shown in Table 1:

Table 1 Random vector for creating an initial solution.

Table 2 Random vector for creating an initial solution.

In this case, all customers are assigned to vehicle 1. Now, based on the ascending sorting of the initial vector, the visit order will be Customer 1$\:\to\:$ Customer 6$\:\to\:$ Customer 2$\:\to\:$ Customer 3$\:\to\:$ Customer 4$\:\to\:$ Customer 5. Finally, the graphical output of the above chromosome will be as shown in Fig. 2.

Fig. 2

An example of the generated initial solution.

Solution representation for determining the job sequence

For this purpose, a random vector of 0s and 1s with a length of I (the number of customers) is formed, and by sorting them in ascending order, the index of each element in the sorted vector indicates the order of the jobs on the machine.

For example, if we have six customers (jobs), we will have a random vector as shown in Table 3:

Table 3 Random vector for creating an initial solution.

Table 4 Random vector for creating an initial solution.

Therefore, the order of the jobs on the machine is: Job 4$\:\:\to\:$ Job 1$\:\to\:$ Job 2$\:\to\:$ Job 3$\:\to\:$ Job 5$\:\to\:$ Job 6.

The graphical output of the above chromosome is shown in Fig. 3:

Fig. 3

An example of the generated initial solution.

In Fig. 3, the vertical lines indicate the maintenance and repair activity intervals, and M represents the maintenance and repair process. It is worth noting that after determining the sequence of jobs based on the availability time of the jobs (the arrival time of the vehicle), the jobs start processing, and the on/off state of the machine is determined based on the start time of each job and the problem constraints.

Ensuring the feasibility of the solution

The above representation determines the visit sequence and assignment of customers to vehicles, as well as the sequence of job execution. However, during the process of updating the chromosomes based on mutation and crossover operators, chromosomes may be generated that are infeasible, i.e., they do not satisfy the constraints. To control this, a penalty function is used. For this purpose, the amount of violation of the constraints is multiplied by a large number and added to the objective functions. This problem has a penalty function. The penalty function of this problem is the amount of violation of the vehicle capacity (parameter Cap). In this penalty function, the amount of violation of the vehicle capacity is obtained, and this value is multiplied by a large number and added to the objective functions. If the amount of violation is zero, no penalty is considered; however, in the case of a violation, a large number is added to the objective functions, making them worse.

$$\:{CV}_{1}=\text{max}\left(0\:.\:\frac{{UC}_{v}}{Cap}-1\right)$$

(46)

In expression (46), $\:{CV}_{1}$ represents the amount of violations, $\:{UC}_{v}$ is the total load carried by vehicle $\:v$, and Cap is the vehicle capacity. Based on the violation functions, the objective functions are considered as (47) and (48):

$$\:{Obj}_{1}=\:{OFV}_{1}+M\left({CV}_{1}\right)$$

(47)

$$\:{Obj}_{2}=\:{OFV}_{2}+M\left({CV}_{1}\right)$$

(48)

In the above expressions, $\:{OFV}_{k}$ is the value of the $\:k$-th objective function obtained, $\:M$ is a large number, and $\:CV$ is the average of the $\:m$ penalty functions, where $\:k=1$ is the emission objective function and $\:k=2$ is the job delay cost objective function.

Crossover operator

To generate new generations, the crossover operator is used. In this research, the computational crossover operator is used. In this type of crossover, if $\:{x}_{1}$ is the first parent and $\:{x}_{2}$ is the second parent, and each has n members, we form a random vector ($\:\alpha\:$) between $\:[-\delta\:,\:1+\delta\:]$ with a length of $\:n$, where $\:\delta\:$ is a parameter, and the first child ($\:{y}_{1}$) and the second child ($\:{y}_{2}$) are obtained as follows:

$$\:{y}_{1}=\alpha\:.{x}_{1}+\left(1-\alpha\:\right).{x}_{2}$$

(49)

$$\:{y}_{2}=\left(1-\alpha\:\right).{x}_{1}+\alpha\:.{x}_{2}$$

(50)

Suppose the first and second parents are as shown in Table 5:

Table 5 Example of crossover operator.

and parameter $\:\delta\:$ is considered equal to $\:0.1$, then a random solution of vector $\:\alpha\:$ can be as shown in Table 6.

Table 6 Example of crossover operator.

Using the above formulas, the first and second children can be obtained as shown in Table 7. This method is used for the crossover and creation of offspring for all 2 chromosomes in this research.

Table 7 Example of crossover operator.

Mutation

The operator used in this research is as follows: µ members are selected from each chromosome, and those members are added to a continuous random number between $\:[-1,\:+1]$.

Solving a numerical study in small dimensions

In addressing NP-HARD models, meta-heuristic algorithms have demonstrated significant potential for finding efficient solutions. Our research utilizes the NSGAII and MOPSO algorithms, drawing upon the parameters employed in prior studies^{1,2,3,4,5,6,7,8,9,10,36}. Recognizing the importance of critical parameters such as $\:maxit$ and $\:npop$ for solution quality, we ensured consistency in their values ($\:maxit=200,\:npop=150$) across both algorithms through a trial and error method (Table 8). Additionally, the Taguchi method was employed to fine-tune other algorithm parameters, enabling us to systematically identify optimal settings and improve overall performance. Further details on the implementation of the Taguchi method can be found in our methodology section, with additional information on its application available in the literature.

Table 8 Parameter levels of the NSGA-II and MOPSO algorithms.

Fig. 4

S/N ratio plot for the NSGAII and MOPSO.

As depicted in Fig. 4, the parameter levels can be distinguished, with some parameters requiring different levels of adjustment. For instance, pc and mu should be set in the first level, while pm is to be adjusted in the second level. This multi-level approach allows for a more nuanced fine-tuning of the algorithm parameters, ultimately improving the performance and accuracy of the model.

In this numerical example, which has been solved using the NSGAII, AEC, and MOPSO methods, 6 customers are considered. There is a workshop, 4 vehicles for collecting pieces from customers (suppliers), and 6 workpieces for processing and placing the pieces. A summary is reported in Table 9, and then the necessary values for solving the problem are created and presented.

Table 9 Introduction of indices for solving the problem.

To create the distance matrix between customers, the Euclidean distance formula was used. First, the coordinates of the customer (piece supplier) were obtained, and then the distance between them was calculated:

$$\:xc\left(i\right)=\left[50\:\:\:50\:\:62\:\:100\:65\:\:33\:\:49\right]$$

(51)

$$\:yc\left(i\right)=\left[50\:\:\:47\:\:32\:\:42\:\:58\:\:69\:\:33\right]$$

(52)

In Eqs. 51 and 52, the coordinates of the customers are presented. For example, for the workshop with a length and width of 50 and 50, and for customer number 5, the coordinates were set to 33 and 69, respectively. In Tables 10 and 11, the necessary values for generating a sample problem are produced and presented.

Table 10 Information needed to solve the sample problem.

Table 11 Information needed to solve the sample problem.

The problem in question was executed using the AEC method in the GAMS software version 24.1.2, and the NSGAII and MOPSO algorithms were run in MATLAB version 2020b on a laptop with 32 GB of RAM and 7 cores. The results are reported. The Pareto fronts generated by the methods are reported in Table 12, and the 3D plot is also provided.

Table 12 Results from the AEC-NSGAII-MOPSO methods.

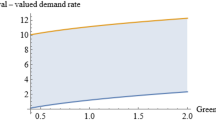
The 2D plot for the problem is presented in Fig. 5. Based on this plot, to reduce the delivery time of the pieces to the customers, the level of emissions increases, and if the goal is to reduce the level of emissions, the delivery time of the pieces to the customers will be delayed, which will cause customer dissatisfaction.

Fig. 5

Pareto front from the solution methods.

Based on Table 11; Fig. 3, the values of the decision variables for this problem with two vehicles, 6 suppliers, one workshop, 6 pieces, and pieces locations are provided. According to Fig. 6, vehicle 1 has collected all the pieces in the order 5-4-3-2-6-1.

Fig. 6

Representation of the vehicle routes for collecting pieces from customers.

The Gantt chart related to scheduling, sequence, and maintenance repairs is presented. The arrival time of the vehicle is 46.111.

Fig. 7

Output of the scheduling problem.

In Fig. 7, the vertical lines indicate the maintenance and repair activity intervals, and M represents the maintenance and repair process. The order of piece processing is 5-1-2-3-4-6, and the values of the decision variable ST (start time of processing on each piece) are shown in Table 13.

Table 13 Start time of processing on the pieces.

Table 14 shows the vehicle load at each node. For example, when the vehicle is at node 5, it has loaded piece 5, which weighs 10 kg.

Table 14 Calculation of vehicle load.

The completion time of pieces processing is shown in Table 15.

Table 15 Completion time of piece processing.

The machine age after the completion of pieces processing is shown in Table 16.

Table 16 Machine age after completion of pieces processing.

The on/off state of the machine is also shown in Table 17.

Table 17 On/off state of the machine.

The total electrical energy consumption for processing all the pieces is $\:{E}_{sum}$=558.65, the total carbon emissions for processing and collecting all the pieces is $\:{C}_{sum}$=152,900.44, and the total fuel consumption for collecting all the pieces is $\:{G}_{sum}$=401,037.71. It is worth noting that after determining the sequence of tasks based on the availability time of the tasks (vehicle arrival time), the tasks start processing, and the on/off state of the machine is determined based on the start time of each task and the problem constraints.

Sensitivity analysis

For the sensitivity analysis of the mathematical model, the important parameters of the model are examined. In this section, the parameter Tr is examined, where this parameter is increased by 50% and decreased by 50%, and the direct impact of this analysis is shown in Figs. 8 and 9, and 10.

Fig. 8

Machine task execution (50% increase).

Fig. 9

Machine task execution (before analysis).

Fig. 10

Machine task execution (50% decrease).

According to the results, this problem did not affect the vehicle routing, as expected, but it did affect the order of task execution. In the initial problem state, the order of task execution was 5-1-2-3-4-6. With a 50% increase in the time required to restart the machine (waiting in idle state), the order of task execution changed to 4-1-2-3-5-6, and if the opposite condition is applied, i.e., a 50% decrease in the parameter tr, the order of task execution becomes 1-5-2-3-4-6. The electrical energy consumption for processing all the pieces is $\:{E}_{sum}$=558.65 for the initial case, $\:{E}_{sum}$=450.65 for the 50% decrease case, and $\:{E}_{sum}$=518.56 for the 50% increase case. The results show that the decrease in electricity consumption for piece processing is greater than the increase.

Vehicle capacity

Based on the results obtained with a 30% and 50% reduction in vehicle capacity, were obtained the following results:

Fig. 11

Vehicle routes (before analysis).

Fig. 12

Vehicle routes (30% reduction in capacity).

Fig. 13

Vehicle routes (50% reduction in capacity).

According to Figs. 11 and 12, and 13, it can be stated that the reduction in capacity should have a direct impact on routing, which is the case. In the initial conditions, only one vehicle is working, and with a 30% reduction, another vehicle visits customer 5, otherwise the problem would be infeasible. Furthermore, with a 50% reduction in vehicle capacity, customers 1-2-6 are visited by the second vehicle, and the pieces are collected. It is also clear that the reduction in vehicle capacity has affected the order of piece processing, and this is because the piece availability time for processing in this research is dependent on the vehicle arrival time, resulting in a different order of processing, as shown in Figs. 14 and 15, and 16.

Fig. 14

Machine task execution (before analysis).

Fig. 15

Machine task execution (30% reduction in capacity).

Fig. 16

Machine task execution (50% reduction in capacity).

Piece processing time

If the piece processing time increases or decreases, it does not affect the vehicle routes, and the routing is done in the same initial form, but the way the pieces are processed changes as shown in Figs. 17 and 18, and 19:

Fig. 17

Machine task execution (before analysis).

Fig. 18

Machine task execution (50% increase in capacity).

Fig. 19

Machine task execution (50% decrease in capacity).

It is clear that in the first step, the way the pieces are processed is different from the initial state, and the completion time is 570 in the initial state, 686 in the case of a 50% increase in processing time, and 456 in the case of a 50% decrease. This is logical because an increase in piece processing time directly affects the completion time and the order of task execution.

The effect of a 20% increase and then a 20% decrease in the parameters of Table 18 was also generally performed. The results are presented in the following:

Table 18 Output of the scheduling problem.

Based on Figs. 20 and 21, and 22, it can be concluded that the increase in energy consumption also affects the scheduling and completion time. As shown in the figure, in the case of a 20% increase, the completion time is 684, while in the initial case, it was 570.

Fig. 20

Machine task execution (before analysis).

Fig. 21

Machine task execution (20% increase).

Fig. 22

Machine task execution (20% decrease in capacity).

This condition also affects the objective function, which is shown in Table 19; Fig. 23:

Table 19 Effect of increased energy consumption on research objectives.

As can be seen, in the case of a 20% decrease, the values of the objective functions decrease (some of the solutions), but in the case of a 20% increase, all Pareto solutions increase. The blue plot is the initial state, the red plot is the 20% decrease state, and the dark plot is the 20% increase state.

Fig. 23

Effect of increased energy consumption on scheduling.

Solving problems in different dimensions

To compare the algorithms used in this research, the following indicators were used: Diversification Metric (DM), Multiobject Coefficient of Variation (MOCV), Mean Ideal Distance (MID), Number of Pareto Solutions (NOS), Spacing, Maximum Spread, and Computation Time. For more details, refer to^{36–37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52–53–54–55–56–57}. First, 30 problem instances in small, medium, and large dimensions were designed. The information about these problem instances is provided in Table 20. These problems were solved using the NSGA-II and MOPSO algorithms in MATLAB. Each problem was executed 10 times for each algorithm, and the average was reported as the final solution for each method.

Based on the points mentioned, it is necessary to design some problems and execute them using both algorithms under the same conditions and compare the results. Table 20 shows the dimensions of the problem, where the smallest problem has 5 customers, 1 vehicle, and 5 types of pieces, and the largest problem includes 150 customers, 10 vehicles, and 150 types of workpieces and their positions. It is worth noting that the numbers required to solve the mathematical model are adopted from a sample problem.

Table 20 Different dimensions of the problem for solving the mathematical model.

Table 21 Output of NSGAII algorithm.

Table 22 output of evaluation indicators for MOPSO algorithm.

Comparison of algorithms using indicators

According to Tables 20 and 21, the comparison between the algorithms is presented. The diversity of the NSGA-II algorithm is greater than MOPSO, which, according to the definition of the diversity index, means that the NSGA-II algorithm performs better in this criterion. For the MID and Spacing indicators, which, according to the definition, have better performance with a decrease, it can be concluded that there is no significant difference between the two algorithms in this indicator. Another indicator examined is NOS, and according to the results and the nature of this indicator, which is better when it is higher, it is clear that the NSGA-II algorithm has performed better than MOPSO. For the DM indicator, which measures the dispersion of non-dominated solutions and a higher value is more desirable, the NSGA-II algorithm has provided the preferred result according to the comparison. Regarding the MOCV criterion, there is no significant difference between the two algorithms, but the MOPSO algorithm has better performance in terms of computation time. In addition, a general analysis can be done. The last row of Tables 21 and 22 shows the overall average of the 7 indicators examined in this research for the 30 problems. Regarding the average, the MOPSO algorithm is superior to the other algorithm in terms of CPU Time, MOCV, MID, and Spacing, and is introduced as the superior algorithm. To accurately assess the algorithms examined in this research, statistical analysis is performed in the next section.

Statistical comparison of algorithm performance

To provide a statistical analysis of the results of the proposed metaheuristic algorithms, a variance analysis test at a 95% confidence level was used. The purpose of the analysis of variance is to compare the means of several populations to determine whether the means of these populations are equal or if there is a significant difference between them. Given the use of two metaheuristic algorithms and the evaluation indicators, the results for the indicators are compared. The results of this test for comparing the indicators using Minitab 18 software are presented. For the Diversity, Spacing, MOCV, and MID indicators, the Prob > F or P-value is greater than 0.05, so there is no significant difference between the two algorithms in these indicators. The P-value is less than 0.05 for the NOS indicator, so there is a significant difference between the two algorithms in this indicator. Therefore, based on Fig. 24, the NSGA-II algorithm performs better in this indicator.

Fig. 24

Statistical analysis result for the NOS indicator.

Since the P-value is less than 0.05, there is a significant difference between the two algorithms in the DM indicator. Therefore, based on Fig. 24, the NSGA-II algorithm performs better in this indicator.

Fig. 25

Statistical analysis result for the DM indicator.

The P-value for CPU Time is less than 0.05, so there is a significant difference between the two algorithms in this indicator. Therefore, based on Fig. 25, the MOPSO algorithm performs better in this indicator.

Fig. 26

Statistical analysis result for the algorithm computation time indicator.

Based on the statistical analysis results, the NSGA-II algorithm is significantly better than the MOPSO algorithm in the DM and NOS indicators, and the MOPSO algorithm is superior in the computation time indicator. Therefore, the NSGA-II algorithm can be introduced as the superior algorithm.

Solving a numerical case study in large dimensions

Based on the results of the statistical analysis and the comparison between the algorithms, it was concluded that the NSGA-II algorithm performed better than the MOPSO algorithm. Therefore, this problem is executed using the NSGA-II algorithm, and the results are reported. In this numerical example, 40 customers, one workshop, 4 vehicles for collecting pieces from customers (suppliers), and are considered 40 workpieces for processing and piece placement. A summary is reported in Table 23, and then the necessary values for solving the problem are created and presented.

Table 23 Introduction of indices for solving the large-scale problem.

The Euclidean distance formula was used to create the distance matrix between customers. First, the coordinates of the customers were obtained, and then the distance between them was calculated. The input parameter values are considered in Table 20. After solving the problem, the Pareto front is presented in Table 24.

Table 24 Set of solutions obtained using the NSGA-II method.

Based on Table 23, the Pareto chart was plotted, as shown in Fig. 26. According to this chart, if the decision-makers goal is to increase customer satisfaction by reducing delivery time (timely delivery of pieces to customers), then the level of emissions will increase, and vice versa. If decision-makers focus on reducing emissions, the machine will be turned off more often, the vehicle loading will be less, and the emissions will decrease, but the on-time delivery will not be achieved, and it will be done later. The presented points are those that decision-makers should choose, depending on the level of emissions they are willing to produce for this logistics process.

Fig. 27

Pareto chart in large dimensions.

For the first Pareto point, the first objective is 3,478,617, and the second objective is 2,137,593. The values of the decision variables are graphically reported in Fig. 28.

Fig. 28

Representation of vehicle routes for collecting pieces to the workshop.

Note that in the problem, the number 1 represents the workshop, and the pieces start from numbers 2 to 41, which are collected by the vehicles from the suppliers or customers. For example, vehicle 4 with the red color has left the origin, which is the workshop ($\:O=1$), and after collecting the pieces, it has returned to the workshop. The arrival times of vehicles 1, 2, 3, and 4 to the workshop are 225.21, 194.20, 315.46, and 113.46, respectively. The order of task execution is also shown in Table 25:

Table 25 Order of task execution.

The Gantt chart is reported in Fig. 29.

Fig. 29

Gantt chart.

The total electrical energy consumption for processing all the workpieces is $\:{E}_{sum}$= 3,457.42, the total carbon emissions for processing and collecting all the workpieces is $\:{C}_{sum}$= 2,284,344.19, and the total fuel consumption for collecting all the workpieces is $\:{G}_{sum}$= 5,987,695.87.

Managerial discussion and analysis

An industrial company whose activities are focused on scheduling and processing pieces generally processes the pieces in such a way that after the job is delivered, the company has the necessary profit to continue its activities and has enough time to distribute it to the final customer. This has resulted in the machine (for processing the pieces) being on until the last piece is processed. During the operation period, the machine is either in the processing state or idle. This problem not only increases the production of pollutants by the machine but also affects the production cost, as the fuel price for keeping the machine on is very expensive and valuable. Therefore, if the carbon emissions during the idle period are greater than restarting the machine, the machine can be turned off. This switching operation is an effective method for saving energy.

This problem leads to a specific delay in the completion time. The processing of a workpiece may be completed late, and some workpieces may even not be delivered on time. However, if the pieces are better planned and made available to the machine for processing, this machine downtime and idle time can be compensated so that no harm is done to the distribution schedule, and the pieces are processed and delivered to the customers on time. The vehicle routing problem (finding the shortest distance traveled by vehicles) allows this possibility, and the pieces are collected before the workshop and delivered to the workshop in less time through optimized transportation and routing. The machine’s access time for processing the pieces is certainly improved when the pieces are transferred to the workshop with a routing plan compared to when they are transferred without a routing plan. Here, the combination of the vehicle routing problem and the workshop scheduling is very useful for such businesses.

Conclusion

The present research aimed to design an integrated mathematical model for combining the vehicle routing and scheduling problem, which ultimately developed a bi-objective model. In addition, environmental and social objectives (timely delivery of the required piece, customer satisfaction) were considered simultaneously. The components of this mathematical model include piece suppliers (customers), the workshop, the pieces and their positions, and finally the vehicles. Decisions were made regarding the allocation of pieces to the vehicles for collection, routing, the number of vehicles, scheduling and prioritizing the pieces for processing, maintenance and repairs, etc. The values of the decision variables were also reported in small and large dimensions.

The proposed mixed-integer linear programming model of this research includes three dimensions: environmental and social (customer satisfaction) simultaneously. First, to find the exact solution, the enhanced epsilon-constraint method was used through the GAMS software. Given the NP-hard nature of the model, for solving larger-scale problems, the metaheuristic methods of NSGA-II and MOPSO were used. 30 examples in small, medium, and large dimensions were solved using these two metaheuristic methods in MATLAB software. The solutions obtained from the enhanced epsilon-constraint method were considered as a basis for comparison with the solutions of the NSGA-II and MOPSO algorithms. The solutions obtained from these algorithms were close to the exact solution and provided acceptable solutions. To compare the two presented algorithms, 7 evaluation criteria were used. According to the DM and NOS criteria, the NSGA-II algorithm was superior, but according to the solution time criterion, the MOPSO algorithm was superior. The statistical comparison of the two algorithms based on the 7 indicators showed that there was a significant difference in the mentioned indicators, but there was no significant difference between the two algorithms in the other indicators. The results showed that to reduce emissions, the on-time delivery parameter to customers is neglected, and in this case, decision-makers must decide on the level of emissions.

Suggestions for future research

Based on the conducted studies, one can propose items to develop the research done and consider new dimensions that have not been addressed so far, as well as solve the proposed models of this problem using various existing methods that are applied according to the nature of each problem, for research in this field. Some of these items are as follows:

• The problem can be designed and solved in a multi-workshop format.

• Uncertainty conditions can be considered.

• An economic objective for achieving sustainability can be included.

• The model can be solved using exact methods such as the Benders algorithm.