Soft-computing models for predicting plastic viscosity and interface yield stress of fresh concrete

Abstract

Interface yield stress and plastic viscosity of fresh concrete significantly influences its pumping ability. The accurate determination of these properties needs extensive testing on-site which results in time and resource wastage. Thus, to speed up the process of accurately determining these concrete properties, this study tends to use four machine learning (ML) algorithms including Random Forest Regression (RFR), Gene Expression Programming (GEP), K-nearest Neighbor (KNN), Extreme Gradient Boosting (XGB) and a statistical technique Multi Linear Regression (MLR) to develop predictive models for plastic viscosity and interface yield stress of concrete. Out of all employed algorithms, only GEP expressed its output in the form of an empirical equation. The models were developed using data from published literature having six input parameters including cement, water, time after mixing etc. and two output parameters i.e., plastic viscosity and interface yield stress. The performance of the developed algorithms was assessed using several error metrices, k-fold validation, and residual assessment etc. The comparison of results revealed that XGB is the most accurate algorithm to predict plastic viscosity (training $\:{R}^{2}=0.959$, testing $\:{R}^{2}=0.947$) and interface yield stress (training $\:{R}^{2}=0.925$, testing $\:{R}^{2}=0.965$). To get increased insights into the model prediction process, shapely and individual conditional expectation analyses were carried out on the XGB algorithm which highlighted that water, cement, and time after mixing are the most influential parameters to estimate both fresh properties of concrete. In addition, a graphical user interface has been made to efficiently implement the findings of this study in the civil engineering industry.

Introduction

In the construction industry, the utmost attention is usually given to the hardened properties of concrete specifically compressive strength. However, the procedure of transporting freshly made concrete from ground to the intended location in the construction of dams, high rise buildings, and long-span bridges etc. is very challenging and requires due attention^1,2,3. Although, the concrete is widely transported to great distances and huge vertical heights by means of a concrete pump in a steel pipe, the problem of blockage of pump and pipes and segregation of concrete while transportations remain a serious issue. These issues not only result in degradation of concrete quality, but also cause loss of time and resources on the worksite^4,5,6.

The ability of a concrete to easily pass through a pipe without altering its fresh and hardened properties using pump is known as pumpability of concrete. There are mainly two types of studies related to this, one those who focus on pump and pipe configuration and those who focus on the concrete fresh properties itself. Since, for a given worksite setting, one doesn’t have much choice in terms of pump and pipe related properties like pump capacity, pipe diameter, pipe length etc. Thus, the study and optimization of fresh concrete properties plays a key role in achieving the desired outcomes^7,8,9. To quote an example, in the construction of world’s tallest building in Dubai, the Burj Khalifa, to ensure a smooth and single stage pumping of concrete over 600 m without blockage, the engineers performed extensive tests to finalize a concrete mixture to achieve the desired properties^10,11. Similarly, the hurdles faced while constructing Head Race Tunnel project in India had been descried by Hazaree and Mahadevan¹². The project required concrete lining up to a distance of 6.3 km which was successfully achieved by extensive testing and meticulous planning done by the engineers. The crucial processes of material selection, equipment and pipeline selection were done by careful evaluation of priming and pumping methodologies and thorough pre-testing before the actual concrete pumping. The plastic viscosity of concrete is of particular importance in this regard. It is a crucial rheological property of concrete to consider in situations where concrete is subjected to shear forces like pumping, casting, and placement etc. It is an indication of how easily the concrete can be mixed, transported, and placed without loss of quality (bleeding & segregation). It is also important to indicate the ease with which concrete passes through the pump without blockage or clogging. Similarly, interface yield stress of concrete is a crucial parameter which that determines the strength of bond between concrete and the reinforcement bars^13,14,15.

Previous studies regarding estimation of fresh concrete properties

The flow profile of concrete inside a pipe along with three layers named as the lubrication layer at the interface between the pipe and concrete, a shear induced region where concrete is under shear and a plug flow zone where concrete flows under translational motion^16,17,18 are shown in Fig. 1. In previous studies, the calculation of concrete pumpability is related to pumping pressure (P) and flow rate (Q) of a concrete mixture. Jang et al.¹⁹ introduced a bi-linear mode to estimate the P-Q relationship. The first assumes that only a boundary layer of small thickness is subjected to shear while the second part considers partial shear during pumping. Scholars have also devised different equations to compute pumping pressure^19,20,21 for the purpose of determining concrete pumpability which are given by Eqs. (1) and (2). In below equations,  is viscous constant of the lubricating layer measured by tribometer ($\:Pa.s/m$), $\:{\tau\:}_{io}$ is the interface yield stress (Pa), while $\:{\tau\:}_{o}$ is the yield stress and µ is plastic viscosity ($\:Pa.s$) of the concrete measured with the help of a viscometer. Also, k represents pipe filling coefficient while R and L are the radius and length of pipe respectively measured in meters. Equation (1) gives the concrete movement to where only a small boundary layer is subjected to shear and Eq. (2) is applicable when bulk concrete is partially sheared during pumping. The concrete pumping pressure is estimated with the help of its rheological and tribological properties when the pumping configuration, concrete flow rate and pipe dimensions are pre-defined²². Thus, predicting plastic viscosity and interface yield stress is crucial to obtaining an optimal pumping pressure.

(1)

(2)

Figure 1

Schematic diagram to show flow of fresh concrete inside a pipe²³.

In another study conducted by Choi et al.²⁴ the authors calculated flow rate by integration of velocity and radius. The developed models utilized rheological properties of each layer, and the four aforementioned parameters were determined via experimentation. More recently, several scholars suggested using a portable tribometer to determine $\:{\tau\:}_{io}$ and ^{15,25,26,27,28,29,30,31}. Similarly, He et al.³² studied the influence of nano titanium oxide on both porous and normal concrete and the authors concluded that the micromechanics approach might be feasible for predicting mechanical concrete properties. However, among these previously developed models, the model developed by Ngo et al.³³ is valid only for normal concrete. In practice, it has been identified that for normal concrete, interfacial properties are crucial to determine pumping pressure^34,35,36,37. So, the interfacial properties which characterize the lubrication layer properties, have been the subject of interest for many researchers. For example, Ngo et al.³³ conducted experiments in which they estimated variation in pumping parameters with change in concrete compositions including variation in superplasticizer, water cement ratio and paste volume etc. The authors concluded that concrete composition affects the lubrication layer formation and concrete tribological properties. Also, Dong et al.³⁸ documented that yield stress generally decreases with increase in finer content of concrete. Similarly, T. Ngo (2009) concluded that increase in cement paste volume results in a linear decrease in viscosity and a minimal decrease in interface yield stress³⁹. Moreover, the variation in water-cement ratio also affects plastic viscosity and yield stress in the same fashion as cement paste volume. The increase in gravel to sand ratio also causes a decrease in viscosity^40,41,42,43. According to Choi et al.⁴⁴ both under question parameter also varied greatly with coarse aggregate size, and plastic viscosity exhibited a linear increasing trend with increase in coarse aggregate size.

Concrete plastic viscosity and yield stress are commonly measured by tribometers^38,45,46. Based on the findings from these tribometers, researchers have attempted to develop empirical prediction models. Ferraris and Larrard⁴⁷ developed a model to investigate the relationship between properties of finer mixtures and mortar parameters. Ngo et al.³³ studied fresh concrete properties in relation to lubrication layer thickness and ratio of solid concentration to maximum compactness of the granular mixture. But all these models are constructed with respect to specific grading of the aggregates and concrete additives, so their application is greatly limited. In addition, there are very few works in the literature about prediction of plastic viscosity and interface yield stress of concrete. Thus, to ensure smooth concrete pumping, it is important to accurately estimate yield stress and plastic viscosity of concrete mixes as accurately as possible based on the mixture composition.

The optimization of concrete mixes to be used for pumping and transportation through pipes also requires the paste-distance correlations to be investigated. But these tests consume significant time and resources. The rheological properties of concrete mixes depend upon its composition and are inherently complex to understand^48,49,50. Also, the properties of concrete mixes in fresh state are time dependent. Therefore, it is imperative to have a thorough understanding of concrete properties during the fresh state to make the concrete pumping process smooth.

Artificial Intelligence (AI) in civil engineering

Since there is a transition to artificial intelligence-based systems in almost every industry, civil and materials industry is also making its transition towards intelligence-based designs and methodologies driven by data. AI in the realm of civil engineering mainly refers to amalgamation of advanced machine learning (ML) and deep learning techniques to optimize material usage, foster sustainable construction practices and intelligent design of infrastructure to improve the overall efficiency and accuracy of construction industry. ML is a subtype of artificial intelligence that enables computers to recognize patterns from the data and use that learning to make accurate predictions for future unseen data without explicit human intervention⁵¹. Machine learning tools have emerged as an effective way to make decisions based on learnings from the data. The ML techniques understand the complex and hidden relationships between independent and dependent variable(s) in the data obtained from experimental investigations. These learnings from the data are then used by professionals like engineers etc. to make accurate decisions without going into the timely and costly testing procedures. In the technologically advanced world of today, ML techniques are seen as a superior alternative of traditional statistical approaches and are extensively used in modelling complex material properties^{52,53,54,55,56,57,58,59,60,61,62,63,64}. Thus, there is a need to apply the robust and widely used ML models to predict fresh concrete properties to solve the aforementioned problems in transportation of concrete over long distances. These ML-based models developed using the generalized data from past studies can be used as reliable tools to predict fresh properties and their use not only results in time and cost savings, but also increases accuracy in estimating rheological concrete properties.

Research significance

From the above discussion, it is evident that a purely experimental approach to assess different rheological properties like plastic viscosity and interface yield stress requires extensive resources and is not the most feasible option given the diverse site conditions. In past, there have been several attempts to develop empirical relationships to obtain concrete plastic constant using statistical techniques^13,39,65. However, these statistical models have limited applicability and are sensitive to the material properties of concrete constituents etc. Also, it is evident from the overview of relevant literature that are few analytical models available for determining plastic viscosity and interface yield stress of concrete but there is a need for exploration on the subject using advanced and accurate ML techniques to predict these properties. The data driven models based on the already available experimental data can help greatly in this regard to accurately predict rheological concrete properties thus eliminating the need for extensive testing and increasing the productivity of the construction industry.

The employment of advance ML techniques will help the professionals to effectively calculate these values without carrying out extensive testing. Thus, this study intends to apply random forest regression (RFR), K-nearest Neighbor (KNN), Extreme gradient Boosting (XGB), Gene Expression Programming (GEP) and also a statistical analysis technique called Multi Linear Regression (MLR) to predict the aforementioned properties of concrete in fresh state and contribute to the literature about predicting plastic viscosity and interface yield stress of concrete mixes using different ML algorithms because the existing literature on the subject is extremely limited. The advantage of using evolutionary technique like GEP alongside other algorithms is that it gives the output in the form of an empirical equation unlike other employed algorithms. This property makes GEP a grey-box model as compared to other black-box model algorithms⁶⁶. GEP provides increased transparency and insights into the prediction process in the form of an empirical equation that relates the predicted parameter to the input parameters. It also offers the advantage of not requiring the pre-optimization of model architecture like Artificial neural networks etc., thus requires less computing power and time to complete the model training and prediction process⁶⁷. Similarly, the tree-based algorithms (RFR and XGB) are known for their accuracy and in giving insights about the importance of different input features. Also, the use of MLR can serve as a way to compare the accuracy of newly developed ML algorithms to predict rheological concrete parameters compared to the conventional statistical approach. The particular significance of this study lies in the fact that it draws a comparison between GEP, tree-based algorithms, KNN, and MLR to highlight their strengths and weaknesses for predicting important rheological properties of concrete. Also, this study intends to utilize a novel explanatory analysis technique (SHAP) analysis on the algorithm of highest accuracy to highlight the importance of different input features in predicting the two outputs. This thing has not been explored in the literature to the best of author’s knowledge.

Research methodology

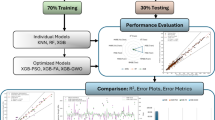
The identification of research problem and collection of data regarding that problem are the most important steps. Thus, the data was collected from literature to be used for training and testing the algorithms. The collected data underwent several statistical analyses to reveal more information about the distribution and correlation of the data. After that, in Step 3, four ML algorithms including GEP, RFR, XGB, KNN and one statistical regression technique i.e., MLR were employed to predict the two concrete properties. After algorithm development, they were validated using several techniques including k-fold cross validation, error assessment, and residual distribution. After the models were validated, they were compared to point out a single accurate model which will be used for further analysis. In step 4, the most accurate model was used for conducting contemporary explanatory analysis techniques including SHAP and individual conditional expectation (ICE) analysis. Finally, a graphical user interface (GUI) has been developed to help implement the findings of this study in the practical settings. The schematic representation of the current study’s methodology is given in Fig. 2 while the explanation of the working mechanism of the employed algorithms is given in the subsequent sections.

Figure 2

Overall research methodology of the study.

Gene expression programming (GEP)

GEP is an AI technique which uses evolutionary algorithms to find solution to a problem. It is an extension of Genetic Programming (GP) and based on Charles Darwin’s principles of natural selection. GEP finds solution to the problem using genes and performing evolutionary rules on these genes⁶⁷. The genes are build using various mathematical functions called primitive functions. These functions range from simple arithmetic functions like addition, subtraction to more complex like square root, sine, cosine etc⁶⁸. These genes which can be expressed as expression trees represent a small piece of code and are combined in various ways using crossover and mutation to create a full program which represents the solution to the given problem⁶⁹. Crossover involves combining two expressions to develop a new one and mutation means changing an existing expression⁷⁰. These processes in GEP are similar to the genetic mutation and crossover in humans. The pictorial representation of the processes of crossover and mutation is given in Fig. 3.

Figure 3

Representation of expression tree and genetic processes⁷¹.

The prediction process starts with the formation of a random population of computer programs called chromosomes. These chromosomes are evaluated for their ability to solve the given problem using a pre-defined fitness function. The chromosomes with good performance based on the fitness function are selected for the next generation while the worst performing ones are deleted from the population⁷². This process repeats several times until a population of chromosomes with the highest accuracy is reached⁷³. The flowchart of the overall process is given in Fig. 4.

Figure 4

Graphical representation of ML models.

K-nearest neighbor (KNN)

KNN is a widely used ML technique which can solve both classification and regression problems⁷⁴. The concept of KNN is based on the principle that if the k closest neighboring samples to a given sample in the space belong to a specific category, then the given sample should also belong to that category. In other words, the KNN algorithm is used to decide the category of an unknown sample by looking at the category of its k closest neighboring samples. For solving a regression problem, the KNN algorithm computes the distance between an input unknown sample and all other samples present in the dataset and selects the first k samples with the shortest distances. KNN algorithm computes the value of unknown data samples by computing the average of relevant variables and comparing the results with the k-nearest samples in the training set⁷⁵. The algorithm’s effectiveness is highly dependent on the k value⁷⁶, which determines the number of samples to be considered in the regression process. A smaller value of k may result in a higher level of noise in the process, while a larger k value may lead to over smoothing and lower accuracy. Therefore, choosing an appropriate k value is crucial for optimization of the KNN performance. The distance between neighboring points used for the regression problems is calculated commonly by using Minkowski function as given in Eq. (3). In Eq. (3), xi and yi are the ith dimensions, and q indicates the order between the points x and y.

$$\:F\left(mi\right)={\left({\sum\:}_{\:i=0}^{\:f}{\left(\right|{x}_{i}-{y}_{i}\left|\right)}^{q}\right)}_{q}^{1}$$

(3)

The KNN method has several benefits over other ML algorithms. Firstly, it is simple and easy to understand. Secondly, it can easily understand nonlinear decision boundaries of both regression and classification problems. Moreover, the flexibility of the KNN approach is enhanced by the ability to adjust the k value to provide a suitable choice limit.

Random forest regression (RFR)

RFR is an ensemble ML algorithm consisting of two components i.e., decision tree (DT) and bagging algorithm and it can be utilized to solve both regression and classification problems based on the given dataset. It can swiftly relate input and output variables to make accurate predictions and has the ability to simulate complex and multivariate relationships between different dependent and independent variables. The algorithm runs by iteratively partitioning the feature space into several sub-regions and this partitioning continues until a stopping criterion is met. Although the decision tree algorithm was robust for solving regression problems in civil engineering, Breiman proposed RFR algorithm to overcome the learning limitations of DTs⁷⁷ and since its development, RFR has proven to be useful in solving various civil and geotechnical related problems^78,79,80,81. RFR treats DT as base learner and uses bagging technique on them to make predictions. It generates a number of DTs that are correlated by using different samples from the bagging technique and the results of all DTs are averaged to make the final predictions to overcome the overfitting issue. It is reported that RFR has several advantages over the traditional DT algorithm including ability to seamlessly handle large data sets, robustness towards outliers and over-fitting⁸². Also, it can simultaneously deal with various variables without skipping any of them and is simpler than other algorithms like ANN etc. The architecture of the RFR algorithm is illustrated in Fig. 4.

Extreme gradient boosting (XGB)

In 2016, Chen and Guestrin developed an ensemble ML algorithm of remarkable accuracy named as XGB⁸³ which uses gradient boosting and DT algorithm to make predictions. Since its development, it has found numerous applications in diverse sectors such as identifying diseases, classifying traffic accidents, and predicting customer behaviours etc^84,85,86. The higher accuracy of XGB as compared to other boosting techniques is by virtue of its ability to learn fast and run several processes in parallel and reduce overfitting⁸⁶. XGB treats DTs as base learners and uses gradient boosting to build more efficient trees. The DTs used in XGB provide useful information about the importance of different variables in predicting the output⁸⁷. The XGB algorithm enhances this ability of DTs by optimizing a loss function to reduce the error of previously generated trees⁸⁸. In simpler words, the process of applying gradient boosting on DTs is simply combining several weak learners to create a strong learner through an iterative process⁸². The XGB algorithm adds new trees in a sequence to reduce the error of previous trees³⁶. This feature enables the algorithm to quickly fit the training data, but it can also become overfitted to the training data if this addition of trees is done at a swift rate. Thus, it is advised to reduce the rate of fitting of algorithm to the training data by means of newly added trees⁸⁹. This limitation of learning rate is done by applying a factor called shrinking rate to the predictions of newly constructed trees. The value of this shrinking rate is advised to be between 0.01 and 0.1 in the literature⁸⁷. The selection of a lower value of shrinking rate or learning rate makes sure that new trees are gradually added to the model to reduce the residual of previously trained trees, and the model is not overfitted. The visual representation of XGB prediction process is given in Fig. 4.

Multi-linear regression (MLR)

It is a common statistical practice to model the relationship between two variables using linear regression. Multiple linear regression (MLR) is an advanced version of basic linear regression which can be used to model linear relationship between several variables. In the current study, MLR model is developed to predict both plastic viscosity and interface yield stress of concrete. The general form of linear regression equation is given by Eq. (4). In Eq. (4), c is the intercept, $\:{\text{X}}_{1},{\text{X}}_{2},\dots\:.{\text{X}}_{\text{n}}$ are variables and $\:{\text{b}}_{1},{\text{b}}_{2},\dots\:.{\text{b}}_{\text{n}}$ are coefficients.

$$\:\text{Y}=\text{c}+{\text{b}}_{1}{\text{X}}_{1}+{\text{b}}_{2}{\text{X}}_{2}+{\text{b}}_{3}{\text{X}}_{3}+\dots\:+{\text{b}}_{\text{n}}{\text{X}}_{\text{n}}$$

(4)

Data collection and analysis

A reliable database plays a crucial role in building ML-based models. Thus, a database of 142 instances was collected from published literature (given in Table A) which contained concrete mixture composition and experimental results for plastic viscosity and interface yield stress. The dataset was used from a study in which the authors designed an experiment to investigate the relationship between concrete mixture composition and the two fresh properties of concrete i.e., plastic viscosity and interface yield stress²³. In particular, the aim of the experiment was to examine the interaction between pipe walls of a concrete pump and the outer layer of concrete as (shown in Fig. 1) using a device called tribometer. A tribometer has three parts: (i) an agitator equipped with a speed electronic control device for measuring the torque, a container, and a steel cylinder. A lubricating layer is formed with the help of two co-axial cylinders and the rheological properties of concrete were computed using the Bingham model. The authors varied the concrete mixture composition to study their effect on the rheological properties of concrete. Also, the effect of time was investigated by measuring the rheological properties at different times after mixing the concrete. The data extracted from the tribometer included rotational velocity V measured in rotations per second and torque T measured in newton meter which were used to calculate plastic viscosity and interface yield stress were using a Bingham model. A detailed description of the procedure of extracting the plastic viscosity and interface yield stress from the measured values of torque and rotational velocity along with the detailed material properties of concrete constituents like type of cement, maximum diameter of aggregate, and type of superplasticizer etc. can be found in²³. The dataset used in current study has six input parameters including cement, water, coarse aggregate, fine aggregate, superplasticizer, and time after mixing. These six input parameters were used in the original experimental setup and are categorized as influencing parameters to predict plastic viscosity and interface yield stress of concrete. According to the recommendations from previous studies, the collected dataset has been divided into training (70%) and testing (30%) sets to make sure that the developed models can perform well on the unseen testing data. The algorithms will be trained using training data and testing data will be used to assess the accuracy of developed models afterwards. This type of data splitting makes sure that models are not overfitted to the training data and can perform equally well on the unseen data and^90,91. The distribution characteristics of data like minimum and maximum value, average, standard deviation, 25%, 50% and 75% percentile value are given in Table 1.

Table 1 Statistical description of dataset.

A statistical analysis tool called correlation matrix is frequently utilized to check the interdependence between various variables used to develop the models. It is used to investigate the effect of explanatory variables on each other because it quantifies the relationship between different variables in the form of coefficient of correlation (R). Th extent of interdependence between variables can be judged by looking at the R values between two variables. Generally, a value above 0.8 indicates the presence of a good correlation between two variables⁹². It is important to check interdependence between variables before developing a ML model. It is due to the fact that if most of the variables are strongly correlated to each other, then it might cause complications in the model, a problem commonly referred to as multi-collinearity⁹³. Notice from Fig. 5 that the correlations between variables are less than 0.8 mostly so they will not give rise to the problem of multi-collinearity.

Figure 5

Correlation matrix of variables.

Violin plots are also constructed to visualize the distribution of parameters used in the study as shown in Fig. 6. In the violin plots, the density of data is shown by the width of the violin plot. Also, the thick black bar represents the 25–75% quartile range, and the small blue dot indicates the median value. Moreover, the extended black line represents the 95% confidence interval. It can be seen from violin plots that both input and output variables are spread across a wide range. The literature recommends having this type of wide data distribution to make widely acceptable and generalized ML models⁹⁴.

Figure 6

Violin plot distribution of parameters.

Performance assessment and model development

Development of GEP model

A software package was used in current study for efficiently for implementing GEP algorithm known as GeneXpro Tools version 5.0. The dataset fed into the software and split into training and testing data. The training was used for training of GEP and after training, the testing data was used to assess the accuracy of trained model. After splitting of the data, the next step was to specify some GEP hyperparameters because each dataset and each algorithm needs a specific set of hyperparameters. The important hyperparameters to tune for GEP algorithm include head size, number of genes, set of functions, and number of chromosomes etc. Each of these hyperparameters control a critical aspect of the GEP algorithm (as indicated by Table 2) and are crucial for the development of a robust GEP model. For instance, head size and number of chromosomes dictate the convergence of the model towards the solution. Similarly, number of genes specify the number of sub expression trees that will be formed by the algorithm and joined by the linking function to get the final equation. The selection of right set of these parameters is crucial since the model’s performance and accuracy is dependent on these hyperparameters. Thus, in current study, these parameters were carefully chosen after consulting previous studies and extensive testing. The initial set of parameter values were chosen using a trial-and-error method and previous literature recommendations^95,96. Then these parameters were varied across a range of possible values and the set of values which yielded highest accuracy were used to build the GEP model for predicting both outputs. The model development was started using chromosome number as 10 and it was varied in increments of 10 until the maximum accuracy was achieved at 100 chromosomes for predicting plastic viscosity and at 80 chromosomes for interface yield stress. In the same way, head size was initially selected as 5, and the model presented in current study achieved maximum accuracy at head size equal to 20 and 30 for plastic viscosity and interface yield stress respectively. The accuracy of the model may be improved by increasing these values however increasing these values beyond a certain point may result in overfitting of the model. Selecting higher values of these parameters also increases the run time and computational power required by the algorithm. Thus, the GEP modelling essentially refers to the process of finding the optimal balance between accuracy, model complexity, and computational power required by the algorithm and the model developed using GEP in this study presents the optimal balance between these aspects. Furthermore, notice that the set of functions used to be included in the final equation consist of simple arithmetic functions and trigonometric functions. It was deliberately done in order to keep the resultant equations simple and compact for fast computation and implementation. The set of GEP hyperparameters employed in current study is represented in Table 2.

Table 2 Hyperparameter settings of ML models.

Development of RFR, XGB, and KNN models

In contrast to GEP algorithm, XGB, RFR, and KNN algorithms were developed with the help of python programming language in Anaconda software. All the prerequisite steps of model development like data loading, data splitting, and actual model development (hyperparameter settings) were done with the help of python codes as shown in Fig. 7. For algorithms like XGB and RFR, the tunning process of hyperparameters holds paramount importance since the accuracy of these algorithms depend directly on these hyperparameter settings⁹⁷. The careful selection of the hyperparameters will enable the algorithms to mitigate overfitting and make them suitable for variable data configurations⁹⁸. There are several approaches available for hyperparameter selection to avoid manual selection of parameters. The grid search approach is the most famous and efficient one out of all the available techniques and is widely used for hyperparameter selection⁹⁹. This approach exhaustively tests all possible combinations of hyperparameters in a gird configuration to find the best set of parameters and it has the advantage that it does not further alter the good-performing values¹⁰⁰. For XGB, RFR, and KNN models in current study, the ‘GridSearchCV’ function in sklearn library of python was used to implement the GridSearch algorithm¹⁰¹. Despite the development of other techniques like random search approach etc. for parameter optimization, GridSearch approach is still the most efficient and widely used technique because:

Figure 7

Model development process using python programming language.

• (i) it is easy to implement.

• (ii) it is reliable and results in low dimensionality.

• (iii) it results in greater accuracy than other optimization techniques¹⁰².

There are two common hyperparameters which need to be tuned in case of XGB and RFR called n-estimators and maximum depth which specify the number of trees build by the algorithm and depth of each tree respectively. The RFR algorithm builds different trees and takes mean of all the predictions made by trees to reach at the final prediction. The number of trees developed by the algorithm is controlled by the parameter “n-estimators”. Thus, the value of this parameter must be carefully chosen so that the algorithm builds a considerable number of trees and takes their mean to make the final prediction. Similarly, the parameter “k-neighbours” of KNN algorithm specifies the number of neighboring samples that the algorithm considers and takes into account in making the decision. The accuracy of KNN algorithm largely depends upon this parameter and selecting an abnormally larger value of this parameter may result in the algorithm being overfitted. The XGB algorithm adds new trees in a sequence to reduce the residual of previously constructed trees and it can fit very quickly to the training data by virtue of this technique, but it can also lead to overfitting of the algorithm to the training data⁸⁹. Thus, it is beneficial to limit the rate at which the algorithm adds new trees to reduce the residual of previous tree. This can be done by applying a shrinking factor to the prediction made by the newly constructed trees. Therefore, a factor called learning rate is applied to the new predictions which limits the rate at which the algorithm fits to the training data. The literature suggests keeping its value between 0.01 and 0.1¹⁰³ so that the residual reduction by each added tree is done slowly. Thus, the value of learning rate has been selected as 0.01 for prediction of both outputs. The values of other hyperparameters used in current study found using grid search approach are given in Table 3 along with the search space in which GridSearch algorithm searched for those values and the significance of each hyperparameter in the development of the ML algorithm.

Table 3 Summary of error evaluation criteria.

Performance assessment of models

The developed models will be checked by means of different error metrices because it is necessary to make sure that the models can effectively solve the given problem without abnormally large errors¹⁰⁴. The coefficient of determination $\:{R}^{2}\:$is used as an indicator of model’s general accuracy¹⁰⁵. However, due to its insensitivity towards some conditions such as a constant value being multiplied or divided with the output¹⁰⁶, several other metrices are used alongside it. The metrices MAE and RMSE are described as crucial for evaluating a ML based model¹⁰⁴. MAE measures average error between real and predicted values and RMSE gives an indication of presence of larger errors¹⁰⁷. The metrices PI and OF are commonly used as indicators of model’s overall performance because they simultaneously consider different metrices and calculates a value based on them¹⁰⁸. Thus, every metric has its own importance. The employed error metrices, their mathematical formulas, their range and suggested criteria for acceptable models are given in Table 3. The criteria given in Table 3 will be used to check the suitability of the resulting ML models.

Results and discussion

GEP results

The empirical equations for predicting plastic viscosity and interface yield stress are given by Eqs. (5) and (6). Since the number of genes were selected as 3 for plastic viscosity modelling, the algorithm yielded three expression trees which were combined using the chosen linking function (addition) to get the final equation. While the number of genes were selected as 5 for interface yield stress prediction thus the algorithm yielded four sub-expression trees which are linked by the addition linking function to get the final result in Eq. (6). The predictive abilities of the GEP algorithm for prediction of both outputs are given in the form of scatter plots for predicting plastic viscosity in Fig. 8. Notice from Fig. 8 (a) that the data points are scattered across the line of linear fit with some points lying at great distances from the line. It depicts that the GEP algorithm failed to accurately predict plastic viscosity at several points. It can also be seen from the training and testing error metrices of GEP given in Table 4. Notice that the $\:{R}^{2}$ value for training and testing of GEP is 0.74 and 0.77 which is less than the recommended value of 0.8. It means that the general performance of GEP algorithm is not satisfactory. The PI values for training and testing set are 0.11 and 0.07 respectively which is less than the upper threshold of 0.2. Also, the OF value of GEP is 0.086 which is also less than the recommended value of 0.2. Although the PI and OF values suggest that the performance of GEP algorithm is satisfactory, the correlation between the actual and predicted values is less than 0.8 which suggests that its general accuracy is not satisfactory.

Figure 8

Scatter plots to GEP training and testing; (a) for plastic viscosity; (b) for interface yield stress.

Table 4 Error metrices of developed models for plastic viscosity prediction.

Regarding the prediction of interface yield stress, the scatter plots in Fig. 8 (b) provide a useful way to visualize the predictive capabilities of the algorithm. The line of linear fit represents the points where actual and predicted values are the same. It can be seen that some data points are lying close to the line while some are scattered in both training and testing plots. It indicates that there are some points at which GEP didn’t accurately predict the interface yield stress. The error evaluation summary of GEP model is also given in Table 5. The $\:{R}^{2}$ value for both training and testing sets lie in the range of 0.6 which is not up to the recommended value for a good model (0.8). Also, the average error between actual and predicted yield stress is 9.17 and 12.80 for training and testing data respectively. The PI value for training is 0.161 and 0.20 for testing while it is recommended to have PI value less than 0.2 for an acceptable model. Thus, despite the advantage that GEP algorithm yielded an empirical Eq. 

$$\:{\text{Y}}_{1}={T}_{1}+{T}_{2}+{T}_{3}$$

(5)

Table 5 Error metrices of developed models for interface yield stress prediction.

Where

$$\:{T}_{1}=\left\{(\frac{\text{F}}{2\text{B}}-\text{tan}\left(\sqrt{\text{A}.{\text{E}}^{5}}\right))({\left(\sqrt{\text{B}}-\text{sin}\text{A}\right)}^{5}-\text{tan}(\sqrt{\text{C}}+\text{cos}\text{D}))\right\}+\sqrt{\text{C}}$$

$$\:{T}_{2}=\left\{\left(\frac{(\text{C}\left(\text{E}.\text{C}\right)+\text{D})}{{\left(\sqrt{\text{B}}\right)}^{4}}-\text{tan}(\text{E}+\text{C})\right)+\sqrt{{\left(\right(\frac{\text{F}}{\text{C}}\left)\right(\text{A}-\text{B}\left)\right)}^{3}}\:\right\}+\text{F}$$

$$\:{T}_{3}=\left(\text{A}-\text{B}\right)+\left\{{\left(\text{cos}\left({(\text{F}}^{6}+{\text{B}}^{6}\right)+{\left(\frac{\sqrt{\frac{2\text{B}.\text{D}}{{\left(\text{tan}(\text{E}-\text{A})\right)}^{4}}}}{\text{B}}\right)}^{3})\right)}^{10}\right\}$$

$$\:{\text{Y}}_{2}={T}_{4}+{T}_{5}+{T}_{6}+{T}_{7}+{T}_{8}$$

(6)

$$\:{T}_{4}=\:\text{tan}\left[\text{tan}[\text{D}.\:(\frac{\left[\text{sin}\left\{\left(-\text{C}\right)(\left(\left(\text{D}.\text{E}\right)-{\text{E}}^{2}\right)+\text{E})\right\}-\left\{\right({\text{E}}^{2}(\text{A}+9.192)\text{C}\left)\right(\text{D}.\text{E}-(\text{B}.\text{E})\left)\right\}\right]\mathbf{C}}{\text{cos}(-9.192)}\left)\right]\right]$$

$$\:{T}_{5}=\:\text{tan}(\text{B}+{\text{D}}^{4})$$

$$\:{T}_{6}=\:\frac{\text{cos}[\left\{\left(\left(0.5827.\left(\text{E}+\text{D}\right)\right)+\frac{\text{cos}\text{D}}{\text{B}+0.285}\right)+\text{C}\right\}+\{\frac{\frac{6.686-\text{A}}{2.5373}}{\text{tan}(\frac{-9.812}{\text{D}}+0.285)}\left\}\right]}{\text{cos}\{{\left(\frac{4.767.\text{C}}{0.285}\right)}^{4}-\text{C}\}}$$

$$\:{T}_{7}=\:{\left([\text{cos}\left\{\left({\text{E}}^{5}+\left(8.45.\text{A}\right)\right)+\left(\frac{76.73.\text{C}}{\text{E}+8.35}\right)\right\}+\left\{\sqrt{\text{tan}\left(\frac{\text{F}}{\text{A}}\right)}\right\}]+6.55\right)}^{2}$$

$$\:T_8=\text{tan}\left\{\text{tan}\left(\text{B}\right)\right\}$$

KNN results

The KNN algorithm didn’t yielded an equation for prediction of interface yield stress and plastic viscosity. However, the KNN results are shown as scatter plots in Fig. 9 for the prediction of both outputs and it can be seen that the points are scattered and not lie much closer to the line of linear fit. The error metrices of KNN for plastic viscosity prediction given in Table 4 also suggest the same. The $\:{R}^{2}$ value is 0.66 for training which shows that there is only 60% accuracy in the predictions made by KNN. The accuracy improved a little in testing set as shown by 0.729 $\:{R}^{2}$ value but it is still less than the recommended value of 0.8. The average errors of KNN are also greater than GEP which shows that KNN will give larger errors than GEP when used to make predictions. The PI values are 0.137 and 0.142 for training and testing which are close to the upper value of 0.2. The OF value is also 0.139 which suggests that the overall performance of KNN algorithm is also marginally satisfactory according to the performance indicators. In the same way, the result for interface yield stress prediction is shown as scatter plots in Fig. 9 (b) and the error evaluation is given in Table 5. It can be seen from Table 5 that the $\:{\text{R}}^{2}$ value is 0.520 for training while it is 0.678 for testing. Both of these values are greater than GEP but lower than the recommended literature value of 0.8. The trend is same for other error metrices of KNN like MAE and RMSE. This shows that the performance of KNN isn’t satisfactory to accurately predict the interface yield stress. This is also visible from the scatter plots in Fig. 9 where the data points are very much scattered and not lie close to the linear fit line. The PI values are 0.168 and 0.17 for training and testing respectively which is less than the recommended value of 0.2. However, despite the PI and OF values lying in the recommended range, the KNN-based predictive model has a difference of 8 to 12 Pa between actual and predicted values.

Figure 9

Scatter plots to KNN training and testing; (a) for plastic viscosity; (b) for interface yield stress.

MLR results

The MLR result for plastic viscosity prediction is given as Eq. (7) while the equation for yield stress is given as Eq. (8). The performance of MLR is also given as scatter plots in Fig. 10 (a) for plastic viscosity and performance evaluation is given in Table 4. Firstly, the $\:{R}^{2}$ value is 0.50 for training and 0.20 for testing which suggests that MLR accuracy is very less than the other algorithms. Similarly, the testing PI and OF value of MLR model are greater than 0.2 which suggests that MLR failed to exhibit overall satisfactory performance to predict plastic viscosity. The scatter plots for interface yield stress prediction are shown in Fig. 10 (b) for MLR training and testing sets. The inability of MLR to accurately predict output and lack of correlation between actual and predicted values is evident from the scatter plots. Also from Table 5, notice that the MAE and RMSE values of MLR are significantly higher than other algorithms while the $\:{\text{R}}^{2}$ value is at the lowest of about 0.2. Notably, both the training and testing PI values of MLR (0.25 and 0.321 respectively) are considerably higher than 0.2 which suggests the overall performance of MLR model is acceptable to be used for prediction. Moreover, the OF value of MLR being 0.292 also suggests that it can’t be used for accurate prediction of the output. It further necessitates the utilization of ML models for predicting properties of concrete.

$$\:{\text{Y}}_{1}=\:-3529.81+3.04\text{A}-0.49\text{B}+1.37\text{C}+1.55\text{D}-10.99\text{E}+4.34\text{F}$$

(7)

$$\:{\text{Y}}_{2}=\:37.89-0.1\text{A}+0.03\text{B}+0.0007\text{C}+0.045\text{D}-5.90\text{E}+0.25\text{F}$$

(8)

Figure 10

Scatter plots to MLR training and testing; (a) for plastic viscosity; (b) for interface yield stress.

RFR results

The error metrices calculated for RFR-based predictive model for plastic viscosity are given in Table 4 and also shown as scatter plots in Fig. 11 (a). Notice that the $\:{R}^{2}$ value for RFR training is 0.91 which indicates that the RFR predicted values are very close to the actual values. It can also be depicted by the very less training MAE value of 46.55. However, the performance of RFR algorithm drops significantly when tested against unseen data of the training set. The $\:{R}^{2}$ drops to a lowest value of 0.64 and MAE increases to 90 Pa/s from 46 Pa/s which is a significant loss in accuracy. Similarly, the training PI suggests that the performance of algorithm is satisfactory in training phase having a value of 0.065 but it increases to 0.12 in testing phase which shows that the algorithm could not exhibit the same level of accuracy when used for unseen data. It shows that the algorithm is overfitted to the training set. Similarly, Fig. 11 (b) shows the RFR result for interface yield stress prediction and the summary of error evaluation of RFR model is also given in Table 5. First of all, the $\:{R}^{2}$ value for RFR training is 0.88 which is greater than the recommended value of 0.8. The good performance of algorithm in training phase can also be depicted by the MAE value of only 4.02 Pa. However, the performance of drops significantly in the testing phase with $\:{R}^{2}$ reaching the value of 0.695. Same trend was observed for RMSE and MAE. Also, the training PI suggests that the performance of algorithm is satisfactory having a value of 0.078 but it increases significantly to 0.2 in testing phase which is equal to the upper threshold for PI values. It depicts that the algorithm could not exhibit the same level of accuracy when used for testing data and is overfitted to the training set. It can also be seen from Fig. 11 that the data points in training plot lie close to the linear fit line while they are scattered in the testing data plot.

Figure 11

Scatter plots to RFR training and testing; (a) for plastic viscosity; (b) for interface yield stress.

XGB results

The XGB algorithm failed to give an empirical equation like GEP, however the result of XGB to predict plastic viscosity is given in the form of scatter plots in Fig. 12 (a). It can be seen from the plots that most of the data points lie close to the linear fit line which shows the excellent accuracy of XGB. Also, the error metrices for XGB is given in Table 4. Notice that the $\:{R}^{2}$ value of XGB is 0.959 and 0.947 for training and testing respectively and the MAE value is also considerably less than the other algorithms. It is an indicator of XGB’s excellent accuracy to predict the plastic viscosity values. The RMSE values are 57.10 for training and 73.32 for testing which suggests that there will not be any abnormally larger errors in the predictions made by the XGB algorithm. Moreover, the OF value of XGB is considerably less than the other algorithms (0.066) which again suggests that its performance is better than all other algorithms. Also, the error metrices calculated for XGB-based predictive model for interface yield stress are given in Table 5 and also shown as scatter plots in Fig. 12 (b). Notice that the $\:{R}^{2}$ value for XGB training is 0.92 which indicates that the XGB predicted values are very close to the actual values. The performance of XGB algorithm doesn’t drop when tested against unseen data of the training set. Similarly, the training PI suggests that the performance of algorithm is satisfactory in training phase having the lowest value of 0.057 and it remained almost same in testing phase (0.053) which shows that the algorithm exhibited the same level of accuracy when used for unseen data. It shows that the algorithm is not overfitted to the training set and can be effectively used for predictions on the new data. This can also be visualized from scatter plots in Fig. 12 where the data points in training and testing plots lie very close to the linear fit line. Thus, from Table 5 it can be concluded that XGB proved to be the most accurate algorithm for prediction of interface yield stress of concrete.

Figure 12

Scatter plots to XGB training and testing; (a) for plastic viscosity; (b) for interface yield stress.

K-fold Validation

K-fold cross-validation is a statistical method for evaluating the generalization abilities of ML models and helps to confirm that the models are resistant to overfitting or underfitting. Overfitting occurs when a model performs exceptionally well on the training data but fails to generalize to unseen data. It can result from the model capturing irrelevant patterns in the training set. K-fold validation mitigates overfitting by ensuring that the model is trained and validated on different subsets of the data, promoting more robust learning patterns. This technique works by dividing the whole dataset into ‘k’ equal-sized subsets, known as folds. During every iteration, one fold is used for testing, while all other folds are cumulatively used for testing. This process is repeated ‘k’ times, enabling each fold to act as testing data exactly one time, as shown by Fig. 13. This ensures that the developed models are generalizable to unseen data, thereby eliminating overfitting. This study utilizes 8-fold cross-validation for all three algorithms, with the accuracy of each algorithm in each fold measured by RMSE, as shown in Figs. 14 and 15.

Figure 13

Schematic representation of k-fold cross validation.

Figure 14

K-fold Validation results of algorithms for prediction of plastic viscosity.

Figure 15

K-fold Validation results of algorithms for prediction of interface yield stress.

Figure 14 shows the k-fold results of algorithms for prediction of plastic viscosity. Plot (a) in Fig. 14 corresponds to the results of GEP algorithm. It can be seen that the RMSE values corresponding to the 8 folds of GEP have some difference in the values. Although it is closer to the RMSE values of GEP given in Table 4, the disparity between the RMSE values of different folds suggests that the performance of algorithm is marginally accurate, and the algorithm may be subject to slight overfitting. Next, plot (b) of Fig. 14 shows the KNN results of k-fold validation. In contrast to GEP, the RMSE values of different folds are very close to each other suggesting that although KNN has less accuracy (as indicated in Table 4), it is not overfitted. Moving on, plot (c) shows MLR results in which some folds yield slightly higher values of RMSE indicating slight overfitting. In contrast, the RFR results in plot (d) show a substantial difference in RMSE values of different folds conforming with the previous findings that RFR model is overfitted to the training set. In particular, RFR yields RMSE values as high as 130 $\:\text{P}\text{a}/\text{s}$ in some folds while this value is only 60 $\:\text{P}\text{a}/\text{s}$ in other folds. It suggests that the performance of RFR algorithm can significantly change based on the distribution of the data. In other words, the RFR model developed in current study is not well generalized for making predictions. It may be due to the fact that RFR algorithm picked up some unnecessary correlations from the data which affected its accuracy. Finally, plot (e) of Fig. 14 show the k-fold validation results of XGB algorithm. It can be seen from the plot that the RMSE values from each fold are lying sufficiently closer to one another. Moreover, these values are also closer to the training and testing RMSE values of XGB given earlier in Table 4. It confirms that XGB is resistant to overfitting and can be used effectively on unseen dataset.

Similarly, the k-fold results of algorithms for prediction of interface yield stress are shown in Fig. 15. The GEP results for yield stress prediction are shown by plot (a) of Fig. 15 from which it can be seen that there is some disparity between the RMSE values of different folds. Previously, in Table 5, GEP algorithm also showed a difference in accuracies for training and testing data. It can be attributed to the fact that GEP is an evolutionary technique which solves the problem by means of chromosomes (mathematical expressions). These expressions are randomly generated and later modified to fit the data. Due to this randomness in the structure of GEP, it is unable to give a generalized and robust model for prediction of interface yield stress. In next plot (b), which has been made with k-fold values for KNN algorithm, the difference between RMSE values for various folds is less prominent compared to GEP. It suggests that KNN is not overfitted to the training data and has good generalization capabilities although with a lower accuracy. It is also true for the MLR results. Its accuracy is less than that of KNN with RMSE values approaching 24 Pa but it is generalized, nevertheless. However, the RFR model again shows prominent signs of overfitting with substantial differences between RMSE values of different folds indicating that the model’s performance varies for diverse data distributions. It highlights that RFR is not generalized well and thus should not be used practically for the prediction of subject output. At last, XGB again stands out having the least difference among different RMSE values. Also, the RMSE values for XGB are very less compared to its counterparts. This suggests that XGB, in addition to accurately predicting plastic viscosity on unseen data, can be effectively leveraged to predict interface yield stress of unseen data too.

Residual assessment

In addition to error evaluation and k-fold validation, it is imperative to check the residuals of individual algorithms to confirm the maximum error which can be encountered while using the algorithm. Also, the residual assessment of algorithm results will help us to understand the range in which the errors lie most of the time. Thus, Fig. 16 shows the residual assessment of developed algorithms for plastic viscosity prediction. Notice from plot (a) (which shows the GEP residuals) that most of the residuals are concentrated in the range − 100 to 200. Although there are some observations for which the residual is more than 300 $\:\text{P}\text{a}/\text{s}$, but mostly the error remains within the range of -150 to 150. It is a fairly larger range considering the importance of accurate predictions for plastic viscosity of concrete. In the next plot, the KNN residuals are depicted which shows a similar range of residuals with some residuals going as high as 500 $\:\text{P}\text{a}/\text{s}$. However, in this plot too, the range for existence of majority of the residual is -200 to 300. It is again a larger range, and it suggests that KNN fails to predict accurate values at various observations. Moving on, plot (3) for MLR shows a similar picture with residuals as high as 600 $\:\text{P}\text{a}/\text{s}$. In contrast to GEP and KNN, larger number of residuals are lying beyond the range − 400 to 400 suggesting that MLR has higher error rates. It can be attributed to the fact that MLR is a simple statistical technique which is unable to capture the complexity of relationships that exist between plastic viscosity and concrete mixture composition. Plot (d) developed using RFR residuals shows significant improvement. There are no errors going beyond − 200 to 300 in the plot while it can be seen that most residuals are concentrated in the range of -100 to 100. It underlines that the accuracy of RFR is better than KNN, MLR, and GEP algorithms. However, it is overfitted to the training data (discussed previously) implying that it may give unexpected errors when tested on unseen data. At last, plot (e) shows the XGB residuals with an impressive improvement in the prediction accuracy. More than 95% of the XGB residuals lie in the narrowest range of -100 to 100. It shows that almost 96% of the times, the XGB error between actual and predicted plastic viscosity will not exceed 100 $\:\text{P}\text{a}/\text{s}$. In addition, there is not a single residual going beyond the range − 200 to 300 further highlighting XGB’s superior performance as compared to other algorithms.

Figure 16

Residual assessment of algorithms for prediction of plastic viscosity.

Figure 17 highlights the residual assessment of models developed for the purpose of prediction of interface yield stress of concrete. Starting from plot (a) of Fig. 17 for GEP algorithm, it can be seen that the range for all residuals is -30 to 50 while most residuals lie in the range − 20 to 20 Pa. This suggests that GEP can give error up to 50 Pa when used to predict interface yield stress values. The KNN residuals are shown next in plot (b) which paints a similar picture to that of plot (a). Most of the residuals are concentrated between − 20 Pa and 30 Pa while the maximum residual goes as high as 48 Pa. In plot (c), the range is increased for MLR with residuals lying in the widest rage of -40 to 80. The maximum observed residual in case of MLR is almost 70 Pa which suggests a significant drop in accuracy compared to GEP and KNN algorithms. The RFR residuals in plot (d) of Fig. 17 highlights an interesting phenomenon. Although there is an improvement in accuracy because most of the residuals are lying from − 10 Pa to 20 Pa. However, there are some residuals which go beyond this range to as large as 60 Pa. It shows that while 95% of the times the error will be around 10 Pa, there can be situations where RFR can yield larger than 50 Pa errors. This abnormal distribution of residuals can be attributed to the fact that RFR showed significant overfitting tendencies in the previous sections and this distribution is a result of that. Finally, the XGB residual assessment is given in plot (e) which highlights two important developments: (i) the range for errors is significantly reduced compared to previous algorithms and now the range is -7 to 7 compared to -30 to 50 for GEP, (ii) most of the errors lie really close to zero and only some errors go beyond the 10 Pa threshold. Thus, it can be confirmed that XGB resulted in the most accurate predictions as compared to all other algorithms used in this study for interface yield stress prediction.

Figure 17

Residual assessment of algorithms for prediction of interface yield stress.

Best model selection

A common problem that can arise when dealing with mathematical modelling is overfitting. It happens when an algorithm fits well to the data it is trained on but cannot maintain its accuracy when exposed to new data¹⁰⁹. It is important to assess a model against the possible issue of overfitting. A model can be checked for overfitting by drawing a comparison between the error metrices of its training and validation data¹¹⁰. If a model gives predictions with large errors on validation data, it implies that the model overfitted to the training data and is not suitable for unseen data and the model is not a generalized one. Notice from Tables 4 and 5 that the correlation values of training and testing sets of all algorithms are very close to each other and doesn’t have a considerable difference. It indicates that the developed ML algorithms retained their accuracy when tested against unseen data. The RFR algorithm suffered slight loss in accuracy when tested against unseen data. It may be due to selecting a higher value for number of trees in the algorithm^111,112. Despite the algorithm being slightly overfitted to the training data, it still proved to be robust and acceptable as indicated by the lower objective function values.

Although Tables 4 and 5 shows error metrices for all the employed algorithms in this study, it is necessary to compare the algorithms based on some criteria to find out which algorithm predicted the fresh properties of concrete with greater accuracy. In this regard, the comparison between different algorithms used in this study can be made by using a Taylor diagram¹¹³. It is a useful technique that gives an indication of model’s performance by using coefficient of determination ($\:{R}^{2}$) and standard deviation of predictions. The distance of the algorithm from the point of actual or reference data is used to assess the accuracy of the algorithm. The more a point is closer to the reference point, the more accurate it is and vice versa. The taylor plots of algorithms used in this study are given in Fig. 18. The comparison of algorithms for plastic viscosity prediction is given by taylor plot in Fig. 18 (a). Notice that the XGB algorithm lies closest to the reference data point. It indicates that the XGB predicted values has higher correlation with actual values and lesser standard deviation. The RFR point is the next point closer to actual data point followed by GEP and lastly KNN. Thus, the order of algorithm accuracy for plastic viscosity prediction is XGB > RFR > GEP > KNN. Figure 18 (b) represents the taylor diagram to compare algorithms for yield stress prediction. In Fig. 18 (b) the XGB algorithm again lies closest to the actual data point depicting the highest correlation with the experimental values. The algorithms KNN and GEP lie very close to each other depicting almost same accuracy to predict interface yield stress of fresh concrete. However, since KNN point lies more closer to the standard deviation line of actual data than GEP, the KNN predicted values has slightly lesser standard deviation than GEP predicted values. Hence, the order of accuracy for yield stress prediction will be XGB > RFR > KNN > GEP.

Figure 18

Taylor plot based comparison of ML models; (a) plastic viscosity prediction; (b) interface yeild stress prediction.

Explanatory analysis

With the increasing use of ML models to predict different properties of concrete, the significance of conducting post-hoc analysis is also increasing for the transparency and interpretability of ML models^114,115. It is due to the fact that in the development of ML models, it is not always clear how the algorithm reached certain predictions and how does the input variables affect the predicted outcome. This drawback can limit the wide use of ML models in predicting critical concrete properties. Thus, explanatory approaches are increasingly getting attention to provide transparency to the ML model’s inner working mechanisms. If the insights from the post-hoc explanations coincide with the observations of previous experimental studies and real-world scenarios, the developed ML models can be deemed acceptable¹¹⁶. These approaches are used to reveal information about the internal working mechanisms of the ML models and are computationally simple and easy to implement. Some of the most common forms of data-based explanatory analysis techniques used in the field of engineering for providing transparency to the black-box models are SHAP, and ICE, analysis etc. These two techniques are most widely used in the realm of civil and materials engineering and thus are used in current study to provide transparency to the XGB model for prediction of plastic viscosity and interface yield stress. Table 6 highlights the benefits and drawbacks of the explanatory techniques used in current study. SHAP will help to identify the most crucial variables for prediction of subject outputs while ICE analysis will help to study the individual and combined effect of inputs on the anticipated outcome.

Table 6 Summary of strengths and weaknesses of employed explanatory techniques.

Shapely analysis

It is imperative to conduct different explanatory analyses on a ML model because a model’s good accuracy on the training and testing dataset cannot be used alone as an indication of a good and reliable model⁵⁴. A good ML model must perform well when used on different data types and configurations. These explanatory analyses impart transparency to the developed models and help to widely implement them by providing useful information to understand the logic behind the prediction process^119,120,121. Thus, Shapley analysis was conducted as an attempt to understand the logic behind the prediction process of the algorithm. As already mentioned in Sect. 5.8 that XGB is the most accurate of all the algorithms employed in current study, so it underwent shapley analysis to help understand the reasoning behind the model prediction process.

The results of shapley analysis of XGB model to predict plastic viscosity are given in Fig. 19. Notice from the mean absolute shap plot given in Fig. 19 (a) that time after mixing is the most important factor to predict plastic viscosity of concrete having absolute shap value of 53.66 followed by water (29.19), fine aggregate (10.27) and the least contributing factor is coarse aggregate (4.55). Although Fig. 19 (a) describes the mean absolute shap values of variables, it does not give an idea about which variables are positively or negatively correlated with the output. To resolve this issue, the SHAP summary plot is given in Fig. 19(b) in which the input parameters are arranged vertically in order of their decreasing importance and the shapley values are given along the horizontal axis. The summary plot helps to find the most influential parameters to predict the output. It also shows that which input parameters relate positively and negatively to the output. Moreover, the feature values on global interpretation plot are colour coded in such a way that blue dot represents low importance and pink dots represents high importance¹²². It can be seen from summary plot that water and time after mixing are the most correlated variables with plastic viscosity.

Figure 19

SHAP global explanation to predict plastic viscosity; (a) mean abolute SHAP values; (b) SHAP summary plot.

The plots given in Fig. 19 are called global explanation plots since they give an overview of the influence of input variables on the output. Although these plots are important for getting information about the prediction process of the model, local interpretability plots are also important to know the dependence between different input variables and corresponding SHAP values. Thus, the variable dependence plots of XGB model to predict plastic viscosity are given in Fig. 20. It can be seen from Fig. 11 that the variables which interact with each other to a higher degree resulting in change in SHAP values are coarse aggregate (D), time after mixing (F), and water. The effect of all other variables on each other is negligible. It can be seen that increase in time after mixing after the value of 50 lead to an increase in SHAP value of coarse aggregate. Moreover, increase in value of fine aggregate causes an increase in water shap values. Also, in Fig. 10, these were the variables whose contribution was maximum in predicting plastic viscosity.

Figure 20

SHAP local dependence plots for plastic viscosity prediction.

In the same manner, the SHAP based feature importance for interface yield stress prediction are given in Fig. 21. The color-coding and rules of vertical arrangement also apply to plots in Fig. 21 like they were discussed earlier for Fig. 20. Notice from Fig. 21 (a) that interface yield stress is highly affected by the superplasticizer dosage (E) having mean absolute sha value of 3.23 followed by time after mixing (3.14) and coarse aggregate (2.7). The role of fine aggregate (0.45) and water (1.29) in predicting yield stress is the least. From the summary plot Fig. 12 (b), it is evident that almost all variables are correlated with interface yield stress, whether positive or negative. However, time after mixing and superplasticizer extend farthest from the zero-line meaning that they have the most effect on interface yield stress. The local dependence plot for yield stress prediction is also given in Fig. 22. It can be seen that the change in SHAP values of a variable with increase in value of another variable is much more prominent than for plastic viscosity prediction. The change in value of F variable (time) causes significant changes in SHAP values of C. Similarly, the changes in C and E bring about change in shap values of B and D respectively.

Figure 21

SHAP global explanation to predict interface yield stress; (a) mean abolute SHAP values; (b) SHAP summary plot.

Figure 22

SHAP local dependence plots for interface yield stress prediction.

ICE analysis

The ICE plots for XGB model developed in current study for plastic viscosity prediction are shown in Fig. 23. These plots are an interactive way to demonstrate the variation in XGB-based output value with change in values of inputs used to build the XGB model. To build an ICE plot, the values of all variables were set to their average values and only one variable was changed across its range. Then, the change in XGB predictions was plotted against the variable values. The curve in the ICE plot corresponds to the averaged value for plots developed for each instance present in the database. Starting with plot (i) of Fig. 23 which shows the effect of cement content (A) on the predicted output. It shows that plastic viscosity doesn’t exhibit a definite relationship with the cement content. The plastic viscosity first drops significantly from 550 Pa/s to almost 470 Pa/s when cement content increases from 400 kg to 450 kg. After that, the output increases again to 500 Pa/s when cement content finally reaches 600 kg. The ICE plot for variable B (water) is shown in plot (ii) from which it can be noticed that the predicted output drops in a stepwise manner from 800 Pa/s to almost 400 Pa/s when water content changes from 140 kg to 180 kg. After that, the plastic viscosity increases slightly to 550 Pa/s at higher water content. Moving forward, plot (iii) shows that there is no definite relationship between variable C (fine aggregate) and the anticipated outcome. The same is true for coarse aggregate as evident from plot (iv). The outcome first remains constant then drops substantially to 480 Pa/s from 510 Pa/s at coarse aggregate values of 950 Kg. Notice from plot (v) which has shows the variation in output values with change in superplasticizer (D) values. It can be noticed that the initial increase in D values from 0 to 1 L cause a decrease in output values from 550 Pa/s to less than 450 Pa/s. However, when superplasticizer values reach 5 L, it causes the output values to rise to 498 Pa/s after being constant for some time.

Figure 23

ICE analysis for investigating relationships between inputs and plastic viscosity.

Figure 24 shows the ICE plots for interface yield stress prediction in the same way they were developed for plastic viscosity prediction. Noticing from plot (i) which shows the effect of variation in cement values on the output, it is evident that the output decreases with increase in cement (A) values. The interface yield stress values suffer a loss from 54 Pa to almost 40 Pa when cement content was changed from 400 kg to more than 600 kg. However, the relationship between water (B) and output is not very straightforward. First the outcome dropped suddenly to almost 30 Pa when water content reached 230 kg from 140 kg. After that, the interface yield stress increased suddenly to more than 70 Pa at water content of about 240 kg and became constant afterwards. From the next plot, it can be seen that fine aggregate has no clear correlation whatsoever with the output values. It can be attributed to the fact that it is the least significant variable in outcome prediction as evident from SHAP analysis. The relationship of coarse aggregate (D) with interface yield stress is almost the same as of its relationship with plastic viscosity with the output first decreasing with coarse aggregate values and then rising gradually before finally becoming constant. In the same way, the relationship between superplasticizer (E) and output is not well defined either. The output first increases substantially, then decreases, and rises slightly again when E values are varied from 0 to 2 L. However, for E values greater than 2.5 L, the output becomes constant. From plot (vi), it is evident that a general increase in output values occurs with increasing time after mixing (F). The output values increase from 30 Pa to 48 Pa when time changes from 0 to 30 min. After that, it remains constant for some interval before falling back to 30 Pa. However, when time goes beyond the 80 min mark, the output rises again to more than 60 Pa. This can be explained by the fact that E is specified as the most significant variable for output prediction and its variation causes significant changes in the outcome values. It must be noted that these plots are developed by varying the content of only one variable while all other variables are kept constant. Therefore, these plots depict only the relationship between a single variable and the outcome. The combined effect of these variables on the predicted output may differ compared to what is shown by these plots. Thus, from the above explanatory analysis of XGB model to predict plastic viscosity and yield stress, it is evident that time after mixing is the common factor which significantly affects both output variables. It is also rigorously identified in experimental investigations that the rheological properties of concrete like plastic viscosity and interface yield stress are time dependent^47,123,124. Also, the crucial role of water in dictating fresh concrete properties has been identified by Ngo et al.³³. The amount of water in the concrete directly impacts the paste volume which in turn affects the plastic viscosity of concrete³⁹. Similarly, the influence of finer content (sand) and additives like superplasticizer on rheological concrete properties have been documented by various studies^17,38,125. Thus, it can be concluded that XGB is the most robust algorithm to predict fresh concrete properties not only because it depicted higher accuracy on training and testing datasets but also because the insights into the XGB prediction process provided by the SHAP, and ICE analyses are also the same as observed in experimental investigations.

Figure 24

ICE analysis for investigating relationships between inputs and interface yield stress.

Practical implications

It is important to highlight the practical implications of such empirical studies to further highlight their importance. It has already been discussed in introduction section that accurate determination of plastic viscosity and interface yield stress are crucial for determining rheology and pumpability of concrete. However, the accurate determination of these properties calls for significant time and resources on-site. Thus, this study was conducted to develop empirical prediction models for determining these two properties of concrete in fresh state. Also, with the recent surge in use of AI and ML in every aspect of the world, it is important to provide these types of frameworks through which the construction industry as a whole and the concrete industry in particular can make its transition towards informed decision-making techniques using the transformative power of ML. This study employed XGB, RFR, GEP, and KNN algorithms for the purpose of fresh properties prediction of concrete. Out of all these algorithms, only GEP expressed its output as an empirical equation for the prediction of subject outputs. However, the accuracy of GEP wasn’t satisfactory compared to the other algorithms. Also, the developed equations are lengthy and computationally extensive which increases the risk of human error while calculating the values. In contrast, the accuracy of XGB was exceptionally good for the prediction of both outputs. However, its black-box nature prevented it from yielding an equation. Thus, to overcome these limitations, a GUI has been developed using python programming language to help compute the plastic viscosity and interface yield stress of concrete automatically based on the set of input variables considered in this as shown in Fig. 25. The user can enter desired input values and upon pressing the predict button, result will be obtained instantly in the output box specified in the GUI. This GUI can serve as an invaluable tool for professionals in the civil engineering industry and different stakeholders to effectively predict concrete properties by entering the mixture composition without requiring extensive technical expertise. Also, with the increasing shift of civil engineering industry towards informed decision making, this GUI is an important tool which reflects the practical application of ML utilization in civil engineering industry. The accurate determination of these properties without going into extensive testing will help the workers to make informed decisions quickly on the site without waiting for the test results. Also, a lot of resources which would have otherwise wasted by conducting the tests on concrete can be saved by employing these ML models. In situations where concrete is used in bulk as batches, there can be several time, resource, and apparatus limitations which can be prevented by using these ML models for predicting concrete properties. The two outputs considered in this study i.e., plastic viscosity and interface yield stress are of particular importance in situations where concrete is subjected to shear forces such as during pumping, placement, and casting etc. Thus, this study holds paramount importance in this regard that it provides a framework to accurately determine these properties using the transformative power of ML. The predictive models in this study can be effectively utilized to determine these properties on site which will save time and help in making swift decisions.

Figure 25

GUI developed for prediction of outputs.

Conclusions

This study was conducted to develop ML-based prediction models for yield stress and plastic viscosity of concrete since efficient pumpability of concrete through pumps for high-rise construction requires accurate estimation of these concrete properties. Four ML algorithms including GEP, XGB, RFR and KNN along with a statistical technique i.e., MLR were used for this purpose using a database of 142 instances and the conclusions of this study were:

• Among all the algorithms employed in this study, only GEP expressed its output in the form of an empirical equation to predict plastic viscosity and interface yield stress.

• The deployed algorithms were validated using error metrices, k-fold validation, and residual assessment which proved that XGB is the most accurate algorithm to predict the subject outputs while GEP and KNN had marginal accuracies. The algorithm comparison by means of taylor plots also confirmed this.

• The results of error evaluation showed that XGB is the most accurate algorithm to predict both outputs having $\:{R}^{2}$ value greater than 0.92 and minimal values of other error metrices like objective function and MAE etc.

• SHAP and ICE analysis were conducted on the XGB algorithm which revealed that time after mixing, water, and cement etc. are the most important features to predict both fresh concrete properties.

Recommendations

Despite the fact that this study is a significant contribution to the literature and a crucial step towards prediction of critical rheological properties of concrete using diverse ML techniques, it is important to highlight its limitations and provide suggestions for future studies:

• The ML models presented in current study were developed using a limited dataset of 142 experimental collected from literature. For the development of more reliable, robust, and widely appliable models, it is recommended to consider much larger datasets in future studies.

• The output variables in this study i.e., plastic viscosity and interface yield stress can be affected by different material properties like nominal aggregate diameter, type of superplasticizer and variable site conditions like mixing and pumping temperature etc. This study doesn’t exclusively incorporate the effect of these variables but recommends considering them in future studies.

• The models presented in this study were developed using data whose range is given in Table 1. For the development of more widely applicable models, it is necessary to consider a wider range of data.

• Other widely used interpretable techniques like partial dependence plots (PDP) and permutation importance analysis etc. must be considered in future studies to reveal more about the nature of black-box models.