Abstract
In this work, we solve a system of fractional differential equations utilizing a Mittag-Leffler type kernel through a fractal fractional operator with two fractal and fractional orders. A six-chamber model with a single source of chlamydia is studied using the concept of fractal fractional derivatives with nonsingular and nonlocal fading memory. The fractal fractional model of the Chlamydia system can be solved by using the characteristics of a non-decreasing and compact mapping. A suggested model with the Lipschitz criteria and linear growth is studied both qualitatively and quantitatively, taking into account boundedness, uniqueness, and positive solutions at equilibrium points with Leray-Schauder results under time scale concepts. We examined the framework of local and global stability and insight into Lyapunov function properties for the infectious disease model. Chaos Control will employ the regulate for linear responses approach to stabilize the system following its equilibrium points. This will take into consideration a fractional order framework with a managed design, where solutions are bounded in the feasible domain and have a greater impact at the lower minimum infectious rate. To illustrate the implications of fractional and fractal dimensions with varying interest rate values through simulations with Newton’s polynomial method under the Mittag-Lefller kernel. Additionally, a comparative analysis of results is also derived by employing power and exponential decay kernels at various fractional orders.
Similar content being viewed by others
Introduction
The most common bacterial sexually transmitted infection in the UK is called Chlamydia trachomatis. The age groups with the highest prevalence of chlamydial infection include women between the ages of 16-19 years and men between the ages of 20-24 years. Since most women with chlamydial infection are asymptomatic, some of them end up developing pelvic inflammatory disease as a result of not receiving treatment1. In 1999, there were approximately 92 million cases of chlamydia worldwide, comprising 42 million cases in men and 50 million cases in women2. Even though genuine resistance to Chlamydia trachomatis is uncommon, cases of recurrent Chlamydia infections are still being reported after treatment with a single one-gram dose of azithromycin or a week’s worth of doxycycline. This raises concerns regarding the possibility of azithromycin treatment failure. Even though reinfections account for most repeat positive cases, new research suggests that treatment failure might also be a factor in3. A unique developmental cycle and obligatory intracellular lifestyle are shared by the evolutionary distinct group of eubacteria known as the chlamydiae, which have been thoroughly studied in4 under ideal cell culture conditions. We design and assess a Chlamydia trachomatous vaccination model with cost-effectiveness optimum control analysis. In5 shows that the model’s disease-free equilibrium is locally asymptotically stable when the reproduction number is less than unity. This allows researchers to examine the impact of various treatment combinations on the host dynamics of chronic genital chlamydial infections, which are characterized by the presence of IFN-\(\gamma\) induced chlamydial persistence. Akinlotan et al.6 create a mathematical framework of within-host Chlamydia dynamics. A mathematical model that describes the kinetics of a Chlamydia trachomatous infection in a human carrier is described by Emuoyibofarhe et al.7. Relevant features like drug administration-assisted recovery were included in the model. The real solution looked at the model’s solutions’ existence and uniqueness. We analyze the model’s stability both locally and globally. Researchers have provided a model to assess chlamydia therapeutic options in8,9,10,11, where they have presented some innovative studies on an epidemic model. Atangana12 combined the two relevant fields of fractional and fractal calculus into a new class of concepts known as fractal-fractional ideas. These operators have two components: the fractal dimension and the order. Differential equations with fractal-fractional derivatives, according to13,14, convert the dimension and order of the putative system into a rational system. It takes fractional calculus to solve issues in the real world. It is frequently used in many different fields related to science, engineering, and finance. The characteristics of the fractional calculus that set it apart comprise fractional order derivatives and fractional integrals. The area of fractional calculus and its diverse aspects have garnered greater attention from scholars in recent times. This is because genetic mutations are an essential tool for understanding how various biological systems operate dynamically. The non-local characteristics of these component operators, such as the integer separator operator15,16,17,18,19,20, give them their strength. The COVID-19 transmission pattern was examined in three severely affected nations in order to provide context for the modeling of COVID-19 transmission in21. For the time discretization and spatial discretization, respectively22,23,24,25,26,27,28, has used redefined extended B-spline functions and the Caputo time fractional derivative. In this work, we constructed several fractal fractional operators and employed various fractal differential operators. The duration of the fractional advection diffusion equation’s approximate solution. Further information is provided in29,30,31,32.
Since fractional mathematical models are more realistic and useful than the traditional integer-order models, fractional calculus has garnered a lot of attention from researchers. Generally speaking, the memory and learning mechanisms are not covered by the integer-order model. If not, take into account the distributed and past effects of any model since the fractional order derivatives and integrals have nonlocal characteristics. According to the nonlocal property, a model’s subsequent state depends on all of its previous states in addition to its current state33,34,35. The governing equations have been subjected to the recently described fractal-fractional differential operator approaches, particularly Atangana-Baleanu and Caputo-Fabrizio fractal-fractional differentiations. The dynamic reactions of a magnetized and non-magnetized conductive fluid model are examined by mathematical analysis based on equilibrium points and stability criteria. Through the use of Adams techniques, often known as the explicit scheme of the Adams-Bashforth approach, numerical simulations have been carried out36,37,38,39,40,41,42,43,44. It is remarkable to note that the techniques used in the study of epidemiological problems are designed to identify the root causes of diseases and other health issues in populations. In epidemiology, the patient represents the population, and researchers view people holistically. The aforementioned branch has garnered significant attention from researchers over the past several decades. Different diseases have been modeled using various concepts of mathematics. Because mathematical models are powerful tools increasingly used to describe real-world problems. For instance, we refer some applications of mathematical models as44,45,46,47,48,49.
A potential approach with several benefits is the use of fractal fractional operators with fractional and dual fractal orders in research studies. This method captures complicated patterns and abnormalities that other methods would miss, allowing for a more nuanced and detailed depiction of complex problems by simultaneously exploiting two orders. This improves our comprehension of complex processes and makes it easier to create more reliable mathematical models that are applicable to a wide range of academic fields. Using fractal fractional operators could transform a variety of industries, from image analysis to signal processing, by providing a flexible toolkit to tackle problems requiring a greater understanding of complex, multi-fractal phenomena. Accepting this novel paradigm opens up new avenues for research and discoveries by promoting a more exact and comprehensive approach in scientific studies. In this case, we analyze a fractal fractional model of contaminated lakes in terms of several distinct attributes.
The following are the remaining sections of this study article: An introduction is given in Section Introduction. The proposed framework and a number of fundamental fractional order derivatives that are useful in addressing the epidemiological framework are thoroughly presented in Section Chlamydia viral mathematical model with FFM. Section Qualitative evaluation of the Chlamydia framework provides a generalized version of the system and examines the qualitative features of the suggested model, such as existence and uniqueness, sensitivity analysis, and illness-free equilibrium. Section Stability analysis of the Chlamydia model examines the stability research of the proposed framework, including Lyapunov stability. We examine the numerical scheme of the Mittag-Leffler kernel in section Numerical scheme with generalized form of fractal fractional operator. Sections Results and discussions and Conclusions include the numerical simulations and findings, respectively.
Chlamydia viral mathematical model with FFM
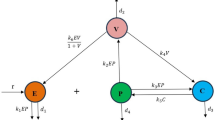
A deterministic compartmental system of the dynamics of Chlamydia illness transmission is presented. Researchers are looking into the causes and recurrence of potential epidemics. In order to understand viral transmission, let’s examine the Vellappandi et al.50 compartmental mathematical epidemic system and a few of its notable features. Using fractional calculus, a mathematical method that deals with derivatives and integrals of non-integer order, systems are analyzed. Patterns and structures that repeat at various scales are the focus of fractal analysis, which has applications in complex systems such as biological ones. Applying fractal fractional analysis to different compartments within a biological system appears to produce consistent and dependable results. This implies that it works well for various components or elements of the system. Long-term consequences of epidemics frequently extend beyond the scope of the original outbreak. These long-term dynamics, such as the possibility of repeat outbreaks, endemic states, and the effects of interventions over protracted periods of time, are better captured by fractal fractional order models. These models can improve the prediction accuracy of epidemic propagation, peak timings, and overall impact by including fractional order derivatives. The following set of nonlinear ordinary differential equations can be used to illustrate the framework with \(^{FFML}D_{0,t}^{(\alpha _{1},\kappa _{1})}\) represents the \((\alpha _{1},\kappa _{1})\) fractal-fractional derivative with Mittag-Leffler type kernel of fractional and fractal orders \(\alpha _{1}\in (0, 1]\) and \(\kappa _{1}\in (0, 1]\), respectively.
Where the starting circumstances are
The proposed framework splits the entire population N into 6 parts at a particular time t. We developed the Chlamydia virus model’s fractional order mathematical variant with vaccination in order to deal with the most Chlamydia model by using the most effective individuals and accounting for six (6) parts of populations. S(t) symbolizes the people’s non-vaccinated susceptibility individuals over time t, V(t) represents the population’s vaccinated susceptibility individuals over time t, E(t) represents the population’s exposed individuals over time t, I(t) represents the population’s infected individuals over time t, T(t) represents the population’s treatment individuals over time t and R(t) represent the population’s recovery over time t, all the parameters are details given in50,51. Thus, everyone in the population is ascertained via
Fundamental ideas of the fractional operator
Firstly, we jot down the following fundamentals of fractional calculus that will be useful in our investigation.
Definition 2.1
Consider the continuous map \(\mathscr {F}(t):(b,c)\rightarrow [0,\infty )\), which has a fractal differentiable dimension of \(\kappa _{1}\). In this case in51, the Riemann-Liouville \((\alpha _{1},\kappa _{1})\) fractal fractional derivative of \(\mathscr {F}(t)\) is provided by given the generalized ML (Mittag-Leffler) type kernel of order \(\alpha _{1}\).
where \(E_{\alpha _{1}}\) is the Mittag-Leffler function \(E_{\alpha _{1}}=\sum _{k=0}^{\infty }\frac{y^{k}}{\alpha _{1}(\alpha _{1}k+^1)}\) and
\(\textrm{AB}(\alpha _{1})=1-\alpha _{1}+\frac{\alpha _{1}}{\Gamma (\alpha _{1})}\) is the fractal derivative with \(\textrm{AB}(1)=\textrm{AB}(0)\).
We also make use of the related concept of the fractal fractional integral in the following.
Definition 2.2
Consider the continuous map \(\mathscr {F}(t):(b,c)\rightarrow [0,\infty )\), which has a fractal differentiable dimension of \(\kappa _{1}\). In this case in51, the Riemann Liouville \((\alpha _{1},\kappa _{1})\) fractal fractional integral of \(\mathscr {F}(t)\) is given by given the generalized ML (Mittag-Leffler) type kernel of order \(\alpha _{1}\).
if it exists, where \(\alpha _{1},\kappa _{1}>0\).
Qualitative evaluation of the Chlamydia framework
We are currently conducting a qualitative analysis of our model of infectious disease with vaccination, which is expressed as a frame work of nonlinear differential equations (1), to better understand its features and the variables that govern the dynamics of infectious disease transmission.
Existence of Chlamydia model in time scale
We start by demonstrating that our framework (1) has a solution. To that, we apply fixed point theory. Let us first define the Banach space \(M=W^{6}\), where \(W = w(J, R)\), in order to perform our qualitative analysis.
for \(|C(t)|=|V|+|I|+|S|+|E|+|T|+|R|\). The fractal fractional Chlamydia viral system (1) on the right side is rewritten as
The fractal fractional Chlamydia virus system (1) in this instance is changed into the system that follows.
We rebuild our tree-state system as the compact initial value conditionsin light of (8).
Where
and
As per the definition of (9), we possess
When we apply the fractional Atangana-Baleanu integral fractal to (11), we obtain
The extended representation of (13) is given by
We now define the self-map \(F: M\rightarrow M\) as follows in order to deduce a fixed-point problem
We employ the Leray Schauder theorem to demonstrate the existence of a solution to our fractal fractional Chlamydia virus system (1).
Theorem 3.1
(Finite point theorem Leray-Schauder52) Let \(H\subseteq G\) be an open set with \(0\in H\), \(G\subseteq M\) a closed convex and bounded set, and M be a Banach space. Next, with respect to the continuous and compact mapping \(F: \widetilde{H}\rightarrow G\), either
-
\(B_{1}\) Then \(y\in \widetilde{H}\) exists such that \(y=F(y)\).
-
\(B_{2}\) In such case, \(y=\mu F(y)\) exists for any \(y\in \partial H\) and \(\mu \in (0,1)\).
The Chlamydia virus system is limited in its existence since it simulates a real-world issue. These limitations, which are represented as \((B_{3})\) and \((B_{4})\) in Theorem 3.2, are essential in determining the dynamics and properties of the system. To define and control the behavior of the Chlamydia virus system within the bounds of pragmatism and realism, \((B_{3})\) and \((B_{4})\) are in fact essential. Acknowledging these limitations is crucial to building a thorough comprehension of the system and creating successful tactics.
Theorem 3.2
(Finite point theorem Leray-Schauder52) Suppose \(Q\in C(J\times M, M)\). If so,
-
\(B_{3}\) Then there exist \(\lambda \in L^{1}(J,R^{+})\) and then there exist \(\alpha _{1}\in C([0,\infty ),(0,\infty ))\), where \(\alpha\) non decreasing such that for all \(t\in J\) and \(A\in M\),
$$\begin{aligned} |Q(t,A(t))|\le \alpha (|A(t)|)\lambda (t). \end{aligned}$$(16) -
\(B_{4}\) Then there exist \(\vartheta >0\), \(\mu \in (0,1)\) such that
$$\begin{aligned} \frac{\vartheta }{A_{0}+\left[ \frac{(1-\alpha _{1})\kappa _{1}t^{\kappa _{1}-1}}{\textrm{AB}(\alpha _{1})}+ \frac{\alpha _{1}\kappa _{1}t^{\alpha _{1}+\kappa _{1}-1}\Gamma (\kappa _{1})}{\textrm{AB}(\alpha _{1})\Gamma (\alpha _{1}+\kappa _{1})}\right] \lambda ^{*}_{0}\alpha (\vartheta )}>1. \end{aligned}$$(17)
Given \(\lambda ^{*}_{0}=\sup _{t\in J}|\lambda (t)|\), the fractal fractional Chlamydia virus system (1) may be solved.
Proof
Let us first take \(F: M \rightarrow M\), as defined by equation (15), and make the following assumptions
for a certain \(r > 0\). It is obvious that since Q is continuous, so is F. Given (\(B_{1}\)), we obtain
for \(A\in N_{r}\). Hence
As a result, on M, F has uniform bounds. Now, let \(t,u\in [0,T]\) such that \(A\in N_{r}\) and \(t<u\). By indicating
we estimate
As \(u\rightarrow t\), we can observe that the right hand (RH) side of equation (19) approaches 0 independently of A. Thus,
As \(u\rightarrow t\). The Arzela-Ascoli theorem uses this to determine the equi-continuity of F and, in turn, the compactness of F on \(N_{r}\). Given the fulfillment of Theorem 3.1 on F, we have \((B_{1})\) or \((B_{2})\). We set from \((B_{2})\)
for some \(\omega >0\), such that
From \((B_{3})\) and equation (18), we have
Assume that \(A= \mu F(A)\) for all \(A\in \partial \Theta\) and all \(0<\mu < 1\).Next, we write using equation (20).
which is untrue. Therefore, by Theorem 3.1, \(\Theta\) admits a fixed point in \(\Theta\) and \((B_{2})\) is not satisfied. This demonstrates that the fractal fractional Chlamydia virus system (1) has an answer. \(\square\)
Uniqueness of the Chlamydia system
To prove the uniqueness of our solution to our problem (1), we first examine a Lipschitz characteristic of the fractal fractional Chlamydia viral system (1).
Theorem 3.3
Now consider \(S,V,E,R,T,I,S^{*},V^{*},E^{*},R^{*},T^{*},I^{*}\in C=C(J,R)\), and consider
-
\(D_{1}\) \(\Vert S\Vert \le \beta _{1}\), \(\Vert V\Vert \le \beta _{2}\), \(\Vert E\Vert \le \beta _{3}\), \(\Vert I\Vert \le \beta _{4}\), \(\Vert T\Vert \le \beta _{5}\), \(\Vert R\Vert \le \beta _{6}\) for some constant \(\beta _{2},\beta _{1},\beta _{5},\beta _{4},\beta _{3},\beta _{6}>0\).
Then, using constants \(k_{1},k_{2},k_{3},k_{4},k_{5}\) and \(k_{6}\) with regard to the pertinent components, \(Q_{1}, Q_{2}, Q_{3}, Q_{4}, Q_{5}\) and \(Q_{6}\) specified in system (7) meet the Lipschitz property, where
Proof
Taking randomly \(S,S^{*}\in C=C(J, R)\) for \(Q_{1}\), we have
We determine that, with the constant \(\beta _{1} > 0\), \(Q_{1}\) is Lipschitz with regard to S(t) based on equation (22).
Similarly, from equation (22) we find out all \(Q_{2}, Q_{3},Q_{4},Q_{5}\) and \(Q_{6}\) is Lipschitz with regard to V(t), R(t), I(t), T(t), E(t) under the constants \(\beta _{2},\beta _{6},\beta _{4},\beta _{5},\beta _{3}>0\) respectively.
Therefore, the kernel functions \(Q_{1}, Q_{2}, Q_{3}, Q_{4}, Q_{5}\) and \(Q_{6}\) are Lipschitz, respectively with constants \(\beta _{1}, \beta _{2}, \beta _{3}, \beta _{4}, \beta _{5}, \beta _{6}>0\). \(\square\)
We now demonstrate the uniqueness of the solution to the fractal fractional problem (1) by using theorem 3.3.
Theorem 3.4
Let condition \(C_{1}\) hold. If
with \(\beta _{i}\in \{1, 2, 3, 4, 5, 6\}\) and the Lipschitz constants introduced by equation (21) set to \(\beta _{i}> 0\), there is only one solution for the fractal fractional Chlamydia virus system (1).
Proof
By contradiction, we carry out the proof. Let us suppose that there is another solution, given starting circumstances, to the fractal fractional Chlamydia virus system (1), which is
From system of equation (15), we have
Similarly, we can developed for others compartments, this can be follow as for all, we estimate
and so
From equation (23), we can state that the inequality mentioned above is true if \(\Vert S(t)-S^{*}(t)\Vert =0\) or \(S(t)=S^{*}(t)\).
Similarly, from equation (23) we can state that the inequality of the compartments like as V(t), E(t), I(t), T(t) and R(t) is true if \(\Vert V(t)-V^{*}(t)\Vert =0\), \(\Vert E(t)-E^{*}(t)\Vert =0\), \(\Vert I(t)-I^{*}(t)\Vert =0\), \(\Vert T(t)-T^{*}(t)\Vert =0\) and \(\Vert R(t)-R^{*}(t)\Vert =0\) respectively.
As a consequence, \((S(t),V(t),E(t),I(t),T(t),R(t))=(S^{*}(t),V^{*}(t),E^{*}(t),I^{*}(t),T^{*}(t),R^{*}(t))\). It demonstrates that the fractal fractional Chlamydia viral system may be solved (1) is unique. \(\square\)
Positivity and bounded of solutions
Given that the proposed model’s responses are bound and guaranteed to be positive, the study looks at the conditions under which it can be applied to significant value real-world scenarios. Regarding classical derivatives, we possess the subsequent information \(\forall t \ge 0\).
We must determine the norm
We discover
For the classical derivative, the outcome is \(\forall t \ge 0\).
While the next section discusses positive options with non-local operators, it states that the system’s (1) solutions will undoubtedly remain positive when all of the beginning criteria for nonlocal operators are satisfied. For \(\forall t>0\), we build a fractal-fractional operator with a Mittag-Leffler kernel.
where the time component is \(\upsilon\).
Lemma 3.1
The region \(\Upsilon _l \in \mathbb {R}_{+}^{6}\)
attracts all of system (1)’s solutions and, for the suggested system in \(\mathbb {R}_{+}^6\), is positively invariant when utilized with initial constraints that are not negative.
Proof
We will illustrate the framework (1) advantageous outcome, and the results are:
In accordance with system (31), the vector field is situated in the area \(\mathbb {R}_{+}^6\) around every hyperplane encircling the non-negative orthant about \(t>0\). Therefore,
is a positively invariant domain.
Remark 3.1
Lemma (3.1) states that for the suggested structure in \(\mathbb {R}_{+}^3\), the region \(\Upsilon _{1}\) is favorably uniform, dependent on non-negative starting restrictions. Said another way, each solution to the system (1) will ultimately come together to and stay within the region \(\Upsilon _l\), guaranteeing the values of the compartments remain non-negative over the course of the system’s dynamics. This feature is crucial for analyzing the model’s behavior and its durability over time because it makes sure the disease dynamics in the compartmental divisions won’t show undesirable or non-material values.
Equilibrium points analysis
This section offers a thorough examination of equilibrium points. First, we solve the framework 1 for equilibrium points. The areas devoid of illness are
The EEPs (Endemic Equilibrium Points) at this time are
where
where, \(P_1=\sigma +\mu , P_2=\eta +\mu +\delta _1+\gamma , P_3=\varphi +\mu +\tau +\delta _2,\)
Reproduction number
Taking the maximum eigen value of the spectral radius \(F V^{-1}\) yields the basic reproduction number \(\mathscr {R}_0\).
where, \(A=\left( S^*+(-\pi +1) V^*\right) , J_1=\omega +\mu , J_2=\sigma +\mu , J_3=\eta +\mu +\delta _1+\gamma , J_4=\varphi +\mu +\tau +\delta _2\), \(N=S^*+T^*+E^*+I^*+V^*+R^*\).
Fixed point theorems for unique and continuous of solution
In order to prove the existence of nonlinear systems, nonlinear functional analysis makes use of fixed-point theorems. The system (1) is assured to have the minimum of one answer inside the range [0, T] by the fixed point concept. The system (1) is considered to be
The following is a reformulation of (33) for the Mittag-Leffler kernel of proposed framework (1) as a fractal fractional integral.
Where \(\Delta _1=\frac{\beta (1-\alpha ) t^{\beta -1}}{\tilde{AB}(\alpha )}\), and \(\Delta _2=\frac{\alpha \beta }{\tilde{AB}(\alpha ) \Gamma (\alpha )}\). Krasnoselski’s fixed point theorem is utilized to illustrate the fundamental concept of concerning equations (34), which are expressed as \(\textrm{P}\) \((\kappa _{1}, \chi _1, \rho _1)\) as contraction maps and \(\textrm{V}\) \((\kappa _{2}, \chi _2, \rho _2)\) as continuous compact integral portions.
Theorem 3.5
Mapping \(\textrm{P}\) \((\kappa _{1}, \chi _1, \rho _1):[0, \mathbb {T}] \rightarrow R^3\) stated in (34) enables constants to have the Lipschitz contractive condition \(\mathcal{M}_{\kappa }, \mathcal{M}_{\chi }, \mathcal{M}_{\textrm{C}}>0\).
Proof
Think about the operator \(\textrm{P}(\kappa _1, \chi _1, \rho _1):[0, \mathbb {T}]\rightarrow R^3\) defined on a space with full norms. Where the norm
(i) First, we’ll demonstrate that \(\textrm{P}(\kappa , \chi , \rho )\) is a map of contractions. In the case of S(t) and \(\overline{S(t)}\), we have
where \(\mathcal{M}_{\kappa }=||(||Y||-m)||\). By applying this strategy to all other compartments, we have \(\mathcal{M}_{\chi }=||(||X||-n)||, \mathcal{M}_{\rho }=||p||\). This suggests that, for the operator \(\textrm{P}(X,Y,Z)\), there are
where \(\mathcal{M}=\max [\mathcal{M}_{\kappa }, \mathcal{M}_{\chi }, \mathcal{M}_{\textrm{C}}]<1\) exists as a Lipschitz constant. This suggests that \(\textrm{P}\) is limited.
(ii) Next, we’ll demonstrate that \(\textrm{V}\) is continuously compact. All positively bound continuous operators’ absolute modulus \(\kappa , \chi , \rho\), supplied by the positive, not equal to zero constants and stated in (34) \(\Theta _{\kappa }, \Theta _{\chi }, \Theta _{\rho }, \Psi _{\kappa }\), \(\Psi _{\chi }, \Psi _{\rho }\), showing the operator’s compactness by satisfying the following bounded inequalities:
Assume that \(\textsf{J}\) has a closed subset called \(\mathbb {Z}\).
For \((\kappa , \chi , \rho ,\varsigma ,\upsilon ,\nu ) \in \textsf{J}\), we find
Show it in a similar fashion for the other compartments in the proposed model. This process leads us to the maximal norm of \(\Vert \tau \Vert\), which we find as
where \(\eta\) is a constant positive number. It follows that the operator \(\Vert \tau \Vert \le \eta \Rightarrow \tau\) is constantly bounded.
We will show that \(\tau\) is now equi-continuous for \(t_a<t_b \in [0, \mathbb {T}]\). We have for \(t_1<t_2 \in [0, \mathbb {T}]\) for this reason.
Similarly,
Since \(t_2 \rightarrow t_1\) is independent of (S, T, E, I, V, R). This implies
\(\Rightarrow \tau\) is an equi-continuous.
\(\Rightarrow \tau\), according to Arzela’s theorem, is relatively compact.
This leads to a Krasnoselski theorem, which states that the contraction and continuity of the \(\textrm{P}\) and \(\textrm{V}\) guarantee the presence of a solitary, distinctive solution. \(\square\)
Theorem 3.6
There is a unique solution for model (1) if
where \(\mathcal{M}=\max \{\mathcal{M}_{\kappa }, \mathcal{M}_{\chi }, \mathcal{M}_{\rho }, \mathcal{M}_{\varsigma }, \mathcal{M}_{\upsilon }, \mathcal{M}_{\nu }\}\).
Proof
Establish an operator \(\textrm{X}=\left( \textrm{X}_1, \textrm{X}_3, \textrm{X}_2, \textrm{X}_5, \textrm{X}_4, \textrm{X}_6 \right) : \mathbb {Z} \rightarrow \mathbb {Z}\) utilizing (1) as
For \((S,T,E,I,V,R), (\overline{S},\overline{T},\overline{E},\overline{I},\overline{V},\overline{R}) \in \mathbb {Z}\), and utilizing (46) we have,
\(\left\| S-\overline{S}\right\| \rightarrow 0\) when \(S \rightarrow \overline{S}\). Hence
with
Following this strategy, we discover
The contraction maps S inherit the characteristics of Schauder’s and Krasnoselski’s theorems and verifies the unique solution of system (1). \(\square\)
Stability analysis of the Chlamydia model
We shall utilize a theorem in this part to demonstrate the mathematical model’s local stability. Using the equation and the theorem, we may determine the model’s local stability. First, the stability characteristics of the chosen model are investigated.
Local asymptotical stability
The system’s Jacobian matrix at the \(E^*\) equilibrium point is
The Jacobian matrix’s characteristic equation \(J(E^*)\) is provided by
The characteristic equation becomes for the equilibrium point \(E_1\) and parameters \(m=3, n=0.1, p=1\)
and eigenvalues of equation (54) are
Since the equilibrium point \(E_1\) is asymptotically stable.
Global stability analysis
To begin, we will go over an essential Lemma to examine the global stability of the suggested system (1) accordingly51.
Lemma 4.1
Consider a continuous function \(\mathbb {G} \in \mathbb {R}^{+}\) in which for each \(t \ge t_0\);
We set all independent variables for the Lyapunov function. For \(\{X,Y,Z\},\mathbb {G}<0\) is the equilibrium.
Theorem 4.1
the reproduction number of a fractional order system is more than 1, its equilibrium points are globally asymptotically stable.
Proof
The Volterra-kind Lyapunov function has the following expression.
where \(v_1,v_2,v_3,v_4,v_5,v_6\) are positive constants that can be altered at a later time. When we plug equation (57) into system (1), we get
By putting, the values of compartments and fitting \(S=S-S^*, V=V-V^*, T=T-T^*, I=I-I^*, E=E-E^*, R=R-R^*\), after simplification, its hold the stabling criteria. We have
\(\square\)
Numerical scheme with generalized form of fractal fractional operator
In this section, we construct numerical algorithm for simulations and results for new finance system (1) with initial condition (2) by using the generalized form of fractal-fractional derivative in Mittag-Leffler function51. So, We can write the system as follows
Where we defined \(\wp = (S,V,E,I,T,R)\), Applying associated integral, we have
where \(\mathfrak {AB}= \frac{\alpha _{1}}{\tilde{AB}(\alpha _{1}) \Gamma (\alpha _{1})}\). By Newton polynomial
After substituting the Newton polynomial into above system, the following is obtained:
Where
From above equations,
As a result, we obtain
Where
Results and discussions
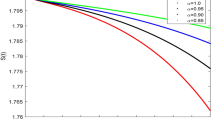
A numerical simulation was conducted to analyze the control of the newly designed complicated fractional chaotic sexually transmitted disease chlamydia in the United States using the fractal fractional approach. \(S(0)=233824096\), \(T(0)=250000\), \(E(0)=500000\), \(V(0)=1000000\), \(I(0)=200904\), and \(R(0)=50000\) are the initial conditions of the proposed system. The variables S(t), T(t), I(t), V(t), E(t), and R(t), respectively, indicate susceptible individuals, treated humans, infectious peoples, vaccinated groups, exposed populations, and humans with recovery. Using the proposed system’s fractal fractional derivative, we can easily see that, according to data from different nations, a more accurate estimate of the minimum illness rate values from50 is given by vulnerable persons, vaccinated susceptible individuals, exposed people, infectious people, treated humans, and humans with a recovery rate. Figures 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 and 12 illustrate this impact at various fractal and fractional order values at different dimensions. Using the FFM fractional derivatives, Figs. 1 and 7 simulate S(t) shows a noticeable decrease in the susceptible population under the influence of control measures, Figs. 2 and 8 simulate V(t) shows a noticeable decrease in the vaccinated susceptible population under the effectiveness of the implemented control is evident; Figs. 3 and 9 show a noticeable decrease in the exposed peoples increase by fractional orders under the influence of control measures; Figs. 4 and 10 simulate I(t) shows a noticeable increase in the infected population under the effectiveness of the implemented control is evident, Figs. 5 and 11 simulate T(t) shows a noticeable decrease in the treated humans population under the effectiveness of the implemented control is evident, and Figs. 6 and 12 simulate T(t) showing a noticeable increase in the recovered humans population under the effectiveness of the implemented control is evident at different fractional orders with different dimensions.
S(t) simulation using parametric values of dimension 1.
V(t) simulation using parametric values of dimension 1.
E(t) simulation using parametric values of dimension 1.
I(t) simulation using parametric values of dimension 1.
T(t) simulation using parametric values of dimension 1.
R(t) simulation using parametric values of dimension 1.
S(t) simulation using parametric values of dimension 0.8.
V(t) simulation using parametric values of dimension 0.8.
E(t) simulation using parametric values of dimension 0.8.
I(t) simulation using parametric values of dimension 0.8.
T(t) simulation using parametric values of dimension 0.8.
R(t) simulation using parametric values of dimension 0.8.
In Figs. 13, 14, 15, 16, 17 and 18, a comparison using a power law kernel, an exponential decay kernel, and a Mittag-Leffler kernel in a fractal sense demonstrates the precision and quick convergence of the proposed operator. Notable responses are obtained from the compartments of the constructed model. The relationship between these variables is a growing or reducing factor with altering fractal values as well as fractional parameter values. In Fig. 13 susceptible individuals rates start to rise in line with the initial conditions decreasing with respect to time t. In Fig. 14, vaccinated individual rates start to rise in line with the initial conditions decreasing with respect to time t. In Fig. 15, exposed group rates start to rise in line with the initial conditions decreasing with respect to time t under vaccination. In Fig. 16, infected individual rates start to decrease in line with the initial conditions to rise with respect to time t. In Figs. 17 and 18, treated and recovered rates start decreasing to rise in line with the initial conditions with respect to time t. The impact factor begins to decrease for those who have received the recommended system’s vaccination, those who have been exposed, those who are infectious, those who have had treatment, and those whose recovery rate is high. For non-integer time-fractional factors, the complex chaotic fractional system is determined to be more appropriate and trustworthy compared to time-integer factors. Comparison of compartments is demonstrated with the power law kernel and exponential decay kernel at different fractional order values in Fig. 19. This study sheds light on how disease control is expected to develop in the future and how we may improve our efforts to reduce the spread of infectious disease in society. Compared to classical derivatives, fractal fractional analysis produces robust results for all compartments when examining steady states with non-integer order derivatives. It’s also important to remember that fractional value reduction improves the accuracy and reliability of solutions for every compartment. Memory influence can be observed with a greater degree of freedom and a solution restricted to a steady state point that lies in a feasible range by varying the fractal dimension. The fractional order results are more dependable than the integer order ones due to the fractional order models’ ability to capture memory effects in a system, despite the fact that both models’ predictive strengths are rather equal.
Comparison S(t) between the Power law, Exponential Decay and Mittag Leffler kernel for order 0.9 with dimension 1.
Comparison V(t) between the Power law, Exponential Decay and Mittag Leffler kernel for order 0.9 with dimension 1.
Comparison E(t) between the Power law, Exponential Decay and Mittag Leffler kernel for order 0.9 with dimension 1.
Comparison I(t) between the Power law, Exponential Decay and Mittag Leffler kernel for order 0.9 with dimension 1.
Comparison T(t) between the Power law, Exponential Decay and Mittag Leffler kernel for order 0.9 with dimension 1.
Comparison R(t) between the Power law, Exponential Decay and Mittag Leffler kernel for order 0.9 with dimension 1.
Comparison between all compartments in chaotic behavior that shows solution of bonded in feasible region (figures generated by MATLAB 2018b,DESKTOP-HFF1O05, Intel(R) Core(TM) i7-8565U CPU @ 1.80GHz 1.99 GHz ).
Conclusions
This research investigates the transmission of Chlamydia in the United States with varying rates using a dynamic, chaotic fractional order model with a fractal fractional derivative. Nonsingular and nonlocal kernels, which emerge in the derivation of the generalized fractal operator, provide the foundation of this fractional model. The uniqueness and positivity of the solutions that fall within the feasible zone were satisfied by the model. The first and second derivative tests are also satisfied by local and global stability. Stable and chaotic Chlamydia system behavior in conceivable locations are the results of the chaos control requirements being satisfied. The Chlamydia model is examined theoretically and numerically using a fractal fractional operator understanding of the Mittag-Leffler function at various fractal and fractional order values. The results are also compared using the exponential decay kernel and power law kernel at various fractional order values, with the proportion of minimum interest rates in various countries used as a proxy. The fractional-order Chlamydia model, which has been adjusted with a fractal fractional derivative, is used to regulate the essential lowest infectious rate of the disease, indicating strong consensus on the system’s Chlamydia disease management. Based on numerical data, the model gives an effect analysis of the essential minimum infectious rate. The graph depicts the influence of variables on the quantity of the critical minimum infectious rate over time. This research approach has significant results for disease coefficients, rate of infection, and demand for recovery. As vaccination demand and infection exponents begin to drop, infectious rates begin to rise in accordance with the initial conditions, exposing the Chlamydia system’s true macroeconomic behavior. It is highlighted here that, for non-integer time-fractional parameters, when compared to time-integer parameters, the intricate chaotic fractional structure yields more reliable and suitable results.
Data availability
The datasets used and/or analysed during the current study available from the corresponding author on reasonable request.
References
Manavi, K. A review on infection with Chlamydia trachomatis. Best Pract. Res. Clin. Obstetr. Gynaecol. 20(6), 941–951 (2006).
Hillis, S. D. & Wasserheit, J. N. Screening for chlamydiaa key to the prevention of pelvic inflammatory disease. N. Engl. J. Med. 334(21), 1399–1401 (1996).
Kong, F. Y. S. & Hocking, J. S. Treatment challenges for urogenital and anorectal Chlamydia trachomatis. BMC Infect. Dis. 15, 1–7 (2015).
Hogan, R. J., Mathews, S. A., Mukhopadhyay, S., Summersgill, J. T. & Timms, P. Chlamydial persistence: Beyond the biphasic paradigm. Infect. Immun. 72(4), 1843–1855 (2004).
Odionyenma, U. B., Omame, A., Ukanwoke, N. O. & Nometa, I. Optimal control of Chlamydia model with vaccination. Int. J. Dyn. Control 10(1), 332–348 (2022).
Akinlotan, M. D., Mallet, D. G. & Araujo, R. P. An optimal control model of the treatment of chronic Chlamydia trachomatis infection using a combination treatment with antibiotic and tryptophan. Appl. Math. Comput. 375, 124899 (2020).
Emuoyibofarhe, O., Olayiwola, R. & Akinwande, N. A mathematical model and simulation of Chlamydia trachomatis in a human carrier. Br. J. Math. Comput. Sci. 7(6), 450–465 (2015).
Sharma, S. & Samanta, G. P. Analysis of a Chlamydia epidemic model. J. Biol. Syst. 22(04), 713–744 (2014).
Heffernan, C. & Dunningham, J. A. Simplifying mathematical modelling to test intervention strategies for Chlamydia. J. Public Health Epidemiol. 1(1), 022–030 (2009).
Sharomi, O. & Gumel, A. B. Mathematical study of in-host dynamics of Chlamydia trachomatis. IMA J. Appl. Math. 77(2), 109–139 (2012).
Akinlotan, M. D., Mallet, D. G. & Araujo, R. P. Mathematical modelling of the role of mucosal vaccine on the within-host dynamics of Chlamydia trachomatis. J. Theor. Biol. 497, 110291 (2020).
Atangana, A. (2017). Fractal-fractional differentiation and integration: connecting fractal calculus and fractional calculus to predict complex system. Chaos Solitons Fractals102, 396-406 (2020).
Farman, M. et al. Yellow virus epidemiological analysis in red chili plants using Mittag-Leffler kernel. Alex. Eng. J. 66, 811–825 (2023).
Xu, C. et al. Lyapunov stability and wave analysis of COVID-19 omicron variant of real data with fractional operator. Alex. Eng. J. 61(12), 11787–11802 (2022).
Toufik, M. & Atangana, A. New numerical approximation of fractional derivative with non-local and non-singular kernel: Application to chaotic models. Eur. Phys. J. Plus 132, 1–16 (2017).
Akgl, E. K. Solutions of the linear and nonlinear differential equations within the generalized fractional derivatives. Chaos Interdiscip. J. Nonlinear Sci. 29(2), 023108 (2019).
Atangana, A. & Akgl, A. Can transfer function and bode diagram be obtained from sumudu transform. Alex. Eng. J. 59(4), 1971–1984 (2020).
Farman, M. et al. A control of glucose level in insulin therapies for the development of artificial pancreas by Atangana Baleanu derivative. Alex. Eng. J. 59(4), 2639–2648 (2020).
Sajjad, A., Farman, M., Hasan, A. & Nisar, K. S. Transmission dynamics of fractional order yellow virus in red chili plants with the Caputo Fabrizio operator. Math. Comput. Simul. 207, 347–368 (2023).
Hasan, A. et al. Epidemiological analysis of symmetry in transmission of the Ebola virus with power law kernel. Symmetry 15(3), 1–29 (2023).
Hashemi, M. S. Some new exact solutions of (2+1)-dimensional nonlinear Heisenberg ferromagnetic spin chain with the conformable time fractional derivative. Opt. Quant. Electron. 50(2), 1–11 (2018).
Aslam, M., Farman, M., Akgl, A. & Sun, M. Modeling and simulation of fractional order COVID-19 model with quarantined isolated people. Math. Methods Appl. Sci. 44(8), 6389–6405 (2021).
Farman, M. et al. Epidemiological analysis of the coronavirus disease outbreak with random effects. Comput. Mater. Continua 67(3), 3215–3227 (2021).
Aslam, M., Farman, M., Akgl, A., Ahmad, A. & Sun, M. Generalized form of fractional order COVID-19 model with Mittag Leffler kernel. Math. Methods Appl. Sci. 44(11), 8598–8614 (2021).
Farman, M., Aslam, M., Akgl, A. & Ahmad, A. Modeling of fractional order COVID-19 epidemic model with quarantine and social distancing. Math. Methods Appl. Sci. 44(11), 9334–9350 (2021).
Farman, M., Akgl, A., Ahmad, A., Baleanu, D. & Umer Saleem, M. Dynamical transmission of coronavirus model with analysis and simulation. Comput. Model. Eng. Sci. 127(2), 753–769 (2021).
Ivorra, B., Ferrndez, M. R., Vela-Prez, M. & Ramos, A. M. Mathematical modeling of the spread of the coronavirus disease 2019 (COVID-19) taking into account the undetected infections. Case China Commun. Nonlinear Sci. Numer. Simul. 88, 105303 (2020).
Atangana, A. & Qureshi, S. Modeling attractors of chaotic dynamical systems with fractal fractional operators. Chaos Solitons Fractals 123, 320–337 (2019).
Chen, W., Sun, H., Zhang, X. & Koroak, D. Anomalous diffusion modeling by fractal and fractional derivatives. Comput. Math. Appl. 59(5), 1754–1758 (2010).
Atangana, A. Fractal fractional differentiation and integration: Connecting fractal calculus and fractional calculus to predict complex system. Chaos Solitons Fractals 102, 396–406 (2017).
Ahmad, S. et al. Fractional order mathematical modeling of COVID-19 transmission. Chaos Solitons Fractals 139, 110256 (2020).
Khan, M. A. The dynamics of dengue infection through fractal fractional operator with real statistical data. Alex. Eng. J. 60(1), 321–336 (2021).
Zuniga Aguilar, C. J., Gomez Aguilar, J. F., Romero Ugalde, H. M., Jahanshahi, H., & Alsaadi, F. E. Fractal fractional neuro adaptive method for system identification. Eng. Comput. 1-24 (2022).
Abro, K. A., Atangana, A. & Gomez Aguilar, J. F. Ferromagnetic chaos in thermal convection of fluid through fractal fractional differentiations. J. Therm. Anal. Calorim. 147(15), 8461–8473 (2022).
Abro, K. A., Atangana, A., Aguilar, Gomez & Chaos, J. F. control and characterization of brushless DC motor via integral and differential fractal fractional techniques. Int. J. Model. Simul. 43(4), 416–425 (2023).
Abro, K. A., & Atangana, A. Mathematical modeling of neuron model through fractal fractional differentiation based on maxwell electromagnetic induction: application to neurodynamics. Neural Comput. Appl. 1-9 (2024).
Siyal, A., & Abro, K. A. A fractal model for thermal analysis of newtonian fluid to forecast thermal behavior. J. Thermal Anal. Calorimetry 1-10 (2024).
Abro, K. A., Atangana, A., Memon, I. Q., & Aziz, A. Analytical and fractional model for power transmission of lossy transmission line. Int. J. Model. Simul. 1-10 (2024).
Abro, K. A., Siyal, A. & Atangana, A. Strange fractal attractors and optimal chaos of memristor memcapacitor via non local differentials. Qual. Theor. Dyn. Syst. 22(4), 156 (2023).
Abro, K. A., Atangana, A. & Gomez Aguilar, J. F. Optimal synchronization of fractal fractional differentials on chaotic convection for Newtonian and non-Newtonian fluids. Eur. Phys. J. Spec. Top. 232(14), 2403–2414 (2023).
Abro, K. A. & Atangana, A. Simulation and dynamical analysis of a chaotic chameleon system designed for an electronic circuit. J. Comput. Electron. 22(5), 1564–1575 (2023).
Abro, K. A., Siyal, A., Atangana, A. & Al-Mdallal, Q. M. Analytical solution for the dynamics and optimization of fractional Klein Gordon equation: An application to quantum particle. Opt. Quant. Electron. 55(8), 1–17 (2023).
Abro, K. A., Atangana, A. & Gomez-Aguilar, J. F. Chaos control and characterization of brushless DC motor via integral and differential fractal fractional techniques. Int. J. Model. Simul. 43(4), 416–425 (2023).
Ghanbari, B., & Gomez Aguilar, J. F. (2019). Analysis of two avian influenza epidemic models involving fractal-fractional derivatives with power and Mittag-Leffler memories. Chaos Interdiscip. J. Nonlinear Sci.29(12).
Gomez Aguilar, J. F., Cordova Fraga, T., Abdeljawad, T., Khan, A. & Khan, H. Analysis of fractalfractional malaria transmission model. Fractals 28(08), 2040041 (2020).
Gomez Aguilar, J. F. & Atangana, A. New chaotic attractors: Application of fractal-fractional differentiation and integration. Math. Methods Appl. Sci. 44(4), 3036–3065 (2021).
Saad, K. M., Alqhtani, M. & Gomez Aguilar, J. F. Fractal fractional study of the hepatitis C virus infection model. Results Phys. 19, 103555 (2020).
Zuniga Aguilar, C. J., Gomez Aguilar, J. F., Romero Ugalde, H. M., Jahanshahi, H. & Alsaadi, F. E. Fractal-fractional neuro-adaptive method for system identification. Eng. Comput. 38, 1–24 (2022).
Abro, K. A., Atangana, A. & Gomez Aguilar, J. F. Chaos control and characterization of brushless DC motor via integral and differential fractal-fractional techniques. Int. J. Model. Simul. 43(4), 416–425 (2023).
Vellappandi, M., Kumar, P. & Govindaraj, V. Role of fractional derivatives in the mathematical modeling of the transmission of Chlamydia in the United States from 1989 to 2019. Nonlinear Dyn. 111(5), 4915–4929 (2023).
Kanwal, T. et al. Dynamics of a model of polluted lakes via fractalfractional operators with two different numerical algorithms. Chaos Solitons Fractals 181, 1–21 (2024).
Granas, A. Fixed Point Theory. Springer Monogr. Math. 14, 15–16 (2003).
Acknowledgements
This study is supported via funding from Prince Sattam bin Abdulaziz University project number (PSAU/2024/R/1445).
Author information
Authors and Affiliations
Contributions
Conceptualization: KSN, MF; Methodology: MF; Software: KSN, MF, EH, AH, PA; Formal analysis: PA, EH; Writing original draft: KSN, MF, EH, AF, PA. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Nisar, K.S., Farman, M., Hincal, E. et al. Chlamydia infection with vaccination asymptotic for qualitative and chaotic analysis using the generalized fractal fractional operator. Sci Rep 14, 25938 (2024). https://doi.org/10.1038/s41598-024-77567-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-024-77567-4
Keywords
This article is cited by
-
Modeling a fractional-order chlamydia dynamic with protected intimacy as a strategic control intervention
Discover Public Health (2025)
-
Analyzing fractional glucose-insulin dynamics using Laplace residual power series methods via the Caputo operator: stability and chaotic behavior
Beni-Suef University Journal of Basic and Applied Sciences (2025)
-
A numerical study on the dynamics of SIR epidemic model through Genocchi wavelet collocation method
Scientific Reports (2025)
-
Monitoring and investigation to control the brain network disease under immunotherapy by using fractional operator
Scientific Reports (2025)
-
Mathematical modeling of tumor-immune dynamics: stability, control, and synchronization via fractional calculus and numerical optimization
Scientific Reports (2025)
