Introduction

The permanent magnet synchronous motor (PMSM) has been considered a promising solution to induction motors (IMs) and DC motors due to their high efficiency and simple structure. These advantages have widened their applications such as tension controls, electric power steering (EPS), home appliances, electric vehicles, and so on1,2,3,4,5.

The torque control is essential for speed and position control system, which can be implemented by the classical direct torque control (DTC) technique. Recently, the rotational coordinate transform based current control scheme has been adopted for the torque control due to its high performance and low current ripple, which is called the vector control technique. In the resulting rotational d-q frame, a simple proportional–integral (PI) regulator has been used to regulate the d-q frame current errors. Their PI gains were tuned through a trial-and-error process and frequency domain analysis technique, called the Bode and Nyquist methods6,7, for a fixed operating point. For wide-range operating range, an extra online gain selector has to be embedded in the control algorithm8. To overcome this limitation, the feedback-linearization (FL) method was applied, which is composed of the PI regulator and a feed-forward compensation for the disturbance from the back EMF effect9,10,11. The PMSM parameter dependent PI gains and feed-forward compensator force the closed-loop dynamics to be a low-pass filter (LPF) with a desired bandwidth via a pole-zero cancellation. To guarantee the desired closed-loop performance, the on-line or off-line parameter identification (ID) algorithms must be combined with the FL controller12,13,14,15. The parameter dependency problem can be alleviated by the sliding mode control method in Ref.16. This scheme requires a conservative lower and upper bounds of the PMSM parameters for the discontinuous sign-function gain and feed-forward compensator, which could produce an excessive control signal. A novel model predictive control (MPC) technique was proposed with a significant reduced computational complexity, compared with classical MPC methods17,18. The closed-loop optimality and control input feasibility can be guaranteed with additional ID algorithms like to the FL controller. It was reported that the disturbance observe (DOB) can be used as an effective solution to construct the feed-forward compensator while eliminating the steady-state errors19,20. Recently, the DOB based current controller was systematically developed for PMSMs with a rigorous closed-loop stability and property analysis21. These surveyed techniques assign the fixed bandwidth to the closed-loop system by their well-tuned control gains. The magnified control gains could improve the transient performance but result in an efficiency degradation in steady-state operations.

Unlike the literature mentioned above, this study devises a novel variable bandwidth-based proportional-type current controller subject to the constraints;

  • (C1) an fixed a high-level of current feedback gain to ensure the desired outer loop bandwidth for speed and position loops;

  • (C2) the requirement of the integral actions for the control loop involving the additional anti-windup mechanisms to ensure the steady-state error rejection;

  • (C3) the true PMSM parameter dependence of the controller to secure the desired closed-loop stability and performance.

The proposed technique considering these constraints makes the following major contributions:

  1. 1.

    The proposed auto-tuner continuously updates the feedback gain according to the simple rule in the analytic form to find the desired closed-loop bandwidth for the transient and steady-state operations, resulting in improved current tracking performance and lowered current ripple level (for (C1)).

  2. 2.

    The proportional-type current controller employs the reduced-order DOB as a subsystem as a replacement of the integrator to simplify the resultant feedback system structure by removing the requirement of the additional anti-windup mechanisms, so that it ensures the performance recovery property (for (C2) and (C3)).

Moreover, practical advantages are shown by providing convincing experimental data using a 700-W prototype PMSM dynamo system.

Current and speed dynamics of PMSMs

In accordance with result9, the PMSM current dynamics are described in the rotational d-q frame as

$$\begin{aligned} L_d \dot{i}_d(t)= & -R_s i_d (t) + L_q \omega _r (t) i_q(t) + u_d (t), \end{aligned}$$
(1)
$$\begin{aligned} L_q \dot{i}_q(t)= & -R_s i_q (t) -L_d \omega _r (t) i_d (t) - \lambda _{PM}\omega _r (t) + u_d (t),~\forall t \ge 0, \end{aligned}$$
(2)

where \(i_x(t)\), \(u_x\), \(x=d,q\), denote the current (in A) and voltage (in V) represented in the rational d-q frame, respectively. The electrical speed is defined as \(\omega _r(t):= P\omega (t)\) with P and \(\omega (t)\) being the pole-pair numbers and rotor speed in rad/s, which is used to transform the reference frame into the rational d-q frame. The inductance values in this frame are given as \(L_x\), \(x=d,q\), (in H) and the stator resistance and flux are represented as \(R_s\) (in \(\Omega\)) and \(\lambda _{PM}\) (in Wb), respectively.

The PMSM mechanical speed dynamics is related to the d-q frame current as

$$\begin{aligned} J\dot{\omega }(t) = - B \omega (t) + T_e(i_d(t),i_q(t)) - T_L(t), \end{aligned}$$
(3)

with the load torque \(T_L(t)\) and electrical torque \(T_e(i_d(t),i_q(t))\) defined as

$$\begin{aligned} T_e(i_d(t),i_q(t)):= \frac{3}{2}P (\Delta L_{dq}i_d(t)i_q(t) + \lambda _{PM}i_q(t)),~\forall t \ge 0, \end{aligned}$$

where J and B represent the inertia and viscous damping constants, respectively, and \(\Delta L_{dq}:= L_d - L_q\). Note that the PMSM speed acts as the internal dynamics in the current control mode. Fortunately, it is proved that any stabilizing current controller stabilizes the internal dynamics coming from the PMSM speed. See21 for details. Thus, this study focuses on developing the current tracking controller without internal dynamics analysis.

The next section designs an advanced current control algorithm under the practical assumptions:

  • (A1) The nominal PMSM parameter values, \(L_{x,0}\), \(x=d,q\), \(R_{s,0}\), \(\lambda _{PM,0}\), are available, but their variations are unknown. e.g., \(L_x = L_{x,0} + \Delta L_x\), \(R_s = R_{s,0} + \Delta R_s\), and \(\lambda _{PM} = \lambda _{PM,0} + \Delta \lambda _{PM}\) with unknown variations \(\Delta L_x\), \(\Delta R_s\), and \(\Delta \lambda _{PM}\).

  • (A2) The d-q frame current \(i_x(t)\), \(x=d,q\), and mechanical speed \(\omega (t)\) are available for feedback using the shut resistors and rotary encoder.

Design of proposed proportional-type robust current controller

Control objective

This subsection introduces the variables as \(I_{x,b}^*(s) = \mathcal {L}\{i_{x,b}^*(t)\}\) and \(I_{x,ref}(s) = \mathcal {L}\{i_{x,ref}(t)\}\) as the Laplace transforms of desired current response \(i_x^*(t)\) and its reference \(i_{x,ref}(t)\), which defines the transfer function as the base feedback system performance:

$$\begin{aligned} \frac{I_{x,b}^*(s)}{I_{x,ref}(s)} = \frac{\omega _{cc}}{s + \omega _{cc}},~x=d,q,~\forall s \in \mathbb {C}, \end{aligned}$$
(4)

with its realization given by

$$\begin{aligned} \dot{i}_{x,b}^*(t) = \omega _{cc} (i_{x,ref}(t) - i_{x,b}^*(t)),~x=d,q,~\forall t \ge 0, \end{aligned}$$
(5)

for given desired bandwidth \(\omega _{cc}\) (in rad/s, \(f_{cc} = \frac{\omega _{cc}}{2\pi }\) Hz) determining the current tracking performance and ripple level in the transient and steady-state operations.

To secure both the transient and steady-state behaviors of the feedback system, this work modifies the base desired system (5) such that \(i_x^*(t) = i_{x,b}^*(t)\bigg |_{\omega _{cc} = \hat{\omega }_{cc}}\) resulting in the time-varying system

$$\begin{aligned} \dot{i}_x^*(t) = \hat{\omega }_{cc}(t) (i_{x,ref}(t) - i_x^*(t)),~\forall t \ge 0, \end{aligned}$$
(6)

for a variable bandwidth \(\hat{\omega }_{cc}(t)\) with property \(\hat{\omega }_{cc}(t) \ge \omega _{cc}\), \(\forall t\), and initial condition \(\hat{\omega }_{cc}(0) = \omega _{cc}\), which is driven by the proposed auto-tuner presented in “Proposed controller” section. This modification constitutes the control objective given by

$$\begin{aligned} \lim _{t\rightarrow \infty } i_x(t) = i_x^*(t),~x=d,q,~\forall t \ge 0, \end{aligned}$$
(7)

exponentially (named the performance recovery) to assign variable bandwidth to the resultant feedback system. The controller including the update logic for \(\hat{\omega }_{cc}(t)\) is designed in “Proposed controller” and “Feedback system analysis results” sections presents the closed-loop system analysis results.

Proposed controller

Open-loop system derivation

Using the notations of (A1) in “Current and speed dynamics of PMSMs” section, the system of (1) and (2) gives an equivalent form given by

$$\begin{aligned} L_{d,0} \dot{i}_d(t)= & -R_{s,0} i_d (t) + L_{q,0} \omega _r (t) i_q(t) + u_d (t) + d_d(t), \end{aligned}$$
(8)
$$\begin{aligned} L_{q,0} \dot{i}_q(t)= & -R_{s,0} i_q (t) - L_{d,0} \omega _r (t) i_d (t) - \lambda _{PM,0}\omega _r (t) + u_d (t) + d_q(t), \end{aligned}$$
(9)

with unknown lumped disturbance defined as

$$\begin{aligned} d_d(t):= & -\Delta R_s i_d(t) + \Delta L_q \omega _r(t)i_q(t) - \Delta L_d \dot{i}_d, \\ d_q(t):= & -\Delta R_s i_q(t) - \Delta L_d \omega _r(t)i_d(t) - \Delta \lambda _{PM}\omega _r(t) - \Delta L_q \dot{i}_q, \end{aligned}$$

which results in the open-loop system for \({\textbf {u}}_{dq}(t) \mapsto {\textbf {i}}_{dq}(t)\):

$$\begin{aligned} {\textbf {L}}_{dq,0}\dot{{\textbf {i}}}_{dq}(t) = -R_{s,0} {\textbf {i}}_{dq}(t) + {\textbf {q}}_0(\omega _r(t),{\textbf {i}}_{dq}(t)) + {\textbf {u}}_{dq}(t) + {\textbf {d}}(t), \end{aligned}$$
(10)

where \({\textbf {L}}_{dq,0}:= \left[ \begin{array}{cc} L_{d,0} & 0 \\ 0 & L_{q,0} \end{array}\right]\), \({\textbf {i}}_{dq}(t):= \left[ \begin{array}{cc} i_d(t) \\ i_q(t) \end{array}\right]\), \({\textbf {u}}_{dq}:= \left[ \begin{array}{cc} u_d(t) \\ u_q(t) \end{array}\right]\), \({\textbf {q}}_0 (\omega _r(t),{\textbf {i}}_{dq}(t)):= \left[ \begin{array}{cc} L_{q,0}i_q(t) \\ -(L_{d,0}i_d(t) + \lambda _{PM}) \end{array}\right] \omega _r(t)\), \({\textbf {d}}(t):= \left[ \begin{array}{cc} d_d(t) \\ d_q(t) \end{array}\right]\), and \(\Vert \dot{{\textbf {d}}}(t)\Vert \le \bar{d}\), \(\forall t \ge 0\).

Implementation of proposed controller

This subsection defines the error \(\tilde{{\textbf {i}}}_{dq}(t):= {\textbf {i}}_{dq,ref}(t) - {\textbf {i}}_{dq}(t)\) for given reference \({\textbf {i}}_{dq,ref}(t):= \left[ \begin{array}{cc} i_{d,ref}(t) \\ i_{q,ref}(t) \end{array}\right]\), which constructs the proposed current controller to stabilize the open-loop system (10) by the rule given by

$$\begin{aligned} {\textbf {u}}_{dq}(t) = -{\textbf {L}}_{dq,0} \hat{\omega }_{cc}(t)\tilde{{\textbf {i}}}_{dq}(t) + R_{s,0} {\textbf {i}}_{dq}(t) - {\textbf {q}}_0(\omega _r(t),{\textbf {i}}_{dq}(t)) - \hat{{\textbf {d}}}(t), \end{aligned}$$
(11)

where the proposed online auto-tuner drives the time-varying feedback gain \(\hat{\omega }_{cc}(t)\) along the system given by

$$\begin{aligned} \dot{\hat{\omega }}_{cc}(t) = \gamma _{at} ( \Vert \tilde{{\textbf {i}}}_{dq}(t)\Vert ^2 + \rho _{at}\tilde{\omega }_{cc}(t) ), \end{aligned}$$
(12)

involving the design parameters \(\gamma _{at} > 0\) and \(\rho _{at} > 0\) where \(\tilde{\omega }_{cc}(t):= \hat{\omega }_{cc}(0) - \hat{\omega }_{cc}(t)\) (\(=\omega _{cc} - \hat{\omega }_{cc}(t)\)), \(\forall t \ge 0\). The disturbance estimate \(\hat{{\textbf {d}}}(t)\) is governed by the reduced-order DOB:

$$\begin{aligned} \dot{{\textbf {z}}}(t)= & -l{\textbf {z}}(t) - l^2 {\textbf {L}}_{dq,0} {\textbf {i}}_{dq}(t) + l( R_{s,0} {\textbf {i}}_{dq}(t) - {\textbf {q}}_0(\omega _r(t),{\textbf {i}}_{dq}(t)) - {\textbf {u}}(t)), \end{aligned}$$
(13)
$$\begin{aligned} \hat{{\textbf {d}}}(t)= & {\textbf {z}}(t) + l{\textbf {L}}_{dq,0} {\textbf {i}}_{dq}(t),~\forall t \ge 0, \end{aligned}$$
(14)

with the DOB gain \(l > 0\). It should be noticed that the reduced DOB of (13) and (14) is derived by referencing the design technique in Ref.20.

The substitution of (11) and (12) to (10) forms the closed-loop current error dynamics as

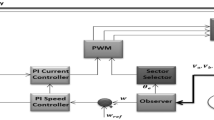
$$\begin{aligned} \dot{{\textbf {i}}}_{dq}(t) = \hat{\omega }_{cc}(t)\tilde{{\textbf {i}}}_{dq}(t) + {\textbf {L}}^{-1}_{dq} {\textbf {e}}_d(t), \end{aligned}$$
(15)

where \({\textbf {e}}_d(t):= {\textbf {d}}(t) - \hat{{\textbf {d}}}(t)\), \(\forall t \ge 0\), which is used for “Feedback system analysis results” section to prove the control objective (7) and closed-loop stability. The configuration of resultant feedback system is shown in Fig. 1.

Figure 1
figure 1

Proposed auto-tuner-based current controller structure.

Full size image

Feedback system analysis results

This section proves that the proposed solution of (11)–(14) guarantees the control objective (7) and exponential current error convergence \(\lim _{t\rightarrow \infty } {\textbf {i}}_{dq}(t) = {\textbf {i}}_{dq,ref}(t)\) through further analysis of the closed-loop dynamics (15) incorporating the subsystem dynamics of (12), (13), and (14). To this end, “Reduced-order DOB analysis results” section begins with the analysis of the reduced-order DOB of (13) and (14).

Reduced-order DOB analysis results

The reduced-order DOB of (13) and (14) does not explicitly show the disturbance estimation tendency for \(\hat{{\textbf {d}}}(t)\), which is clarified in Lemma 1.

Lemma 1

The reduced-order DOB of (13) and (14) guarantees that

$$\begin{aligned} \dot{\hat{{\textbf {d}}}}(t) = l ({\textbf {d}}(t) - \hat{{\textbf {d}}}(t)),~\forall t \ge 0. \end{aligned}$$
(16)

Proof

The time derivative of (14) adopting (13) gives

$$\begin{aligned} \dot{\hat{{\textbf {d}}}}= & \dot{{\textbf {z}}} + l{\textbf {L}}_{dq,0}\dot{{\textbf {i}}}_{dq} \\= & -l (\hat{{\textbf {d}}} - l{\textbf {L}}_{dq,0} {\textbf {i}}_{dq}) - l^2 {\textbf {L}}_{dq,0} {\textbf {i}}_{dq} + l( R_{s,0} {\textbf {i}}_{dq} - {\textbf {q}}_0 - {\textbf {u}}) + l{\textbf {L}}_{dq,0}\dot{{\textbf {i}}}_{dq} \\= & l ( {\textbf {L}}_{dq,0}\dot{{\textbf {i}}}_{dq} + R_{s,0} {\textbf {i}}_{dq} - {\textbf {q}}_0 - {\textbf {u}}_{dq} -\hat{{\textbf {d}}} ) \\= & l({\textbf {d}} - \hat{{\textbf {d}}}),~\forall t \ge 0, \end{aligned}$$

where the open-loop system (10) showing \({\textbf {d}} = {\textbf {L}}_{dq,0}\dot{{\textbf {i}}}_{dq} + R_{s,0} {\textbf {i}}_{dq} - {\textbf {q}}_0 - {\textbf {u}}_{dq}\) validates the last equation above; completes the proof. \(\square\)

Remark 1

The result (16) of Lemma 1 derives the system for \({\textbf {e}}_d = {\textbf {d}} - \hat{{\textbf {d}}}\) satisfying

$$\begin{aligned} \dot{{\textbf {e}}}_d = -l{\textbf {e}}_d + \dot{{\textbf {d}}}, \end{aligned}$$
(17)

which shows \(\dot{V}_{e_d}\) for \(V_{e_d}:= \frac{1}{2}\Vert {\textbf {e}}_d\Vert ^2\) such that

$$\begin{aligned} \dot{V}_{e_d}= & {\textbf {e}}_d (-l{\textbf {e}}_d + \dot{{\textbf {d}}}) = - \frac{l}{2}\Vert {\textbf {e}}_d\Vert ^2 + {\textbf {e}}_d \bigg ( -\frac{l}{2} {\textbf {e}}_d + \dot{{\textbf {d}}} \bigg ) \nonumber \\\le & - l V_{e_d},~\forall t \ge 0, \end{aligned}$$
(18)

for any \(l > 0\) such that \(\frac{2\bar{d}}{l}\approx 0\); used for the remaining analysis.

Online auto-tuner analysis results

The proposed online auto-tuner (12) updating the variable bandwidth \(\hat{\omega }_{cc}(t)\) has a lower bound of its initial bandwidth \(\omega _{cc}\), which helps to prove the closed-loop properties in Theorems 1 and 2. See Lemma 2 for details.

Lemma 2

The proposed online auto-tuner (12) renders the variable bandwidth \(\hat{\omega }_{cc}(t)\) to satisfy the inequality

$$\begin{aligned} \hat{\omega }_{cc}(t) \ge \omega _{cc}, \forall t \ge 0. \end{aligned}$$
(19)

Proof

The system (12) can be written as

$$\begin{aligned} \dot{\hat{\omega }}_{cc} = - \gamma _{at}\rho _{at}\hat{\omega }_{cc} + \gamma _{at}\rho _{at}\omega _{cc} + \gamma _{at}\Vert \tilde{{\textbf {i}}}_{dq}\Vert ^2, \end{aligned}$$

whose lower bound can be found by integrating both side:

$$\begin{aligned} \hat{\omega }_{cc}= & e^{-\gamma _{at}\rho _{at}t} \omega _{cc} + \int _0^t e^{-\gamma _{at}\rho _{at}(t-\tau )} (\gamma _{at}\rho _{at}\omega _{cc} + \gamma _{at} \Vert \tilde{{\textbf {i}}}_{dq}\Vert ^2 ) d\tau \\\ge & e^{-\gamma _{at}\rho _{at}t} \omega _{cc} + \gamma _{at}\rho _{at}\omega _{cc} e^{-\gamma _{at}\rho _{at} t} \int _0^t e^{\gamma _{at}\rho _{at}\tau } d\tau \\= & \omega _{cc},~\forall t \ge 0, \end{aligned}$$

which verifies the result of this lemma. \(\square\)

Control loop analysis results

This subsection ends the feedback system analysis tasks by proving the design objective (7), exponential current error convergence \(\lim _{t\rightarrow \infty } {\textbf {i}}_{dq}(t) = {\textbf {i}}_{dq,ref}(t)\), and offset-free property using the results (18) and (19) obtained from “Reduced-order DOB analysis results” and “Online auto-tuner analysis results” sections. Theorem 1 begins with the proof of the design objective (7).

Theorem 1

The proposed feedback system shown in Fig. 1 guarantees

$$\begin{aligned} \lim _{t\rightarrow \infty } {\textbf {i}}_{dq}(t) = {\textbf {i}}_{dq}^*(t), \end{aligned}$$

exponentially for \({\textbf {i}}_{dq}^*(t):= \left[ \begin{array}{cc} i_d^*(t) \\ i_q^*(t) \end{array}\right]\) satisfying

$$\begin{aligned} \dot{{\textbf {i}}}_{dq}^*(t) = \hat{\omega }_{cc}(t) ({\textbf {i}}_{dq,ref}(t) - {\textbf {i}}_{dq}^*(t)),~\forall t \ge 0,~ \end{aligned}$$
(20)

(e.g., accomplishment of the control objective (7)) for any \(\frac{2\bar{d}}{l}\approx 0\).

Proof

The deviation \(\varvec{\epsilon }:= {\textbf {i}}_{dq}^* - {\textbf {i}}_{dq}\) gives the system along (22) and (20):

$$\begin{aligned} \dot{\varvec{\epsilon }} = -\hat{\omega }_{cc}\varvec{\epsilon } - {\textbf {L}}_{dq,0}^{-1} {\textbf {e}}_d,~\forall t \ge 0, \end{aligned}$$

which makes \(V_\epsilon := \frac{1}{2}\Vert \varvec{\epsilon }\Vert ^2 + \kappa _{e_d}V_{e_d}\) with \(\kappa _{e_d} > 0\) to be

$$\begin{aligned} \dot{V}_\epsilon= & \varvec{\epsilon }^T(-\hat{\omega }_{cc}\varvec{\epsilon } - {\textbf {L}}_{dq,0}^{-1} {\textbf {e}}_d) + \kappa _{e_d}\dot{V}_{e_d} \nonumber \\\le & -\frac{\omega _{cc}}{2}\Vert \varvec{\epsilon }\Vert ^2 - \bigg (\kappa _{e_d}l - \frac{\Vert {\textbf {L}}_{dq,0}^{-1}\Vert ^2}{\omega _{cc}}\bigg ) V_{e_d}, \end{aligned}$$
(21)

using the results (18) and (19) and fact \({\textbf {x}}^T {\textbf {y}} \le \frac{\epsilon }{2}\Vert {\textbf {x}}\Vert ^2 + \frac{1}{2\epsilon }\Vert {\textbf {y}}\Vert ^2\), \(\forall {\textbf {x}}\), \({\textbf {y}} \in \mathbb {R}^n\), \(\forall \epsilon > 0\) (Young’s inequality). Then, the selection \(\kappa _{e_d} = \frac{1}{l}\big (\frac{\Vert {\textbf {L}}_{dq,0}^{-1}\Vert ^2}{\omega _{cc}} + 1\big )\) concludes

$$\begin{aligned} \dot{V}_\epsilon \le -\alpha _\epsilon V_\epsilon ,~\forall t \ge 0, \end{aligned}$$

where \(\alpha _e:= \min \big \{\omega _{cc}, \frac{1}{\kappa _{e_d}}\big \}~(>0)\); completing the proof. \(\square\)

Theorem 2 proves the exponential current error convergence \(\lim _{t\rightarrow \infty } {\textbf {i}}_{dq}(t) = {\textbf {i}}_{dq,ref}(t)\) using the result (18) obtained in “Reduced-order DOB analysis results” section. Before proceeding with the formal analysis, rewrite the closed-loop system (15) with the online auto-tuner (12) as

$$\begin{aligned} \dot{\tilde{{\textbf {i}}}}_{dq}(t)= & -\frac{\omega _{cc}}{2}\tilde{{\textbf {i}}}_{dq}(t) + \frac{\tilde{\omega }_{cc}(t)}{2}\tilde{{\textbf {i}}}_{dq}(t) - \frac{\hat{\omega }_{cc}(t)}{2}\tilde{{\textbf {i}}}_{dq}(t) - {\textbf {L}}_{dq,0}^{-1} {\textbf {e}}_d(t) + {\textbf {w}}(t), \end{aligned}$$
(22)
$$\begin{aligned} \dot{\tilde{\omega }}_{cc}(t)= & - \gamma _{at}( \Vert \tilde{{\textbf {i}}}_{dq}(t)\Vert ^2 + \rho _{at}\tilde{\omega }_{cc}(t) ), \end{aligned}$$
(23)

where \({\textbf {w}}(t):= \dot{{\textbf {i}}}_{dq,ref}(t)\) and \(\Vert {\textbf {w}}(t)\Vert \le \bar{w}\), \(\forall t \ge 0\), which is used for a basis to prove the result of Theorem 2

Theorem 2

The proposed feedback system shown in Fig. 1 guarantees

$$\begin{aligned} \lim _{t\rightarrow \infty } {\textbf {i}}_{dq}(t) = {\textbf {i}}_{dq,ref}(t), \end{aligned}$$
(24)

exponentially for any design parameters \(\gamma _{at} > 0\) and \(\rho _{at} > 0\) of the auto-tuner resulting in \(\frac{2\bar{w}}{\hat{\omega }_{cc}(t)}\approx 0\).

Proof

The closed-loop trajectories (22) and (23) yield \(\dot{V}\) for \(V:= \frac{1}{2}\Vert \tilde{{\textbf {i}}}_{dq}\Vert ^2 + \frac{1}{4\gamma _{at}}\tilde{\omega }_{cc}^2 + \beta _{e_d}V_{e_d}\) with \(\beta _{e_d} > 0\) as

$$\begin{aligned} \dot{V}= & \tilde{{\textbf {i}}}_{dq}^T \bigg (-\frac{\omega _{cc}}{2}\tilde{{\textbf {i}}}_{dq} + \frac{\tilde{\omega }_{cc}}{2}\tilde{{\textbf {i}}}_{dq} - \frac{\hat{\omega }_{cc}}{2}\tilde{{\textbf {i}}}_{dq} - {\textbf {L}}_{dq,0}^{-1} {\textbf {e}}_d + {\textbf {w}}\bigg ) + \frac{1}{2\gamma _{at}}\tilde{\omega }_{cc} \bigg (- \gamma _{at}( \Vert \tilde{{\textbf {i}}}_{dq}\Vert ^2 + \rho _{at}\tilde{\omega }_{cc} )\bigg ) + \beta _{e_d}\dot{V}_{e_d} \nonumber \\\le & -\frac{\omega _{cc}}{4}\Vert \tilde{{\textbf {i}}}_{dq}\Vert ^2 - \frac{\rho _{at}}{2}\tilde{\omega }_{cc}^2 - \bigg ( \beta _{e_d} l - \frac{2\Vert {\textbf {L}}_{dq,0}^{-1}\Vert ^2}{\omega _{cc}}\bigg ) V_{e_d} + \tilde{{\textbf {i}}}_{dq}^T \bigg ( -\frac{\hat{\omega }_{cc}}{2}\tilde{{\textbf {i}}}_{dq} + {\textbf {w}} \bigg ),~\forall t \ge 0, \end{aligned}$$
(25)

where the result (18) and Young’s inequality justify the inequality above. Then the selection \(\beta _{e_d} = \frac{1}{l}\bigg (\frac{2\Vert {\textbf {L}}_{dq,0}^{-1}\Vert ^2}{\omega _{cc}} + 1\bigg )\) concludes

$$\begin{aligned} \dot{V} \le - \alpha V,~\forall t \ge 0, \end{aligned}$$
(26)

where \(\alpha := \min \big \{\frac{\omega _{cc}}{2}, 2\rho _{at}\gamma _{at}, \frac{1}{\beta _{e_d}}\big \} >0\) subject to the variable bandwidth \(\hat{\omega }_{cc}\) (\(\ge \omega _{cc}\), \(\forall t \ge 0\), by Lemma 2) satisfying \(\frac{2\bar{w}}{\hat{\omega }_{cc}}\approx 0\); completing the proof. \(\square\)

The closed-loop system could suffer from a steady-state error because the proposed controller includes the proportional component of current tracking error. However, the reduced-order DOB of (13) and (14) contributes the steady-state error rejection property to the closed-loop system without current tracking error integrators, which is investigated in Theorem 3.

Theorem 3

The proposed feedback system shown in Fig. 1 guarantees

$$\begin{aligned} {\textbf {i}}_{dq}(\infty ) = {\textbf {i}}_{dq,ref}(\infty ), \end{aligned}$$
(27)

for any steady-state, where \(\lim _{t\rightarrow \infty } {\textbf {i}}_{dq}(t) = {\textbf {i}}_{dq}(\infty )\) and \(\lim _{t\rightarrow \infty } {\textbf {i}}_{dq,ref}(t) = {\textbf {i}}_{dq,ref}(\infty )\).

Proof

The closed-loop system of (22) and (17) results in the static relationships such that

$$\begin{aligned} {\textbf {0}}= & - \hat{\omega }_{cc}(\infty ) \tilde{{\textbf {i}}}_{dq}(\infty ) - {\textbf {L}}^{-1}_{dq} {\textbf {e}}_d(\infty ), \end{aligned}$$
(28)
$$\begin{aligned} {\textbf {0}}= & {\textbf {e}}_d(\infty ), \end{aligned}$$
(29)

which completes the proof since the combination of (29) and (28) implies \(\tilde{{\textbf {i}}}_{dq}(\infty ) = {\textbf {0}}\). \(\square\)

Experimental results

This section provides the experimental data to convince the practical merits of the proposed controller and adopts the FL controller for comparison study. The Texas Instruments (TI) DSP28335 implemented the control algorithms under pulse-width modulation (PWM) periods 0.1 ms synchronized to the analog-to-digital conversion and control interrupts. The TI DRV8302-HC-C2-KIT was used as the three-phase inverter with the DC voltage level \(V_{dc} = 15\) V. Figure 2 depicts the hardware setup. A 700 W prototype PMSM was used for this experiment where the rated current and speed are 30 A and 3000 rpm, respectively. The PMSM parameters are given by \(R_s = 0.0315~\Omega\), \(L_d = 0.126\) mH, \(L_q = 0.34\) mH, \(\lambda _{PM} = 0.0109\) Wb, \(P = 3\), \(J = 0.000341\) kg\(\cdot\)m2, \(B = 0.001\) Nm/rad/s. It was assumed that the nominal PMSM parameters were given to be not equal to their true values to taking the model-plant mismatches into account, whose values were selected as \(R_{s,0} = 0.7R_s\), \(L_{d,0} = 0.8L_d\), \(L_{q,0} = 0.5L_q\), \(\lambda _{PM,0} = 0.7\lambda _{PM}\).

Figure 2
figure 2

Hardware setup.

Full size image

For the proposed controller, the bandwidth update algorithm (12) was set to be initiated from its initial bandwidth \(f_{cc} = 30\) Hz for \(\omega _{cc} = 2\pi f_{cc} = 188.49\) rad/s. The rest of design parameters were chosen as \(\gamma _{at} = 10\times 10^3\), \(\rho _{at} = 50/\gamma _{at}\), and \(l = 1885\). The FL controller (presented in Ref.9) given by

$$\begin{aligned} u_d(t)= & L_{d,0} \omega _{cc} \tilde{i}_d(t) + R_{s,0}\omega _{cc}\int _{0}^{t}\tilde{i}_d(\tau ) d\tau - \omega _r(t)L_{q,0} i_q(t), \end{aligned}$$
(30)
$$\begin{aligned} u_q(t)= & L_{q,0}\omega _{cc}\tilde{i}_q(t) + R_{s,0}\omega _{cc}\int _{0}^{t}\tilde{i}_q(\tau ) d\tau + \omega _r(t)\bigg ( L_{d,0} i_d (t) + \lambda _{PM,0} \bigg ),~\forall t \ge 0, \end{aligned}$$
(31)

is used for comparison with the bandwidth \(\omega _{cc}\), which is the same as the initial bandwidth of the proposed controller. Note that the FL controller results in the closed-loop transfer function \(\frac{I_x(s)}{I_{x,ref}(s)} = \frac{\omega _{cc}}{s + \omega _{cc}}\), \(x=d,q,\) \(\forall s \in \mathbb {C}\), through a pole-zero cancellation, if \(R_s = R_{s,0}\), \(L_{d} = L_{d,0}\), \(L_q = L_{q,0}\), and \(\lambda _{PM} = \lambda _{PM,0}\), i.e., there are no plant-model mismatches.

Pulse reference tracking test under constant speed load

The first experiment verified the q-frame current tracking performance for a pulse-wave reference with \(i_{d,ref} = 0\). This experiment was repeated for three speed loads of \(\omega _{rpm} = 500\), 1000, and 2000 rpm. The resulting d-q frame current responses are shown in Fig. 3, which observes that the proposed technique considerably enhances the robustness of the feedback system by effectively attenuating the performance degradation from model-plant mismatches and operating mode changes due to the improved feedback system structure including the online auto-tuner and DOBs. Figure 4 presents the corresponding DOB and bandwidth responses.

Figure 3
figure 3

d-q frame current tracking performance comparisons for pulse-wave reference under three speed loads \(\omega _{rpm} = 500\), 1000, and 1500 rpm.

Full size image
Figure 4
figure 4

DOB and bandwidth responses for pulse-wave reference tracking test under speed load \(\omega _{rpm} = 2000\) rpm.

Full size image

Sinusoidal reference tracking test under sinusoidal speed load

This subsection demonstrates the improvement of frequency response characteristics by the proposed technique under the same setting as the first experiment. To this end, the speed load was set to in a biased sinusoidal form as \(\omega _{rpm} = 1200 + 70 \sin (2\pi 10 t)\), \(\forall t \ge 0\), and three kinds of references were applied to the feedback system such that \(i_{q,ref}(t) = 15 + 10 \sin (2\pi f t)\) A, \(f=20,~40,~60\) Hz. The upper side of Fig. 5 shows the resulting closed-loop current responses, which implies that the proposed technique considerably enhances the frequency response characteristics (e.g., the reductions of magnitude distortion and phase delay) of the feedback system by boosting the bandwidth, accordingly, despite a severe operating mode change. The lower side of Fig. 5 shows the corresponding bandwidth behaviors.

Figure 5
figure 5

q-frame current tracking performance comparison result and variable bandwidth behaviors under sinusoidal speed load and sinusoidal references with three kinds of bandwidths, 20, 40, 60 Hz.

Full size image

Current regulation test under sinusoidal speed load

In the third experiment, the q-frame current regulation performance was investigated for \(i_{q,ref}(t) = 20\) A under the time-varying speed load \(\omega _{rpm} = 1200 + 70 \sin (2\pi 10 t)\), \(\forall t \ge 0\). As can be seen from Fig. 6, the proposed controller makes the current oscillation smaller about three-times than the FL controller through effective cooperation by the subsystems, such as DOB and online auto-tuner, which leads to a considerable torque ripple reduction resulting in an improved ride comfort for the electrical vehicle applications.

Figure 6
figure 6

q-frame current regulation performance comparison under sinusoidal speed load.

Full size image

Numerical performance comparison result

This subsection concludes this section by presenting the numerical comparison result for the closed-loop performances demonstrated in “Pulse reference tracking test under constant speed load” to “Current regulation test under sinusoidal speed load” sections using the metric function defined as \(f_{RMS}:= \sqrt{\int _0^\infty |i_{q,ref}(t) - i_q(t)|^2 + |i_{d,ref}(t) - i_d(t)|^2 dt}\). Here, additional comparison result was included in this numerical performance evaluation using the PI controller tuned for the bandwidth \(f_{cc} = 30\) Hz (\(\omega _{cc} = 2\pi 30\) rad/s) under the constant speed load \(\omega _{rpm} = 500\) rpm. Figure 7 tabulates the numerical performance comparison result showing a 39% performance improvement by the proposed technique. From this experimental evidence, the useful properties proven in “Feedback system analysis results” section were experimentally confirmed, and the proposed technique could be qualified as a promising solution for actual industrial systems, such as home appliances, electric vehicles, and so on.

Figure 7
figure 7

Numerical performance comparison result.

Full size image

Conclusions

A robust current control technique was suggested for PMSMs, which includes the online auto-tuner and DOBs with closed-loop analysis. The beneficial closed-loop properties obtained by the auto-tuner and DOBs were proven theoretically and experimentally verified by convincing experimental data. Especially, the proposed auto-tuner played a crucial role in improving the current tracking performance and frequency response characteristics in the experimental study by increasing and restoring the closed-loop bandwidth accordingly. In future work, a combination of DOBs and integrators will be devised to secure improved closed-loop robustness with a closed-loop performance optimization process through the order-reduction technique.