Mathematical model of velocity and distribution law in gas lift reverse circulation well washing flow field for drilling shaft sinking

Abstract

To reveal the velocity distribution law of a gas lift reverse circulation well washing flow field in drilling shaft sinking, a velocity mathematical model of well washing flow field is established. The theoretical analytical solutions and velocity distribution laws in the drill pipe and bottom hole were provided and validated through numerical simulations and similar model tests. Furthermore, this study explores the impacts of mud circulation, wind pressure, rock debris, and mud properties on the flow field distribution, presenting the sensitivity order of the factors. This study indicated the following findings. (1) The velocity theoretical model of well washing flow field was validated through numerical simulation and similar model tests, and the relative error ranged from 4.2 to 18.5%, demonstrating the high consistency. (2) The rock debris and mud experienced slight and consistent deceleration within the drill pipe. Upon reaching the gas input end, the axial upward return of the multiphase flow resulted in a “jumping” sharp increase. (3) The mud circulation, wind pressure, and void fraction positively correlated with the multiphase fluid velocity in the drill pipe, but negatively correlated with the mud density and slag content. The axial upward velocity of the rock debris decreased with increasing particle size and density. (4) The sensitivity of each factor to the discharge speed of rock debris was summarized as follows: air content > mud circulation > wind pressure > mud density > rock debris density > rock debris particle size > slag content. These findings could offer a theoretical basis for selecting well washing parameters and enhancing drilling and washing efficiency.

Introduction

Based on China’s “double carbon” goal, the energy industry has intensified efforts to adjust its industrial structure, prioritizing clean, green, and low-carbon energy sources. However, by 2023, the coal consumption has still accounted for 55.3% of the total energy consumption, indicating that coal would remain the “ballast stone” and “stabilizer” of China’s energy^1,2,3. The objective of achieving “double carbon” emissions in China has catalyzed a shift in the mode of coal mine development. It has also promoted the development of coal resources towards high-quality, intelligent, safe, efficient, and green practices. This transition is the only pathway for ensuring the high-quality development of the coal industry in the new era^1,4,5,6.

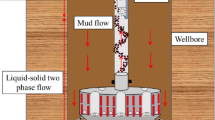
Currently, China’s coal resource development is increasingly focused on the western mining area, where most of the coal reserves are situated within Cretaceous-Jurassic water-bearing weak cemented rock formations. In new well construction, freezing methods are commonly employed to construct deep and large vertical shafts. Compared with those techniques, drilling methods offer advantages such as high mechanization, automated drilling control, and unmanned underground operations. This aligns with the development trend of the coal industry with few people, enhanced safety, environmental friendliness, and intelligence^4,5,7,8. In coal mine shaft construction using the drilling method, the upward return path of rock debris at the bottom of the well is lengthy and the mud column exerts significant pressure. This can inhibit the achievement of substantial upward return speeds through positive circulation well washing. Consequently, gas lift reverse circulation well washing is commonly employed in coal mine shaft drilling. This method involves injecting compressed air into the drill pipe to mix it with mud, creating a low-density mixed fluid. Mud, along with rock debris, is then discharged from the bottom of the well owing to the pressure differential between the internal and external mud columns^9,10,11. In engineering, challenges such as difficult rock debris discharge and low well washing efficiency frequently arise, directly affecting the drilling effectiveness. Therefore, understanding the velocity distribution pattern of the well washing flow fields is crucial for enhancing washing effectiveness.

In recent years, both domestic and international scholars have investigated the velocity distribution patterns of well-washed flow fields, yielding significant findings. Jiao et al.,¹² investigated the distribution of air washing flow fields from shaft boring machines using fluid simulation software. Their analysis included the radial, tangential, and vertical velocity components of air within slag discharge pipes, as well as the vortex distributions in bottom hole flow fields, leading to the optimization of well washing system parameters. Similarly, Cai et al.¹³, utilizing the underbalanced gas drilling technology, investigated the velocity distribution patterns of PDC-bit high-pressure CO₂ jet bottom-hole flow fields. Through a combination of numerical simulations and model testing, they analyzed the effects of nozzle diameter, injection distance, and injection pressure on bottom-hole flow field velocities. Fu et al.¹⁴, utilized multiphase flow simulation software to explore the migration patterns of drilling slag during positive circulation well washing of anchor holes in roadway floors. The study revealed that the drilling slag underwent a uniform deceleration motion around the center hole of the drill bit and quasi-uniform motion in the annular passage. In a separate study, Fan et al.¹⁵, examined the migration behavior of drilling slag in shale gas horizontal well drilling through numerical simulations. The analysis explored the impacts of the drilling rod speed, displacement, eccentricity, and well deviation angle on the axial migration speed of the drilling slag using a control variable approach. Additionally, Qu et al.¹⁶, established a numerical simulation model of PDC bit bottom-hole flow fields and analyzed the distribution patterns of bit speed, jet injection speed, and cross-sectional area of flow channels on the bottom-hole flow field velocity. In summary, scholars have extensively researched the velocity distribution patterns of drilling flow fields, primarily focusing on small-diameter oil and gas wells or anchor holes on roadway floors. Additionally, the predominant well washing methods employed are air washing or annular positive circulation washing. These methods typically involve gas–solid or liquid–solid two-phase flow patterns. Although numerical simulation research is predominant, there have been few theoretical breakthroughs. Therefore, a significant disparity exists between the aforementioned research and the velocity distribution patterns of well washing in large-diameter coal mines, rendering the existing findings insufficient to meet the current demands.

This study focused on φ5m advanced drilling in the Beifeng Well of the Taohutu Coal Mine. Based on the principles of energy conservation and fluid mechanics, a mathematical model was established for the velocity distribution of the well washing flow fields. The analysis included the distribution patterns of fluid velocity in the drill pipe and bottom hole and investigates the impact of mud circulation, wind pressure, rock debris, and mud properties on the velocity distribution within the well washing flow field. This study could offer a theoretical foundation for setting well washing parameters and enhancing drilling and washing efficiency.

Research background

Taohutu Coal Mine is located in Ordos City and has a designed production capacity of 8 Mt/a. The main shaft, auxiliary shaft, and center air shaft were created in this coal mine simultaneously using the freezing method, while the north wind shaft was developed using the drilling method. Taohutu North wind shaft is another vertical shaft built using the drilling method in western China, following the Kegai Coal Mine’s central air inlet and return shaft, and it has a considerable diameter and depth. The north wind well in Taohutu has a net diameter of 6.5 m and an excavation depth of 751 m. The ZMD120/1200 vertical shaft drilling rig (see Fig. 1) is used to carry out the drilling construction of "one drill and one expansion," which is embodied in the advanced drilling of φ5.0 m truncated cone bit and the reaming drilling of φ9.4 m. The well washing method uses the gas lift reverse circulation slurry suspension slag removal process.

Fig. 1

ZMD120/1200 shaft drilling rig and other drilling equipment.

Mathematical model of velocity for well washing flow field

Velocity model of multiphase fluid in drill pipe

Basic assumptions

The well washing process involved the cleaning of bottom-hole rock debris and the transportation of the multiphase fluid inside the drill pipe. To uncover the velocity distribution pattern of the multiphase fluid in this flow field, it could be imperative to establish a mathematical model for the fluid velocity inside the drill pipe and at the bottom of the well. Prior to this, several assumptions were made.

• (1) There could be no interaction between the phases, and each phase could be uniformly distributed within the drill pipe.

• (2) All phases could be considered incompressible fluids, and the expansibility of the gas phase could be disregarded.

• (3) The well-washing model could function as an insulation system, maintaining no heat exchange with the external environment.

Velocity model of fluid in liquid–solid section

According to the principles and fundamental assumptions of gas lift reverse circulation well cleaning, the velocity model for the multiphase fluid in the liquid–solid section of the drill pipe was established, as depicted in Fig. 2. In this model, the drill pipe inlet served as the reference point. Within the liquid–solid section, two-stage elementary flows $v_{i} {\text{d}}_{t}$ and $v_{j} {\text{d}}_{t}$ were considered, with respective lengths and cross-sectional areas ${\text{d}}A_{1}$. The average velocities of these elementary flows were $v_{i}$ and $v_{j}$. The velocity, density, and volume fraction of each phase in the elementary flow are shown in Fig. 2.

Fig. 2

Mathematical model of multiphase fluid velocity in liquid–solid section of drill pipe.

The energy conservation principle applied to the initial element flow as the drill pipe liquid–solid section moved. Hence, the energy conservation equation for the two-element flow is as follows:

$$E_{Po} + E_{Ko} + E_{po} = E_{P1} + E_{K1} + E_{p1} + \Delta h_{L}$$

(1)

where $E_{Po}$, $E_{P1}$ are gravity potential energy at the entrance of drill pipe and two-phase flow; $E_{Ko}$,$E_{K1}$ are the kinetic energy of two element flow; $E_{po}$,$E_{p1}$ are static pressure energy of two element flow; $\Delta h_{L}$ is the along-the-way loss.

The gravitational potential energy of the element flow starts at zero at the drill pipe inlet and can be expressed as it moves through the liquid–solid section:

$$E_{P1} = Z_{i} \int_{{A_{1} }} {\gamma_{j} } v_{j} {\text{d}}A_{1} {\text{d}}t$$

(2)

Among them, the average velocities $v_{i}$ and $v_{j}$ of two-dimensional flow in the liquid–solid section can be expressed as:

$$\left\{ \begin{gathered} v_{i} = v_{l} \alpha_{l} + v_{s} \alpha_{s} \hfill \\ v_{j} = v_{l1} \alpha_{l} + v_{s1} \alpha_{s} \hfill \\ \end{gathered} \right.$$

(3)

where $v_{l}$ and $v_{l1}$ are the real velocity of mud in the binary flow; $v_{s}$ and $v_{s1}$ are the real velocity of rock debris;$\alpha_{l}$ and $\alpha_{s}$ are the liquid content and slag content of the binary flow respectively.

Among them,

$$\alpha_{l} + \alpha_{s} = 1$$

(4)

The average gravity of the binary flow can be expressed as follows:

$$\gamma_{i} = \gamma_{j} = (\alpha_{l} \rho_{l} + \alpha_{s} \rho_{s} )g$$

(5)

where $\rho_{s}$ and $\rho_{l}$ are the densities of rock debris and mud respectively.

The continuity equation of the mud flow at the slurry return tank and the binary flow of the drill pipe and the initial velocity of mud in the binary flow of the drill pipe are then determined, given a constant circulating amount of mud:

$$v_{l} = \frac{{v_{c} A_{2} }}{{A_{1} }}$$

(6)

where $v_{c}$ is the velocity of slurry in the slurry return tank; and $A_{2}$ is the area of mud flow in the slurry return tank.

The velocity of the rock debris relied on two factors, including the velocity of the mud and the free settling velocity of the rock debris in the mud¹⁷. Therefore, the migration speed of rock debris in the drill pipe can be expressed as¹⁸:

$$\left\{ \begin{gathered} v_{s} = v_{l} - u_{s} \hfill \\ v_{s1} = v_{l1} - u_{s} \hfill \\ \end{gathered} \right.$$

(7)

The free settling velocity of rock debris in mud can be expressed as¹⁸:

$$u_{s} = K(1 - \delta^{2} )\sqrt {\frac{{d_{s} (\rho_{s} - \rho_{l} )}}{{\rho_{sl} }}}$$

(8)

where $K$ is the shape coefficient of rock debris, and when the rock debris is spherical particles, the value is 4 ~ 4.5; $\delta$ is the relative size of rock particles and the diameter of drill pipe, which can be expressed as $\delta = d_{s} /d$, $d_{s}$ is the size of rock debris, $d$ is the diameter of drill pipe; $\rho_{sl}$ is the mixed density of liquid and solid phases.

The kinetic energy of two elementary flows can be expressed as:

$$\left\{ \begin{array}{l}{E_{Ko}} = \frac{{v_i^2}}{{2g}}\int_{{A_1}} {{\gamma _i}} {v_i}{\text{d}}{A_1}{\text{d}}t\\{E_{{K_1}}} = \frac{{v_j^2}}{{2g}}\int_{{A_1}} {{\gamma _j}} {v_j}{\text{d}}{A_1}{\text{d}}t\end{array} \right.$$

(9)

The static pressure energy of two elementary flows can be expressed as:

$$\left\{ \begin{array}{l}{E_{po}} = \int_{{A_1}} {{\gamma _i}} {H_t}{v_i}{\text{d}}{A_1}{\text{d}}t\\{E_{p1}} = \int_{{A_1}} {{\gamma _j}} {H_i}{v_j}{\text{d}}{A_1}{\text{d}}t\end{array} \right.$$

(10)

where $H_{t}$ and $H_{i}$ are the buried depth of two-dimensional flow respectively.

The energy loss of yuan flow in the liquid–solid section can be expressed as:

$$\Delta h_{L} = \int_{Q} {h_{f} \gamma_{l} } {\text{d}}Q{\text{d}}t$$

(11)

where, $h_{f}$ is the energy loss of mud; $\gamma_{l}$ is the severity of mud; $Q$ is the circulating amount of mud.

Among them,

$$h_{f} = \lambda \frac{{Z_{i} v_{l}^{2} }}{2gd}$$

(12)

where $\lambda$ is the resistance coefficient along the way; $Z_{i}$ is the length of pipeline channel.

The resistance coefficient along the path was determined according to the Nicholas experiment¹⁹. When the mud in the drill pipe flows upward, its Reynolds number can be expressed as:

$${\text{Re}} = \frac{{\rho_{l} v_{l} d}}{\mu }$$

(13)

where $\mu$ is the viscosity of mud, Pa·s.

The mud flow in the drill pipe was in a turbulent smooth region²⁰. Its resistance coefficient along the way can be expressed by the Blasius²¹ formula as follows:

$$\lambda = \frac{0.3164}{{\sqrt[4]{{\text{Re}}}}}$$

(14)

By substituting Eqs. (2) ~ (14) into Eq. (1), the mathematical expression of the velocity of multiphase fluid in the liquid–solid section of the drill pipe can be obtained through simplification as follows:

$$\begin{aligned} & \frac{{A_{1} }}{2}\left[ {(v_{l} - \alpha_{s} u_{s} )^{3} - (v_{l1} - \alpha_{s} u_{s} )^{3} } \right] + A_{1} g\left[ {H_{t} (v_{l} - \alpha_{s} u_{s} ) - H_{i} (v_{l1} - \alpha_{s} u_{s} )} \right] \\ & \quad = Z_{i} A_{1} g(v_{l1} - \alpha_{s} u_{s} ) + \lambda \frac{{Z_{i} (v_{l1} - \alpha_{s} u_{s} )^{2} Q}}{2d} \\ \end{aligned}$$

(15)

Velocity model of fluid in liquid–solid-gas section

Based on the velocity model in "Velocity model of fluid in liquid–solid section", we extended this to establish the velocity model for the multiphase fluid in the liquid–solid–gas section of the drill pipe, as depicted in Fig. 3. The velocity, density, and volume fraction of each phase in the binary flow are shown in Fig. 3. When $Z_{i} = L_{1}$, the meta-flow marked the transition from the end of the liquid–solid section to the beginning of the liquid–solid–gas section, reaching a critical velocity $v_{jt}$ as it exited the liquid–solid section.

Fig. 3

Mathematical model of multiphase fluid velocity in liquid–solid–gas section of drill pipe.

The energy conservation equation for the two-element flow in the three-phase flow section of the drill pipe can be derived as follows:

$$E_{Pt} + E_{Kt} + E_{pt} + W = E_{P2} + E_{K2} + E_{p2} + h_{L1}$$

(16)

where $E_{Pt}$, $E_{Kt}$, $E_{pt}$ and $W$ are gravity potential energy, kinetic energy, static pressure energy and input energy of critical element flow respectively; $E_{{P_{2} }}$, $E_{K2}$, $E_{p2}$ and $\Delta h_{L1}$ are respectively the gravitational potential energy, kinetic energy, static pressure energy and loss along the way of any one-dimensional flow in the three-phase flow section.

The wind pressure at the outlet of the air duct serves as the input energy for accelerating the three-phase flow and can be expressed as follows:

$$W = \int_{{A_{o} }} {pv} {\text{d}}A_{o} {\text{d}}t$$

(17)

To determine the velocity of the air flow discharged from the air duct, we established Bernoulli equations for both the air outlet of the surface air pump and the air outlet of the air duct:

$$\frac{{p_{o} }}{{\rho_{o} g}} + H_{t} = \frac{p}{{\rho_{g} g}} + L_{1} + \frac{{\alpha_{1} v^{2} }}{2g} + a\frac{{\alpha_{1} v^{2} }}{2g}$$

(18)

where, $p_{o}$ and $p$ are the output wind pressures of air pump and air duct respectively, $\rho_{o}$ and $\rho_{g}$ are the densities of the two gases respectively, $\alpha_{1}$ is the kinetic energy correction coefficient, generally 1²⁰ can be taken, and $a$ is the proportional coefficient.

When the gas velocity in the air duct is below 0.3 Ma, the gas can be treated as an incompressible fluid¹². Therefore, $\rho_{o} = \rho_{g}$, and the gas output velocity from the air duct can be derived by simplifying Eq. (18):

$$v = \sqrt {\frac{{2(\Delta p + \rho_{g} gL_{2} )}}{{(a + 1)\rho_{g} }}}$$

(19)

where $\Delta p$ is the pressure loss from the air pump to the outlet of the air duct, and $L_{2}$ is the length of the air duct.

The gravitational potential energy of the two-dimensional flow in the three-phase flow section can be expressed as follows:

$$\left\{ \begin{gathered} E_{Pt} = L_{1} \int_{{A_{1} }} {\gamma_{j} } v_{jt} {\text{d}}A_{1} {\text{d}}t \hfill \\ E_{P2} = Z_{k} \int_{{A_{1} }} {\gamma_{k} } v_{k} {\text{d}}A_{1} {\text{d}}t \hfill \\ \end{gathered} \right.$$

(20)

The kinetic energy of the two-dimensional flow in the liquid–solid-gas section can be expressed as follows:

$$\left\{ \begin{gathered} E_{Kt} = \frac{{v_{jt}^{2} }}{2g}\int_{{A_{1} }} {\gamma_{j} } v_{jt} {\text{d}}A_{1} {\text{d}}t \hfill \\ E_{K2} = \frac{{v_{k}^{2} }}{2g}\int_{{A_{1} }} {\gamma_{k} } v_{k} {\text{d}}A_{1} {\text{d}}t \hfill \\ \end{gathered} \right.$$

(21)

The static pressure energy of two-dimensional flow in the liquid–solid-gas section can be expressed as:

$$\left\{ \begin{array}{l}{E_{pt}} = \int_{{A_1}} {{\gamma _j}} {H_j}{v_{jt}}{\text{d}}{A_1}{\text{d}}t\\{E_{p2}} = \int_{{A_1}} {{\gamma _k}} {H_k}{v_k}{\text{d}}{A_1}{\text{d}}t\end{array} \right.$$

(22)

where, $H_{j}$ and $H_{k}$ are the buried depth of two-dimensional flow in liquid–solid–gas section respectively.

The average flow velocity $v_{k}$ and critical flow velocity $v_{jt}$ of the liquid–solid–gas section can be expressed as:

$$\left\{ \begin{gathered} v_{k} = v_{l2} \alpha_{l2} + v_{s2} \alpha_{s2} + v_{g2} \alpha_{g2} \hfill \\ v_{jt} = v_{lt} \alpha_{l} + v_{st} \alpha_{s} \hfill \\ \end{gathered} \right.$$

(23)

where, $v_{s2}$, $v_{l2}$ and $v_{g2}$ are the real velocities of rock debris, mud, and air in the three-phase flow section respectively; $\alpha_{l2}$, $\alpha_{s2}$ and $\alpha_{g2}$ are the liquid content, slag content and air content of the liquid–solid–gas section, respectively, where $\alpha_{l2} + \alpha_{s2} + \alpha_{g2} = 1$.

The average bulk density $\gamma_{k}$ of the liquid–solid–gas section can be expressed as:

$$\gamma_{k} = (\rho_{l} \alpha_{l2} + \rho_{s} \alpha_{s2} + \rho_{g} \alpha_{g2} )g$$

(24)

The energy loss of the elementary flow can be expressed as:

$$\Delta h_{L1} = \int_{Q} {h_{f1} \gamma_{l} } {\text{d}}Q{\text{d}}t$$

(25)

By substituting Eqs. (17) ~ (25) into Eq. (16), we can derive the velocity expression of the multiphase fluid in the drill pipe as follows:

$$\begin{aligned}& {A_o}p\sqrt {\frac{{2(\Delta p + {\rho _g}g{L_2})}}{{(a + 1){\rho _g}}}} + {L_1}\left[ {(1 - {\alpha _s}){\rho _l} + {\alpha _s}{\rho _s}} \right]g({v_{lt}} - {\alpha _s}{u_s}){A_1}\\& \quad + \frac{{{A_1}{{({v_{lt}} - {\alpha _s}{u_s})}^3}}}{2}\left[ {(1 - {\alpha _s}){\rho _l} + {\alpha _s}{\rho _s}} \right]\\& \quad + \left[ {(1 - {\alpha _s}){\rho _l} + {\alpha _s}{\rho _s}} \right]g{H_j}({v_{lt}} - {\alpha _s}{u_s}){A_1}\\& \quad = {Z_k}({\rho _l}{\alpha _{l2}} + {\rho _s}{\alpha _{s2}} + {\rho _g}{\alpha _{g2}})g({v_{l2}}{\alpha _{l2}} + {v_{s2}}{\alpha _{s2}} + {v_{g2}}{\alpha _{g2}}){A_1}\\& \quad + \frac{{{A_1}{{({v_{l2}}{\alpha _{l2}} + {v_{s2}}{\alpha _{s2}} + {v_{g2}}{\alpha _{g2}})}^3}}}{2}({\rho _l}{\alpha _{l2}} + {\rho _s}{\alpha _{s2}} + {\rho _g}{\alpha _{g2}})\\& \quad + ({\rho _l}{\alpha _{l2}} + {\rho _s}{\alpha _{s2}} + {\rho _g}{\alpha _{g2}})g{H_k}({v_{l2}}{\alpha _{l2}} + {v_{s2}}{\alpha _{s2}} + {v_{g2}}{\alpha _{g2}}){A_1}\\& \quad + \lambda \frac{{{L_2}{{({v_{l2}}{\alpha _{l2}} + {v_{s2}}{\alpha _{s2}} + {v_{g2}}{\alpha _{g2}})}^2}}}{{2d}}({\rho _l}{\alpha _{l2}} + {\rho _s}{\alpha _{s2}} + {\rho _g}{\alpha _{g2}})Q\end{aligned}$$

(26)

Equation (26) is intricate and challenging to solve. To simplify the calculation, if we disregard the relative slip between the mud and air when the gas–liquid slip speed ratio is 1²², we can simplify Eq. (26) to obtain the velocity expression of the multiphase fluid in the drill pipe:

$$\begin{aligned} & \frac{{A_{o} }}{{A_{1} }}p\sqrt {\frac{{2(\Delta p + \rho_{g} gH_{j} )}}{{(a + 1)\rho_{g} }}} { + }(v_{lt} - \alpha_{s} u_{s} )\left[ {(1 - \alpha_{s} )\rho_{l} + \alpha_{s} \rho_{s} } \right]\left[ {H_{t} g + \frac{{(v_{lt} - \alpha_{s} u_{s} )^{2} }}{2}} \right] \\ & \quad = (\rho_{l} \alpha_{l2} + \rho_{s} \alpha_{s2} + \rho_{g} \alpha_{g2} )(v_{l2} - \alpha_{s2} u_{s2} ) \\ & \quad \left[ {H_{t} g + \frac{{(v_{l2} - \alpha_{s2} u_{s2} )^{2} }}{2} + \lambda \frac{{L_{2} (v_{l2} - \alpha_{s2} u_{s2} )}}{{2dA_{1} }}Q} \right] \\ \end{aligned}$$

(27)

Velocity model of bottom hole fluid

Under the rotation of the drill bit, the fluid at the bottom of the well flows tangentially $v_{t}$, and under the adsorption of the slag suction port, it flows radially $v_{r}$.These velocities combine to generate a horizontal velocity $v_{h}$ parallel to the bottom hole working face, along with an upward velocity $v_{a}$ perpendicular to the working face. The combined effects of these flows result in a circulating mudflow washing the bottom hole in a spiral flow pattern. Therefore, combined with the flow form of fluid, the velocity model of bottom-hole fluid was established²³, as depicted in Fig. 4.

$$\left\{ \begin{gathered} v_{t} = 2\pi R_{i} wK_{1} /60 \hfill \\ v_{r} = Q/(2\pi R_{i} h) \hfill \\ v_{h} = \delta \sqrt {v_{t}^{2} + v_{r}^{2} } \hfill \\ v_{a} = \alpha Q/(\pi R_{i}^{2} ) \hfill \\ \end{gathered} \right.$$

(28)

where $w$ is the rotating speed of drill bit; $R_{i}$ is bottom hole radius, m;$K_{1}$ is an empirical constant; $h$ is the bottom-hole clearance height; $\alpha$ is the vertical velocity distribution coefficient.

Fig. 4

Bottom-hole fluid velocity distribution model.

Verification of velocity model

Numerical model and test platform

To reveal the distribution pattern of the multiphase fluid velocity in the well washing flow field, we developed a numerical model employing the CFD-DEM method^18,24. This model incorporated the well washing construction technique in the drilling methods, along with the hydraulic structure of drill bit and arrangement of cutters. In addition, we independently developed a test device to simulate the well washing in drilling methods, as illustrated in Figs. 5 and 6. The numerical simulation procedure is detailed in Reference^4,5, and the development of the test platform is outlined in Reference^4,5.

Fig. 5

Numerical model of well washing.

Fig. 6

Well washing test device.

Fluid velocity verification in drill pipe

To test the correctness of the multiphase fluid velocity model within the drill pipe, we have carried out corresponding numerical simulation and model test. The high-speed cameras were employed to capture the rock debris movement within the drill pipe, and the PIV test technology^25,26 was utilized to measure the velocity of the rock debris. The multiphase fluid velocity model within the drill pipe was verified through a combination of numerical simulations and model tests. Table 1 is the selection of model parameters, and the comparative results of the mathematical model, numerical simulation, and model test are presented in Fig. 7.

Table 1 Parameter selection table.

Fig. 7

Comparative verification of multiphase fluid velocity in drill pipe. (a) Comparative verification of mud velocity. (b) Comparison and verification of rock debris velocity.

Figure 7 shows the movement of the rock debris and mud within the drill pipe, motion interval was segmented into liquid–solid and liquid–solid–gas sections. The theoretical calculations indicated the average upward velocities of mud in these sections as 4.14 m/s and 10.86 m/s, respectively, while the numerical simulation results are 4.32 m/s and 11.36 m/s. The relative errors of the average upward velocities of mud in these two sections were 4.2% and 4.4%, respectively. In liquid–solid section, theoretical, numerical, and model test results for the velocity of rock debris were 3.35 m/s, 4.11 m/s, and 3.86 m/s, respectively. In liquid–solid–gas section, the average velocities of the rock debris in the theoretical calculation, numerical simulation, and model test were 9.81 m/s, 8.46 m/s, and 10.41 m/s, respectively. The relative errors of the average velocity of rock debris in these two sections of the drill pipe were 18.5% and 16%, respectively. The relative errors compared to the model test results were 13.2% and 5.8%, respectively. The theoretical calculation results agreed well with the numerical simulation and model test results, proving the correctness of the multiphase fluid velocity model in the drill pipe.

Verification of bottom hole fluid velocity

To verify the correctness of the velocity distribution of bottom hole fluid, the standard deviation and relative standard deviation of the tangential, radial, horizontal, and axial velocities of the bottom-hole fluid were analyzed through a method involving mutual verification of theoretical calculations and numerical simulation results²⁷. The evaluation index was presented in Eq. (29), with the error analysis outcomes of the velocity in bottom-hole depicted in Fig. 8 and Table 2. As observed from Fig. 8 and Table 2, the standard deviation range of the flow velocity of bottom-hole fluid in the theoretical calculations and numerical simulations fell between 0.055 m/s and 0.53 m/s, with an average value of 0.3 m/s. The relative standard deviation ranged from 10.8 to 27.7%, with an average relative standard deviation of 18.6%. The theoretical calculation results closely aligned with the numerical simulation results, thus providing further evidence of the accuracy and reliability of the bottom-hole fluid velocity model.

$$\left\{ \begin{gathered} S = \sqrt {\frac{{\sum\limits_{i = 1}^{n} {\left( {v_{u} - v_{w} } \right)^{2} } }}{n - 1}} \hfill \\ f = \frac{S}{{v_{m} }} \hfill \\ \end{gathered} \right.$$

(29)

where $S$ is the standard deviation, $f$ is the relative standard deviation, $v_{u}$ and $v_{w}$ is the flow velocity at the bottom of the numerical calculation and theoretical calculation results, respectively; $n$ is the number of dates; $v_{m}$ is the maximum velocity.

Fig. 8

Comparison and verification of bottom hole fluid velocity. (a) Tangential velocity. (b) Radial velocity. (c) Horizontal speed. (d) Axial velocity.

Table 2 Velocity error analysis of bottom hole fluid.

Factor analysis of well flushing flow field

Analysis of influencing factors of fluid velocity in drill pipe

• (1) Mud circulation

The remaining model parameters in Table 1 were kept constant while the mud circulation within the range of 0.8 to 1.12 m³/s was varied, and the impact of mud circulation on fluid velocity within the drill pipe was assessed.

The analysis in Fig. 9 revealed a consistent and slight deceleration of the rock debris and mud within the drill pipe. As they reached the gas injection point, the introduction of gas accelerated the multiphase fluid, significantly increasing the axial upward velocity of both rock debris and mud. For instance, at a mud circulation rate of 1.04 m³/s, the axial upward speeds of rock debris and mud surged by 162.3% and 192.8%, respectively. This was attributed to the significant reduction in the density and pressure of the multiphase fluid within the drill pipe owing to the gas injection, enabling a high-velocity return under the pressure differential between the inner and outer mud columns of the drill pipe.

Fig. 9

Effect of mud circulation on mixed fluid velocity in drill pipe.

Increasing the mud circulation could significantly enhance the upward velocity of rock debris and mud within the drill pipe. Specifically, when the mud circulation increased from 0.8 m³/s to 1.12m³/s, there could be a notable rise in the average upward velocity of rock debris and mud in both the liquid–solid and liquid–solid–gas sections. This increases were 39.8% and 52.9% for the former and 14% and 15.6% for the latter. This could be attributed to the enhancement of both the radial and axial velocities of the circulating mudflow at the bottom hole. Moreover, this augmented circulation intensified the scouring effect on the broken rock debris and enhanced the adsorption capacity of the slag suction port. Furthermore, the increased mud circulation notably increased the axial velocity of the mud within the drill pipe, thereby augmenting the momentum exchange between the rock debris and mud particles. This exchange resulted in a greater drag force that facilitated the axial migration of the rock debris¹⁵, thus accelerating the axial migration of both the rock debris and mud.

• (2) Wind pressure

Keep the other model parameters in Table 1 unchanged and change the wind pressure to 0.3 ~ 0.7 Mpa respectively, and analyze the influence of wind pressure on the fluid velocity in the drill pipe.

Based on the findings depicted in Fig. 10, a positive correlation was observed between the wind pressure and the axial upward velocity of rock debris and mud within the liquid–solid–gas section of the drill pipe. As the wind pressure increased from 0.33 to 0.7 Mpa, the average axial upward velocity of rock debris and mud in the liquid–solid–gas section of the drill pipe increased by 34.6% and 38.7%, respectively. This escalation was attributed to the increased output pressure of the air pipe within the drill pipe resulting from the heightened air compressor output. This in turn augmented the input energy of the well washing system. Consequently, the gas overcame the gravitational potential energy of the multiphase fluid in the drill pipe and the pressure-holding effect of the mud column with greater kinetic energy. The gas then converted its kinetic energy into static pressure energy, gravitational potential energy, and the kinetic energy of the multiphase fluid. This process facilitated a higher flow rate, allowing rock debris and mud within the drill pipe to flow back more effectively. Conversely, a higher wind pressure could increase the air content within the drill pipe to a certain degree. Furthermore, the mixing density and pressure of the multiphase fluid decreased, enabling the discharge of the multiphase fluid to the ground at an increased flow rate. This was facilitated by the substantial pressure difference exerted by the mud column outside the drill pipe. Therefore, increasing the wind pressure facilitated a higher upward flow rate of rock debris and mud within the liquid–solid section of the drill pipe.

• (3) Particle size and density of rock debris

Fig. 10

Influence of wind pressure on fluid velocity in liquid–solid–gas section of drill pipe.

Keep other model parameters in Table 1 unchanged, change the particle size of rock debris to 0.01 ~ 0.05 m and the density of rock debris to 2100 kg/m³ ~ 2500 kg/m³ respectively, and analyze the influence of the physical properties of rock debris on its axial upward velocity.

Upon examination of Figs. 11 and 12, the axial upward velocity of the rock debris within the drill pipe decreased as both the particle size and density increased. As the particle size of rock debris increased from 0.01 to 0.05 m, the axial upward velocity decreased by 17.6% in the liquid solid section and by 7.8% in the liquid solid gas section. When the density of the rock debris increased from 2100 to 2500 kg/m³, the axial upward velocity decreased by 4% in the liquid–solid section and by 2.5% in the liquid–solid gas section. This was because larger particle sizes and higher densities of rock debris corresponded to greater gravity, flow resistance, and free settling velocity. The transportation of such large and high-density rock debris particles required a higher mud flow rate. Additionally, the large and high-density rock debris particles exerted significant critical rolling torque at the bottom of the well. The failure to sufficiently counteract this torque with the scouring effect of the circulating mud flow and the adsorption force of the slag suction port led to cutting accumulation at the bottom of the well. Therefore, the large and high-density rock debris particles impede effective washing. It could be crucial to carefully select the hydraulic structure of the drill bit and arrange the tools to ensure thorough rock fragmentation²⁸.

• (4) Mud density

Fig. 11

Effect of particle size of rock debris on velocity of rock debris in drill pipe.

Fig. 12

Influence of rock debris density on rock debris velocity in drill pipe.

Keep the other model parameters in Table 1 unchanged, and change the mud density to 1050 ~ 1250 kg/m³ respectively, and analyze the influence of mud density on the axial upward velocity of fluid in the drill pipe.

The analysis in Fig. 13 revealed a significant impact of mud density on the axial upward velocity of rock debris and mud within the liquid–solid–gas section, indicating a negative correlation between these velocities and mud density. Specifically, as the density of mud increased from 1050 to 1250 kg/m³, the axial velocities of rock debris and mud within the liquid–solid–gas section decreased by 5.2% and 3.9%, respectively. Although enhancing the mud density could elevate the buoyancy of rock debris to a certain degree, it also substantially increased the resistance along the flow path. In addition, the high-density mud required a greater starting wind pressure and mud circulation to achieve higher flow rates, resulting in increased energy consumption. Conversely, the high-density mud elevated the mixing density of the multiphase fluid within the drill pipe, which could inhibit the formation of a low-pressure environment and hindering the attainment of high flow velocities of rock debris and mud. Therefore, the low-density mud should be selected to ensure the pressure balance of the well wall, wall protection effect of the well wall, and suspension ability of the well wall to improve the flow velocity of rock debris and mud.

• (5) Slag content and air content

Fig. 13

Effect of mud density on mixed fluid velocity in drill pipe.

Keep the other model parameters in Table 1 unchanged, change the slag content to 1–5% and the void content to 35–55% respectively, and analyze the influence of slag content and void content on the axial upward velocity of multiphase fluid in liquid–solid–gas section of drill pipe.

Through the analysis of Figs. 14 and 15, both the slag content and void fraction exerted the significant effects on the axial upward velocity of the multiphase fluid within the liquid–solid–gas segment of the drill pipe. Specifically, the axial upward velocity of the rock debris and mud within this segment decreased with increasing slag content but increased with increasing void fraction. For instance, when the slag content increased from 1 to 5%, the axial upward velocity of the rock debris and mud in the liquid–solid-gas section decreased by 5.3% and 5.4%, respectively. Conversely, as the air content increased from 35 to 55%, the axial upward velocity of rock debris and mud in the liquid–solid–gas section increased by 28.6% and 29.8%, respectively. This phenomenon arose from the relatively high density of the rock debris. An increased slag content elevated the mixing density of the multiphase fluid within the liquid–solid–gas section, inhibiting the formation of a low-pressure, low-density flow state within the drill pipe. Consequently, better rheological properties of mud were required to accommodate more rock debris. Conversely, when the void fraction within the liquid–solid–gas section of the drill pipe increased, the mixing density of the multiphase fluid decreased markedly. This facilitated the formation of a substantial pressure difference force inside and outside the drill pipe, enabling the rock debris and mud to achieve a higher flow rate and facilitate return.

Fig. 14

Effect of slag content on fluid velocity in drill pipe.

Fig. 15

Effect of void fraction on fluid velocity in drill pipe.

Analysis of influencing factors of fluid velocity at bottom Hole

Keep the other model parameters in Table 1 unchanged, change the bit speed to 5 ~ 9 r/min and the mud circulation to 0.8 m³/s ~ 1.12 m³/s, and analyze the influence of bit speed and mud circulation on the Various flow velocities of bottom hole fluid.

Analysis of Fig. 16 shows that,

• (1) The tangential velocity of the bottom hole mud demonstrated a linear increase as the bottom hole radius expanded. Elevating the bit rotation speed significantly enhanced the circulation efficiency of the bottom-hole circulating mud flow. For instance, when the bit speed increased from 5 to 9 r/min, the maximum tangential velocity increased by 81.5%.

• (2) The radial velocity was only related to the mud circulation through the bottom-hole flow section and rose in tandem with increased circulation. The proximity to the slag suction port corresponded to a higher radial velocity. For instance, when mud circulation escalated from 0.8 to 1.12 m³/s, the maximum radial velocity at the slag suction port increased by 40.1%.

• (3) The horizontal flow at the bottom-hole working face resulted from a combination of tangential and radial flows. Within a radius of 0.5 m (the area encompassing the slag suction port), the predominant flow was radial, and the radial flow rate decreased as the radius of the flow field expanded. Beyond the 1 m radius of the bottom hole (the peripheral area of the drill bit), the flow primarily consisted of tangential motion, with the tangential speed augmenting with the expansion of the flow field radius. Elevating the bit speed or mud circulation enhanced both the tangential and radial synthetic horizontal velocities. Increasing the cutter head speed effectively improved the horizontal velocity of the circulating mudflow around the bit. Moreover, augmenting the mud circulation effectively improved the radial velocity of the circulating mud flow in the adsorption area of the slag suction port.

• (4) The predominant movement of the bottom-hole fluid was horizontal flow, with the vertical upward flow occurring primarily near the slag suction port, and the upward flow speed increased with the enhanced mud circulation. The horizontal flow at the bottom of the well consisted mainly of tangential motion, with radial flow being evident primarily in the vicinity of the slag suction port.

Fig. 16

Influence of various factors on bottom hole fluid velocity. (a) Influence of bit speed on tangential velocity. (b) Influence of mud circulation on radial velocity. (c) Influence of bit speed on horizontal velocity. (d) Influence of mud circulation on horizontal velocity. (e) Influence of mud circulation on axial velocity.

Factor sensitivity analysis

Factor sensitivity analysis quantifies the impact of various factors on a research object^29,30. Focusing on the discharge speed of rock debris in the drill pipe, factors such as mud circulation $Q$, wind pressure $p$, rock debris particle size $d_{s}$, rock debris density $\rho_{s}$, mud density $\rho_{l}$, slag content $\alpha_{s2}$, and air content $\alpha_{g2}$ were examined. The analysis evaluated the influence of these factors on discharge speed. The sensitivity coefficient was calculated according to Eq. (30), and the functional relationship outlined in Eq. (31) governs the relationship between the research object and influencing factors.

$$i = \delta_{y} /\delta_{x}$$

(30)

where $i$ is the factor sensitivity coefficient, $\delta_{x}$ is the rate of change of influencing factors, and $\delta_{y}$ is the rate of change of the research object.

$$v_{s2} = f(Q,p,d_{s} ,\rho_{s} ,\rho_{l} ,\alpha_{s2} ,\alpha_{g2} )$$

(31)

When examining the impact of an individual factor on the research object, it is essential to keep other factors constant while varying the specific factor within a reasonable range to assess its sensitivity. The values of the influencing factors remained consistent with those outlined in "Analysis of influencing factors of fluid velocity in drill pipe", and their initial values are listed in Table 1. The sensitivity of each parameter, as calculated from the findings in "Analysis of influencing factors of fluid velocity in drill pipe", is shown in Fig. 17.

Fig. 17

Sensitivity analysis of rock debris discharge speed factors.

Figure 17 shows the sensitivity coefficients for mud circulation, wind pressure, rock debris particle size, rock debris density, mud density, slag content, and void fraction, which were 0.434, 0.350, − 0.057, − 0.141, − 0.197, − 0.039, and 0.576, respectively. Factors such as the particle size, density, mud density, and slag content of rock debris were negatively correlated with the discharge speed of the rock debris. Conversely, the mud circulation, wind pressure, and air content were positively correlated with the discharge speed. Overall, the sensitivity of each factor to the discharge speed of rock debris was summarized as follows: air content > mud circulation > wind pressure > mud density > rock debris density > rock debris particle size > slag content.

Conclusion

• (1) Based on the principles of energy conservation and fluid mechanics, we established a mathematical model for gas-lift reverse circulation well washing. This model provided the theoretical analytical solutions for the multiphase fluid velocity distribution within the drill pipe, liquid–solid gas section, and bottom hole. Consequently, we derived the fluid velocity distribution law in the well washing flow field, which was verified through numerical simulations and similar model tests.

• (2) In the drill pipe, the rock debris and mud experienced gradual and uniform deceleration. Upon reaching the gas input end, the multiphase fluid underwent the acceleration owing to gas injection, significantly boosting the axial upward return of rock debris and mud. The bottom hole fluid migration primarily occurred as horizontal flow, with the vertical upward flow concentrated near the slag suction port, and its speed increased with the elevated mud circulation. At the bottom of the well, the horizontal flow predominantly took the form of tangential motion, with the radial flow noticeable only in proximity to the slag suction port.

• (3) Within the drill pipe flow field, mud circulation, wind pressure, and void fraction exhibited positive correlations with multiphase fluid velocity and inversely correlated with mud density and slag content. Moreover, the axial upward velocity of the rock debris decreased with increasing particle size and density. In the bottom-hole flow field, increasing the mud circulation significantly enhanced the axial and radial velocities of the mud at the slag suction port. Furthermore, increasing the bit speed effectively augmented the circulation effect of the circulating mudflow at the bottom hole.

• (4) Using the factor sensitivity analysis method, the sensitivity of each factor to the discharge speed of rock debris can be summarized as follows: air content > mud circulation > wind pressure > mud density > rock debris density > rock debris particle size > slag content.