Introduction

The spontaneous combustion of coal is a common cause of coal fires, which has been reported around the world. Coal gangue is solid waste discharged during coal mining, washing and other production processes1, accounting for 10% of coal production2. Due to the low comprehensive utilization rate of coal gangue, most of it is piled up as industrial solid waste in the open air to form coal gangue dumps3. However, these coal gangue dumps are exposed to the environment and often experience spontaneous combustion4. This not only causes significant economic losses and energy waste, but also generates toxic and harmful substances such as sulfur dioxide, carbon monoxide, and hydrogen sulfide, seriously endangering human life, health, and the ecological environment system5,6,7,8. Therefore, controlling the spontaneous combustion of coal gangue dumps is of great significance for protecting personnel safety and ecological environment.

Scholars have proposed various solutions for the prevention and control of spontaneous combustion of coal gangue dump, such as compacting the coal gangue dumps, covering the surface of the coal gangue dump with a layer of soil that isolates oxygen9,10, and injecting alkaline or colloidal fire extinguishing slurry into the spontaneous combustion area of the coal gangue dump through drilling11,12. But these methods have their limitations and cannot fundamentally destroy the thermal storage environment inside coal gangue dumps. The efficiency of compacting coal gangue dumps to suppress spontaneous combustion is very low, and the covering method cannot control internal spontaneous combustion. For large coal gangue dumps, the comprehensive difficulty of overall covering is large, and it is easy to rekindle in the later period. The yellow mud grouting material in the grouting method is easy to produce gaps, and gel fire prevention and extinguishing materials will produce irritating odor, which will deteriorate the environment. From the perspective of isolating oxygen, these methods can temporarily prevent the spontaneous combustion of coal gangue dumps, but they cannot fundamentally destroy the heat storage environment inside the coal gangue dumps. Therefore, Xu Lihua conducted a coal pile cooling test by heat pipe at the Hepingmen Coal Mine in 1991, and the test showed that the HPs had a significant cooling effect on the coal pile13. An heat pipe (HP) is an efficient heat transfer device that can transfer heat at very small axial temperature differences through the evaporation and condensation phase transformation of working fluid inside the pipe14. Due to its simple structure, strong environmental friendliness, and excellent working performance, it has been widely used in solar energy systems15, industrial waste heat recovery16 and other fields.

At present, the research and application technology of heat pipes (HPs) in the prevention and control of coal or coal gangue spontaneous combustion is constantly developing. Li Bei (2018) systematically studied the changes in cooling performance of HPs under factors such as time, distance, and different heating temperatures through indoor experiments of coal pile with HPs17. Cheng Fangming (2019) established a cooling model for coal pile with HPs and analyzed the influence of HP insertion angle on the temperature field, self-igniting zone, and highest temperature point of the coal pile18.Gao Hong (2023)explored the effect of working fluid concentration on suppressing coal spontaneous combustion through indoor experiments. The experiment showed that as the concentration of HP working fluid increased, the radius of heat transfer effect first increased and then decreased, with the optimal concentration of about 8.5–9%19. In HPs cooling experiments, most scholars conduct small-scale indoor HPs cooling performance tests without considering external environmental factors. Wang Jiao (2018) constructed a finite element model of coal pile heat pipe cooling and heat transfer, and analyzed the influence of HPs insertion depth and layout density on the cooling effect of coal pile20. But the model has not been verified by experimental data. Ai Chunming (2024), by arranging water-cooled steel pipes within coal piles and utilizing the COMSOL multiphysics coupling model for simulation analysis, found that water-cooled steel pipes can effectively delay the spontaneous combustion period of coal piles by 11 days and extend the spontaneous combustion period by 56 days, significantly enhancing the prevention and control effects of coal pile spontaneous combustion21. The distribution of heat sources on the actual site does not match. Existing research has found that the number, insertion depth and angle, and filling rate of HPs can affect the distribution of internal temperature field in coal gangue dumps. Previous research in the field of spontaneous combustion control in coal gangue dumps has largely focused on small-scale experiments or the application of single HP, lacking direct guidance for large-scale field applications. These studies often overlook how to effectively deploy multiple HPs in actual coal gangue dumps for efficient heat dissipation and rarely delve into the optimal geometric configuration, such as the equilateral triangular arrangement. Moreover, few studies have conducted a detailed analysis of the internal temperature field changes within coal gangue dumps under different HP arrangements, with most work focusing on the cooling effects of HPs and neglecting long-term efficacy and cost–benefit analysis. This results in decision-makers lacking references for economic viability and long-term stability when considering the application of HP technology, which limits the practical application and promotion of research findings.

This paper bases on the heat transfer theory model of HPs, establishes a wind driven cooling model for coal gangue dumps with HPs, analyzes the change of internal temperature of coal gangue dump under different insertion depths and insertion spacings of HPs, compares the cooling effect of insertion spacings and insertion depths of HPs on the coal gangue dump, and obtains the optimal arrangement of HPs. It is important to optimize the layout scheme of HPs and strengthen the cooling effect of spontaneous combustion coal gangue dumps, providing theoretical guidance for the selection and layout of HPs.

Testing procedures

Test background

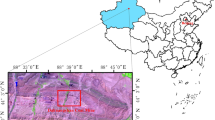
The Danaoliang Coal Mine is located in the Yangquan City of China’s Shanxi Province (Fig. 1). It is formed by direct accumulation without rolling treatment. It covers an area of 4848m2. The east and west of the Danaoliang Coal Mine are windward slopes, the south is a sharp corner of the mountain, and the north is in contact with low-temperature coal gangue that has not yet spontaneous combustion.

Fig. 1
figure 1

Schematic diagram of the research scope of coal gangue dumps.

Full size image

Layout of HPs

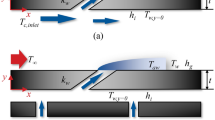
An HP consists of evaporation section, insulation section, and condensation section. Its working principle is to absorb heat in the evaporation section, evaporate the internal fluid and flow to the condensation section. The fluid releases heat into the air in the condensation section, condenses back into liquid, and flows back to the evaporation section under the action of gravity, continuously transferring the heat of the coal gangue to the atmosphere.

An HP used in this test is 7 m long with an 89 mm outer diameter and 6 mm wall thickness (Fig. 2). It has a 5 m evaporative section, 0.1 m adiabatic section, and a 1.9 m condensing section (including a 1.2 m finned part)22. The HP is made of heat-resistant and corrosion-resistant material with high thermal conductivity. Its internal working fluid is a water-based inorganic compound, operating effectively between 50 °C and 800 °C.

Fig. 2
figure 2

Layout of HPs.

Full size image

The heat pipes are arranged in parallel and staggered in an equilateral triangle (Fig. 3). In addition, in order to control the temperature of the deep and shallow layers at the same time, the long and short heat pipes are arranged alternately.

Fig. 3
figure 3

Schematic diagram of the cooling principle of the equilateral triangle HPs.

Full size image

The layout scheme of HPs is shown in Fig. 4. Two rows of HPs are arranged at a spacing of 2 m on the windward face in the west of the coal gangue dumps, and the rest are arranged at a spacing of 4 m. A total of 393 HPs were laid in the study area.

Fig. 4
figure 4

Schematic diagram of the layout of HPs and temperature monitoring points.

Full size image

Layout of monitoring points

The layout scheme of Monitoring Points is shown in Fig. 4. The temperature monitoring points are arranged at 13 temperature monitoring positions (No. T1-T13), and the measuring points are located at the center of the equilateral triangle. Two sets of temperature measuring equipment were deployed at the same monitoring point to measure the temperature at 3 m and 6 m respectively. The temperature measurement device mainly consists of K-type high temperature thermocouple sensors, wireless modules, transmitting and receiving devices, and monitoring platform, and the diagrams of each device are shown in Fig. 5. The installation process of the temperature measurement device is to lay the temperature measurement pipe at the monitoring point, insert the high temperature thermocouple into the bottom position of the pipe and fix it, and then block the pipe holes after the completion of the installation process. Through wireless LORA ultra long-distance transmission, the temperature data can be sent to the system terminal platform, which can achieve real-time monitoring and recording of temperature data.

Fig. 5
figure 5

Method of temperature measurement.

Full size image

Model mechanism

COMSOL multiphysics 6.0, a commercial software based on finite element method, is a multiphysics simulation software that simulates real physical phenomena by solving partial differential equations23. Therefore, COMSOL multiphysics 6.0, which has high flexibility and ease of use in multi physical field coupling, was selected as the simulation software for this study. In this model, the Brinkman equation represents the air percolation velocity field, the dilute matter transfer in the porous medium represents the oxygen concentration field, and the porous medium heat transfer represents the temperature field. In this model, the solver for numerical calculations is Parallel Direct Sparse Solver Interface.

Heat transfer mechanism and model of coal gangue dumps

(1) Air seepage velocity field equation.

The internal pores of coal gangue dumps are large, and the particle size is also large, resulting in strong shear force from the airflow. The Brinkman equation can reflect the kinetic energy dissipation caused by viscous shear and is applicable to rapidly moving fluids in porous media. According to the conservation of momentum, the Brinkman equation expression applicable to the fluid dynamics of porous media in coal gangue dumps is as follows (1):

$$\mu \nabla^{2} v = \frac{\mu }{k}v + \nabla P$$
(1)

where, v is the air infiltration velocity (m/s); μ is the dynamic viscosity coefficient (kg/(m·s)); k is the permeability of the porous medium (m2); P is the pressure (Pa).

Regarding the spontaneous combustion of coal gangue dumps, it is necessary to consider the thermal buoyancy caused by internal combustion, which is the reason for the “chimney effect”. The internal combustion of coal gangue causes a change in gas density, and the difference in gas density leads to further gas flow, which mainly occurs in the vertical direction. Therefore, it is necessary to introduce the Boussinesg hypothesis and supplement the Brinkman equation. The complete expression is as follows (2):

$$\mu \nabla^{2} v = \frac{\mu }{k}v + \nabla P - \rho_{g} g\left( {1 - \frac{{T_{a} }}{T}} \right)$$
(2)

where, \(\rho_{g} g\left( {1 - \frac{{T_{a} }}{T}} \right)\) is the added term, which is the Boussinesq assumption of thermal buoyancy; \(\rho_{g}\) is the density of air (kg/m3); Ta is the external environmental temperature (K); T is the temperature of the coal gangue (K).

(2) Oxygen concentration field equation.

Oxygen from the external environment continues to enter the interior of coal gangue dumps with air. When conditions are ripe, oxygen reacts chemically with coal gangue, consuming oxygen during combustion. At the same time, the supply of oxygen also provides power for combustion. Due to the large pores between unconsolidated and loosely stacked coal gangue, the mechanical dispersion of oxygen concentration in the pores can be ignored, and its permeation and molecular diffusion are the main modes of movement24. According to the law of conservation of heat and mass transfer in porous media, the equilibrium formula of the oxygen concentration transport field is as follows (3):

$$e\frac{\partial c}{{\partial t}} + v\nabla c = D\nabla^{2} c - (1 - e)r$$
(3)

where, c is the oxygen concentration (mol/m3); e is the internal porosity of the coal gangue dumps; D is the air diffusion coefficient (m2/s); r is the reaction rate (mol/(m3·s)), and as follows (4):

$$r = c^{m} A\exp ( - E/RT)$$
(4)

where, A is the pre-factor (s-1); E is the activation energy (mol/J); T is the absolute temperature of the environmen (K); R is the gas constant(J/(mol·K)); m is the reaction constant. According to Smith and Lazzara25, the range of m is generally between 0.5 and 1.0.

(3) Coal pile temperature field equation.

Without considering the thermal radiation effect on the surfaceof the coal gangue dumps, the heat exchange mode between the internal coal gangue is mainly through heat conduction and heat convection26. Based on the theory of energy conservation in porous media heat transfer, this study considers the heat trans fer equilibrium between coal gangue (solid phase) and permeated air (gas phase) as local heat equilibrium, which means that the contact temperature of the solid phase and the gas is consistent. The heat balance equation of porous media is as follows (5):

$$\left[ {(e\rho_{g} C_{g} ) + (1 - e)\rho_{s} C_{s} } \right]\frac{\partial T}{{\partial t}} = \left( {(1 - e)\lambda_{s} + e\lambda_{g} } \right)\nabla^{2} T - \left( {v\nabla } \right)\left( {\rho_{g} C_{g} T} \right) + \left( {1 - e} \right)r\Delta H$$
(5)

where, ρg, and ρs respectively represent the density of gas and solid (kg/m3); Cg and Cs are the specific heat capacities of gas and solid (J/(kg·K)); λg and λs are the thermal conductivity coefficients of gas and solid (W/(m·K)); (1-e) λs+eλg is the comprehensive equivalent thermal conductivity coefficient of solid and gas phases; (1-e)r∆H is the heat source term, which refers to the heat generated by the consumption of oxygen and the occurrence of chemical reactions during combustion; ∆H is the enthalpy change value, which refers to the amount of heat released by consuming unit mole of oxygen coal gangue under standard conditions (J/mol).

The above heat source term refers to the heat released by the oxidation reaction of carbon containing substances in coal gangue, which is a function of oxygen concentration c in the equation. The oxygen consumption term in the oxygen transport field is a function of temperature T. By combining the basic equations of three physical fields, the mutual coupling between air flow velocity v. oxygen concentration c, and temperature T is achieved, thereby constructing a mathematical model for the spontaneous combustion of coal gangue dumps. In this study, the porosity and permeability of the coal gangue dump are assumed to be homogeneous across the entire domain. This assumption simplifies the numerical model by treating the coal gangue dump as a uniform porous medium, which allows for easier computation of heat transfer and fluid flow within the dump.

Heat transfer mechanism and model of HPs

The heat pipe is assumed to extract heat uniformly along its length; the evaporation–condensation process inside the heat pipe is assumed to be very efficient, that is, the internal heat transfer resistance is not considered; the heat pipe is assumed to start working effectively immediately after contacting the heat source; the heat loss during the heat transfer process of the heat pipe is not considered, that is, the heat absorbed by the evaporation section is assumed to be equal to the heat released by the condensation section; the heat pipe is simplified to a linear cold source acting uniformly along its length, and the actual geometric shape of the heat pipe and the influence of the heat dissipation fins are ignored18.

The process of releasing heat from an HP can be considered as part of the temperature field. In this paper, the heat pipe in the evaporation section is generalized as a linear cold source of the temperature field, the material type is set as solid. The heat transferred to the outside world from the evaporating section of the heat pipe is equated to a linear cold source consistent with the heat transfer efficiency of the heat pipe, which continuously absorbs the latent heat inside the gangue mountain and transfers the heat continuously24.

In the heat transfer process, the heat transfer of an HP is related to thermal resistance. The heat transfer Q of an HP is the ratio of the temperature difference ∆T at both ends to the thermal resistance R, which is generally linearly correlated. Its expression is as follows (6):

$$Q = \frac{\Delta T}{R}$$
(6)

where, Ris the overall thermal resistance of the coal gangue—HP system, which consists of seven thermal resistances17. The R can be simplified by dividing it into three variables expressed in Eq. (7):

$$R = R_{a} + R_{b} + R_{c} = \sum\limits_{j = 1}^{7} {R_{j} }$$
(7)

The first variable, conduction heat resistance (Ra = R1) between coal gangue and external wall of the evaporator section, is given by Eq. (8):

$$R_{1} = \frac{{\ln (2r_{c} /D_{{{\text{ex}}}} )}}{{2\pi \lambda_{s} L_{{\text{e}}} }}$$
(8)

where, \(r_{c}\) is the cooling radius (m); \(D_{{{\text{ex}}}}\) is the external radius of HP (m); \(L_{{\text{e}}}\) is the evaporator tube length (m).

The second variable, thermal resistance (Rb = R2 + R3 + R4 + R5 + R6) inside the HP, is described using the following correlation.

For the HP evaporator section, the conduction heat resistance (R2) between the external wall and the internal wall is estimated using Eq. (9):

$$R_{2} = \frac{{\ln (D_{{{\text{ex}}}} /D_{in} )}}{{2\pi \lambda_{{\text{w}}} L_{{\text{e}}} }}$$
(9)

where, \(D_{in}\) is the internal radius of HP (m); \(\lambda_{{\text{w}}}\) is the thermal conductivity of HP material (W/(m·k)).

The convection heat resistance (R3) between the internal wall of the evaporator section and working medium can be expressed by Eq. (10).

$$R_{3} = \frac{1}{{\pi D_{in} L_{e} h_{e} }}$$
(10)

where, he is the evaporative heat transfer coefficient (W/(m2·°C)). hecan be calculated according to Imura’s correlation27:

$$h_{{\text{e}}} = 0.32\left( {\frac{{\rho_{1}^{0.65} \lambda_{1}^{0.3} C_{1}^{0.7} g^{0.2} q_{{\text{e}}}^{0.4} }}{{\rho_{{\text{v}}}^{0.25} h_{{{\text{fg}}}}^{0.4} \mu_{1}^{0.1} }}} \right)\left( {\frac{{p_{1} }}{{p_{2} }}} \right)^{0.3}$$
(11)

where, \(\rho_{1}\) is the density of specific liquid (kg/m3); \(\lambda_{1}\) is the liquid working medium heat transfer coefficient (W/(m·K)); \(C_{1}\) is the Specific liquid working medium heat capacity (J/(kg·°C));\(g\) is the acceleration due to gravity (m/s2); \(q_{e}\) is the heat flux in evaporator (J/(m2·s)); \(\rho_{v}\) is the steam working medium (kg/m3); \(\mu_{1}\) is the dynamic viscosity of liquid working medium (N/s·m2);\(p_{1}\) is the inside pressure of HP (Pa); \(p_{2}\) is the ambient pressure (Pa).

The steam flow resistance (R4) between the evaporator section and the condenser section can be expressed by Eq. (12):

$${\text{R}}_{4} = \left\{ {\begin{array}{*{20}c} {0, {\text{Working state}}} \\ { + \infty , {\text{Stoping work}}} \\ \end{array} } \right.$$
(12)

The convection heat resistance (R5) between the steam working medium and the internal wall of the condenser section can be expressed by Eq. (13).

$$R_{5} = \frac{1}{{\pi D_{in} L_{c} h_{c} }}$$
(13)

where, \(L_{c}\) is the convection tube length (m); he is the condensation heat transfer coefficient (W/(m2·°C)). hccan be calculated according to Nusselt’s correlation28:

$$h_{{\text{c}}} = 0.925\lambda_{1} (\frac{{(\rho_{1} - \rho_{{\text{v}}} )/\rho_{1} }}{{\nu_{1}^{0.1} /g}})^{1/3} {\text{Re}}^{{^{1} /_{3} }}$$
(14)

where, \(\nu_{1}\) is the kinematic viscosity (m2/s); \({\text{Re}}\) is the number for liquid working medium Reynolds.

For the HP condenser section, the conduction heat resistance (R6) between the external wall and the internal wall is estimated using Eq. (15):

$$R_{6} = \frac{1}{{2\pi \lambda_{w} L_{c} }}\ln \left( {\frac{{D_{ex} }}{{D_{in} }}} \right)$$
(15)

The third variable, conduction heat resistance (Rc = R7) between the air and external wall of the condenser section, is given by Eq. (16):

$$R_{7} = \frac{1}{{A_{{\text{c}}} \alpha }}$$
(16)

where, \(A_{{\text{c}}}\) is the outer surface area of the condensation section (m2); \(\alpha\) can be calculated according to reference Northwest Research Institute Co., Ltd. of C.R.E.C (2002):

$$\alpha = 2.75 + 1.51\nu_{{{\text{air}}}}^{0.2}$$
(17)

where, \(\nu_{{{\text{air}}}}\) is the air velocity (m/s).

Numerical simulation of coal gangue dump

Model setup and grid

According to the schematic layout of HPs and temperature monitoring points (Fig. 4), a simplified geometric model of the coal gangue dump with HPs is established. The HPs scheme of the model is the same as that of the field test, which was used to rate model parameters and validate the model. The model consists of two main parts, as shown in Fig. 6. The first part is the top of the coal gangue dump with HPs. The shape is a trapezoid with a right-angled in the top view. The west side of the right-angled trapezoid is the longest, and the side length is set to162m. The east direction is the short side, and the side length is set to 40 m. The side length in the north direction is 48 m. The second part is the slope of the coal gangue dump. It is a four-sided pyramid hexahedron, closely located on the west side of the coal gangue dump. In order to approach the actual slope, the inclination angle of the slope is set at 22.6°. The total height of the coal gangue dump is 10 m.

Fig. 6
figure 6

Schematic diagram of the geometric model.

Full size image

The model used the physical field to control the mesh, which was divided into tetrahedron. The grid section of coal gangue dump is shown in Fig. 7. The mesh number is 80547. The average size of the computing mesh is 2.8281m, and minimum unit mass: 0.021708.

Fig. 7
figure 7

Model mesh construction diagram.

Full size image

Model parameters, initial and boundary conditions

The initial temperature field is the temperature monitoring data of 13 monitoring points in the coal gangue dump on the first day. The initial oxygen concentration21 was 9.375 mol/m3. In the natural environment, the wind speeds naturally flows into the coal gangue body. However, due to seepage losses, the wind speeds decreases to approximately zero within the coal gangue dump. Therefore, the wind speeds for air seepage inside the coal gangue dump is set to v = 0.0001 m/s21.

Each direction of the coal gangue dump is represented by letters (Fig. 6). Taking the positive direction of the x-axis as the actual north direction. The air inlet (B5) is set as an constant flux boundary. The air outlet (B1) is set as constant pressure boundary. The inlet and outlet interface of oxygen is the same as that of air. In the temperature field, B1 is the heat flux boundary. There is no heat and oxygen exchange around the remaining boundary of the model. The main parameters of the model are obtained from the coal gangue sample test results of Danaoliang coal mine in Shanxi, as shown in Table1. The thermal property values in Table 1 are based on assumptions from previous studies and field conditions at Danaoliang Coal Mine.

Table 1 Thermal properties of coal gangue and air.
Full size table

Model validation

The validation was conducted for conditions with cooling the coal gangue dump using HPs. The variation of actual and simulated temperatures at different monitoring points at 3 m below ground (z = 3 m) and 6 m below ground (z = 6 m) are shown in Fig. 8 and Fig. 9. The relative error of the verification is the relative error of the simulation result to the measurement results. The overall trend of the actual temperature at each monitoring point is consistent with that of the simulated temperature data, and the maximum relative error is less than 20%, indicating that the model established in this study is feasible.

Fig. 8
figure 8figure 8

Analysis of temperature variation errors at different measuring points z = 3 m.

Full size image
Fig. 9
figure 9figure 9

Analysis of temperature variation errors at different measuring points z = 6 m.

Full size image

Simulation scheme

This study mainly focuses on investigating the influence of different insertion spacings and insertion depths of HPs on the cooling effect of spontaneous combustion coal gangue dump. The simulation scheme is shown in Table 2.

Table 2 Scheme of different insertion spacings and insertion depths of HPs.
Full size table

The HPs deployment method in this numerical simulation adopts the equilateral triangle uniform deployment. The plane schematic diagrams of different spacing are shown in Fig. 10.

Fig. 10
figure 10

The plane schematic diagrams of different spacing schemes.

Full size image

Results and discussion

Influence of HPs with different insertion spacings on the heat transfer behaviour of coal gangue dumps

Effect of HP insertion spacing on the temperature field of coal gangue dumps

Simulation experiments were carried out with spacing values (S) of the HPs of 3 m,4 m, 5 m, and 6m32,33. The influence of HPs spacing on the temperature distribution in each depth plane is shown in Fig. 11. The temperature field distribution of coal gangue dump at the same depth under different HPs insertion spacing is similar, but the temperature values are different.

Fig. 11
figure 11

Temperature distribution of coal gangue dump under different HPs insertion spacings.

Full size image

Overall, the temperature on the windward side of the coal gangue dump is relatively low, while the temperature on the leeward side is very high. The reasons are that the airflow passes through the top of the coal gangue dump, the pressure on the upper part of the leeward surface is greater than the pressure at the bottom. Due to the pressure difference, the airflow flows towards the bottom of the leeward surface, forming a turbulent vortex. The formation of this turbulent vortex reverses the direction of wind flow and generates backflow. Due to the low reflux speed, the convective heat transfer ability of the condensation section surface of HPs is weaker than that of the corresponding windward end. Therefore, the oxidation heat cannot be discharged in time, and the spontaneous combustion zone appears at the bottom of the leeward side.

The temperature difference in the same plane of the spontaneous combustion coal gangue dump is significant, ranging from several hundred degrees Celsius. At the same location, the temperature at a depth of 6 m is generally higher than at a depth of 3 m. The reasons are that the heat storage conditions at a depth of 6 m are better, and the combustion of coal gangue is more intense, resulting in higher temperatures.

Effect of HPs insertion spacing on the spontaneous combustion area of coal gangue dumps

According to reference 34, this study assumed that the value of 280 °C is the beginning of the spontaneous combustion zone (SCDZ) of the coal gangue dump34. Figures 12a-d illustrate the distribution of the SCDZ (T > 280℃) at various depths under different HP insertion spacings. It is observed that as the HP insertion spacing increases, the SCDZ expands both laterally and vertically, indicating that closer spacing of HPs is more effective in controlling temperature and reducing the risk area. This is due to the fact that smaller HP spacing leads to increased heat dissipation efficiency, as there are more points of heat extraction, ensuring that heat does not accumulate in any localized area and effectively reducing the overall temperature of the coal gangue dump. When S = 3 m, the SCDZ area at different depths is minimized, amounting to 7.0 and 3204.1 m2, respectively; meanwhile, the low-temperature area (T < 280℃) is maximized, reaching 4841 m2 and 1643.9 m2.

Fig. 12
figure 12

SCDZ area of coal gangue dump under different HPs insertion spacings.

Full size image

Additionally, the insertion spacing of HPs affects the shape and area of the SCDZ. This is attributed to the fact that closer spacing increases the total surface area available for heat exchange. Each HP has a certain radius of influence; therefore, a greater number of HPs means a larger covered area, which in turn reduces the temperature gradient and the size of the SCDZ.

Effect of HPs insertion spacing on the spontaneous combustion volume of coal gangue dumps

The spontaneous combustion volume (V) of coal gangue dumps varies with time under different insertion spacings of HPs, as shown in Fig. 13, and the overall trend follows a monotonic function. In the coal gangue dump, with the passage of time, the spontaneous combustion volume continues to decrease. The reasons are that under the continuous action of the HPs, internal heat is continuously released, and the spontaneous combustion volume continues to decrease. When S = 3 m, the spontaneous combustion volume is the least, and the prevention and control effect is better.

Fig. 13
figure 13

Spontaneous combustion volume variation under different insertion spacings of HPs.

Full size image

The variation of the spontaneous combustion volume difference(∆V) of coal gangue dump with the insertion spacing is shown in Fig. 14, and the overall trend shows a gradual decrease. The HPs insertion spacing is directly proportional to the spontaneous combustion volume difference. The smaller the HPs insertion spacing, the smaller spontaneous combustion volume difference. When S = 3 m, the spontaneous combustion volume difference is lower than that of 4, 5, and 6 m, respectively. The reasons are that the smaller the insertion spacing between HPs, the higher the layout density, the stronger the heat transfer ability, the more heat is released inside the coal gangue mountain, the smaller the spontaneous combustion area, and the corresponding low-temperature area expands.

Fig. 14
figure 14

Changes in spontaneous combustion volume difference under different HPs insertion spacing.

Full size image

Effect of HPs insertion spacing on the high-temperature point of coal gangue dumps

The temperature variation at the high temperature center under different HPs insertion spacing is shown in Fig. 15. The cooling process of coal gangue dump can be divided into two stages, namely the significant cooling stage and the slow cooling stage. Taking S = 3 m as an example, the period from 0 to la is a significant cooling stage. During this stage, the temperature of the coal gangue dump is higher and the external environment temperature is lower. Due to the influence of air convection heat transfer and HP heat transfer, the temperature of the high-temperature heatsource point drops sharply. The cooling rate of the coal gangue dump slows down during the slow decrease stage from 2 to 5a. The reasons are that the temperature of the coal gangue dump decreases, and the temperature difference with the outside world decreases. As the temperature of the coal gangue dump decreases, the working efficiency of the HP also decreases, leading to slow cooling.

Fig. 15
figure 15

Temperature changes at high temperature points of coal gangue dump under different HPs insertion spacing.

Full size image

As time goes on, the temperature drop caused by the decrease in HPs insertion spacing becomes increasingly significant. During different time periods after the insertion of HPs, when S = 3 m, the temperature at the high-temperature center always lower than 4, 5, and 6 m. The reasons are that the smaller the spacing between HPs, the closer the heat conduction distance between the layout center and the evaporation section of the HP, making it easier for heat to be transferred out through the HP and resulting in a greater decrease in temperature.

The temperature difference in the case of S = 3 m increases overtime. When the time gradually increases from la to 5a, the temperature reduction of S = 3 m is greater than that of other cases. The reasons are that as time goes on, due to the decrease in HPs spacing and increase in HPs density, the internal heat of the coal gangue dump is continuously and efficiently released, resulting in a greater difference in cooling effect between different spacing arrangements.

The temperature difference at the high-temperature center (∆Tmax) varies with the HPs insertion spacing, as shown in Fig. 16, and the overall trend shows a gradual decrease. The temperature decrease at the high-temperature center is inversely proportional to the HPs insertion spacing. The smaller the HPs insertion spacing, the greater the magnitude of temperature decrease.

Fig. 16
figure 16

Temperature difference at high temperature points under different HPs insertion spacings.

Full size image

Influence of HPs with different insertion depths on the heat transfer behaviour of coal gangue dumps

Effect of HP insertion depth on the temperature field of coal gangue dumps

Simulation experiments were carried out with depth values (D) of the HPs of 4,5, 6, and 7 m. The influence of HPs depth on the temperature distribution of the x–z and y–z profiles is shown in Fig. 17. The temperature field distribution of coal gangue dumps in the same section is similar at different HPs insertion depths, and the difference is manifested by different temperature values.

Fig. 17
figure 17

Temperature distribution of coal gangue dump under different HPs insertion depths.

Full size image

Overall, the temperature is low in the upper layer and high in the middle and lower layers. The reasons are that the coal gangue located in the upper layer is exposed to the environment and has significant thermal convection with the airflow. This results in a relatively slow rate of temperature rise. In the middle and lower layers of coal gangue dumps, due to low airflow velocity, there is less heat exchange between the environment and coal gangue, resulting in less heat loss and gradual accumulation of heat.

The temperature distribution within the coal gangue dump reflects how heat accumulates and dissipates, with ground temperature acting as a crucial factor for this process. In areas where the ground temperature is higher, the coal gangue dump tends to experience an overall increase in internal temperatures. This leads to a steeper temperature gradient within the pile, especially in the deeper layers, where heat from both spontaneous combustion and the environment accumulates. Consequently, the spontaneous combustion danger zone (SCDZ) expands, as the high ground temperature accelerates the coal oxidation process. In such cases, heat continues to build up over time, raising the overall fire risk. Conversely, lower ground temperatures can release internal heat more efficiently. The temperature gradient is less steep, and cooling from the environment helps reduce the heat build-up in the deeper layers of the coal gangue dump.

Effect of HPs insertion depth on the spontaneous combustion area of coal gangue dumps

Figure 18 show the distribution of the SCDZ of the x–z and y–z profiles under different HPs insertion depth. As the HPs insertion depth increases, the SCDZ at different profiles decrease sequentially. The x–z and y–z profiles show a consistent trend, which indicates that the insertion depth is an important parameter affecting the spontaneous combustion of coal gangue. In both the x–z and y–z profiles, it is observed that when D = 7 m, the area of the SCDZ is the smallest, and is sequentially lower than the cases of D = 6 m, D = 5 m, and D = 4 m.

Fig. 18
figure 18

SCDZ area of coal gangue dump under different HPs insertion depths.

Full size image

This phenomenon occurs because as the HPs insertion depth increases, the contact area between the evaporative section of the HP and the coal gangue expands. This larger surface area facilitates more effective heat absorption from the coal gangue dump. Additionally, the HPs can penetrate into regions with higher thermal gradients, enabling more efficient heat transfer from the coal gangue to the HP and subsequently to the surrounding environment. This reduces the likelihood of heat accumulation within the core of the coal gangue dump. The deeper HPs can extract heat from the deeper layer in the coal gangue dump, which not only reduces the temperature at the depth, but also prevents heat accumulation and spontaneous combustion.

Effect of HPs insertion depth on the spontaneous combustion volume of coal gangue dumps

The spontaneous combustion volume (V) of coal gangue dumps varies with time under different insertion depths of HPs, as shown in Fig. 19, and the overall trend follows a monotonic function. In the coal gangue dump, with the passage of time, the spontaneous combustion volume continues to decrease. The reason is that under the continuous action of the HPs, internal heat is continuously released, and the spontaneous combustion area continues to decrease. When D = 7 m, the spontaneous combustion volume is the least, and the prevention and control effect is good.

Fig. 19
figure 19

Spontaneous combustion volume variation under different insertion depths of HPs.

Full size image

The variation of the spontaneous combustion volume difference(∆V) of coal gangue dump with the insertion depth is shown in Fig. 20, and the overall trend is increasing. The spontaneous combustion volume difference of coal gangue dump is directly proportional to the insertion depth. This means that the greater the depth of heat pipe layout, the greater the magnitude of temperature reduction.

Fig. 20
figure 20

Changes in spontaneous combustion volume difference under different HPs insertion depth.

Full size image

Effect of HPs insertion depth on the high-temperature point of coal gangue dumps

The temperature variation at the high temperature center under different HPs insertion depths is shown in Fig. 21. The temperature decreases over time when HP is inserted at different depths, indicating that the insertion depth of the HP has a significant impact on the temperature of the high-temperature heat source point inside the coal gangue dump. The reasons are that as the insertion depth of the HP increases, the bottom of the HP is closer to the high-temperature heat source point of the coal gangue dump, and the temperature of the working fluid in the HP is greatly affected by the high-temperature heat source point. The work efficiency of the HP is higher, which promotes the extraction of deep heat and lowers the temperature.

Fig. 21
figure 21

Temperature changes at high temperature points of coal gangue dump under different HPs insertion depths.

Full size image

The temperature difference at the high-temperature center (∆Tmax) varies with the HPs insertion depth, as shown in Fig. 22, and the overall trend is increasing. The insertion depth of the HP is directly proportional to the temperature drop. This means that the deeper the HP is inserted, the greater the temperature difference at the high-temperature center. When the heat pipe is inserted at a depth of 7 m, the temperature difference at the reference point is the highest, and the cooling effect is good.

Fig. 22
figure 22

Temperature difference at high temperature points under different HPs insertion depths.

Full size image

Two factor analysis of variance

Based on single factor experiments, four levels were designed for each factor to establish an orthogonal experiment, as shown in Table 3. Taking into account the influence of insertion spacing and insertion depth on the spontaneous combustion volume. Table 3 shows that the scheme with the smallest spontaneous combustion volume is S = 3 m and D = 7 m.

Table 3 Results of orthogonal experiments.
Full size table

It is clear that the S and D directly impacts both the cost and the reduction of the spontaneous combustion volume (Fig. 23). At a smaller spacing and the greater the depth, the reduction in the spontaneous combustion volume is more substantial, which enhances the cooling effect significantly. However, this comes with higher costs due to increased number and material requirements. There is not a simple positive correlation between cost and reduction in spontaneous combustion.

Fig. 23
figure 23

The relationship between cost and spontaneous combustion volume difference.

Full size image

The optimal layout method should balance cost and cooling performance. Based on the data analysis, the configuration of S = 3 m and D = 7 m appears to be the most effective. While this option is associated with higher costs, it offers the greatest reduction in the spontaneous combustion volume and provides superior cooling efficiency. This layout is particularly advantageous in scenarios where fire risk must be minimized, as it provides the most robust suppression of spontaneous combustion.

Thus, the configuration of S = 3 m and D = 7 m represents the optimal solution, as it balances the trade-offs between cost and effective combustion control, ensuring both financial feasibility and enhanced fire prevention in coal gangue dumps.

Factor 1 (Spacing, S) and Factor 2 (Depth, D) are independent variables, and the response variable is the spontaneous combustion volume (V). The general form of the model can be expressed by Eq. (18):

$${V}_{ij}=\mu +{\alpha }_{i}+{\beta }_{j}+{\epsilon }_{ij}$$
(18)

where, \(\mu\) is the overall mean of the response (spontaneous combustion volume); \({\alpha }_{i}\) represents the effect of spacing (S) at level i; \({\beta }_{j}\) represents the effect of depth (D) at level j; \({\epsilon }_{ij}\) is the error term, assumed to be normally distributed with mean 0 and variance σ2.

For two-factor ANOVA, the null hypothesis (H0) of spacing and depth can be expressed by Eqs. (19) and (20):

$${\text{H0 (Spacing): }}\;\alpha_{1} = \alpha_{2} = \alpha_{3} = \alpha_{4} = 0$$
(19)
$${\text{H0 (Depth):}}\;\beta_{1} = \beta_{2} = \beta_{3} = \beta_{4} = 0$$
(20)

It can be seen from the Table 4 that the P-values of spacing and depth are both less than 0.05, indicating that the two factors have a significant impact on the cooling value. The significance of the impact on the spontaneous combustion area is: spacing > depth.

Table 4 Results of two-factor variance experiment.
Full size table

Optimal cooling solution results

According to Fig. 24, the overall temperature at z = 3 m and z = 6 m in the spontaneous combustion coal gangue dump continues to decrease with time, and the horizontal direction has an obvious trend of high temperature center spreading to low temperature, and the fire source moves to the low temperature area. Based on the characteristics of temperature field changes, corresponding treatment measures can be taken at specific locations, such as increasing the density of HPs or adding grouting curtain walls to timely control the diffusion of the fire source center to the low-temperature area and prevent the expansion of spontaneous combustion danger areas.

Fig. 24
figure 24figure 24

Temperature distribution variation of coal gangue dump under optimal HPs layout.

Full size image

The spontaneous combustion volume (V) and high-temperature point temperature(Tmax) changes of the coal gangue dump under the optimal HPs layout is shown in Fig. 25. After 5 years of heat transfer, the V and Tmax of the coal gangue dump decreased by, 11755m3(39.75%)and 302.57 ℃ (46.68%), respectively. The cooling efficiency was about 2351 m3/a and 60.51 ℃/a. The V and Tmax of the coal gangue dump decrease over time, due to the removal of oxidation heat by the HPs, which destroys the thermal storage environment of the coal gangue dump and leads to a decrease in temperature.

Fig. 25
figure 25

Diagram of V and Tmax changes of coal gangue dump under optimal HPs layout.

Full size image

Therefore, HPs can be inserted into the coal gangue dump in the optimal solution as a heat transfer device, clearing the accumulated heat in the coal gangue dump and accelerating the removal of SCDZ in the dump. The optimal solution obtained in this study can provide theoretical reference for the design and optimization of actual HPs layout schemes in future coal fire prevention practices.

Conclusion

This study encompassed comprehensive predictive and experimental investigations, aiming to delve into the influence of heat pipe layout parameters on the cooling effect of spontaneous combustion coal gangue dumps. Several conclusions can be made:

  1. 1.

    The smaller the spacing between HPs, the more effective the cooling, particularly reducing the area of the Spontaneous Combustion Danger Zone (SCDZ). An HP spacing of 3 m was optimal, keeping temperatures below 280 °C by the fifth year and improving cooling efficiency over time.

  2. 2.

    The deeper the HP is inserted, the more pronounced the cooling effect will be in the deep layers of the coal gangue dump. At a depth of 7 m, a significant temperature difference of up to 154 °C was observed in the high-temperature center, effectively suppressing the rate of deep combustion.

  3. 3.

    The influence of the insertion spacing of HPs on the spontaneous combustion volume of coal gangue dumps is greater than the influence of the insertion depth of HPs. When S = 3 m and D = 7 m, the spontaneous combustion volume and highest point temperature of coal gangue dumps were reduced by 39.75% and 46.68%, respectively, demonstrating the effectiveness of HP technology in controlling coal gangue combustion.

The results provide an important reference for the control of spontaneous combustion of coal gangue dumps and the engineering design of waste heat utilization, and have certain application value. In practical applications, the spacing between HPs is determined based on the influence radius of the HP, and an appropriate length of HP is selected to be inserted into the high-temperature center range in combination with temperature distribution, in order to economically and efficiently prevent the spontaneous combustion of coal gangue dumps.