Introduction

Cardiovascular system is crucial for human life and extensive researches have been done for the evaluation of this system in different conditions1,2,3. Cerebral aneurysms present a significant health risk due to the potential for rupture, which can lead to life-threatening hemorrhagic strokes4,5,6. The two most common endovascular techniques used to treat aneurysms are stenting and coiling7. Both methods aim to reduce the risk of rupture by altering the hemodynamics within the aneurysm and decreasing the stress on the aneurysm wall8,9. However, these techniques differ in their approach, efficacy, and applicability to various types of aneurysms10,11. This comparison will explore the strengths and limitations of stent and coiling techniques, with a focus on how each method influences hemodynamic changes and contributes to rupture risk reduction in different types of cerebral aneurysms12,13,14.

Comprehensive research has been conducted to improve the treatment of the biological systems15,16,17. Stents, particularly flow-diverting stents (FDS), have become a popular treatment for cerebral aneurysms. Stents are mesh-like structures deployed inside the parent blood vessel, covering the aneurysm neck. They work by redirecting blood flow away from the aneurysm sac, promoting clot formation within the aneurysm and stabilizing the aneurysm wall18,19,20. By reducing the blood flow into the aneurysm, stents aim to lower the wall shear stress (WSS) on the aneurysm wall, which is a key factor in rupture risk21,22.

Stents, especially flow diverters, significantly alter the hemodynamics of cerebral aneurysms. By acting as a barrier between the parent vessel and the aneurysm, stents reduce the velocity of blood entering the aneurysm sac23,24. This reduction in inflow velocity encourages the formation of thrombus (clot) inside the aneurysm, gradually reducing the pressure on the aneurysm wall and lowering the risk of rupture. Flow-diverting stents create a more uniform distribution of WSS along the parent vessel and aneurysm wall, contributing to vascular stabilization and brain injury25,26,27.

The hemodynamic changes induced by stenting have been extensively studied using Computational Fluid Dynamics (CFD)28,29. Studies have shown that flow-diverting stents can lead to a significant reduction in WSS and energy dissipation inside the aneurysm sac. These changes are particularly effective in reducing the risk of rupture in aneurysms with large necks and those located at bifurcations where flow patterns are more complex30,31.

Stenting is most effective for large, wide-necked aneurysms that are difficult to treat with other methods, such as coiling32,33,34. These aneurysms often have more complex flow patterns, and the wide neck allows for significant blood flow into the aneurysm sac. Stents are also beneficial in treating fusiform aneurysms, which are characterized by the dilation of the entire circumference of the vessel. Flow diverters can stabilize these aneurysms by reconstructing the blood vessel and promoting flow redirection18,19,35.

However, stenting may not be suitable for small aneurysms or aneurysms located in distal vessels where deploying a stent can be technically challenging36. Additionally, stents require patients to take long-term antiplatelet therapy to prevent clot formation on the stent itself, which may not be ideal for certain patients37.

This study examines critical hemodynamic factors associated with aneurysm rupture in stented Middle Cerebral Artery (MCA) aneurysms. Using computational fluid dynamics, the researchers analyzed pulsatile blood flow in patient-specific 3D MCA aneurysm models, comparing hemodynamics before and after simulated stent deployment. By comparing these factors in the original and stented aneurysm geometries, the study aimed to evaluate how effectively stent placement reduces rupture risk. The finite volume method was employed to model pulsatile blood flow within the aneurysms. This computational approach allowed for detailed examination of flow patterns and stresses acting on the aneurysm wall. Through this comparative analysis of pre- and post-stent hemodynamics, the researchers sought to quantify the impact of stent deployment on key risk factors for aneurysm rupture. The findings provide insights into the mechanisms by which stents may help stabilize aneurysms and prevent catastrophic bleeding events.

Modeling

Geometry

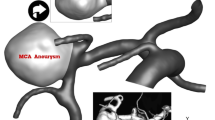
The selected MCA aneurysm is shown in Fig. 1, with the geometrical details of the model provided in Table 1. The original geometry was sourced from the Aneurisk webpage38. Figure 2 illustrates the shape of the selected case in two stages of deformation. The primary concept behind the deformed aneurysms relates to the alignment of the parent vessel due to stent placement. Specifically, the first deformation model represents an intermediate stage of the final deformation, labeled as the second deformation in the figure. As depicted, the parent vessel is considered fully aligned, allowing only limited blood flow to enter the sac region.

Fig. 1
figure 1

Selected aneurysm.

Full size image
Table 1 Geometrical details of selected aneurysms.
Full size table
Fig. 2
figure 2

Deformation-effect of stent.

Full size image

Coiling

The use of coiling in conjunction with stent treatment is also examined in this study. The main approach to coiling implementation involves filling the entire saccular region with porous materials, each with varying permeability factors, K, representing fluid conductivity within the porous medium. This factor indicates the surface area to volume ratio of the porous domain39,40. The study employed the Kozeny model to calculate permeability. Table 2 provides the details of the applied permeability factors and their corresponding porosity values41.

Table 2 Porosity details of coiled aneurysms.
Full size table

The Kozeny model, also known as the Kozeny-Carman equation, is a widely used empirical model for estimating the permeability of porous media. It relates the permeability to the geometric characteristics of the porous structure, such as porosity and specific surface area. The model assumes that the porous medium can be represented as a bundle of capillary tubes, where fluid flows through these channels, and it accounts for both the porosity and the complexity of the pore structure.

The permeability K in the Kozeny model is given by the following equation:

$$K=\frac{{\epsilon }^{3}}{c(1-\epsilon )^{2}{S}^{2}}$$
(1)

Where K is the permeability, \({\epsilon }\) is the porosity of the medium (the fraction of the total volume that is void space), S is the specific surface area (the surface area of the solid material per unit volume), c is the Kozeny constant, a dimensionless factor that accounts for the geometry and tortuosity of the flow paths through the porous material.

The model assumes laminar flow through the porous medium and is often applied in cases where the pore structure is relatively uniform. In this study, the Kozeny model is used to estimate the permeability of the coiled aneurysm, which is filled with a porous material to simulate the effect of the coiling treatment. By varying the permeability factors, the model allows for the evaluation of how different degrees of porosity and fluid conductivity within the coiled sac affect the hemodynamic performance of the treatment.

Governing equations

The simulation of pulsatile flow within the cerebral vessel containing the aneurysm is conducted using the Navier-Stokes equations, while the energy equation is excluded due to the minimal temperature variation in real blood flow. Since the flow is pulsatile, a transient simulation is required, and the Casson model, a widely used non-Newtonian model, is applied to estimate blood viscosity. The simulations are carried out using ANSYS FLUENT software42.

Applied boundary condition and grid production

Pulsatile blood flow is applied at both the inlet and outlet of the domain (Fig. 3). The boundary conditions used are a mass flow rate at the inlet and a pressure outlet at the outlet for the selected models. The blood flow cycle represents that of a normal body, with four stages of the cycle considered. The peak systolic stage corresponds to the maximum blood flow rate.

Fig. 3
figure 3

Boundary conditions at inlet and outlet43.

Full size image

Figure 4 shows the generated grid for the selected aneurysm. The cells are uniformly distributed along the surface, while the resolution of the grid varies across the cross-section, with a finer grid near the sac wall compared to the vessel’s center. This refinement is necessary to optimize the grid for capturing critical hemodynamic factors near the wall. A grid study was conducted for both models by generating five grids. The quality of the grid was verified by comparing blood velocity at the ostium section across these grids, and the final grid was selected when increasing the grid size and number resulted in minimal changes in blood velocity at the neck area. As a result, the final grid for the selected model consists of 568,522 cells.

Fig. 4
figure 4

Grid sample.

Full size image

Results and discussion

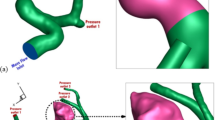
Figure 5 shows the variation of wall shear stress (WSS) on the sac surface for chosen case, across three porosity conditions and two deformation states, at peak systolic. As shown in Fig. 5, the WSS distribution on the sac surface, without coiling but after two stages of deformation treatment, reveals that the critical high wall shear stress is concentrated near the ostium region. The aneurysm’s deformation leads to a reduction in blood flow entering the sac surface region. In the model with low porosity (high permeability), blood entry is further restricted, resulting in lower WSS at the ostium section. The primary reason for rupture in this case is the high tension at the ostium. Coiling treatment has a limited effect on the WSS in this model. Figure 6 also illustrates and compares the effects of coiling and deformation on the average wall shear stress (AWSS) on the sac surface. The AWSS analysis further underscores the significance of deformation in this case.

Fig. 5
figure 5

Wall shear stress contour on different conditions.

Full size image
Fig. 6
figure 6

Average wall shear stress contour on different conditions.

Full size image

Figure 7 illustrates the pressure variations on the sac surface for selected model at two stages of deformation and two porosity conditions during stage II (peak systolic). The pressure contour on the aneurysm and vessel wall shows that coiling treatment reduces the extent of the high-pressure region, though it has minimal effect on the pressure gradient across the sac surface. However, the aneurysm’s deformation significantly lowers the high-pressure values near the ostium. Indeed, the effect of coiling is minimal due to the limited blood flow entering the sac region. On the other hand, the deformation caused by the stent significantly reduces the pressure on the sac surface.

Fig. 7
figure 7

Pressure contour on different conditions.

Full size image

Figure 8 shows the blood flow structure within the sac region and parent vessel, using iso-velocity surfaces to compare the effects of coiling and stenting on blood hemodynamics. The stent proves to be a more effective treatment method for chosen case, which features a low sac volume. Additionally, the stent-induced deformation plays a crucial role in obstructing blood flow into the sac region, making it a more impactful factor in reducing flow into the aneurysm.

Fig. 8
figure 8

Pressure contour on different conditions (V = 0.1 m/s).

Full size image

The evaluation of the Oscillatory Shear Index (OSI) at the end of the cardiac cycle was conducted to identify regions with a high risk of aneurysm rupture. Figure 9 presents a comprehensive OSI contour for the models. The OSI contour reveals that the maximum OSI is located at the top dome and the ostium region. Deformation of the aneurysm reduces the extent of the high OSI region, while coiling alone has little effect on decreasing OSI on the aneurysm wall. However, the combination of stenting and coiling effectively reduces OSI on the sac surface.

Fig. 9
figure 9

OSI contour on different aneurysm conditions over cardiac cycle.

Full size image

Figure 10 compares the quantitative evaluation of a chosen case under the impacts of coiling and stent treatments. The image shows a 3D bar plot illustrating the maximum Oscillatory Shear Index (OSI) on the sac surface under various conditions. The x-axis represents different deformation states (without deformation, deformation 1, and deformation 2), while the z-axis indicates different porosity levels (without porosity, porosity = 0.85, and porosity = 0.65). The y-axis represents the maximum OSI values. It is observed that, in the absence of porosity and deformation, the OSI reaches its highest value. Besides, deformation significantly reduces the maximum OSI, especially in the second deformation state. This plot effectively demonstrates how porosity and deformation influence the OSI, which is critical for understanding the potential rupture risk of aneurysms. Similar results also observed for the mean OSI.

Figure 10c and d display a 3D bar plot that illustrates the max Average Wall Shear Stress (AWSS) and mean AWSS, respectively, on the aneurysm sac surface under different porosity and deformation conditions. The x-axis indicates various deformation states (without deformation, deformation 1, and deformation 2), while the z-axis represents porosity levels (without porosity, porosity = 0.85, and porosity = 0.65). The highest AWSS occurs without porosity or deformation, indicating the largest wall shear stress is present in this scenario. The introduction of deformation (particularly deformation 2) significantly reduces AWSS. This plot emphasizes the role of deformation and porosity in controlling wall shear stress, which is essential for understanding aneurysm progression and potential rupture risk.

Fig. 10
figure 10

Quantitative comparison of hemodynamic factors related to rupture of aneurysms.

Full size image

Conclusion

In this study, an inclusive assessment of hemodynamic features was conducted on single cerebral saccular MCA aneurysms with different endovascular treatment. computational fluid dynamics (CFD) is used to compare stent and coiling treatments to assess their effectiveness in reducing aneurysm rupture risk by analyzing hemodynamic factors. Coiling was modeled as a porous condition, while the effects of the stent were represented by aneurysm deformation. The contours of wall shear stress (WSS), pressure, and oscillatory shear index (OSI) were compared across two stages of aneurysm deformation and varying coiling porosities. The results indicate that stent and coiling treatments have a lesser impact on hemodynamic factors in large aneurysms, but they can effectively reduce rupture risk in aneurysms with smaller sac volumes. Introducing porosity (at values of 0.85 and 0.65) further reduces the OSI, with porosity = 0.65 showing a greater reduction. The combined effect of deformation and porosity leads to the lowest OSI values, highlighting the importance of these factors in minimizing the OSI on the aneurysm sac surface. Adding porosity (values of 0.85 and 0.65) further decreases the AWSS, with the lower porosity value (0.65) showing a more pronounced reduction in shear stress. The combined effects of deformation and porosity lead to the lowest AWSS values, showing that both factors are critical for minimizing shear stress on the aneurysm sac.