Reliable numerical scheme for coupled nonlinear Schrödinger equation under the influence of the multiplicative time noise

Abstract

In this study, we consider the coupled nonlinear Schrödinger equation under the influence of the multiplicative time noise. The coupled nonlinear Schrödinger equation, which shows the complex envelope amplitudes of the two modulated weakly resonant waves in two polarisations and is used to describe the pulse propagation in high birefringence fibre, has several uses in optical fibres.query:Journal instruction requires a city for affiliations; however, these are missing in affiliation [6]. Please verify if the provided city are correct and amend if necessary. The underlying model is analyzed numerically and analytically as well. For the computational results, the proposed stochastic backward Euler scheme is developed and its consistency is derived in the mean square sense. For the linear stability analysis, Von-Neumann criteria is used, given proposed stochastic scheme is unconditionally stable. The exact optical soliton solutions are constructed with the help of the $\phi ^6$-model expansion technique, which provided us with the Jacobi elliptic function solutions that will explore optical solitons and solitary waves as well. The initial and boundary conditions are constructed for the numerical result by some optical soliton solutions. The 3D, 2D and corresponding contour plot are drawn for the different values of noise. Mainly, the comparison of results is shown graphically in 3D and line plots for some newly constructed solutions by selecting suitable parameters value.

Introduction

Mathematical models are generally the most accurate way to present the nonlinear physical phenomena in nature. The different types of partial differential equations (PDEs) have been modeled to explore and comprehend the different physical phenomena^1,2. These PDEs have much interest in the field of optics, finance, engineering, biology, physics, control theory, systems identification, and many others. Optical wave structures are widely used in the telecommunication industry, plasma physics, the internet industry, and other fields^3,4. When all these phenomena are analyzed at the macrolevel they show random behaviors. The Wiener process, often known as the Brownian motion, is a physical process. It is a frequently employed stochastic process in a dispersive environment^5,6. The stochastic PDEs are the best mathematical expressions when noise and random effects are involved in complex physical systems. Then the stochastic PDEs are employed in the analysis of chemical, biological, optics, and physical systems which are affected by the random factors^7,8,9,10.

The stochastic partial differential equation (SPDEs) are crucial to deal with numerically and analytically due to noise terms. Nowadays many researchers are working on the stochastic PDEs numerically and analytically. Yasin et al. working on the numerical simulations of nonlinear stochastic such as Newell–Whitehead–Segel equation¹¹, Fisher-type equations¹² predator-prey model¹³, Gross-Pitaevskii equation in dispersive media^14,15 etc. They dealing the stochastic PDEs to propose the numerical scheme and discussed their stability and consistency as well under the effect of noise. Nouy developed spectral stochastic methods for the numerical solution of stochastic PDEs¹⁶. Luo dealt with the Wiener chaos expansion and numerical solutions of stochastic partial differential equations¹⁷. Germain proposed a backward Euler scheme to find the approximate solution of stochastic PDEs^18,19,20. Jiang visualized the stochastic nonlinear Schrödinger equation by stochastic multi-symplectic integrator²¹. Jentzen proposed the higher order numerical approximations of SPDEs with additive noise²².

Meanwhile, many other researchers investigate the stochastic exact wave solutions for nonlinear PDEs by using different techniques. Alkhidhr investigates the stochastic solutions for the non-linear Schrödinger’s equations using the unified technique²³, and Abdelrahman et al. constructed the stochastic wave structure by unified solver method²⁴. Mohammed has done much work on the stochastic PDEs analytically, such as considering fractional order KdV, and constructed the analytical solutions by using the tanh-coth and Jacobi elliptic function methods²⁵. He also constructed the exact solutions of the stochastic Ginzburg-Landau equation²⁶, Al-Askar et al. investigated the analytical solutions of the space-fractional stochastic approximate long water wave equation²⁷. Shaikh et al. considered the stochastic Konno–Oono system and obtained the soliton solutions²⁸.

Ohta et al. considered the coupled nonlinear Schrödinger equations (CNLSEs) and explored the N-dark soliton solutions²⁹. Zhang et al. found the interaction of anti-dark solitons for CNLSEs using the Hirota method³¹, and Inc, M., investigated the optical solitons solutions for the CNLSEs³². Mo et al. used the deep learning algorithm to solved CNLSEs³³ while, Radhakrishnan and Lakshmanan extracted the exact solutions for the CNLSEs by the help of Hirota bilinear approach³⁴. Wazwaz gained the optical envelope soliton solutions for CNLSEs applicable to high birefringence fibers³⁵. Kanna explored the different Shape-changing collisions for the CNLSEs³⁶, Sakkaravarthi explored the bright solitons for CNLSEs using the Hirota bilinearization method³⁷. Wazwaz used the variational iteration method and extracted the different optical soliton solutions for CNLSEs. In optical systems of modeling waves with multiple components, the single nonlinear model normally normally extend to coupled nonlinear equations that include the solutions F(x, t) and G(x, t). The CNLSE exhibits physical and optical significance to birefringent fibers, bimodal, one-dimensional propagation in any material with the existence of Kerr effects, and other features as well³⁸. Moreover, the two CNLSEs explore the propagation of two or more pulses with different polarizations and frequencies in an optical fiber, physics of plasmas, the propagation of light pulses in birefringent (means fiber mediums having two-different refractive indices) fibers, and incoherent beam propagation in photo refractive media, and other phenomena³⁹. The research area on optical solitons has attracted an intense research work in theoretical physics, lasers, plasma physics, atmosphere, matter waves (Bose-Einstein condensate), medical image processing, ultrafast optics, optical communications, and nonlinear optics⁴⁰. The growing research on optical fields examines well beyond optical fiber and goes to quite a number of other fields such as rogue oceanic waves, atmosphere, lasers, space and laboratory plasma physics, Bose-Einstein condensates, and many others. There are many forms of the nonlinear Schrödinger equation but in this study, we consider the coupled nonlinear Schrödinger equation under the influence of the multiplicative time noise as, for more detail see³⁵.

$$\begin{aligned} i F_t+ i \mu F_{x} +\frac{1}{2}F_{xx} +\left( |F|^2+\beta |G|^2\right) F -i\sigma _1 F W_t(t)=0, \end{aligned}$$

(1)

$$\begin{aligned} i G_t- i \mu G_{x} +\frac{1}{2}G_{xx} +\left( |G|^2+\beta |F|^2\right) G -i\sigma _2 G W_t(t)=0, \end{aligned}$$

(2)

where the unknown functions F and G indicate the complex envelope amplitudes of the two modulated weakly resonant waves in two polarizations which are used to describe the pulse propagation in high birefringence fiber. Also, the quadratic dispersive and cubic terms are modeled. The nonlinear terms of the coupled system (1-2) contribute to the pulse compression and nonlinear birefringence due to the optical Kerr effect. $\mu$ is a group velocity mismatch (GVM) due to normal group velocity dispersion GVD, and $\beta$ is a real parameter that stands for cross-phase modulation coefficient. $\sigma _1$, $\sigma _2$ are the control parameters with the W(t) is Brownian motion and $W_t(t)=\frac{d W(t)}{d t}$ is multiplicative noise respectively. Different phenomena are described by the CNLSEs including linear pulse splitting, nonlinear pulse stabilization, and pedestal removal in compressed pulses.

The perturbed Chen–Lee–Liu equation was analyzed by two techniques⁴¹. 2D regularized long-wave equation was considered for the analytical solutions⁴². The soliton solutions of the Mikhailov–Novikov–Wang integrable equation was obtained⁴³. The innovative solitary wave solutions for the Kadomtsev–Petviashvili equation was obtained⁴⁴. The author considered fractional Caudrey–Dodd–Gibbon and used the Bernoulli sub-equation function and extended Khater method for the analytical study⁴⁵. The solitary wave solutions of the Mikhailov–Novikov–Wang integrable equation was obtained by various analytical techniques⁴⁶. The generalized modified Equal-Width equation was considered and analyzed for the solitary wave solutions⁴⁷. The abundant families of the solutions was gained⁴⁸. Kai et al. extracted the exact solutions for the fourth-order time-fractional PDE⁴⁹, and for the regularized long wave equation⁵⁰. Zhu et al. used the Chaffee-Infante equation⁵¹ and modified Schrödinger’s equation to gained the exact soliton solutions⁵². Wang et al. recently worked on the (2+ 1)-dimensional variable coefficient Broer–Kaup system for the sake of elastic integrations⁵³, while they are also used the modified tanh-function method to re-studied the localized structures of NLPDEs⁵⁴. Kong et al also used the Riccati equation expansion method⁵⁵. Recently, Si et al. worked on the multi-wavelength soliton and shows their experimental results⁵⁶. Albayrak et al. explored the pure-cubic optical solitons⁵⁷, Altun et al. considered the Biswas-Milovic equation and constructed the optical solitons using the new Kudryashov’s method⁵⁸. Zayed et al. gained the highly dispersive optical solitons for the stochastic Lakshmanan–Porsezian–Daniel equation⁵⁹.

In this study, the system (1-2) is investigated by both techniques i.e., numerically and analytically. In the literature mentioned above, many researchers worked separately on numerical and exact solitary wave solutions but there is a gap in their study to compare their results. To gain the numerical results, the proposed backward Euler scheme is developed for the stochastic CNLSE, and the sake of exact optical solutions, we applied the $\phi ^6$-model expansion. The $\phi ^6$-model expansion method gives us the different stochastic optical solitons and solitary wave solutions successfully^65,66. The motivation of this study is to compare the numerical results with the newly constructed optical soliton solutions via simulations. To compare these results, we need the initial and boundary value problems that are constructed by selecting some stochastic optical soliton solutions. The $\phi ^6$-model expansion strategy was employed to investigate the solutions for solitary waves. When we select $C\rightarrow 1$ and $C\rightarrow 0$, respectively, this fundamental analytical tool will provide us with the solutions in the form of JEF solutions that illustrate the solitons and solitary wave solutions. Under the influence of noise, the many forms of Dark, Bright, Dark-Bright, mixed, and periodic mixed solutions are investigated. The stochastic Backward Euler scheme that is proposed computes the numerical results. To ensure uniformity, the suggested numerical scheme is examined using mean square analysis. Von-Neumann criteria are applied for the linear stability analysis, demonstrating the unconditional stability of the proposed stochastic scheme. The exact solutions for the optical solitons are obtained by applying the analytical method, specifically the $\phi ^6$-model expansion. The Jacobi elliptic function solutions, which yield the exact optical solitons and solitary wave solutions, investigate these solutions. Plots in both two and three dimensions are generated for a few soliton scenarios with varying noise levels. For the numerical result, some optical soliton solutions are used to generate the initial and boundary conditions. For some freshly developed solutions, the comparison of outcomes is primarily displayed graphically in 3D and line plots by choosing appropriate values for the parameters.

The article is divided into the following sections: Section “Preliminaries” gives a short overview of the Ito calculus. Section “Proposed scheme” presents the proposed scheme, Section “Analysis of scheme” is about the analysis of the scheme. Section “Optical stochastic waves transformation” is about the Optical stochastic wave transformation, Section “$\phi ^6$-model expansion method” deals with the $\phi ^6$-model expansion method and Section “Graphical results” presents the graphical results. The Section “Conclusion” is about the conclusion and Section “Parameters to draw plots” has the Appendix of parameters values.

Preliminaries

In this section, we give short overview about the It${\hat{o}}$ calculus.

Wiener process and It${\hat{o}}$ integral

The Brownian motion W(t) is said to be stochastic process $\{W(t)\}_{t\ge 0}$ if it satisfy the following properties^67,68:

• 1. $W(0)=0$ with probability 1;

• 2. W(t) is the continues function of $t\ge 0$;

• 3. $W(t_2)-W(t_1)$ and $W(t_4)-W(t_3)$ are independent increments for all $0\le t_1<t_2\le t_3<t_4$;

• 4. $W(t_2)-W(t_1)$, $W(t_4)-W(t_3)$ has normal distribution ${\mathfrak {N}}(0,(t_2-t_1),(t_4-t_3))$;

• 5. ${\mathbb {E}}\bigg [W_t\bigg ]=0$ for each value $t\ge 0$;

• 6. ${\mathbb {E}}\bigg [W_t^2\bigg ]=t$ for each value $t\ge 0$;

• 7. ${\mathbb {E}}\bigg [W_t-W_s\bigg ]=0$;

• 8. ${\mathbb {E}}\bigg [(W_t-W_s)^2\bigg ]=t-s$.

It${\hat{o}}$ stochastic integral

The square property of an It${\hat{o}}$ integral is $\int _0^t \sigma _t dW(t)$ has the following property:

$$\begin{aligned} {\mathbb {E}} \bigg |\int _0^t \sigma _t dW(t)\bigg |^2=\int _0^t {\mathbb {E}}\bigg | \sigma _t\bigg |^2 dt. \end{aligned}$$

(3)

Von-Neumann technique

To examine the stability of the proposed scheme, we can apply the Von-Neumann technique, such that

$$\begin{aligned} \Phi _l^m=\frac{1}{\sqrt{2 \pi }}\int _{\frac{-\pi }{\Delta x}}^{\frac{\pi }{\Delta x}}e^{il\Delta \rho }{\hat{\Phi }}_{l}^{m}(\rho )d\rho . \end{aligned}$$

(4)

In this technique ${\hat{\Phi }}_{l}^{m}$ is Fourier transformation which is defined as

$$\begin{aligned} {\hat{\Phi }}_{l}^{m}=\frac{1}{\sqrt{2\pi }}\sum _{-\infty }^{\infty } e^{-il\Delta \rho } \Phi _l^m \Delta x, \end{aligned}$$

(5)

where $\rho$ is the real variable, by substituting this into the proposed scheme we get

$$\begin{aligned} {\hat{\Phi }}_{l}^{m+1}(\rho )= {\hat{\Phi }}_l^m \Upsilon (\rho \Delta x,\Delta t,\Delta x). \end{aligned}$$

(6)

Hence, the necessary and sufficient condition for the stability of the scheme via Von-Neumann technique is

$$\begin{aligned} {\mathbb {E}}\bigg |\Upsilon (\rho \Delta x,\Delta t,\Delta x)\bigg |^2\le 1+k\Delta t. \end{aligned}$$

(7)

Proposed scheme

This section deals with the proposed numerical scheme namely as Backward Euler scheme. To construct the stochastic Backward Euler scheme we approximate the derivatives such as:

$$\begin{aligned} F_t \approx \frac{F_l^{m+1}-F_l^m}{\Delta t},\qquad F_x \approx \frac{F_{l+1}^{m}-F_l^m}{\Delta x}, \qquad F_{xx}\approx \frac{F_{l+1}^{m+1}-2 F_l^{m+1}+F_{l-1}^{m+1}}{\Delta x^2}, \end{aligned}$$

(8)

$$\begin{aligned} G_t \approx \frac{G_l^{m+1}-G_l^m}{\Delta t},\qquad G_x \approx \frac{G_{l+1}^{m}-G_l^m}{\Delta x}, \qquad G_{xx}\approx \frac{G_{l+1}^{m+1}-2 G_l^{m+1}+G_{l-1}^{m+1}}{\Delta x^2}, \end{aligned}$$

(9)

here $\Delta t$ and $\Delta x$ are time and space stepsizes respectively. Now, substitute these values in the system (1-2) and after some basic calculations we get the following forms

$$\begin{aligned} & (i-2\delta )F_{l}^{m+1}+\delta F_{l+1}^{m+1}+\delta F_{l-1}^{m+1}=-\gamma F_{l+1}^m+(\gamma +i) F_l^m- \Delta t (|F_l^m|+\beta |G_l^m|)F_l^m\nonumber \\ & \quad + i \sigma _1 F_l^m(W^{(m+1)\Delta t}-W^{m\Delta t}),\end{aligned}$$

(10)

$$\begin{aligned} & \quad (i-2\delta )G_{l}^{m+1}+\delta G_{l+1}^{m+1}+\delta G_{l-1}^{m+1}=\gamma G_{l+1}^m-(\gamma -i) G_l^m-\Delta t (|G_l^m|+\beta |F_l^m|)G_l^m\nonumber \\ & \quad + i \sigma _2 G_l^m(W^{(m+1)\Delta t}-W^{m\Delta t}). \end{aligned}$$

(11)

Where $\gamma =\frac{i \mu \Delta t}{\Delta x}$ and $\delta =\frac{ \Delta t}{2\Delta x^2}$. So, the Eq. (10) is the proposed Backward Euler schemes for the Eqs. (1–2).

Analysis of scheme

This current section is deals with the consistency under the mean square sense and stability analysis via Von-Neumann criteria^69,70.

Consistency of scheme

Here, we check that our proposed scheme is consistent under the mean square sense.

Definition 1

A proposed stochastic scheme ${\mathbb {L}}|_{l,m} P|_{l,m}=\Upsilon |_{l,m}$ is consistent with their corresponding stochastic PDE ${\mathbb {L}} P=\Upsilon$ at the point (x, t), if the continually differentiable functions are $F=F(x, t)$ and $G=G(x, t)$ then,

$$\begin{aligned} \mathbb {E}\bigg ||\left( {\mathbb {L}} P-\Upsilon \right) |_{l,m}-\bigg [{\mathbb {L}}|_{ l,m} P|_{ l\Delta x,m \Delta t}-\Upsilon |_{l,m}\bigg ]\bigg |^2\rightarrow 0, \end{aligned}$$

(12)

here we let $h=\Delta x$ and $k=\Delta t$.

So, as $h \rightarrow 0$, $k \rightarrow 0$ and $(l h, (m+1)k)\rightarrow (x, t)$.

Theorem 1

The proposed Backward Euler scheme in Eqs. (10, 11) is consistent in the mean square sense corresponding to the stochastic PDEs in Eqs. (1, 2).

Proof

Let us consider the smooth functions F(x, t) and G(x, t) and using the operator ${\mathbb {L}}(F)=\int _{m k}^{(m+1)k} F ds$ on Eq. (1). Thus we obtain

$$\begin{aligned} & {\mathbb {L}}(F)|_{l,m}=i F(l h, (m+1)k) - i F(l h, m k)+ i\mu \int _{m k}^{(m+1)k} F_x(l h, s)ds~~~\nonumber \\ & \quad + \frac{1}{2} \int _{mk}^{(m+1)\Delta t} F_{xx}(l h, s)ds+ \int _{m k}^{(m+1)k} |F(l h, s)|^2F(l h, s)ds \nonumber \\ & \quad + \beta \int _{m k}^{(m+1)k} |G(l h, s)|^2F(l h, s)ds-i \sigma _1 \int _{m k}^{(m+1) k} F(l h, s)dW|_s. \end{aligned}$$

(13)

Further, we use the proposed stochastic Backward Euler scheme on Eq. (1) and get

$$\begin{aligned} & {\mathbb {L}}|_{l,m}(F)=i F(l h, (m+1)k) - i F(l h, m k)+ i\mu k \frac{F_{l+1}^{m}-F_l^m}{h}~~~~~~\nonumber \\ & \quad + \frac{1}{2} k \frac{F_{l+1}^{m+1}-2 F_l^{m+1}+F_{l-1}^{m+1}}{h^2}+ k |F(l h, s)|^2F(l h, s)~~~~\nonumber \\ & \quad + \beta k |G(l h, s)|^2F(l h, s)-i \sigma _1 F(l h, s)(W^{(l+1)k}-W^{lk}), \end{aligned}$$

(14)

by the help of mean square sense the above expression can be written as

$$\begin{aligned} & {\mathbb {E}}\bigg |{\mathbb {L}}(F)|_{l,m}-{\mathbb {L}}|_{l,m}(F)\bigg |^2\le 5\mu ^2 {\mathbb {E}}\bigg | \int _{m k}^{(m+1)k} \left( F_x(l h, s)-\frac{F_{l+1}^{m}-F_l^m}{h}\right) ds\bigg |^2~~~ \nonumber \\ & \quad + \frac{5}{4} {\mathbb {E}}\bigg |\int _{m k}^{(m+1)k} \left( F_{xx}(l h, s)-\frac{F_{l+1}^{m+1}-2 F_l^{m+1}+F_{l-1}^{m+1}}{h^2}\right) ds\bigg |^2~~~\nonumber \\ & \quad +5{\mathbb {E}} \bigg |\int _{m k}^{(m+1)k}\left( |F(l h, s)|^2F(l h, s)-|F(l h, s)|^2F(l h, s)\right) ds\bigg |^2~~~\nonumber \\ & \quad +5 \beta {\mathbb {E}} \bigg |\int _{m k}^{(m+1)k} \left( |G(l h, s)|^2F(l h, s)- |G(l h, s)|^2F(l h, s)\right) ds\bigg |^2~~~\nonumber \\ & \quad - 5\sigma _1^2 {\mathbb {E}}\bigg |\int _{m k}^{(m+1)k} \left( F(l h, s)+F(l h, s)\right) dW|_s\bigg |^2.~~ \end{aligned}$$

(15)

Now, we apply the symmetric property of It${\hat{o}}$’s integral

$$\begin{aligned} & {\mathbb {E}}\bigg |{\mathbb {L}}(F)|_{l,m}-{\mathbb {L}}|_{l,m}(F)\bigg |^2\le 5\mu ^2 {\mathbb {E}}\bigg | \int _{m k}^{(m+1)k} \left( F_x(l h, s)-\frac{F_{l+1}^{m}-F_l^m}{h}\right) ds\bigg |^2~~~\nonumber \\ & \quad + \frac{5}{4} {\mathbb {E}}\bigg |\int _{m k}^{(m+1)k} \left( F_{xx}(l h, s)-\frac{F_{l+1}^{m+1}-2 F_l^{m+1}+F_{l-1}^{m+1}}{h^2}\right) ds\bigg |^2~~~\nonumber \\ & \quad +5{\mathbb {E}} \bigg |\int _{m k}^{(m+1)k}\left( |F(l h, s)|^2F(l h, s)-|F(l h, s)|^2F(l h, s)\right) ds\bigg |^2~~~\nonumber \\ & \quad +5 \beta {\mathbb {E}} \bigg |\int _{m k}^{(m+1) k} \left( |G(l h, s)|^2F(l h, s)- |G(l h, s)|^2F(l h, s)\right) ds\bigg |^2~~~\nonumber \\ & \quad -5 \sigma _1^2 \int _{m k}^{(m+1)k}{\mathbb {E}}\bigg | \left( F(l h, s)+F(l h, s)\right) \bigg |^2ds. \end{aligned}$$

(16)

Hence ${\mathbb {E}}\bigg |{\mathbb {L}}(F)|_{l,m}-{\mathbb {L}}|_{l,m}(F)\bigg |^2\rightarrow 0$, as $l\rightarrow \infty$ and $m \rightarrow \infty$, so proposed scheme Eq. (10) is consistent with SPDE (1). Further, we also check the consistency for the Eq. (11) with SPDE Eq. (2) such as, we take the operator ${\mathbb {L}}(G)=\int _{m k}^{(m+1)k} G ds$ on Eq. (2). Thus we obtain

$$\begin{aligned} & {\mathbb {L}}(G)|_{l,m}=i G(l h, (m+1)k) - i G(l h, m k)- i\mu \int _{m k}^{(m+1)k} G_x(l h, s)ds~~~\nonumber \\ & \quad + \frac{1}{2} \int _{mk}^{(m+1)k} G_{xx}(l h, s)ds+ \int _{m k}^{(m+1)k } |G(l h, s)|^2G(l h, s)ds\nonumber \\ & \quad + \beta \int _{m k}^{(m+1)k} |F(l h, s)|^2G(l h, s)ds-i \sigma _2 \int _{m k}^{(m+1)k} G(l h, s)dW|_s. \end{aligned}$$

(17)

Further, we use the proposed stochastic Backward Euler scheme on Eq. (2) and get

$$\begin{aligned} & {\mathbb {L}}|_{l,m}(G)=i G(l h, (m+1)k) - i G(l h, m k)- i\mu k \frac{G_{l+1}^{m}-G_l^m}{h}~~~~~~\nonumber \\ & \quad + \frac{1}{2} k \frac{G_{l+1}^{m+1}-2 G_l^{m+1}+G_{l-1}^{m+1}}{h^2}+ k |G(l h, s)|^2G(l h, s)~~~~\nonumber \\ & \quad + \beta k |F(l h, s)|^2G(l h, s)-i \sigma _2 G(l h, s)(W^{(l+1)k}-W^{l k}), \end{aligned}$$

(18)

by the help of mean square sense the above expression can be written as

$$\begin{aligned} & {\mathbb {E}}\bigg |{\mathbb {L}}(G)|_{l,m}-{\mathbb {L}}|_{l,m}(G)\bigg |^2\le 5\mu ^2 {\mathbb {E}}\bigg | \int _{m k}^{(m+1)k}\left( G_x(l h, s)-\frac{G_{l+1}^{m}-G_l^m}{h}\right) ds\bigg |^2~~~\nonumber \\ & \quad + \frac{5}{4} {\mathbb {E}}\bigg |\int _{m k}^{(m+1)k} \left( G_{xx}(l h, s)-\frac{G_{l+1}^{m+1}-2 G_l^{m+1}+G_{l-1}^{m+1}}{h^2}\right) ds\bigg |^2~~~\nonumber \\ & \quad +5{\mathbb {E}} \bigg |\int _{m k}^{(m+1)k} \left( |G(l h, s)|^2G(l h, s)-|G(l h, s)|^2G(l h, s)\right) ds\bigg |^2~~~\nonumber \\ & \quad +5 \beta {\mathbb {E}} \bigg |\int _{m k}^{(m+1)k}\left( |F(l h, s)|^2G(l h, s)- |F(l h, s)|^2G(l h, s)\right) ds\bigg |^2~~~\nonumber \\ & \quad -5 \sigma _2^2 {\mathbb {E}}\bigg |\int _{m k}^{(m+1)k} \left( G(l h, s)+G(l h, s)\right) dW|_s\bigg |^2.~~ \end{aligned}$$

(19)

Now, we apply the symmetric property of It${\hat{o}}$’s integral

$$\begin{aligned} & {\mathbb {E}}\bigg |{\mathbb {L}}(G)|_{l,m}-{\mathbb {L}}|_{l,m}(G)\bigg |^2\le 5\mu ^2 {\mathbb {E}}\bigg | \int _{m k}^{(m+1)k}\left( G_x(l h, s)-\frac{G_{l+1}^{m}-G_l^m}{h}\right) ds\bigg |^2~~~\nonumber \\ & \quad + \frac{5}{4} {\mathbb {E}}\bigg |\int _{m k}^{(m+1)k} \left( G_{xx}(l h, s)-\frac{G_{l+1}^{m+1}-2 G_l^{m+1}+G_{l-1}^{m+1}}{h^2}\right) ds\bigg |^2~~~\nonumber \\ & \quad +5{\mathbb {E}} \bigg |\int _{m k}^{(m+1)k} \left( |G(l h, s)|^2G(l h, s)-|G(l h, s)|^2G(l h, s)\right) ds\bigg |^2~~~\nonumber \\ & \quad +5 \beta {\mathbb {E}} \bigg |\int _{m k}^{(m+1)k}\left( |F(l h, s)|^2G(l h, s)- |F(l h, s)|^2G(l h, s)\right) ds\bigg |^2~~~\nonumber \\ & \quad -5 \sigma _2^2 \int _{m k}^{(m+1)k}{\mathbb {E}}\bigg | \left( G(l h, s)+G(l h, s)\right) \bigg |^2ds. \end{aligned}$$

(20)

Hence ${\mathbb {E}}\bigg |{\mathbb {L}}(G)|_{l,m}-{\mathbb {L}}|_{l,m}(G)\bigg |^2\rightarrow 0$, as $l\rightarrow \infty$ and $m \rightarrow \infty$, so proposed scheme Eq. (11) is consistent with SPDE (2). $\square$

Stability of scheme

In this section, we check the stability of the stochastic Backward Euler scheme by using the Von-Neumann technique^69,70,71,72.

Theorem 2

The proposed Backward Euler scheme in Eqs. (10, 11) is unconditionally stable.

Proof

The Von-Neumann technique is used to the linear scheme, so linearizing the schemes in Eqs. (10, 11). We get expressions such as:

$$\begin{aligned} (i-2\delta )F_{l}^{m+1}+\delta F_{l+1}^{m+1}+\delta F_{l-1}^{m+1}=-\gamma F_{l+1}^m+(\gamma +i) F_l^m+ \sigma _1 F_l^m(W^{(m+1)\Delta t}-W^{m\Delta t}), \end{aligned}$$

(21)

$$\begin{aligned} (i-2\delta )G_{l}^{m+1}+\delta G_{l+1}^{m+1}+\delta G_{l-1}^{m+1}=\gamma G_{l+1}^m-(\gamma -i) G_l^m+ \sigma _2 G_l^m(W^{(m+1)\Delta t}-W^{m\Delta t}). \end{aligned}$$

(22)

By the help of this technique, we change $F_l^m$ and $G_l^m$ in the difference equations as follows

$$\begin{aligned} F_l^m= & \Upsilon (t)e^{i\zeta x}, \end{aligned}$$

(23)

$$\begin{aligned} G_l^m= & \Lambda (t)e^{i\zeta x}, \end{aligned}$$

(24)

using the Eqs. (23, 24) the Eqs. (21, 22) take the following forms

$$\begin{aligned} & (i-2\delta +\delta e^{i\zeta \Delta x}+\delta e^{-i\zeta \Delta x}) \Upsilon (t+\Delta t)e^{i\zeta x}=(-\gamma e^{i\zeta \Delta x}\\ & \quad +(\gamma +i)+\sigma _1(W^{(m+1)\Delta t}-W^{m\Delta t})) \Upsilon (t)e^{i\zeta x},\\ & \quad (i-2\delta +\delta e^{i\zeta \Delta x}+\delta e^{-i\zeta \Delta x}) \Lambda (t+\Delta t)e^{i\zeta x}=(\gamma e^{i\zeta \Delta x}\\ & \quad -(\gamma -i)+\sigma _2(W^{(m+1)\Delta t}-W^{m\Delta t})) \Lambda (t)e^{i\zeta x}, \end{aligned}$$

after some calculations, and taking the expectation on the amplification factor. Further, we use the independence of Wiener process increments, and get

$$\begin{aligned} & {\mathbb {E}}\bigg |\frac{\Upsilon (t+\Delta t)}{\Upsilon (t)}\bigg |^2\le \bigg |\frac{-\gamma e^{i\zeta \Delta x}+(\gamma +i)}{i-2\delta +2\delta (1-2\sin ^2(\frac{\zeta \Delta x}{2}))}\bigg |^2+\bigg |\frac{\sigma _1}{i-2\delta +2\delta (1-2\sin ^2(\frac{\zeta \Delta x}{2}))}\bigg |^2\Delta t,\\ & \quad {\mathbb {E}}\bigg |\frac{\Lambda (t+\Delta t)}{\Lambda (t)}\bigg |^2\le \bigg |\frac{\gamma e^{i\zeta \Delta x}-(\gamma -i)}{i-2\delta +2\delta (1-2\sin ^2(\frac{\zeta \Delta x}{2}))}\bigg |^2+\bigg |\frac{\sigma _2}{i-2\delta +2\delta (1-2\sin ^2(\frac{\zeta \Delta x}{2}))}\bigg |^2\Delta t. \end{aligned}$$

So, $\bigg |\frac{-\gamma e^{i\zeta \Delta x}+(\gamma +i)}{i-2\delta +2\delta (1-2\sin ^2(\frac{\zeta x}{2}))}\bigg |\le 1$, $\bigg |\frac{\gamma e^{i\zeta \Delta x}-(\gamma -i)}{i-2\delta +2\delta (1-2\sin ^2(\frac{\zeta \Delta x}{2}))}\bigg |\le 1$ and$\bigg |\frac{\sigma _1}{i-2\delta +2\delta (1-2\sin ^2(\frac{\zeta \Delta x}{2}))}\bigg |^2=\kappa _1$,

$\bigg |\frac{\sigma _2}{i-2\delta +2\delta (1-2\sin ^2(\frac{\zeta \Delta x}{2}))}\bigg |^2=\kappa _2$. Hence, from the necessary and sufficient of the stability Eq. (7) such as:

$$\begin{aligned} & {\mathbb {E}}\bigg |\frac{\Upsilon (t+\Delta t)}{\Upsilon (t)}\bigg |^2\le 1+\kappa _1 \Delta t, \end{aligned}$$

(25)

$$\begin{aligned} & \quad {\mathbb {E}}\bigg |\frac{\Lambda (t+\Delta t)}{\Lambda (t)}\bigg |^2\le 1+\kappa _2 \Delta t. \end{aligned}$$

(26)

Hence, our proposed scheme is unconditionally stable. $\square$

Optical stochastic waves transformation

In this section, we mainly focus on the optical stochastic soliton solutions^71,72. The complex stochastic wave transformation is use to get the optical soliton solution for the system (1, 2) as follows

$$\begin{aligned} F(x, t)= f(\rho )e^{[i\theta +\sigma _1 W(t)-\frac{\sigma _1^2}{2}t]}, \qquad G(x, t)= g(\rho )e^{[i \theta +\sigma _2 W(t)-\frac{\sigma _2^2}{2}t]}, \nonumber \\ \text {where} \qquad \rho =l_1 x- l_2 t, \quad \text {and} \quad \theta =m_1 x-m_2 t. \end{aligned}$$

(27)

Where $l_1, l_2$ are represents the speeds of light, $m_1, m_2$ are the wave numbers, W(t) is the Brownian motion and $\sigma _1$, $\sigma _2$ are the control parameters of noise. Substituting these transformation using the derivatives as

$$\begin{aligned} & \frac{d F}{d t}= (-l_2 f^{'}-i m_2 f^{'}+\sigma _1 f W_t-\frac{\sigma _1^2}{2}f+\frac{\sigma _1^2}{2} f) e^{[i\theta +\sigma _1 W(t)-\frac{\sigma _1^2}{2}t]},\\ & \frac{d G}{d t}= (-l_2 g^{'}-i m_2 g^{'}+\sigma _2 g W_t-\frac{\sigma _2^2}{2}g+\frac{\sigma _2^2}{2} g) e^{[i\theta +\sigma _2 W(t)-\frac{\sigma _2^2}{2}t]}, \end{aligned}$$

Where the terms $\frac{\sigma _1^2}{2} f$ and $\frac{\sigma _2^2}{2} g$ is the It${\hat{o}}$ correction (for more detail see^73,74).

$$\begin{aligned} & \frac{d F}{d x}=\left( l_1 f^{'}+i m_1 f\right) e^{[i\theta +\sigma _1 W(t)-\frac{\sigma _1^2}{2}t]},\\ & \frac{d^2 F}{d x^2}=\left( l_1^2 f^{''}+2 i l_1 m_1 f^{'}-m_1^2 f\right) e^{[i\theta +\sigma _1 W(t)-\frac{\sigma _1^2}{2}t]},\\ & \frac{d G}{d x}=\left( l_1 g^{'}+i m_1 g\right) e^{[i\theta +\sigma _2 W(t)-\frac{\sigma _2^2}{2}t]},\\ & \frac{d^2 G}{d x^2}=\left( l_1^2 g^{''}+2 i l_1 m_1 g^{'}-m_1^2 g\right) e^{[i\theta +\sigma _2 W(t)-\frac{\sigma _2^2}{2}t]}. \end{aligned}$$

Substituting the complex stochastic wave transformation Eq. (27) and its derivatives into the system in Eqs. (1, 2). After simplification we compare the real and imaginary parts as follows

$$\begin{aligned} -m_2 f^{'} -\mu m_1 f+\frac{1}{2} l_1^2 f^{''}-\frac{1}{2} m_1^2 f+f^3+\beta g^2 f=0, \end{aligned}$$

(28)

$$\begin{aligned} m_2 g^{'}+\mu m_1 g +\frac{1}{2} g^{''} -\frac{1}{2} m_1^2 g+g^3+\beta f^2 g=0, \end{aligned}$$

(29)

imaginary part is

$$\begin{aligned} (-l_2+\mu l_1 +l_1 m_1) f^{'}=0, \end{aligned}$$

(30)

$$\begin{aligned} (-l_2 -\mu l_1 +l_1 m_1)g^{'}=0. \end{aligned}$$

(31)

from the imaginary part we find the constraint condition such as:

$$\begin{aligned} l_1=\frac{\pm m_1+l_2}{\pm \mu +m_1}. \end{aligned}$$

(32)

$\phi ^6$-model expansion method

This section deals, with the we use the exact stochastic wave solutions via $\phi ^6$-model expansion method. The general solutions of the Eqs. (28, 29) is suppose in the polynomial form such as^75,76.

$$\begin{aligned} f(\zeta )= \sum _{j=0}^{2K} c_j \phi ^j(\zeta ), \end{aligned}$$

(33)

$$\begin{aligned} g(\zeta )= \sum _{j=0}^{2K} d_j \phi ^j(\zeta ), \end{aligned}$$

(34)

where $c_j \& d_j (0\le j\le 2K)$ are real constants that are found later and $c_{2k}\ne 0$ and $d_{2k}\ne 0$. Here $\phi ^j(\zeta )$ is satisfying the following auxiliary equation such as:

$$\begin{aligned} \phi ^{'2}(\zeta )= & \varrho _0+\varrho _2 \phi ^2(\zeta )+\varrho _4\phi ^4(\zeta )+\varrho _6\phi ^6(\zeta ), \end{aligned}$$

(35)

$$\begin{aligned} \phi ^{''}(\zeta )= & \varrho _2\phi (\zeta )+2\varrho _4 \phi ^3(\zeta )+3 \varrho _6\phi ^5(\zeta ). \end{aligned}$$

(36)

The Eq. (36) has the well know solution

$$\begin{aligned} \phi (\zeta )=\frac{\Lambda (\zeta )}{\sqrt{h_1 \Lambda ^2(\zeta )+h_2}}, \end{aligned}$$

(37)

where $h_1 \Lambda ^2(\zeta )+h_2>0$ while $\phi (\zeta )$ is the solution of the following Jacobian elliptic equation

$$\begin{aligned} \Lambda ^{'2}(\zeta )=\kappa _0+\kappa _2 \Lambda ^2(\zeta )+\kappa _4\Lambda ^4(\zeta ), \end{aligned}$$

(38)

where $\kappa _0, \kappa _2, \kappa _4$ are real coefficients to be determined later with the condition $\kappa _4\ne 0$ and $h_1$, $h_2$ are taken such as:

$$\begin{aligned} h_1=\frac{\varrho _4(\kappa _2-\varrho _2)}{(\kappa _2-\varrho _2)^2+3\kappa _0\kappa _4-2\kappa _2(\kappa _2-\varrho _2)}, \end{aligned}$$

(39)

$$\begin{aligned} h_2=\frac{3\kappa _0\varrho _4}{(\kappa _2-\varrho _2)^2+3\kappa _0\kappa _4-2\kappa _2(\kappa _2-\varrho _2)}. \end{aligned}$$

(40)

The solutions of Eq. (38) are expressed in the forms of Jacobi elliptic function (JEF) $\Lambda (\zeta )$ solutions such as:

$\Lambda (\zeta , C)$	$C\rightarrow 1$	$C\rightarrow 0$	$\Lambda (\zeta , C)$	$C\rightarrow 1$	$C\rightarrow 0$
$sn(\zeta , C)$	$\tanh (\zeta )$	$\sin (\zeta )$	$ns(\zeta , C)$	$\coth (\zeta )$	$\csc (\zeta )$
$cn(\zeta , C)$	$sech(\zeta )$	$\cos (\zeta )$	$dn(\zeta , C)$	$sech(\zeta )$	1
$cd(\zeta , C)$	1	$\cos (\zeta )$	$cs(\zeta , C)$	$csch(\zeta )$	$\cot (\zeta )$
$sc(\zeta , C)$	$\sinh (\zeta )$	$\tan (\zeta )$	$sd(\zeta , C)$	$\sinh (\zeta )$	$\sin (\zeta )$
$ds(\zeta , C)$	$csch(\zeta )$	$csc(\zeta )$	$nc(\zeta , C)$	$\cosh (\zeta )$	$\sec (\zeta )$

Now, we need the value of K in the expressions (33–34). To get the value of positive integer K we apply the homogenous balancing principle formula⁷⁷ on highest derivative term $f''$ and nonlinear term $f^3$ ( or $g''$ and $g^3$) respectively, then obtain $K =1$. Putting this value into the Eqs. (33, 34) and they express as follow

$$\begin{aligned} f(\zeta )= c_0+c_1 \phi (\zeta )+c_2 \phi ^2(\zeta ), \end{aligned}$$

(41)

$$\begin{aligned} g(\zeta )= d_0+d_1 \phi (\zeta )+d_2 \phi ^2(\zeta ), \end{aligned}$$

(42)

where $c_j$ and $d_j$ $(j=0,1,2)$ are real constants that are found to be later. Placing the Eqs. (41, 42) into the Eqs. (28, 29) with the help of Eqs. (36,35). Then we collect the same powers of $\phi ^j(\zeta )[\phi ^{'}(\zeta )]^k$ where $j=0,1,\cdots$ and $k=0,1$. Taking all of them equal to zero and obtain the system of strategic equations easily. Further we solve this strategic equations with the aid of Mathematica 11.1 and get the solution set as follows

$$\begin{aligned} \left\{ \begin{array}{ll} c_0=0,~~c_1=c_1,~~c_2=0,~~d_0=\frac{7 c_1^2}{4 l_1 \sqrt{-\varrho _6}},~~d_1=0,~~d_2=-2 l_1 \sqrt{-\varrho _6},~~\varrho _0=-\frac{7 \left( 256 c_1^2 l_1^2 m_1^2 \varrho _6+665 c_1^6\right) }{2560 l_1^6 \varrho _6^2},\\ ~~\varrho _2=\frac{273 c_1^4}{64 l_1^4 \varrho _6}+\frac{2 m_1^2}{5 l_1^2},~~\varrho _4=-\frac{29 c_1^2}{8 l_1^2},~~\beta =\frac{3}{8},~~\mu =\frac{63 c_1^4}{64 l_1^2 m_1 \varrho _6}-\frac{3 m_1}{10},~~m_2=0. \end{array} \right. \end{aligned}$$

These constant values and the JEF solutions chosen from the table are used to construct the various families of stochastic optical soliton solutions for equation (1–2). The following is a summary of the solutions $\Rightarrow$ If we take $\kappa _0=1$, $\kappa _2=-(1-C^2)$, $\kappa _4=C^2$, $0<C<1$, then $\Lambda (\zeta )=sn(\zeta , C)$ or $\Lambda (\zeta )=cd(\zeta , C)$. So, JEF solutions is retrieved such as:

$$\begin{aligned} F_{1,C}(\zeta )= \frac{c_1 sn(\zeta )^2}{\sqrt{h_{1} sn(\zeta )^2+h_{2}}}, \end{aligned}$$

(43)

or

$$\begin{aligned} F_{2,C}(\zeta )= \frac{c_1 cd(\zeta )^2}{\sqrt{h_{1} cd(\zeta )^2+h_{2}}}, \end{aligned}$$

(44)

$$\begin{aligned} G_{1,C}(\zeta )= \frac{7 c_1^2}{4 l_1 \sqrt{-\varrho _6}}-\frac{2 l_1 \sqrt{-\varrho _6} sn(\zeta )^4}{h_{1} sn(\zeta )^2+h_{2}}, \end{aligned}$$

(45)

or

$$\begin{aligned} G_{2,C}(\zeta )=\frac{7 c_1^2}{4 l_1 \sqrt{-\varrho _6}}-\frac{2 l_1 \sqrt{-\varrho _6} cd(\zeta )^4}{h_{1} cd(\zeta )^2+h_{2}}, \end{aligned}$$

(46)

where

$$\begin{aligned} \left\{ \begin{array}{ll} h_1=\frac{1160 c_1^2 l_1^2 \varrho _6 \left( 1365 c_1^4+64 l_1^2 \varrho _6 \left( 5 l_1^2 \left( C^2+1\right) +2 m_1^2\right) \right) }{349440 c_1^4 l_1^2 m_1^2 \varrho _6+1863225 c_1^8-4096 l_1^4 \varrho _6^2 \left( 25 l_1^4 \left( C^4-C^2+1\right) -4 m_1^4\right) },\\ h_2= -\frac{1113600 c_1^2 l_1^6 \varrho _6^2}{349440 c_1^4 l_1^2 m_1^2 \varrho _6+1863225 c_1^8-4096 l_1^4 \varrho _6^2 \left( 25 l_1^4 \left( C^4-C^2+1\right) -4 m_1^4\right) }. \end{array} \right. \end{aligned}$$

Remark

If $C\rightarrow 1$ in Eq. (43), the stochastic dark optical soliton of Eq. (1) are extracted such as:

$$\begin{aligned} F_{1,1}(x, t)=\left( \frac{c_1 \text {tanh}^2\left( l_1 x-l_2 t\right) }{\sqrt{h_{11} \text {tanh}^2\left( l_1 x-l_2 t\right) +h_{22}}}\right) e^{i m_1 x-\frac{1}{2} \sigma _1^2 t-\sigma _1 W(t)}, \end{aligned}$$

(47)

the stochastic optical dark soliton of Eq. (2) are extracted such as:

$$\begin{aligned} G_{1,1}(x, t)= \left( \frac{7 c_1^2}{4 l_1 \sqrt{-\varrho _6}}-\frac{2 l_1 \sqrt{-\varrho _6} \text {tanh}^4\left( l_1 x-l_2 t\right) }{h_{1} \text {tanh}^2\left( l_1 x-l_2 t\right) +h_{2}}\right) e^{i m_1 x-\frac{1}{2} \sigma _1^2 t-\sigma _1 W(t)}. \end{aligned}$$

(48)

Remark

If $C\rightarrow 0$ in Eq. (43), the stochastic optical solitary wave solution of Eq. (1) are extracted such as:

$$\begin{aligned} F_{1,0}(x, t)= \left( \frac{c_1 \sin ^2\left( l_1 x-l_2 t\right) }{\sqrt{h_{1} \sin ^2\left( l_1 x-l_2 t\right) +h_{2}}}\right) e^{i m_1 x-\frac{1}{2} \sigma _1^2 t-\sigma _1 W(t)}, \end{aligned}$$

(49)

or

$$\begin{aligned} F_{2,0}(x, t)= \left( \frac{c_1 \cos ^2\left( l_1 x-l_2 t\right) }{\sqrt{h_{1} \cos ^2\left( l_1 x-l_2 t\right) +h_{2}}}\right) e^{i m_1 x-\frac{1}{2} \sigma _1^2 t-\sigma _1 W(t)}, \end{aligned}$$

(50)

the stochastic optical solitary wave solution of Eq. (2) are extracted such as:

$$\begin{aligned} G_{1,0}(x, t)= \left( \frac{7 c_1^2}{4 l_1 \sqrt{-\varrho _6}}-\frac{2 l_1 \sqrt{-\varrho _6} \sin ^4\left( l_1 x-l_2 t\right) }{h_{1} \sin ^2\left( l_1 x-l_2 t\right) +h_{2}}\right) e^{i m_1 x-\frac{1}{2} \sigma _1^2 t-\sigma _1 W(t)}, \end{aligned}$$

(51)

or

$$\begin{aligned} G_{2,0}(x, t)= \left( \frac{7 c_1^2}{4 l_1 \sqrt{-\varrho _6}}-\frac{2 l_1 \sqrt{-\varrho _6} \cos ^4\left( l_1 x-l_2 t\right) }{h_{1} \cos ^2\left( l_1 x-l_2 t\right) +h_{2}}\right) e^{i m_1 x-\frac{1}{2} \sigma _1^2 t-\sigma _1 W(t)}. \end{aligned}$$

(52)

$\Rightarrow$ If we take $\kappa _0=1-C^2$, $\kappa _2=2C^2-1$, $\kappa _4=-C^2$, $0<C<1$, then $\Lambda (\zeta )=cn(\zeta , C)$. So, JEF solution is retrieve such as:

$$\begin{aligned} F_{3,C}(\zeta )=\frac{c_1 cn(\zeta )^2}{\sqrt{h_{1} cn(\zeta )^2+h_{2}}}, \end{aligned}$$

(53)

$$\begin{aligned} G_{3,C}(\zeta )= \frac{7 c_1^2}{4 l_1 \sqrt{-\varrho _6}}-\frac{2 l_1 \sqrt{-\varrho _6} cn (\zeta )^4}{h_{1} cn (\zeta )^2+h_{2}}, \end{aligned}$$

(54)

where

$$\begin{aligned} \left\{ \begin{array}{ll} h_1=\frac{1160 c_1^2 l_1^2 \varrho _6 \left( 1365 c_1^4+64 l_1^2 \varrho _6 \left( \left( 5-10 C^2\right) l_1^2+2 m_1^2\right) \right) }{349440 c_1^4 l_1^2 m_1^2 \varrho _6+1863225 c_1^8-4096 l_1^4 \varrho _6^2 \left( 25 \left( C^4-C^2+1\right) l_1^4-4 m_1^4\right) },\\ h_2= -\frac{1113600 c_1^2 \left( C^2-1\right) l_1^6 \varrho _6^2}{-349440 c_1^4 l_1^2 m_1^2 \varrho _6-1863225 c_1^8+4096 l_1^4 \varrho _6^2 \left( 25 \left( C^4-C^2+1\right) l_1^4-4 m_1^4\right) }. \end{array} \right. \end{aligned}$$

Remark

If $C\rightarrow 1$ in Eq. (53), the stochastic optical bright soliton of Eq. (1) are extracted such as:

$$\begin{aligned} F_{3,1}(x, t)= \left( \frac{c_1 \text {sech}^2\left( l_1 x-l_2 t\right) }{\sqrt{h_{1} \text {sech}^2\left( l_1 x-l_2 t\right) +h_{2}}}\right) e^{i m_1 x-\frac{1}{2} \sigma _1^2 t-\sigma _1 W(t)}, \end{aligned}$$

(55)

the stochastic optical bright soliton of Eq. (2) are extracted such as:

$$\begin{aligned} G_{3,1}(x, t)= \left( \frac{7 c_1^2}{4 l_1 \sqrt{-\varrho _6}}-\frac{2 l_1 \sqrt{-\varrho _6} \text {sech}^4\left( l_1 x-l_2 t\right) }{h_{1} \text {sech}^2\left( l_1 x-l_2 t\right) +h_{2}}\right) e^{i m_1 x-\frac{1}{2} \sigma _1^2 t-\sigma _1 W(t)}. \end{aligned}$$

(56)

Remark

If $C\rightarrow 0$ in Eq. (53), the stochastic optical solitary wave solution of Eq. (1) are extracted such as:

$$\begin{aligned} F_{3,0}(x, t)= \left( \frac{c_1 \cos ^2\left( l_1 x-l_2 t\right) }{\sqrt{h_{1} \cos ^2\left( l_1 x-l_2 t\right) +h_{2}}}\right) e^{i m_1 x-\frac{1}{2} \sigma _1^2 t-\sigma _1 W(t)}, \end{aligned}$$

(57)

the stochastic optical solitary wave solution of Eq. (2) are extracted such as:

$$\begin{aligned} G_{3,0}(x, t)= \left( \frac{7 c_1^2}{4 l_1 \sqrt{-\varrho _6}}-\frac{2 l_1 \sqrt{-\varrho _6} \cos ^4\left( l_1 x-l_2 t\right) }{h_{1} \cos ^2\left( l_1 x-l_2 t\right) +h_{2}}\right) e^{i m_1 x-\frac{1}{2} \sigma _1^2 t-\sigma _1 W(t)}. \end{aligned}$$

(58)

$\Rightarrow$ If we take $\kappa _0=C^2-1$, $\kappa _2=2-C^2$, $\kappa _4=-1$, $0<C<1$, then $\Lambda (\zeta )=dn(\zeta , C)$. So, JEF solutions are retrieved such as:

$$\begin{aligned} F_{4,C}(\zeta )=\frac{c_1 dn(\zeta )^2}{\sqrt{h_{1} dn(\zeta )^2+h_{2}}}, \end{aligned}$$

(59)

$$\begin{aligned} G_{4,C}(\zeta )= \frac{7 c_1^2}{4 l_1 \sqrt{-\varrho _6}}-\frac{2 l_1 \sqrt{-\varrho _6} dn (\zeta )^4}{h_{1} dn (\zeta )^2+h_{2}}, \end{aligned}$$

(60)

where

$$\begin{aligned} \left\{ \begin{array}{ll} h_1=\frac{1160 c_1^2 l_1^2 \varrho _6 \left( 1365 c_1^4+64 l_1^2 \varrho _6 \left( 5 \left( C^2-2\right) l_1^2+2 m_1^2\right) \right) }{349440 c_1^4 l_1^2 m_1^2 \varrho _6+1863225 c_1^8-4096 l_1^4 \varrho _6^2 \left( 25 \left( C^4-C^2+1\right) l_1^4-4 m_1^4\right) },\\ h_2= -\frac{1113600 c_1^2 \lambda _0 l_1^6 \varrho _6^2}{349440 c_1^4 l_1^2 m_1^2 \varrho _6+1863225 c_1^8-4096 l_1^4 \varrho _6^2 \left( 25 \left( C^4-C^2+1\right) l_1^4-4 m_1^4\right) }. \end{array} \right. \end{aligned}$$

Remark

If $C\rightarrow 1$ in Eq. (59), the stochastic optical bright soliton of Eq. (1) are extracted such as:

$$\begin{aligned} F_{4,1}(x, t)= \left( \frac{c_1 \text {sech}^2\left( l_1 x-l_2 t\right) }{\sqrt{h_{1} \text {sech}^2\left( l_1 x-l_2 t\right) +h_{2}}}\right) e^{i m_1 x-\frac{1}{2} \sigma _1^2 t-\sigma _1 W(t)}, \end{aligned}$$

(61)

the stochastic optical bright soliton of Eq. (2) are extracted such as:

$$\begin{aligned} G_{4,1}(x, t)= \left( \frac{7 c_1^2}{4 l_1 \sqrt{-\varrho _6}}-\frac{2 l_1 \sqrt{-\varrho _6} \text {sech}^4\left( l_1 x-l_2 t\right) }{h_{1} \text {sech}^2\left( l_1 x-l_2 t\right) +h_{2}}\right) e^{i m_1 x-\frac{1}{2} \sigma _1^2 t-\sigma _1 W(t)}. \end{aligned}$$

(62)

$\bullet$ If we take $\kappa _0=C^2$, $\kappa _2=-(1+C^2)$, $\kappa _4=1$, $0<C<1$, then $\Lambda (\zeta )=sn(\zeta , C)$ or $\Lambda (\zeta )=dc(\zeta , C)$. So, JEF solutions are retrieved such as:

$$\begin{aligned} F_{5,C}(\zeta )=\frac{c_1 sn(\zeta )^2}{\sqrt{h_{1} sn(\zeta )^2+h_{2}}}, \end{aligned}$$

(63)

or

$$\begin{aligned} F_{6,C}(\zeta )= \frac{c_1 dc(\zeta )^2}{\sqrt{h_{1} dc(\zeta )^2+h_{2}}}, \end{aligned}$$

(64)

$$\begin{aligned} G_{5,C}(\zeta )= \frac{7 c_1^2}{4 l_1 \sqrt{-\varrho _6}}-\frac{2 l_1 \sqrt{-\varrho _6} sn (\zeta )^4}{h_{1} sn (\zeta )^2+h_{2}}, \end{aligned}$$

(65)

or

$$\begin{aligned} G_{5,C}(\zeta )=\frac{7 c_1^2}{4 l_1 \sqrt{-\varrho _6}}-\frac{2 l_1 \sqrt{-\varrho _6} dc (\zeta )^4}{h_{1} dc (\zeta )^2+h_{2}}, \end{aligned}$$

(66)

where

$$\begin{aligned} \left\{ \begin{array}{ll} h_1=\frac{1160 c_1^2 l_1^2 \varrho _6 \left( 1365 c_1^4-64 l_1^2 \varrho _6 \left( 5 \left( C^2-1\right) l_1^2-2 m_1^2\right) \right) }{349440 c_1^4 l_1^2 m_1^2 \varrho _6+1863225 c_1^8-4096 l_1^4 \varrho _6^2 \left( 25 \left( C^4-5 C^2+1\right) l_1^4-4 m_1^4\right) },\\ h_2=-\frac{1113600 c_1^2 \lambda _0 l_1^6 \varrho _6^2}{349440 c_1^4 l_1^2 m_1^2 \varrho _6+1863225 c_1^8-4096 l_1^4 \varrho _6^2 \left( 25 \left( C^4-5 C^2+1\right) l_1^4-4 m_1^4\right) }. \end{array} \right. \end{aligned}$$

Remark

If $C\rightarrow 1$ in Eq. (64), the stochastic optical singular soliton of Eq. (1) are extracted such as:

$$\begin{aligned} F_{5,1}(x, t)= \left( \frac{c_1 \coth ^2\left( l_1 x-l_2 t\right) }{\sqrt{h_{1} \coth ^2\left( l_1 x-l_2 t\right) +h_{2}}}\right) e^{i m_1 x-\frac{1}{2} \sigma _1^2 t-\sigma _1 W(t)}, \end{aligned}$$

(67)

the stochastic optical singular soliton of Eq. (2) are extracted such as:

$$\begin{aligned} G_{5,1}(x, t)= \left( \frac{7 c_1^2}{4 l_1 \sqrt{-\varrho _6}}-\frac{2 l_1 \sqrt{-\varrho _6} \coth ^4\left( l_1 x-l_2 t\right) }{h_{1} \coth ^2\left( l_1 x-l_2 t\right) +h_{2}}\right) e^{i m_1 x-\frac{1}{2} \sigma _1^2 t-\sigma _1 W(t)}. \end{aligned}$$

(68)

Remark

If $C\rightarrow 0$ in Eq. (64), the stochastic optical solitary wave solution of Eq. (1) are extracted such as:

$$\begin{aligned} F_{5,0}(x, t)= \left( \frac{c_1 \csc ^2\left( l_1 x-l_2 t\right) }{\sqrt{h_{1} \csc ^2\left( l_1 x-l_2 t\right) +h_{2}}}\right) e^{i m_1 x-\frac{1}{2} \sigma _1^2 t-\sigma _1 W(t)}, \end{aligned}$$

(69)

the stochastic optical solitary wave solution of Eq. (2) are extracted such as:

$$\begin{aligned} G_{5,0}(x, t)= \left( \frac{7 c_1^2}{4 l_1 \sqrt{-\varrho _6}}-\frac{2 l_1 \sqrt{-\varrho _6} \csc ^4\left( l_1 x-l_2 t\right) }{h_{1} \csc ^2\left( l_1 x-l_2 t\right) +h_{2}}\right) e^{i m_1 x-\frac{1}{2} \sigma _1^2 t-\sigma _1 W(t)}. \end{aligned}$$

(70)

$\Rightarrow$ If we take $\kappa _0=-C^2$, $\kappa _2=-1+2C^2$, $\kappa _4=1-C^2$, $0<C<1$, then $\Lambda (\zeta )=nc(\zeta , C)$. So, JEF solutions are retrieved such as:

$$\begin{aligned} F_{7,C}(\zeta )=\frac{c_1 nc(\zeta )^2}{\sqrt{h_{1} nc(\zeta )^2+h_{2}}}, \end{aligned}$$

(71)

$$\begin{aligned} G_{7,C}(\zeta )= \frac{7 c_1^2}{4 l_1 \sqrt{-\varrho _6}}-\frac{2 l_1 \sqrt{-\varrho _6} nc (\zeta )^4}{h_{1} nc (\zeta )^2+h_{2}}, \end{aligned}$$

(72)

where

$$\begin{aligned} \left\{ \begin{array}{ll} h_1=\frac{1160 c_1^2 l_1^2 \varrho _6 \left( 1365 c_1^4+64 l_1^2 \varrho _6 \left( \left( 5-10 C^2\right) l_1^2+2 m_1^2\right) \right) }{349440 c_1^4 l_1^2 m_1^2 \varrho _6+1863225 c_1^8-4096 l_1^4 \varrho _6^2 \left( 25 \left( C^4-C^2+1\right) l_1^4-4 m_1^4\right) },\\ h_2= -\frac{1113600 c_1^2 \lambda _0 l_1^6 \varrho _6^2}{349440 c_1^4 l_1^2 m_1^2 \varrho _6+1863225 c_1^8-4096 l_1^4 \varrho _6^2 \left( 25 \left( C^4-C^2+1\right) l_1^4-4 m_1^4\right) }. \end{array} \right. \end{aligned}$$

Remark

If $C\rightarrow 1$ in Eq. (71), the stochastic optical periodic soliton of Eq. (1) are extracted such as:

$$\begin{aligned} F_{7,1}(x, t)= \left( \frac{c_1 \cosh ^2\left( l_1 x-l_2 t\right) }{\sqrt{h_{1} \cosh ^2\left( l_1 x-l_2 t\right) +h_{2}}}\right) e^{i m_1 x-\frac{1}{2} \sigma _1^2 t-\sigma _1 W(t)}, \end{aligned}$$

(73)

the stochastic optical periodic soliton of Eq. (2) are extracted such as:

$$\begin{aligned} G_{7,1}(x, t)= \left( \frac{7 c_1^2}{4 l_1 \sqrt{-\varrho _6}}-\frac{2 l_1 \sqrt{-\varrho _6} \cosh ^4\left( l_1 x-l_2 t\right) }{h_{1} \cosh ^2\left( l_1 x-l_2 t\right) +h_{2}}\right) e^{i m_1 x-\frac{1}{2} \sigma _1^2 t-\sigma _1 W(t)}. \end{aligned}$$

(74)

Remark

If $C\rightarrow 0$ in Eq. (71), the stochastic optical solitary wave solution of Eq. (1) are extracted such as:

$$\begin{aligned} F_{7,0}(x, t)=\left( \frac{c_1 \sec ^2\left( l_1 x-l_2 t\right) }{\sqrt{h_{1} \sec ^2\left( l_1 x-l_2 t\right) +h_{2}}}\right) e^{i m_1 x-\frac{1}{2} \sigma _1^2 t-\sigma _1 W(t)}, \end{aligned}$$

(75)

the stochastic optical solitary wave solution of Eq. (2) are extracted such as:

$$\begin{aligned} G_{7,0}(x, t)= \left( \frac{7 c_1^2}{4 l_1 \sqrt{-\varrho _6}}-\frac{2 l_1 \sqrt{-\varrho _6} \sec ^4\left( l_1 x-l_2 t\right) }{h_{1} \sec ^2\left( l_1 x-l_2 t\right) +h_{2}}\right) e^{i m_1 x-\frac{1}{2} \sigma _1^2 t-\sigma _1 W(t)}. \end{aligned}$$

(76)

$\Rightarrow$ If we take $\kappa _0=-1$, $\kappa _2=2-C^2$, $\kappa _4=-(1-C^2)$, $0<C<1$, then $\Lambda (\zeta )=nd(\zeta , C)$. So, JEF solutions are retrieved such as:

$$\begin{aligned} F_{8,C}(\zeta )=\frac{c_1 nd(\zeta )^2}{\sqrt{h_{1} nd(\zeta )^2+h_{2}}}, \end{aligned}$$

(77)

$$\begin{aligned} G_{8,C}(\zeta )= \frac{7 c_1^2}{4 l_1 \sqrt{-\varrho _6}}-\frac{2 l_1 \sqrt{-\varrho _6} nd (\zeta )^4}{h_{1} nd (\zeta )^2+h_{2}}, \end{aligned}$$

(78)

where

$$\begin{aligned} \left\{ \begin{array}{ll} h_1=\frac{1160 c_1^2 l_1^2 \varrho _6 \left( 1365 c_1^4+64 l_1^2 \varrho _6 \left( 5 \left( C^2-2\right) l_1^2+2 m_1^2\right) \right) }{349440 c_1^4 l_1^2 m_1^2 \varrho _6+1863225 c_1^8-4096 l_1^4 \varrho _6^2 \left( 25 \left( C^4-C^2+1\right) l_1^4-4 m_1^4\right) },\\ h_2= -\frac{1113600 c_1^2 \lambda _0 l_1^6 \varrho _6^2}{349440 c_1^4 l_1^2 m_1^2 \varrho _6+1863225 c_1^8-4096 l_1^4 \varrho _6^2 \left( 25 \left( C^4-C^2+1\right) l_1^4-4 m_1^4\right) }. \end{array} \right. \end{aligned}$$

Remark

If $C\rightarrow 1$ in Eq. (77), the stochastic optical periodic soliton of Eq. (1) are extracted such as:

$$\begin{aligned} F_{8,1}(x, t)= \left( \frac{c_1 \cosh ^2\left( l_1 x-l_2 t\right) }{\sqrt{h_{1} \cosh ^2\left( l_1 x-l_2 t\right) +h_{2}}}\right) e^{i m_1 x-\frac{1}{2} \sigma _1^2 t-\sigma _1 W(t)}, \end{aligned}$$

(79)

the stochastic optical periodic soliton of Eq. (2) are extracted such as:

$$\begin{aligned} G_{8,1}(x, t)= \left( \frac{7 c_1^2}{4 l_1 \sqrt{-\varrho _6}}-\frac{2 l_1 \sqrt{-\varrho _6} \cosh ^4\left( l_1 x-l_2 t\right) }{h_{1} \cosh ^2\left( l_1 x-l_2 t\right) +h_{2}}\right) e^{i m_1 x-\frac{1}{2} \sigma _1^2 t-\sigma _1 W(t)}. \end{aligned}$$

(80)

Remark

If $C\rightarrow 0$ in Eq. (77), the stochastic optical solitary wave of Eq. (1) are extracted such as:

$$\begin{aligned} F_{8,0}(x, t)= \left( \frac{c_1 \cot ^2\left( l_1 x-l_2 t\right) }{\sqrt{h_{1} \cot ^2\left( l_1 x-l_2 t\right) +h_{2}}}\right) e^{i m_1 x-\frac{1}{2} \sigma _1^2 t-\sigma _1 W(t)}, \end{aligned}$$

(81)

the stochastic optical solitary wave of Eq. (2) are extracted such as:

$$\begin{aligned} G_{8,0}(x, t)= \left( \frac{7 c_1^2}{4 l_1 \sqrt{-\varrho _6}}-\frac{2 l_1 \sqrt{-\varrho _6} \cot ^4\left( l_1 x-l_2 t\right) }{h_{1} \cot ^2\left( l_1 x-l_2 t\right) +h_{2}}\right) e^{i m_1 x-\frac{1}{2} \sigma _1^2 t-\sigma _1 W(t)}. \end{aligned}$$

(82)

$\Rightarrow$ If we take $\kappa _0=1$, $\kappa _2=2-C^2$, $\kappa _4=1-C^2$, $0<C<1$, then $\Lambda (\zeta )=sc(\zeta , C)$. So, JEF solutions are retrieved such as:

$$\begin{aligned} F_{9,C}(\zeta )=\frac{c_1 sc(\zeta )^2}{\sqrt{h_{1} sc(\zeta )^2+h_{2}}}, \end{aligned}$$

(83)

$$\begin{aligned} G_{9,C}(\zeta )= \frac{7 c_1^2}{4 l_1 \sqrt{-\varrho _6}}-\frac{2 l_1 \sqrt{-\varrho _6} sc(\zeta )^4}{h_{1} sc(\zeta )^2+h_{2}}, \end{aligned}$$

(84)

where

$$\begin{aligned} \left\{ \begin{array}{ll} h_1=\frac{1160 c_1^2 l_1^2 \varrho _6 \left( 1365 c_1^4+64 l_1^2 \varrho _6 \left( 5 \left( C^2-2\right) l_1^2+2 m_1^2\right) \right) }{349440 c_1^4 l_1^2 m_1^2 \varrho _6+1863225 c_1^8-4096 l_1^4 \varrho _6^2 \left( 25 \left( C^4-C^2+1\right) l_1^4-4 m_1^4\right) },\\ h_2= -\frac{1113600 c_1^2 \lambda _0 l_1^6 \varrho _6^2}{349440 c_1^4 l_1^2 m_1^2 \varrho _6+1863225 c_1^8-4096 l_1^4 \varrho _6^2 \left( 25 \left( C^4-C^2+1\right) l_1^4-4 m_1^4\right) }. \end{array} \right. \end{aligned}$$

Remark

If $C\rightarrow 1$ in Eq. (83), the stochastic optical periodic soliton of Eq. (1) are extracted such as:

$$\begin{aligned} F_{9,1}(x, t)= \left( \frac{c_1 \sinh ^2\left( l_1 x-l_2 t\right) }{\sqrt{h_{1} \sinh ^2\left( l_1 x-l_2 t\right) +h_{2}}}\right) e^{i m_1 x-\frac{1}{2} \sigma _1^2 t-\sigma _1 W(t)}, \end{aligned}$$

(85)

the stochastic optical periodic soliton of Eq. (2) are extracted such as:

$$\begin{aligned} G_{9,1}(x, t)= \left( \frac{7 c_1^2}{4 l_1 \sqrt{-\varrho _6}}-\frac{2 l_1 \sqrt{-\varrho _6} \sinh ^4\left( l_1 x-l_2 t\right) }{h_{1} \sinh ^2\left( l_1 x-l_2 t\right) +h_{2}}\right) e^{i m_1 x-\frac{1}{2} \sigma _1^2 t-\sigma _1 W(t)}. \end{aligned}$$

(86)

Remark

If $C\rightarrow 0$ in Eq. (77), the stochastic optical solitary wave of Eq. (1) are extracted such as:

$$\begin{aligned} F_{9,0}(x, t)= \left( \frac{c_1 \tan ^2\left( l_1 x-l_2 t\right) }{\sqrt{h_{1} \tan ^2\left( l_1 x-l_2 t\right) +h_{2}}}\right) e^{i m_1 x-\frac{1}{2} \sigma _1^2 t-\sigma _1 W(t)}, \end{aligned}$$

(87)

the stochastic optical solitary wave of Eq. (2) are extracted such as:

$$\begin{aligned} G_{9,0}(x, t)= \left( \frac{7 c_1^2}{4 l_1 \sqrt{-\varrho _6}}-\frac{2 l_1 \sqrt{-\varrho _6} \tan ^4\left( l_1 x-l_2 t\right) }{h_{1} \tan ^2\left( l_1 x-l_2 t\right) +h_{2}}\right) e^{i m_1 x-\frac{1}{2} \sigma _1^2 t-\sigma _1 W(t)}. \end{aligned}$$

(88)

$\Rightarrow$ If we take $\kappa _0=1$, $\kappa _2=2C^2-1$, $\kappa _4=-C^2(1-C^2)$, $0<C<1$, then $\Lambda (\zeta )=sd(\zeta , C)$. So, JEF solutions are retrieved such as:

$$\begin{aligned} F_{10,C}(\zeta )=\frac{c_1 sd(\zeta )^2}{\sqrt{h_{1} sd(\zeta )^2+h_{2}}}, \end{aligned}$$

(89)

$$\begin{aligned} G_{10,C}(\zeta )= \frac{7 c_1^2}{4 l_1 \sqrt{-\varrho _6}}-\frac{2 l_1 \sqrt{-\varrho _6} sd(\zeta )^4}{h_{1} sd(\zeta )^2+h_{2}}, \end{aligned}$$

(90)

where

$$\begin{aligned} \left\{ \begin{array}{ll} h_1=\frac{1160 c_1^2 l_1^2 \varrho _6 \left( 1365 c_1^4+64 l_1^2 \varrho _6 \left( \left( 5-10 C^2\right) l_1^2+2 m_1^2\right) \right) }{349440 c_1^4 l_1^2 m_1^2 \varrho _6+1863225 c_1^8-4096 l_1^4 \varrho _6^2 \left( 25 \left( C^4-C^2+1\right) l_1^4-4 m_1^4\right) },\\ h_2= -\frac{1113600 c_1^2 \lambda _0 l_1^6 \varrho _6^2}{349440 c_1^4 l_1^2 m_1^2 \varrho _6+1863225 c_1^8-4096 l_1^4 \varrho _6^2 \left( 25 \left( C^4-C^2+1\right) l_1^4-4 m_1^4\right) }. \end{array} \right. \end{aligned}$$

Remark

If $C\rightarrow 1$ in Eq. (89), the stochastic optical periodic soliton of Eq. (1) are extracted such as:

$$\begin{aligned} F_{10,1}(x, t)= \left( \frac{c_1 \sinh ^2\left( l_1 x-l_2 t\right) }{\sqrt{h_{1} \sinh ^2\left( l_1 x-l_2 t\right) +h_{2}}}\right) e^{i m_1 x-\frac{1}{2} \sigma _1^2 t-\sigma _1 W(t)}, \end{aligned}$$

(91)

the stochastic optical periodic soliton of Eq. (2) are extracted such as:

$$\begin{aligned} G_{10,1}(x, t)=\left( \frac{7 c_1^2}{4 l_1 \sqrt{-\varrho _6}}-\frac{2 l_1 \sqrt{-\varrho _6} \sinh ^4\left( l_1 x-l_2 t\right) }{h_{1} \sinh ^2\left( l_1 x-l_2 t\right) +h_{2}}\right) e^{i m_1 x-\frac{1}{2} \sigma _1^2 t-\sigma _1 W(t)}. \end{aligned}$$

(92)

Remark

If $C\rightarrow 0$ in Eq. (89), the stochastic optical solitary wave solution of Eq. (1) are extracted such as:

$$\begin{aligned} F_{10,0}(x, t)= \left( \frac{c_1 \sin ^2\left( l_1 x-l_2 t\right) }{\sqrt{h_{1} \sin ^2\left( l_1 x-l_2 t\right) +h_{2}}}\right) e^{i m_1 x-\frac{1}{2} \sigma _1^2 t-\sigma _1 W(t)}, \end{aligned}$$

(93)

the stochastic optical solitary wave solution of Eq. (2) are extracted such as:

$$\begin{aligned} G_{10,0}(x, t)=\left( \frac{7 c_1^2}{4 l_1 \sqrt{-\varrho _6}}-\frac{2 l_1 \sqrt{-\varrho _6} \sin ^4\left( l_1 x-l_2 t\right) }{h_{1} \sin ^2\left( l_1 x-l_2 t\right) +h_{2}}\right) e^{i m_1 x-\frac{1}{2} \sigma _1^2 t-\sigma _1 W(t)}. \end{aligned}$$

(94)

$\Rightarrow$ If we take $\kappa _0=1-C^2$, $\kappa _2=2-C^2$, $\kappa _4=1$, $0<C<1$, then $\Lambda (\zeta )=cs(\zeta , C)$. So, JEF solutions are retrieved such as:

$$\begin{aligned} F_{11,C}(\zeta )=\frac{c_1 cs(\zeta )^2}{\sqrt{h_{1} cs(\zeta )^2+h_{2}}}, \end{aligned}$$

(95)

$$\begin{aligned} G_{11,C}(\zeta )= \frac{7 c_1^2}{4 l_1 \sqrt{-\varrho _6}}-\frac{2 l_1 \sqrt{-\varrho _6} cs(\zeta )^4}{h_{1} cs(\zeta )^2+h_{2}}, \end{aligned}$$

(96)

where

$$\begin{aligned} \left\{ \begin{array}{ll} h_1=-\frac{5 c_2^2 \left( \beta c_0 c_2-2 \beta c_1^2\right) \left( 16 \beta c_1^4+40 \beta c_0 c_2 c_1^2+3 c_2^2 \left( C^2-2\right) l_1^2\right) }{-256 \beta ^2 c_1^8-1280 \beta ^2 c_0 c_2 c_1^6-1600 \beta ^2 c_0^2 c_2^2 c_1^4+9 c_2^4 \left( C^4-C^2+1\right) l_1^4},\\ h_2= \frac{45 c_2^4 \lambda _0 l_1^2 \left( \beta c_0 c_2-2 \beta c_1^2\right) }{-256 \beta ^2 c_1^8-1280 \beta ^2 c_0 c_2 c_1^6-1600 \beta ^2 c_0^2 c_2^2 c_1^4+9 c_2^4 \left( C^4-C^2+1\right) l_1^4}. \end{array} \right. \end{aligned}$$

Remark

If $C\rightarrow 1$ in Eq. (95), the stochastic optical periodic soliton of Eq. (1) are extracted such as:

$$\begin{aligned} F_{11,1}(x, t)= \left( \frac{c_1 \cosh ^2\left( l_1 x-l_2 t\right) }{\sqrt{h_{1} \cosh ^2\left( l_1 x-l_2 t\right) +h_{2}}}\right) e^{i m_1 x-\frac{1}{2} \sigma _1^2 t-\sigma _1 W(t)}, \end{aligned}$$

(97)

the stochastic optical periodic soliton of Eq. (2) are extracted such as:

$$\begin{aligned} G_{11,1}(x, t)= \left( \frac{7 c_1^2}{4 l_1 \sqrt{-\varrho _6}}-\frac{2 l_1 \sqrt{-\varrho _6} \cosh ^4\left( l_1 x-l_2 t\right) }{h_{1} \cosh ^2\left( l_1 x-l_2 t\right) +h_{2}}\right) e^{i m_1 x-\frac{1}{2} \sigma _1^2 t-\sigma _1 W(t)}. \end{aligned}$$

(98)

Remark

If $C\rightarrow 0$ in Eq. (95), the stochastic optical solitary wave solution of Eq. (1) are extracted such as:

$$\begin{aligned} F_{11,0}(x, t)= \left( \frac{c_1 \sin ^2\left( l_1 x-l_2 t\right) }{\sqrt{h_{1} \sin ^2\left( l_1 x-l_2 t\right) +h_{2}}}\right) e^{i m_1 x-\frac{1}{2} \sigma _1^2 t-\sigma _1 W(t)}, \end{aligned}$$

(99)

the stochastic optical solitary wave solution of Eq. (2) are extracted such as:

$$\begin{aligned} G_{11,0}(x, t)=\left( \frac{7 c_1^2}{4 l_1 \sqrt{-\varrho _6}}-\frac{2 l_1 \sqrt{-\varrho _6} \sin ^4\left( l_1 x-l_2 t\right) }{h_{1} \sin ^2\left( l_1 x-l_2 t\right) +h_{2}}\right) e^{i m_1 x-\frac{1}{2} \sigma _1^2 t-\sigma _1 W(t)}. \end{aligned}$$

(100)

$\Rightarrow$ If we take $\kappa _0=C^2(1-C^2)$, $\kappa _2=2C^2-1$, $\kappa _4=1$, $0<C<1$, then $\Lambda (\zeta )=ds(\zeta , C)$. So, JEF solutions are retrieved such as:

$$\begin{aligned} F_{12,C}(\zeta )=\frac{c_1 ds(\zeta )^2}{\sqrt{h_{1} ds(\zeta )^2+h_{2}}}, \end{aligned}$$

(101)

$$\begin{aligned} G_{12,C}(\zeta )= \frac{7 c_1^2}{4 l_1 \sqrt{-\varrho _6}}-\frac{2 l_1 \sqrt{-\varrho _6} ds(\zeta )^4}{h_{1} ds(\zeta )^2+h_{2}}, \end{aligned}$$

(102)

where

$$\begin{aligned} \left\{ \begin{array}{ll} h_1=\frac{1160 c_1^2 l_1^2 \varrho _6 \left( 1365 c_1^4+64 l_1^2 \varrho _6 \left( 5 \left( C^2-2\right) l_1^2+2 m_1^2\right) \right) }{349440 c_1^4 l_1^2 m_1^2 \varrho _6+1863225 c_1^8-4096 l_1^4 \varrho _6^2 \left( 25 \left( C^4-C^2+1\right) l_1^4-4 m_1^4\right) },\\ h_2= -\frac{1113600 c_1^2 \left( C^2-1\right) l_1^6 \varrho _6^2}{-349440 c_1^4 l_1^2 m_1^2 \varrho _6-1863225 c_1^8+4096 l_1^4 \varrho _6^2 \left( 25 \left( C^4-C^2+1\right) l_1^4-4 m_1^4\right) }. \end{array} \right. \end{aligned}$$

Remark

If $C\rightarrow 1$ in Eq. (101), the stochastic optical singular soliton of Eq. (1) are extracted such as:

$$\begin{aligned} F_{12,1}(x, t)= \left( \frac{c_1 \text {csch}^2\left( l_1 x-l_2 t\right) }{\sqrt{h_{1} \text {csch}^2\left( l_1 x-l_2 t\right) +h_{2}}}\right) e^{i m_1 x-\frac{1}{2} \sigma _1^2 t-\sigma _1 W(t)}, \end{aligned}$$

(103)

the stochastic optical singular soliton of Eq. (2) are extracted such as:

$$\begin{aligned} G_{12,1}(x, t)= \left( \frac{7 c_1^2}{4 l_1 \sqrt{-\varrho _6}}-\frac{2 l_1 \sqrt{-\varrho _6} \text {csch}^4\left( l_1 x-l_2 t\right) }{h_{1} \text {csch}^2\left( l_1 x-l_2 t\right) +h_{2}}\right) e^{i m_1 x-\frac{1}{2} \sigma _1^2 t-\sigma _1 W(t)}. \end{aligned}$$

(104)

Remark

If $C\rightarrow 0$ in Eq. (101), the stochastic optical solitary wave solution of Eq. (1) are extracted such as:

$$\begin{aligned} F_{12,0}(x, t)= \left( \frac{c_1 \text {csc}^2\left( l_1 x-l_2 t\right) }{\sqrt{h_{1} \text {csc}^2\left( l_1 x-l_2 t\right) +h_{2}}}\right) e^{i m_1 x-\frac{1}{2} \sigma _1^2 t-\sigma _1 W(t)}, \end{aligned}$$

(105)

the stochastic optical solitary wave solution of Eq. (2) are extracted such as:

$$\begin{aligned} G_{12,0}(x, t)= \left( \frac{7 c_1^2}{4 l_1 \sqrt{-\varrho _6}}-\frac{2 l_1 \sqrt{-\varrho _6} \text {csc}^4\left( l_1 x-l_2 t\right) }{h_{1} \text {csc}^2\left( l_1 x-l_2 t\right) +h_{2}}\right) e^{i m_1 x-\frac{1}{2} \sigma _1^2 t-\sigma _1 W(t)}. \end{aligned}$$

(106)

$\Rightarrow$ If we take $\kappa _0=\frac{1-C^2}{4}$, $\kappa _2=\frac{1+C^2}{2}$, $\kappa _4=\frac{1-C^2}{4}$, $0<C<1$, then $\Lambda (\zeta )=nc(\zeta , C)\pm sc(\zeta , C)$. So, JEF solutions are retrieved such as:

$$\begin{aligned} F_{13,C}(\zeta )=\frac{c_1 (cn(\zeta )\pm sc(\zeta ))^2}{\sqrt{h_{1} (cn(\zeta )\pm sc(\zeta ) )^2+h_{2}}}, \end{aligned}$$

(107)

$$\begin{aligned} G_{13,C}(\zeta )= \frac{7 c_1^2}{4 l_1 \sqrt{-\varrho _6}}-\frac{2 l_1 \sqrt{-\varrho _6} (cn(\zeta )\pm sc(\zeta ) )^4}{h_{1} cn (cn(\zeta )\pm sc(\zeta ) )^2+h_{2}}, \end{aligned}$$

(108)

where

$$\begin{aligned} \left\{ \begin{array}{ll} h_1=\frac{1160 c_1^2 l_1^2 \varrho _6 \left( 1365 c_1^4-32 l_1^2 \varrho _6 \left( 5 \left( C^2+1\right) l_1^2-4 m_1^2\right) \right) }{349440 c_1^4 l_1^2 m_1^2 \varrho _6+1863225 c_1^8-256 l_1^4 \varrho _6^2 \left( 25 \left( C^4+14 C^2+1\right) l_1^4-64 m_1^4\right) },\\ h_2= -\frac{278400 c_1^2 \left( C^2-1\right) l_1^6 \varrho _6^2}{-349440 c_1^4 l_1^2 m_1^2 \varrho _6-1863225 c_1^8+256 l_1^4 \varrho _6^2 \left( 25 \left( C^4+14 C^2+1\right) l_1^4-64 m_1^4\right) }. \end{array} \right. \end{aligned}$$

Remark

If $C\rightarrow 1$ in Eq. (107), the stochastic optical dark soliton of Eq. (1) are extracted such as:

$$\begin{aligned} F_{13,1}(x, t)= \left( \frac{c_1 \text {sech}^2\left( l_1 x-l_2 t\right) }{\left( \tanh \left( l_1 x-l_2 t\right) +1\right) ^2 \sqrt{\frac{h_{1} \text {sech}^2\left( l_1 x-l_2 t\right) }{\left( \tanh \left( l_1 x-l_2 t\right) +1\right) ^2}+h_{2}}}\right) e^{i m_1 x-\frac{1}{2} \sigma _1^2 t-\sigma _1 W(t)}, \end{aligned}$$

(109)

the stochastic optical dark soliton of Eq. (2) are extracted such as:

$$\begin{aligned} G_{13,1}(x, t)= \left( \frac{7 c_1^2}{4 l_1 \sqrt{-\varrho _6}}-\frac{2 l_1 \sqrt{-\varrho _6} \text {sech}^4\left( l_1 x-l_2 t\right) }{\left( \tanh \left( l_1 x-l_2 t\right) +1\right) ^4 \left( \frac{h_{1} \text {sech}^2\left( l_1 x-l_2 t\right) }{\left( \tanh \left( l_1 x-l_2 t\right) +1\right) ^2}+h_{2}\right) }\right) \nonumber \\e^{i m_1 x-\frac{1}{2} \sigma _1^2 t-\sigma _1 W(t)}. \end{aligned}$$

(110)

Remark

If $C\rightarrow 0$ in Eq. (107), the stochastic optical solitary wave solutions of Eq. (1) are extracted such as:

$$\begin{aligned} F_{13,0}(x, t)= \left( \frac{c_1 \text {cos}^2\left( l_1 x-l_2 t\right) }{\left( \sin \left( l_1 x-l_2 t\right) +1\right) ^2 \sqrt{\frac{h_{1} \text {cos}^2\left( l_1 x-l_2 t\right) }{\left( \sin \left( l_1 x-l_2 t\right) +1\right) ^2}+h_{2}}}\right) e^{i m_1 x-\frac{1}{2} \sigma _1^2 t-\sigma _1 W(t)}, \end{aligned}$$

(111)

the stochastic solitary wave solutions of Eq. (2) are extracted such as:

$$\begin{aligned} G_{13,0}(x, t)= \left( \frac{7 c_1^2}{4 l_1 \sqrt{-\varrho _6}}-\frac{2 l_1 \sqrt{-\varrho _6} \text {cos}^4\left( l_1 x-l_2 t\right) }{\left( \sin \left( l_1 x-l_2 t\right) +1\right) ^4 \left( \frac{h_{1} \text {cos}^2\left( l_1 x-l_2 t\right) }{\left( \sin \left( l_1 x-l_2 t\right) +1\right) ^2}+h_{2}\right) }\right) \nonumber \\e^{i m_1 x-\frac{1}{2} \sigma _1^2 t-\sigma _1 W(t)}. \end{aligned}$$

(112)

Graphical results

This section, divided into two subsection firstly we will discussed the optical soliton solutions and their effect under the noise and secondly we will compare these result with the stochastic Backward Euler schemes

Optical soliton solutions

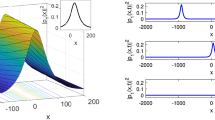
In this subsection, we will discussed the graphical behavior of our results of the coupled nonlinear Schrödinger equation under the influence of the multiplicative time noise.query:Reference [30, 60, 61, 62, 63, 64] was provided in the reference list; however, this was not mentioned or cited in the manuscript. As a rule, if a citation is present in the text, then it should be present in the list. Please provide the location of where to insert the reference citation in the main body text. Kindly ensure that all references are cited in ascending numerical order. We have drawn some solution in the form of 3D, 2D, and corresponding contour under the different effect of noise. We choose $\sigma _1,\sigma _2$ zero and our obtained result are provided us the classical optical soliton solutions under no influence of noise. Further we choose $\sigma _1,\sigma _2$ equal to 0.3, 0.6 that will gives us the randomness in the behaviors. The Fig. 1 is drawn for the solution $F_{1,1}(x,t)$ and this is the bright soliton solutions that is clearly obtained from the Fig. 1a,d,g when we choose the noise zero. Moreover, Fig. 1b,e,h are drawn by choosing $\sigma _1=0.3$ and Fig. 1c,f,i when $\sigma _1=0.6$ respectively. The Figs. 2 and 4 are gives us the solitary wave solutions and Fig. 3 is also gives us the bright soliton behavior.query:Figure cittaion 4 was manually cited here for sequential order, kindly check and confirm. These solutions are very effective for the complex envelope amplitudes of the two modulated weakly resonant waves in two polarizations which are used to describe the pulse propagation in high birefringence fiber (Fig. 4).

Fig. 1

The figure (a–c) show the 3D, figure (d–f) show the 2D, and figure (g–i) show the contours for the solution $F_{1,1}(x,t)$ under the different noise strengths.

Fig. 2

The figure (a–c) show the 3D, figure (d–f) show the 2D, and figure (g–i) show the contours for the solution $F_{2,0}(x,t)$ under the different noise strengths.

Fig. 3

The figure (a–c) show the 3D, figure (d–f) show the 2D, and figure (g–i) show the contours for the solution $G_{3,1}(x,t)$ under the different noise strengths.

Fig. 4

The figure (a–c) show the 3D, figure (d–f) show the 2D, and figure (g–i) show the contours for the solution $G_{1,0}(x,t)$ under the different noise strengths.

Comparisons of the results

In this subsection, the comparison of the results that are constructed successfully. The computational results are gained by proposed stochastic Backward Euler schemes (10–11) and the exact stochastic wave structures are gained by using the $\phi ^6$-model expansion. The main idea of the study is to compare the computational results with optical stochastic wave structure by constructing the initial conditions (ICs) and boundary conditions (BCs). These ICs and BCs are constructed by selecting the newly constructed optical soliton solutions. Here different five test problems are constructed and compare the results via simulations using MATLAB2015a. The 3D and line plots are drawn for the numerical schemes and different optical soliton solutions under the control parameter $\sigma _1$ and $\sigma _2$ which control the randomness in their behaviors. Test problem 1 is taken to draw the Fig. 5 for the numerical results the proposed schemes (10–11) are taken while comparing their results with $F_{1,0}(x,t)$ and $G_{1,0}(x,t)$. The Fig. 5a plot for the real values of F(x, t) and exact optical solution for the real values of $F_{1,0}(x,t)$ are shown in Fig. 5c while the combine line plot is shown in Fig. 5e that are displaced in (left-side) of Fig. 5. While similarly Fig. 5b plot for the real values of G(x, t) and exact optical solution for the real values of $G_{1,0}(x,t)$ are shown in Fig. 5d while the combine line plot is shown in Fig. 5f that are displaced in (right-column) side of Fig. 5. Their result is clearly shown the randomness in their behavior and gives us almost the same behavior for the computational result and exact optical solitary wave solutions. In Fig. 6 the numerical results the proposed schemes (10-11) are taken while compare their results with $F_{1,1}(x,t)$ and $G_{1,1}(x,t)$. The Fig. 6a,c,e are plotted for the real values of F(x, t) while Fig. 6b,d,f for the real values of G(x, t) in 3D and line shapes. The solutions $F_{5,1}(x,t)$ and $G_{5,1}(x,t)$ compare numerical results the are dispacted in Fig. 7 and the Fig. 7a,c,e for real(F(x, t)) while the Fig. 7b,d,f for real(G(x, t)). Same as the Fig. 8 are plots by selecting the $F_{9,1}(x,t)$ and $G_{9,1}(x,t)$ and $F_{9,0}(x,t)$ and $G_{9,0}(x,t)$ respectively. These graphs were created for the various parameter values listed in the Appendix (9). These results are interesting and new under the effect of the multiplicative time noise. So, these solutions successfully provided us with the same physical behaviors as the solutions under the influence of multiplicative time noise. Some test problems for the ICs and BCs are given as follows,

Test problem 1

The proposed Backward Euler schemes (10–11) is taken for the approximate solutions while Eqs. (49)and (51) as exact optical soliton solutions. The ICs and BCs are chooses such as

$$\begin{aligned} F(x, 0)= & \frac{0.08 e^{0.01849+(1.2 i) x} \sin ^2( -0.02 x)}{\sqrt{0.02043 \sin ^2( -0.02 x)-0.00002}} \end{aligned}$$

(113)

$$\begin{aligned} G(x, 0)= & e^{0.01849+( 1.2 i) x} \left( (0.634075 i)-\frac{(0.035327 i) \sin ^4(-0.02 x)}{0.02043 \sin ^2( -0.02 x)-0.00002}\right) , \end{aligned}$$

(114)

the BCs are as follows,

$$\begin{aligned} F(0, t)= & \frac{0.08 e^{-0.00045 t+(0.01849)} \sin ^2(0.987 t)}{\sqrt{0.02043 \sin ^2(0.987 t)-0.00002}}, \end{aligned}$$

(115)

$$\begin{aligned} G(0, t)= & e^{-0.00045 t+(0.01849)} \left( (0.634075 i)-\frac{(0.035327 i) \sin ^4(0.987 t)}{0.02043 \sin ^2(0.987 t+0.)-0.00002}\right) , \end{aligned}$$

(116)

$$\begin{aligned} F(5, t)= & \frac{0.08 e^{-0.00045 t+(0.01848\, +6. i)} \sin ^2(0.1\, -0.987 t)}{\sqrt{0.02043 \sin ^2(0.1\, -0.987 t)-0.00002}},~~~ \end{aligned}$$

(117)

$$\begin{aligned} G(5, t)= & e^{-0.00045 t+(0.01849\, +6. i)} \left( (0.634075 i)-\frac{(0.035327 i) \sin ^4(0.1\, -0.987 t)}{0.02043 \sin ^2(0.1\, -0.987 t)-0.00002}\right) . \end{aligned}$$

(118)

Using these conditions, the Fig. 5 is plotted to compare the results of Proposed Backward schemes (10-11) with the solutions $F_{1,1}(x,t)$ $G_{1,1}(x,t)$.

Fig. 5

The figure (a, c, e) are representations of the solutions F(x, t), $F_{1,1}(x,t)$ while figure (b, d, f) are representations of the solutions G(x, t), $G_{1,1}(x,t)$. The different values of parameters are use to construct these plots are mentioned in Appendix 9.

Test problem 2

The proposed Backward Euler schemes (10–11) is taken for the approximate solutions while Eqs. (47)and (48) as exact optical soliton solutions. The ICs and BCs are chooses such as

$$\begin{aligned} F(x, 0)= & \frac{0.08859 e^{i x} \tanh ^2(0.02 x)}{\sqrt{0.01527 \tanh ^2(0.02 x)-0.00001}}, \end{aligned}$$

(119)

$$\begin{aligned} G(x, 0)= & e^{i x} \left( (0.99303 i)-\frac{(1.81146 i) \tanh ^4(0.02 x)}{\tanh ^2(0.02 x)-0.00079}\right) , \end{aligned}$$

(120)

the BCs are as follows,

$$\begin{aligned} F(0, t)= & \frac{0.08859 e^{-0.005 t} \tanh ^2(1.1 t)}{\sqrt{0.01527 \tanh ^2(1.1 t)-0.00001}}, \end{aligned}$$

(121)

$$\begin{aligned} G(0, t)= & e^{-0.005 t} \left( (0.99304 i)-\frac{(1.81146 i) \tanh ^4(1.1 t)}{1. \tanh ^2(1.1 t)-0.00079}\right) , \end{aligned}$$

(122)

$$\begin{aligned} F(5, t)= & \frac{(0.02513\, -0.08495i) e^{-0.005 t} \tanh ^2(0.1\, -1.1 t)}{\sqrt{0.01527 \tanh ^2(0.1\, -1.1 t)-0.00001}}, \end{aligned}$$

(123)

$$\begin{aligned} G(5, t)= & e^{-0.005 t} \left( (0.95225\, +0.28169 i)-\frac{(1.73705\, +0.51384 i) \tanh ^4(0.1\, -1.1 t)}{1. \tanh ^2(0.1\, -1.1 t)-0.00079}\right) . \end{aligned}$$

(124)

Using these conditions, the Fig. 5 is plotted to compare the results of Proposed Backward schemes (10–11) with the solutions $F_{1,0}(x,t)$ $G_{1,0}(x,t)$.

Fig. 6

The figure (a, c, e) are representations of the solutions F(x, t), $F_{1,0}(x,t)$ while figure (b, d, f) are representations of the solutions G(x, t), $G_{1,0}(x,t)$. The different values of parameters are use to construct these plots are mentioned in Appendix 9.

Test problem 3

The proposed Backward Euler schemes (10–11) is taken for the approximate solutions while Eqs. (67) and (68) as exact optical soliton solutions. The ICs and BCs are chooses such as

$$\begin{aligned} F(x, 0)= & \frac{0.08 e^{0.10203+i x} \text {sech}^2( -0.02 x)}{\sqrt{0.02574 \text {sech}^2( -0.02 x)-0.00003}},\end{aligned}$$

(125)

$$\begin{aligned} G(x, 0)= & e^{0.10203+i x} \left( ( +0.60038 i)-\frac{(+0.0373095 i) \text {sech}^4( -0.02 x)}{0.0257 \text {sech}^2( -0.02 x)-0.00003}\right) , \end{aligned}$$

(126)

the BCs are as follows,

$$\begin{aligned} F(0, t)= & \frac{0.08 e^{0.10203\, -0.005 t} \text {sech}^2(1.1 t)}{\sqrt{0.0257 \text {sech}^2(1.1 t)-0.00003}},\end{aligned}$$

(127)

$$\begin{aligned} G(0, t)= & e^{0.10203\, -0.005 t} \left( (0.60038 i)-\frac{( 0.0373 i) \text {sech}^4(1.1 t)}{0.0257 \text {sech}^2(1.1 t)-0.00003}\right) ,\end{aligned}$$

(128)

$$\begin{aligned} F(5, t)= & \frac{0.08 e^{-0.005 t+(0.10203\, +5. i)} \text {sech}^2(0.1\, -1.1 t)}{\sqrt{0.02574 \text {sech}^2(0.1\, -1.1 t)-0.00003}},\end{aligned}$$

(129)

$$\begin{aligned} G(5, t)= & e^{-0.005 t+(0.10203\, +5. i)} \left( (0.6004 i)-\frac{(0.\, +0.0373 i) \text {sech}^4(0.1\, -1.1 t)}{0.02574 \text {sech}^2(0.1\, -1.1 t)-0.00003}\right) . \end{aligned}$$

(130)

Using these conditions, the Fig. 7 is plotted to compare the results of Proposed Backward schemes (10–11) with the solutions $F_{5,1}(x,t)$ $G_{5,1}(x,t)$.

Fig. 7

The figure (a, c, e) are representations of the solutions F(x, t), $F_{5,1}(x,t)$ while figure (b, d, f) are representations of the solutions G(x, t), $G_{5,1}(x,t)$. The different values of parameters are use to construct these plots are mentioned in Appendix 9.

Test problem 4

The proposed Backward Euler schemes (10–11) is taken for the approximate solutions while Eqs. (85)and (86) as exact optical soliton solutions. The ICs and BCs are chooses such as

$$\begin{aligned} F(x, 0)=\frac{1.2 e^{0.083+(2.1 i) x} \sinh ^2( -0.98 x)}{\sqrt{0.7758 \sinh ^2(-0.98 x)-0.4649}}, \end{aligned}$$

(131)

$$\begin{aligned} G(x, 0)=e^{(2.1 i) x-} \left( (1.6956 i)-\frac{(2.9725 i) \sinh ^4( -0.98 x)}{0.7758 \sinh ^2( -0.98 x)-0.4649}\right) , \end{aligned}$$

(132)

the BCs are as follows,

$$\begin{aligned} F(0, t)= & \frac{1.2 e^{-0.005 t+(0.08316)} \sinh ^2(0.56 t)}{\sqrt{0.7758 \sinh ^2(0.56 t)-0.4649}}, \end{aligned}$$

(133)

$$\begin{aligned} G(0, t)= & e^{-0.005 t+(0.08316)} \left( (1.69555 i)-\frac{(2.97249 i) \sinh ^4(0.56 t)}{0.77578 \sinh ^2(0.56 t)-0.4649}\right) , \end{aligned}$$

(134)

$$\begin{aligned} F(5, t)= & \frac{1.2 e^{-0.005 t+(0.08316\, +10.5 i)} \sinh ^2(4.9\, -0.56 t)}{\sqrt{0.7758 \sinh ^2(4.9\, -0.56 t)-0.4649}}, \end{aligned}$$

(135)

$$\begin{aligned} G(5, t)= & e^{-0.005 t+(0.08316\, +10.5 i)} \left( ( 1.69555 i)-\frac{(2.9725 i) \sinh ^4(4.9\, -0.56 t)}{0.77578 \sinh ^2(4.9\, -0.56 t)-0.4649}\right) . \end{aligned}$$

(136)

Using these conditions, the Fig. 8 is plotted to compare the results of Proposed Backward schemes (10-11) with the solutions $F_{9,1}(x,t)$ $G_{9,1}(x,t)$.

Fig. 8

The figure (a, c, e) are representations of the solutions F(x, t), $F_{9,1}(x,t)$ while figure (b, d, f) are representations of the solutions G(x, t), $G_{9,1}(x,t)$. The different values of parameters are use to construct these plots are mentioned in Appendix 9.

Conclusion

In this manuscript, we investigated the numerical and analytical results of the stochastic coupled nonlinear Schrödinger equation. This system is considered under the multiplicative time noise which has wide applications in optical fibers and indicates the intricate envelope amplitudes of the two modulated weakly resonant waves in the two polarisations that are utilised to characterise pulse propagation in high birefringence fibre. The numerical results are computed by the proposed stochastic Backward Euler scheme. The proposed numerical scheme is analyzed under the mean square sense to check the consistency. For the linear stability analysis, Von-Neumann criteria are used and which shows that the given proposed stochastic scheme is unconditionally stable. The analytical approach namely as $\phi ^6$-model expansion is applied to obtain the exact optical solitons solutions. These solutions are explored by the Jacobi elliptic function solutions that will provide the exact optical solitons and solitary wave solutions. 3D and 2D plots are dispatched for some solitons under the different effects of noise. The initial and boundary conditions are constructed for the numerical result by some optical soliton solutions. Mainly, the comparison of results is shown graphically in 3D and line plots for some newly constructed solutions by selecting suitable parameters value. Before and after an explosion, a soliton experiences convergence and separation, relative phase oscillation, chaos, and oscillation. Single-soliton oscillation, multi-wavelength solitons, and chaos are observed in simulations and experiments with increasing pump power-related parameters, demonstrating the validity and consistency of the results from simulations and experiments.