Remote sensing of mercury sodium exospheric patterns in relation to particle precipitation and interplanetary magnetic field

Abstract

The ground-based solar telescope THEMIS performed several observations of Mercury’s sodium exosphere in years 2011–2013, when the MESSENGER spacecraft was orbiting around the planet. Typical two-peak exospheric patterns were frequently identified. In previous studies, some specific cases of THEMIS Na two-peak observations were characterized and related to IMF conditions, during specific extreme cases, in the occasion of CME arrival. The present study aims to perform a statistical analysis of Na two-peak emissions in nominal IMF conditions at Mercury, as measured by MESSEGER. The comparison between parameters of Na two-peak exospheric patterns (relative distances and intensities) versus the IMF intensity and Z-component is analysed, demonstrating, in average conditions, the existance of a direct relationship between Na peaks distance/intensity and IMF intensity. Moreover, only when IMF is very low, the shear angle seems to detrmine the occurrence of dayside reconnection when IMF-Z is negative (similarly to the Earth’s case), whereas at higher IMF, it seems that reconnection may occur independently from shear angle. This study supports the idea that particle precipitation is a significant driver of the shaping of Na exosphere morphology, and that only when IMF intensity is particularly low, the dayside magnetospheric structure appears to be more similar to the Earth’s configuration. These results allow to better understand the way the planet reacts to IMF conditions, thus providing interesting clues for the incoming BepiColombo measurement objectives.

Introduction

The Na doublet emission at 5890-96 Å, thanks to its good visibility also from the ground, is broadly used to study the exosphere of Mercury. Since the discovery of Na component in Mercury’s exosphere¹, a large dataset of ground-based images has been collected in which both recurrent and variable patterns have been identified^{2,3,4,5,6,7,8}. Starting from 2007, the ground-based campaign performed at the solar telescope THEMIS in Tenerife (Canary Islands) have collected several sequences of data for many hours per day that have been used to study the morphology and the high dynamism of the Na exosphere (see Mangano et al.⁹, and reference therein). In particular, Mangano et al.¹⁰ showed, on a dataset of 5 years, that the exospheric Na ground-based observations quite often (61%) exhibit a two-peak distribution: a couple of column density maxima located at high latitudes in both hemispheres. These “two-peak” patterns usually persist for several hours/day, or even for days, even if superposed to a global modulation in intensity⁹ that may also occur on time scales down to few minutes¹¹.

The explanation of this peculiar behaviour of Mercury’s Na exosphere is still not fully clear. The dynamics of Mercury’s exosphere is certainly related to the surface release processes induced by environmental agents¹². Since this planet is very close to the Sun, with a weak internal magnetic field and without a dense atmosphere to shield it, it’s surface is strongly exposed to solar radiation (thermal and UV) and it is heavily bombarded by micrometeoroids and by solar wind plasma^13,14,15.

A strong variability of the global sodium exospheric intensity with true anomaly angle (TAA) is well known^16,17,18, and interpreted as the composite effect of two factors: one related to the variability of the radiation pressure acceleration along the orbit of Mercury, and the other related to the processes of condensation and migration of Na in the interaction between surface and exosphere^6,19,20. The Na photoionization rate also contribute to deplete the Na exosphere especially at closest distances from the Sun; in fact, a statistical study of Na+ observations by MESSENGER²¹ showed that Na+ is in good agreement with the photoionized Na+ estimated from the Na ground-based images obtained with the THEMIS solar telescope²².

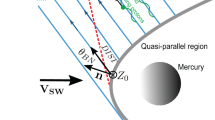
The typical two-peak pattern in intensity approximately corresponds to the exospheric region above the planetary magnetic cusp footprints , thus supporting the idea that solar wind precipitation through the polar cusps plays a key role in the exospheric Na generation²³. In fact, as it happens at the Earth, the open-closed field line boundaries of Mercury’s magnetosphere map to high latitude dayside regions. The magnetospheric cusps is a highly variable region, and also wider in Mercury’s case where the internal magnetic field is weaker. Thanks to the MESSENGER magnetic field data a cusp extension in between $\sim \,56^\circ$ and $84^\circ$ magnetic latitudes and $\sim$ 7–16 h local times. was derived²⁴. Later, Raines et al.²⁵ presented a more comprehensive statistical cusp characterization with respect not only to the magnetic field, but also to the solar wind toward the surface. In that study, the proton precipitation ranges between $45^\circ$ and $85^\circ$ magnetic latitudes and a similar 7–16 h local time range for the southern hemisphere is found. The northern hemisphere cusp appears to be less extended in local time due to the northward shift of the internal dipole that produces a smaller open-closed region at the surface. That study showed that the cusp mean magnetic latitude drops with increasing magnetic field strength, especially for IMF > 25 nT. The short-term variability of particle precipitation and related Na emission seems to be justified only in relation to solar wind and Interplanetary Magnetic Field (IMF) variability. In fact, any other known process would have a different geometry (for example photon fluxes onto the surface maximize at low latitudes at subsolar point) and are not expected to exhibit a variability on a time scale of minutes. Also, the overall micrometeoroid flux impacting the surface should impinge in a wide, about hemispheric, region (expected to peak at dawn). Finally, sporadic bigger meteoroids would produce a short-time variation in the exosphere, but they could not produce a regular increase of the signal at mid latitudes simultaneously in both hemispheres. Only the solar wind deflected by the planetary magnetic field and driven to the surface along the open field lines on the cusp could produce a geometry and a variability compatible with the observed Na distributions. As a further proof of the relationship of ion precipitation with Na surface release, recently Sun et al.²² showed a clear correlation in MESSENGER data between intense flux transfer event showers (and, hence, intense solar wind fluxes toward the surface) and contemporary detection of intense up-welling sodium ions (Na+) originating from the planet. Since the precipitation at Mercury depends on the IMF intensity and orientation $|\text {B}|$, Bx, By, Bz with respect to the internal magnetic field²⁶, Orsini and co-authors²⁷ analysed some individual cases in which contemporary exospheric sodium patterns from THEMIS and in-situ IMF data from MESSENGER were available. In the cases analysed, the two-peak pattern is the configuration observed during nominal IMF conditions (an intensity between 25 and 50 nT). In that paper it is shown that IMF intensity $|\text {B}|$ is related to the observed two-peaks pattern, while the Bx, By, Bz components seem to not play a significant role in shaping the Na exosphere, when $|\text {B}|$ is $\gtrsim$ 25 nT.

This result is in agreement with DiBraccio et al.²⁸ outcome, which stated that Mercury’s dayside magnetopause is frequently experiencing reconnection, resulting from the low Alfvénic Mach number ($M_A= V_{SW}/V_A$) conditions, where $V_{SW}$ is the solar wind bulk velocity and $V_{A}$ is the Alfvén speed given by:

$$\begin{aligned} V_A=B / \sqrt{\rho \mu _0 }, \end{aligned}$$

where B is the magnitude of the magnetic field, $\rho$ is the mass density of the plasma and $\mu _{0}$ is the permeability of free space. Low $M_A$, which often characterizes the inner heliosphere, means also low plasma $\beta$ value in the magnetosheath (where $\beta$ is the ratio of plasma thermal to magnetic pressure). Zomerdiijk-Russell et al.²⁹, by means of MESSENGER data, have shown indeed that the reconnection at Mercury does occur independently by shear angles. By taking into consideration the mean values of both solar wind speed and density at the orbit of Mercury (e.g.:³⁰), Massetti et al.¹¹ indicate that a value of $|\text {B}|$ > 25 nT is likely to be associated to a low Mach Alfvenic number $M_{A}$ (< 5) upstream. This condition causes high reconnection rate at Mercury, nearly regardless of the IMF orientation, hence independently from the magnetic field shear angle²⁸. Because of this scenario, when $|\text {B}|$ is lower than 25 nT, $M_{A}$ is generally higher, so that it would be possible that the magnetic field components (especially Bz, as in the Earth’s case) should play a role in enhancing the reconnection rate at the dayside magnetopause, thus determining in these specific conditions an Earth-like mini-magnetosphere structure. The average subsolar magnetopause standoff point distance from the surface at Mercury is $\sim$ 1.45 $R_{M}$³¹. On the contrary, during extreme events, like ICME passages, the stand-off point could be much closer to the surface³². During a ICME passage with $|\text {B}| >50$ nT, a diffused Na emission over the whole dayside was observed²⁷. Given that the Na release is linked to the ion impact onto the surface, that observation is confirming that in extreme conditions the precipitation onto the surface is not limited to the footprint of open field lines regions, but it spreads over almost the whole enlightened portion of the surface.

Orsini et al.²⁷ concluded that particle precipitation is a significant driver of Na surface release and consequent exospheric pattern, so that the localized Na emission is a proxy of planetary space weather features at Mercury, even if the study shown by Massetti et al.¹¹ do not allow the identification of the detailed mechanism responsible for surface release and exospheric Na refilling. Possible mechanisms responsible for Na release after ion impacts involve also solar UV photons²² and diffusion inside the regolith grains³³.

The objective of the present work is the study of possible relationships between two-peak Na emission parameters (relative distances and intensities) and plasma precipitation at Mercury in nominal IMF conditions This original approach, pursued by applying the rationale of Orsini et al.²⁷ (based on individual cases), allows to perform a statistical analysis of the two-peak parameters over an extended dataset of THEMIS Na emission images and simultaneous IMF data from MESSENGER, in non-extreme conditions (i.e. only cases with $|\text {B}| < 40$ nT). In the following, we analyse the peak distances and intensities in relation to $|\text {B}|$ and Bz component. In Section 2, the criteria for data selection are described, and the observed relationships between two-peaks patterns and IMF data are analyzed; in Section 3, the observed results are discussed, and conclusions and clues for possible future work are given. Methods used for data analysis are discussed in the last section.

Results

THEMIS Na remote sensing images

The sodium maps of Mercury’s exosphere were obtained with observations at the solar telescope THEMIS in Tenerife, Canary Islands (Spain). As widely described in previous papers, THEMIS is 90 cm f/16 Ritchey-Chretien telescope with an altitude-azimuthal mounting and a helium filled telescope tube, and a spectropolarimeter working in the spectral range 400–1000 nm^4,5. The subsets of THEMIS data used in this study were collected during several observation runs from 2011 to 2013, i.e., when contemporary in-situ IMF data from MESSENGER spacecraft were also available. Data were selected according to their quality, i.e.: the scan sequence to build a single image occurred with no abrupt changes in seeing values or problems in the image locking (tip-tilt) and generated a regular disk of the planet in solar reflected light (taken from the spectrum continuum around the Na D lines). Examples of these scans are shown in Fig. 1.

By considering data with seeing values < 3” , we selected 77 images with contemporary IMF values available (summarized in Table 1). These images were collected at different values of TAA and, given the well-known dependence of the Na exosphere emission intensity along the Mercury orbit⁶, a normalization to the average value at each TAA was performed for all the images, so that at the end only relative intensity values were shown in the images with respect to the expected average intensity value (same method as in Mangano et al.⁹). Such an approach was necessary to be able to compare images during different periods of the Hermean year. Details of Na intensity profile versus TAA are given in Fig. 2. In particular, it can be noted that the selected observations were not taken in the low intensity TAA regions.

For each of these images, we wanted to derive the distance between the two peaks. To do this, we have integrated the values along the Sun-Mercury direction projected along the perpendicular of the line of sight (X axis in Fig. 3), and we have derived a 1D plot of the integral intensity along the S-N axis of each image (Fig. 3, left panel). The resolution of the THEMIS ground-based observations does not allow to estimate the exospheric altitude profile above the disk.

The Na exosphere includes atoms released by different processes, like the sunlight-induced thermal desorption and photon stimulated desorption. We want to analyse specifically the peak characteristics, so that we have generated a simulated background of Na exosphere profile to take into account the average exosphere that is supposed to exist ‘below’ the two-peaks feature, by using a similar method used in Mangano et al.⁹. By subtracting this ’background exosphere’ to the profile obtained from the previous analysis, we may derive the integrated latitudinal profile of the exosphere superposed to the average contribution, and the real position of the two peaks (when present) and their distance can be identified with higher precision. In Fig. 4, an example of a profile before and after the subtraction is shown. The peaks distance is calculated as the distance between the median position of the two peaks. In order to take into account possible signal oscillations within the 1-h observation period, the peak intensities are calculated as the average of the 5 values around the position of each maximum. Then, the intensity is calculated as the average between the two peak intensities (i.e. N-S anisotropies are not considered here).

MESSENGER magnetic field data selection

By using the 1-min averaged IMF data from MESSENGER, we have extracted the IMF magnitude $|\text {B}|$ with the three components in solar ecliptic reference system, Bx, By, Bz. Data when MESSENGER was inside Mercury’s magnetosphere have been excluded, and by a case-by-case visualization of magnetic field measurements, we have also excluded periods when signatures of foreshock regions have been identified. By taking the start time of each Na emission hourly image, the IMF data have been computed by means of running averages within a 30-min time interval, starting 15 min before each Na image start time, and ending 15 min after. According to our present knowledge on cause-effects timing in the exosphere generation, such kind of average is able to take into account the delay time between the measured IMF and the effects acting on the exosphere by plasma precipitation inside the magnetosphere. This temporal delay has been assumed by considering the timescales for stabilization of the Na exospheres, as investigated by Mura³⁴, which are quite short. At perihelion, the timescale is less than 2 h for an extreme event, so that one can assume that in 1 h or less the Na exosphere adjusts to a modification of the plasma precipitation. Whenever the time interval includes magnetosphere traversal, interpolated IMF values are used, provided that the actual values outside the magnetosphere are contributing to the computed average for more than 15 min (i.e. 50% of the selected 30-min interval).

The use of observations with ’interpolated’ IMF data is crucial to keep a significant set of data. This approach is supported also by the not-instantaneous reaction time of the exosphere, so that by looking for the exact values of the IMF at the time of observations would be wrong. The 30-min averages certainly show less variability than the 50–60% of cases cited by James et al³⁵, where there is no variation beyond 10nT within 2 (or 4) h. The trend of data would not be affected by randomly adding or subtracting 10 nT. Nevertheless, such IMF averages are to be taken with some caveats:

• 1. The exosphere has a reaction/latency time that induces a moderate random error,

• 2. The interpolated B value will add another random error

Thus, we have two random errors that add to the real value of B. Actually, If we use the value of B affected by these two random errors and still obtain a correlation, this evidence can only inprove the validity of the trend and partially justify the observed data points scatter.

Fig. 1

The images above show two examples of the solar continuum light as reflected from the disk of Mercury. These images are extracted from each Mercury image, and are used for the flux calibration, but they are also an immediate way to visualize the quality of the scan building, i.e. if the seeing was very variable during the exposition, it will produce a continuum image very uneven (as in the left panel); instead, if the scan occurs during constant conditions of seeing, the continuum image appear very regular (right panel).

Fig. 2

Global Na emission dependance with TAA. This plot is the outcome of several Na observation campaigns from two ground-based stations (Themis in red and McMath-Pierce in blue). Before interpreting the signal significance, any Na intensity detection has been normalized with respect to this experimental profile. In fact, the selected data (black points at the plot bottom) stay where the observed intensity is not too low.

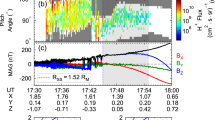
Figure 5 shows a typical profile of the MESSENGER magnetic field detection during one of the selected data. Blue line refers to IMF $|\text {B}|$ instant values over 1 min. The purple thick line shows the 30-min running averages. Straight line in the center of the figure indicates the start time of the Na hourly data image. The running average linked to the Na image is taken within 30 min around the start time (i.e.: the running average just 15 min after the image start time). Interpolated profiles of IMF data during magnetosphere crossings are also shown (dashed purple line). They are computed by considering the last running average before magnetosphere traversal, and the first running average after the magnetosphere traversal. They take part to the average computation only if at least 50 % of the actual data contribute to the computed average $|\text {B}|$ values.

Fig. 3

Na intensity image. The right panel shows a typical Na image, exhibiting a well-defied two peak structure. In the left panel the longitude-integrated signal is plotted versus latitude.

The histogram of occurrence of $|\text {B}|$ in the selected periods (Fig. 6) confirms the hypothesis that the most frequent magnetic condition at Mercury corresponds to a $|\text {B}|$ value ranging between 15 and 35 nT. Even if the IMF data considered are just a small subset of all the MESSENGER measurements, the derived average range (including an indetermination of 10 nT) is not so far away from the average range (10–30 nT) indicated by James et al.³⁵.

Data analysis

In the 77 selected exospheric Na images, the double peaks show variable intensities and relative distances. In Fig. 7 typical examples of 4 different Na patterns occurring in the THEMIS selected data are shown, together with the corresponding $|\text {B}|$ values measured by the magnetometer onboard MESSENGER. In just a few occasions, $|\text {B}|$ exceeds 40 nT (top left panel): in such cases the two peaks distance is hardly discernible and they appear to be fragmented in spots, as if the peak was moving much faster than the 1-h time needed to build an image). In other two cases (top right and bottom left panels), $|\text {B}|$ ranges around 30 nT (the most frequently observed value), and in such cases a clear two-peak structure is observed. Finally, when $|\text {B}| < 24$ nT, (bottom right panel) the peaks become so much fainter that they can hardly be identified. Starting from this eye-by-eye simple analysis, we began our investigation on whether the peaks position and intensity might be related to the local $|\text {B}|$ conditions.

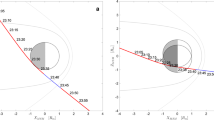
In Fig. 8, we plot the distance of the two peaks versus $|\text {B}|$. Given the presence of many processes that produce Na exosphere, in principle we should not expect a strong dependence between Na morphology and $|\text {B}|$. The scatter plot instead shows a relationship between the two parameters. In the figure, single points are shown, together with average values and standard deviations in steps of 4 nT. The red arrows at the bottom of the plot indicate cases where the signal is too faint to determine a two-peak configuration. We use the test of Student/Pearson to determine the significance of the correlation coefficient with respect to the number of available samples. With the available data set, the critical limit coefficient = 0.2569 indicates no relationship at all. By applying the Student/Pearson test to the data we derive a correlation coefficient = 0.4594, indicating that, despite the complexity of the Na generation mechanisms, there seems to be a significant correlation between the exospheric Na peak distance and the intensity of the IMF $|\text {B}|$. As a consequence, the generation process induced by plasma precipitation is able to prevail above the others. The trend shown in Fig. 8, indicates that the distances is directly related to $|\text {B}|$. The cases shown by the red arrows, where the distance cannot be well determined occurs when $|\text {B}| <27$ nT. In addition, the two histograms in Fig. 9 show that the peak distance is slightly different if we compute it for $|\text {B}| < 24$ nT, being maximum occurrence at 1.2 Mercury radii ($R_{M}$), and for |IMF| > 24 nT, being peak distances maximum occurrence at 1.3 $R_{M}$, identifying an increasing trend in the distance of the peaks with increasing $|\text {B}|$.

A second parameter analyzed is the maximum intensity of the two peaks, even though this parameter has a higher uncertainty because it is affected by atmospheric seeing during the observations. Similarly to Fig. 8, a scatter plot of the peak maximum intensity versus the IMF magnitude is produced, with the signal intensity computed as described in previous section (Fig. 10). In this case, the wide data dispersion does not reveal any clear trend versus $|\text {B}|$ (correlation = 0.1149). As in the previous plot, at low $|\text {B}|$ values, there are cases where the intensity is too low to be actually computed (see red arrows). Nevertheless, if we plot the histograms of the peak maximum intensity occurrence (Fig. 11) in two B ranges, in a similar way as done in Fig. 9, we can notice a maximum occurrence of lower intensity when $|\text {B}| < 24$ nT, and of higher values in the higher $|\text {B}|$ range. Hence, it is worth to check if the two peaks distance and their maximum intensity are related one to each other, at least when we exclude extreme conditions with $|\text {B}| >40$ nT.

Figure 12 shows the scatter plot of peak distance vs peak intensity with an increasing trend confirmed by the correlation coefficient = 0.5229. This result shows that when the two peaks are closer one to each other, they are also much less intense. As a consequence, it is more difficult to clearly distinguish them with respect to the exospheric background used for the data analysis (see description above), resulting in a less intense Na peak signal. This trend seems to confirm the scenario that such Na exosphere signals are linked to plasma precipitation. In fact, at lower latitudes the magnetic field lines are less affected by reconnection when $|\text {B}|$ is very low and are hardly open to particle precipitation.

As described in the introduction, it is expected that at Mercury when $|\text {B}| > 24$ nT, assuming mean solar wind conditions at Mercury (i.e. density and velocity less relevant respect to IMF), both the Mach number and the plasma $\beta$ are low ($<5$). In these conditions the magnetosphere dayside reconnection occurs almost independently with respect to the Bz orientation. Conversely, when IMF $|\text {B}| < 24$ nT, the Mach number and $\beta$ are higher, so that the magnetosphere conditions are much more Earth-like, and dayside reconnection may occur only when Bz is negative.

Given the previous considerations, we investigate if the Bz component plays a role in Na peak distance, i.e. in the dayside particle precipitation (assuming that these two quantities are correlated), for the two mentioned IMF magnitude ranges. In Fig. 13 we plot the two peaks distance versus Bz/$|\text {B}|$, for three different ranges of $|\text {B}|$: (a) < 24 nT (left panel); (b) > 24 nT (middle panel); (c) < 22nT (right panel). As a matter of fact, the middle panel (b) does not show any trend (correlation = 0.1015), thus confirming that particle precipitations generating the two Na peaks do not depend on the z component of the IMF. In left panel (a), the correlation is still too low (0.2). The existence of a clear trend (correlation = 0.7706; critical limit= 0.7070) is confirmed if we look at right panel (c) that includes only cases where $|\text {B}|$ is < 22 nT, confirming the expectation that the two peaks are better defined when Bz/$|\text {B}|$ is negative. Even if the number of data is poor, a clear trend is evident (correlation = 0.7706, critical limit = 0.7070), and a linear best fit can be easily superposed to the single points.

Discussion

This study tries to answer some important questions linked to the plasma precipitation patterns at Mercury (and relative Na two peak emission of the exosphere), and consequently to the reconnection rate occurring in the Mercury dayside magnetosphere with respect to the IMF magnitude and direction. Cases with $|\text {B}| >40$ nT have not been considered, since when Mercury is affected by very strong solar perturbations, the whole magnetopause can be compressed toward the planet and particles precipitate on almost the whole dayside surface, as shown in Orsini et al.²⁷.

If particle precipitation induced by dayside reconnection is generating the exospheric Na two-peak emission, their latitudes and intensities should be dependent on $|\text {B}|$ (assumed to be a significant driver of $M_{A}$ and $\beta$ in the magnetosheath). Actually, the solar wind velocity and density could also affect $M_{A}$ and $\beta$. Unfortunately, such quantities are not available in the MESSENGER data. It follows that we could not investigate their effect onto the precipitation or onto the Na surface release, so that we assume that their variations are minor with respect to IMF effects. For investigating the relation between Na distribution and the IMF intensity, we have plotted the distances between the two-peak Na emissions observed by THEMIS versus $|\text {B}|$ as observed by MESSENGER (see Fig. 8). The few events at $|\text {B}| >40$ nT (not included in the Figure) show a decrease in the distance. They are associated to a CME and/or very perturbed solar events hitting Mercury as proved by Orsini et al.²⁷. In fact, the peak distance goes down with increasing IMF: as reconnection takes place, the cusps move to lower latitudes²³. Such perturbed cases are probably related to the precipitation of solar wind ions onto the planet surface at low latitudes due to strong compression of the magnetopause and finite gyroradius effects, as discussed in DiBraccio et al.²⁸ (see also Zomerdiijk-Russell et al.²⁹). Anyway, such cases are out of the ‘normal’ (and more frequent) conditions that we want to analyze in this paper. For this reason, we decided to include in our analysis only cases with $|\text {B}| <40$ nT.

The plot of Fig. 8 exhibits two different regimes:

• 1. $|\text {B}| < 24$ nT: the distances/latitudes of Na emission are lower;

• 2. $24< |\text {B}| < 40$ nT: generally higher distance/latitudes are observed.

It follows that a dependence of the two peaks distance as a function of the IMF magnitude is observed, especially for $|\text {B}| < 24$ nT.

We have applied a similar approach to investigate the peak intensity versus $|\text {B}|$. Even if no clear trend is observed, probably due to the high variability of this parameter (induced by both instrumental effects and general exospheric conditions), it is anyway clear that on average two different regimes may be identified:

• 1. $|\text {B}| < 24$ nT: the peaks generally have lower intensities;

• 2. $24 < |\text {B}|<$ 40 nT: the peaks generally have higher intensities and a more scattered distribution.

The previous considerations suggest a relationship between the two peak distances and intensities. In fact, the scatter plot of the two parameters reveals a clear relationship, confirming the fact that when the two peak distances are lower, even their intensity is lower. We could infer that when the two peaks appear to be closer one to each other, in reality their intensity is so low that they are no more visible and anyway mixed-up with other Na emission sources. Considering the expected trend of the average latitudes of the solar wind precipitation versus $|\text {B}|$ obtained by Raines et al.²⁵ (that shows a decrease in average cusp latitude at magnetic field increase when $|\text {B}|$ is $>25$ nT), the results of this study seem to be in disagreement with ours. Nevertheless, their study shows that, when $|\text {B}|$ increases, the cusp becomes wider: it extends indeed at lower latitudes, but the precipitating flux increases even more at high latitudes. In our study we do not evaluate the latitudinal extension of the Na peaks, we just consider the latitudes where the highest Na intensity is observed. Then, the two studies are in agreement, and the flux intensity versus latitude profile do not contradict our Na two-peaks observations.

The problem of the influence of the solar wind pressure in our analysis cannot be assessed, because this information is not available in the MESSENGER data. Actually, this quantity is certainly not constant, hence, we have to assume that the data scattered distributions observed in the figures could be partially caused by solar wind pressure variations, which we cannot consider at present. Probably the BepiColombo data will allow more improvements in the near future. Since the solar wind speed and density variations are not considered here, we have to assume that these are minor and that IMF is the major driver: at $|\text {B}| > 25$ nT, $\beta$ is low (the magnetic pressure is high with respect to plasma pressure) and the reconnection rate is high, whatever the shear angle is²⁸. In this condition, the precipitation is always present below the cusps, hence the two Na peaks are frequently observed. At lower $|\text {B}|$ values (< 24 nT), the reconnection rate is lower, and the precipitation is relevant only for negative Bz, as it happens in the Earth’s magnetosphere.

Fig. 4

Example of the treatment applied to each image after performing the sum over the E-W direction to highlight the peaks. Left panel: profile of the summed intensity (black) and the ‘bulk’ profile of the exosphere (red) along the S-N direction over the planet. Right panel: the profile after subtraction of the ‘bulk’ exosphere. The red dots mark the position of maxima, the blue dots the position of the maxima weighted over the five central points. The horizontal dashed line highlight the half maximum value and the horizontal solid line shows the associated FWHM.

Fig. 5

Example of the magnetic field profile during one of the selected periods. The blue line are the regions of IMF estimates, and they are $|\text {B}|$ instant values averaged over 1 min. The purple thick line shows the 30-min running averages. The vertical dashed line indicates the start time of the Na hourly data image. The $|\text {B}|$ running average linked to the Na image is taken within 30 min around the start time (i.e.: the running average just 15 min after the image start time). Interpolated profiles of IMF data during magnetosphere crossings are also shown (dashed purple line).

Fig. 6

Histogram of IMF magnitude ($|\text {B}|$) occurrence within the selected data set. Red boxes indicate $|\text {B}|$ values out of the nominal data used in our analisys.

We have investigated if for low $|\text {B}|$, when $M_{A}$ and $\beta$ are similarly higher, the reconnection is more effective when Bz component is anti-parallel to planetary magnetic field at the magnetopause, i.e.: Bz is negative. According to the hypothesis of Na release proportional to particle precipitation, we analysed the Na two-peak emission distance with respect to Bz/$|\text {B}|$. As a matter of fact, the scatter plot of the two peaks distance versus Bz/$|\text {B}|$ (>24 nT) does not show any particular trend, indicating that the plasma precipitation may occur independently from the shear angle. This situation is very different to what happens at the Earth. Conversely, for weak $|\text {B}|$ cases (<24 nT), a dependence is slightly observed in the plot of two peak distance vs Bz/$|\text {B}|$. This appearance is even more evident if we limit the scatter plot to cases when $|\text {B}|$ is < 22 nT, so that more stable Na peaks at high distances/latitudes are noticed only when the angle is negative, whereas a more scattered condition occurs when such an angle is close to zero or positive. Hence, it is reasonable to assume that only when occasionally $|\text {B}|$ is weak, the dayside reconnection leading particle precipitation in the polar regions could be controlled by Bz, like it happens at the Earth³⁶. In conclusion, the structure of Mercury’s dayside magnetosphere in the most frequent conditions is very different from the Earth’s one. Actually, it becomes more similar to the Earth’s case when $|\text {B}|$ is quite lower respect to the nominal conditions.

Fig. 7

Examples of 4 different exospheric Na emission images occurring in the selected THEMIS database. The average IMF magnitude value (as measured by the MESSENGER magnetometer, white boxes), and a roughly estimated distance is also given (dashed line). Question marks indicate that in some cases the distance cannot be easily estimated.

Fig. 8

Scatter plot of the two peaks distance in Mercury radii ($R_M$) versus the IMF magnitude ($|\text {B}|$). Single points are shown, together with average values and standard deviations in steps of 4 nT (red crosses). The red arrows at the bottom of the plot indicate cases where the signal is too faint to determine a two peak configuration. The correlation coefficient is 0.4594, above the limit of no relationship at all (0.2569).

Fig. 9

Histograms of the two peaks distance frequency for $|\text {B}|$ lower (right panel) or higher (left panel) than 24 nT, respectively.

In summary, remote observations of Na emission in the Mercury dayside are an interesting way to infer information on the IMF-magnetosphere interaction on a global scale. A relationship between cusp particle precipitation and two-peaks Na emission in Mercury’s exosphere was previously shown in Orsini et al.²⁷ in extremely high IMF cases. In this study, we have selected 77 Na images in 2011–2013, when in-situ IMF data were available from MESSENGER. We have shown that the two-peaks Na emission locations in Mercury’s exosphere are dependent on IMF magnitude. When considering the two peaks intensity, the Na two-peak distributions appear to be more discernible when $|\text {B}|$ is $<\sim 24$ nT.

If we select only cases with $|\text {B}| <24$ nT, a dependence of the two-peak distances versus Bz/$|\text {B}|$ is noticed, so that more stable Na peaks at high distances/latitudes are observed when Bz/$|\text {B}|$ is negative, whereas a more scattered conditions occur when such an angle is close to zero or positive. This could be the effect of dayside reconnection process control by Bz/$|\text {B}|$, like in Earth’s case.

Further investigations will be possible once the ESA-JAXA BepiColombo double spacecraft mission will be operative around Mercury. In fact, thanks to this new mission, parameters like $M_{A}$ and $\beta$ could be fully computed, thanks to simultaneous observation of solar wind, IMF, ion precipitation, internal magnetic field and exospheric Na component. During BepiColombo operations, simultaneous ground-based observation campaigns would be very useful for better understanding the global dynamics of the Na exosphere.

Methods

THEMIS data analysis

VM performed a long Earth-based campaign of observations of the Na exosphere of Mercury in years 2007–2014 with the THEMIS solar telescope, located in Tenerife (Canary islands, Spain) by using MTR spectrograph and two independent cameras to investigate simultaneously small spectral regions around D1 and D2 emission lines (5896–5890 Å). The Mercury exosphere was automatically scanned over by a slit (put in the planetary North-South direction) along the Sun-antiSun direction (i.e. E-W or W-E direction) and the image recomposed in a second step. Tip-tilt corrections at  1 kHz were performed to assure perfect coverage of the planetary disk. For each position of the slit, 20 exposures of 20 seconds each were taken. Bias correction was applied and flat-field correction was performed by using the solar spectrum (taken in between usual Mercury observations throughout the day). Spectral calibration was performed by using solar spectrum too and by identifying telluric lines. Sky background was removed by using ‘line-free’ regions of the same spectra, and solar reflected spectrum too. Resulting exospheric emission line was then integrated and calibration in brightness was performed by using Hapke theory to model the solar light reflected from Mercury surface. Best fit of modelled Hapke reflected solar light with the observed one allowed us to derive exact position of the Mercury disk above the emission and estimate seeing values. More details of the analysis can be found in⁹. Finally, bi-dimensional map of the Na exospheric intensity emission, superposed on the disk of Mercury, are obtained. Such maps are then normalized over the average intensity emission expected at the TAAs of observations to evidence the relative intensity with respect to the average condition and remove seasonal effects.

Fig. 10

Scatter plot of the two peaks maximum intensity (arbitrary units) versus $|\text {B}|$. Single points are shown, together with average values and standard deviations in steps of 4 nT (see red crosses). The red arrows at the bottom of the plot indicate cases where the signal is too faint to determine a clear intensity estimate. The correlation coefficient of 0.1149 states that there is no relationship.

MESSENGER IMF data analysis

By using the 1-min averaged IMF data from MESSENGER, we have extracted the IMF magnitude $|\text {B}|$ with the three components in solar ecliptic reference system, Bx, By, Bz. Data inside the Mercury magnetosphere down from the bow shock (including foreshock regions) have been carefully excluded. By taking the start time of each Na emission hourly image, the IMF data have been computed by means of running averages within a 30-min time interval, starting 15 min before each Na image start time, and ending 15 min after the Na observations start time. Whenever the time interval includes magnetosphere traversals, interpolated IMF values are used, provided that the actual values outside the magnetosphere are contributing to the computed average for more than 50% of the selected 30-min interval.

The student/Pearson test

The Student’s t-test, in statistics, is a way of testing hypotheses concerning the mean of a set of samples from a normally distributed population when their standard deviation is unknown. In case of two variables linear regression, this test can be applied to check if the Pearson correlation coefficient is significantly different from zero. based on the sample surveyed. If r is the Pearson correlation coefficient and n is the sample size, a p-value can then be calculated from the t-test. According to this procedure, the critical value for significance of the correlation is then also derived. For more details see Cramér³⁷.

Fig. 11

Histograms of the two peaks maximum intensity (arbitrary units) for $|\text {B}| <24$ nT (left panel) or $|\text {B}| >24$ nT (right panel).

Table 1 List of the selected THEMIS data used for the present analysis. For each event, date, start time, seeing conditions, IMF average magnitude and TAA values are listed.

Fig. 12

Scatter plot of the two peaks maximum distance versus intensity. Single points are shown, together with average values and standard deviations (red crosses). The correlation coefficent is 0.5229, so that the existance of a clear trend is confirmed.

Fig. 13

Scatter plots of the two peaks distance versus Bz/$|\text {B}|$, for $|\text {B}| <24$ nT (left panel); $|\text {B}| >24$ nT (middle panel); $|\text {B}| <22$ nT (right panel). Middle panel does not show any trend (correlation = 0.1015); in the left panel the correlation is still too low (0.2); in the right panel a clear trend is evident (correlation = 0.7706, critical limit = 0.7070). The linear best fit is shown. (y=-0,43x+1,07).