Introduction

With the mining of deep coal and the construction of deep underground engineering, the causes of rock mass deformation and failure are becoming increasingly complex1,2. The mechanical properties of rock mass are greatly affected by mining disturbance, joint surface, different stress states, loading and unloading along different stress paths, and static and dynamic loads3,4,5. However, the classical viscoelastic–plastic theory cannot well determine and predict the mechanical and deformation characteristics of rocks under the influence of the above factors6. In turn, major problems, such as roadway support instability in engineering practice, cannot be solved appropriately7. When the rock mass is in a deep complex geological environment, it is subjected to high temperature, high ground stress, high pressure, and strong disturbance of engineering excavation, and a certain amount of microfracture defects will be generated inside the rock mass9,10. These initial microscopic defects will not only affect the final failure mode of rock mass but also make the mechanical properties of deep surrounding rocks change greatly11. According to the first law of thermodynamics, the essence of material deformation and failure belongs to the instability phenomenon under the action of energy accumulation and dissipation transformation. Therefore, the deformation and failure process of all materials in nature can be explained by the energy conservation theorem. The excavation of deep rock mass has been accompanied with energy input, accumulation, release, and dissipation. These four energy forms are constantly transformed into one another in the process of surrounding rock deformation12,13,14. The surrounding rock and the later support body will experience the above different forms of energy conversion in the process of load–deformation15,16,17. Therefore, using the law of conservation of energy to solve the problem of rock deformation and reveal the failure mechanism of rocks has been a popular research direction in recent years. Domestic and foreign scholars have carried out in-depth research on the relationship between the deformation and failure law and the energy evolution law of surrounding rocks under different geological conditions. They have also achieved fruitful results.

Griggs et al.18 conducted indoor rheological tests on rocks of different lithologies and found the range of ultimate failure load required for rock creep. For the first time, a custom logarithmic function was used to fit the creep curve (the first empirical constitutive model was established). Hou et al.19 proposed a method for predicting the creep characteristics of sandstone under different initial damage states by changing creep parameters. The model cannot only describe three typical creep stages but can also reflect the influence of initial damage on the creep characteristics of the rock. Liu et al.20 replaced the traditional viscous elements in the nonlinear rheological model of rock with fractional differential elements. The viscosity coefficient of the traditional model was transformed into a function related to stress and time. A nonlinear variable parameter creep model of rock was established. Zhang et al.21 carried out a shear creep test of the key element rock of the potential sliding surface of a landslide and proposed a new plastic nonlinear model (PFY model). Yang et al.22 established fractional-order components on time and stress changes. They replaced the viscoplastic model with the traditional model and established a constitutive model that can describe the accelerated creep of rocks. The correctness of the model was verified by comparing the test curve with the model curve.

The above theory and method are used to study the creep characteristics of rocks from the perspective of pure mechanics. The law of conservation of energy is the basic principle in classical physics. It can clearly reveal the law of energy transfer and transformation within a system. The establishment of a rock creep model based on the law of conservation of energy has a solid physical foundation. The law of conservation of energy can describe the process of energy balance and change in the system concisely through mathematical Eq.s. The rock creep model established on the basis of this law can facilitate mathematical symbolic representation and computational solution. At the same time, the law of conservation of energy is applicable to various materials and material systems. Therefore, the rock creep model based on this law has wide applicability. It can be used to predict and analyze the creep properties of different rock types and actual engineering conditions. Therefore, this study takes the tunnel surrounding rock as the research object and carries out creep tests under different confining pressures. A new nonlinear creep constitutive model is constructed by energy theory and strain energy theory. Furthermore, the creep deformation failure mechanism of surrounding rocks under different confining pressures is revealed. It provides a theoretical basis for the solution of practical engineering problems, such as tunnel support and prevention of surrounding rock instability.

Construction of a creep model

Uniaxial creep model

Under the action of external load, the deformation includes instantaneous strain, viscoelastic deformation, and viscoplastic deformation. Instantaneous strain includes instantaneous elastic strain and instantaneous plastic strain. To simplify the calculation, this study disregards the instantaneous plastic strain and considers only the instantaneous elastic strain as the instantaneous strain. Therefore, the generalized Hooke’s law can be used to describe the instantaneous strain.

The instantaneous strain can be expressed as23,24

$$\varepsilon = \varepsilon_{{\text{e}}} + \varepsilon_{{{\text{ve}}}} + \varepsilon_{{{\text{vp}}}}$$
(1)

where εe is the elastic strain, εve is the viscoelastic strain, and εvp is the viscoplastic strain.

The elastic strain can be expressed as25,26,27

$$\varepsilon_{e} = \frac{\sigma }{{E_{0} }}$$
(2)

where E0 is the instantaneous elastic modulus, and σ is the stress.

The viscoelastic strain can be expressed as28,29

$$\varepsilon_{ve} = \frac{\sigma }{{E_{1} }}\left[ {1 - \exp ( - \frac{{E_{1} }}{{\eta_{1} }}t)} \right]$$
(3)

where E1 is the viscoelastic modulus, and η1 refers to viscosity coefficients.

The Perzyna viscoplastic model is used to describe the viscoplastic strain rate of rock during creep deformation30.

$$\left\{ {\varepsilon^{\prime}_{vp} } \right\} = \eta \left\langle {\phi \left( F \right)} \right\rangle \left\{ m \right\}$$
(4)

where η is the viscosity coefficient of the viscoplastic model, φ(F) is an arbitrary function of the yield function, and{m} is the direction of viscoplastic flow. In this study, the associated flow rule is used, and {m} = 1.

From literature research, creep deformation is not only affected by stress state but also by temperature, osmotic pressure, chemical corrosion, and other factors31,32,33. Therefore, the main factors determining the creep mechanical behavior of a material should be considered. In this study, the method in the literature is used to construct the viscoplastic model by strain energy theory. According to strain energy theory, the creep mechanical behavior of rock is related to its internal energy change. The viscoplastic creep model based on strain energy theory can be expressed as34

$$\varepsilon^{\prime}_{vp} = \eta_{2} \left( {\frac{{\sigma \varepsilon_{r} }}{{\sigma_{s} \varepsilon_{s} }}} \right)^{n}$$
(5)

where εs is the initial creep strain of steady-state creep, and εr is the creep deformation.

The stress in the creep test is always a constant value. εr can be simplified as a function of time. Polynomial infinite approximation can be used to obtain the following equation35:

$$\varepsilon_{r} = \varepsilon_{s} f\left( t \right)$$
(6)

where f(t) is a polynomial function of time.

The polynomial function of time f(t) is expressed as

$$f\left( t \right) = a_{0} + a_{1} t + \cdots + a_{i} t_{i} + \cdots + a_{k} t_{k} ,k = 0,...,N$$
(7)

where ai is a constant coefficient.

On the basis of Eqs. (5)–(7), the following equation can be obtained:

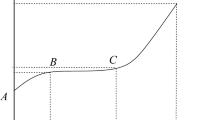
$$\varepsilon^{\prime}_{vp} = \eta_{2} \left[ {\frac{\sigma f\left( t \right)}{{\sigma_{s} }}} \right]^{n}$$
(8)

Three stages of rock creep are analyzed from the perspective of energy. (1) Deceleration creep stage36,37: This stage is mainly dominated by elastic deformation, at which the external work is mainly transformed into elastic potential energy. (2) Steady-state creep stage: This stage is mainly plastic deformation, at which the external work of the rock is mainly converted into plastic deformation energy. (3) Accelerated creep stage: At this stage, the external work is mainly converted into kinetic energy. The traditional Nishihara model can reflect the variation in instantaneous strain and viscoelastic strain but cannot describe the deformation law of accelerated creep38. According to the literature39, the Nishihara model explains that rock transforms into two creep deformation stages of elastic potential energy and plastic potential energy under the condition of external work. For the accelerated creep stage, the conversion of external work into the kinetic energy stage cannot be interpreted. The accelerated creep of rock is studied by the law of conservation of energy without considering the internal heat exchange of rock. The correction coefficient λ is introduced to ensure that the kinetic energy of the system is caused by the material strain. The energy of the input system is equal to the corrected kinetic energy.

$$\sigma SL\Delta \varepsilon_{vp} = \frac{1}{2}\lambda M\left( {\Delta \varepsilon^{\prime}_{vp} } \right)^{2}$$
(9)

where S is the end face area, L is the height, M is the mass, Δεvp is the microvolume viscoplasticity strain, and Δε’vp is the microvolume viscoplasticity strain rate.

Substituting Eq. (8) into Eq. (7), we get

$$\frac{{d\varepsilon_{vp} }}{dt} = \frac{{\lambda M\sigma^{2n - 1} \eta_{2}^{2} }}{{2\sigma_{s}^{2} SL}}\left[ {f\left( t \right)} \right]^{2n}$$
(10)

When the creep deformation of rock enters into a steady-state creep, the steady-state creep rate of rock is a fixed value. In Eq. (7), k = 0, then

$$f\left( t \right) = a_{0}$$
(11)

Substituting Eq. (11) into Eq. (10) provides

$$\frac{{d\varepsilon_{vp1} }}{dt} = \frac{{\lambda_{2} M\sigma^{{2n_{1} - 1}} \eta_{2}^{2} }}{{2\sigma_{s}^{2} SL}}a_{0}^{{2n_{1} }}$$
(12)

The initial conditions are t = 0 and εvp1 = 0. The following equation is obtained by integrating Eq. (12):

$$\varepsilon_{vp1} = \frac{{\lambda_{2} M\sigma^{{2n_{1} - 1}} \eta_{2}^{2} }}{{2\sigma_{s}^{2} SL}}a_{0}^{{2n_{1} }} t,t_{b} \ge t \ge t_{a}$$
(13)

where ta is the time node at the junction of steady-state creep and primary creep.

When the creep deformation enters the accelerated creep deformation stage, the creep deformation rate is variable. The time function f(t) can be expressed as

$$f\left( t \right) = a^{\prime}_{0} + a_{1} t$$
(14)

where a’0 and a1 are constants.

Substituting Eq. (14) into Eq. (10), we get

$$\frac{{d\varepsilon_{vp2} }}{dt} = \frac{{\lambda_{3} M\sigma^{{2n_{2} - 1}} \eta_{3}^{2} }}{{2\sigma_{s}^{2} SL}}\left( {a^{\prime}_{0} + a_{1} t} \right)^{{2n_{2} }}$$
(15)

The initial conditions are t = 0 and εvp2 = 0. The following equation is obtained by integrating Eq. (15):

$$\varepsilon_{vp2} = \frac{{\lambda_{3} M\sigma^{{2n_{2} - 1}} \eta_{3}^{2} }}{{2\sigma_{s}^{2} SL}}\frac{{\left( {a^{\prime}_{0} + a_{1} t} \right)^{{2n_{2} + 1}} }}{{a_{1} \left( {2n_{2} + 1} \right)}},t \ge t_{b}$$
(16)

Through substituting Eqs. (2), (3), (13), and (16) into Eq. (1), Eq. (20) can be obtained40,41.

When σ ≤ σs and t ≤ ta,

$$\varepsilon = \frac{\sigma }{{E_{0} }} + \frac{\sigma }{{E_{1} }}\left[ {1 - \exp ( - \frac{{E_{1} }}{{\eta_{1} }}t)} \right]$$
(17a)

When σ > σs and ta≤t ≤tb,

$$\varepsilon = \frac{\sigma }{{E_{0} }} + \frac{\sigma }{{E_{1} }}\left[ {1 - \exp ( - \frac{{E_{1} }}{{\eta_{1} }})t} \right] + \frac{{\lambda_{2} M\sigma^{{2n_{1} - 1}} \eta_{2}^{2} }}{{2\sigma_{s}^{2} SL}}a_{0}^{{2n_{1} }} t$$
(17b)

When σ > σs and t > tb,

$$\varepsilon = \frac{\sigma }{{E_{0} }} + \frac{\sigma }{{E_{1} }}\left[ {1 - \exp ( - \frac{{E_{1} }}{{\eta_{1} }})t} \right] + \frac{{\lambda_{2} M\sigma^{{2n_{1} - 1}} \eta_{2}^{2} }}{{2\sigma_{s}^{2} SL}}a_{0}^{{2n_{1} }} t + \frac{{\lambda_{3} M\sigma^{{2n_{2} - 1}} \eta_{3}^{2} }}{{2\sigma_{s}^{2} SL}}\frac{{\left( {a^{\prime}_{0} + a_{1} t} \right)^{{2n_{2} + 1}} }}{{a_{1} \left( {2n_{2} + 1} \right)}}$$
(17c)

where ta is the time corresponding to the demarcation point of primary creep and steady-stable creep. tb is the time corresponding to the boundary point of steady-stable creep and accelerated creep. They can be obtained by test curves.

Triaxial creep model

Deep underground engineering often occurs in a complex geological environment. The stress state of the underground structure is no longer a simple uniaxial stress state but a multidirectional stress state. Therefore, the creep model under one-dimensional stress state cannot be used to predict the long-term deformation of surrounding rocks in practical engineering. The above one-dimensional model should be transformed into a three-dimensional model by analogy and yield function. To make the derivation of an unsteady creep model solve the problem of support and prediction of surrounding rock deformation in practical engineering, the creep constitutive model should be in line with the actual creep deformation characteristics of the surrounding rock. Therefore, Eq. (17) is transformed from a one-dimensional to a three-dimensional model.

In the three-dimensional state, the stress tensor σij can be decomposed into spherical stress tensor σm and deviatoric stress tensor Sij. Similarly, strain tensor εij can be decomposed into spherical strain tensor εm and deviatoric strain tensor eij42,43,44

$$\left\{ \begin{gathered} \sigma_{ij} = S_{ij} + \delta_{ij} \sigma_{m} \hfill \\ \varepsilon_{ij} = e_{ij} + \delta_{ij} \varepsilon_{m} \hfill \\ \end{gathered} \right.$$
(18)

where δij is the Kronecker function, the spherical stress tensor σm=(σ1 + 2σ3)/3, the spherical strain tensor εm=(ε1 + 2ε3)/3, and Sij = σij − σm.

The above parameters satisfy the following equations45,46:

$$\left\{ \begin{gathered} S_{ij} = 2G_{1} e_{ij} \hfill \\ \sigma_{m} = 3K\varepsilon_{m} \hfill \\ \end{gathered} \right.$$
(19)

where G1 is the initial shear modulus, and K is the initial bulk modulus.

The instantaneous strain and viscoelastic strain can be three-dimensionalized by the analogy method. The viscoplastic strain includes plastic potential function and yield function. It cannot be transformed by analogy47. Therefore, the three-dimensional viscoplastic strain should be redefined by yield function and plastic potential function.

Under normal temperature and medium- and low-temperature conditions, hydrostatic pressure (stress sphere tensor) is generally believed to exert a minimal effect on creep, whereas stress deviation plays a major role in creep. Thus, the yield function can take the following form48,49:

$$F = \sqrt {J_{2} } - \frac{{\sigma_{s} }}{\sqrt 3 }$$
(20)

where J2 is the second invariant of the stress tensor.

When σ ≤ σs and t ≤ ta,

$$\varepsilon_{11} = \frac{{\sigma {}_{1} - \sigma_{3} }}{{3G_{0} }} + \frac{{\sigma {}_{1} + 2\sigma_{3} }}{9K} + \frac{{\sigma {}_{1} - \sigma_{3} }}{{3G_{1} }}\left[ {1 - \exp \left( { - \frac{{G_{1} }}{{\eta_{1} }}t} \right)} \right]$$
(21a)

When σ > σs and ta≤t ≤tb,

$$\varepsilon_{11} = \frac{{\sigma_{1} + 2\sigma_{3} }}{{9K_{e} }} + \frac{{\sigma_{1} { - }\sigma_{3} }}{{3G_{e} }} + \frac{{\sigma {}_{1} - \sigma_{3} }}{{3G_{ve} }}\left[ {1 - \exp \left( { - \frac{{G_{ve} }}{{H_{ve} }}t} \right)} \right] + \frac{{2\lambda_{2} MH_{2}^{2} }}{{\sigma_{s}^{2} SL}}a_{0}^{{2n_{1} }} t\left( {\frac{{\sigma_{1} - \sigma_{3} - \sigma_{s} }}{\sqrt 3 }} \right)^{{2n_{1} - 1}}$$
(21b)

When σ > σs and t > tb,

$$\begin{gathered} \varepsilon_{11} = \frac{{\sigma_{1} + 2\sigma_{3} }}{{9K_{e} }} + \frac{{\sigma_{1} { - }\sigma_{3} }}{{3G_{e} }} + \frac{{2\lambda_{3} MH_{3}^{2} }}{{\sigma_{s}^{2} SL}}\frac{{\left( {a^{\prime}_{0} + a_{1} t} \right)^{{2n_{2} + 1}} }}{{a_{1} \left( {2n_{2} + 1} \right)}}\left( {\frac{{\sigma_{1} - \sigma_{3} - \sigma_{s} }}{\sqrt 3 }} \right)^{{2n_{2} - 1}} \hfill \\ \frac{{\sigma {}_{1} - \sigma_{3} }}{{3G_{ve} }}\left[ {1 - \exp \left( { - \frac{{G_{ve} }}{{H_{ve} }}t} \right)} \right] + \frac{{2\lambda_{2} MH_{2}^{2} }}{{\sigma_{s}^{2} SL}}a_{0}^{{2n_{1} }} t\left( {\frac{{\sigma_{1} - \sigma_{3} - \sigma_{s} }}{\sqrt 3 }} \right)^{{2n_{1} - 1}} \hfill \\ \end{gathered}$$
(21c)

Equation (21) is a three-dimensional nonlinear viscoelastic–plastic constitutive model based on energy conservation and strain energy theory.

Triaxial mechanical property test of rock

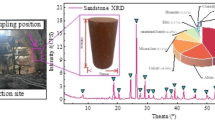
The rock sample is collected from the surrounding rock of a tunnel. After detection, the rock type is determined to be sandstone. The surrounding rock is simply cut on site and brought back to the laboratory for finishing. The final standard rock sample is shown in Fig. 1. The rock specimen is a standard cylindrical specimen with a height of 100 mm and a diameter of 50 mm. The flatness of the upper and lower ends of the rock is less than 0.05 mm. The errors of height and diameter are within 0.3 mm. The porosity is 1.456%.

Fig. 1
figure 1

Rock sample.

Full size image

The test equipment is a real-time high-temperature conventional triaxial test system (Fig. 2). It includes a confining pressure chamber, an axial pressure chamber, a test chamber, a confining pressure closed-loop servo metering pump, and an axial pressure closed-loop servo metering pump. The highest confining pressure can reach 100 MPa. The pressure control accuracy is less than 0.01 MPa. Pressure control methods include flow control and constant pressure control. The test systems are connected to the computer host. Real-time monitoring and control of data are realized using a computer. The real-time high-temperature conventional triaxial test system can carry out high-temperature conventional triaxial compression (rheological) test, temperature–stress coupling test, seepage–stress–chemical corrosion coupling test, and temperature–seepage–stress–chemical corrosion coupling test, fully meeting the test requirements.

Fig. 2
figure 2

Real-time high-temperature conventional triaxial test system.

Full size image

The maximum principal stress range of the rock area is 7.91–11.37 MPa, and the minimum principal stress range is 4.14–7.30 MPa. The horizontal ground stress value of the surrounding rock of the tunnel is in the range of 4–11 MPa. For assessing the stress–strain characteristics and strength characteristics of tunnel surrounding rock in this stress range, the confining pressure values of 5 and 10 MPa are selected.

The loading steps of the triaxial test are as follows.

  1. (1)

    For preventing sudden brittle failure of rock, the upper limit safety value of displacement should be set before the axial stress is applied.

  2. (2)

    Axial stress is applied at a loading rate of 1 ml/min. When the rock reaches the peak strength failure, the axial displacement of the same rate is continued until the residual strain of the rock is measured.

  3. (3)

    The measured data need to be saved.

  4. (4)

    The confining pressure should be unloaded first, followed by the axial stress.

  5. (5)

    After the hydraulic oil in the cabin is extracted, the damaged rock samples are taken out, marked, and stored.

  6. (6)

    On the basis of the test data, the axial and radial stress–strain curves of rock are drawn.

In accordance with the test steps, the mechanical property test under triaxial loading conditions is carried out, and the stress–strain curve of rock under triaxial loading conditions is drawn, as shown in Fig. 3.

Fig. 3
figure 3

Stress–strain curve of rock under triaxial loading conditions.

Full size image

According to Fig. 3, the variation in rock under different confining pressures is similar. In the prepeak deformation stage, the rock stress increases with the increase in strain until the peak strength. In the postpeak deformation stage, the rock stress decreases with the increase in strain until the residual strength. In the residual deformation stage, the rock stress shows a constant trend with the increase in strain. At the same time, the peak strength of the rock increases with the increase in confining pressure. This phenomenon is due to the restriction of confining pressure on the circumferential deformation during the loading process, which improves the bearing capacity of the rock.

Triaxial creep test of rock

Creep test steps

The loading steps of the triaxial creep test are as follows:

  1. (1)

    A single specimen is gradually loaded.

  2. (2)

    The confining pressures are 5 and 10 MPa. The initial stress level is 50% of the peak strength of the triaxial test rock.

  3. (3)

    The initial value of stress is an integer. The stress levels of the samples with a confining pressure of 5 MPa are divided into 40, 50, 60, 70, and 80 MPa.

  4. (4)

    The confining pressure is applied to the predetermined value at the oil loading rate of 1 ml/min. After the surrounding rock stabilizes, the axial stress is applied, and the confining pressure needs to be kept constant throughout the test.

  5. (5)

    The axial stress is applied to the predetermined value at the oil loading rate of 1 ml/min. After the first stage of load–deformation becomes stable, the next stage of load is applied. Each load is increased by 15 MPa until the specimen is deformed and destroyed.

  6. (6)

    After the test is completed, the confining pressure is unloaded to zero, then the axial pressure is unloaded to zero. The test data storage interval is 5 s, and the final test data can be exported.

Analysis of axial creep test curve

The axial creep test curves of different confining pressures are shown in Fig. 4.

Fig. 4
figure 4

Axial creep test curves.

Full size image

On the basis of Fig. 4, the main characteristics of the axial creep curves are discussed in the following aspects. (1) Instantaneous strain: Under the confining pressure of 10 MPa, the instantaneous deformation of rock is 0.150%, 0.204%, 0.285%, 0.394%, and 0.516%. The instantaneous strain of rock is related to the applied stress level. With the increase in stress, the instantaneous strain also increases gradually, and a linear trend occurs between the instantaneous strain and the stress level. The percentage of instantaneous strain to total strain first increases and then decreases because the rock itself has a large number of pores. The rock pores are compressed at the initial loading time. After complete compaction, a large number of cracks exist in the rock. This condition leads to a large instantaneous strain in the initial stage of the rock and a small instantaneous strain in the later stage. (2) Creep deformation: The proportion of creep deformation to total deformation shows a trend of first decreasing and then increasing, which implies that the internal pores of the rock continue to develop, leading to obvious deterioration characteristics of the rock. (3) Creep time: The greater the confining pressure, the longer the accelerated creep time of the rock.

Analysis of isochronous stress–strain curve

The isochronous stress–strain curve is a broken line segment of the relationship between stress and strain50. The abscissa is generally the applied external stress load value. The ordinate is the strain value corresponding to the stress at a certain moment. The isochronous stress–strain curves of rock under different confining pressures are shown in Fig. 5.

Fig. 5
figure 5

Rock isochronous stress–strain curves under different confining pressures.

Full size image

From Fig. 5, the variation in rock strain at and before the divergence point is small under the same stress level. It is concentrated at one point, and the stress and strain before the divergence point are linear. However, after the divergence point, as the stress increases, the variation in rock strain under the same stress level increases, and the stress generally shows a nonlinear change trend. For example, at the confining pressure of 5 MPa, the long-term strength of the rock is 60 MPa.

Parameter identification and model validation

Parameter identification

When the creep of rock is carried out to about t = 0–ta, the deformation of rock is only instantaneous creep and primary creep. However, when the creep proceeds to about t = ta–tb, the rock deformation shows steady-state creep. When the creep proceeds to about t > tb, the rock deformation gradually transits to the accelerated creep stage. In this stage, the creep velocity increases with time until the instability of rock and soil. Therefore, the critical point can be distinguished according to the above variation characteristics of creep rate. With the confining pressure of 5 MPa as an example, the corresponding parameter values of the critical point are shown in Table 1.

Table 1 Corresponding parameters of the critical point.
Full size table

After the actual size and quality of the rock sample are measured, the basic parameters of the rock are obtained, as shown in Table 2.

Table 2 Basic parameters of the rock.
Full size table

Through the least square method (Levenberg–Marquardt optimization algorithm)51,52 under a confining pressure of 5 MPa are identified. The creep model parameter values under a confining pressure of 5 MPa are shown in Table 3.

Table 3 Creep model parameter values under a confining pressure of 5 MPa.
Full size table

Model validation

The model parameters are obtained by inversion of the five-stage creep test curve under a confining pressure of 25 MPa. They are substituted into the nonlinear creep model, and a comparison between the model and experimental creep curves is shown in Fig. 6.

Fig. 6
figure 6

Comparison between the model and experimental creep curves.

Full size image

From Fig. 6, the change rule of the model curve of the nonlinear creep damage model deduced under different confining pressures is similar to the change rule of the experimental creep curve. According to the comparison between the model curve and the experimental data, the creep deformation of the creep model in this paper has a high fitting degree under low stress. However, under the last level of failure load, although the model curve is higher than the test curve, a significant deviation occurs in the local creep deformation stage, especially in the accelerated creep deformation stage. In general, establishing a nonlinear creep constitutive model is feasible. The model can truly reflect the creep deformation law and stress state of sandstone. It has a guiding significance for solving the long-term stability of surrounding rocks in practical engineering.

For verifying the advantages of the proposed model over the Nishihara model, the curves of the proposed model, the Nishihara model, and the test data are drawn in Fig. 7.

Fig. 7
figure 7

Curves of the proposed model, the Nishihara model, and the test data.

Full size image

Figure 7 demonstrates that the fitting degree of the creep model curve and the test curve is considerably greater than that of the Nishihara model curve and the test curve. The model not only describes the whole process of rock primary creep, steady-state creep, and accelerated creep well. It also compensates for the shortcomings of traditional models in describing accelerated creep.

To verify whether the derived model is only applicable to the rock described in this paper, this study tests the applicability of the model by using the experimental data in the literature53. The rock type used in this study is green shale. The comparison between the model curve and the test curve is depicted in Fig. 8.

Fig. 8
figure 8

Comparison between the model curve and the test curve in the literature48.

Full size image

From Fig. 8, the creep model curve is highly fitted with the test curve. The whole process of rock decay creep, constant creep, and accelerated creep is clearly described. The model addresses the shortcomings of traditional models in characterizing accelerated creep. Hence, the established creep model can also describe the long-term deformation of other types of rocks.

Conclusions

From the perspective of energy, the creep characteristics of rock are studied through the conversion relationship between the external work and internal energy of rock, and the corresponding creep model is established. This model can depict the accelerated creep stage of rock. The ability to store energy inside rock is optimized, and the external work is mainly converted into kinetic energy.

The fitting degree of the creep model curve and test curve is remarkably greater than that of the Nishihara model curve and test curve. The creep deformation of the established nonlinear creep model is highly fitted under low stress. Under the last level of failure load, the model curve and the test curve fit well. However, obvious deviations also occur in the local creep deformation stage, especially in the accelerated creep deformation stage. On the whole, the model can thoroughly describe the whole process of creep deformation. It also compensates for the shortcomings of the traditional creep model in describing accelerated creep deformation characteristics. Therefore, the construction process of the model can be considered to be correct and reasonable.