Rotor angle stability of a microgrid generator through polynomial approximation based on RFID data collection and deep learning

Abstract

The article proposes a novel approach to assess rotor angle stability in microgrids by enhancing the Modified Galerkin Method (MGM), which is based on the Polynomial Approximation, using real-time RFID data acquisition. Due to their reliance on assumptions, traditional rotor angle stability methodologies frequently fail in online transient stability testing. MGM successfully captures the dynamic behavior of microgrids by approximating state variables using a sequence of polynomials and coefficients. Redundant data, like as vibrations or noise signals, can cause delays in defect diagnosis and decrease diagnostic accuracy. This problem is addressed by integrating RFID technology. RFID technology could potentially be used with a hybrid CNN-LSTM model to develop a sophisticated fault diagnostic system. This entails identifying fault characteristics through the use of signal processing techniques and feature extraction methods, such as the Fourier transform and time-domain statistical features. In addition, we use Total Harmonic Distortion (THD) to reduce superfluous data. The suggested techniques significantly increase fault detection efficiency and precision, outperforming existing techniques with a 0.94 classification accuracy. An extensive case study on an IEEE 3-machine 9-bus system is used to illustrate its efficacy, showing observable improvements in fault detection speed and accuracy that make microgrid operations safer and more dependable.

Introduction

Retaining the operational integrity and dependability of multi-machine microgrids requires rotor angle stability. It describes the capacity of the microgrid’s synchronous machines to maintain synchronism with one another in the face of disruptions like breakdowns, load variations, or switching activities. In order to prevent extensive blackouts and provide a consistent and dependable power supply, these systems must be stable. Because it makes a case that the Centre of Inertia (COI) can accurately represent the system’s overall behavior—an assumption that is not always true, particularly during large disturbances—the traditional rotor angle stability approach is criticised for being inadequate for online transient stability assessment. Instead, COI does the rotor angle difference calculation utilising only the active and reactive power outputs from the local generator, obviating the requirement for a complex communication infrastructure and precise rotor angle measurements. In order to get accurate power measurement derivatives, COI requires high sample rates. Additionally, the approach relies on assumptions that could not hold true in all real-world situations, especially when complex system dynamics and disturbances are present^1,2. The concept of the COI is highly relevant in microgrids, particularly in terms of stability and control. COI helps analyze the dynamic response of distributed energy resources (DERs) during disturbances, enabling an assessment of how inertia affects system stability, especially with the integration of renewable energy sources that typically exhibit lower inertia³. It is crucial for frequency stability, as traditional power systems rely on the inertia of synchronous machines. In microgrids with high inverter-based resource penetration, understanding COI facilitates the development of control strategies that can emulate inertial responses, thereby smoothing frequency variations and enhancing resilience. Moreover, the distribution of load and generation within a microgrid influences the location of the COI, necessitating careful planning and operation to stabilize the grid effectively. As microgrids are modular, changes in generation and load require dynamic reassessment of system performance, making the COI a vital concept for ensuring reliable and efficient microgrid operation. The paper presents a novel method for handling parametric issues in the analysis of the rotor angle stability of the microgrid. By combining MGM with polynomial approximation, the Modified Galerkin method (MGM) aims to accurately and efficiently represent the dynamic behaviour of a microgrid that is impacted by changing parameters^4,5,6. Robust rotor angle is made possible by MGM’s worldwide adjustable precision across a variety of factors.

Conventional defect diagnostic techniques have long been used to extract characteristics from sensor data. Examples of these techniques include Data Acquisition Systems (DAQ) and Phasor Measurement Units (PMUs). These methods, however, frequently need the manual extraction of characteristics, which may be laborious and may not be well suited to intricate dynamics of contemporary microgrids^7,8. In hectic setting of contemporary microgrids, the manual nature of these approaches might cause delays in failure detection and diagnosis. Due to intermittent nature of renewable energy sources, microgrids are characterized by rapid variations in demand and generation patterns. The static nature of classic feature extraction approaches was unable to fully capture these complicated and shifting dynamics.

Machine learning has revolutionized automated feature extraction, improved diagnostic accuracy, and defect diagnostics procedures. Algorithms like Support Vector Machines (SVM), Decision Trees, and Artificial Neural Networks (ANN) have been extensively utilized in this field. Although machine learning approaches have become more adept at identifying faults, they are still unable to fully capture the temporal dynamics that are peculiar to microgrid systems⁹. For example, support vector machines (SVMs) are useful for classifying errors because of their resilience while processing high-dimensional data and their capacity to identify the best hyperplanes that maximise the margin between classes. The capacity of SVMs to construct ideal hyperplanes that maximise the margin between classes is very helpful in precisely recognising and categorising problems in microgrid systems¹⁰​​. Because they offer unambiguous decision rules that are simple to comprehend and use, decision trees are preferred for their simplicity and interpretability. Using the characteristics taken from sensor data to create binary splits, they have been effectively used in defect diagnostics. When diagnosing fresh defect data, the reliability of the training data is influenced by its quality¹¹. The problem of manually constructing features which is frequently time-consuming and needs subject expertise is addressed by decision trees. The study¹² shows that this automated feature engineering technique can effectively identify and construct informative features, improved diagnostic accuracy, by evolving a population of candidate features and optimising them based on their performance in fault classification tasks.

The Discrete Wavelet Transform (DWT) is used for feature extraction in wavelet-based ANN fault detection and classification, whereas ANN is used for fault identification in microgrids. ANN-based techniques, as opposed to conventional methods, give improved diagnostic accuracy by modelling non-linear correlations within the data​​¹³. Notwithstanding these developments, the temporal dynamics and transient states of microgrid systems are sometimes difficult for traditional machine learning algorithms to capture. This is particularly important as microgrid failures might display temporal features that call for the understanding of time-dependent behaviours in models. Although it is very accurate, it is sensitive to excessive vibration and noise, computationally complex, may overfit, has limited scalability, and requires additional validation for generalising fault localisation across various microgrid configurations¹⁴. Deep learning designs with varying degrees of effectiveness are Convolutional Neural Networks (CNNs) and Long Short-Term Memory (LSTM) networks. While LSTMs are skilled at identifying temporal patterns, CNNs excel at extracting features. The benefits of both may be utilised by integrating CNNs and LSTMs. With this combined method, LSTM layers take care of the temporal correlations while CNN layers concentrate on obtaining spatial characteristics from Radio Frequency Identification (RFID) data. By outperforming traditional methods, this CNN-LSTM hybrid has proven to be highly effective in defect diagnostic tasks^9,15. RFID technology improves fault diagnostics by providing more precise and quick defect detection by permitting real-time data tracking and collection¹⁶.

Defect diagnostics are improved by the real-time data tracking and capturing provided by RFID technology. Fault identification becomes quicker and more accurate as a result¹⁷. System monitoring of changing state variables is critical in the complicated microgrid context. These variables are associated with the temporal derivatives of the system’s algebraic states and dynamics, respectively, in differential-algebraic equations (DAEs)¹⁸. Generators, loads, and transmission lines are common components that DAEs are used to simulate. They do this by illustrating the changes in both algebraic and dynamic variables over time, such as magnitudes and phase angles and rotor angles, voltages, and currents^19,20. These models typically make the assumption that the system’s parameters are constant, which may not adequately capture the system in changing circumstances. For the analysis of transitory stability, polynomial approximation techniques have gained popularity recently²¹. Through the use of polynomial functions of time and system characteristics to describe state variables, these approaches consistently approximate DAE solutions.

The stability of multi-machine microgrids, particularly rotor angle stability, is essential for maintaining synchronism among synchronous machines under disruptions such as faults, load variations, or switching activities. Traditional rotor angle stability methods often rely on simplifying assumptions, which may not hold during transient conditions, particularly in microgrids where dynamic, non-linear, and complex behaviors are prevalent⁴. To address these challenges, this study proposes an innovative approach that integrates real-time data collection using RFID technology with Polynomial Approximation-based MGM to enhance the accuracy and reliability of rotor angle stability analysis.

RFID technology gathers precise, real-time data¹⁶, addressing the limitations of traditional stability assessment techniques. The methodology incorporates a hybrid CNN-LSTM model, which processes RFID data for enhanced fault detection accuracy. The MGM, paired with polynomial approximation, is used to model the dynamic stability of rotor angles under varying conditions, offering a robust solution to transient stability challenges in microgrids.

In this study, we provide a novel method that combines RFID data collection with MGM based on Polynomial Approximation to enhance transient stability analysis in microgrids. This technique improves the responsiveness and accuracy of fault detection systems by addressing the problems with non-linearity and non-polynomial behaviour that are common in traditional approaches. Our extensive case study of an IEEE 3-machine 9-bus system demonstrates the effectiveness of this technique and identifies significant gains in fault detection speed and accuracy. Consequently, this method helps to improve the consistency and dependability of microgrid operations. Here is a summary of our contributions:

• a) This work proposes a novel strategy using Polynomial Approximation-based MGM to overcome the inherent non-linear and non-polynomial difficulties commonly seen in classic rotor angle stability analysis methods. This projection of the system model’s equations yields a clear approximation for the implicit parameter-state function.

• b) Microgrids use RFID technology for fast and accurate data collection as well as real-time defect identification. This makes it possible for vital measurements like voltage and current to be collected instantly, which improves the microgrids’ capacity to identify and track failures.

• c) An innovative method for identifying flaws is presented, which involves positioning RFID sensors in strategic areas. These sensors acquire essential data, compute RMS, analyse harmonics, and compute Total Harmonic Distortion (THD) in order to thoroughly evaluate the microgrid’s operational integrity.

• d) A CNN-LSTM algorithm and RFID technology are used to diagnose errors. This approach works well, with a 94% accuracy rate in identifying single, two, and three-phase faults in microgrids. The LSTM layers, which capture temporal relationships while the CNN layers gather spatial properties from the RFID data, improve the accuracy and responsiveness of fault detection systems.

For ease of understanding, the material is divided into several sections. The topology of the system is described in Sect. 2. Section 3 provides an explanation of the CNN-LSTM algorithm used in fault diagnostics. Section 4 explores the IEEE 3-machine 9-bus microgrids using PSCAD simulation, with the article appearing in the last section.

System topology

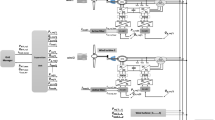
The increasing complexity and integration of several renewable energy sources in microgrids has made rotor angle stability a major problem as these systems continue to develop. The dynamic and non-linear properties of microgrids are typically too much for traditional fault diagnostic approaches^8,22, which usually rely on signal processing and human feature extraction. This paper proposes a novel approach to address these problems by combining real-time RFID data collection with MGM based on Polynomial Approximation. This technique greatly increases the speed and precision of defect detection by using an RFID for fast and precise data collecting and a CNN-LSTM model for enhanced issue diagnosis. The foundation of this methodology lies in using the MGM with polynomial approximation to model and analyze the dynamic stability of rotor angles in microgrids. MGM provides an efficient mathematical framework to approximate the system’s state variables, capturing transient dynamics essential for real-time stability assessment. This approach is particularly effective in dealing with non-linear and complex behaviors in microgrid systems, as it minimizes residual functional errors by employing polynomial functions to project state equations. The MGM’s ability to handle parametric variations in a microgrid’s components, such as voltage, current, and rotor angle, makes it highly suitable for this application. A flowchart outlining this process is shown in Fig. 1.

Fig. 1

Proposed work methodology flowchart.

System model

Parameters like as reactance, resistance, and capacitance are typically regarded as constants in conventional transient models. These variables, which include voltage, current, power, and so on, must be taken into consideration while solving parametric issues in microgrid modelling⁵. This is accomplished by using a collection of DAEs, as follows, to mathematically express these transitory parametric issues:

$$\:\left\{\begin{array}{c}\dot{x}=F\left(x,y;L\right)\:\:\:\:\\\:0=G\left(x,y;L\right)\end{array}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\right.$$

(1)

Here, $\:y\:\ \in \,{R}^{m}$ represents the algebraic state variables, such as voltage magnitude and angle, and $\:L\: \in\:{R}^{d}$ is the parameter under consideration. $\:x\:\in\:{R}^{n}$ represents the dynamic state variables, such as the rotor angle, voltage, and current of a generator. A variable parameter L determines how the system behaves according to the DEAs. The DEAs, which are represented as $\:F:{R}^{n}\times\:{R}^{m}\times\:{R}^{u\:}\to\:{R}^{n}$, are dynamic models of components, including generators, and describe their internal states. $\:G:\:{R}^{n}\times\:{R}^{m}\times\:{R}^{u}\to\:{R}^{m}$ is an algebraic equation of order $\:(n+m)$ that is used to interface equations and network models. It is important to keep in mind that when switching events occur, $\:x$ changes gradually while $\:y$ changes suddenly, necessitating the appropriate adaptation of functions $\:F$ and $\:G$.

Impulsive switched model

A series of equations, including ones that account for situations like queue tripping in the DEA, replace Eq. (1) to represent the circumstances before and after the event.

$$\:0=G\left(x,y\right)\triangleq\:\left\{\begin{array}{c}{G}^{-}\left(x,y\right),\:\:if\:s\left(x,y\right)<0\\\:{G}^{+}\left(x,y\right),\:\:if\:s\left(x,y\right)>0\end{array}\right.$$

(2)

The two sorts of DAEs are denoted by “-” and “+” in this case. The reason for emphasising the importance of the crossing idea is that a switching event occurs when the trigger function intersects zero²³. We may define $\:s\left(x,y\right)$ as a function that changes sign at the precise 0-crossing point when this occurrence coincides with the function’s zero crossing. Furthermore, it’s critical to manage the circumstance cautiously when the trajectory crosses the triggering surface:

$$\:S=\left\{\left.(x,y)\right|s\left(x,y\right)=\left.0\right\}\right.\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$

(3)

Switching events alone is not enough to capture many discrete behaviour types in microgrids efficiently. Impulsive behaviours are better at capturing abrupt dynamic fluctuations, as those caused by resetting protection timers or altering transformer taps. Usually, the state of the system just prior to the event is taken into account by the reset equation:

$$\:h\left({x}^{-},{y}^{-}\right)=\:{x}^{-}+\varDelta\:x\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$

(4)

Hence the function characterizing the change of state variables is denoted by $\:h:{\mathbb{R}}^{n+m}\to\:{\mathbb{R}}^{n}$. To be more precise, the variables $\:{x}^{-}$ and $\:{y}^{-}$ denote the values of the dynamic state variables and algebraic state variables just before sudden events. When $\:x$ changes predetermined as a result of this occurrence, it is indicated by the phrase $\:\varDelta\:x$. Function h, sometimes called the reset equation, captures the effect of the impulsive action by introducing discontinuous leaps into the dynamic -states when $\:s\left(x,y\right)=0$.

$$\:{x}^{+}=h\left({x}^{-},{y}^{-}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$

(5)

The original meaning of the superscript notation is retained, where $\:{x}^{+}$ indicates the value of $\:x$ immediately following the initialisation event. Similar to a switching event, a reset event occurs anytime $\:s(x,y)$ crosses zero.

Modified Galerkin’s method based on polynomial approximation

By staying orthogonal to the trial basis functions $\:\varPhi\:$, the MGM approach aims to minimise the residual functional J and uncover the coefficients $\:{A}_{k}^{x}$ and $\:{A}_{k}^{y}$. By reducing $\:J$, a measure of the difference between an issue’s estimated and genuine solutions, MGM seeks to increase the approximation’s accuracy. The definition of the dot product may be used to generate the Galerkin criterion Eqs^24,25. To get the unknown coefficients $\:{A}_{k}^{x}$ and $\:{A}_{k}^{y}$, Eq. (6) is crucial.

$$\:\left\{\begin{array}{c}\langle{R}_{F}\left({A}_{k}^{x},{A}_{k}^{y};L\right),{{\Psi\:}}_{k}\left(L\right)\rangle=0\\\:\langle{R}_{G}\left({A}_{k}^{x},{A}_{k}^{y};L\right),{{\Psi\:}}_{k}\left(L\right)\rangle=0\end{array}\:,\:\:0\le\:\left|k\right|\le\:N\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\right.$$

(6)

The basic polynomial function of the MGM is $\:{{\Phi\:}}_{k}\left(L\right)$, the trial basis function. It uses a trial basis function $\:{{\Psi\:}}_{k}\left(L\right)$ inside a set of polynomials $\:{\mathbb{P}}_{N}^{u}\left(L\right)$ for evaluation purposes. Typically, $\:{{\Psi\:}}_{k}\left(L\right)$ is set to be equal to $\:{{\Phi\:}}_{k}\left(L\right)$, and the number of $\:{{\Psi\:}}_{k}\left(L\right)\:$functions should match the number of coefficients that are not known. $\:{R}_{F}$ stands for the differential, while $\:{R}_{G}$ stands for the system’s algebraic components

$$\:{f}_{x}\left(t,{A}_{k}^{x},{A}_{k}^{y}\right)=\dot{x}\left(t\right)-F\left(x\left(t\right),y\left(t\right),L\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$

(7)

here, the coefficients $\:x\left(t\right),\:\text{a}\text{n}\text{d}\:y\left(t\right)$ are used to represent x(t) and y(t). The difference between the dynamic state variables’ actual and expected rates of change, as determined by function F, is measured by the function $\:{f}_{x}$​.

$$\:{f}_{y}\left(t,{A}_{k}^{x},{A}_{k}^{y}\right)=G\left(x\left(t\right),y\left(t\right),L\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$

(8)

here, the algebraic restrictions are indicated by the symbol$\:{f}_{y}$, while $\:y\left(t\right)$ is specified using the coefficients of $\:{A}_{k}^{x}$. The representation of Eq. (6) will be as follows in order to include it into the residual functional $\:J$:.

$$\:J={\int\:}_{L}{\parallel\:\varvec{R}\parallel\:}^{2}dL\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$

(9)

Introduce a minor change in $\:\delta\:J$ using $\:{A}_{k}^{x}$ and $\:{A}_{k}^{y}$. Then, by applying the chain rule to equation $\:\left(9\right)$, you will obtain:

$$\:\left\{\begin{array}{c}\frac{dJ}{{dA}_{k}^{x}}={\int\:}_{L}\frac{{\partial\:\parallel\:\varvec{R}\parallel\:}^{2}}{\partial\:{A}_{k}^{x}\text{}}dL\\\:\frac{dJ}{{dA}_{k}^{y}}={\int\:}_{L}\frac{{\partial\:\parallel\:\varvec{R}\parallel\:}^{2}}{\partial\:{A}_{k}^{y}\text{}}dL\end{array}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\right.$$

(10)

The squared norm of the residual vector, denoted as $\:{\parallel\:\varvec{R}\parallel\:}^{2}$, may be expressed as follows in terms of its components, $\:{R}_{i}$: $\:{\parallel\:\varvec{R}\parallel\:}^{2}=\sum\:{\left({R}_{i}\right)}^{2}$. This equation determines the overall size of the residual vector inside the given vector space by summing the squares of each residual vector component²⁶. Thus, Eq. (10) will be as follows:

$$\:\left\{\begin{array}{c}\partial\:J=2{\int\:}_{L}\sum\:_{i}{R}_{i}\left(\frac{\partial\:{R}_{i}}{\partial\:{A}_{k}^{x}}\partial\:{A}_{k}^{x}+\frac{\partial\:{R}_{i}}{\partial\:{A}_{k}^{y}}\partial\:{A}_{k}^{y}\right)dL\\\:\partial\:J=2{\int\:}_{L}\left(\frac{\partial\:{R}_{i}}{\partial\:{A}_{k}^{x}}\:\partial\:{A}_{k}^{x}+\frac{\partial\:{R}_{i}}{\partial\:{A}_{k}^{y}}\:\partial\:{A}_{k}^{y}\right)dL\end{array}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\right.$$

(11)

Upon establishing the functional $\:J$=0 variation and replacing the formulas for $\:\frac{\partial\:J}{\partial\:{A}_{k}^{x}}$ and $\:\frac{\partial\:J}{\partial\:{A}_{k}^{y}}$, we derive:

$$\:{\int\:}_{L}\left(\varvec{R}.\frac{\partial\:\varvec{R}}{\partial\:{A}_{k}^{x}}\partial\:{A}_{k}^{x}+\varvec{R}.\frac{\partial\:\varvec{R}}{\partial\:{A}_{k}^{y}}\partial\:{A}_{k}^{y}\right)dL=0\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$

(12)

The MGM is utilised to minimise the functional $\:\partial\:J$, as expressed in Eq. (12). This is achieved by taking the residual vector R and calculating the inner product of the variations in the coefficients $\:{A}_{k}^{x}$ and $\:{A}_{k}^{y}$. Equation (12) is just an MGM projection of Eq. (1). After the DAEs are solved, a projection equation of dimension $\:\left(n+m\right)\times\:{N}_{b}$ is obtained, where $\:{N}_{b}$ is the number of time steps in Eq. (1). This yields the coefficients A_k^x and A_k^y. Only the coefficients $\:{A}_{k}^{x}$ and $\:{A}_{k}^{y}$ are involved in the differential-algebraic equation system represented by Eq. (6). Every discrete time step $\:{t}_{0},{t}_{1},\dots\:,{t}_{N}$ sees the evaluation of these coefficients. For a time period $\:{t}_{n}$​ to $\:{t}_{n+1}$, the MGM adjusts the equations accordingly.

Based on the initial conditions $\:t=0$, the MGM determines the state variables for the subsequent time step, $\:{t}_{1}$. The accuracy and stability of the numerical solution depend significantly on these initial conditions, which are typically set as $\:\left(0\right)={x}_{0}$ and $\:y\left(0\right)={y}_{0}$. Consequently, the updates for the coefficients $\:{A}_{k}^{x}$ and $\:{A}_{k}^{y}$ are determined as follows:

$$\:{A}_{k}^{x}\left({t}_{1}\right)={A}_{k}^{x}\left(0\right)+\frac{\varDelta\:t}{2}\left({f}_{x}\left(0,{A}_{k}^{x}\left(0\right),{A}_{k}^{x}\left(0\right)\right)+{f}_{x}\left(\varDelta\:t,{A}_{k}^{x}\left(\varDelta\:t,{A}_{k}^{x}\left(\varDelta\:t\right)\right),{A}_{k}^{x}\left(\varDelta\:t\right)\right)\right)$$

(13)

$$\:{A}_{k}^{y}\left({t}_{1}\right)={A}_{k}^{y}\left(0\right)+\frac{\varDelta\:t}{2}\left({f}_{y}\left(0,{A}_{k}^{y}\left(0\right),{A}_{k}^{y}\left(0\right)\right)+{f}_{y}\left(\varDelta\:t,{A}_{k}^{y}\left(\varDelta\:t,{A}_{k}^{y}\left(\varDelta\:t\right)\right),{A}_{k}^{y}\left(\varDelta\:t\right)\right)\right)$$

(14)

The initial conditions also guarantee that the results generated by the projection equations and the MGM are relevant and coherent. The trajectory of the state variables $\:x\left(t\right)$and $\:y\left(t\right)$ is defined by the system’s initial dynamic reaction. For solving the DAEs accurately over time, we therefore provide these frameworks. The updates for the coefficients $\:{A}_{k}^{x}$ and $\:{A}_{k}^{y}$ for $\:t={t}_{n+1}$ come from the sources listed below:

$$\:{A}_{k}^{x}\left({t}_{n+1}\right)={A}_{k}^{x}\left({t}_{n}\right)+\frac{\varDelta\:t}{2}\left({f}_{x}\left({t}_{n},{A}_{k}^{x}\left({t}_{n}\right),{A}_{k}^{x}\left({t}_{n}\right)\right)+{f}_{x}\left({t}_{n+1},{A}_{k}^{x}\left({t}_{n+1},{A}_{k}^{x}\left({t}_{n+1}\right)\right),{A}_{k}^{x}\left({t}_{n+1}\right)\right)\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$

(15)

$$\:{A}_{k}^{y}\left({t}_{n+1}\right)={A}_{k}^{y}\left({t}_{n}\right)+\frac{\varDelta\:t}{2}\left({f}_{y}\left({t}_{n},{A}_{k}^{y}\left({t}_{n}\right),{A}_{k}^{y}\left({t}_{n}\right)\right)+{f}_{y}\left({t}_{n+1},{A}_{k}^{y}\left({t}_{n+1},{A}_{k}^{y}\left({t}_{n+1}\right)\right),{A}_{k}^{y}\left({t}_{n+1}\right)\right)\right)\:\:$$

(16)

here $\:{f}_{x}$​ and $\:{f}_{y}$​ denote the dynamic and algebraic parts of the residuals. The procedure is repeated, modifying $\:{A}_{k}^{x}$ and $\:{A}_{k}^{y}$​ iteratively until the integral equation meets a defined tolerance level. When events like short circuit faults occur at time $\:t={t}_{f}$ the projection equations must shift from pre-fault DAEs to those that incorporate the fault. The coefficients $\:{A}_{k}^{x}\left(t\right)$ are maintained continuously throughout this process:

$$\:{A}_{k}^{x}\left({t}_{f}^{-}\right)={A}_{k}^{x}\left({t}_{f}^{+}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$

(17)

While the coefficients $\:{A}_{k}^{y}\left(t\right)$ undergo abrupt changes and must be reassessed according to the fault-on DAEs:

$$\:{A}_{k}^{y}\left({t}_{f}^{-}\right)\ne\:{A}_{k}^{y}\left({t}_{f}^{+}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$

(18)

The MGM approach employs continuous integration of the DAEs across time, where the coefficients $\:{A}_{k}^{x}\left(t\right)$ and $\:{A}_{k}^{y}\left(t\right)$ are updated at each time step by iterative solution of a discrete system of equations. This guarantees the smoothness of $\:{A}_{k}^{x}$and modifies $\:{A}_{k}^{y}$ as needed, with the goal of minimising residuals and offering a dependable solution to the parametric difficulties presented by the DAEs. When events trigger modifications, such as a short circuit failure happening at time $\:t\:=\:{t}_{f}$​, the projection equations will adjust correspondingly. At time $\:{t}_{f}$, the projection equation transitions from the pre-fault differential-algebraic equations (DAEs) to the fault-on DAEs. The algebraic variable $\:{A}_{k}^{y}$will experience discontinuities in its coefficients and will need to be updated according to the fault-on differential-algebraic equations (DAEs). However, the coefficients of the state variable $\:{A}_{k}^{x}$ remain continuous both before and after the faults $\:{t}_{f}^{-}$ and $\:{t}_{f}^{+}$. By reducing the reliance on simplified assumptions, MGM enhances the accuracy of stability analysis. For instance, during transient events like faults, MGM projects the system’s DAE, ensuring that real-time updates to rotor angle stability are both accurate and computationally feasible. This method serves as the mathematical core of the study, setting the groundwork for the integration of RFID data and machine learning techniques to improve diagnostic precision.

Architecture of RFID sensor tags

RFID sensor tags offer a powerful, practical, and independent means of defect detection and real-time monitoring in microgrids. Advanced data processing techniques are applied to these tags after they are installed in a network, significantly enhancing the dependability and stability of microgrid operations. RFID tags are capable of measuring not just voltage and current but also magnetic fields, temperature, and vibration. An innovative method for keeping an eye on and identifying microgrid issues is the use of RFID sensor tags. By combining RFID technology with sensors and power management systems, these tags provide continuous, wireless monitoring without the need for an external power source^17,27. By leveraging RFID’s capabilities for real-time data collection, the MGM can perform dynamic adjustments to the mathematical model, ensuring that it accurately reflects the rotor’s and microgrid behavior under varying conditions. This integration supports enhanced rotor angle stability, allowing for proactive measures to be implemented before potential instabilities occur. The combination of MGM’s predictive modeling and RFID’s instantaneous data feedback creates a robust framework for decision-making in automated systems. It facilitates rapid response to changes in system behavior, thereby optimizing performance and ensuring reliability.

RFID data acquisition significantly impacts the computational complexity of real-time fault detection systems by introducing challenges related to data volume, processing latency, and integration with other data sources. The high throughput of RFID tags necessitates advanced data filtering and aggregation techniques to isolate relevant information for fault detection, which can elevate computational demands²⁸. Additionally, stringent latency requirements compel the use of optimized algorithms, often involving parallel processing or machine learning methods, further complicating system architecture. As the scale of the RFID deployment increases, the need for scalable solutions becomes critical to ensure efficient handling of data influx while maintaining real-time responsiveness. The incorporation of error detection and correction mechanisms adds an additional layer of complexity, necessitating continuous monitoring and adaptation to ensure data integrity. Thus, the interplay between RFID data acquisition and computational complexity requires careful design considerations to achieve effective real-time fault detection.

Relevant data are collected throughout the feature extraction step, including harmonics, frequency components, and RMS values. To begin gathering and analysing vibration data from microgrids using these RFID sensor tags, the system’s voltage and current must be evaluated. In the microgrid, the current is expressed as:

$$\:I\left(t\right)={I}_{max}sin(\omega\:t+\varphi\:)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$

(19)

In Eq. 19, $\:\varphi\:$ is the phase angle, $\:{I}_{max}$ is the maximum current, and ω is the angular frequency. The time-varying characteristics of AC are captured by Eq. (19), which is crucial for the microgrid’s dynamic behaviour. In the microgrid, the voltage is expressed as:

$$\:V\left(t\right)={V}_{max}sin\left(\omega\:t\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$

(20)

In Eq. 20, $\:{V}_{max}$ is the highest voltage that can be obtained by capturing the sinusoidal change of the voltage in order to precisely characterise the system’s electrical potential differences. The instantaneous power is obtained by multiplying the voltage by the current in order to comprehend the power dynamics

$$\:P\left(t\right)=V\left(t\right)\cdot\:I\left(t\right)\cdot\:cos\left(\theta\:\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$

(21)

here $\:\theta\:$ shows the phase difference between voltage and current. Equation (21) is essential as evaluation of the microgrid’s energy transfer and efficiency depends on power computation. First recording electrical properties, the RFID sensors next compile raw vibration data shown by this model

$$\:v\left(t\right)=asin(\omega\:t+\varphi\:)+\epsilon\left(t\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$

(22)

here $\:\omega\:$ is the angular frequency; $\:\varphi\:$ is the phase angle; $\:\epsilon\left(t\right)$ denotes noise. Reflecting actual situations, Eq. (22) captures the signal and noise components of the vibration data. Crucially, vibration signals indicate mechanical and electrical problems in microgrid components. Raw RFID data is sent via a band-pass (BP) filter to eliminate vibration and extraneous components:

$$\:{v}_{bp}\left(t\right)=\mathcal{F}\left(v\right(t\left)\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$

(23)

here $\:\mathcal{F}$ specifies the filtering action. Since it lets frequencies within a given range relevant to the vibration signals—pass through while attenuating frequencies outside this range. This makes a band-pass filter the ideal. By concentrating on the pertinent frequency ranges where problem signals are likely to show, this improves the quality of the signal and so increases the accuracy of next analysis. Then the Fourier Transform turns the filtered signal into the frequency domain:

$$\:V\left(f\right)={\int\:}_{-{\infty\:}}^{{\infty\:}}{v}_{bp}\left(t\right){e}^{-j2\pi\:ft}dt\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$

(24)

The Fourier Transform breaks apart a time-domain signal into its component frequencies. Understanding the vibration properties and spotting any aberrant patterns suggestive of problems depends on the identification of the prominent frequencies and their amplitudes, so this metamorphosis is essential. Key characteristics are collected from the processed vibration signal to help fault diagnosis. Calculating the root mean square (RMS) value requires:

$$\:RM{S}_{v}=\sqrt{\frac{1}{T}{\int\:}_{0}^{T}{V}_{bp}^{2}\left(t\right)dt}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$

(25)

CNN-LSTM model

For RFID-based fault detection in microgrids, a hybrid model comprising CNNs and LSTMs is a suitable choice for the following reasons. CNNs²⁹. help to identify localised features in sensor data that can point to transient flaws. LSTMs allow one to record the temporal sequence of events, which is necessary to understand how mistakes evolve over time.

Figure 2show the CNN-LSTM model-based fault detection method. This model uses convolutional layers to extract spatial features from the data while combining LSTM layers—which control temporal interactions³⁰. The max-pooling layers enhance the feature maps and reduce their size^9,31. after filters have produced them. As the LSTM layers process these features consecutively, the in-put gate refreshes the candidate information; the forget gate eliminates extraneous data from previous stages; and the output gate creates the new hidden state. Information is flowed under control using gates. By combining CNNs and LSTMs, this model effectively captures the temporal and spatial aspects of the data, hence enhancing its potential to precisely and consistently identify microgrid faults.

Fig. 2

Microgrid Fault Diagnosis Overview.

The CNN-LSTM model’s mathematical representation is shown below:

• i. By means of filters, convolutional layers examine and identify properties from incoming data. One defines each filter using a weight matrix $\:{W}_{i}$ and a bias term $\:{\varvec{b}}_{i}$. These filters let one find the convolutional layer’s output from the input.

$$\:{Z}_{i}=X*{W}_{i}+{\varvec{b}}_{i}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$

(26)

$\:{Z}_{i}$ is the output feature map here; $\:X$ is the sample count; $\:*$ is the convolution operation; $\:{W}_{i}\:$and $\:{\varvec{b}}_{i}$ are the weights and biases of the filter, respectively. Max pooling layers lowers the spatial dimensions of the feature maps. Applying max pooling results in calculated output $\:{Z}_{i}^{{\prime\:}}$ for every feature map $\:{Z}_{i}$:

$$\:{Z}_{i}^{{\prime\:}}=MaxPool\left({Z}_{i}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$

(27)

• ii. LSTM layers seek to capture the temporal dependencies in the data. Every LSTM cell has many gates: an input gate, an output gate, an update gate, a forget gate, and a cell state evolving throughout time. The LSTM output H at a given time step t is computed by the following process: The following procedure is used to calculate the LSTM output $\:H$ at a specific time step $\:t$:

• a) The joint forgetting gate decides which parts of the previous cell state $\:{C}_{t-1}$ should be kept or discarded. It takes in the previous hidden state $\:{H}_{t-1}$ and the current input $\:{X}_{t}$. Based on this information, it produces a forget-gate vector $\:{f}_{t}$ with values between 0 and 1, which adjusts the previous cell state accordingly.

$$\:{f}_{t}=\sigma\:\left({W}_{f}\cdot\:\left[{H}_{t-1},{X}_{t}\right]+{b}_{f}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$

(28)

here, $\:\sigma\:$ is the sigmoid activation function, and $\:\left[{H}_{t-1},{X}_{t}\right]$ is the combination of the prior hidden state $\:{H}_{t-1}$and the current input $\:{X}_{t}$. The weight matrix and bias vector for the forgetting gate are denoted by $\:{W}_{f}$ and $\:{b}_{f}$.

• b) The input gate is denoted as $\:{i}_{t}$, decides which portions of the candidate updates $\:\stackrel{\sim}{C}$ will be incorporated into the cell state $\:{C}_{t-1}$. These candidate updates $\:\stackrel{\sim}{C}$ represent possible new values that might be added to the existing cell state.

$$\:\stackrel{\sim}{{C}_{t}}=tanh({W}_{C}.[{H}_{t-1},{X}_{t}]+{b}_{C})\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$

(29)

here, the weight matrix and bias vector used to calculate the candidate updates are denoted as $\:{W}_{C}$ and $\:{b}_{C}$. One can ascertain the input gate $\:{i}_{t}$ as follows:

$$\:{i}_{t}=\sigma\:\left({W}_{f}\cdot\:\left[{H}_{t-1},{X}_{t}\right]+{b}_{i}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$

(30)

• c) To update the new cell state, we use the joint forgetting gate $\:{f}_{t}$, the previous cell state $\:{C}_{t-1}$, the input gate $\:{i}_{t}$, and the candidate values $\:\stackrel{\sim}{{C}_{t}}$.

$$\:{g}_{t}={f}_{t}.{C}_{t-1}+{i}_{t}.\stackrel{\sim}{{C}_{t}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$

(31)

• d) The output gate $\:{\text{O}}_{\text{t}}$ controls what portion of the current cell state $\:{C}_{t}$ will be shown as the hidden state $\:{H}_{t}$. It decides which aspects of the cell state are passed on.

$$\:{O}_{t}=\sigma\:\left({W}_{O}\cdot\:\left[{H}_{t-1},{X}_{t}\right]+{b}_{O}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$

(32)

$$\:{H}_{t}={O}_{t}.tanh\left({C}_{t}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:$$

(33)

here, the weight matrix and bias vector used to calculate the output gate are denoted as $\:{W}_{O}$ and $\:{b}_{O}$.

Data is gathered and used into MATLAB during the first step of modeling; the acquired database is used to train a CNN-LSTM for better estimate. The network is trained in the case study using a dataset of 10,48,575 samples considering coding rate, payload, and spreading factor. The dataset is split then into a validation set to assess the performance of the network and a learning set for training. Using a scaled conjugate gradient backpropagation method, assigning 70% of the data for training, 15% for validation, and 15% for testing, network training is undertaken. RMS and regression analysis constitute part of the evaluation of network performance. Finding the smallest error value helps to maximize non-constraint parameters; thereafter, these values are used to identify the optimal value of acquired power.

Table 1 CNN-LSTM information fusion technique using entropy identity attributes metrics values.

Using entropy identification attribute measurements throughout a variety of epochs—more especially, from 930 to 1030—Figure 3 displays the performance of a CNN-LSTM in a multifactor authentication system. Table 1 shows that CNN-LSTM performance increases with training progress; its best validation performance of 87.3123 at epoch 1000. With minimum errors ranging from 0.01 to 0.03, the inputs (P, B, D) fed into the CNN-LSTM provide outputs that rather closely match the target values. This shows great dependability and precision in the authentication procedure as it shows the capacity of the model to correctly forecast and confirm identification traits. The CNN-LSTM effective learning and optimization across the training epochs is highlighted by declining error values and convergence of out-puts to target values, hence producing peak performance at the designated epoch.

Fig. 3

Performance of CNN-LSTM during Training and Validation.

Figure 4 presents the combined data set together with the performance of a CNN-LSTM model in target value prediction across training, validation, and testing phases. With a strong correlation coefficient $\:(R\:=\:0.9995)$, every regression figure reveals almost perfect linear link between goal and output values. Every plot’s fit lines show low error and great accuracy as they rather closely match the perfect $\:Y=T$ line. More specifically, the training plot $\:(R\:=\:0.9953)$, validation plot $\:(R\:=\:0.99956)$, and test plot $\:(R\:=\:0.\:99949)$ all support the CNN-LSTM model’s strong performance and capacity for generalizing effectively to unknown data. Showcasing its great predictive power across all data splits, the combined figure further supports the general dependability and precision of the CNN-LSTM model.

Fig. 4

Regression Plots for Training, Validation, and Testing Phases of CNN-LSTM Performance.

Case study

The rotor angle stability of an IEEE 3-machine, 9-bus power system under $\:100$ base MVA at $\:50\:Hz$ frequency operation is investigated in this part. This system uses a hydroelectric generator connected to slack bus 1 as generator 1 ($\:{G}_{1}$). Generator 3 ($\:{G}_{3}$) is another hydroelectric generator attached to bus bar 3; Generator 2 ($\:{G}_{2}$) runs on wind power linked to bus 2. Bus bars five, six, and eight are set aside for loads A, B, and C respectively. After the system was built in PSCAD, three different types of faults were added at the sites shown in Fig. 5. The brief circuit started at six seconds and lasted for $\:0.20$s. Stability and reliability of modern microgrids depend on continuous monitoring and prompt fault identification. The application of RFID sensors for real-time monitoring and fault detection of microgrids^32,33 is examined in this work. Important parameters like active power, voltage, and current are efficiently tracked using RFID sensor tags together with sophisticated signal processing and deep learning approaches.

The IEEE 3-machine, 9-bus system, traditionally part of larger power system studies, is treated as a microgrid primarily due to its modular configuration, diverse generation sources, and the implementation of real-time monitoring technologies for improved resilience. In this paper, the IEEE 3-machine 9-bus system is adapted to microgrid characteristics by introducing advanced monitoring techniques, including RFID technology integrated with a CNN-LSTM fault detection model, to mimic microgrid behavior under high-penetration renewable energy conditions. This setup allows for dynamic responses to faults and stability monitoring at a smaller scale, reflecting the essential qualities of a microgrid. The study addresses rotor angle stability—a core concern in microgrids with renewable energy sources due to low inertia—by using a MGM for transient stability analysis. This focus on resilience and localized stability is characteristic of microgrid systems rather than traditional centralized grids.

Fig. 5

IEEE 3- Machine 9-Bus System Single Line Diagram.

In the case of two winding transformers, the primary winding is the one that takes the input from the supply. While the secondary winding is connected to a load for supplying energy to the load. The data for the Two-Winding Transformer of the microgrid is provided in Table 2.

Table 2 Two-winding Transformer Data.

Busbars are incredible pieces of technology that make complicated power distribution much easier, less expensive, and more flexible. Busbars, also known as busbar trucking systems, distribute electricity with greater ease and flexibility than other more permanent installation and distribution forms. Sometimes spelled bus bar or buss bar, they are often metallic strips of copper, brass, or aluminum that both ground and conduct electricity. The data for the Bus Bar of the microgrid is provided in Table 3.

Table 3 Bus Bar Data.

Transmission line parameters are characteristics that describe the behavior and performance of the transmission lines used to transfer electrical power from one place to another. These parameters are essential for designing, analyzing, and optimizing the performance of the transmission lines. The parameters include Impedance and resistance. Table 4 shows the Impedance and resistance of the microgrid.

Table 4 Line parameters.

The power transformer is a type of transformer and a type of toroidal transformer. Power transformers are a device that uses the principle of electromagnetic induction to change voltage. Its function is voltage conversion and safety isolation in power technology and power electronics. It is widely used in technology. These parameters play a critical role in understanding, designing, and analyzing the operation of transformers in an electrical network. Table 5 shows the Transformer Parameters of the microgrid.

Table 5 Transformer parameters.

Load Data refers to information about the electrical energy consumption patterns of the consumers within the microgrid network. Load data provides insights into how much electrical power is being drawn from the system by various consumers at different times, allowing power utilities and operators to efficiently manage electricity generation, transmission, and distribution. Below Table 6 shows the Load Data of the microgrid.

Table 6 Load data.

CNN-LSTM model training outcomes

Comparatively to the overall number of problems the model identifies, its accuracy is found by counting the flaws it properly classifies. Table 7 shows that for the CNN-LSTM model accuracy reaches $\:0.98$ for single-phase faults but falls to 0.90 for three-phase faults. To determine the re-call rate—which indicates how well the model finds all actual defects—divide true positives by the sum of false negatives. For single and three-phase faults, the CNN-LSTM model boasts a recall rate of $\:0.98$. A high recall rate indicates that the model reduces missed detections and effectively finds most real defects. Combining accuracy and recall, the F1 score points out the general performance of the model. Regarding single-phase faults, a high F1 score shows that, by properly balancing accuracy and recall, the CNN-LSTM model lowers false positives as well as false negatives. The model has to balance identifying the bulk of flaws with minimizing too many false alarms if it is to properly categorize errors.

Table 7 Performance of Fault classification.

By use of the Receiver Operating Characteristic (ROC) curve, the CNN-LSTM model’s performance in fault categorization is assessed. Larger ROC curve area denotes higher performance. Figure 6 shows the ROC curve of the CNN-LSTM model to differentiate among three various fault types. With a ROC curve area of $\:0.99$ for every one of the three varieties of defects, the CNN-LSTM model shines in identifying and classifying these errors.

Fig. 6

CNN-LSTM Fault Classification ROC Curve.

RFID model training outcomes

Reconstructing the vibration data for each RFID tag with CNN-LSTM model¹⁷ yields the residual error (RE). Figure 7 demonstrate the RE values for the three separate faults influencing RFID tags $\:1,\:2,$ and $\:3$ ranging from $\:0.04$ to $\:0.12$. Strongly associated with the RE, the position of the RFID tags and the problem itself suggest that the fault is most likely near to RFID tags $\:1$ and $\:2$. Moreover, RFID tag $\:2$ exhibits higher RE values than tag $\:1$, implying that tag $\:2$ is nearer the fault. This remark fits the stance of intelligent mistakes.

Fig. 7

REs Value of RFID Under Fault Conditions.

Figure 8 shows several strategies’ outcomes. Whereas the blue lines show the normal trajectories produced by the collecting approach $\:({\theta\:}_{21}=120^\circ\:),\:$the yellow lines show the standard trajectories of $\:{\theta\:}_{21}$ as decided upon by the sampling method $\:({\theta\:}_{21}=136^\circ\:)$. The green lines show the standard trajectories of the HM approach for $\:({\theta\:}_{21}=137^\circ\:)$; the black lines show the standard trajectories of the TM method for $\:({\theta\:}_{21}=134^\circ\:)$. The red lines show the typical paths of $\:({\theta\:}_{21}=113^\circ\:)$ from the recommended MGM method. Moreover, Fig. 8 illustrates how well MGM controls the rotor angle under a failure in the area of $\:135 MW\le\:{G}_{2}\le\:160MW$. MGM is a preferred choice as its shorter recovery time and higher performance highlight its quick stabilization angle reduction, thereby ensuring microgrid stability in fault conditions.

Fig. 8

Relative Swing Angle $\:{\theta\:}_{21}$ Curve.

A breakdown between generators $\:{G}_{1}$ and $\:{G}_{2}$in the IEEE 3-machine 9-bus power system clearly alters the rotor angles of the generators⁵. This change greatly influences the voltage of the system as differences in rotor angle cause changes in power, which then influences voltage levels. As Fig. 9 shows, the voltage across the buses will so vary in reaction to the malfunction.

Because RFID-based fault detection can accurately collect voltage changes and vibration signals with high precision and little interference, it becomes especially successful in this environment. An RFID system based on CNN-LSTM is especially qualified to extract a range of signals, including vibrations from generators, so enabling more precise analysis. When a failure emerges at $\:6.2s$, the CNN-LSTM-based RFID system displays more advanced fault detection and signal extracting capabilities than DAQ, Decision Trees, and SVM systems based on considerable increase in data.

Suggesting typical functioning, the voltage first remains constant at $\:0kV$ for $\:0$ to $\:6s$. A breakdown occurs at $\:6s$ a rapid increase in voltage from $\:0kV$ to $\:10kV$. Following this abrupt spike, the voltage stabilizes at $\:10kV$, which stands for the continually high voltage resulting from the ongoing fault condition. This paper underlines the need of microgrid systems having quick fault detection and efficient response techniques as well as the extent of voltage variations during a fault occurrence.

Fig. 9

Voltage Comparison.

When a fault occurs between $\:{G}_{1}$ and $\:{G}_{2}$ in the IEEE 3-machine 9-bus power system depicted in Fig. 5, the load moves from one generator to the other and the disturbance causes notable changes in the rotor angle $\:\delta\:$ of these generators. This change in rotor angle indicates generators losing synchronism, which causes variations in the electrical current output $\:I\left(t\right)$. The clearly visible spike or fluctuation in the affected lines will indicate the dynamic reaction of the system to the failure. Because of its great resilience to electromagnetic interference and its high signal processing capability, RFID-based defect detection is very good in extracting vibration signals. Figure 10 shows the present stability to help to demonstrate this. Precise, high-resolution data offered by RFID technology produces a quasi-stationary current signal with minimum departure from zero, therefore indicating strong signal integrity and durability. Reflecting possible noise and instability in these systems, conventional approaches such DAQ, Decision Trees, and SVM tend to show more pronounced stochastic fluctuations in the present signal.

Fig. 10

Current Comparison.

With the fault incidence shown by a red dashed line, Fig. 11displays the active power over time. The power measurements obtained by many techniques are matched to the real power both before and after the problem³⁴. The power-angle equation $\:P=EV/Xsin\left(\delta\:\right)$ characterizes the link between rotor angle and power. A failure causes the rotor angle to vary, therefore changing the sine component and hence the power flow. This connection suggests that variations in the power output follow from any change in the rotor angle. Unlike more erratic data from conventional measurement systems, Fig. 10 illustrates that RFID-based fault detection precisely monitors the real power, therefore capturing the dynamic reaction of the system. RFID data’s reliability and accuracy make it the better approach for real-time monitoring and fault diagnostics in power systems.

Fig. 11

Active Power Comparison.

Comparisons with existing approaches

Table 8 compares fault detection methodologies for microgrids, concentrating on four approaches: SVM and decision trees, DWT with ANN, and a new method that uses RFID-based CNN-LSTM architecture. The SVM-based method, while cost-effective, exhibits low sensitivity to vibrational perturbations and medium scalability. The decision tree approach offers moderate improvements in sensitivity and similar scalability. The ANN method, employing DWT, provides high sensitivity and scalability, balancing diagnostic accuracy with computational complexity. The proposed RFID based CNN-LSTM method demonstrates superior performance across all metrics, offering very high sensitivity to dynamic disturbances and scalability with reduced maintenance overhead cost, underscoring its efficacy in real-time fault detection and robust fault diagnosis in complex microgrid systems.

Table 8 Comparisons with Existing Approaches.

Conclusion

To further expand transient stability analysis in microgrids, this work presents a novel method combining Polynomial Approximation based MGM with RFID-enhanced data collecting. By means of more precise and fast data collecting, RFID technology improves the precision and responsiveness of defect detection systems. Moreover, the CNN-LSTM algorithm integration enhances fault diagnostic capabilities, thereby producing a 94% fault classification accuracy. The case study on IEEE 3-machine 9-bus system shows notable increase in fault detection speed and accuracy. These advances produce more consistent and trustworthy microgrid operations by overcoming the limits of traditional methods in managing non-linear and non-polynomial situations. The research stresses the advantages of combining strong analytical algorithms with modern data-gassing technology in order to offer smarter grid enhancements and real-time RFID-based fault identification.

Future work

To expand the scope of our transient stability analysis, we plan to apply the proposed methodology to the New England 10-generator, 39-bus system. This more complex system will allow us to rigorously test and validate our approach across a broader range of operating conditions and fault scenarios. By utilizing a larger network, we aim to capture a wider array of transient behaviors and interdependencies, offering a more comprehensive and representative assessment of the methodology’s effectiveness. This transition to a larger power system model will also provide valuable insights into scalability and robustness, both of which are crucial for real-world applications.

Additionally, we intend to incorporate wavelet transform techniques to enhance the sensitivity and accuracy of fault detection within our stability analysis. Wavelet transforms offer significant advantages for analyzing transient and non-stationary signals typical of fault conditions in microgrids. Integrating these techniques will complement our existing CNN-LSTM-based fault detection framework, enabling finer signal processing and improved feature extraction for more precise identification of transient events. These future enhancements aim to strengthen the model’s diagnostic capabilities and broaden its applicability to diverse and dynamic microgrid environments.