An efficient personalized federated learning approach in heterogeneous environments: a reinforcement learning perspective

Abstract

In order to address the problem of data heterogeneity, in recent years, personalized federated learning has tailored models to individual user data to enhance model performance on clients with diverse data distributions. However, the existing personalized federated learning methods do not adequately address the problem of data heterogeneity, and lack the processing of system heterogeneity. Consequently, these issues lead to diminished training efficiency and suboptimal model performance of personalized federated learning in heterogeneous environments. In response to these challenges, we propose FedPRL, a novel approach to personalized federated learning designed specifically for heterogeneous environments. Our method tackles data heterogeneity by implementing a personalized strategy centered on local data storage, enabling the accurate extraction of features tailored to the data distribution of individual clients. This personalized approach enhances the performance of federated learning models when dealing with non-IID data. To overcome system heterogeneity, we design a client selection mechanism grounded in reinforcement learning and user quality evaluation. This mechanism optimizes the selection of clients based on data quality and training time, thereby boosting the efficiency of the training process and elevating the overall performance of personalized models. Moreover, we devise a local training method that utilizes global knowledge distillation of non-target classes, which combined with traditional federated learning can effectively address the issue of catastrophic forgetting during global model updates. This approach enhances the generalization capability of the global model and further improves the performance of personalized models. Extensive experiments on both standard and real-world datasets demonstrate that FedPRL effectively resolves the challenges of data and system heterogeneity, enhancing the efficiency and model performance of personalized federated learning methods in heterogeneous environments, and outperforming state-of-the-art methods in terms of model accuracy and training efficiency.

Federated learning¹ (FL) is a rapidly evolving distributed machine learning paradigm that enables collaborative model training across multiple data owners while preserving data privacy^2,3. The predominant FL architecture follows a server-client model, where a central server is responsible for aggregating global models, and clients (i.e., data owners) perform local model training. Through iterative communication, FL produces a global model that is adaptive to the diverse data distributed across clients, thereby addressing the specific tasks of each client.

In practical applications, clients are often networked devices such as mobile phones, wearable devices, and autonomous vehicles, each of which generates and collects data with varying distributions. For example, in handwriting recognition on mobile devices, different users writing the same word may exhibit variations in stroke width and tilt, leading to significant discrepancies in the feature distributions of handwritten characters. This variability, known as data heterogeneity, results in client data being non-independent and identically distributed (non-IID⁴). This heterogeneity poses a major challenge for the unified global model, as it may find it difficult to generalize effectively across the varying data distributions, thereby reducing the classification performance on certain local datasets. Additionally, variations in hardware, network connectivity, and battery life across clients, termed system heterogeneity, further complicate the FL process. System heterogeneity causes training time to be determined by the slowest client, thereby underutilizing the computational resources of more capable clients and diminishing the overall training efficiency. Thus, data and system heterogeneity are fundamental challenges⁵ in FL, hindering the model performance and efficiency of traditional FL methods in heterogeneous environments.

To address the issue of data heterogeneity, personalized federated learning has emerged as a promising solution, focusing on creating customized models tailored to each client’s unique data characteristics, thereby enhancing local model performance. Personalized federated learning strategies can be broadly categorized into two approaches⁶: “global model personalization” and “learning personalized models.” The former involves training a global model and subsequently adapting it locally for each client, whereas the latter integrates model aggregation with various local training methods to simultaneously generate personalized models during federated training. However, most existing personalized federated learning approaches primarily focus on mitigating data heterogeneity, often neglecting system heterogeneity. As a result, in heterogeneous environments these methods may improve the model performance but fail to enhance training efficiency, thereby limiting their practical applicability. Consequently, there is a need for a novel personalized federated learning method that simultaneously addresses both data and system heterogeneity, thereby improving model performance and training efficiency in heterogeneous environments.

In addition to the challenges of data and system heterogeneity, personalized federated learning on mobile devices faces other obstacles, such as limited wireless network connectivity and unstable device availability. Due to these limitations, it is impractical for FL to involve all devices in each round of model updates and aggregation. In most FL methods, a group of devices is randomly chosen for training during each round. However, because of data and system heterogeneity, clients contribute differently to global model training based on their data distribution, communication latency, and computational speed. Most existing FL methods overlook these disparities, and their random selection approaches fail to leverage client characteristics to optimize the FL process. Therefore, optimizing client subset selection is crucial for improving model performance and training efficiency in FL within heterogeneous environments.

Moreover, FL is susceptible to the catastrophic forgetting phenomenon^7,8, similar to that observed in continual learning^9,10. As the central server aggregates local models from clients, the varying data distributions and selective training of client subsets can lead to significant shifts in data distributions across training rounds. These shifts may cause the global model to overwrite critical parameters learned from previous tasks, leading to the loss of previously obtained knowledge. However, existing FL methods lack effective mechanisms to mitigate this forgetting phenomenon. Addressing this issue is essential for maintaining model performance and ensuring the continuous learning capability of FL models in heterogeneous environments.

In this study, we propose an innovative personalized federated learning approach tailored for heterogeneous environments, aimed at addressing the challenges mentioned above. The contributions of our work can be outlined as below:

• We devise a novel personalized federated learning method, FedPRL, specifically crafted to tackle the challenges of data and system heterogeneity in heterogeneous environments. FedPRL boosts the performance of tailored models for each client while also enhancing the efficiency of the model’s training process in heterogeneous environments.

• We design a client selection approach leveraging reinforcement learning (RL) and user quality evaluation. This approach evaluates clients according to their impact on the global model and local training time, using a double deep Q-learning (DDQL) algorithm to select the optimal client subset. This method optimizes client selection, leading to more efficient global model training in heterogeneous environments and improved model performance.

• In FedPRL, we propose a local training method that incorporates global knowledge distillation of non-target classes. This method leverages knowledge distillation techniques to mitigate the forgetting phenomenon in FL, enhancing the model’s adaptability to new tasks while retaining knowledge from previous tasks. This approach improves the model’s continual learning ability and boosts global model performance.

• Comprehensive experiments conducted on both standard and real-world datasets show that, in heterogeneous environments, FedPRL surpasses state-of-the-art methods in both model classification performance and training efficiency. Additionally, it shows strong potential for application in the medical and healthcare field, where it can effectively handle classification tasks.

The remainder of this study is organized as follows: Section “Related works” reviews existing literature on addressing data and system heterogeneity in FL, along with related works on RL and continual learning in FL. Section “Methods” offers an in-depth explanation of the algorithm we propose. Section “Experiments” outlines the key questions to be explored and provides detailed information on datasets, parameter settings, and experimental procedures. It also presents the full experimental results along with an in-depth analysis, addressing the key questions. Finally, Sect. “Conclusion” summarizes the study’s contributions and suggests directions for future research.

Related works

Guided by the challenges identified in FL, we conducted a comprehensive review across four key dimensions: data heterogeneity, system heterogeneity, RL-based federated learning, and continuous learning-based federated learning.

Data heterogeneity

Personalized federated learning has been extensively explored as a strategy to mitigate data heterogeneity, with numerous diverse methodologies proposed in recent years. They mainly include five underlying strategies: model-agnostic meta-learning, clustering, multi-task learning, dual-model integration, and simultaneous learning of shared representation and local model.

(1) Model-agnostic meta-learning (MAML): FedAvg+¹¹ was designed as a straightforward personalized federated learning method that leverages MAML. This method initially trains a global model and subsequently fine-tunes it locally on each client using stochastic gradient descent over several epochs, thereby personalizing the model to the local data. Later, personalized federated learning was formally connected with MAML, leading to the proposal of algorithms^12,13 that train meta-models optimized for local personalization.

(2) Clustering: ClusteredFL^14,15 was devised under the approach that clients could be grouped into clusters, where each cluster would share a common model while allowing models to differ between clusters. Clients learn their cluster assignments and models during training. Similarly, FedEM, proposed by Marfoq et al.¹⁶, operates as a soft clustering algorithm, treating personalized model learning as a mixture of a finite set of component models.

(3) Multi-task learning (MTL): This strategy captures subtle relationships between client models by framing federated multi-task learning as an optimization problem with a penalty term that reflects client differences. Smith et al.¹⁷ pioneered this approach, introducing an algorithm that handles general penalties but is limited to learning linear models or pre-trained linear combinations. Subsequent work^18,19,20,21 extended this framework to train more general models, albeit with simpler penalties, such as the distance to the average model.

(4) Dual-model integration: This strategy integrates both global and local models for each client. Corinzia and Buhmann²² and Mansour et al.¹⁵ initially proposed this idea, which was later expanded by Zhang et al.²³, allowing clients to integrate the local models from other participants by using appropriate weights that are dynamically acquired through the training process.

(5) Simultaneous learning of shared representation and local model: This strategy is employed by approaches such as FedRep²⁴, FedPer²⁵ and pFedGP²⁶. In these methods, the local models in FedRep and FedPer are linear, whereas pFedGP utilizes a Gaussian process. The local models operate on global latent representations, though pFedGP’s reliance on Gaussian processes for learning semi-parametric models in a federated context results in significant computational costs during training and inference.

Summary: Among the various approaches for addressing data heterogeneity, those involving the simultaneous training of shared representations and local models have shown promise. However, refining local models while accommodating changes in shared representations increases computational complexity. Consequently, the refinement of local models is often constrained, limiting the potential performance gains of personalized models in heterogeneous environments.

System heterogeneity

In personalized federated learning, addressing system heterogeneity involves designing personalized models with varying architectures tailored to each client’s computational and storage capabilities. This approach optimizes hardware resource utilization and enhances the efficiency of model training in heterogeneous environments.

Building on this concept, Horváth et al.²⁷ proposed a method in which each client trains a portion of the global model, with the size of this portion being adjusted according to the client’s computational capabilities. This method is especially beneficial for clients that utilize only a limited subset of channels in a convolutional neural network. Similarly, Tan et al.²⁸ devised a method where “prototypes”-representing the mean features of all data points in a specific class-are exchanged between client devices and servers instead of the model’s gradients or parameters. This technique allows for diverse model architectures and input spaces across clients.

Another method that considers both system heterogeneity and data heterogeneity is pFedHN, designed by Shamsian et al.²⁹. In this approach, a global hypernetwork processes local client representations to produce personalized, heterogeneous models. However, a significant drawback of this method is the substantial memory usage of the hypernetwork, which, in Shamsian et al.’s experiments, required 100 times more parameters than the output model.

Summary: Research on system heterogeneity in personalized federated learning is notably less developed than research on data heterogeneity. Few effective methods address both challenges concurrently. The current methods’ insufficient consideration of system heterogeneity limits the potential for personalized models to achieve both superior performance and efficient training in heterogeneous environments.

RL-based federated learning

RL is a powerful optimization technique that excels in managing and optimizing complex decision-making processes through its adaptive learning capabilities. Recent research^30,31,32,33 has demonstrated the significant potential of applying RL to client selection in FL. These studies propose frameworks that facilitate dynamic client selection by considering multiple aspects, including data distribution and hardware capabilities. Based on the different perspective of the problems concerned, existing methods can be divided into the following three aspects: data heterogeneity only, system heterogeneity only, and both data and system heterogeneity.

(1) Data heterogeneity only: FAVOR³⁰ was devised as a control framework that utilizes experiential learning, which incorporates the DDQL algorithm to select clients. However, the reliance on a single client for training the DDQL model may impede the agent’s ability to converge rapidly.

(2) System heterogeneity only: Zhang et al.³¹ and Rjoub et al.³² also utilized DDQL for client selection, with Zhang et al.³¹ uniquely considering the dynamic nature of the client pool in their approach.

(3) Both data and system heterogeneity: In this regard, a multi-agent reinforcement learning³³ (MARL) framework was designed, where each agent corresponds to a client. While this method effectively considers both heterogeneities, having multiple agents involved substantially raises resource consumption, leading to a more resource-intensive process.

Summary: Current RL-based client selection methods seldom address both data and system heterogeneity concurrently and often struggle to balance model performance with training efficiency.

Continuous learning-based federated learning

So far, the challenge of knowledge forgetting in FL within the context of continual learning has received relatively limited attention. Below, we present a chronological overview of the key research developments in this area.

In the early stages, Casado et al.³⁴ explored scenarios where data distributions shift over time in FL. Hendryx et al.³⁵ proposed the concept of “federated reconnaissance,” where new categories gradually emerge during training, and proposed the use of prototype networks to address this challenge. Guo et al.³⁶ advanced the field by developing a regularization-based algorithm along with a novel theoretical framework. During this period, researchers increasingly recognized and analyzed the phenomenon of knowledge forgetting by dynamically examining the FL process.

Subsequently, Usmanova et al.³⁷ designed a distillation-based approach to counteract catastrophic forgetting by leveraging previous models alongside the global model to guide the training of local models. Yoon et al.³⁸ proposed an innovative federated graph parameter isolation method that splits network weights into global parameters and those specific to individual tasks. Dong et al.³⁹ addressed the federated class incremental setting by employing a distillation-based method aimed at reducing catastrophic forgetting from both local and global perspectives. More recently, Qi et al.⁴⁰ proposed a generative replay-based method called ACGAN, incorporating model integration and consistency enforcement to further alleviate forgetting. During this phase, a variety of techniques were developed to tackle the problem of knowledge forgetting.

Summary: Current research highlights the detrimental effects of knowledge forgetting on FL. Addressing this challenge is crucial for enhancing the performance of global model.

Methods

Overall structure

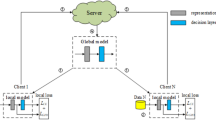
To tackle the challenges posed by data and system heterogeneity in heterogeneous environments, we propose a novel personalized federated learning method called FedPRL. The primary goal of FedPRL is to enhance both the generalization capability and training efficiency of the global model through optimized client selection and refined local training processes. Following this, the global model is subsequently tailored into personalized models for each client by applying an optimized personalization strategy, ultimately boosting the classification performance and efficiency of these personalized models in heterogeneous environments. To this end, the workflow of our FedPRL algorithm is organized into six steps, as illustrated in Fig. 1.

Step 1: Client selection: The server performs client selection by utilizing the method of RL and user quality evaluation. The selection strategy adapts according to the current stage of exploration in optimizing the client combination. In the early stages of training, when exploration is crucial, the method favors unselected clients to test new combinations. In later stages, once the optimal combination has been identified, the selection process prioritizes the best-performing clients to maximize the global model’s effectiveness.

Step 2: Local training: The selected clients employ a FL algorithm that incorporates global knowledge distillation for non-target classes. This approach preserves the global model’s prior knowledge within each client’s model while simultaneously updating the local model with the client’s specific dataset.

Step 3: Client local models upload: Clients upload their updated local model parameters to the central server.

Step 4: Global aggregation: The server then aggregates these parameters to update the global model.

Step 5: Global model distribution: The server distributes the updated global model parameters back to each client, setting the foundation for the next round of local updates and FL.

Step 6: Global model personalization: Each client personalizes the global model using a strategy based on local data storage. In this step, the client processes sample features from its local dataset through the global model, generating transitional representations. These are then paired with corresponding sample labels to create key-value pairs, which are stored locally to complete the local data storage setup. During personalized model inference, the k-nearest neighbors (kNN) model generates local predictions based on this local data storage, while the global model provides a global prediction. The final personalized model prediction is derived by combining these local and global predictions through a model interpolation technique.

Below, we will provide a detailed explanation of the methods we designed and optimized, which are integrated into Step 1, Step 2, and Step 6. The remaining steps Step 3, Step 4, and Step 5 retain the operations in the FedAvg¹ algorithm and will not be further elaborated.

Fig. 1

Overall structure of the FedPRL algorithm.

Client selection

During this step, we designed our method based on RL and user quality evaluation to optimize the client selection process. Therefore, in this section, we begin by introducing the user quality evaluation function that we devised, which assesses each client’s contribution to mitigating the challenges posed by system heterogeneity and data heterogeneity in heterogeneous environments. Following this, we detail our proposed DDQL-based client selection method. This method incorporates the user quality evaluation function into the reward mechanism, enabling the selection of the optimal client combination for each training round.

User quality evaluation function

In order to overcome the challenges of system and data heterogeneity in heterogeneous environments, our quality evaluation function assesses clients based on two key factors: total training time and their impact on improving global model accuracy. This dual assessment enables the client selection method to effectively tackle both challenges simultaneously.

(1) System heterogeneity: Clients in a FL network vary in computing power and network connectivity, leading to differences in the time required for model training and communication. To address this, we evaluate each client based on the time they spend on data transmission and model training. By prioritizing clients with shorter total times, we can enhance the efficiency of the FL process, thereby mitigating the effects of system heterogeneity. The total time spent by client n in the i-th round of federated training is calculated as follows:

$$\begin{aligned} T^i_n=t^i_n+\tilde{t}^i_n, \end{aligned}$$

(1)

where $t^i_n$ represents the local training time, and $\tilde{t}^i_n$ denotes the data transmission time. Local training time refers to the computational time needed for local iterations using gradient descent, estimated based on the client’s hardware capabilities. Data transmission time is the time required to transmit the client’s local model parameters to the server, calculated based on the model’s parameter size and the network bandwidth.

(2) Data heterogeneity: Owing to differences in data distribution among clients, the degree to which each client’s model parameters contribute to optimizing the global model varies. To address this issue, we established a scoring mechanism that assesses each client’s impact on the global model during each training round, allowing for the selection of the most advantageous clients and thereby reducing the negative impacts of data heterogeneity. The client quality evaluation function is expressed as follows:

$$\begin{aligned} \mathscr {Q}^i_n={\varvec{\theta}} \cdot (A^i_n-A^{i-1})+(1-{\varvec{\theta}} )\cdot \mathscr {Q}^{i-1}_n, \end{aligned}$$

(2)

where $A^i_n$ represents the local model accuracy of client n in the i-th round of training, and $A^{i-1}$ refers to the global model’s accuracy from the preceding round. This function accounts for each client’s historical contributions, offering a fairer and more comprehensive evaluation over the long term and addressing potential fluctuations in model performance.

However, calculating client accuracy ($A^i_n$) in each round is time-consuming, as it requires model inference using validation set samples, thereby reducing training efficiency. To overcome this, we designed an alternative function based on the normalized model difference⁴¹, which replaces the $A^i_n - A^{i-1}$ component in the quality evaluation function, thereby reducing computational overhead. The new function is defined as:

$$\begin{aligned} \zeta ^i_n=\left\{ \begin{array}{lr} \text {exp}\left\{ -|d(w^i_n,w^i)|\right\} ,& \text {if}\ \ P_i>P_{i-1} \\ 1-\text {exp}\left\{ -|d(w^i_n,w^i)|\right\} ,& \text {if}\ \ P_i\le P_{i-1} \end{array} \right. , \end{aligned}$$

(3)

where P denotes the performance metrics utilized in our study, including measures like accuracy or F1 score, and $d(w^i_n, w^i)$ quantifies the average difference in model weights for client n during the i-th training round when comparing the local model to the global one. This difference, similar to $A^i_n - A^{i-1}$, reflects the disparity between these models. The calculation is as follows:

$$\begin{aligned} d(w^i_n,w^i)=\frac{1}{|w^i|}\sum \limits ^{|w^i|}_{j=1}\left| \frac{w^i_{n,j}-w^i_j}{w^i_j}\right| , \end{aligned}$$

(4)

where $w^i_{n,j}$ and $w^i_j$ are the j-th weights of the local and global models, respectively. This approach significantly reduces computational complexity by avoiding the need for model inference, relying instead on arithmetic operations on model parameters.

In summary, by combining the accuracy-based quality evaluation function with the computational efficiency of the $\zeta ^i_n$ function, we designed a final optimized user quality evaluation function:

$$\begin{aligned} \mathscr {Q}^i_n={\varvec{\theta}} \cdot (\alpha _1\zeta ^i_n-\alpha _2T^i_n)+(1-{\varvec{\theta}} )\cdot \mathscr {Q}^{i-1}_n. \end{aligned}$$

(5)

This function evaluates each client’s contribution to the generalization and training efficiency of the global model, guiding the system to select the optimal client combination to address both data and system heterogeneity. The total time $T^i_n$ is assigned a negative sign to encourage the RL agent to minimize it, thus enhancing overall system efficiency.

DDQL-based client selection method

In this section, we provide an in-depth explanation of our client selection method in two parts: Markov decision process formulation and detailed DDQL-based client selection optimization.

(1) Markov decision process formulation: To apply RL for client selection in FedPRL, we constructed a Markov decision process with three essential components: state set, action set, and reward set.

(a) State set: We defined the state set using a state vector $s^i$, representing the status of the i-th round of federated training:

$$\begin{aligned} s^i=\left( s^i_1,s^i_2,\ldots ,s^i_N\right) . \end{aligned}$$

(6)

This vector comprises the states of all clients, encapsulating critical factors such as each client’s local model weights, local data size, computing capacity, and available network bandwidth during the current training round. To manage the complexity of the model weight vector, we applied principal component analysis³⁰ (PCA) to reduce its dimensionality, enabling it to effectively contribute to the training of the RL agent.

(b) Action set: The action set is defined by an action vector, where each vector contains N Boolean components, with N representing the total number of clients. Each component indicates whether a particular client is selected for the current training round. Specifically, if the n-th component is set to 1, it indicates that client n is chosen. The agent utilizes this action vector to determine the optimal set of clients for the current round of federated training. The action vector is represented as:

$$\begin{aligned} a^i=\{a^i_1,a^i_2,\cdots ,a^i_n,\ldots ,a^i_N\},\ \text {where}\ a_n^i\in \{0,1\}. \end{aligned}$$

(7)

(c) Reward set: The reward set is defined using the user quality evaluation function as the reward function within the RL algorithm. The higher the quality evaluation of a client, the greater the benefit of selecting that client, making the client’s quality score equivalent to the reward in RL. The reward vector for each round is expressed as:

$$\begin{aligned} r^i=\left( r^i_1,r^i_2,\ldots ,r^i_n,\ldots ,r^i_C\right) , \end{aligned}$$

(8)

where $r^i_n$ denotes the reward associated with selecting client n during the i-th training round, and C represents the total number of clients selected. Here, $r^i_n$ is directly equivalent to the client quality evaluation score $\mathscr {Q}_n^i$.

(2)Detailed DDQL-based client selection optimization: To improve the client selection process, we proposed a DDQL-based client selection method. DDQL employs two neural networks, i.e., (1) the main network and (2) the target network. The main network is responsible for training and selecting the best action, and the target network evaluates the action for the subsequent state. To maintain the training stability, parameters of the main network are periodically copied to the target network every R rounds. This dual-network architecture mitigates the risk of overestimating Q-values by decoupling action selection from action evaluation, thus enhancing strategy accuracy. Each of the two networks follows a multi-layer perceptron architecture, incorporating multiple hidden layers activated by the ReLU function. This activation function improves both the nonlinear representational capacity and convergence speed of the network. To prevent overfitting, dropout is applied after the hidden layers. In this study, both networks utilize a structure of linear layer + ReLU + Dropout + linear layer. The network architecture, including the number of layers and neurons, should be tailored to align with the dataset’s scale and feature complexity, optimizing the model’s capacity for expressive representation and generalization.

The loss function of the DDQL is defined by the Mean Squared Error (MSE), which quantifies the disparity between the Q-value predicted by the main network and the target Q-value. MSE is chosen to minimize approximation bias, thereby contributing positively to the algorithm’s stability. The loss function incorporates both immediate rewards and discounted future rewards, and can be calculated as follows:

$$\begin{aligned} \mathscr {L}^i_n(\phi ^i)=\left( \mathscr {Y}^i_n-Q(s^i, a^i_n; \phi ^i)\right) ^2, \end{aligned}$$

(9)

where $\mathscr {Y}^i_n$ represents the target Q-value of action $a^i_n$ in round i, and can be described as follows:

$$\begin{aligned} \mathscr {Y}^i_n=r^i_n+\gamma Q\left( s^i, \text {argmax}\ Q(s^i, a^i_m; \phi ^i); \tilde{\phi }^i\right) , \end{aligned}$$

(10)

where $r^i_n$ denotes the reward linked to selecting client n in training round i, with $\phi ^i$ and $\tilde{\phi }^i$ representing the parameters of the main and target networks, respectively. The discount factor $\gamma$, confined to the interval $0 \le \gamma \le 1$, modulates the significance of future rewards relative to current outcomes. For each training round, the loss function is individually calculated to optimize client selection based on current and projected contributions.

Selecting an appropriate discount factor $\gamma$ is critical for algorithmic performance. A $\gamma$ value near 1 causes the agent to prioritize future rewards, whereas a smaller $\gamma$ focuses on the immediate rewards of the agent. Through systematic testing, we determine an optimal $\gamma$ for each dataset, balancing short-term gains with long-term benefits. This tuning enables the reinforcement learning model to adapt client selection more flexibly in a federated learning environment, thus enhancing performance and training efficiency under system heterogeneity.

During action selection, we design an $\epsilon$-greedy strategy to manage exploration-exploitation trade-offs. Initially, a high exploration probability $\epsilon$ encourages random action selection to gather diverse sample data. Once the midpoint of total training rounds is reached, $\epsilon$ is rapidly decreased, guiding the agent toward actions with higher Q-values based on the learned experience. In this manner, $\epsilon$ decreases progressively from a high initial value to a predefined minimum, with its rate of decrease proportional to the number of training rounds. This approach enables broad exploration early on and a shift to optimal action selection as training progresses, bolstering the reliability of the learned strategy.

The learning rate determines the update step size in neural network training. A high learning rate may cause excessive Q-value fluctuations, while a low learning rate will slow down the convergence rate. Thus, we employ a grid search to select an initial learning rate that is incrementally reduced during training to ensure model convergence. By utilizing the Adam optimizer, the learning rate is further dynamically adjusted based on gradient shifts, allowing an adaptable step size through various training stages.

To enhance the sample efficiency, we incorporate an experience replay mechanism within DDQL that retains state transitions $(s^i, a^i, s^{i+1}, r^{i+1}, d^i)$ collected during training, where $d^i$ is a Boolean value indicating whether a terminal state has been reached. By randomly sampling small batches from such stored experience for each update, the algorithm can leverage a more diverse range of historical data. This mechanism mitigates the adverse effects of sample correlation, thereby enhancing both the efficiency and stability of model training.

Notably, to address the computational and memory challenges stemming from the exponential growth of the action space when considering all possible client subsets as actions, we have improved this RL algorithm. Traditional RL methods face significant complexity and memory demands under such conditions. Our approach enables the RL agent to simultaneously learn and select multiple actions, streamlining the process. Specifically, we replace the exhaustive subset-based actions with an N-dimensional action space representing all clients, where each action corresponds to the selection of an individual client. We define a Q-value function $Q(s^i, a^i_n)$, which quantifies the value of choosing client n in state $s^i$, allowing the agent to assess each client’s potential within the current state. The top C clients with the highest Q-values are then selected to form an optimized client set. This method effectively reduces the action space, minimizing computational and memory costs while maintaining flexibility and optimization in client selection.

Local training

During this step, we proposed our method based on global knowledge distillation of non-target classes to optimize local training. This is because, in our personalization strategy based on local data storage, each client utilizes both a global model and a local kNN model to generate a personalized model. The global model is also responsible for computing transition representations for the client. To ensure that all clients benefit from a robust global model with strong generalization capabilities, in FedPRL we designed this local training method that incorporates global knowledge distillation of non-target classes. This method can be integrated with the FedAvg algorithm, utilizing knowledge distillation techniques to mitigate knowledge forgetting during joint training, ultimately resulting in a shared global model with enhanced generalization capabilities.

This method applies optimization specifically to the local model’s loss function. The key idea is to preserve the global model’s existing knowledge of non-target classes, thereby maintaining the implicit relationships between different categories that the global model has learned. In this context, “non-target classes” refer to all classes other than the current sample’s label. The global knowledge distillation is achieved through a linear combination of loss functions $\mathscr {L}$, facilitating the transfer of knowledge from the global model to local model while retaining older knowledge. The loss function integrates cross-entropy loss $\mathscr {L}_{CE}$ with non-target class distillation loss $\mathscr {L}_{KL}$ as follows:

$$\begin{aligned} \mathscr {L}=\mathscr {L}_{CE}\left( p_{D_n},{\textbf {1}}_y\right) +\eta \cdot \mathscr {L}_{KL}\left( \tilde{p}^T_{D_n},\tilde{p}^T_D\right) , \end{aligned}$$

(11)

where the hyperparameter $\eta$ controls the extent of knowledge retention beyond the local distribution. The non-target class distillation loss $\mathscr {L}_{KL}$ is defined as the KL divergence between the softmax prediction vectors $\tilde{p}^T_{D_n}$ and $\tilde{p}^T_D$ for the local and global models, respectively, at temperature T:

$$\begin{aligned} \mathscr {L}_{KL}\left( \tilde{p}^T_{D_n},\tilde{p}^T_{D}\right) =-\sum \limits ^H_{h=1,h\ne y}\tilde{p}^T_D(h)\cdot \text {log}\left[ \frac{\tilde{p}^T_{D_n}(h)}{\tilde{p}^T_D(h)}\right] . \end{aligned}$$

(12)

Here, $\tilde{p}^T_{D_n}$ and $\tilde{p}^T_D$ represent the non-target class logits of the local and global models after applying the softmax function at temperature T. Figure 2 visually summarizes the complete calculation process for the local model’s loss function in our algorithm.

Fig. 2

Calculation process of the local model loss function in our algorithm.

According to the loss function (Eq. 11), the local model uses cross-entropy loss $\mathscr {L}_{CE}$ to incorporate target class information from the dataset, acquiring new knowledge specific to the local distribution. Concurrently, the global model provides non-target class information, and the non-target class distillation loss $\mathscr {L}_{KL}$ ensures that this global knowledge is preserved within the local model. This dual approach allows the local model to perform regular training while also mimicking the global model to learn the relationships between categories from a global perspective.

After the local model update, the server aggregates the client model parameters using a weighted average, updating the global model. This procedure guarantees that the global model retains the non-target class knowledge from previous rounds while integrating the new target class knowledge generated by the clients. As a result, the global model continues to evolve without suffering from knowledge forgetting, allowing for continuous, robust updates.

Global model personalization

In this step, we devised our method based on local data storage to optimize global model personalization. Specifically, we actually designed an enhanced “global model personalization” strategy to train personalized models, which involves initially training a global model through conventional FL and subsequently tailoring it to meet the specific needs of each client. The traditional FL process, optimized by our designed local training method, has been described in detail above. This section focuses on our local data storage-based personalization strategy that generates personalized models for individual clients, as well as the local data storage update strategy that we devise to enhance the robustness and scalability of our method for real-time learning in dynamic data distribution.

Local data storage-based personalization strategy

Our approach begins with the construction of a local data store on each client device. The kNN algorithm is then utilized to generate local predictions based on this stored data. To achieve personalization, these local predictions are combined with the global model’s predictions through a process of model interpolation, effectively customizing the global model to suit each client’s unique data and requirements.

(1)Building local data storage: Our personalization strategy begins with the construction of a local data store on each client device, which stores key-value pairs in the form of (transition representation, label). The transition representation is a fixed-length output derived by processing a feature vector through the global model, such as the output of the final convolutional layer in a CNN model.

The construction process involves the following steps: the client selects a sample from its local dataset, inputs the corresponding feature vector into the global model to generate the transition representation, and then pairs this representation with the sample’s label to create a key-value pair. This pair is then stored in the local data store. Each sample in the local dataset undergoes this forward pass to complete the data store construction. The formal representation of the key-value pair in the local data store is outlined in Eq. (13):

$$\begin{aligned} \left( \mathscr {S}^{key}_n,\mathscr {S}^{value}_n\right) =\left\{ \left( \rho _{M_D}\left( x^{(i)}_n\right) ,y^{(i)}_n\right) ,\forall \left( x^{(i)}_n,y^{(i)}_n\right) \in D_n\right\} , \end{aligned}$$

(13)

where $D_n$ denotes the local dataset of client n, $(x^{(i)}_{n},y_n^{(i)})$ represents the feature vector and label of the i-th sample in the local dataset, $\rho _{M_D}(x_n^{(i)})$ represents the transition representation of the feature vector $x^{(i)}_n$, and $M_D$ refers the global model.

(2)Calculating local predictions: Next, we generate the client’s local prediction. This process begins by inputting the feature vector into the global model, which produces both the global model prediction and the corresponding transition representation, denoted as $\rho$. The client then applies the kNN regression algorithm. This algorithm uses the transition representation $\rho$ to search the local data store for the k nearest neighbors.

For each of these neighbors, the algorithm calculates the conditional probability of each label, given the current feature vector. The conditional probability of a label is determined by checking whether the label in each of the k nearest key-value pairs matches the label being predicted. When a match is found, a Gaussian kernel function is employed to quantify the similarity between the transition representations. These similarity values are then aggregated to form the conditional probability of the label.

Finally, the client’s local prediction is derived by calculating a weighted average across all possible labels, where each label’s weight corresponds to its conditional probability. The equation for calculating the conditional probability of a label y is presented as follows:

$$\begin{aligned} P_n(y|x)=\left[ M^{(k)}_{D_n}(x)\right] _y=\sum \limits ^k_{i=1} {\textbf {1}}_{\left\{ y=y_i\right\} }\times \text {exp}\left\{ -d\left( \rho _{M_D}(x),\rho _{M_D}(x_i)\right) \right\} . \end{aligned}$$

(14)

(3)Generating personalized models: After obtaining both the global model prediction and the local model prediction, the final step is to interpolate between the two to create the client’s personalized model. This process involves using a parameter $\lambda _n \in (0,1)$ to blend the global model distribution with the nearest neighbor distribution generated by the local model. Specifically, the global model prediction $M_D(x)$ is weighted by $(1-\lambda _n)$, and the local model prediction $M^{(k)}_{D_n}(x)$ is weighted by $\lambda _n$. The sum of these weighted predictions yields the personalized model prediction $M_{n,\lambda _n}(x)$. The equation for generating the personalized model is as follows:

$$\begin{aligned} M_{n,\lambda _n}(x)=\lambda _n\cdot M^{(k)}_{D_n}(x)+(1-\lambda _n)\cdot M_D(x). \end{aligned}$$

(15)

The parameter $\lambda _n$ determines the extent of personalization. When $\lambda _n$ is set to 0, the personalized model defaults to the global model, maximizing generalization but offering minimal adaptation to the local data distribution. As $\lambda _n$ increases, the global and local models are increasingly blended, enhancing the degree of personalization. At $\lambda _n = 1$, the personalized model relies entirely on the local model, achieving the highest adaptation to local data but with reduced generalization.

In summary, our proposed personalization strategy based on local memory involves several key steps: all clients utilize a shared global model, each client constructs a local data store, and learns a local kNN model. Then, using Eq. (15), model interpolation is performed to combine the global and local models, resulting in personalized models that effectively balance generalization and personalization. The specific process for generating personalized models during the inference stage is illustrated in Fig. 3.

Fig. 3

Inference process of the personalized model based on local data storage.

Local data storage update strategy

Local data storage acts as a feature extraction mechanism for client samples, utilizing the global model to filter out irrelevant features from the original data while simultaneously enabling the global model to learn the specific data characteristics of each client during the personalization process. The effectiveness of local predictions increases with the size of the data storage, as it captures a broader range of local data features, thereby improving classification performance for the types of samples already present in the local dataset. However, this approach has limitations: it may underperform on unseen data types and could even mislead the global model. This challenge arises when users alter their habits, introducing new categories of samples into the local dataset, leading to a decline in the personalized model’s performance, which indicates the model’s less robustness to shifts in data distribution and scalability.

To enhance the personalized model’s resilience to changes in local data distribution, we have designed three strategies for updating the data storage when new samples are introduced:

• First-in-First-out (FIFO): This strategy replaces the oldest key-value pair in the data storage with the key-value pair of the new sample.

• Insert: This strategy directly adds the new sample’s key-value pair to the existing data storage.

• NoUpdate: In this strategy, the data storage remains unchanged when new samples are introduced.

We simulated a dynamic environment to test these strategies. Initially, client n has a local data storage constructed from samples drawn from distribution $D_n$. During each time unit $t < t_0$, client n continues to receive batches of samples from $D_n$. However, at time $t_0$, a shift in data distribution occurs, and for $t_0 \le t \le T$, client n begins receiving samples from a different distribution, $D'_n$ ($D'_n \ne D_n$). The client can then apply one of the three update strategies to the local data storage to adapt to the new data distribution. This adaptability prevents local predictions from negatively impacting global predictions, thereby preserving the overall performance of the personalized model.

Experiments

We conducted extensive experiments on both standard and real-world datasets to address the following seven key research questions:

• Q1: How does our approach outperform the state-of-the-art personalized federated learning methods in heterogeneous environments? (see Result 1)

• Q2: How does our approach perform on new clients that appear after training? (see Result 2)

• Q3: How do the size of local data storage and the extent of data heterogeneity affect the performance of our model? (see Result 3)

• Q4: How sensitive is our approach to hyperparameters - the model mixing parameter $\lambda _n$ and the number of nearest neighbors k? (see Result 4)

• Q5: How robust is our approach to changes in data distribution? (see Result 5)

• Q6: How do the model performance and training efficiency of our method fare in the fall detection task? (see Result 6)

• Q7: What is the specific contribution of each component in our approach to overall model performance and training efficiency under heterogeneous environments? (see Result 7)

Datasets

We utilize the CIFAR-10, CIFAR-100, FEMNIST, and MobiAct datasets for training and testing, covering two domains: image recognition and fall detection. The first three datasets, CIFAR-10, CIFAR-100, and FEMNIST, are well-established in the field, offering rich content and diverse application scenarios that simulate real-world data distribution effectively. The MobiAct dataset, as a real-world example of fall detection in smart home environments, provides a robust test for evaluating the practical effectiveness of our proposed algorithm.

Dataset introduction

• CIFAR-10: This widely used computer vision dataset consists of 60,000 color images at a resolution of 32$\times$32 pixels, spread across 10 categories, with 6,000 images in each category. The dataset is divided into 50,000 images for training and 10,000 images for testing.

• CIFAR-100: While structurally similar to CIFAR-10, CIFAR-100 comprises 60,000 color images at a resolution of 32$\times$32 pixels but is organized into 100 distinct categories, with each category containing 600 images. This dataset offers more fine-grained classification, with subcategories such as “bees” and “beetles” under the broader “insects” category.

• FEMNIST: An extension of the MNIST dataset and a benchmark for FL, FEMNIST contains 805,263 grayscale images at a resolution of 28$\times$28 pixels. These images are distributed across 62 character classes, including 10 digits, 26 lowercase letters, and 26 uppercase letters. The data originates from 3,500 users, reflecting the diversity and non-IID nature of real-world handwriting samples.

• MobiAct⁴²: Designed for human activity recognition and fall detection research, the MobiAct dataset captures data from 67 volunteers using smartphone sensors (e.g., accelerometers and gyroscopes) across more than 3,200 tests. It includes 12 different daily activities (such as walking, running, and stair climbing) and simulates four types of falls (forward, backward, left, and right). The heterogeneity of data stems from the varying physical conditions of the volunteers.

Non-IID data partitioning

To rigorously evaluate personalized federated learning methods, it is essential to simulate FL environments realistically and partition datasets in a manner that reflects non-IID conditions. Below, we detail the partitioning processes for each dataset:

• CIFAR-10: Since there is no natural partitioning method, we use the Dirichlet distribution to allocate data among clients. The parameter $\alpha$ controls the uniformity of the distribution-larger values of $\alpha$ result in more similar client data distributions, while smaller values increase the differences. For each label y, an N-dimensional vector $p_y$ is sampled from the Dirichlet distribution, where $p_{y,n}$ represents the proportion of label y data assigned to the n-th client. This approach ensures that each client’s dataset is composed of samples from multiple labels, with varying distributions.

• CIFAR-100: Utilizing the dataset’s hierarchical label structure (coarse and fine labels), we partition the data using the Pachinko allocation method⁴³. This technique employs two-level Dirichlet distributions: the first assigns a distribution with parameter $\alpha$ to each client to determine the probability of coarse labels appearing, and the second assigns a distribution with parameter $\beta$ to determine the probability of fine labels within each coarse label. Data is then allocated to clients according to these distributions, allowing for controlled variation in data distribution at both levels.

• FEMNIST: Data is partitioned based on the authorship of characters, with all characters written by a single individual forming a client’s dataset. The inherent variability in handwriting styles across different authors ensures a non-IID distribution.

• MobiAct: Data is divided based on the volunteers who contributed it, creating two groups of client datasets with distinct data heterogeneity. In the “volunteer-based partitioning” group, each volunteer represents a client, reflecting natural non-IID datasets resulting from individual habits and distinct physical conditions. In the “label skew” group, volunteers are assigned different sets of activities, introducing varying degrees of label skew. Specifically, we create three partitions: “natural partition,” where each client’s dataset is based on a single volunteer’s data; “label skew 8,” where each client has 8 activities distinct from others, introducing moderate label skew⁴; and “label skew 4,” where each client has 4 distinct activities, introducing significant label skew.

These partitioning strategies ensure that the datasets realistically simulate FL conditions, enabling a thorough evaluation of personalized federated learning algorithms.

Experimental tasks

To thoroughly evaluate the performance, training efficiency, and overall effectiveness of our FedPRL algorithm across various classification tasks, and to validate the characteristics we designed into the algorithm, we developed four specific classification tasks, each aligned with a particular dataset. Table 1 provides a summary of the datasets, models, and transition representation details for each experimental task.

For the datasets including CIFAR-10, CIFAR-100, and FEMNIST, we selected MobileNet-v2⁴⁴ as the base model. The model’s weights are initialized using the default pre-trained weights provided by the torchvision library. We use the output from the model’s last hidden layer as the transition representation for these tasks.

For the MobiAct dataset, we implemented gated recurrent unit (GRU) model as the base model. Each GRU layer consists of 256 hidden units, with model weights randomly initialized within a uniform distribution ranging from [-0.1, 0.1]. The input to the model’s final linear layer is used as the transition representation.

Table 1 Experimental tasks information.

Implementation details

Heterogeneous hardware setup

To simulate a FL environment with system heterogeneity, we introduced a variety of edge devices and transmission protocols, as detailed in Tables 2 and 3. This setup is designed to replicate the differing computing and transmission capabilities of various edge platforms. The specific configurations are inspired by devices such as the Intel Core i7, Raspberry Pi PI3, Jetson AGX Orin, Jetson Nano, and Jetson Xavier NX. The frequencies and bandwidths listed represent average operational values for these platforms. To reflect real-world dynamic conditions, we modeled these values using normal distributions with varying standard deviations. During each training round, a value is randomly drawn from the relevant distribution to represent the client’s CPU frequency or network bandwidth. This approach effectively simulates the variability in computing resources and communication capabilities in practical situations, thereby highlighting how system heterogeneity can impact the process of FL.

Table 2 Specifications of simulated edge devices.

Table 3 Transmission protocols specifications.

Experimental environment

All experiments were conducted on a remote server running Ubuntu 20.04.5, equipped with an Intel(R) Xeon(R) Platinum 8255C CPU, an RTX 3080 GPU with 10GB of video memory, 40GB of RAM, and 80GB of storage capacity.

Parameter setting

For experiments involving the CIFAR-10, CIFAR-100, and FEMNIST datasets, federated training was carried out over 300 rounds. In each round, 10% or 20% of the clients were selected using our intelligent client selection method. After completing local training, clients adjusted the learning rate to 99% of its original value. For the MobiAct dataset, the training spanned 500 rounds, with a similar selection of 10% of clients per round and the same learning rate adjustment strategy.

In all experiments, our method utilized Euclidean distance as the metric for calculating local predictions, with the kNN model implemented using the IndexFlatL2 class from the FAISS library⁴⁵ for accurate nearest neighbor searches. The hyperparameters for other baseline methods were set according to their original papers, with grid search employed to optimize these parameters in the current experimental environment. The hyperparameters used in our method for each dataset during the experiments are summarized in Table 4.

Table 4 Hyperparameter settings.

Evaluation metrics

To evaluate the performance, training efficiency, and overall effectiveness of our method on classification tasks, we utilize three key metrics: the average accuracy of personalized models, total training time, and F1 score.

Average accuarcy of personalized models: This metric represents the weighted average accuracy across all personalized models on individual clients, providing a comprehensive measure of the personalized federated learning method’s performance across the complete set of clients. It can be calculated as follows:

$$\begin{aligned} \text {Accuracy}=\frac{\sum ^N_{n=1}(TP_n+TN_n)}{\sum ^N_{n=1}|D_n|}, \end{aligned}$$

(16)

where $TP_n + TN_n$ represents the count of correctly predicted samples by client n’s personalized model, while $|D_n|$ indicates the total number of samples in client n’s local dataset.

Total training time: This metric captures the cumulative sum of local training and data transmission time for all participating clients throughout the global model training process, reflecting the general efficiency of the federated training process. It can be calculated as follows:

$$\begin{aligned} \text {Total Training Time}=\sum \limits ^I_{i=1}\sum \limits ^N_{n=1}T^i_n, \end{aligned}$$

(17)

where $T^i_n$ is the sum of local training and data transmission time for client n in the i-th round of federated training.

F1 score: The F1 score offers a balanced evaluation of the model’s classification performance by integrating both precision and recall. It can be calculated as follows:

$$\begin{aligned} \text {F1}=2\times \frac{\text {precision}\cdot \text {recall}}{\text {precision}+\text {recall}}, \end{aligned}$$

(18)

where presion = $\frac{TP}{TP+FP}$ and recall = $\frac{TP}{TP+FN}$. Here, TP, TN, FP, and FN indicate true positives, true negatives, false positives, and false negatives, respectively.

Comparison methods

We compare our FedPRL against three state-of-the-art baseline methods in federated learning and personalized federated learning.

• FedAvg¹: A foundational algorithm in FL, FedAvg aggregates local models from multiple devices by averaging their parameters to create a global model.

• Ditto²⁰: An advanced personalized federated learning algorithm, Ditto leverages regularization techniques to generate personalized models for each client, enhancing model accuracy, fairness, and robustness in FL.

• FedRep²⁴: A state-of-the-art personalized federated learning algorithm, FedRep achieves superior personalized model performance by training the representation layer on local clients while optimizing the classifier layer on the server.

Results

We conducted a series of experiments and performed a detailed analysis of the results to address the key research questions Q1-Q7.

Result 1: Comparison of average performance and training efficiency in personalized models (for Q1)

To address Q1, we evaluated the average performance and training efficiency of personalized models produced by various algorithms across the natural partition, label skew 8 partition, and label skew 4 partition of the CIFAR-10, CIFAR-100, FEMNIST, and MobiAct datasets. The algorithms tested included our FedPRL algorithm as well as established FL algorithms: FedAvg, Ditto, and FedRep. To assess the general performance of these algorithms across all clients, we calculated the average accuracy of personalized models, with weights proportional to the number of samples in each client’s dataset. Additionally, we evaluated the model training efficiency of each algorithm by measuring the total training time and recording the number of training rounds required to achieve the target accuracy.

(1) Comparison of average accuarcy in personalized models: The results of average accuracy and training rounds are presented in Table 5, where MobiAct (v1), MobiAct (v2), and MobiAct (v3) correspond to the natural partition, label skew 8 partition, and label skew 4 partition of the MobiAct dataset, respectively. Our FedPRL algorithm consistently achieved the highest accuracy across all datasets, outperforming the state-of-the-art methods FedAvg, Ditto, and FedRep. Specifically, on the CIFAR-10 dataset, FedPRL outperformed the baseline algorithms by 21.70%, 7.36%, and 6.32%, respectively. On CIFAR-100, the accuracy improvements were 20.70%, 7.21%, and 5.50%, respectively. On FEMNIST, FedPRL surpassed the baselines by 13.11%, 3.34%, and 2.34%. For the MobiAct dataset, FedPRL improved accuracy by 17.33%, 14.22%, and 12.06% on the natural partition (v1), 18.92%, 15.56%, and 12.53% on the label skew 8 partition (v2), and 9.61%, 6.25%, and 5.98% on the label skew 4 partition (v3). Overall, our algorithm demonstrated an average accuracy improvement of 16.90%, 8.99%, and 7.46% over the baseline algorithms.

(2) Comparison of training efficiency in personalized models: Figure 4 illustrates the total training time of our FedPRL algorithm compared to three baseline algorithms (FedAvg, Ditto, and FedRep) across the CIFAR-10, CIFAR-100, and FEMNIST datasets. On each of these datasets, FedPRL achieved the shortest final total training time, significantly outperforming the state-of-the-art methods FedAvg, Ditto, and FedRep. Specifically, on the CIFAR-10 dataset, FedPRL demonstrated accelerations of 26.54%, 23.86%, and 28.32% compared to the baseline algorithms, respectively. For CIFAR-100, these accelerations were 26.42%, 27.73%, and 29.48%, while on FEMNIST, FedPRL achieved improvements of 22.99%, 22.34%, and 24.98%, respectively. Overall, FedPRL averaged a speedup of 25.32%, 24.64%, and 27.59% against the baseline algorithms.

Furthermore, since Ditto and FedRep primarily address data heterogeneity without optimizations for system heterogeneity, their total training times remain comparable to FedAvg. Ditto’s personalized strategy involves lower computational demands, while FedRep’s additional fine-tuning steps introduce computational overhead, generally resulting in a total training time order of Ditto < FedAvg < FedRep, as shown in Fig. 4. Notably, in Fig. 4, after reaching the midpoint (150) of total training rounds, FedPRL’s total training time consistently became markedly lower than that of the baseline algorithms, with this advantage widening progressively as training advanced. This improvement is due to FedPRL’s reinforcement learning mechanism, which, upon reaching halfway through the training rounds, shifts focus from exploring new client combinations to leveraging previously identified optimal combinations, thereby maximizing both model performance and training efficiency.

In addition to reporting average accuracy, Table 5 presents the number of training rounds required for each algorithm to achieve predefined target accuracies across datasets. For each dataset, we set target accuracies at 77.0%, 59.6%, 64.3%, 80.2%, 78.8%, and 75.8%, respectively. Our proposed FedPRL consistently achieves these targets with the fewest training rounds across all datasets, outperforming all baseline algorithms. These results demonstrate that FedPRL offers superior convergence speed.

Summary 1: The results clearly highlight the superiority of the FedPRL algorithm, demonstrating its enhanced effectiveness over FedAvg, Ditto, and FedRep in addressing both data and system heterogeneity in heterogeneous environments. FedPRL effectively mitigates the adverse effects of data heterogeneity, leading to notable improvements in the performance of FL models across diverse client datasets. Additionally, it addresses system heterogeneity, reducing model total training time, accelerating convergence, and thereby significantly enhancing model training efficiency.

Table 5 Average accuracy (%) and training rounds to achieve target accuracy for personalized models.

Fig. 4

The variation of total training time during federated training on CIFAR-10, CIFAR-100, and FEMNIST.

Result 2: Performance on new clients (for Q2)

In real-world scenarios, the model trained through FL must not only perform well on the clients that participated in the training process but also generalize effectively to new clients that join afterward. Ensuring excellent performance on these new clients requires the model to have strong generalization capabilities. To address Q2, we conducted experiments in which only 80% of the clients took part in the initial training phase, while the remaining 20% were introduced subsequently to test the adaptability of our FedPRL algorithm to new clients. Specifically, we assessed whether the algorithm could generate personalized models that are effective for these new clients.

Table 6 presents the accuracy of the personalized models generated by the FedPRL algorithm for these new clients. When compared to the results in Table 5, we observe that the personalized models created by FedPRL perform similarly for both the clients involved in the training and those that joined later. Specifically, across the six datasets, the accuracy of personalized models for new clients is only slightly lower-by 5.30%, 5.90%, 4.04%, 1.90%, 2.23%, and 0.12%, respectively-resulting in an average decrease of just 3.25%.

Summary 2: The FedPRL algorithm demonstrates strong generalization to new clients, as the accuracy for these new clients is only marginally lower than for those that participated in training. Thanks to the design of the FedPRL algorithm, new clients can easily obtain the global model from the server, use it to build their local data storage for the kNN model, and quickly generate high-quality personalized models. This confirms that FedPRL is highly effective at adapting to new clients and efficiently producing accurate personalized models for them.

Table 6 Average accuracy of personalized models for new clients (%). Accuracy of clients participating in training is shown in parentheses.

Result 3: Impact of local data storage size and data heterogeneity (for Q3)

Distinguishing between new and old clients is essential not only for practical scenarios but also for understanding how various factors impact the performance of the FedPRL algorithm. In this context, “new clients” are those that join after federated training has concluded and did not participate in global model training, while “old clients” are those that contributed to the global model training.

To address Q3, we proportionally reduced the local data storage size for new clients while keeping the global model unchanged, and then tested the average accuracy of the personalized models generated for these new clients. For each client n, the local dataset size is $|D_n|$, and a capacity parameter $w_n$ determines the size of the data storage, calculated as $w_n\cdot |D_n|$. By adjusting the capacity parameter, we modified the local data storage size to observe its impact on model accuracy. Additionally, we introduced a parameter $\alpha$ to represent data heterogeneity, where $\alpha$ ranges from 0 to 1, with smaller values indicating stronger data heterogeneity. We created five sub-datasets with varying degrees of data heterogeneity (i.e., 0.1, 0.3, 0.5, 0.7, and 1.0) on the CIFAR-10 and CIFAR-100 datasets and adjusted the capacity parameters on these datasets to evaluate the corresponding model accuracy. This approach allowed us to assess the impact of data heterogeneity on personalized model performance.

The experimental results are presented in Fig. 5. The data shows that as the size of the local data storage decreases, the accuracy of the personalized model also declines. However, even when reducing the local data storage from the full dataset size to one-third (with a capacity parameter of 0.33), the accuracy remains close to that of the maximum storage size, with changes not exceeding 0.83%. This suggests that the FedPRL algorithm is not highly sensitive to the size of local data storage, offering considerable flexibility. Devices with limited storage capacity can still achieve high accuracy by setting local data storage to one-third of the dataset size, while those with larger storage capacity can maximize accuracy by utilizing the full dataset.

It is important to note that if the local data storage size for old clients is also altered during the experiment, the global model and transition representation would change, introducing multiple variables that could obscure the impact of local data storage size on algorithm performance. Figure 6 shows the results of experiments where these variables were introduced.

Fig. 5

The relationship between local data storage size and accuracy under different data heterogeneity (global model unchanged).

Fig. 6

The relationship between local data storage size and accuracy under different data heterogeneity (global model changed).

From Figs. 5 and 6, it is also evident that with a fixed capacity parameter, the accuracy of the personalized model increases as $\alpha$ decreases. This indicates that stronger data heterogeneity leads to higher accuracy in the personalized model, demonstrating the FedPRL algorithm’s effectiveness in handling diverse client data distributions. Additionally, when the capacity parameter is set to 0 (indicating no local data storage), the global model is used, and the test accuracy reflects the global model’s performance. In Fig. 5, where the global model is fixed, the test accuracy at the starting point (capacity parameter 0) remains constant across different $\alpha$ values. However, in Fig. 6, where the global model changes with $\alpha$, the accuracy at the starting point decreases as data heterogeneity increases, but it recovers as the local data storage size increases, indicating that larger data storage can offset the negative impact of data distribution heterogeneity on the global model.

Summary 3: As local data storage size decreases, personalized model accuracy diminishes, but the FedPRL algorithm remains largely insensitive to storage size, achieving optimal accuracy with storage set to between one-third and the full size of the local dataset. Moreover, stronger data heterogeneity enhances personalized model accuracy, underscoring the algorithm’s effectiveness in managing data heterogeneity challenges.

Result 4: Hyperparameter sensitivity (for Q4)

To address Q4, we designed an experiment to assess the sensitivity of the FedPRL algorithm to its hyperparameters. Since the algorithm’s personalization strategy involves a model interpolation method and a kNN model, it is crucial to assess the impact of the model mixing parameter $\lambda _n$ in the interpolation method and the number of nearest neighbors k in the kNN model, as these parameters influence the prediction performance of personalized models.

(1) Impact of $\lambda _n$ on algorithm performance: We conducted a series of experiments using the control variable method to test the average accuracy of personalized models at various $\lambda _n$ values. The experiments were performed on the CIFAR-10 and CIFAR-100 datasets, with data heterogeneity $\alpha$ set to 0.3. Fifty clients participated in the FL process, each with non-IID datasets of varying sizes. The number of nearest neighbors k in the kNN model was fixed at 10 and 12, with Euclidean distance used as the distance metric.

Figure 7 illustrates the relationship between $\lambda _n$ and the average accuracy of personalized models. The four lines represent clients with different sample sizes. The results indicate that the optimal $\lambda _n$ is approximately 0.8 for CIFAR-10 and 0.9 for CIFAR-100, with the optimal value increasing as the number of client samples grows. Additionally, the accuracy of personalized models varies significantly with changes in $\lambda _n$, demonstrating that the FedPRL algorithm is sensitive to the interpolation parameter $\lambda _n$.

This sensitivity can be explained by the principle of model personalization: clients with more local data typically experience greater differences in data distribution compared to other clients. Because the global model, which is based on an averaged distribution, may not accurately reflect these specific distributions, the local model becomes more critical for capturing the client’s data characteristics. Consequently, clients with larger datasets rely more heavily on their local models, leading to a higher optimal $\lambda _n$ value to achieve the best personalized model performance.

Fig. 7

The relationship between model interpolation parameter $\lambda _n$ and accuracy in clients with different sample sizes.

(2) Impact of k on algorithm performance: We also tested the impact of the number of nearest neighbors k on the FedPRL algorithm’s performance by evaluating the average accuracy of personalized models across various k values. These experiments were conducted on the CIFAR-10 and CIFAR-100 datasets, with data heterogeneity $\alpha$ set to 0.1. Again, fifty clients participated, with varying sample sizes and non-IID data distributions. The distance metric was Euclidean distance, and the k values tested were 1, 3, 5, 7, 10, 12, 14, 16.

Figure 8 shows the relationship between k and the average accuracy of personalized models. For CIFAR-10, the optimal k value lies between 5 and 12, where the average accuracy is both highest and most stable. Within this range, the accuracy varies by no more than 0.25%. For CIFAR-100, the optimal k value range is between 5 and 14. Given the broad range of optimal k values and the minimal fluctuation in accuracy, we conclude that the FedPRL algorithm is not sensitive to the k parameter.

Fig. 8

The relationship between the number of nearest neighbors k and the average accuracy of personalized models.

Summary 4: The performance of the FedPRL algorithm is sensitive to the interpolation parameter $\lambda _n$, with the optimal value increasing as the quantity of client samples increases. However, the algorithm is not sensitive to the k value in the kNN model. For the CIFAR-10 and CIFAR-100 datasets, optimal k values can be chosen from the ranges 5-12 and 5-14, respectively, without significant impact on performance.

Result 5: Robustness to data distribution shifts (for Q5)

As discussed earlier, the FedPRL algorithm incorporates three strategies for updating local data storage in response to changes in client data distribution within a dynamic environment: First-in-First-out (FIFO), Insert, and NoUpdate.

To address Q5 and assess the effectiveness of these local data storage update strategies, we simulated the dynamic environment described and conducted experiments to assess the performance of personalized models under each strategy as client data distribution changed.

Figure 9 illustrates how the accuracy of personalized models varies with the three local data storage update strategies as client data distribution evolves. The horizontal axis represents time, during which new sample data is incrementally added to the client dataset. At time $t_0=14$, data from a new distribution begins to be introduced. Before $t_0$, the client adds samples from the original distribution, and after $t_0$, it starts incorporating samples from the new distribution.

If the client does not update its data store (NoUpdate strategy), accuracy drops sharply at $t_0=14$ when the data distribution changes, and it struggles to recover. Under the FIFO strategy, we observe some fluctuations in accuracy before $t_0$, caused by changes in data storage affecting kNN predictions. Although accuracy decreases at $t_0$, it gradually improves as the data store is populated with samples from the new distribution. The Insert strategy produces similar results to FIFO, but with notable differences: before $t_0$, the growing number of samples in the data store enhances kNN predictions, leading to improved accuracy. After $t_0$, accuracy also increases, but at a slower rate compared to FIFO, due to the retention of samples from the older distribution.

Summary 5: Of the local data storage update strategies tested, the FIFO and Insert strategies significantly enhance the robustness of the FedPRL algorithm in environments where data distribution is dynamically changing. The FIFO strategy proves to be more robust than the Insert strategy, as it effectively clears out outdated samples. In contrast, the NoUpdate strategy results in a substantial and irrecoverable decline in personalized model accuracy following a change in data distribution.

Fig. 9

Personalized model accuracy under three strategies with changing data distributions.

Result 6: Model performance and training efficiency in fall detection task (for Q6)

To address Q6, we evaluated the performance and training efficiency of the FedPRL algorithm on the MobiAct dataset, using natural partition, label skew 8 partition, and label skew 4 partition settings. This assessment focused on the algorithm’s effectiveness in the fall detection task within a smart home environment. We used F1 score (%) and total training time (s) as the evaluation metrics, with the FedAvg algorithm serving as the baseline for comparison.

Figure 10 illustrates the F1 score and total training time for both the FedPRL and FedAvg algorithms during training, highlighting their convergence behavior across these two metrics. The results clearly show that the FedPRL algorithm reaches the target F1 score more quickly than FedAvg. For example, with a target F1 score of 77.8% under the label skew 4 partition, FedAvg needs 200 training rounds to achieve the target, while FedPRL reaches it in just 83 rounds, reducing the training rounds by 58.5%. Similarly, under the label skew 8 partition with an F1 score target of 86.75%, FedAvg takes 448 rounds to meet the goal, whereas FedPRL accomplishes this in only 72 rounds, reducing the training rounds by 83.93%.

Moreover, the total client training time for FedAvg increases linearly, whereas FedPRL converges to a constant time, indicating that FedPRL effectively identifies the optimal client combination. This balance between maximizing the F1 score and minimizing total training time demonstrates the effectiveness of the client selection method used by FedPRL.

Summary 6: The client selection method developed for the FedPRL algorithm intelligently identifies the optimal client combination, enhancing both model performance and training efficiency in heterogeneous environments. This approach effectively tackles the challenges associated with data and system heterogeneity, with real-world validations underscoring the superiority and practical applicability of the FedPRL algorithm, indicating its potential for integration with the medical and healthcare field.

Fig. 10

The variation of F1 score and total training time during federated training on MobiAct.

Result 7: Ablation study (for Q7)

To address Q7, we conducted comprehensive ablation studies on the CIFAR-10 dataset to assess each component’s specific contributions on the performance and efficiency of the FedPRL algorithm. The FedPRL algorithm incorporates three specifically designed and optimized components: (1) client selection based on RL and user quality evaluation, (2) local training based on global knowledge distillation of non-target classes, and (3) global model personalization based on local data storage. In our visualizations, these components are labeled as “client selection”, “local training”, and “personalization” in both Table 7 and Fig. 11. Our ablation studies use the FedAvg baseline across datasets exhibiting data heterogeneity degrees of 0.1 (highest heterogeneity), 0.3, 0.5, 0.7, and 1.0 (lowest heterogeneity), incrementally adding one or two components until reaching the full FedPRL configuration, with each intermediate combination serving as a distinct training method in our study. Evaluation metrics include model accuracy (%) and total training time (s). By systematically comparing different component combinations, we gain insights into each component’s specific contributions to both overall model performance and training efficiency.

Table 7 reports the model accuracy across different combinations of FedPRL components when trained on datasets with varying degrees of data heterogeneity. The results indicate that each component contributes positively to accuracy compared to the baseline FedAvg, though with differing magnitudes. Specifically, the client selection component alone yields a modest average accuracy increase of 1.70%, while the local training component alone achieves a slightly higher average improvement of 3.79%. Notably, the global model personalization component alone drives the most substantial accuracy gain, with an average improvement of 15.47%, outperforming the other components. Each component independently enhances model accuracy across datasets with varying data heterogeneity levels. The improvements become more pronounced as heterogeneity increases, as greater distribution differences diminish FedAvg’s performance, allowing FedPRL’s components to deliver more impactful optimization. Although both the client selection and local training components offer modest improvements, they fall short on highly heterogeneous datasets, where accuracy remains lower than on less heterogeneous datasets. In contrast, the global model personalization component achieves significant accuracy gains, aligning or even exceeding performance on highly heterogeneous datasets compared to those with less heterogeneity. Therefore, the global model personalization component plays a critical role in effectively addressing data heterogeneity, consistently boosting model accuracy across all levels of heterogeneity, particularly on datasets with pronounced distribution differences.

Moreover, compared to methods utilizing a single component, adding additional components consistently enhances model accuracy, underscoring the contribution of each component to overall performance. Specifically, incorporating the client selection component yields an average accuracy increase of 1.41% over the single-component method. Adding the local training component results in a further average improvement of 3.27%. Most significantly, integrating the global model personalization component elevates accuracy by an average of 15.01%. In terms of model performance, the client selection and local training components specifically support and amplify the impact of the global model personalization component. This synergy further enhances model accuracy across datasets with varying degrees of data heterogeneity, illustrating the complementary roles of each component in strengthening model adaptability and robustness.

Figure 11 illustrates the total training time for different combinations of FedPRL components following 300 rounds of federated learning. Due to the high efficiency of our designed personalization step, which can be performed after global model training, the global model personalization component minimally impacts overall training time. Consequently, the inclusion of the global model personalization component results in only a marginal increase in total training time, averaging a mere 0.55%. Furthermore, the computational overhead introduced by the optimized local training component is minimal, exerting negligible influence on the total training time, as evidenced by the nearly identical total training times observed before and after its integration. Notably, the figure clearly demonstrates that the total training time for methods incorporating the client selection component are markedly lower than those without it, with an average reduction of 26.65%. This observation highlights the client selection component’s role in enhancing training efficiency, as it reduces total training time and accelerates convergence, thereby significantly enhancing the overall efficiency of the federated learning process.

Summary 7: The ablation experiments demonstrate that the three key components in FedPRL are critical for enhancing both model performance and training efficiency. The client selection component enables the algorithm to adapt effectively to heterogeneous environments, addressing system heterogeneity issues. By selecting an optimal subset of clients, this component significantly reduces total training time and accelerates convergence, thus boosting training efficiency. Moreover, it contributes to a modest improvement in model performance while maintaining efficiency gains. The local training component complements the global model personalization component, further enhancing model performance across datasets with varying degrees of data heterogeneity. The global model personalization component is crucial for addressing data heterogeneity, leading to substantial improvements in model performance, especially on datasets with high heterogeneity. In sum, FedPRL, incorporating these three components, effectively addresses both data and system heterogeneity in heterogeneous environments, delivering marked improvements in both model performance and training efficiency.

Table 7 Ablation study on FedPRL: accuracy of different component combinations across varying degrees of data heterogeneity (%).

Fig. 11

Ablation Study on FedPRL: Total training time across different component combinations after 300 rounds.

Conclusion

In this study, we propose a novel personalized federated learning algorithm tailored for heterogeneous environments, FedPRL, designed to effectively tackle the challenges posed by data and system heterogeneity in FL. Our method integrates local data storage, RL, and knowledge distillation to simultaneously enhance model performance and training efficiency in heterogeneous environments. Specifically, we implement local data storage on the client side and employ the kNN algorithm to generate local predictions, enabling the model to better capture data features and especially enhance its performance on highly heterogeneous data. Additionally, we optimize client selection by leveraging RL and user quality evaluation, focusing on minimizing training time while maximizing contributions to the global model. Moreover, our use of knowledge distillation helps preserve global knowledge of non-target classes, mitigating the issue of catastrophic forgetting to improve the model’s performance on data with varying degrees of heterogeneity. Comprehensive experiments conducted on both standard and real-world datasets validate the superior performance and exceptional training efficiency of our algorithm in heterogeneous environments, and further indicate that FedPRL can be effectively integrated into the medical and healthcare field.

For future research, we aim to incorporate advanced pipeline techniques into our method to achieve additional reductions in training time within the FL framework.