Foot fractures diagnosis using a deep convolutional neural network optimized by extreme learning machine and enhanced snow ablation optimizer

Abstract

The current investigation proposes a novel hybrid methodology for the diagnosis of the foot fractures. The method uses a combination of deep learning methods and a metaheuristic to provide an efficient model for the diagnosis of the foot fractures problem. the method has been first based on applying some preprocessing steps before using the model for the features extraction and classification of the problem. the main model is based on a pre-trained ZFNet. The final layers of the network have been substituted using an extreme learning machine (ELM) in its entirety. The ELM part also optimized based on a new developed metaheuristic, called enhanced snow ablation optimizer (ESAO), to achieve better results. for validating the effectiveness of the proposed ZFNet/ELM/ESAO-based model, it has been applied to a standard benchmark from Institutional Review Board (IRB) and the findings have been compared to some different high-tech methods, including Decision Tree / K-Nearest Neighbour (DT/KNN), Linear discriminant analysis (LDA), Inception-ResNet Faster R-CNN architecture (FRCNN), Transfer learning‑based ensemble convolutional neural network (TL-ECNN), and combined model containing a convolutional neural network and long short-term memory (DCNN/LSTM). Final results show that using the proposed ZFNet/ELM/ESAO-based can be utilized as an efficient model for the diagnosis of the foot fractures.

Introduction

Background

A bone fracture is the cracking or breaking of a bone in the body¹. This condition occurs when bone strength is compromised. Bone fractures can occur anywhere in the body, including the arms, legs, heels, hands, back, spine, and other parts of the body². Bone fractures are usually the result of severe impact, high pressure, intense sports activity, traumatic factors, diseases that weaken bone strength³. Certain medical conditions and forces that are applied repeatedly to the bones (such as running) can also increase the risk of certain types of fractures⁴.

Fractures in bones occur when the force applied to the bone is robust than the bone could structurally withstand⁵. This disrupts the bone’s strength and structure, making pain, loss of function, and occasionally bleeding and damage round the location.

Bone fractures are a very common injury and can affect anyone at any age⁶. In some cases, this injury may occur at the age of over 50 years, because with increasing age, the probability of fracture increases with decreasing bone density⁷. However, this does not mean that bone fractures are only for the elderly, and young people and even children may suffer this type of injury.

A doctor diagnoses a broken bone with a physical exam and imaging tests. Usually, after an injury in the emergency department, the fracture and injury are stabilized first⁸. Once stabilized, imaging tests are needed to confirm the fracture⁹. Different types of methods based on artificial intelligence and medical imaging have been presented for early diagnosis of the foot fractures.

Traditional techniques like X-ray and MRI are commonly employed for identifying and categorizing foot fractures¹⁰. Nevertheless, these approaches possess certain limitations, including their expensive nature, time-consuming process, exposure to radiation, and reliance on expert interpretation¹¹. Furthermore, these methods may fail to capture intricate or intricate characteristics crucial for diagnosing foot fractures.

Literature analysis

Consequently, there is a necessity for alternative and supplementary techniques that can surmount these constraints and offer a more precise and efficient diagnosis of foot fractures. For example, Myint et al.¹² introduced a method for the Tibia as the lower leg bone’s classification fractures in X-ray images. Preprocessing involved applying the USM (Unsharp Masking) technique to enhance the image and using the Harris corner detection algorithm to extract corner feature points. The classification was performed using a Decision Tree (DT) for fracture or non-fracture classification and K-Nearest Neighbour (KNN) for classifying fracture types. Four fracture types were defined: Oblique, Comminute, Normal, and Transverse. The system achieved an accuracy of 82% for classifying fracture types. However, some limitations of this work may include the reliance on specific image processing techniques that may not generalize well to other datasets, potential variations in imaging protocols and quality, and the need for validation on a larger and more diverse dataset to assess the system’s performance in real-world clinical settings. Moreover, the study did not compare the system’s performance to that of human experts, which could provide valuable insights into its practical utility and potential limitations.

Sahin et al.¹³ utilized various machine learning techniques to detect and classify bone fractures. The purpose was to alleviate the workload of physicians by accurately identifying fractures in X-ray images, thereby reducing the chances of misdiagnosis and minimizing treatment durations. To achieve this, the X-ray images underwent preprocessing and feature extraction using edge detection methods and Harris corner detection. The extracted features were then fed into twelve different machine learning classifiers, which were fine-tuned using hyperparameters through the grid search method. The classifiers were subsequently evaluated using 10-fold cross-validation. Among the classifiers, the linear discriminant analysis (LDA) exhibited the highest accuracy rate of 88.67% and an AUC of 0.89. However, it is important to acknowledge certain limitations of this study. These limitations encompass the necessity for validation on a larger dataset that encompasses more diverse populations and imaging protocols. Additionally, the reliance on specific image processing and machine learning techniques employed in this study may not generalize well to other datasets. Furthermore, the absence of a comparison with human experts hinders the assessment of the system’s practical utility in real-world clinical settings.

Thian et al.¹⁴ used convolutional neural network (CNN) for fracture detection and localization on wrist radiographs. A total of 7356 wrist radiographic studies were utilized to train fracture localization models, with the dataset divided into validation and training groups. The deep learning model, utilizing Inception-ResNet Faster R-CNN architecture, was tested on a separate test set and demonstrated high sensitivity and specificity in detecting and localizing radius and ulna fractures. The specificity, per-study sensitivity, and AUC were, in turn, 72.9%, 98.1%, and 0.895. However, limitations of the work may include the retrospective nature of the study, potential biases in the dataset, and the need for further validation in diverse clinical settings to assess generalizability. Additionally, the study did not compare the model’s performance to that of human radiologists, which could provide valuable insights into its practical utility in a clinical setting.

Rashid et al.¹⁵ offered a method for diagnose of the wrist fractures. They proposed a combined model comprising a convolutional neural network (CNN) and long short-term memory (LSTM) to identify wrist fractures from X-ray images. The offered model’s behavior, both with and without augmentation, was compared with other deep learning models and existing algorithms in different terms. The outcomes revealed that the fusion of DCNN-LSTM achieved superior accuracy and exhibited potential for implementation as a secondary option in medical applications. However, it is important to acknowledge certain limitations of present research, such as the dataset’s relatively tiny size, which may impact the generalizability of the proposed model to larger and more diverse populations. Furthermore, the study did not evaluate the practical utility and performance of the model in real-world clinical settings, nor did it compare the model’s diagnostic accuracy to that of human experts. Therefore, it would be advantageous to conduct further validation on a larger dataset and assess the reliability and effectiveness of the proposed model through evaluation in clinical practice.

Kim et al.¹⁶ focused on the development and evaluation of an AI-assistant system designed to diagnose foot fractures. The foot’s compound figure often poses challenges in accurately diagnosing fractures, and while AI has been introduced as a potential solution, its accuracy in this particular context still falls short compared to conventional methods. To address this issue, the researchers employed contrast-limited adaptive histogram equalization to enhance the radiographs’ visibility, along with information augmentation techniques to avoid overfitting. They trained a collective model consisting of three transfer learning-based convolutional neural networks (CNNs)-InceptionResNetV2, MobilenetV1, and ResNet152V2 - using preprocessed radiographs. The behavior of the model was assessed with metrics such as the receiver operating characteristic (ROC) curve, area under the curve (AUC), and F1-Score. The findings of the study demonstrated that the ensemble model exhibited superior classification ability, with an F1-Score of 0.837, an AUC of 0.95, and a precision of 86.1%, when compared to individual models which achieved a precision of 82.4%. Furthermore, when the AI aid was provided to orthopedic fellows, residents, interns, and students, the precision of every group enhanced. Additionally, the diagnosis time was reduced for these respective groups. However, it is important to acknowledge the limitations of this study. One limitation is the reliance solely on radiographs as the input for diagnosis, which may not capture all the relevant information or provide a comprehensive understanding of the fracture. Moreover, the study did not compare the performance of the AI assistant to that of experienced experts, making it challenging to determine its effectiveness in comparison to human diagnosis. Furthermore, the generalizability of the AI model may be limited to the specific dataset and population used in the study. Therefore, further validation on a larger and more diverse dataset would be necessary to establish its broader applicability.

Motivation and contribution

Recently, medical image analysis has witnessed the emergence of powerful tools, namely deep learning and metaheuristic techniques. These techniques have confirmed to be extremely effective in solving a wide range of problems, including segmentation, detection, classification, and diagnosis. Deep learning techniques excel at extracting high-level features from vast amounts of data, enabling them to attain high-tech behavior in numerous tasks. On the other hand, metaheuristic techniques possess the ability to optimize complex and nonlinear problems, providing near optimal solutions in a reasonable timeframe. Despite the potential of these techniques, there is a scarcity of studies that combine deep learning and metaheuristic techniques in a hybrid approach for diagnosing foot fractures. This scarcity has motivated us to propose a novel hybrid methodology that harnesses the strengths of both techniques, resulting in an efficient model for foot fracture diagnosis. Our contributions can be summarized as follows:

• A new hybrid methodology is proposed for diagnosing foot fractures, which integrates deep learning and metaheuristic techniques. This methodology comprises 3 foremost stages: pre-processing, property extraction, and classification.

• In order to extract high-level features from the medical images, a pre-trained deep convolutional neural network known as ZFNet has been employ.

• For the classification task, an extreme learning machine (ELM) that offers fast and straightforward learning capabilities. ELM demonstrates excellent generalization performance with minimal human intervention.

• To optimize the ELM, introduce a novel metaheuristic algorithm called enhanced snow ablation optimizer (ESAO) has been proposed.

• The effectiveness of the offered method has been assessed using a standard benchmark dataset obtained from the Institutional Review Board (IRB).

ZFNet/extreme learning

A new technique has been made to recognize foot fractures using deep learning and pre-processing. By employing foot fractures dataset, the previously trained ZFNet was optimized at first. Then, the rest of the layers of enhanced ZFNet were adapted through applying an Extreme Learning Machine. Eventually, the generalization skills of the ELM were enhanced via ESAO.

ZFNet

ZFNet could win the competition of ILSVRC in 2013. In that year, the scholars invented an approach to picture extracted features in all layers of Convolutional Neural Network¹⁷. by getting help from it, the features gained from AlexNet have been illustrated. There exist two obstacles in the whole construction of the AlexNet. Moreover, some alterations are done for solving those problems. The initial obstacle is all the features that have been extracted through AlexNet within the second and first layers comprise high and low-frequency alteration.

However, there are fewer middle-frequency alterations. For solving the present obstacle, the first layer is altered from $\:11\times\:11$ to $\:7\times\:7$. The subsequent obstacle is relevant to the extracted features’ interference within the subsequent layer that happened because of the massive size of step of the convolution¹⁸. That is why, the size of step altered from 4 to 2. Therefore, ZFNet can help to gain more various attributes; moreover, the efficacy of the network has been contrasted with the AlexNet. So, a CNN and ZFNet have been utilized in the present study.

Extreme learning machine

Each application that uses machine learning extensively utilize single-concealed layer neural networks like ELM. Initially, input layer’s biases and weights have been made stochastically. Moreover, the output layer’s biases and weights have been calculated on the basis of the stochastic values that had been produced. Learning techniques of conventional neural network possess a lesser proportion of efficacy and a slower learning pace¹⁹. Within the layer of input, the quantity of neuron has been depicted by $\:n$, and the values of neurons in the output and concealed layer have been, in turn, depicted by $\:m$ and $\:L$.

The equation of the activation function has been illustrated in the following way:

$$X_{i} = \mathop \sum \limits_{{j = 1}}^{L} Y_{j} f\left( {v_{j} \times d_{j} \times c_{j} } \right)$$

(1)

here, the input link’s weight has been illustrated by $\:{v}_{j}$, the bias of the concealed neuron $\:j$ has been illustrated by $\:{d}_{j}$, the output link’s weight has been depicted by $\:{c}_{i}$, and the ultimate output of the Extreme Learning Machine has been demonstrated by $\:{X}_{i}$. The matrix procedure of the Eq. (1) has been defined by the use of Eq. (3).

$${X}^{T}=GY$$

(2)

where the move of matrix $\:X$ has been represented by $\:X$, and $\:G$ and $\:Y$ are expressed subsequently:

$$ G = \left[ {\begin{array}{*{20}c} {f\left( {v_{1} \times d_{1} \times c_{1} } \right)} & {f\left( {v_{2} \times d_{2} \times c_{2} } \right)} & {\begin{array}{*{20}c} \cdots & {f\left( {v_{L} \times d_{L} \times c_{1} } \right)} \\ \end{array} } \\ \vdots & \vdots & {\begin{array}{*{20}c} {} & \vdots \\ \end{array} } \\ {f\left( {v_{1} \times d_{1} \times c_{\gamma } } \right)} & {f\left( {v_{2} \times d_{2} \times c_{\gamma } } \right)} & {\begin{array}{*{20}c} \cdots & {f\left( {v_{L} \times d_{L} \times c_{\gamma } } \right)} \\ \end{array} } \\ \end{array} } \right]_{{\gamma \times L}} $$

(3)

$$\:Y={\left[{Y}_{1},{Y}_{2},\:.\:.\:.\:,\:{Y}_{L}\right]}^{T}$$

(4)

The primary purpose of the ELM is decreasing the quantity of errors made during the procedure of training. For appropriately carrying out a conventional ELM, the biases and weight of the input must be selected randomly; additionally, the function of activation must be extremely distinguished. The training procedure of Extreme Learning Machine results in the weight of output $\:Y$ that is learned by increasing the function of the least least-squares to the most in Eq. (5). Moreover, the result might be specified by the use of Eq. (6).

$$ \mathop {\min }\limits_{Y} \left\| {GY - X^{T} } \right\| $$

(5)

$$\:\widehat{Y}={G}^{+}{X}^{T}$$

(6)

where the comprehensive Moore-Penrose inverse of the matrix $\:G$ has been represented by $\:{G}^{+}$.

Evolved ZFNet

An approach has been invented for detecting cancer of breast, which is named ZFNet-ESAO-ELM. The present approach has been inspired from ELM, ESAO, and ZFNet. Features of imaging can be extracted from mammography pictures of breast by employing a trained ZFNet.

Employing an enhanced chimp optimizer to make an ELM

The time of procedure should decrease by substituting the ultimate entirely connected layer with Extreme Learning Machine. Once the ELM has been utilized, there exists an uncertainty level that is relevant to the ultimate system, because the weights of connection and biases of the layer of input have been randomly adapted. In fact, this has been considered to be a significant problem²⁰. So, ESAO has been used as stabilizer system for increasing resilience of network and maintaining the actual-time processing at the same time within the subsequent step²¹. The present approach prevents from divergence of network by adapting the biases and weights of the layer of input.

Within the problem explanation of the present scenario, biases and weights of the ELM are as search candidates of ESAO, and specification of problem-solving errors are as a performance index of ESAO. Furthermore, several search candidates, which are based on vector, have been suggested in the present study due to the fact that ESAO requires vectors to be as sources. It has been thoroughly explained subsequently:

$$ individualsolution = [V_{{11}} ,~V_{{12}} ,~ \ldots ,~V_{{nT}} ,~d_{1} ,~d_{2} ,~ \ldots ~,~b_{T} ] $$

(7)

where the weight between the input $\:j$ of the prior pooling layer of ZFNet and input node $\:i$ of the ELM has been represented by $\:{V}_{ji}$, and the biases of the neuron $\:i$ has been illustrated by $\:{d}_{i}$. The present algorithm must have an approach to measure the efficacy of its search candidates just like other algorithms. The current part assesses the appropriateness of the search candidates of the present algorithm by the use of performance index or categorization MSE. The utilized performance index is explained in the following:

$$\:perfindex=\frac{1}{2}\sqrt{\frac{\sum\:_{j=0}^{T}{\left(z-\widehat{z}\right)}^{2}}{T}}$$

(8)

where real and expected outputs have been, in turn, demonstrated by $\:z$ and $\:\widehat{z}$, and the entire quantity of instance utilized for training has been represented by $\:T$. Figure 1 illustrates the results of different stages of the process.

Fig. 1

The results of different stages of the process.

Enhanced snow ablation optimizer (ESAO)

In this section, the main idea for the Snow Ablation Optimizer (SAO)’s motivation, which rooted in the process of snow sublimation and melting, is described. Then, this algorithm is modeled mathematically.

Inspiration

one of the most attractive and stunning sceneries in nature is snow. Particularly in winter, the snow’s melting has a major impact on the ecosystem, which influences human health and harvests’ evolution and progress. Based on physics, snow could change into 2 shapes: steam and liquid water. sublimation and melting as the physical procedures are related formats of steam and liquid water. In the meantime, the liquid water transformed from snow defrost could be exchanged into vapor by disappearing.

The motivation’s resource for SAO rises from the snow’s melting and sublimation manner. In the subsequent sections, in the SAO algorithm, the initialization phase, exploration phase, exploitation phase, and binary-population apparatus would be presented.

Initialization phase

In the context of SAO, the iteration process commences with a swarm that is produced in a stochastic manner. As indicated in the following equation, the total swarm is typically demonstrated as a matrix with $\:D$ columns and $\:N$ rows, in which $\:N$and $\:D$ signify the size of the swarm, and the of the solution space’s dimensionality, respectively.

$$ Y = l + \varepsilon \times \left( {u - l} \right) = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {y_{{1,1}} } & {y_{{1,2}} } \\ \end{array} ~~~\begin{array}{*{20}c} { \ldots ~~~~y_{{1,D - 1}} } & {y_{{1,D}} } \\ \end{array} } \\ {\begin{array}{*{20}c} {y_{{2,1}} } & {y_{{2,2}} } \\ \end{array} ~~~\begin{array}{*{20}c} { \ldots ~~~~y_{{2,D - 1}} } & {y_{{2,D}} } \\ \end{array} } \\ {\begin{array}{*{20}c} \vdots \\ \end{array} ~~~~~~~~~~~~~~~~~~\begin{array}{*{20}c} { \vdots ~~~~} & {~~~~ \vdots ~~~~~~~~~~} & \vdots \\ \end{array} } \\ {\begin{array}{*{20}c} {y_{{N - 1,1}} } & {y_{{N - 1,2}} } \\ \end{array} ~~~\begin{array}{*{20}c} { \ldots ~~~~y_{{N - 1,D - 1}} } & {y_{{N - 1,D}} } \\ \end{array} } \\ {\begin{array}{*{20}c} {y_{{N,1}} } & {y_{{N,2}} } \\ \end{array} ~~~\begin{array}{*{20}c} { \ldots ~~~~y_{{N,D - 1}} } & {y_{{N,D}} } \\ \end{array} } \\ \end{array} } \right] $$

(9)

Here, the solution space’s lower and upper boundary is determined by $\:l$ and $\:u$, respectively. $\:\varepsilon\:$ signifies a number stochastically that is from 0 to 1.

Exploration phase

The exploration method in SAO is designated by its features in this section. Once the liquid water or snow malformed from snow changes into steam, the search agents show high-decentralized properties because of the unequal motion. The current research takes advantage of the Brownian movement to simulate this condition. As a random procedure, Brownian motion is broadly employed to compete with the seeking for food animals’ manner, the elements’ limitless and asymmetrical motion, and the stock price’s oscillation manner to name but a few. The phase’s size is calculated by the possibility density function on the basis of the normal distribution using variance one and mean zero for standard Brownian motion. This is determined by the next Eq. 

$$\:{F}_{B}(x;\text{0,1})={\left(2\pi\:\right)}^{-0.5}\times\:{e}^{-0.5{x}^{2}}$$

(10)

With uniform and dynamic phase duration, the Brownian motion allows several potential areas in the search space to be discovered. Therefore, the steam distribution’s condition of in the search space can be well mirrored by Brownian motion. This situation in the procedure of exploration is modeled mathematically as follows:

$$\:{Y}_{i}\left(t+1\right)=E\left(t\right)+{B}_{i}\left(t\right)\otimes\:({\varepsilon\:}_{1}\times\:\left(G\left(t\right)-{Y}_{i}\left(t\right)\right)+{(1-\varepsilon\:}_{1})\times\:\left(Y\left(t\right)-{Y}_{i}\left(t\right)\right))$$

(11)

In which, $\:{Y}_{i}\left(t\right)\:$defines the $\:i-th$ member throughout the $\:t-th$ iteration, $\:{B}_{i}\left(t\right)$ designates a vector counting stochastic amount based on Gaussian distribution signifying the Brownian motion, the $\:\otimes\:$ defines entry-wise multi-plications, $\:{\varepsilon\:}_{1}$indicates a number stochastically that is from 0 to 1. Additionally, $\:G\left(t\right)$ denotes the existing greatest solution, $\:E\left(t\right)$ is a stochastic member chosen from a group of some elites that is in the swarm, and $\bar{Y}\left( t \right)$ represents the total swarm’s centroid situation. The mathematical models are represented as below:

$$ \bar{Y}\left( t \right) = (1/N)\sum\limits_{{i = 1}}^{N} {Y_{i} \left( t \right),} $$

(12)

$$\:E\left(t\right)\in\:G\left(t\right),{Y}_{2nd}\left(t\right),{Y}_{3rd}\left(t\right),{Y}_{c}\left(t\right)$$

(13)

here $\:{Y}_{2nd}\left(t\right)$ and $\:{Y}_{3rd}\left(t\right)\:$signify, in turn, the 2nd-greatest member and the 3rd-greatest member in the existing population. $\:{Y}_{c}\left(t\right)\:$signifies the members’ centroid situation whose fitness amounts are classified in the top fifty percents. The members whose fitness amounts are classified in the top fifty percents are called leaders in present research. Furthermore, $\:{Y}_{c}\left(t\right)\:$is computed by the next Eq. 

$$ Y_{c} \left( t \right) = (1/N_{1} )\sum\limits_{{i = 1}}^{{N_{1} }} {Y_{i} \left( t \right),} $$

(14)

here the leaders’ number is determined by$\:\:{N}_{1}\:$, that is, $\:{N}_{1}\:$is equivalent to half of the total swarm’s size, and $\:{Y}_{i}\left(t\right)\:$signifies the $\:i-th$ greatest leader.

Consequently, throughout every iteration, the $\:E\left(t\right)$ is stochastically chosen from a group that contains the existing greatest solution, 2nd-greatest member, 3rd-greatest member, and leaders’ centroid situation.

The parameter$\:\:{\varepsilon\:}_{1}\:$that controls the motion towards the existing greatest member and the leaders’ motion to the centroid position. The above 2 cross terms’ integration is mostly applied to mirror the communication among members.

Exploitation phase

This section presents the SAO’s exploitative characteristics. Instead of increasing through a highly dispersed property in the solution space, search agents are encouraged to get high-quality solutions throughout the entire solution space when the snow undergoes its melting behavior and transitions into liquid water. The degree-day method as one of the furthermost traditional snowmelt methods, is applied to mirror the snow-melting’s procedure. This method’s overall arrangement is offered as follows:

$$\:S=DDF\times\:(T-{T}_{1})$$

(15)

where $\:S$ signifies the snow-melt ratio, a major factor to imitate the melting performance in the exploitation phase. The average day-to-day temperature is determined by $\:T$. $\:{T}_{1}\:$mentions the foundation temperature that is generally regulated to zero. This outcome is shown as follows:

$$\:S=DDF\times\:T$$

(16)

here $\:DDF\:$depict the degree-day parameter situated between 0.35 and 0.6. The formula for renewing the amount of DDF is provided in every iteration of the mathematical model.

$$\:DDF=0.35+0.25\times\:\left({(e}^{\frac{t}{{t}_{max}}}-1)/(e-1)\right)$$

(17)

here $\:{t}_{max\:}$signifies the conclusion standard. Then in SAO, the snow-melt ratio is computed by applying the next formula:

$$\:S=0.35+0.25\times\:\left({(e}^{\frac{t}{{t}_{max}}}-1)/(e-1)\right)\times\:T\left(t\right),\:T\left(t\right)={e}^{\frac{-t}{{t}_{max}}}$$

(18)

At that time in the SAO’s exploitation phase, the situation renewing formula is offered in the next formula:

$$ Y_{i} \left( {t + 1} \right) = S \times G\left( t \right) + B_{i} \left( t \right) \otimes \le \left( {\varepsilon _{2} \times \left( {G\left( t \right) - Y_{i} \left( t \right)} \right) + (1 - \varepsilon _{2} ) \times \left( {\bar{Y}\left( t \right) - Y_{i} \left( t \right)} \right)} \right) $$

(19)

here $\:S$ is the snow-melt ratio, $\:{\varepsilon\:}_{2}\:$designates the stochastic amount selected between − 1 and1. This parameter simplifies the statement between members.

During this phase, with the assistance of the cross terms $\:{\varepsilon\:}_{2}\times\:\left(G\left(t\right)-{Y}_{i}\left(t\right)\right)\:$and $(1 - \varepsilon _{2} ) \times \left( {\bar{Y}\left( t \right) - Y_{i} \left( t \right)} \right),$the members are further likely to achieve hopeful areas on the basis of data of the existing greatest search agent and centroid situation of the swarm.

Dual-population mechanism

Understanding an interchange among exploitation and exploration is so substantial in meta-heuristic algorithms.

Likewise, some liquid water transformed from melted snow could be converted into steam to achieve exploration procedure. That is, during sometimes, the probability of members undertaking asymmetrical motions using a highly decentralized feature upsurge. After that, the algorithm slowly tends to discover the solution space. During this research, the dual population mechanism is developed to mirror this condition and preserve exploration and exploitation. The entire population is stochastically separated into 2 equal-sized sub-populations at the initial stage of iteration. The entire population and these 2 sub-populations are defined as $\:P$ ,$\:{P}_{a}$, and $\:{P}_{b}$, correspondingly. Furthermore, the $\:P$ ,$\:\:{P}_{a}$, and $\:{P}_{b}$, sizes are signified as $\:N$, $\:{N}_{a}$, and $\:{N}_{b}$, in turn.

In which, $\:{P}_{a}\:$is charged with the exploration, while $\:{P}_{b}\:$is allocated to accomplish the exploitation. Next, in the succeeding iterations, $\:{P}_{b}\:$size slowly drops and the $\:{P}_{a}$ size is consequently amplified.

Taken together, the SAO algorithm’s comprehensive situation renewing equation is determined by the next formula:

$$ Y_{i} \left( {t + 1} \right) = \left\{ \begin{gathered} E\left( t \right) + B_{i} \left( t \right) \otimes \left( {\varepsilon _{1} \times \left( {G\left( t \right) - Y_{i} \left( t \right)} \right) + (1 - \varepsilon _{1} )} \right) \times \left( {Y\left( t \right) - Y_{i} \left( t \right)} \right),~i \in indx_{a} \hfill \\ S \times G\left( t \right) + B_{i} \left( t \right) \otimes \left( {\varepsilon _{2} \times \left( {G\left( t \right) - Y_{i} \left( t \right)} \right) + (1 - \varepsilon _{2} )} \right) \times \left( {\bar{Y}\left( t \right) - Y_{i} \left( t \right)} \right),~i \in indx_{b} \hfill \\ \end{gathered} \right. $$

(20)

The total population is a situation matrix as defined by Eq. (10). Hence, in above equation$\:\:\:{indx}_{a}$ and $\:\:\:{indx}_{b}$ signify a collection of indexes counting line numbers of members in $\:{P}_{a}$ and $\:{P}_{b}$in the whole situation matrix, correspondingly.

Enhanced version

By striking an equilibrium among exploration and exploitation within the solution space, SAO effectively avoids premature convergence. Nevertheless, SAO does possess certain limitations, including the insufficient diversity and stability of its search agents, as well as its sensitivity to parameter settings. Consequently, this paper introduces an enhanced version of SAO algorithm that incorporates a heat transfer and condensation strategy. This improvement aims to bolster the performance of SAO when tackling intricate and constrained optimization problems.

Two modifications have been implemented in this study to enhance the algorithm. The first improvement utilizes Chaos theory, which introduces randomness and unpredictability into the search process of the fish migration optimizer. By doing so, the algorithm is able to explore a wider range of solutions, resulting in improved performance.

Furthermore, Chaos theory offers better exploration strategies, enabling the algorithm to quickly identify and exploit the most promising solutions. Additionally, the algorithm minimizes the risk of being stuck in local optima, enhances the probabilities of discovereing the global optimum. Among the various types of chaotic processes, the Bernoulli shift map is widely recognized and has been extensively studied in relation to chaotic behavior in dynamical systems²².

The Bernoulli shift map can be utilized to examine the dynamics of intricate systems comprising multiple variables. It is characterized by a binary parameter $\:{Y}_{\left(j+1\right)}$, which equals the modulo 2 sums of two binary variables $\:{Y}_{\left(j\right)}$ and $\:{Y}_{\left(j-1\right)}$. When the Bernoulli shift map has been applied to the initial population of the optimizer, this map can introduce chaotic behavior by incorporating randomness through a set of binary numbers. The outcome of this process is as follows:

$$ Y_{i} \left( {t + 1} \right) = \left\{ \begin{gathered} \frac{{Y_{i} \left( t \right)}}{{1 - \theta }},~~~0 < Y_{i} \left( t \right) \le 1 - \theta \hfill \\ \frac{{Y_{i} \left( t \right) - \left( {1 - \theta } \right)}}{\theta },1 - \theta \le Y_{i} \left( t \right) < 1 \hfill \\ \end{gathered} \right. $$

(21)

where $\:\theta\:=0.3$.

The Lévy flight mechanism is also implemented as another modification. This mechanism is a mathematical model inspired by the movement patterns of swarm. It finds extensive application in the field of metaheuristics. The core principle behind the Lévy flight is to deviate from a linear path and instead incorporate random jumps when searching for the optimal solution. This approach enables a more effective search in contrast to a purely linear strategy. Notably, it is widely used in population-based metaheuristic algorithms to discover different areas of the search space and avoid Random walk has been utilized here for mathematically simulating of the method:

$$\:Levy\left(w\right)\approx\:\frac{w}{1+\theta\:}$$

(22)

$$\:w=\frac{A}{{\left|B\right|}^{1/\theta\:}}$$

(23)

$$\:{\sigma\:}^{2}={\left\{\frac{{\Gamma\:}(1+\theta\:)}{\theta\:{\Gamma\:}\left(\right(1+\theta\:)/2)}\frac{\text{s}\text{i}\text{n}(\pi\:\tau\:/2)}{{2}^{(1+\theta\:)/2}}\right\}}^{\frac{2}{\tau\:}}$$

(24)

where $\:w$ represents the step size, $\:\theta\:$ describes the Levy index between 0 and 2 (with $\:\theta\:=1.5$). $\:A$ and $\:B$ have been distributed normally by the mean of 0, and $\:\varGamma\:(.)$ describes the Gamma function.

In this study, we employ this mechanism to enhance $\:{r}_{1}$. Through the implementation of Lévy flight, we have achieved significant improvements.

$$\:{S}^{New}=0.35+0.25\times\:\left({(e}^{\frac{t}{{t}_{max}}}-1)/(e-1)\right)\times\:T\left(t\right),\:T\left(t\right)=Levy$$

(25)

Such that, $\:{S}^{New}$ defines the new snow-melt ratio.

Validation of model

In order to validate the proposed Enhanced Snow Ablation Optimizer (ESAO), a thorough and unbiased validation process was conducted. Firstly, the algorithm was applied to 23 well-known classical benchmark functions. Subsequently, the outcomes gained from the ESAO were compared to five other high-tech algorithms: Gaining-Sharing Knowledge-based algorithm (GSK)²³, Teamwork Optimization Algorithm (TOA)²⁴, Butterfly Optimization Algorithm (BOA)²⁵, Manta Ray Foraging Optimization (MRFO)²⁶, and Arithmetic Optimization Algorithm (AOA)²⁷. Table 1. Indicates the parameter values used for each of these analyzed algorithms.

Table 1 Parameter values used for each of these analyzed algorithms.

The benchmark functions utilized in the study were categorized into 3 kinds: unimodal (F1 to F7), multimodal (F8 to F13), and fixed-dimensional (F14 to F23). All functions were assumed to have a dimension of 30.

The main aim of this investigation is to provide the minimum value for all 23 functions mentioned above. Essentially, the algorithm that yields the smallest value will demonstrate the best results. To conduct a comprehensive and reliable analysis, the mean value and standard deviation (StD) are utilized to assess the analyzed algorithms’ optimization solutions. In order to ensure a fair and robust comparison, all algorithms were subjected to the identical population size and iterations’ maximum number, in turn, set at 60 and 200. Additionally, repeating the optimization process 30 times allows for more reliable and robust algorithmic solutions. The comparison analysis of the ESAO toward the other algorithms is shown in Table 2.

Table 2 The comparison analysis of the ESAO toward the other algorithms.

Based on the table, it can be seen that the ESAO algorithm consistently outperforms the other algorithms across most benchmark functions. The mean values for the ESAO algorithm are generally lower, indicating better optimization outcomes, and the StD values are also relatively smaller, suggesting more stable and consistent results. For instance, in Function F1, the ESAO algorithm achieves a mean value of 2.57E-59, which is significantly lower than the other algorithms’ mean values.

Similarly, in Functions F5, F8, F9, and F16, the ESAO algorithm surpasses the other algorithms in terms of both mean and StD. These findings demonstrate the efficiency and competitiveness of the offered ESAO algorithm in resolving the optimization problems represented by the benchmark functions. The algorithm exhibits superior behavior in terms of precision, convergence, and stability. It is important to acknowledge that the evaluation and comparison presented in Table 4 provide evidence of the ESAO algorithm’s capabilities. However, further validation and testing on different problem domains and real-world applications would be necessary to establish its broader applicability and robustness.

Table 3 Optimal parameter value achieved for the optimal network.

Table 4 Outcomes of the performance assessment and comparison conducted on the five models utilization of eight metrics and 2-fold validation.

Optimizing extreme learning machine based on ESAO

Replacing the final fully connected layer with the ELM can lead to a reduction in processing time. However, using the ELM introduces a level of ambiguity in the last model since the input layer biases and connection weights are adjusted stochastically. This uncertainty is a important drawback. To address this, we employ the ESAO fir the next phase.

By adjusting the biases and weights of the input layer, this method prevents network divergence while maintaining real-time processing. In this scenario, we incorporate ELM biases and weights as search agents for the ESAO and use diagnostic errors (calcification errors) as a cost function. Furthermore, to accommodate the requirements of the ESAO, we propose vector-based search agents instead of matrix and binary-state-based agents. This vector encoding is illustrated in the following Equation:

$$\:decision\:variables=\left[{W}_{11},{W}_{12},\cdots\:,{W}_{nT},{b}_{1},{b}_{2},\cdots\:,{b}_{T}\right]$$

(26)

The weight among the$\:\:{j}^{th}$ input node of ELM and the ith input from the preceding pooling layer of ZFNet is represented by $\:{W}_{ij}$, whereas the biases of the $\:{j}^{th}$ neuron are denoted by $\:{b}_{j}$. In order to ensure the efficient operation of ESAO, it is important to assess the behavior of its search agents. The purpose of this part is to evaluate the appropriateness of the search agents generated by ESAO by employing the cost function or classification Mean Square Error (MSE). The utilized objective function (OF) can be stated as follows:

$$\:OF=\frac{1}{2}\sqrt{\frac{{\sum\:}_{j=0}^{T}{\left(z-\widehat{z}\right)}^{2}}{2}}$$

(27)

where $\:T$ describes the total sample quantity for training, $\:z$ and $\:z{\prime\:}$ describe the real and the predicted output by the model, respectively.

The optimization procedure is executed through the following stages:

• (1) Iteration 1–10: The algorithm begins by initializing a population of search agents and assessing their fitness values. Based on these values, search agents are selected, and the most effective agents are retained to generate the subsequent generation.

• (2) Iteration 11–20: The algorithm engages in exploration, exploitation, and employs a Dual-population mechanism on the chosen search agents to produce new offspring.

• (3) Iteration 21–30: The fitness values of the newly generated population are evaluated, and the top-performing search agents are selected to constitute the next generation.

• (4) Iteration 31–40: The algorithm reiterates the process, incorporating additional mechanisms such as the Bernoulli shift map and Lévy flight to generate new offspring.

• (5) Iteration 41–50: The fitness values of the new offspring are assessed, and the best search agents are chosen to form the next generation.

Figure 2 illustrates the convergence plot of the ESAO algorithm.

Fig. 2

The convergence plot of the ESAO algorithm.

The convergence plot indicates that the algorithm reaches the optimal solution at Iteration 47, with a corresponding fitness value of 0.7015 at which point the algorithm reaches convergence to the best solution. Table 3 represents the optimal parameter value achieved for the optimal network.

The learning rate is a vigorous hyperparameter that dictates the magnitude of each update during the training process. A minimal learning rate, such as 1e-6, is employed to prevent overshooting and to promote stable convergence of the model. This particular value is selected for several reasons:

• A high learning rate may result in overshooting, leading the model to deviate from the optimal solution.

• Conversely, a low learning rate fosters more stable convergence, although it may result in prolonged training times.

• Through empirical testing, we determined that a learning rate of 1e-6 strikes an effective balance between the speed of convergence and stability.

The maximum number of epochs signifies the upper limit of iterations permitted during training. This figure is determined for the following reasons:

• An excessive number of epochs can result in overfitting, causing the model to become overly tailored to the training data.

• A limited number of epochs may prevent the model from reaching the optimal solution.

• Our experimental findings indicate that a maximum epoch count of 5 offers a suitable compromise between achieving convergence and avoiding overfitting.

The mini batch size indicates the quantity of training examples utilized in each iteration. This parameter is selected for several reasons:

• A larger mini batch size may result in slower convergence and reduced accuracy.

• Conversely, a smaller mini batch size can facilitate quicker convergence but might compromise the accuracy of the results.

• Our experiments have demonstrated that a mini batch size of 50 strikes an effective balance between the speed of convergence and the accuracy of outcomes.

The number of hidden nodes in the Extreme Learning Machine (ELM) signifies the model’s complexity. This figure is determined for the following reasons:

• An excessive number of hidden nodes can lead to overfitting and a decrease in convergence speed.

• In contrast, a limited number of hidden nodes may fail to yield accurate results.

• Our experimental findings indicate that utilizing 500 hidden nodes in the ELM provides a suitable equilibrium between complexity and accuracy.

The maximum iteration denotes the upper limit on the number of iterations permitted during the training process. This value is determined for several reasons:

• An excessively high iteration count may result in overfitting and a decrease in convergence speed.

• Conversely, a low iteration count might prevent the model from reaching the optimal solution.

• Our experimental findings indicate that setting the maximum iteration count to 200 strikes an effective balance between the speed of convergence and the accuracy of the model.

The number of candidates refers to the quantity of search agents employed in the optimization procedure. This value is selected for the following reasons:

• A high number of candidates can contribute to slower convergence and less precise outcomes.

• In contrast, a low number of candidates may fail to yield accurate results.

• Based on our experiments, we have determined that utilizing 50 candidates offers a favorable balance between convergence speed and accuracy.

In summary, the parameter values outlined in Table 3 ensure an optimal balance among convergence speed, accuracy, and complexity, thereby facilitating the achievement of the best possible results.

Simulation results

Dataset description

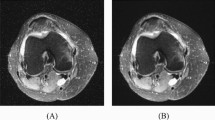
Dataset used in this study consists of 1,099 radiographs of anteroposterior views of the pelvis, taken from patients who visited the Pusan National University Hospital between Jan. 2011 and Dec. 2017. The radiographs were categorized as fracture or normal by two expert radiologists, who also classified the fracture types as oblique, transverse, or comminuted. The patients’ mean age was 52.5 years, that is ranging from 17 to 93 years. The dataset had a balanced distribution of sex, with 562 female and 537 male patients. The dataset was stochastically divided into testing and training groups, with 85% of the pictures (934) used for training the convolutional neural networks (CNNs) and 15% of the images (165) used for testing and validating the model performance¹⁶. Figure 3 displays a compilation of sample images that depict various cases of foot fractures within the Pusan National University Hospital.

Fig. 3

Sample images that depict various cases of foot fractures within the Pusan National University Hospital.

The complete dataset is separated into 2 groups: the test group and the training group. The training set constitutes 75% of the dataset and includes a diverse collection of foot fracture images. On the other hand, the test set accounts for the remaining 25% of the dataset and is exclusively reserved for evaluating the model’s behavior. This partitioning strategy ensures that the model is rigorously tested on unfamiliar data, providing an authentic assessment of its capabilities.

Data augmentation

Synthetic minority oversampling technique (SMOTE) is a method utilized to produce synthetic samples from the minority class in an excessive dataset. Its process involves identifying a minority class instance’s k-nearest neighbors and selecting one of them randomly to create a new example along the line connecting them.

Consider $\:X$ as the original dataset with $\:n$ samples and $\:d$ features, and $\:y$ as the class label vector. Let $\:{X}_{m}$ represent the subset of $\:X$ that belongs to the minority class, and $\:{X}_{M}$ represent the subset belonging to the majority class. Let nm and $\:{n}_{M}$ denote the number of samples in $\:{X}_{m}$ and $\:{X}_{M}$ respectively. Let $\:r$ be the desired oversampling ratio, which determines the number of synthetic samples to be added. The final dataset will have $\:nf=\:{n}_{M}+r\times\:{n}_{m}$ samples.

To apply SMOTE, we first calculate the k-nearest neighbors of each sample in $\:{X}_{m}$ using a distance metric such as Euclidean distance. Then, for each sample $\:{x}_{i}$ in $\:{X}_{m}$, we randomly choose one of its neighbors $\:{x}_{j}$ from $\:{X}_{m}$ and generate a new synthetic sample $\:{x}_{s}$ through linear interpolation.

$$\:{x}_{s}={x}_{i}+\lambda\:({x}_{j}-{x}_{i})$$

(28)

where $\:\lambda\:$ represents a stochastic amount that ranges [0,1].

We continue this procedure until we acquire a final dataset $\:{X}_{f}$ with $\:{n}_{f}$ samples by incorporating $\:r\times\:{n}_{m}$ synthetic samples.

SMOTE can be applied to mitigate the problem of class imbalance in foot fracture discovery using X-ray radiography. This problem arises when there are significantly more normal images than fracture images in the dataset²⁸. By utilizing SMOTE, it becomes possible to generate synthetic fracture images, thereby balancing the dataset. This approach aids the model in effectively learning the characteristics and patterns of fracture images, potentially enhancing the accuracy and sensitivity of fracture detection. Nonetheless, it is significant to acknowledge that SMOTE does have specific restrictions. These include the potential risk of overfitting, challenges in handling high-dimensional data, and the generation of noisy or unrealistic samples.

Augmentation enhances the model’s ability to learn precise features through various methods. By implementing a range of augmentations, including rotation, scaling, flipping, and the introduction of Gaussian noise, the model encounters a broader spectrum of variations. This exposure facilitates the acquisition of more robust and generalizable features. Consequently, there is an improvement in performance on validation and test datasets, an increase in data diversity, a reduction in overfitting, and enhanced regularization. The application of augmentation serves as a regularizing mechanism, compelling the model to focus on simpler features that can be generalized to unfamiliar data. Through the use of diverse augmentations, the model is better equipped to generalize to new, unseen data and to learn invariant features that remain unaffected by specific transformations.

Results and analysis

The research utilized the Pusan National University Hospital dataset for modeling and validation. During each iteration of the fine-tuning process, 75% of the information was used for training, while the residual 25% was reserved for testing. After 20 iterations, all of the data underwent testing to determine the final accuracy. The final accuracy was derived by calculating the average accuracy across the ten iterations.

This section presents the simulation results of our proposed ZFNet/ELM/ESAO model, which addresses the deep learning problem. The system ran on the Windows 11 operating system, utilizing Intel Core i7 CPU 2.00 GHz, 2.5 GHz, 8GB RAM and 64-bit operating system for both training and testing. The execution was performed with 32GB of RAM.

The effectiveness of the suggested approach, ZFNet/ELM/ESAO, was compared to many sophisticated models listed in the literature in this section. The models mentioned are Decision Tree / K-Nearest Neighbour (DT/KNN)¹², Linear discriminant analysis (LDA)¹³, Inception-ResNet Faster R-CNN architecture (FRCNN)¹⁴, Transfer learning‑based ensemble convolutional neural network (TL-ECNN)¹⁶, and combined model including a convolutional neural network and long short-term memory (DCNN/LSTM)¹⁵. The collection of these models was on the basis of their ability to exemplify diverse methodologies and frameworks for image classification and segmentation problems.

In order to evaluate the efficacy of ZFNet/ELM/ESAO, a range of assessment measures were employed to measure various facets of the model’s performance. These measurements offer a thorough comprehension of the performance of our suggested approach.

Accuracy, however, quantifies the proportion of accurate forecast cases to the entire amount of instances, demonstrating the general effectiveness of the model’s classification, that is:

$$\:Accuracy=\frac{{T}_{P}+{T}_{N}}{{T}_{P}+{T}_{N}+{F}_{P}+{F}_{N}}$$

(29)

where $\:{F}_{P}$, $\:\:{F}_{N}$, $\:{T}_{P}$, and $\:{T}_{N}$, in turn, define the false positive, false negative, true positive, and true negative, respectively.

Correctness is a measure of the model’s ability to precisely forecast positive samples out of all the samples predicted as positive. This evaluation assesses the model’s aptitude to accurately recognize examples of the positive class, that is:

$$\:Precision=\frac{{T}_{P}}{{T}_{P}+{F}_{P}}$$

(30)

where $\:{T}_{P}$, and $\:{T}_{P}\:$describe the true positive and false positive, respectively.

Recall specifies the model ability for correctly positive samples prediction during all of the actual positive samples, that is:

$$\:Recall=\frac{{T}_{P}}{{T}_{P}+{F}_{N}}$$

(31)

The F1 Score, calculated as the harmonic mean of correctness and specificity, serves as a balanced assessment that considers both specificity and accuracy, that is:

$$\:F1=2\times\:\frac{Precision\times\:Sensitivity}{Precision+Sensitivity}$$

(32)

The F-beta ($\:{F}_{\beta\:}$) score is a mathematical measure that combines memory and precision in a weighted harmonic mean. It enables the optimization of precision and recall by adjusting their relative importance with a parameter $\:\beta\:$.

$$\:{F}_{\beta\:}=\left(1+{\beta\:}^{2}\right)\times\:\frac{\left(1+{\beta\:}^{2}\right)\times\:TP}{\left(1+{\beta\:}^{2}\right)\times\:TP+{\beta\:}^{2}\times\:{F}_{N}+{F}_{P}}$$

(33)

where $\:\beta\:$ specifies a constant that is here equal to 2.

The Kappa-score ($\:{\kappa\:}_{sc}$), which ranges in the interval [-1, 1], which measures the agreement between the ground truth and the model’s forecast, taking into account chance, that is:

$$\:{\kappa\:}_{sc}=\frac{{P}_{o\left(w\right)}-{P}_{e\left(w\right)}}{1-{P}_{e\left(w\right)}}$$

(34)

where

$$\:{P}_{o\left(w\right)}=\frac{1}{N}{\sum\:}_{i=1}^{k}{\sum\:}_{j=1}^{k}{w}_{ij}{f}_{ij}$$

(35)

$$\:{P}_{e\left(w\right)}=\frac{1}{{N}^{2}}{\sum\:}_{i=1}^{k}{\sum\:}_{j=1}^{k}{w}_{ij}{r}_{i}{c}_{j}$$

(36)

here, $\:n$ describes the number of observers, $\:k$ describes the number of classes, $\:N$ specifies the number of observations, $\:{r}_{i}$ signifies the row sums, $\:{c}_{j}$ determines the column sums, and $\:{w}_{ij}$ as wight is achieved as follows:

$$\:{w}_{ij}=1-\frac{\left|i-j\right|}{k-1}$$

(37)

Specificity evaluates the model’s ability to accurately forecast negative samples out of the total number of actual negative samples, demonstrating its capacity to prevent false positives, that is:

$$\:Specificity=\frac{{T}_{N}}{{T}_{N}+{F}_{P}}$$

(38)

Finally, Area Under the ROC Curve (AUC) assesses the overall effectiveness of the model by displaying the true positive proportion versus the false positive rate across each of potential thresholds.

To assess the resilience and applicability of the models, three distinct cross-validation methods have been employed: 2-fold, 3-fold, and 5-fold. The results of the efficacy evaluation and comparison of the five models, using eight metrics and 2-fold validation, are shown in Table 4.

Based on the data offered in Table 4, it can be seen that the ZFNet/ELM/ESAO-based model exceeds the additional approaches in terms of most metrics. It attains the highest values for precision, accuracy, recall, F-beta score, Kappa score, and specificity. This indicates that the suggested model possesses a superior capability to accurately identify foot fractures with great precision and accuracy, while minimizing the occurrence of false negatives and false positives.

Moreover, when compared to other cutting-edge methods like DT/KNN, LDA, FRCNN, TL-ECNN, and DCNN/LSTM, the ZFNet/ELM/ESAO-based model consistently exhibits superior performance across the majority of the assessed metrics. This implies that the proposed hybrid approach effectively utilizes deep learning techniques, extreme learning machine, and the enhanced snow ablation optimizer to enhance the diagnosis of foot fractures. The results of the efficacy evaluation and comparison of the five models, using eight metrics and 3-fold validation, are shown in Table 5.

Table 5 Outcomes of the performance assessment and comparison conducted on the five models utilization of eight metrics and 3-fold validation.

Table 5 reveals that the ZFNet/ELM/ESAO-based model exhibits superior performance compared to the alternative approaches across various metrics. It consistently achieves the highest values for precision, accuracy, recall, F-beta score, Kappa score, specificity, F1 score, and AUC. These findings indicate that the proposed model consistently outperforms the other methods in accurately identifying foot fractures while maintaining a more accuracy and precision.

Additionally, the ZFNet/ELM/ESAO-based model surpasses additional high-tech methods namely DT/KNN, LDA, FRCNN, TL-ECNN, and DCNN/LSTM across the majority of the evaluated metrics. This suggests that the combination of deep learning techniques with extreme learning machine and the enhanced snow ablation optimizer effectively enhances the diagnostic capabilities for foot fractures.

The results of the efficacy evaluation and comparison of the five models, using eight metrics and 5-fold validation, are shown in Table 6.

Table 6 Outcomes of the performance assessment and comparison conducted on the five models utilization of eight metrics and 5-fold validation.

Table 6 presents the findings, which obviously designate that the ZFNet/ELM/ESAO-based model consistently performs better than additional methods in terms of various metrics. The model achieves the highest values for precision, accuracy, recall, F-beta score, Kappa score, specificity, F1 score, and AUC. This determines the superior behavior of the offered model in diagnosing foot fractures, even when subjected to a rigorous validation process using five-fold cross-validation.

Moreover, the ZFNet/ELM/ESAO-based model surpasses other state-of-the-art methods such as DT/KNN, LDA, FRCNN, TL-ECNN, and DCNN/LSTM across most of the evaluated metrics. These findings highlight the efficiency of the anticipated methodology in enhancing the accuracy and precision of foot fracture diagnosis, thereby minimizing the occurrence of false negatives and false positives.

In the following, a discussion about the tradeoff has been made between model capacity and computational efficiency based on the proposed ZFNet/ELM/ESAO model. Model capacity signifies a model’s capability to learn and represent intricate patterns within the data. Enhancing model capacity can improve performance; however, it also heightens the likelihood of overfitting and necessitates greater computational resources.

Conversely, computational efficiency pertains to a model’s ability to process data swiftly and effectively. While increasing computational efficiency can result in quicker training and inference times, it may also detract from overall model performance.

In our proposed model, ZFNet/ELM/ESAO, we have intentionally sought to strike a balance between model capacity and computational efficiency. A variety of techniques has been employed to achieve this equilibrium:

• 1. ELM: The ELM has been integrated as the output layer of our model, which possesses a lower model capacity relative to other neural network architectures. This approach mitigates the risk of overfitting and enhances computational efficiency.

• 2. ESAO: The ESAO has been implemented as the optimization algorithm, a metaheuristic method that can effectively navigate the search for optimal solutions within a high-dimensional space. This contributes to improved computational efficiency and minimizes the risk of overfitting.

• 3. ZFNet: The ZFNet is used as the feature extractor, which offers a moderate level of model capacity. This enables us to extract pertinent features from the data while maintaining computational efficiency.

The tradeoff between model capacity and computational efficiency has been have verified using 2, 3, and 5-fold cross-validation. The results are shown in Table 7.

Table 7 Verification with cross-validation.

The results indicated that the proposed ZFNet/ELM/ESAO model provides an effective balance between model capacity and computational efficiency. It possesses a moderate capacity, enabling it to learn and represent intricate patterns within the data while maintaining computational efficiency. Furthermore, the results suggest that enhancing model capacity can improve performance; though, this also heightens the risk of overfitting and necessitates greater computational resources.

For instance, the ZFNet/ELM model exhibits a higher capacity than our proposed model, yet it demonstrates lower accuracy and demands more computational power. Conversely, reducing model capacity may result in quicker training and inference times, but it could also detract from overall model performance. For example, the ESAO model has a lower capacity compared to our proposed model, which corresponds to its diminished accuracy.

Discussions

The identification of foot fractures presents significant challenges due to several factors. These include the diverse nature of fracture patterns, which may be linear, comminuted, or spiral, complicating accurate identification. Additionally, the resemblance between normal and fractured bones can hinder differentiation, while the scarcity of training data specific to foot fractures poses difficulties in developing a reliable model.

To enhance the system’s accuracy, a range of features from the dataset were extracted. These features encompassed texture characteristics, such as Gabor filters, Local Binary Patterns (LBP), and Histogram of Oriented Gradients (HOG), aimed at capturing the patterns and textures of the bones. Furthermore, shape features like moments, Fourier descriptors, and shape context were included to represent the shape and structure of the bones. Intensity features, including mean, standard deviation, and entropy, were also used to analyze the intensity patterns of the bones, along with fractal features such as fractal dimension and lacunarity to reflect the complexity and self-similarity inherent in the bone structures.

To enhance accuracy further, several strategies can be implemented. These include data augmentation through transformations such as rotation, scaling, and flipping, which serve to increase both the size and diversity of the dataset. Additionally, transfer learning can be employed by using pre-trained models and fine-tuning them on our specific dataset, thereby capitalizing on the knowledge acquired from other datasets. Ensemble methods, including bagging and boosting, can be utilized to amalgamate the predictions of multiple models, thereby enhancing overall accuracy.

Furthermore, feature engineering can be conducted to create new features that effectively capture the underlying patterns and structures of the bones, potentially through the application of wavelet or curvelet transforms. Active learning can also be integrated by selecting the most informative samples for annotation, which will contribute to improving model accuracy.

Looking ahead, we intend to investigate the application of deep learning models, such as convolutional neural networks (CNNs) and recurrent neural networks (RNNs), to further refine system accuracy. We will also explore multimodal fusion techniques to integrate features from various modalities, including X-ray, CT, and MRI scans. Moreover, we aim to implement explainability techniques to shed light on the model’s decision-making process, thereby enhancing its interpretability. This comprehensive approach will enable us to improve the accuracy of the system in identifying foot fractures and provide a robust and reliable tool for clinicians and researchers.

Conclusions

A foot fracture refers to the act of breaking or shattering one or more bones within the leg. This can occur due to various factors such as a forceful impact on the foot, falling from a significant height, excessive pressure exerted on the foot, improper usage of the foot (commonly seen in club sports), wearing inappropriate footwear, structural abnormalities in the bones, or underlying conditions like osteoporosis (a condition characterized by reduced bone density) or bone cancer. These fractures typically occur in the leg region. Following such an incident, individuals often experience intense pain in the affected area, swelling, redness, bruising, limited mobility, significant deformity in the leg, and a sensation of either heat or coldness in the fractured region. The root cause of foot pain in these cases is the misalignment or displacement of the bones. The accurate and timely judgement of these fractures is crucial for effective recovery and treatment. In this research paper, a novel hybrid methodology was proposed for diagnosing foot fractures by combining deep learning and metaheuristic techniques. The proposed approach included of three primary steps: preprocessing, feature extraction, and classification. Throughout the preprocessing step, some techniques were employed to enhance the quality of input images. This ensures better accuracy in subsequent stages. In the feature extraction step, a pre-trained deep convolutional neural network (ZFNet) was utilized to extract high-level properties from the images. This enables us to capture important features and patterns related to foot fractures. For the classification step, an extreme learning machine (ELM) was employed to categorize the images as either normal or fractured. To optimize the ELM, a new metaheuristic algorithm called enhanced snow ablation optimizer (ESAO) was introduced, which mimics the natural process of snow ablation. This algorithm enhances the performance of the ELM in accurately classifying foot fractures. To evaluate the efficiency of the offered method, experiments were conducted utilizing a standard benchmark dataset from the Institutional Review Board (IRB). The results were compared with those obtained from state-of-the-art methods, including Decision Tree / K-Nearest Neighbour (DT/KNN), Linear discriminant analysis (LDA), Inception-ResNet Faster R-CNN architecture (FRCNN), Transfer learning‑based ensemble convolutional neural network (TL-ECNN), and combined model containing a convolutional neural network and long short-term memory (DCNN/LSTM). Findings demonstrated that the proposed method achieves high levels in different terms. In the future work, our objective will be to enhance our approach by integrating more sophisticated models in deep learning and metaheuristics. These techniques include attention mechanisms, adversarial learning, multi-objective optimization, and swarm intelligence. Subsequently, we will aspire to expand the scope of our approach to encompass other types of fractures and medical images, such as ankle, wrist, spine, and chest.