Research on geological hazard characteristics and susceptibility of the Duku Highway based on SBAS-InSAR and improved spatiotemporal clustering

Abstract

The high-altitude Duku Highway is characterized by complex terrain changes and frequent geological hazards, which severely impact the lives of local residents and the sustainable development of the regional economy. The lack of understanding of terrain deformation, coupled with scarce foundational observation data, makes it challenging to apply mainstream susceptibility assessment methods such as slope modeling and causality analysis. Consequently, this study utilizes Sentinel-1 A data and employs the SBAS-InSAR technique to extract and analyze the deformation characteristics of 184 hazard areas along the Duku Highway over nearly three years. Furthermore, the Correlation Clustering Evaluation Model is proposed, attributing hazard properties to unsupervised spatial clustering results, thus enabling the study of hazard susceptibility in data-scarce regions without prior knowledge. The results indicate that the SBAS-InSAR coherence is 0.64, with a validation accuracy of 85%. The high, relatively-high, and moderate susceptibility areas account for 24.7%, 17.1%, and 32.6% of the total area, respectively. The rapid uplift of terrain due to plate compression is a major factor leading to frequent hazards in high and relatively-high susceptibility areas. These regions may spontaneously experience cyclic hazards (minimum of 2 months) without extreme external factors. The research findings offer new insights into regional hazards and provide a basis for the sustainable management of highways.

Introduction

With the rapid development of society, technology, and the economy, highway construction has gradually shifted from plain regions to mountainous areas with complex geological environments¹. Due to continental plate movements, mountainous terrain has undergone small-scale changes. Combined with local climate, slope, and surface cover, even with protective measures for artificial slopes during construction, mountain highways also face significant geological risks, threatening people’s personal safety and property², making the evaluation of hazard susceptibility essential.

Currently, the research methods for the susceptibility of highway hazards can be broadly categorized into three main types: (1) Empirical methods involve statistically analyzing indicators such as the frequency and scale of hazard occurrences to determine susceptibility^3,4. (2) Physical modeling methods include finite element methods and limit equilibrium methods. The primary approach is to construct three-dimensional models of highway slopes and determine the stability of these slopes in three-dimensional space through the calculation of indicators under different geological conditions^5,6. (3) Causal analysis methods can be mainly divided into machine learning methods and evaluation system methods. The primary idea of machine learning is to use the factors that affect the stability of slopes as input variables to construct a high-dimensional nonlinear mapping model between slope safety coefficients and influencing factors with different methods, and predict the stability of remaining slope^7,8. The evaluation system method determines the susceptibility by performing weight analysis on each influencing factor and judging the degree of influence^9,10,11. All of these methods have been widely applied in highway hazard research and have proven their accuracy. However, due to the different principles of each method, there are certain limitations in research on different regions. Empirical methods cannot determine the exact location of the hazard mountain sources, and the spatial-temporal precision of their analytical results is often low¹². Physical modeling methods require the collection of a large amount of slope terrain and geological data, and research in mountainous areas with diverse geological conditions and fast terrain deformation rates can be challenging^13,14. Causal analysis method is currently the most mainstream research method, which requires a large amount of basic observational data and has high requirements for the spatiotemporal scale, quantity, and accuracy of the data. It is difficult to study and analyze regions with complex causes, scarce observational data, and variable geological conditions^15,16. In particular, this method requires a certain understanding of the hazard occurrence mechanism in the region, and prior knowledge of the hazard causes is needed to train samples or score the contribution rate of factors, which is not available for the scarce foundational observation data area. The key scientific problem this paper focuses on is how to achieve high-precision, large-scale susceptibility assessments for geological hazards in mountainous areas with complex terrain and limited observational data.

The Duku Highway, the southern section of National Highway G217, connects the northern and southern parts of Xinjiang, China¹⁷. It is one of the most famous scenic highways in China¹⁸and also one of the highways most frequently affected by geological hazards, experiencing over 400 geological hazards annually. Due to mountain barriers and undulating terrain, various local mountain climate patterns are formed along the highway. Field verification shows that the characteristics of the winding mountain roads, combined with the region’s complex and variable climate, soil, lithology, land cover, and topographic distribution, make most remote sensing derived products inaccurate in this area. Additionally, the poor construction of ground observation networks for meteorological, hydrological, and geomorphological monitoring makes this region a typical data-scarce area. These characteristics make it difficult for mainstream hazard causation analysis methods, including machine learning and evaluation systems¹⁶, to ensure analytical accuracy. The frequent geological hazards and changing terrain also significantly increase the difficulty of physical modelling for slope stability¹⁴. As a result, there is currently almost no research on the geological hazards along this highway, including hazard susceptibility. The region especially lacks understanding of spontaneous terrain deformation, which is a characteristic manifestation and key inducement of regional hazards. Many studies believe that terrain deformation exhibits specific trends before and after geological hazards, which is of great significance for hazard understanding and prevention^19,20,21.

The characteristics of terrain deformation trends are a direct reflection of regional hazard occurrences and a specific manifestation of hazard formation mechanisms. High-precision terrain deformation quantification methods have consistently been a research hotspot worldwide. Developed in the 1990s, Differential Interferometric Synthetic Aperture Radar (D-InSAR) uses Synthetic Aperture Radar (SAR) to obtain interferometric fringes of large-scale terrain changes^22,23. This technology has been successfully applied to monitor surface micro-deformations such as ground subsidence, earthquakes, volcanic activities, and landslides²⁴. As D-InSAR technology has been increasingly applied to landslide monitoring, traditional methods can hardly meet the requirements for advanced research. The Small Baseline Subset Interferometric Synthetic Aperture Radar (SBAS-InSAR) technology, based on distributed target small baseline sets, improves upon traditional D-InSAR by enabling long-term time-series terrain deformation monitoring²⁵. SBAS technology involves more SAR images in deformation calculations, increases the distribution density of high-coherence points, overcomes decoherence issues from large spatio-temporal baselines, and improves image utilization²⁶. Compared to Permanent Scatterer Interferometric Synthetic Aperture Radar (PS-InSAR), which relies on permanent scatterers and is suitable for environments with numerous stable reflection points like urban areas, SBAS-InSAR (Small Baseline Subset Interferometric Synthetic Aperture Radar) is applicable to various environments and can conduct long-term monitoring of areas with complex terrain²⁷. It has been widely studied for monitoring temporal changes in hazard time series in areas with poor microwave image coherence²⁸, making it particularly suitable for the Duku Highway. Therefore, this paper uses SBAS-InSAR technology to obtain long-term time series data of terrain deformation in the study area, providing support for extracting regional terrain deformation characteristics and studying hazard susceptibility.

Classification is an effective approach for identifying terrain deformation characteristics in hazard-prone areas and is also the basis for hazard susceptibility grading. Currently, remote sensing classification methods can be divided into supervised classification, unsupervised classification, and deep learning classification. Mainstream supervised classification methods include Support Vector Machines, Random Forests, Maximum Likelihood Classification, and Neural Networks. These methods achieve high classification accuracy and can address complex nonlinear classification problems²⁹. However, they require a large number of training samples, and the quality and quantity of these samples are critical²⁹. Unsupervised classification methods, such as k-means clustering and hierarchical clustering, are highly adaptable but have high computational complexity. These methods generally require prior knowledge of the number of classes to be classified³⁰. Deep learning classification methods, including Convolutional Neural Networks and Generative Adversarial Networks, are suitable for handling high-dimensional and complex remote sensing data³¹. Similar to supervised classification, these methods also require a large amount of labeled data for training, have high computational resource demands, and require long training times³². Due to the lack of prior knowledge about the terrain deformation characteristics of regional hazard events, supervised classification cannot be used to classify the deformation trends and summarize their characteristics^33,34. Spatial hierarchical clustering of time series is an unsupervised classification method that aims to group unlabeled ordered arrays with spatial attributes based on an effective measure of similarity in time series trends³⁵. This method can select the optimal number of clusters by evaluating differences and similarities in trends within and between data groups³⁶, providing the best description of unknown data. Therefore, this method can directly and efficiently extract trend characteristics of terrain deformation that lead to hazards in different regions. By statistically analyzing the frequency of hazards in each hazard characteristic curve, this paper can directly and effectively calculate the susceptibility corresponding to each hazard characteristic curve, thus obtaining the susceptibility grading of known hazard areas.

However, for the susceptibility grading of unrecorded hazard events or non-hazard areas across the entire region, a single spatiotemporal clustering classification method is challenging. This difficulty arises because a large number of non-hazard pixels act as noise, increasing the computational load³⁷. Determining the optimal number of spatial clusters solely based on differences between arrays and similarities within arrays often fails to reflect true hazard characteristics, as described earlier, potentially leading to errors in susceptibility grading. To address this issue, this paper proposes the Correlation Clustering Evaluation Model (CCEM). This method evaluates the correlation between large-area spatial clustering results and hazard event area clustering results to determine the optimal number and results of spatial clusters that best match hazard characteristics, thus enabling large-area hazard susceptibility studies.

In summary, this study addresses the scientific question of how to assess hazard susceptibility in areas with complex terrain and limited data. It aims to understand the geological hazard characteristics of the Duku Highway, explore the potential mechanisms of geological hazard formation on the Duku Highway, and serve the practical problem of sustainable management of geological hazards on the Duku Highway. The study is divided into three parts: (1) Verification of SBAS-InSAR output results based on coherence and field measurements. (2) Using spatial hierarchical clustering to classify the terrain deformation time series of 184 hazard areas, analysing the spatial and temporal distribution characteristics (trends, periodicity, change rates) of each category of terrain deformation. (3) Proposing the CCEM to achieve hazard susceptibility studies of mountainous roads with complex terrain and scarce data, exploring potential mechanisms of regional hazard formation. This study is the first exploration of hazard research on the Duku Highway, employing the CCEM model to classify terrain deformation trends, which are direct reflections and key inducements of hazards. This approach effectively addresses the challenges faced by traditional methods in evaluating susceptibility in areas with complex terrain and sparse observational data. It provides a theoretical foundation for regional hazard prevention and control efforts and future research, offering valuable insights for studies in other areas with similar characteristics.

Materials and methods

Historical background, geographical location, hazard events, and climate and land cover conditions of the Duku Highway

Overview of the Duku Highway, construction background, and geographical environment

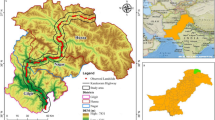
The Tianshan Mountain Range is one of the seven largest mountain ranges in the world. It spans four countries, with two-thirds of it located in the central part of Xinjiang, China. The range is the boundary between the north and south regions of Xinjiang. The Duku Highway, which runs north-south, was built in 1983 and is an important road connecting the northern and southern parts of Xinjiang (Fig. 1). The entire highway is 562.79 km long (a third-class highway) and shortens the distance between the northern and southern parts of Xinjiang by almost 600 km. The Duku Highway has a unique terrain with many sharp curves and steep slopes. More than 280 km of the road are at an altitude of over 2000 m, and a third of the road runs along cliffs and precipices with one-fifth above the snowline. The highway crosses four main rivers in Tianshan and connects five main roads while passing through four ice-covered slopes with perpetual snow. The difficulty of its construction is regarded as the highest in history, with 168 builders sacrificing their lives and thousands injured during its construction in the 70s and 80s. Currently, the Duku Highway has become one of the most famous tourist attractions in China due to its unique climate, scenery, and terrain.

Fig. 1

Research area geographic location, water system, road network, elevation, vegetation normalization index, slope, geological map.

Overview of geological gazards on the Duku Highway

Affected by regional adverse geological effects and the characteristics of special rock and soil, geological hazards occur frequently in the region. Adverse geological hazards include collapses, falling rocks, debris flows, wind-blown snow, landslides, roadbed water damage, and thermal thawing collapses of alpine frozen soil, among which collapses, falling rocks, landslides, and debris flows are the most frequent. According to statistics from various highway management bureaus in Xinjiang, the Duku Highway has experienced a total of 4256 geological hazards in the past decade. Among them, from July 2018 to October 2021, a total of 299 locations experienced geological hazards such as falling rocks, collapses, and debris flows during the 15-month period when the road was open to traffic. The highway management department monitored 192 hazard locations, with 184 concentrated in the northern section of the Duku Highway, most of which were repetitive occurrences. Within ten years, a total of 3891 occurrences were recorded, with the most repetitions at one location reaching 74 times. Especially after the 150-kilometer mark, the density of hazards is high, posing significant risks. Another 107 occurrences were observed by staff during highway inspections, so only observation locations were recorded without noting the time of occurrence. Based on this, this study focuses on the northern section of the Duku Highway (0–210 km region) as the main research object. At the same time, to delineate the susceptibility range of highway hazards, a 5 km buffer zone is established along the highway to define the research area.

Climate and land cover conditions of the Duku Highway

The climate of the Duku Highway mainly belongs to the continental monsoon climate zone. Influenced by the Siberian cold air, there is a large temperature difference between seasons, with windy springs, rainy summers, dry autumns, and snowy winters³⁸. The annual average temperature is 9.6℃, with an average temperature of −15℃ in January and an extreme low temperature of −35℃. The average temperature in July is 18℃, and the extreme high temperature is 32℃. The area is semi-arid, except for summer when the precipitation is more, and the amount of precipitation is generally low in other seasons. The majority of precipitation is in the form of torrential rain or shower, and almost every year the areas along the road experiences heavy rain, with more than 50% occurring from June to August³⁹. The annual average precipitation is 641.5 mm, with more than 50% occurring in July and August, while the precipitation from December to February of the following year is less, accounting for only about 3% of the annual total precipitation. The annual average evaporation is 1579 mm, which is 2.5 times the precipitation. Due to the influence of altitude and climate, the land cover within the 5 km buffer zone along the highway is primarily alpine grassland, accounting for approximately 84.2% of the total area. The overall vegetation coverage index (NDVI) is relatively high, with the average NDVI of the entire region being 0.53, and 0.74 in the southern part, which has a certain impact on the coherence of the imagery. The second largest land cover type is bare land, mainly distributed in the central part of the study area, accounting for 13% of the total area. Within the bare land, about 1.2% of the area is permanently covered by snow and ice, corresponding to a lower NDVI index (ranging from − 0.92 to 0.3).

Data availability

The data required for this study mainly include measured hazard data and remote sensing data. The hazard data are actual measurements from the county highway management bureaus in Xinjiang. The copyright of this data is owned by the local highway management department and has not been used by any research institution to date. The data comprises two main datasets: (1) The 2021 Highway Hazard Information Database, which includes the occurrence times of 113 hazards on the Duku Highway in 2021, the start and end coordinates of these hazards, the types of hazards (including 11 landslides and 102 rockfalls), and the scale of the hazards. (2) The 2011–2021 Decadal Key Highway Hazard Area Statistics Database, which includes the geographic coordinates of the start and end points of 184 highway segments with frequent hazard occurrences and the number of repeated hazard occurrences over the ten-year period. According to the requirements of this study, the 113 data points with recorded times are used for the verification of SBAS-InSAR output results and the clustering of hazard deformation characteristic curves. The hazard data from 184 locations are used for the extraction of hazard deformation characteristics.

The selection of remote sensing data is crucial for hazard monitoring. Considering factors such as the characteristics of geological hazards, temporal coherence, satellite revisit cycle, sensitivity of deformation detection, image resolution, and data continuity⁴⁰, this study chooses the European Space Agency (ESA) Sentinel-1 A data. Sentinel-1 A is selected for its sensitivity in long-term deformation monitoring and detection, strict orbit control, high-frequency revisit cycle, high-quality imaging, and provision of POD precise orbit data⁴¹. The basic information of Sentinel-1 A data is shown in Table 1.

Table 1 The basic information of the Sentinel-1 data used in this study.

At the same time, during the SBAS-InSAR processing, we utilized the Precise Orbit Data (POD) corresponding to Sentinel-1, ERA-Interim atmospheric parameter data, and SRTM 30 m DEM data to correct for sensor orbit, atmospheric delay, and topographic phase, respectively. These datasets are extensively used in mainstream InSAR processing research to enhance the coherence accuracy of consecutive image pairs in complex mountainous terrains⁴² However, Sentinel-1 data also have limitations, such as speckle noise, seasonal vegetation changes, and seasonal rainfall and drought. These factors can affect image quality, radar signal return intensity, and radar reflectivity, thereby impacting subsequent analysis results.

Research methods

The research methodology of this paper is divided into three parts. The first part employs the SBAS-InSAR technique for processing SAR images, ultimately producing terrain deformation measurements for the entire study area over three years. The second part utilizes hierarchical clustering to perform time-series clustering on the terrain deformation measurements of hazard areas obtained in the first part, extracting the terrain deformation characteristics of various hazards. The third part conducts spatial-temporal clustering for the entire area within a 5-kilometer buffer zone of the highway, using the CCEM method proposed in this paper. This paper completes the assessment of regional hazard susceptibility and analyzes the mechanisms of regional hazard occurrence. Figure 2 presents the detailed technical route of this study.

Fig. 2

Research technical roadmap (rectangle represents research intermediate processes and methods, parallelogram represents input data and output results, red font represents main research methods, bold font represents main research results).

The following sections will only introduce the methods related to the output of key results, including the evaluation method for SBAS-InSAR results, the hierarchical clustering method, and the hazard susceptibility assessment method based on correlation clustering.

Construction and result validation of SBAS-InSAR

(1) Construction of SBAS-InSAR

Small baseline set (SBAS) technology is an extension of the PSI technique proposed by Ferreiti⁴⁰. This technique adopts a multi-master image interferogram pair mode, which maximizes the number of interferograms involved in deformation calculation within the same monitoring period compared to the single-master image mode of PSI. At the same time, unlike PSI, which directly models the original interferograms without unwrapping, SBAS models the differenced interferograms after unwrapping and solves them through the Singular Value Decomposition (SVD) method⁴¹. SBAS suppresses the spatial decorrelation effect by simply and efficiently combining all available small baseline interferogram pairs. By combining isolated subsets, it maximizes the utilization of each acquired image and improves the temporal sampling rate of the observation data. It can provide more continuous spatial deformation results and more reliable results for research⁴⁰. Since SBAS-InSAR technology has been widely used, the SBAS-InSAR calculation process has been shown in the technical roadmap, so this paper will not elaborate on the calculation process of SBAS technology.

This study employs ENVI version 5.6.3 for SBAS-InSAR processing, except for the results explicitly indicating direction, all calculated results in this paper are in the line-of-sight (LOS) direction. The primary processing steps include setting parameters such as time baseline threshold, spatial baseline threshold, coherence threshold, and the selection of stable scatterers. When setting the spatiotemporal and coherence threshold parameters, it is essential to consider the complex terrain of high-altitude mountainous areas and the objectives of long-term deformation observation. For long-term observations, the time baseline is generally set within 60–180 days^43,44, and the spatial baseline is maintained within 50–100 m^45,46.

To capture the long-term trends of surface deformation, this study sets the temporal and spatial baselines to 180 days and 100 m, respectively, to generate more coherent pairs. Subsequently, pairs with poor coherence are manually removed to achieve higher accuracy. For the selection of the coherence threshold, most studies choose a threshold between 0.3 and 0.5, with high-precision requirements generally considered to be between 0.4 and 0.6 [47,48,49⁹. Given the objective of this study is long-term time series monitoring, it is necessary to statistically analyze the change trends of all pixels within the study area. Although a lower coherence threshold might increase noise and cause decorrelation, impacting deformation monitoring results, the study aims to ensure spatial continuity of the pixels and avoid spatial gaps. Therefore, the coherence threshold is set at the lower limit of the high-precision requirement, which is 0.4. For the selection of stable scatterers, this process is fundamental to InSAR data processing and is crucial for the accuracy of InSAR results⁴⁹. The version of ENVI used in this study provides an automatic module for selecting stable scatterers in SBAS-InSAR. The principle behind this module is to conduct a time series analysis of the coherence of multi-temporal SAR images, identifying pixels that maintain high coherence at all or most time points. These pixels are considered stable scatterers.

(2) Validation of SBAS-InSAR result

SBAS-InSAR technology is actually a process of measuring the phase difference between radar waves and converting them into deformation values. The phase difference indicates spatial geometric information, but the phase signal obtained from radar images not only contains actual measurement signal information but also a large amount of noise signal. Therefore, to make the phase difference meaningful, it is necessary to measure the correlation degree between the radar interferometric signals. The coherence coefficient is commonly used to evaluate the quality of the interferometry between two radar images. If the interferometry quality is good, it means that the deformation phase information obtained by InSAR technology calculation is complete and meaningful. Conversely, if the coherence is low and the quality of interferometry is poor, the integrity of the phase difference measurement is destroyed and there is no actual meaning in the phase information representing the deformation value⁵⁰. The formula for calculating the coherence coefficient is as follows⁵¹:

$$\:\gamma\:=\frac{{\sum\:}_{n=1}^{N}{\sum\:}_{m=1}^{M}{u}_{1}(n,m){{u}_{2}}^{*}(n,m)}{\sqrt{{\sum\:}_{n=1}^{N}{\sum\:}_{m=1}^{M}{\left|{u}_{1}(n,m)\right|}^{2}{\sum\:}_{n=1}^{N}{\sum\:}_{m=1}^{M}{\left|{u}_{2}(n,m)\right|}^{2}}}$$

(1)

In the equation, $\:*$ represents the plural conjugate, that is, taking the opposite value of the imaginary part of the plural value. $\:{u}_{1}(n,m)$ and $\:{u}_{2}(n,m)$ represent the complex values at the image coordinate row and column (n, m) within the main and secondary image data blocks, respectively. $\:{\left|{u}_{1}(n,m)\right|}^{2}$ represents the second-order norm of the data. ($\:M$) and ($\:N$) represent the size of the data block used to calculate coherence, i.e., calculating the correlation coefficient with a window size of ($\:N\times\:M$) centered on any pixel. The obtained correlation coefficient γ at each point serves as an indicator to evaluate the interference phase quality of the pixel⁵². From the coherence coefficient calculation model, it can be understood that the coherence coefficient is a physical quantity related to the phase information. The denominator of the equation actually serves to normalize, i.e., the range of γ is [0, 1]. When $\:{u}_{1}(n,m)={u}_{2}(n,m)$, γ = 1, indicating that two pixels are completely correlated, and the obtained deformation phase information is complete and meaningful. If γ = 1, then the two pixels are completely incoherent, and the phase information loses practical significance. This paper evaluates the results of SBAS-InSAR using coherence.

For field validation, similar to this study, most research areas lack specific measured deformation data to accurately validate the precision of SBAS-InSAR. Therefore, the mainstream approach for validating SBAS-InSAR results is generally through the ability of SBAS-InSAR to accurately identify the occurrence of hazards⁵³. As mentioned in Sect. 2.2, most hazards along the Duku Highway are collapses and landslides. These types of hazards often exhibit movement away from the Line-Of-Sight (LOS) in previous InSAR hazard monitoring studies⁵⁴, numerically expressed as negative values. This can serve as an important basis for determining the occurrence of hazards. The specific method in this study is to reclassify 113 hazardous areas based on the occurrence time, according to the satellite revisit interval. Hazardous areas with the same revisit period are grouped together. The average deformation value of the terrain in the hazard occurrence area between two scenes is calculated. Generally, the average deformation value should be less than 0. That is, when the difference is less than 0, it is considered that a geological hazard may have occurred, which is a qualitative understanding of hazard occurrence.

In addition, one of the main characteristics of geological hazards is the abrupt change in terrain that differs from the normal terrain change trend within a short period⁵⁵. This characteristic can serve as an important basis for identifying hazards. Therefore, to further improve the credibility of result validation, this study extracts the daily terrain change rate within the satellite revisit period (12 days) during the hazard occurrence in the hazard area. By statistically analyzing the difference between this value and the average daily change rate of the entire region for the year (hazard occurrence is characterized by the deformation rate in the hazard area being higher than the average change rate of the entire region), it is determined whether geological hazards have occurred in these areas. This is a quantitative understanding of hazard occurrence. By combining both qualitative and quantitative understandings of hazards, this study aims to achieve the purpose of validating the accuracy of SBAS-InSAR.

Principles of hierarchical clustering for Time Series and methods for evaluating its results

The Hierarchical Clustering, as a classic clustering algorithm⁵⁶, automatically divides samples based on the set similarity linkage method. Hierarchical clustering methods can be divided into two types. Divisive Hierarchical Clustering and Agglomerative Hierarchical Clustering. Generally, Divisive Hierarchical Clustering has poor quality and a narrow applicability range, so the Agglomerative Hierarchical Clustering is often the most common Hierarchical Clustering method⁵⁷. Agglomerative hierarchical clustering is a bottom-up approach with the following specific steps: Step 1): Initialization: Treat each data point as an independent cluster. If there are n data points, then initially there are n clusters. Step 2): Compute the Distance Matrix: Calculate the distance between all clusters to generate an n×n distance matrix. Step 3): Merge the Closest Clusters: Identify the two clusters that are closest to each other based on the distance metric and merge them into a new cluster. After merging, the number of clusters is reduced by one. Step 4): Update the Distance Matrix Recalculate the distances between the new cluster and the remaining clusters, and update the distance matrix. Step 5): Repeat Steps 3 and 4Continue the process of merging and updating the distance matrix until all data points are merged into a single cluster or the desired number of clusters is reached.

The core of hierarchical analysis is to calculate the similarity or distance between each pair of samples. Common similarity or distance measurement methods include Euclidean distance, Manhattan distance, cosine similarity, etc⁵⁸. For sample data of time series, the similarity of trend changes in sample data time series is an important indicator for classifying time series data. Pearson correlation is a measure of trendiness and is widely used⁵⁹. Generally, the greater the difference between groups and the higher the similarity within the groups, the better the clustering results are considered to be. Both inter-group differences and intra-group similarities in this paper are measured by the correlation coefficient. The calculation of the inter-group correlation coefficient is as follows:

First, for each pair of time series $\:{X}_{i}$ and $\:{X}_{j}$within the same cluster, calculate their Pearson correlation coefficient:

$$\:{r}_{ij}=\frac{{\sum\:}_{t=1}^{T}({X}_{i}-\stackrel{-}{{X}_{i}})({X}_{j}-\stackrel{-}{{X}_{j}})}{\sqrt{{\sum\:}_{t=1}^{T}{\left({X}_{i}\right(t)-\stackrel{-}{{X}_{i}})}^{2}}\sqrt{{\sum\:}_{t=1}^{T}{\left({X}_{j}\right(t)-\stackrel{-}{{X}_{j}})}^{2}}}$$

(2)

Where T is the length of the time series. Then, for each cluster, calculate the average correlation of all pairs of time series. Assuming the K-th cluster contains $\:{n}_{k}$​time series, the average correlation coefficient for that cluster is:

$$\:{R}_{k}=\frac{2}{{n}_{k}({n}_{k}-1)}\sum\:_{i=1}^{{n}_{k}-1}\sum\:_{j=i+1}^{{n}_{k}}{r}_{ij}$$

(3)

Finally, take the average of the average correlations of all clusters to obtain the overall intra-cluster correlation (where K is the total number of clusters)::

$$\:{R}_{\text{I}\text{n}\text{t}\text{e}\text{r}-\text{g}\text{r}\text{o}\text{u}\text{p}}=\frac{\sum\:_{k=1}^{K}{R}_{k}}{K}$$

(4)

The inter-cluster correlation coefficient is calculated as follows:

First, for each pair of time series $\:{X}_{i}$ and $\:{X}_{j}$ from different clusters, compute their Pearson correlation coefficient:

$$\:{r}_{ij}=\frac{{\sum\:}_{t=1}^{T}({X}_{i}-\stackrel{-}{{X}_{i}})({X}_{j}-\stackrel{-}{{X}_{j}})}{\sqrt{{\sum\:}_{t=1}^{T}{\left({X}_{i}\right(t)-\stackrel{-}{{X}_{i}})}^{2}}\sqrt{{\sum\:}_{t=1}^{T}{\left({X}_{j}\right(t)-\stackrel{-}{{X}_{j}})}^{2}}}$$

(5)

For each pair of clusters $\:{n}_{a}$ and $\:{n}_{b}$, calculate the average correlation of all time series between them. Assuming cluster $\:{n}_{a}$ contains i time series and cluster $\:{n}_{b}$ contains b time series, the average correlation between them is:

$$\:{R}_{ab}=\frac{1}{{n}_{a}{n}_{b}}\sum\:_{i=1}^{{n}_{a}}\sum\:_{j=1}^{{n}_{b}}{r}_{ij}$$

(6)

The overall inter-cluster correlation is obtained by averaging the average correlation coefficients of all pairs of clusters. If there are K clusters in total, the overall inter-cluster correlation is:

$$\:{R}_{\text{I}\text{n}\text{t}\text{r}\text{a}-\text{g}\text{r}\text{o}\text{u}\text{p}}=\frac{2}{K(K-1)}\sum\:_{a=1}^{K-1}\sum\:_{b=a+1}^{K}{R}_{ab}$$

(7)

Method of delimiting the mountain slope hazard areas

The delimitation of hazard areas is the basis for extracting the terrain deformation characteristic curves of various types of hazards. Since the coordinates of the hazard points recorded by the transportation management department are on the road, it is impossible to determine which part of the mountain slope has undergone deformation causing the occurrence of hazards. Therefore, it is necessary to divide the areas where hazards may occur in mountainous areas. In this paper, the specific method is based on high-resolution multispectral images, using the road 5 m outside the coordinates of the starting and ending points of the hazard as the bottom boundary of the hazard occurrence. A line segment upward from the bottom boundary point is used as the left and right boundary of the hazard occurrence. The ridge line is used as the top boundary to delimit the potential mountainous terrain deformation areas that may cause a single hazard event. The delimitation method is shown in the Fig. 3: this method can ensure that the areas of the mountain slope in the hazard area causing the hazard are included.

Fig. 3

Diagram of the method for determining hazard areas to verify the output results of SBAS (The basemap was captured by the drone of the author’s institution and has only undergone graphical and textual editing.).

Using this delimitation method, the scope of 184 regions with frequent geological hazard was determined, and the SBAS-InSAR output results were extracted and masked based on this scope. The hazard characteristics of the masked units in the 184 geological hazard areas were calculated. The specific method is detailed in Formula 8.

Correlation clustering evaluation model (CCEM) for the susceptibility of geological hazards

Clustering is an unsupervised classification method. Spatial clustering results lack hazard attributes, cannot indicate hazard characteristics, and cannot determine the specific number of spatial clusters. Therefore, it is necessary to use hazard clustering results to correct the spatial clustering results, thereby deriving the susceptibility of regional hazards. This new approach uses the clustering results of pre-determined samples with attributes to correct the overall environmental clustering. It aims to address the issues of determining the optimal number of clusters and the lack of attribute characteristics in environmental clustering methods. It can be divided into four steps:

(1) Extraction of feature functions of hazard area clustering and spatial clustering results

A feature function refers to a time series function that can characterize the trend of terrain deformation changes for a specific category. The calculation method is as follows:

$$\:{f}_{i}\left(x\right)=\frac{{f}_{1i}\left(x\right)+{f}_{2i}\left(x\right)+\dots\:+{f}_{ni}\left(x\right)}{n}$$

(8)

In the formula, $\:i$ represents the type of clustering, and $\:n$ represents the number of functions corresponding to class $\:i$ that contain the temporal variation of terrain deformation. $\:{f}_{i}\left(x\right)$ is the feature function of class $\:i$, and the value at a specific moment is the average value of all pixel values in the hazard area at $\:x$ moment, $\:x\:$represents the time axis. According to this formula, the feature function of each category in the hazard area can be obtained, serving as the basis for spatial clustering association. At the same time, this method is also the basic algorithm for extracting spatial clustering feature functions.

Temporal-spatial clustering involves categorizing the temporal trends of all pixels in the study area based on their similarity, with pixels as the basic unit. However, a large sample size can lead to significant differences between the clustering results and the hazard area. Within a hazard area, there may be multiple spatial clustering results. Therefore, the deformation characteristic function of spatial clustering in a hazard area should be the weighted average of the characteristic functions of various categories within the same area, expressed as:

$$\:{G}_{h}\left(x\right)=\frac{{\sum\:}_{1}^{j}{(f}_{jh}\left(x\right)\text{*}{k}_{jh})}{\sum\:{k}_{jh}}$$

(9)

In the formula, $\:h$ represents the number of the hazard area, and there are a total of 186 hazard areas in the study area. Therefore, the maximum value of $\:h$ is 186. $\:{G}_{h}\left(x\right)$ represents the terrain deformation characteristic function of spatial clustering results in the $\:h$ region. $\:j$ represents the spatial clustering types included in the $\:h$ region, and $\:{f}_{jh}\left(x\right)$ represents the terrain deformation characteristic function of spatial clustering category $\:j$ in the $\:h$ region. $\:{k}_{jh}$ represents the number of pixels in the $\:h$ region belonging to category $\:j$. Thus, the deformation curves of spatial clustering in all 186 hazard areas can be obtained through $\:{G}_{h}\left(x\right)$.

(2) Determination of the optimal number of spatial clusters

The spatial distribution of hazard susceptibility is based on spatial clustering. Therefore, determining the optimal number of spatial clusters that best match the hazard characteristics is a fundamental requirement in hazard susceptibility research. To accomplish this, this paper proposes the concept of association indicators to measure the degree of correlation between the hazard feature clustering results and the spatial clustering results. This will determine the optimal number of spatial clusters. To maintain consistency in research objectives and results, the method of calculating association indicators should be consistent with the method of calculating clustering metrics. Therefore, this paper selects the Pearson correlation coefficient as the association indicator between spatial clustering and hazard clustering. The closer the association indicator is to 1, the more the spatial clustering results possess the characteristics of the hazard. The correlation indicator for the $\:h$ region should be the correlation coefficient between the feature function of the hazard clustering in that region and the feature function of the spatial clustering. The correlation indicator between the $\:i$ category hazard clustering and the $\:j$ type spatial clustering should be the average of all hazard areas, calculated as follows:

$$\:{T}_{ij}=\frac{\sum\:COR({f}_{ih}\left(x\right),{G}_{jh}\left(x\right))}{h}$$

(10)

In the formula, $\:{T}_{ij}$ is defined as the correlation indicator between the $\:i$ type hazard clustering and the $\:h$ type spatial clustering. To determine the optimal number of spatial clusters, this paper establishes a correlation matrix between the spatial clustering results and the hazard clustering results. This calculates the correlation between the feature functions of each category of spatial clustering and each category of hazard clustering:

$$\:\:A=\left|\begin{array}{ccc}{T}_{11}&\:\cdots\:&\:{T}_{1i}\\\:\vdots&\:\ddots\:&\:\vdots\\\:{T}_{j1}&\:\cdots\:&\:{T}_{ij}\end{array}\right|$$

(11)

By calculating the average value $\:{T}_{avg}$ of the same spatial clustering T within the matrix, when $\:{T}_{avg}$ is maximized, the corresponding $\:j$ is the optimal number of spatial clusters that best match the hazard attributes.

(3) Association between spatial clusters and hazard clusters

After calculating the optimal clustering number, to imbue the spatial clustering results with hazard attributes, it is necessary to utilize the association between hazard clustering and the optimal spatial clustering results. Similarly, correlation is used as the measure:

$$\:B=\left|\begin{array}{ccc}COR({f}_{1i}\left(x\right),{f}_{1j}\left(x\right))&\:\cdots\:&\:COR({f}_{ii}\left(x\right),{f}_{1j}\left(x\right))\\\:\vdots&\:\ddots\:&\:\vdots\\\:COR({f}_{1i}\left(x\right),{f}_{jj}\left(x\right))&\:\cdots\:&\:COR({f}_{ii}\left(x\right),{f}_{jj}\left(x\right))\end{array}\right|$$

(12)

In the formula, $\:j$ and $\:i$ respectively represent the optimal number of spatial clusters and hazard clusters. Due to a larger sample size, the optimal number of spatial clusters is usually greater than the optimal number of hazard clusters. Therefore, for each $\:i$, there may be one or more $\:j$ with higher correlation. However, for each $\:j$, it should not have high correlation with multiple $\:i$. Hence, a correlation threshold needs to be established to prevent multiple hazard categories from corresponding to the same spatial clustering category, which would make it impossible to assign attributes to spatial clustering results based on hazard clustering results. If the correlation between $\:i$ and $\:j$ is greater than this threshold, it is considered that $\:i$ and $\:j$ can be associated, that is, $\:i=j$. Mechanically, the higher the threshold, the less likely the many-to-one situation occurs. Therefore, the establishment of this threshold needs to be sufficiently high to prevent many-to-one situations while maintaining highly correlated corresponding combinations.

(4) Rating of spatial hazard susceptibility

Spatial hazard susceptibility can be understood as the frequency of hazard occurrences⁶⁰. Therefore, this paper first grades the susceptibility of hazard areas based on the frequency of observed hazard occurrences. Then, through the spatial correlation described earlier, the spatial clustering results are made to have ratings of hazard susceptibility, thus achieving the rating of spatial hazard susceptibility.

Results

Verification of the coherence of SBAS-InSAR results and their accuracy in identifying geological hazards

The SBAS-InSAR output results form the basis of this study. To ensure spatial and temporal continuity, a minimum coherence threshold of 0.4 and a time baseline of 400 days were set to obtain the interferometric connection graph (Fig. 3 left). After manually removing low-coherence image pairs, 411 interferograms were obtained, with all vertical baselines between − 150 m and 150 m. The average coherence coefficient of the 411 interferograms is 0.64, primarily distributed between 0.55 and 0.65, followed by 0.65 to 0.7 and 0.5 to 0.55. Based on the method described in Sect. 2.3.3, this paper also used a mask to extract the coherence of 184 frequently occurring hazard areas. The average coherence coefficient of the 184 hazard areas is 0.68, slightly higher than the regional average (Fig. 4right). Due to regional vegetation coverage and heavy rainfall, high-coherence interferometric images are less common²⁶. To verify the accuracy of the results, the study also applies the average difference deformation quantity of two images during 113 hazard occurrence periods to verify the SBAS-InSAR output results.

Fig. 4

SBAS-InSAR interferometric connection graph (left), overall coherence coefficient of the study area and coherence coefficient of hazard areas (right).

The 113 hazard validation areas primarily cover the 70–100 km and 150–220 km sections of the highway. Most hazards (over 100) are concentrated in the 150–220 km section, characterized by dense occurrence points and varying occurrence times. Based on the relationship between occurrence time and image revisit cycle, the 113 hazards are divided into 13 time periods (hazards occurring within the same satellite revisit cycle are grouped together). Figure 5 shows the spatial distribution of all 113 hazards used for verification and the average difference in deformation quantity between two images in the hazard area.

Fig. 5

The differential values of terrain deformation in 113 hazard areas before and after the occurrence of hazards in 2021.

Statistically, the average difference in deformation quantity in the hazard area for 101 of the 113 hazard occurrence periods is negative, while 12 areas show positive values. Among the positive value areas, 11 correspond to hazards that occurred in the satellite revisit cycle from August 6, 2021, to August 18, 2021, with a hazard identification rate of 62% for this cycle. Overall, the recognition rate of SBAS-InSAR output results for a single hazard occurrence is 85%. Excluding lower periods, the recognition rate of SBAS-InSAR for hazard occurrence can reach 98%.

Fig. 6

Distribution statistics of the absolute terrain deformation rates for the 101 hazard areas within the corresponding satellite revisit periods, and a comparison with the absolute value of the overall average terrain deformation rate for the entire region.

Subsequently, the terrain deformation rates of these 101 hazard areas, which exhibit negative values, were statistically analyzed to determine whether they meet the criteria for hazard identification based on deformation rates, as illustrated in Fig. 6. In 2021, the overall average terrain deformation rate for the region was 0.0058 mm/day. Compared to this standard, the terrain deformation rates in all 101 hazard areas identified by SBAS-InSAR exceeded this threshold. Generally, at the time of hazard occurrence, the minimum, average, and maximum deformation rates in these areas were 0.014 mm/day, 0.29 mm/day, and 1.04 mm/day, respectively. Although this does not quantify the deformation rate thresholds for different hazards, it indicates that SBAS-InSAR detected terrain changes in these areas that were inconsistent with the overall deformation trend, aligning with the characteristics of terrain deformation in geological hazard areas. These results, combined with the study of coherence coefficients, indicate that the SBAS-InSAR output results are reliable.

Extraction of terrain deformation trends of Duku highway and characteristics of geological hazard areas

Based on the SBAS-InSAR output results, the cumulative deformation and overall deformation rate for each time period in the study area are calculated and shown in Fig. 7. The legend classification is based on the natural breakpoint method, using the maximum and minimum deformation values within each time period as boundaries. Additionally, to better illustrate the undulating changes in the terrain, the LOS data has been processed and displayed alongside the Vertical Direction (VD) data. It can be observed that the spatial distribution of the cumulative deformation and deformation rates for each year in both the LOS and the VD are completely consistent. However, the absolute values in the VD are greater than those in the LOS. Among them, 2018 to 2019 showed a decline in the central area (80–130 km), while the rest of the region showed an upward trend. From 2019 to 2020, there was a slight decline in the northern central region (10–130 km) and an upward trend in the southern region. From 2020 to 2021, there was a decline in all areas outside the 20–40 km, 60–90 km, and 205–220 km regions. During the validation period of the SBAS-InSAR results (May to September 2021), there was a decline along the northern region (10–50 km) and a significant decline along the southern (130–200 km) highway, while the rest of the region showed an upward trend. In terms of cumulative deformation, the annual changes in different areas vary, but there are commonalities. All areas exhibit a decrease between 90 km and 130 km, and an increase beyond 205 km.

Fig. 7

Spatial distribution of terrain cumulative variables and average change rates for each year from May 2018 to September 2021 on the Duku Highway.

In terms of terrain deformation rates, in the LOS, the terrain deformation rate of each pixel in the entire region ranges from − 13.8 mm/a to 48 mm/a, with the region rising at an average speed of 2.1 mm/a. Specifically, the region can be divided into six significant change areas based on highway locations at 15 km, 60 km, 90 km, 130 km, and 205 km: north of 15 km shows a slow upward trend with an average deformation rate of 0.78 mm/a; 15 to 60 km shows a slow downward trend with an average rate of −1.23 mm/a; 60 to 90 km shows a slow upward trend with an average rate of 1.86 mm/a; 90 to 130 km shows a significant decreasing trend with an average rate of −3.76 mm/a; 130 to 205 km shows alternating rising and falling regions with average rates of −3.85 mm/a and 6.82 mm/a respectively; and beyond 205 km shows a significant rising trend with an average rate of 23.39 mm/a. In the vertical direction, the terrain deformation rates of all pixels across the entire region range from − 18.4 mm/a to 67.6 mm/a, with an average uplift rate of 3.2 mm/a. The vertical terrain deformation rates for the corresponding six areas are 1.05 mm/a, −1.61 mm/a, 2.48 mm/a, −5.01 mm/a, −5.2 mm/a, and 9.23 mm/a, 32.0 mm/a. It is noteworthy that the terrain uplift and subsidence between 130 km and 205 km are quite complex and significant, with substantial uplift observed beyond 205 km. These two regions are also where hazards are most densely concentrated.

To identify the characteristics of hazard occurrence, this study extracted the deformation time series of 184 hazard areas based on SBAS-InSAR results and applied hierarchical clustering to identify terrain deformation characteristics. The maximum number of clusters was set to 16, and the average correlation within and between groups was calculated for different cluster numbers, as shown in the table below. Intra-group correlation increased from 2 to 10 clusters, while inter-group correlation decreased during this period. At 10 clusters, intra-group correlation is highest and inter-group correlation is lowest. After 10 clusters, these correlations begin to fluctuate. Therefore, 10 clusters is identified as the optimal number of clusters, indicating that the terrain deformation characteristics of hazard areas can be classified into 10 categories based on their changing trends (Table 2).

Table 2 Inter- and intra-group correlations for clusters 2 to 16 in hazards areas.

Based on the extraction results of the 10 categories of terrain deformation change trends, this study has extracted the feature values, trend, intra-group range and periodicity of terrain deformation in the hazard area, as shown in the Fig. 8.

Fig. 8

Three-year terrain deformation characteristic curves, trends, intra-group variation ranges and periodic analysis results based on wavelet analysis for the 10 clusters in the hazard area.

The overall change in terrain deformation shows volatility. Based on the trend of terrain changes, hazards can be classified into ascending-type (clusters: 4, 5, 6, 9, 10) and descending-type (clusters: 1, 2, 3, 7, 8). Ascending-type hazards have a general upward trend in terrain deformation, with average rising velocities from 1.19 mm/a to 12.5 mm/a. These hazards often experience sudden, significant drops during the rising process, implying hazard occurrences. Except for cluster 10, all clusters show periodicity at certain time scales: cluster 4 has a two-month period, cluster 5 has two- and six-month periods, cluster 6 has a two-month period, and cluster 9 has a one-year periodicity. Descending-type hazards exhibit a general downward trend in terrain deformation, with average declining velocities from 0.66 mm/a to 2.52 mm/a. Except for cluster 2, which has two- and six-month periodicity, these hazards exhibit a one-year cyclic change.

Table 3 Terrain change rates, numbers of hazards and susceptibility classifications for 10 types of hazards.

Table 3 shows the locations where hazards occurred frequently and the total number of hazards at the same locations over ten years. There are significant differences in hazard frequency across different categories. Cluster 9 has the highest frequency, with 93 geological hazards areas and 1886 hazards over ten years, accounting for 48.5% of all hazards. Cluster 8 is the second most frequent, with 32 hazards areas and 925 over ten years, making up 27.8% of all hazards. Although cluster 8 shows a significant decrease compared to cluster 9, it is still significantly higher than cluster 4, ranked third. Clusters 4, 1, 2, 5, and 7 have similar hazard occurrences, as do clusters 3, 6, and 10. is noteworthy that the number of hazard occurrences and the frequency of hazards recurring over a ten-year period are significantly positively correlated with the absolute value of the terrain deformation rate for the corresponding categories, with correlation coefficients of 0.90 and 0.88, respectively. These results indicate that the rate of terrain deformation is a critical factor in triggering hazard events.

Simultaneously, to determine the hazard susceptibility of the entire region, it is necessary to classify the hazard susceptibility of the areas already affected by hazards and then analyze the entire region using the CCEM method. The classification of hazard susceptibility in affected areas essentially involves further categorizing the clustering results of terrain change trends based on the frequency of hazard occurrences. It can be observed that the data to be classified in this study are characterized by a small sample size and a discrete numerical distribution. According to statistical literature⁶¹, for the classification of such data, it is necessary to analyze the distribution characteristics and perform subjective classification based on the classification objectives. It can be seen that Clusters 9 and 8 (with hazard frequencies of 1886 and 925, respectively) are outliers in the overall sample. To avoid the influence of these outliers on other data points and to ensure a more uniform distribution of the remaining data points for further analysis, these outliers need to be classified separately. Additionally, Clusters 1, 2, 4, 5, and 7 (with hazard frequencies of 218, 148, 158, 182, and 219, respectively, mean: 184) and Clusters 3, 6, and 10 (with hazard frequencies of 28, 85, and 46, respectively, mean: 53) are concentrated and exhibit low variability, thus each group is classified into a single category. Based on this principle, ten hazard clusters can be classified into five categories based on hazard occurrence frequency and susceptibility level: high-risk (more than 100 hazards annually), relatively high-risk (50–100 annually), moderate-risk (10–50 annually), relatively low-risk (less than 10 annually), and low-risk (few or no hazards annually). This classification forms the basis for susceptibility analysis.

Susceptibility and attribution analysis of geological hazards on the Duku Highway and recommendations for highway management

The previous sections evaluated the terrain deformation trends at hazard points and the risks in hazard areas. To determine the susceptibility of road hazards across the entire area, this section applies the method described in 2.3.3 to correct the spatial clustering results and produce a susceptibility map of road hazards. The first step is to determine the optimal cluster number in CCEM.

Fig. 9

Matrix of correlation indices ($\:{\varvec{T}}_{\varvec{x}\varvec{j}}$) between the 20 spatial clustering results and 10 hazard clustering results (left), and matrix of correlation between the optimal spatial clustering result and the 10 hazard clustering results (right).

According to formulas (3) and (4), the relationship between spatial clustering result and feature functions of hazard area clustering is shown in Fig. 9 (left). The maximum spatial cluster number is set to 20. The results indicate that when the classification is 16, $\:{T}_{avg}$ is the highest, identifying 16 as the optimal clustering number for hazard requirements (Fig. 10a). To attribute hazard characteristics to spatial clustering, a correlation matrix (Fig. 9 right) of 10-class and 16-class clustering results is drawn based on formula (5). The results show that a 0.9 correlation threshold is optimal. This threshold ensures no multiple hazard clusters correspond to spatial clustering results and maintains a high correlation coefficient, ensuring a strong link between hazard and spatial clustering. Based on this correlation matrix, the categories with the highest correlation in 16 classes are selected for each of the 10 classes to derive the spatial clustering results that best represent regional hazard changes, as shown in Fig. 8b. The correspondence between spatial clustering and the improved spatial classification results is shown in Table 4.

Table 4 Spatial clustering reclassification results and spatial hazard susceptibility grading based on CCEM.

Figure 10b shows that except for the two categories in the north and south, more terrain change categories are observed in the middle region (15–130 km), mostly in a strip-like pattern. The eighth and ninth types which are the highest frequency of hazards are widely distributed in the southern 130–220 km range, and the seventh type is mostly in the 100–130 km range, while the remaining types are concentrated in the 20–100 km range. Due to the lower correlation between the feature functions of the second, fourth, fifth, and eighth categories of the original 16 and the characteristics of the tenth type, they are considered very low risk. However, due to the intense geological activity in the study area, there is still some potential risk, so they are defined as low-risk areas. Base on above, the hazard susceptibility map (Fig. 10c and d) was plotted.

Fig. 10

Spatial clustering results of 3-year terrain deformation(a), reclassification of spatial clustering results based on CCEM(b), spatial distribution map of geological hazard susceptibility(c), and 3D version spatial distribution map of geological hazard susceptibility(d).

The susceptibility distribution map shows that hazard susceptibility is geographically similar to the terrain deformation rate. Boundaries can be set at 15 km, 90 km, 130 km, and 205 km: the area north of 15 km is low-risk; from 15 km to 90 km, mainly moderate-risk and relatively-low-risk areas; from 90 km to 130 km, moderate-risk; from 130 km to 205 km, relatively-high-risk and high-risk; from 205 km to 220 km, high-risk. Statistically, high-risk, relatively-high-risk, moderate-risk, relatively-low-risk, and low-risk areas account for 24.7%, 17.1%, 32.6%, 11.5%, and 14.1% of the total area, respectively.

Combining the results of Sect. 3.1 and 3.2, a strong connection is evident between hazard risk and terrain deformation variation in the study area. The spatial correlation coefficient between risk levels 1–5 (from low to high risk) and the absolute value of the terrain deformation rate is 0.74, indicating a positive correlation. High-risk, relatively-high-risk, and moderate-risk areas are primarily in regions with rapid terrain deformation and large fluctuations. High-risk areas show distinct terrain changes compared to other regions with similar land cover, climate, and slope, featuring a high-rise rate (9.57 mm/year). The denser the hazard points, the more frequent the hazards. Relatively high-risk areas, adjacent to high-risk areas, exhibit rapid terrain descent (descent rate − 0.81 mm/year), lower than moderate-risk areas. This suggests that frequent hazards in these areas result from significant rises in surrounding areas. Moderate-risk and relatively-low-risk areas, within 15 km to 130 km, show mixed rising and falling hazards. In moderate-risk areas, the average rise rate is 0.95 mm/year and the fall rate is −1.43 mm/year. In relatively-low-risk areas, the rise and fall rates are lower, at 0.78 mm/year and − 0.43 mm/year, respectively. Low-risk areas are mostly in the flat northern region, with an average terrain change rate of −0.09 mm/year.

As described in the study area’s overview, the Duku Highway lies between multiple geological fault zones, with the highway’s boundary points aligning closely with these fault zones. Plate movement causes differences in terrain change trends and rates between regions separated by fault zones, which fundamentally explains the varying susceptibility to regional hazards⁶². The trend of terrain change significantly influences regional hazards, especially the rapid rise of terrain, which is a key factor leading to frequent hazards in the northern section of the Duku Highway. This indicates that regional hazards have spontaneity. Moreover, since the terrain deformation trend in almost all hazard areas shows periodicity, these hazards are likely to recur over time, particularly in high and relatively high-risk areas. The spontaneity and recurrence of hazards in these areas mean they can occur without strong external conditions (extreme rain, steep terrain, abundant loose deposits) and may even recur without external factors. If strong external conditions arise, these areas may face a greater risk of hazards and larger-scale hazards. In medium and relatively low-risk areas, diverse terrain change trends and relatively low rates of change lead to varied causes of regional hazards, with a higher proportion of external factors contributing. This explains why the spatial correlation between terrain change rate and hazard risk, although positive, has a correlation coefficient of only 0.74.

Therefore, highway management personnel must focus on daily road maintenance and hazard prevention in high-risk and relatively high-risk areas, while emphasizing the prevention of hazards caused by extreme events, such as heavy rain, in moderate-risk and relatively low-risk areas. Specifically, in terms of infrastructure construction and maintenance, more robust road design and construction methods need to be adopted in high-risk areas, such as reinforcing roadbeds, adding drainage facilities, and building protective walls. Regular inspections of road conditions in these areas are essential, and timely application of techniques such as rockfall shelters, protective nets, shotcrete, retaining walls, and frame beams at specific locations is necessary. Regular maintenance and repairs are crucial to ensure road safety. To monitor geological hazards in real-time, management personnel should install real-time monitoring equipment in high-risk, relatively high risk and Moderate risk areas, such as landslide monitors, rain gauges, and seismometers. Establishing a comprehensive real-time monitoring and early warning system is also vital. Based on the monitoring data, timely warnings should be issued to relevant departments and the public to enable preemptive measures. Finally, using actual work results to continuously update the geological hazard susceptibility maps ensures the accuracy and timeliness of the data. This supports and promotes research related to high-altitude geological hazards, exploring new hazard prevention and mitigation technologies and methods, thereby continuously enhancing the scientific and effective management of highways.

Discussion

The main contribution of this paper is the use of SBAS-InSAR technology to extract long-term trend features of hazard deformation and achieve high-precision research on hazard susceptibility in areas with scarce basic observation data, using terrain deformation trend features as key indicators. Methodologically, this paper establishes a correlation clustering evaluation method (CCEM) to correct spatiotemporal clustering results, enabling the spatial clustering results of unsupervised classification to possess hazard attributes. This provides a framework for classifying spatiotemporal data with attribute features but no prior knowledge. Consequently, this paper reveals the characteristics and formation mechanisms of hazards on the Duku Highway, analyzes regional hazard susceptibility, and provides a theoretical basis for highway management for local departments. It also serves as a reference for managing and researching hazards on other high-altitude highways.

The output of SBAS-InSAR is the foundation of this study. As noted in most current SBAS-InSAR research in mountainous regions, SBAS-InSAR is susceptible to atmospheric⁴⁴, orbital⁶³, registration⁶⁴, terrain⁶⁵, and interference factors⁵². Particularly for long-term monitoring in mountainous areas with complex terrain, dynamic changes in snow cover, and high NDVI vegetation cover, these factors can variously affect the coherence of consecutive interferograms, thereby impacting the SBAS-InSAR results. To mitigate these effects, this study implemented DEM correction to reduce the impact of complex terrain on coherence. Precision orbit data were used to correct for multiple observations, shadowing, mid-pass stops, and foreshortening effects of the sensor. Atmospheric delay correction was performed to reduce coherence degradation caused by frequent atmospheric disturbances in complex mountainous areas. The final overall average coherence of 0.64 indicates that, similar to many studies in complex mountainous regions^66,67,68,69, the SBAS-InSAR results possess high data accuracy⁴⁴.

However, due to the absence of descending orbit data from Sentinel-1 for the study area, the SBAS-InSAR results are unable to fully capture the complexity of surface deformation, leading to shadow effects in the terrain. This is particularly problematic for accurately separating the east-west deformation components. These limitations in the data source inevitably introduce environmental noise into the results, affecting the accuracy, completeness, and continuity of the SBAS-InSAR time series analysis^43,70. Therefore, addressing the issues arising from the lack of descending orbit data in certain areas is a topic that requires future attention. Although filtering can effectively mitigate noise, the applicability of different filtering methods in specific regions needs further investigation. Moreover, the absence of descending orbit data as a control group also complicates the validation of the SBAS-InSAR results presented in this paper. Currently, the validation of SBAS-InSAR results for geological hazard identification primarily relies on cross-verification using ascending and descending orbit data, combined with optical remote sensing imagery or field surveys²⁵. However, the study area in this paper includes a total of 113 hazard events over three years, making individual validation of these events highly labor-intensive. Therefore, this study determines whether SBAS-InSAR identified the 113 hazard events and quantifies the identification accuracy from both qualitative and quantitative perspectives based on the topographic characteristics of the hazards. The final geological hazard identification rate is 85%, indicating a certain level of accuracy in the SBAS-InSAR results. This method has general significance for hazard identification, reducing the workload of optical image-assisted validation. However, due to different regions and hazard scales representing different average deformation rates, there are still limitations. Accurately determining the deformation rate threshold for hazards requires a high coherence (above 0.8)⁴⁴ and further in-depth and detailed studies in different regions. Additionally, the sudden and transient nature of geological hazards makes it challenging for SBAS-InSAR results using Sentinel-1 data with a 12-day revisit cycle to accurately identify all hazard events and measure the exact volume of the hazards. These issues pose challenges for the Sentinel-1 satellite in accurately identifying geological hazards and quantifying the extent of damage in regions with scarce observational data, and they remain scientific problems that need to be addressed in future research.

Classification is crucial to the susceptibility rating in this paper. Due to the lack of prior knowledge about terrain deformation for hazards, this paper directly analyzes unmarked data through unsupervised classification to discover potential structures or patterns, thereby gaining prior knowledge of terrain deformation characteristics. Based on this, the paper uses correlation to associate the results of spatial clustering and corrects these results using prior knowledge of hazard temporal clustering, thus endowing the unsupervised classification results with attribute features. This method (CCEM) is versatile. When applying it to other regions, attention should be paid to selecting association indicators, establishing the number of spatial clusters, and setting the correlation threshold. However, this method also has drawbacks. The overall calculation of the spatiotemporal cube in spatial clustering requires a large amount of memory (120GB in this study) and high research equipment standards, making it difficult to achieve higher accuracy and larger research scope. For the application scenarios of susceptibility evaluation, this method also has limitations. It is more suitable for evaluating the likelihood of hazards caused by a single hazard factor (in this study, the rapid terrain changes rate of the fault zone itself, whereas in other study areas, rainfall is generally the dominant single-factor susceptibility evaluation⁷¹). For the evaluation of multi-factor hazard environments, it is necessary first to use the CCEM method to evaluate each single factor individually and then assign susceptibility weights to different factors to obtain a comprehensive result. Therefore, further in-depth research can be conducted on the advantages and disadvantages of this method’s application scenarios in the future. A primary focus should be distinguishing its adaptability compared to other susceptibility evaluation methods, such as mainstream machine learning, in the same regions. Using prior knowledge obtained from clustering, utilizing machine learning to perform supervised classification on spatial regions, comparing and analyzing the differences between the research methods proposed in this paper and supervised classification methods. Further analysis will be done on the advantages and disadvantages of both methods, improving the spatial clustering method, and optimizing the classification approach proposed in this paper.

If we categorize the conditions under which geological hazard events occur, they can be divided into the environmental factors that nurture the hazard, the hazard-causing factors that directly lead to the occurrence of hazards, and the manifestation forms of the hazard, known as hazard carriers (such as debris flows, landslides)⁷². All three are indispensable. Geological hazards on highways are usually caused by the combined effects of multiple factors. Most studies focus on the environmental factors that nurture hazards, and the contribution rates of different factors (altitude and human factors⁷³, climate⁷⁴, NDVI⁷⁵) obtained from different studies vary. In this study, unlike the general mountainous regions where rainfall-induced hazards are common, the most significant characteristic of hazards along the Duku Highway is spontaneous collapses and rockfalls, which do not require any special external environmental factors. This is the fundamental reason why this study directly chose spontaneous terrain changes as the hazard-causing factor for investigation. The study found that the trend of terrain deformation is strongly correlated with hazard susceptibility. In other words, the occurrence of hazards is closely related to spontaneous geological activities in mountainous areas, a view supported by many other regional studies^76,77,78. The study found that regions with faster terrain deformation rates tend to have higher hazard susceptibility. When the deformation rate of a region significantly exceeds the average mountain deformation rate, these regions are more prone to hazards. For the formation mechanisms of collapse and rockfall hazards, rapid topographic changes can lead to the development of new faults and fractures. These faults and fractures often serve as potential initiation points for geological hazards because they reduce the overall strength of the rock mass, making it more susceptible to failure under external forces⁷⁹. Simultaneously, newly exposed surfaces, such as cliffs and bare rock layers, typically lack vegetation cover and surface protection, rendering them more vulnerable to weathering and erosion processes. Weathering can cause the rock to become loose, and erosion can further weaken the stability of the rock mass, thereby increasing the risk of geological hazards⁸⁰. Moreover, for landslides and debris flow hazards, topographic changes can alter the pathways of groundwater flow, leading to the formation of new subsurface water seepage channels. The movement of groundwater can increase the pore water pressure within the rock mass, reducing its shear strength and thus increasing the likelihood of landslides and debris flows. It is evident that regions with slower rates of topographic deformation have generally reached a relatively stable state. Compared to unstable regions, these stable areas require more extreme external conditions to trigger hazards, resulting in a lower frequency of geological hazards⁸¹. In this study, the rapid rise of terrain due to the mutual compression of fault zones is identified as the primary cause of the high frequency of geological hazards along the Duku Highway. A direct analysis of hazard-causing factors can effectively uncover the mechanisms of hazard development in a region. However, this approach has limitations, as this study only analyzed a single hazard-causing factor. For regions where hazards are caused by multiple factors, especially moderate-risk areas, analyzing only terrain changes is not comprehensive.

In summary, this study is a preliminary exploration of the terrain change characteristics and hazard research along the Duku Highway, conducted in an area with scarce data and no prior knowledge. The basic observation network for this highway is currently being planned. Given the limitations of this study and the characteristics of the Duku Highway, deeper research is essential. Future research will build on the prior knowledge gained from this study, using different methods to process noise in SBAS-InSAR results, improve result coherence, and conduct higher precision hazard identification studies. For hazard susceptibility, it is necessary to integrate hazard-prone environmental factors, hazard-causing factors, and hazard manifestations. Analyzing the hazard thresholds of different hazard-causing factors under various hazard-prone environments for different hazard forms will result in a comprehensive regional geological hazard study. This will contribute to the prevention and control of highway hazards and provide a reference for the study of hazards on other high mountain highways.

Conclusions

Exploring the spatial patterns of hazard susceptibility is crucial for sustainable highway management. Using long-term terrain deformation results from SBAS-InSAR technology, this study identifies the characteristics of regional hazard-induced terrain deformation and proposes a method (CCEM) to associate these characteristics with spatial terrain deformation clustering results. This method endows unsupervised classification results with hazard attributes, enabling high-precision susceptibility assessments in areas with scarce data and no prior knowledge. The research results provide strong support for local highway maintenance departments in sustainable road management and offer a theoretical basis for further studies in the region, which could benefit research on hazards in other high-altitude mountainous areas. The main conclusions are as follows:

• 1. SBAS-InSAR analysis shows that the average coherence coefficient of 411 interferograms is 0.64, primarily distributed between 0.55 and 0.65. The average coherence coefficient for 113 hazard areas is 0.68, with 101 of these areas showing negative average differential deformation values. The SBAS-InSAR results identify 85% of single hazard occurrences, demonstrating a certain level of reliability.

• 2. From 2018 to 2021, the terrain of the Duku Highway has been rising at a rate of 2.1 mm/a. Six significant change areas have been identified, with boundaries at 15 km, 60 km, 90 km, 130 km, and 205 km, and average velocity changes ranging from − 3.85 to 23.39 mm/a.

• 3. The terrain change trends in the hazard areas of the Duku Highway can be divided into ten categories. Clusters 9 and 8, with a 1-year cycle, an ascending velocity of 12.5 mm/a, and a descending velocity of −1.81 mm/a, have hazard occurrence rates of 48.5% and 27.8%, respectively, and are rated as high and relatively-high susceptibility categories.

• 4. The correlation between hazard susceptibility and spatial clustering shows that the Duku Highway’s hazard features are spontaneous and recurrent. High-risk, relatively-high-risk, moderate-risk, lower-risk, and low-risk areas account for 24.7%, 17.1%, 32.6%, 11.5%, and 14.1% of the total areas, respectively. The deformation rate positively correlates with risk level, and areas with rapidly rising deformation rates are more likely to experience hazards.

• 5. For sustainable highway management, greater attention is needed for daily road maintenance and hazard prevention in high-risk and relatively-high-risk areas. These areas require timely application of techniques such as rockfall barriers at specific locations, as well as regular maintenance and repair of equipment. Meanwhile, moderate-risk and relatively-low-risk areas should focus on preventing hazards from extreme events like heavy rain. Additionally, all areas should be equipped with real-time monitoring devices such as landslide detectors, rain gauges, and seismometers, and a comprehensive real-time monitoring and early warning system should be established.