Introduction

Large-scale brain network models based on biologically plausible local dynamics and interconnected using structural connectivity data derived from human imaging studies have offered a principled framework for studying the emergence of global brain dynamics. Simulated brain activity based on these models resembles realistic neural processes and can be used to make predictions about neurological disorders1,2,3.

Insights from large-scale brain network models include efficient information processing due to small-world network properties (dense local and sparse long-range connections)4,5; the presence of hubs for information integration and transfer6, “rich clubs” of highly interconnected hub regions for rapid communication7, and networks associated with specific cognitive functions, such as the default mode network for introspection and the salience network for attention and emotion 8.

One of the most revealing insights from large-scale brain network models is the dynamic nature of the brain’s functional networks and their rapid reconfiguration, spontaneously or in response to tasks and stimuli9, and that this dynamic functional connectivity (FC) is essential for adaptability and flexibility of cognition10,11. This capacity for fast transitioning between different functional network configurations that persist over time in response to cognitive and environmental demands is called metastability12.

Inter-regional coupling strength and connection delays play important roles in brain metastability. The strength of coupling between different brain regions affects the degree of synchronization between them. Stronger coupling promotes synchronization, i.e., regions become more coordinated and aligned for longer durations, while weaker coupling results in desynchronization or more independent neural activity.

The balance between strong and weak coupling is essential for achieving both integration (communication between brain regions) and segregation (specialized processing within regions)13. Metastability involves maintaining this balance, allowing the brain to transition between integrated and segregated states as needed for different cognitive functions14.

On the other hand, connection delays, or the time it takes for signals to propagate between brain regions, introduce temporal dynamics into the brain’s patterns of FC and contribute to the emergence of metastable states as the brain navigates through different network configurations15,16,17. The timing of transitions between states can depend on the combination of delays within the network18.

The interplay between coupling strength and connection delays is complex and can result in various dynamic states. When brain regions are weakly-coupled with long delays, their activity is independent. As the coupling strength increases and the delay reduces, the system transitions towards fully synchronized dynamics.

The dynamic interplay between these factors allows the brain to balance synchronization and desynchronization, integration and segregation, the temporal coordination of neural activity, and the peak synchronization frequency18. Understanding how coupling strength and connection delays influence brain metastability is a crucial aspect of neuroscience19,20,21.

The emergence of functional coherent subnetworks at different fundamental frequencies during the resting-state regime of the brain occurs spontaneously. A similar emergence of subnetworks or oscillatory modes is also expected from a multi-state metastability regime. It is important to highlight that the coherent subnetworks in the brain also present a spatial preference for a subset of the brain regions and a preferred fundamental frequency18,22.

Previous studies have shown that the subnetworks patterns related to the leading-eigenvector23 or ICA components24 of fMRI resemble the resting-state networks25. These patterns have been well characterized by statistical tools on neuroimaging data, showing fluidity and coalescence of the frequency-specific subnetworks22,26,27. Also, computational models have shown the transition between these patterns, but without specific frequency28 or without resemblance to resting state networks18. How these frequency-specific patterns emerge from neural dynamics, persist during short times, and co-occur with patterns preferring other frequencies was usually attributed to stochastic resonance14. Therefore, the dynamical features of the subnetworks patterns were attributed to multistability rather than metastability.

This paper aims to demonstrate the emergence of multiple oscillatory modes, their corresponding coherent functional networks, and their persistence in time from a network of Kuramoto oscillators. The network nodes correspond to brain regions connected according to the Automatic Anatomical Labelling (AAL90) Atlas29 using a single configuration of coupling and delay parameters. The emergence of the oscillatory modes and their transitions over time does not require more than selecting the configuration of parameters to achieve maximal metastability. We do not include intrinsic noise or any external perturbation.

We assume spectral entropy to be a proxy for metastability and identify the set of coupling and delay parameters that maximises this metric. We also present the emergent spectrum and metastable dynamics of the brain regions at that set of parameters. Further, we characterize the FC at specific frequency bands, showing the emergence of tempo-spatial and frequency-specific functional subnetworks. Finally, we compute subnetworks’ temporal features searching for differences in their fractional occupancy and duration distributions.

We show a correlation between spectral entropy and wakeful brain states. When spectral entropy reaches its peak, the resulting coherent subnetworks from our model resemble the expected networks observed in empirical human resting-state EEG. This resemblance encompasses both spatial and temporal features.

Results

The emerging dynamics from delayed interactions among identical oscillators exhibit a spectrum with frequency components different from the single intrinsic frequency of each individual oscillator. We are interested in how many different peaks and how much broader this emergent spectrum becomes when we vary the global parameters: the global coupling coefficient K and the mean conduction delay \(MD\).

Parameters set for metastable dynamics

Multi-state metastable dynamics have at least two attractor basins by definition. This implies that the system’s average spectral profile will exhibit a shape distinct from a single frequency peak (see Supplementary Fig. S1, for examples of the average spectral profiles resultant from the Kuramoto model). The relevant frequency components increase with the number of attractor basins in the system.

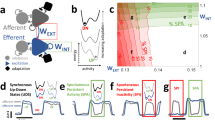
There is no specific numerical quantity that directly measures metastability. Instead, various quantitative and at times qualitative metrics are employed to assess the features of brain function associated with metastability30. Here, we use the spectral entropy as a proxy for metastability while varying the global coupling K (adimensional) and the mean conduction delay \(MD\) (in a biophysical-inspired range31,32). Figure 1 shows a colored heatmap of the corresponding spectral entropy for each set of parameters in our model. Figure 1 also includes the average spectrum for each set of parameters.

The maximum value obtained for the spectral entropy is highlighted with a white square corresponding to \(K = 4\) and \(MD = 21\) ms. This set of parameters also presents low synchrony assessed by the average of the Kuramoto order parameter (KOP) (Supplementary Fig. S2a presents the average of the KOP), and it is not the maximal set of parameters for the KOP standard deviation (Supplementary Fig. S2b presents the standard deviation of the KOP).

The best fit with FC profiles of resting-state MEG is marked with a magenta square (\(K = 3\), \(MD = 16\) ms) as found in Cabral et al.33. The point of the best fit correlating the Kuramoto model average spectrum to resting-state EEG average spectrum is marked with a dark-blue square (\(K = 5\), \(MD = 20\) ms, average Pearson’s coefficient = 0.49)34. The point of best correlation with anesthesia EEG spectrum is marked with a cyan square (\(K = 10\), \(MD = 40\) ms, average Pearson’s coefficient = 0.34)35, and the correlation with slow-wave sleep EEG spectrum is marked with a grey square (\(K = 9\), \(MD = 38\) ms, average Pearson’s coefficient=0.43)36. Resting-state, anesthesia, and slow-wave sleep EEG spectra are corrected by 1/f to remove the aperiodic component before correlating with the model spectra. The marked operational point corresponds to the maximal average Pearson’s coefficient from correlating five subjects’ spectra.

The coupling value and mean delay in anesthesia and slow-wave sleep are higher than in the resting-state case. Thus, these brain stages have higher synchrony but lower spectral entropy (see Supplementary Fig. S2a, b).

Fig. 1
figure 1

Spectral entropy heatmap. Spectral entropy as a metric of metastability from the parameters space exploration of global coupling, K, and mean delay \(MD\). The white square marks the maximum value obtained for the spectral entropy at \(K=4\) and \(MD =21\) ms. The dark-blue square marks the best correlation fit with resting-state EEG spectrum at \(K=5\) and \(MD =20\) ms, and the magenta square marks the best fit from Cabral et al. 33 at \(K=3\) and \(MD =16\) ms. The cyan square marks the best fit with anesthesia EEG at \(K=10\) and \(MD =40\) ms. The grey square marks the best fit with slow-wave sleep EEG at \(K=9\) and \(MD =38\) ms.

Full size image

Emerging spectrum and time switching between attractor basins

The average spectrum of the system indicates the frequencies in which the system’s power is highly concentrated. We assume that the frequency peaks are associated with the existence of limit-cycle attractors. We focus on the system activity at the frequency peaks indicated in Fig. 2a because these correspond to the major EEG and MEG wavebands found in human brain data37,38. Further, this spectrum comes from using the structural features of the human connectome. Changes in the structural features, keeping the network topology, result in different average spectra (see Supplementary Fig. S3). We band-pass filtered the time-series data using a bandwidth of 1 Hz around these peak frequencies. Then, we extracted the envelopes to determine the dominance of every peak frequency at each time point (see "Selection of envelopes threshold" section for details of fractional occupancy calculation by thresholding the envelopes).

As the spectrum corresponds to the set of parameters that determine maximum metastability, the visualization of the time excerpts of the Kuramoto model simulations in Fig. 2b shows how some nodes ‘switch’ between attractors (see, for example, simulations from nodes relating to the brain areas Right Precuneus and Right Heschl). These nodes have low variance in their fractional occupancy at each peak frequency (see Supplementary Fig. S4). On the other hand, some nodes have a preferred frequency most of the time (see, for example, Right Occipital Inferior). We note here that some nodes have most of their power in frequencies other than the frequency peaks defined here, i.e., the power of their oscillations in these bands did not pass the occupancy threshold (see, for example, Left Cingulum Mid).

On the other hand, the Kuramoto dynamics from a set of parameters that determine lower spectral entropy does not present several peak frequencies (see Supplementary Fig. S5a), neither “switch” between attractors (see Supplementary Fig. S5b).

Fig. 2
figure 2

Model dynamics at the maximum metastability set of parameters. (a) The average spectrum of the ninety nodes with \(K=4\) and \(MD =21\) ms. (b) Time-series of the nodes’ activity filtered below 50 Hz. The shaded regions highlight when the nodes’ envelopes pass a threshold = 0.232 for each frequency band. As the maximum possible envelope amplitude is 1, the selected threshold (for threshold selection details, see "Selection of envelopes threshold" section in Methods) indicates when at least 5.3% of the node’s instantaneous power is present at each narrow frequency band.

Full size image

Functional sub-networks emerging at each frequency peak

FC relates to all the pairs of brain regions with correlated activities during a determined period39. We use sliding windows with an overlap of 50% to determine the FC matrix by examining the spectral coherence at each frequency peak. Figure 3 shows the subnetworks with higher fractional occupancy at each peak frequency (see "FC matrices clustering" section for clustering details, see Supplementary Fig. S6 for region labels and positions reference). We found that emerging subnetworks at lower frequencies (Fig. 3a,b) have a greater number of interhemispheric connections than the higher frequency subnetworks (Fig. 3c–e).

The functional subnetworks at 13 Hz and 15 Hz (Fig. 3a,b) resemble the Default Mode Network (DMN)22,40. These include the medial prefrontal cortex (ORBsupmed, SFGmed, REC), the posterior cingulate cortex (PCG), the cuneus (CUN), the precuneus (PCUN), the angular gyrus (ANG), and the thalamus (THA). Note that the medial regions are connected to the occipital regions with a negative value of the imaginary coherence, while the interhemispheric connections have positive imaginary coherence. This is an example of anticorrelated, but coherent, simultaneous activity.

The subnetwork that emerges at 29.4 Hz (Fig. 3c) resembles a combination of the salience network with the sensory systems41. This subnetwork includes the right insula (INS), the anterior cingulate cortex (ACG), the posterior cingulate cortex (PCG), the occipital superior gyrus (SOG - visual), the supplementary motor area (SMA), the postcentral gyrus (PoCG - motor), the superior temporal gyrus (TPOsup-auditory), and the middle temporal gyrus (TPOmid-visual).

The subnetworks at 41.2 and 43 Hz (Fig. 3d,e) resemble the fronto-parietal network42,43, which includes the frontal superior gyrus (SFG), the frontal inferior gyrus (IFG), the inferior parietal lobule (IPL), and the caudate (CAU), and the inferior temporal gyrus (ITG). However, it seems that the networks also include part of the salience network, given that they include the insula (INS) and the right posterior cingulate cortex (PCG).

The putamen (PUT), the pallidum (PAL), and the right caudate (CAU) require a mention, as they participate in all the subnetworks at all the five frequencies. On the other hand, the imaginary coherence of the right precentral gyrus (PRECg), left frontal inferior operculum (IFGoperc), and left supramarginal (SMG) do not participate in any functional network, as they do not have enough coherence with other regions at the five frequencies.

The additional subnetworks at each frequency band share a “core” of participant brain regions (see Supplementary Figs. S10 and S11). The regions “out of the core” are recruited/excluded at different times with as many different connectivity patterns such as the number of detected subnetworks.

Fig. 3
figure 3

Functional emerging subnetworks. Functional subnetworks with the maximal fractional occupancy for each frequency peak (a–e). The average spectral coherence FC matrix of each cluster is masked by the structural connectivity matrix, and only the highest 10% of the connections are shown. The color of the brain regions corresponds to the colors previously used for each frequency band. The color of the edges in the circular network plot indicates the imaginary part of the coherence (icoh). Supplementary Fig. S7 shows the real part of the coherence. Brain plots were generated using adapted code from the repository “PyBP” available at https://github.com/alexandershaw4/PyBP-Py-BrainPlotter-for-AAL90. The circular networks were generated using the Python library “MNE-connectivity 0.7.0” available at https://mne.tools/mne-connectivity/stable/index.html.

Full size image

Fractional occupancy and duration of the frequency-related sub-networks

Using the sliding windows, we can calculate the fractional occupancy and duration of the subnetworks in each frequency band using the window length. The subnetwork’s fractional occupancy comes from the number of time windows belonging to each cluster in each frequency peak. The violin plots in Fig. 4a show the occupancy of the subnetworks for each frequency peak. There are statistical differences between certain groups at 13, 15, and 29.4 Hz (Kruskal–Wallis H-test \(p<\)0.05). All subnetworks at 13 and 15 Hz are pair-wise statistically different from each other (\(p<\)0.01, Wilcoxon t-test, Bonferroni corrected for multiple comparisons). Almost all subnetworks at 29.4 Hz also are pair-wise statistically different.

The median of the maximal fractional occupancy is 33.3% at 13 Hz and 27.8% at 15 Hz. The median of the maximal fractional occupancy at the medial frequency at 29.4 Hz is 39.7%. The median of the maximal fractional occupancy is 15.1% at 41.2 Hz (subnetwork 7), and 15.4% at 43 Hz (subnetwork 7).

Although the subnetworks’ occurrences are similar in their fractional occupancy at the two higher frequency peaks, it is possible to select one subnetwork with the highest fractional occupancy at each peak frequency.

The boxplots in Fig. 4b present the duration of the individual appearances of the functional subnetworks. Using six-cycle windows, we obtain a longer median duration for the lower frequency peaks. Interestingly, there are significant differences (\(p<\)0.01, Wilcoxon t-test, Bonferroni corrected for multiple comparisons) in the subnetworks duration between almost all the pairs of subnetworks at the three lower frequencies. At higher frequencies, there are fewer significant differences in the distribution of the subnetworks’ duration between all pairs. As multiple-group, there are statistical differences (Kruskal–Wallis H-test \(p<\)0.01) for four of the five peak frequencies. The exception in multiple-group comparison is at 41.2 Hz.

The maximal duration at each frequency are 4.389 s (subnetwork 4), 3.8 s (subnetwork 4), 2.856 s (subnetwork 4), 1.022 s (subnetwork 7), and 0.98 s ( subnetworks 4 and 7), respectively.

Fig. 4
figure 4

Subnetworks’ fractional occupancy and duration. (a) Fractional occupancy of the spectral coherence FC sub-networks. (b) Duration distributions of the coherent sub-networks. Each vertical panel corresponds to the previously defined frequency bands. A diamond below the distributions indicates multi-group statistical difference (Kruskal–Wallis H-test \(p<\)0.05 in (a), \(p<\)0.01 in (b), p-values are corrected for multiple comparisons). The horizontal lines above the distributions indicate a statistically significant difference between the indicated pairs (\(p<\)0.01 Wilcoxon t-test).

Full size image

Discussion

Model choice: Kuramoto network as a large-scale brain model

The Kuramoto model assigns a key role to the oscillators’ coupling. This model becomes a whole-brain model when the coupling corresponds with a human brain connectome inheriting the coupling strengths and connection delays16,44,45,46,47. The Kuramoto model simplifies the dynamics of each region to a unitary amplitude harmonic oscillator. This simplification contrasts with biophysically-inspired oscillatory dynamics19 or amplitude-varying oscillators18, but provides a mechanistic explanation of oscillatory phenomena in the human brain cortex1,33,48,49,50. Not surprisingly, the Kuramoto model was proposed from the beginning by Kuramoto51 as a plausible model of the brain alpha-rhythm.

In this work, we show that we obtain metastable dynamics using adequate scaling parameters for coupling the whole brain model. The model reaches the maximum metastability at a particular set of global coupling and mean delay \(\{K = 4, MD = 21 \text {ms}\}\).

The spectral properties that emerge from the model at this maximum metastability are correlated with the spectral properties of awake resting state EEG of young, healthy adults. On the other hand, spectral properties of EEG from altered cognitive brain states e.g. anaesthesia, sleep, epilepsy correspond to alterations in the model’s global delay and coupling parameters away from maximum metastability. For example, the slow-wave sleep spectrum matches with the model results using a larger K and larger MD. That makes sense as slow-wave sleep dynamics are more synchronized and involve larger networks20,52.

Moreover, at global maximum metastability, the system spontaneously switches between multiple coherent subnetworks. The emergent subnetworks oscillate at specific frequencies and resemble the topography of functional resting-state networks25. Thus, linking cognitive states to model states.

Metric for multi-state mestastability

Emergence of metastable dynamics

Our results show the emergence of different sub-networks exhibiting a preferred frequency. Similar to the work of Roberts et al.53 and Cabral et al.18, the subnetworks are visited in sequence, and none of them persist indefinitely (Fig. 2b), suggesting that the simulated dynamics exhibit metastable behaviour. It is worth mentioning that we used conduction delays informed by the structural connectivity18,33, in contrast to the homogeneous delay used in Roberts et al.53 Also, we used a single natural frequency of 40 Hz for all nodes rather than retrieving different natural frequencies for each node from a distribution as in the work of Pang et al.54 Finally, we highlight that our model33 does not include any external stimulation or intrinsic noise.

Measuring the metastability

The standard deviation of the Kuramoto order parameter, which has been used as a proxy measurement of metastability21,30, indicates the global variation between synchronized and non-synchronized states. However, a multi-state metastable system does not only interchange between synchronized/not-synchronized states within a single average frequency. Instead, it shows different spectral coherence levels around multiple peak frequencies. The spectral entropy of each node indicates the richness of its dynamics and can be thought of as a measure of the information contained in its frequency spectrum. The sum of the entropy spectrum from all the nodes gives a global measurement of the diversification of the states/modes of the system55,56,57. A system with all nodes oscillating at the same single frequency has the same, and the minimal, spectral entropy as a system with each node oscillating at a distinct single frequency. These are the two extremes of full coherence and full incoherence, respectively. Thus, we start by determining the global maximum value of spectral entropy for a specific combination of the global coupling and mean conduction delay.

We select the point in the model’s parameter space that maximizes the global spectral entropy to ensure greater diversity in the dynamics of the simulated time series. However, using entropy to measure the “richness” of emerging dynamics in the brain or any other complex system could be ill-determined given that the entropy value is maximal for white noise58. Nonetheless, it is an adequate metric for diverse emerging dynamics when all the nodes start with a single peak in their spectrum by imposing the natural frequency on the model, i.e., the minimum possible entropy. We suggest the maximum value of global spectral entropy is limited by the structural features of the employed network, as expected from geometrical constraints on brain dynamics54.

Further work could analyze the entropy at each node, and if possible over time (selecting an adequate time window). Functional networks with a spatial distribution of entropy could indicate the potential of each node to be recruited by distinct functional networks.

Emergence of coherent subnetworks

We argue that the different emerging frequency peaks correspond to several limit-cycle attractor basins. Following this presence of multiple frequencies, spectral coherence is an adequate measurement of frequency-specific synchronization59,60. Moreover, spectral coherence indicates the presence of phase-locking pairs at all frequency ranges. We limited the analysis and results to the peak frequencies of the average spectrum (Fig. 2a), but this approach could be used in other central frequencies. However, some caution must be taken when using frequency-domain measurements. The main disadvantage of coherence with respect to the instantaneous Kuramoto order parameter is the need to use time windows. We use a different time window length for each frequency peak, and an overlap of 50% to counteract the temporal disadvantage and to get a higher temporal resolution. Then, the obtained subnetworks represent different phase-locking patterns at each peak frequency. The frequency specificity of our analysis goes beyond previous works that have shown the emergence of multiple broadband functional subnetworks using different computational models fitted to the complexity of awake state28,61 or fMRI data62.

Regions participate in different subnetworks

We present the subnetworks with the highest participation during the simulation period at the five peak frequencies (Fig. 3). The coherence subnetworks at the two lower frequencies resemble the DMN and the Visual Network. The subnetworks of the middle frequency (29.4 Hz) are a combination of the salience network and sensory networks. Finally, the subnetworks at the two higher frequencies resemble the fronto-parietal or central executive network. These networks are also called the three core neurocognitive networks, and dysregulation of these networks correlates with various neuropathologies3. Our frequency-specific resemblance of resting state networks is aligned with the work of Mantini et al.24 using EEG and fMRI data, and the work of Petkoski and Jirsa16 using the Kuramoto model with other methodology to scale the connectivity. Instead of naming our peak frequencies and relating them to canonical EEG bands, we highlight the relative frequency value of the peaks: lower, middle, and higher (see Supplementary Fig. S8 for the similarity between our found subnetworks and Supplementary Fig. S9 for the similarity with the resting-state networks and the three core neurocognitive networks).

The basal ganglia regions: pallidum (PAL) (structural features on left hemisphere: strength \(I_n=88.27\), degree \(k_n=53\); right: \(I_n=82.44\), \(k_n=58\). See "Structural features of human-connectome" section in Methods for details of \(I_n\) and \(k_n\) computation), putamen (PUT) (left: \(I_n=130.84\), \(k_n=57\); right: \(I_n=141.29\), \(k_n=62\)), and the right caudate (CAU) (\(I_n=97.46\), \(k_n=63\)) participate in all the subnetworks at all peak frequencies. But their participation is mainly via connections between themselves. However, the left caudate (\(I_n=77.77\), \(k_n=57\)) does not participate in the networks of 29.4 Hz and 41.2 Hz. Perhaps the lack of the left caudate to complete the basal ganglia is a threshold artifact or could come from the lower structural connection strength than the other basal ganglia regions. In any case, the predominant presence of the basal ganglia indicates the importance of including sub-cortical regions to study brain dynamics63.

In this work, we explored the emergent dynamics of the whole-brain Kuramoto model using the same intrinsic frequency for all brain regions to simplify the network configuration. Using a single intrinsic frequency also ensures that the emergent dynamics are a consequence of the connectome configuration and that intrinsic cross-frequency interaction does not alter the dynamics. However, the intrinsic cross-frequency interactions between cortical and subcortical regions could be necessary to match the maximal metastability frequency peaks to the EEG canonical peak frequencies. Further work will explore the dynamics when subcortical intrinsic frequencies are lower than the cortical intrinsic frequency64, or even assigning different intrinsic frequencies to each brain region65.

According to the presence of brain regions in each subnetwork (see Supplementary Fig. S11), the thalamus (THA) (left: \(I_n=89.06\), \(k_n=64\); right: \(I_n=79.88\), \(k_n=64\)), right insula (INS) (\(I_n=93.51\), \(k_n=43\)), right posterior cingulum gyrus (PCG) (\(I_n=149.00\), \(k_n=61\)), and left anterior cingulum gyrus (ACG) (\(I_n=124.84\), \(k_n=42\)) are present in almost all the subnetworks at all peak frequencies. These regions present connections between them and other regions. Particularly, the cingulum regions present interhemispheric connections. The active presence of cingular regions in networks of resting-state dynamics has been demonstrated to be correlated with the anatomy of the cingulum bundle66,67,68. This bundle, or collection of white matter tracts, connects regions of the frontal lobe with the precuneus (PCUN), posterior cingulate cortex (PCG), thalamus (THA), hippocampus (HIP), and parahippocampus (PHG)69.

The remaining 80 regions are absent in the subnetworks for at least one peak frequency. These regions are recruited by the subnetworks at different peak frequencies with preference in the effective frequencies of the region, which result from the interaction of all the ninety nodes. There are still open questions at the functional level: Could the activity of the functional hub (basal ganglia, thalamus, insula, and cingulum gyrus) modify the recruitment of the other 80 regions? What is the result of malfunction/disconnection of one node of the functional hub?

Regarding the relation with structural features of the regions, note that the right PCG has the highest strength \(I_n=149.00\) but this region does not participate in all the subnetworks. Neither, the thalamus regions in both hemispheres having the highest degree \(k_n=64\) participate in all the subnetworks.

On the other hand, the right precentral (PreCG) (\(I_n=65.94\), \(k_n=26\)), the left frontal inferior operculum (IFGoperc) (\(I_n=82.88\), \(k_n=28\)) and the left supramarginal (SMG)(\(I_n=59.10\), \(k_n=22\)) are absent from all the subnetworks. However, the region with lowest strength \(I_n=46.78\) is the right paracentral lobule (PCL) participating in five subnetworks. The region with lowest degree \(k_n=18\) is the right rolandic operculum (ROL) participating also in five subnetworks. Thus, we can expect more participation in functional subnetworks from the highly connected regions, but we can not predict how much greater it may be.

Temporal features of the coherent subnetworks

There is a “core” of participating regions that recruits more regions by increasing the spectral coherence (or excludes regions by decreasing the coherence). As the coherence takes into account both zero-lag and constant-lag synchrony, the coherent functional subnetworks include distant regions that are phase-locked but not in-phase with each other70.

High activity of a region at a peak frequency, measured by the fractional occupancy of each region (Supplementary Fig. S3), does not distinguish the presence of the region in multiple functional subnetworks. In fact, a region with a broader spectrum than a single peaky frequency, i.e., with a high spectral entropy, could be participating in more than one functional subnetwork instantaneously. For example, empirical data has demonstrated that sensory networks exhibit interaction of theta and gamma bands of EEG71,72, relating to a bottom-up and a top-down functional network, respectively.

On the other hand, the fractional occupancy of each functional subnetwork (Fig. 4) indicates the switching of the pattern of coherence for each frequency band. In this way, it offers a perspective of how the synchronization patterns distribute differently over time. We remark that as the fractional occupancy is a ratio over the total simulation period, the different time window length does not matter to qualitatively compare this metric result between frequency bands.

We found that for the two lower-frequency peaks, there exists a difference in fractional occupancy between all subnetworks. Taking into account that the duration distribution of the subnetwork with higher fractional occupancy also has a longer tail, it indicates a temporal preference of the dynamics to remain in that subnetwork. Thus, at the lower frequency peaks the simulated brain signals show an “idle” mode, that as mentioned before, spatially resembles the DMN73. In contrast, there are no statistical differences for the occupancy at the two higher frequency peaks. Considering their resemblance with the executive control network, the lack of differences in fractional occupancy indicates that the resting brain does not prefer a cognitive task.

We use sliding windows containing several cycles for our coherence calculation. This meant that the median duration of each subnetwork is larger than the typical microstates duration of 50 ms27,74. Reliable coherence measurements are possible with just a fraction of the cycle22, but we preferred to be conservative in the analysis. In any case, our subnetworks are concurrent at the different frequency peaks. The combined overlap of the subnetworks results in states with a median duration lower than 50 ms (see Supplementary Fig. S13), but the number of possible clusters combination (M=3925) renders the analysis unfeasible. However, this is explained by the fact that microstates duration is based on transition times of statistical models (Hidden Markov Model (HMM) and variants74). Thus, the statistics of the transitions between the different combinations of the coherent subnetworks could be used in future work to link the emerging dynamics from the Kuramoto model with results from literature using HMM and variants.

Networks occurrence could be related to the modularity of the broadband functional connectivity dynamic (FCD) matrix75. The modularity of the correlation FCD matrix describes the switching between different spatial configurations, but without reference to their oscillatory modes. Spectral entropy increases as long-range subnetworks’ presence broadens the spectrum. However, FCD modularity is higher for lower global coupling values, where each spatial configuration is more dissimilar than configurations occurring at other times (see Supplementary Fig. S14). Thus, spectral entropy indicates the switching between frequency-specific subnetworks, rather than just changes in spatial configurations by lag differences (see Fig. 2).

Conclusions

The increase of the dynamical richness by the human-connectome interaction of single intrinsic frequency oscillators is well described by the spectral entropy. We propose that spectral entropy is a proxy measurement of multi-state metastability, which is expected to be high at the awake resting-state brain. In line with this approach, the emerging coherent subnetworks at the point of maximal spectral entropy resemble the Default Mode Network, the Salience Network, and the Executive Control Network, not only in their spatial regions, but also near the respective well-known EEG brain rhythms. Further, the correlations fit with the average spectrum from other brain states EEG are located at points in the parameters-space of lower spectral entropy, suggesting a relation of this dynamical measurement of neural activity with behavior calm.

In addition, we found that the multiple coherent subnetworks at lower frequencies, resembling the DMN, have different fractional occupancy. On the other hand, the executive control-like subnetworks are similar in their fractional occupancy. However, the duration distributions have differences for almost all the frequencies. These findings indicate the presence of a default “idle” stage without preference to switch into a preferred executive subnetwork on the maximal spectral entropy dynamics. That was what we expected from the brain in resting-state, which makes the model suitable for its use as a baseline for the simulation of awake brain interventions.

Methods

Kuramoto model

The Kuramoto model describes the synchrony dynamics of a harmonic oscillator coupled inside an oscillator network. The differential equation of Kuramoto model describes the time evolution of the phase of one oscillator subjected to perturbations from neighboring oscillators48. The simple Kuramoto model equation, with equal connection strengths and all-to-all coupling between oscillators, becomes:

$$\begin{aligned} \dot{\theta }_n(t)=\omega _n+\frac{K'}{N} \sum _{m=1}^{N} \sin {(\theta _m(t)-\theta _n(t))}, \end{aligned}$$
(1)

where \(\omega _n\) is the natural frequency of the nth oscillator, \(K'\) is the global coupling strength between all oscillators, N is the total number of nodes, and \(\theta _n\) and \(\theta _m\) are the phase shifts between two oscillators, respectively.

In order to use human connectome data, we employed a modified Kuramoto model with heterogeneous coupling coefficients and delays between the connections. The model is represented by:

$$\begin{aligned} \dot{\theta }_n(t)=\omega _n+K\sum _{m=1}^{N} c_{nm} \sin {(\theta _m(t-\tau _{nm})-\theta _n(t))}, \end{aligned}$$
(2)

where \(c_{nm}\) is the element from the weighted adjacency matrix that represents the coupling strength, and \(\tau _{nm}\) represents the delay. We simplified the term \(K'/N\) from Eq. (1) to K, as \(N=90\) is the same for all simulations. We used the AAL9029 connectivity matrices with volume correction, as in Cabral et al.33.

As an additional global parameter, we also vary \(\tau _{nm}\) by a mean delay factor \(MD\). To achieve this modulation, the matrix \(\mathbf {\tau }\) of delays is normalized by the average of the nonzero elements and then multiplied by the mean delay factor. As our connectome data is a distance matrix between brain regions, the applied mean delay is a proxy for the inverse of the mean conduction speed1.

We simulate 300 s for each set of the parameters’ space in Fig. 1. We perform twenty simulations, each of 30 min, with different initial conditions for \(\theta _n\) using the point of maximal spectral entropy.

Structural features of human-connectome

AAL90 consists of two non-negative matrices: one matrix, C, of the connection weights with elements \(c_{nm}\), and another matrix, D, of the distances between regions.

The matrix D is symmetric, but the matrix C is not. Then, we calculate the connectivity strength of each region/node n as if we use a symmetric version of the C matrix by averaging the directed weights using \(c'_{nm}=(c_{nm}+c_{mn})/2\)65, then

$$\begin{aligned} I_n=\sum _{m=1}^{N} c'_{nm}, \end{aligned}$$

and the node degree as:

$$\begin{aligned} k_n=\sum _{m=1}^{N} \delta (c'_{nm}), \end{aligned}$$

where the function \(\delta (c'_{nm})\) is 1 if \(c'_{nm}>0\) and zero otherwise.

To vary the mean delay, the D matrix is normalized by its average taking into account only the values where the \(c_{nm}>0\). Then, \(\tau _{nm}\) is defined by

$$\begin{aligned} \tau _{nm}=( MD )d_{nm}, \end{aligned}$$
(3)

where \(d_{nm}\) is an element of the normalized D matrix.

Dynamic measurements on simulated signals

Kuramoto order parameter

The measure of the global synchronization between oscillators as a function of time uses the average phase value, the KOP48, expressed by:

$$\begin{aligned} r(t)=\left| \frac{1}{N}\sum _{n=1}^{N} e^{i \theta _n(t)}\right| . \end{aligned}$$
(4)

Frequency spectrum

All the nodes in the Kuramoto model have an intrinsic frequency (\(\omega _n\)). The intrinsic frequency of auditory evoked responses of a vast amount of cortical regions is around 40 Hz76, and this intrinsic frequency was previously used in Cabral et al33. Thus, we use \(\omega _n=2\pi (40)\) rad for all nodes. However, inter-node interactions may cause individual phase shifts leading to changes in the frequency of each node and the frequency of the system as a whole33. Then, the spectrum of each oscillator could have a broader bandwidth with additional frequency peaks. We calculate the power spectral density of each node using a windowed Fourier transform of \(\sin {(\theta _n(t))}\) via Welch’s method. We use a Hann time window of 5 s, overlapping by 50%, to get a frequency resolution of 0.2 Hz.

Spectral entropy

The normalized power spectral density by the sum of the power along all the frequencies could be considered a probability distribution function. Also, taking advantage of the quantization of the frequency domain in discrete bins by the numerical calculation of the Fourier transform, we take the Shannon entropy of the normalized power spectral density57, given by:

$$\begin{aligned} H_n=-\sum p(f_j) \log {(p(f_j))}, \end{aligned}$$
(5)

where \(f_j\) indicates the j-th frequency bin, and \(p(f_j)\) the normalized power spectral density at that frequency bin. Further, we get a global metric by summing the spectral entropy over all the nodes.

$$\begin{aligned} H=\sum _{n=1}^{N} H_n. \end{aligned}$$
(6)

Preferred frequencies at maximal spectral entropy

The frequency peaks are the bins for which the average spectrum (taken over all nodes) has a local maximum. As the amplitude signal of each node is unitary \(\left( sin(\theta _n(t))\right)\), the frequency peaks also correspond to the preferred frequencies of the system with longer occupation time. Using \(K=4\) and \(\textit{MD}=21\ \text {ms}\) results in five frequency peaks in the emerging spectrum. The peak frequencies are the set \(\textbf{p}=\{13,15,29.4,41.2,43\}\) Hz.

Selection of envelopes threshold

A proxy to the instantaneous power of each node at a particular frequency was calculated with the envelope of the narrow-band filtered signals. This comes from the amplitude or magnitude of the Hilbert transform of the filtered signals. To discretize the time a node occupies in each frequency peak, we employed a binary classification approach with a single threshold for all the 90 nodes and the 5 frequency-band envelopes. Then, we select the threshold of the maximum F1-score considering: True Positives: time samples where just one envelope overpass the threshold; False Positives: time samples where more than one envelope overpass the threshold; Negatives: time samples where none of the envelopes overpass the threshold.

Functional connectivity matrices

The FC matrices were calculated with the spectral coherence between the nodes’ activity77. The stride length comes from expecting to include at least six complete oscillations. Then, the time windows were \(\{462, 400, 204, 146, 140\}\) ms for the correspondent peak frequency. The spectral densities calculation employs shorter windows of three complete oscillations with an overlap of 50%78. In addition to disentangling the networks that co-occur but have different phase synchrony, we also calculated the FC matrices with the imaginary part of the coherence.

The spectral coherence is defined by

$$\begin{aligned} coh_{xy}(f)=\frac{|S_{xy}(f)|}{\sqrt{|S_{xx}(f)| |S_{yy}(f)|}}, \end{aligned}$$

where \(S_{xy}(f)\) is the cross-spectral density of signal x and signal y. \(S_{xx}(f)\) and \(S_{yy}(f)\) are their respective spectral densities.

The imaginary part of the coherence79,80 is defined by

$$\begin{aligned} icoh_{xy}(f)=\frac{\text {imag}(S_{xy}(f))}{\sqrt{|S_{xx}(f)| |S_{yy}(f)|}}. \end{aligned}$$

FC matrices clustering

The FC matrices are symmetric, and all diagonal elements are one. Then, before clustering, we re-arrange the lower triangular matrix excluding the diagonal as a vector. This gives an array \(FC^{(s)}(p)\in \mathcal {R}^{w \times 4005}\), where w is the number of time windows, for each trial s, and for each frequency peak in \(\textbf{p}\).

We used the SpectralClustering method from the scikit-learn Python library, with ’nearest_neighbors’ as the affinity parameter to cluster the data. This algorithm was performed over the PCA transformation of the FC array data using ten components. Before using the clustering algorithm, we normalized the PCA-transformed data by subtracting the minimum value and then dividing it by the difference between the maximum and the minimum value.

The number of clusters, M, is a parameter of the clustering algorithm. We employed two criteria to select the quantity of the clusters. The first is the inter-trial correlation between the most similar centroids of the clusters from each trial (see Supplementary Fig. S12a).

The second is the correlation of the cluster size between trials, which corresponds with the fractional occupancy of each cluster (see Supplementary Fig. S12b). This second criterion reduces the search range to \(M<11\).

In particular, we selected the number of clusters, M, that is the maximum of the inter-trial correlation for the peak frequencies 13 Hz, 15 Hz, and 29.4 Hz. For the peak frequencies 41.2 Hz and 43 Hz, we selected \(M=7\), just before the ’elbow’ at \(M=8\).

The subnetworks shown in Fig. 3 correspond to the centroid of the clusters. For visualization, we pruned the not-present edges in the structural matrix C, the edges with a standard deviation intra-cluster above the 80% percentile, and the edges with coherence below the 90% percentile, this is keeping the 10% of connections with higher coherence.

Duration and fractional occupancy of the sub-networks

The subnetworks’ duration was calculated from the consecutive stride lengths of each subnetwork occurrence. The fractional occupancy comes from adding the duration of all the occurrences of a subnetwork over the total simulation time (30 min). We used the Kruskal–Wallis H test from stats.multicomp of the statsmodels Python library to perform the statistical analysis correcting for multiple comparisons.