A novel convolutional neural network for enhancing the continuity of pavement crack detection

Abstract

Pavement cracks affect the structural stability and safety of roads, making accurate identification of crack for assessing the extent of damage and evaluating road health. However, traditional convolutional neural networks often struggle with issues such as missed detection and false detection when extracting cracks. This paper introduces a network called CPCDNet, designed to maintain continuous extraction of pavement cracks. The model incorporates a Crack align module (CAM) and a Weighted Edge Cross Entropy Loss Function (WECEL) to enhance the continuity of crack extraction in complex environments. Experimental results show that the proposed model achieves mIoU scores of 77.71%, 80.36%, 91.19%, and 71.16% on the public datasets CFD, Crack500, Deepcrack537, and Gaps384, respectively. Compared to other networks, the proposed method improves the continuity and accuracy of crack extraction.

Introduction

Highways serve as the backbone of the national comprehensive transportation system, playing a vital foundational role in the overall socioeconomic development of the country. Due to factors such as road structure, climate conditions, and traffic loads, roads often suffer varying degrees of damage. Therefore, comprehensive promotion of technical condition detection is a necessary means to improve the scientific decision-making level of highway maintenance. Intelligent detection of road surface cracks is a major technological bottleneck in this field.¹

Traditional image processing techniques for road surface crack segmentation mainly consist of several categories: filtering-based segmentation², segmentation based on texture and fractal geometric features³,threshold-based segmentation⁴, edge detection-based segmentation⁵ , and methods based on minimum distance⁶. Although traditional crack extraction algorithms have low computational costs, they are susceptible to issues such as lighting conditions and camera imaging making it difficult to directly extract crack features from the original images. The performance of these methods largely depends on the quality of the images being processed.

With the rapid development of computer vision technology, machine learning methods identify cracks by learning patterns on the image surface, which can mitigate the interference of background noise⁷. Its main techniques include Random Forest⁸,Support Vector Machine⁹, Artificial Neural Networks¹⁰ among others. Due to traditional machine learning methods relying on manually setting color or texture features to simulate cracks, they depend on domain experts to extract features, which can result in strong feature quality. The features manually set in these methods can only satisfy crack detection under certain specific conditions. When new crack environments emerge, these methods require reconfiguration, making them unable to meet the detection requirements for all road crack scenarios.

In recent years, deep learning has been widely used in the field of computer vision, which brings new opportunities for automatic identification of pavement cracks through automatic learning instead of manual feature setting¹¹. Researchers achieve automatic identification and extraction of road crack by constructing various deep convolutional neural network models and iteratively training them using a dataset of road crack samples.¹² proposed a Rectangular Convolutional Pyramid and Edge Enhanced Network, which utilizes a deep network architecture to construct a rectangular convolutional pyramid module to describe crack features of different structures. Then, through hierarchical feature fusion refinement modules and boundary refinement modules, they effectively promote the fusion of features at different scales. Tang et al.¹³ proposed EDNet to address the issue of class imbalance in crack segmentation. The encoder fits feature maps with road surface images, enhancing segmentation accuracy, while the decoder generates feature maps from ground truth images in an autoencoding manner, reducing the imbalance between crack and non-crack pixels. Guo et al.¹⁴ proposed BARNet, a network that adaptsively adjusts and refines crack boundaries. However, it requires manual adjustment of penalty weights for different types of cracks. Qu et al.¹⁵ proposed a deep supervised convolutional neural network for crack detection, utilizing a multi-scale convolutional feature fusion module. High-level features are directly introduced into low-level features at different convolutional stages, providing integrated direct supervision for convolutional feature fusion. AlHuda et al.¹⁶ proposed a road surface crack segmentation network based on class activation maps and an encoder-decoder architecture, fused the crack localization map generated by a classification network with an encoder, and then achieved accurate segmentation of road surface cracks through a decoder network.Yu et al.¹⁷ proposed the CCapFPN, which enhances the accuracy of crack detection by integrating features from different levels and scales. Wang et al. Yang et al.¹⁸proposed the PAFNet for road crack segmentation, which addresses the issue of information loss in crack detection through context fusion, dual attention, and dynamic weight learning. Jaziri et al.¹⁹ introduced a fractal-based crack simulator along with a corresponding crack dataset. They generated crack images using simulation techniques and obtained generalization ability to real cracks through effective learning methods.

The Transformer model was initially designed for natural language processing tasks. However, with further research, it has also been successfully applied in the field of computer vision. Some Transformer-based models and methods have also achieved success in crack detection. CrackFormer²⁰ adopts the SegNet architecture and introduces self-attention blocks and local attention. It enhances crack detection clarity through multi-stage lateral fusion. Another CrackFormer²¹ employs a multi-scale window strategy, utilizing four parallel feature extraction branches for local and global crack feature extraction. The model undergoes multiple stages of transformation, gradually reducing spatial resolution while increasing feature channel dimensions. It merges multi-scale feature representations to enhance performance. Compared to traditional convolutional neural networks, Transformers perform better in handling long range dependencies. However, they lack the ability to capture local relationships and have high computational complexity. As a result, some researchers have begun to combine CNNs and Transformers for crack detection tasks. Quan et al.²² proposed a model for crack extraction by utilizing a hybrid CNN and Transformer architecture. They leverage the advantages of convolutional neural networks in capturing local correlations while combining the strengths of Transformers in modeling global relationships to enhance fine extraction of crack boundaries. Bai et al.²³ proposed a Dual Encoding Multi-Scale Fusion Network (DMFNet) based on CNN and Transformer networks. By learning global and local feature interactions, they introduced attention enhancement and deep supervision mechanisms, achieving efficient crack detection. Guo et al.²⁴ utilized the Swin Transformer as an encoder to provide global crack semantic features and employed UperNet as a decoder to retrieve more detailed crack information, thus enhancing the accuracy of crack detection. Wang et al.²⁵ proposed CGTrNet, which incorporates a Transformer and convolutional feature fusion module to address the issue of dimension inconsistency and semantic gap between CNN and Transformer outputs. This effectively integrates both local and global information of cracks.

While existing crack detection and segmentation models have made significant progress in automation and accuracy, they still face several challenges. The slender structures of cracks may cause the network to fail to cover a sufficiently long area to maintain continuity. Even if continuous crack features exist, they may be partially covered by some convolution kernels, resulting in the network unable to fully extract continuous cracks. Additionally, pooling operations reduce the resolution of feature maps, which may lead to the loss or blurring of part of the cracks, further affecting continuity. To address this problem, this paper proposes for maintaining crack continuity extraction network CPCDNet.The main contributions of this paper are as follows:

• 1) Cracks, being long and narrow structures, typically appear as slender and curved features in images. Traditional convolutional neural networks, while performing exceptionally well in many image processing tasks, may lack sensitivity to such specific structures. In particular, traditional convolutional kernels may not adequately capture the details and shape variations of long, narrow features like cracks. To address this issue, this paper introduces the Dynamic Snake Convolution method, which dynamically adjusts the convolutional kernels to better accommodate the elongated structure of cracks, thereby improving crack detection performance.

• 2) In convolutional neural networks, the resolution of feature maps is often reduced due to downsampling operations. During the upsampling phase, these low-resolution feature needs to be restored to the original image size. However, due to the complexity of the downsampling process, pixel position discrepancies often arise during the restoration, leading to cracks appearing broken or discontinuous. To address this issue, this paper proposes the Crack Align Module, which uses learned offset values from the model to guide the restoration of pixel values during upsampling, ensuring the continuity of crack structures.

• 3) A weighted edge cross entropy loss function has been designed, which adjusts weights by applying different penalties based on the distance of each pixel point from the crack edge. Since pixels near the crack edges often exhibit higher uncertainty, the distance transform values near the edges require smoothing. This paper addresses the limited precision issue at the crack edges by attenuating the distance transform values near the edges, thereby slowing down the model’s learning in these areas.

The remaining organization of this paper is as follows: “Related work” reviews crack extraction methods based on convolution, feature fusion, and loss functions. Then, in “CPCDNet model overview”, we describe our proposed model approach. In “Experiments and results”, we present and analyze experimental results. Finally, in “Conclusions”, we summarize our work and discuss future prospects.

Related work

Due to the proposed method in this paper involving convolution-based, feature fusion-based, and loss function-based crack detection methods, we will introduce related work on each of these aspects in the following subsections.

Methods based on convolution

Due to the elongated structure of cracks, conventional square convolutions only extract a small portion of crack features during the extraction process, while extracting more irrelevant background features. Inspired by Inception-v3, Zhou²⁶ designed the Enhanced Convolution Block, which splits a 3$\times$3 convolution into a 1$\times$3 convolution, a 3$\times$1 convolution, and a 3$\times$3 convolution to extract crack features separately and then fuse them, enriching the feature representation of cracks. Qin et al.²⁷ introduced deformable convolutional blocks to address the issue of irregular shapes in crack detection. Deformable convolutions allow for the formation of deformable kernels by adding learnable offsets to fixed sampling positions in standard convolutions. These offsets are learned from previous feature maps through additional convolutional layers, enabling the convolution operation to adaptively adjust object deformations in a better way, thus better accommodating cracks of different shapes. Cracks occupy a small proportion of the entire image pixels and are widely distributed. Regular convolutions have limited receptive fields and can only perceive input data within a limited range. This limitation may result in the failure to capture the global features of cracks. Although dilated convolutions can increase the receptive field to some extent, they may produce poor segmentation results for small cracks. Lin et al.²⁸ combined dilated convolutions with dilation rates of 1, 2, and 3 to detect cracks. This approach enlarges the receptive field while retaining more crack information and prevents the loss of small cracks. Choi et al.²⁹ applied depthwise separable convolutions in reverse order within the module, aiming to improve computational speed and reduce costs. This approach optimizes feature propagation, accelerates training and inference processes, and is suitable for efficient deep learning tasks, thereby enhancing crack detection more effectively.

Methods based on features fusion

In crack detection tasks, due to the complexity and diversity of cracks, a single feature often struggles to comprehensively capture all the characteristics of cracks. Therefore, by feature fusion, various features can be combined to enhance the overall performance of the model, making it more suitable for different types and complexities of crack detection scenarios. Zhong et al.³⁰ proposed W-SegNet, which utilizes multi-scale feature fusion, employs upsampling and cascading operations, and combines convolutions to comprehensively segment road crack of different sizes in the image, thereby enhancing pixel segmentation performance. Ye et al.³¹ proposed a UNet-based network that combines ASPP and dilated convolutions. This network preserves and fuses information from different scales to improve the model’s accurate segmentation ability for cracks. Liu et al.³²proposed a feature fusion method based on attention mechanisms, where the model adaptively adjusts channel weights to emphasize features contributing more significantly to the information. This approach improves the segmentation performance for small cracks. Qu et al.³³ preserved more detailed information through multi-scale upsampling and enhanced the context information transmission between feature maps using attention mechanisms, thereby improving segmentation accuracy. Yan et al.³⁴ proposed the dual channel network CycleADCNet. One channel focuses on extracting strong contextual information of targets distributed around and in corners of cracks, while the other channel extracts feature with global contextual information.

Methods based on loss function

In road crack segmentation tasks, there is a significant imbalance between pixels belonging to the background and those belonging to cracks. If the model treats all pixels equally, the pixel loss will be predominantly guided by the background region, while the influence from the crack region will be relatively minor, this imbalance leads to lower accuracy in crack segmentation. Currently, many researchers have proposed different loss functions to address this issue. Du et al.³⁵ compared twelve commonly used loss functions on four benchmark datasets. The results showed that weighted binary cross-entropy loss, Focal loss, Dice-based loss, and composite loss functions significantly outperformed other functions. Mei et al.³⁶ transformed the pixel-level crack detection problem into a connectivity problem. By generating eight connectivity graphs and considering the connectivity between pixels and their neighboring pixels, designed a new loss function to optimize neural network parameters. This method comprehensively considers the morphological features of cracks, enhances the neural network’s ability to learn crack connectivity structures, and thus improves the accuracy and robustness of pixel-level crack detection. Ali et al.³⁷ proposed a weighted cross-entropy loss function. They utilized local weighting factors to calculate the reciprocal of the ratio between crack pixels and non-crack pixels in each image. This approach assigns smaller weights to background regions and larger weights to crack regions. Fang et al.³⁸ proposed a weighted loss function based on the traditional cross-entropy loss function. Considering the severe imbalance in crack data, they introduced weighted classification loss by assigning different importance weights to different classes, alleviating the impact of imbalanced data on model training. Li et al.³⁹ introduced power functions, logarithmic functions, and exponential functions on top of the cross-entropy function. They dynamically adjusted penalties based on crack sample statistics, providing a comprehensive approach to achieve accurate crack detection.

CPCDNet model overview

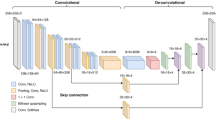
This paper proposed a CPCDNet based on the UNet architecture. Due to the elongated shape of cracks, traditional convolutions with fixed shapes struggle to capture both global and detailed features comprehensively. In this paper, we introduce Dynamic Snake Convolution at the first of convolutional layer to better adapt to and capture crack structures, significantly enhancing sensitivity to elongated structures while effectively controlling the network’s parameter count. During the decoding stage, UNet requires continuous upsampling operations and feature fusion with the corresponding parts from the encoder after each upsampling step. However, bilinear interpolation-based upsampling cannot accurately restore the position information of crack edges. Therefore, this paper proposes the Crack Align Module to address this issue. The module adjusts the upsampling of high-level feature maps accurately through learned offset values, enabling better alignment of feature maps at different levels to accurately restore the position information of crack edges. In the loss function part, this paper designs the Weighted Edge Cross Entropy Loss Function, which leverages the distance of each pixel in the image to the crack boundary and the characteristics of crack edges to allocate loss weights, thereby enhancing the focus on crack boundaries. The architecture of CPCDNet is illustrated in Fig. 1.

Figure 1

The structure of CPCDNet.

Dynamic snake convolution

Since cracks are usually long in the image and the shape of the conventional convolution is fixed, this may cause the model to be limited by the fixed shape of the convolution kernel in learning the crack structure, making it difficult to capture the global and detailed features of the cracks. While deformable convolution⁴⁰ allows the convolutional kernel to dynamically adjust its shape during the learning process, better adapting to the elongated structure of cracks, but it also has drawbacks, manipulating all biases of a single convolutional kernel deformation is learned all at once in the network, and the range of this bias is very large, allowing for arbitrary translation within the receptive field range. This operation can easily cause the model to lose fine structural features, which is not a very reasonable setting for tasks involving segmentation of elongated crack structures. Dynamic Snake Convolution (DSC)⁴¹ incorporates continuity constraints into the design of convolutional kernels. At each convolutional position, the previous position serves as the reference point, allowing for free selection of the oscillation direction while ensuring the continuity of feature extraction. Therefore, compared to deformable convolutions, where the learned positions may be discrete, the position variations of constrained deformable convolutions are continuous, continuous positions enable better extraction of information from elongated edges. Therefore, we embed Dynamic Deformable Convolution into UNet, enhancing the model’s sensitivity to elongated structures and better capturing crack structures. This improves the performance of crack detection. However, since DSC introduces additional parameters, applying it to all layers of UNet may result in excessive parameterization, increasing computational complexity. Given that cracks in images are relatively small in proportion, we choose to add Dynamic Deformable Convolution only to the first layer of UNet to balance model performance and computational efficiency. This approach allows us to retain sensitivity to elongated structures in crack detection tasks while effectively controlling the number of parameters, avoiding excessive model complexity. DSC is illustrated in Fig. 2.

Figure 2

The structure of dynamic snake convolution.

In Fig. 2, the changes along the x-axis and y-axis within the receptive field are given by the following equations:

$$\begin{aligned} {{K}_{i\pm c}}= & \left\{ \begin{matrix} ({{x}_{i+c}},{{y}_{i+c}})=({{x}_{i}}+c,{{y}_{i}}+\Sigma _{i}^{i+c}\Delta {y}), \\ ({{x}_{i-c}},{{y}_{i-c}})=({{x}_{i}}-c,{{y}_{i}}+\Sigma _{i-c}^{i}\Delta {y}), \\ \end{matrix} \right. \end{aligned}$$

(1)

$$\begin{aligned} {{K}_{j\pm c}}= & \left\{ \begin{matrix} ({{x}_{j+c}},{{y}_{j+c}})=({{x}_{j}}+\Sigma _{j}^{j+c}\Delta {x},{{y}_{j}}+c), \\ ({{x}_{j-c}},{{y}_{j-c}})=({{x}_{j}}+\Sigma _{j-c}^{j}\Delta {x},{{y}_{j}}-c), \\ \end{matrix} \right. \end{aligned}$$

(2)

where K represents the fractional positions in Eqs. (2) and (3), and $K^{'}$ enumerates all integer spatial positions. As shown in Fig. 3, due to the mismatch between the elongated structure of the ruler and the cracks in the image, the attention of UNet towards the ruler significantly decreases after adding DSC, compared to the original UNet, which pays more attention to the cracks. This demonstrates the effectiveness of DSC.

Figure 3

Feature map visualization during training with or without DSC addition. After adding DSC, the focus on the ruler in the feature map is significantly reduced, while the crack extraction is significantly more refined.

Crack align module

The occurrence of positional shifts of cracks in the up-sampled recovery pixels is one of the causes of missed detection of edges, and such pixel positional shifts may result in blurred or shifted edges, leading to missed identification of edges, as shown in Fig. 4. For coarser cracks, the occurrence of leakage detection inside the crack does not cause discontinuity in crack extraction, as in (a). In contrast, in (b), the leakage occurs at the edge location of the crack, which leads to a fracture situation. (c) is a finer crack with low contrast, there is no internal or external distinction, which basically results in a fracture situation as long as a missed detection occurs. (d) is a complex structure consisting of alligator crack, in which case the cracks are also very susceptible to extraction discontinuities.

Figure 4

Discontinuity in crack identification.

UNet requires continuous upsampling operations during the decoding stage, and after each upsampling, it performs feature fusion with the corresponding part of the encoder. However, the upsampling method using bilinear interpolation cannot accurately restore the position information of the crack edges, resulting in discontinuities in crack extraction. This is because during the downsampling process, positional information gradually gets lost, which may result in different input images yielding the same output after downsampling, as shown in Fig. 5. The pixel values at positions A and B in the same image, after downsampling, converge to position C. However, during upsampling, position C cannot definitively determine which of the same results should be restored. When the feature maps from the encoder part are pixel-wise fused with these misaligned results, it is easy to result in incorrect fusion outcomes, and continuous upsampling and downsampling exacerbate this misalignment.

Figure 5

Schematic diagram of the downsampling process.

The Crack Align Module proposed in this paper addresses this issue, as shown in Fig. 6.

Figure 6

The structure of crack align module.

The Crack Align Module first performs upsampling on high-level feature maps and concatenates them with low-level feature maps. Then, it introduces a $1\times 1$ convolution to generate a feature map with a depth of 2, where the first layer encodes the shift information in the x-direction, and the second layer encodes the shift information in the y-direction. Adjustments are made through learnable offset values. By predicting the position deviation offset values based on traditional bilinear interpolation upsampling, the model corrects the results of traditional upsampling, enabling more accurate localization of crack pixel positions. The expression is as follows:

$$\begin{aligned} {{F}_{offset}}= & Con{{v}_{1\times 1}}(Concatenate(UpSample({{H}_{high}}),{{H}_{low}}),W) \end{aligned}$$

(3)

$$\begin{aligned} {{I}_{translated}}= & Translate(I,{{F}_{offset\_x}},{{F}_{offset\_y}}) \end{aligned}$$

(4)

Where W is offset weight, after generating the translation information, CAM utilizes this information to guide the upsampling of high-level feature maps, aligning feature maps at different levels more effectively to preserve more boundary position information of cracks. At the same time, the model can adjust the upsampling positions more accurately, thereby reducing or eliminating discontinuities caused by interpolation, making the pixel value changes in the crack area smoother, thus improving the continuity of cracks. Finally, by fusing the feature maps from the encoder at each pixel, the occurrence of misalignment is reduced, resulting in a reasonable fusion result. The final expression is as follows:

$$\begin{aligned} H=Fuse({{H}_{low}},UpSample({{H}_{high}},{{F}_{offset\_x}},{{F}_{offset\_y}})) \end{aligned}$$

(5)

Figure 7

Feature map visualization during training with or without CAM addition. After adding CAM, the extraction of tiny crack in the feature map is significantly more continuous.

From Fig. 7, it can be observed that the small cracks in the image are very similar to the background. With the addition of CAM, UNet can accurately capture these cracks, while the original UNet pays less attention to them, resulting in discontinuities. This demonstrates the effectiveness of CAM.

Weighted edge cross entropy loss function

The accuracy of the crack edge extraction is crucial to maintain the continuity of the crack extraction; incorrect detection or missed identification at the edges will result in incomplete shape and contour of the crack, which in turn will affect the continuity of the crack. This paper proposes a weighted edge cross entropy loss function to enhance the edge features of pavement cracks. In Fig. 8, assuming the green region A represents the actual crack area and the blue region represents the model’s prediction, the yellow region B denotes the incorrectly predicted parts. These errors contribute to the loss value.

Figure 8

A represents the actual crack area, B represents the model’s predicted result, and C represents the background area.

Near the edges of cracks, the model’s accuracy is limited. If a prediction error occurs, a smaller penalty should be applied. However, in regions far away from the crack edges, where the characteristics are significantly different from those of the crack area, the model has a high probability of identifying this region as a background region. In case of a prediction error, a larger penalty should be applied. In this paper, the distance transform method is used to calculate the nearest distance L from each pixel to the edge. Pixels near the edge will have smaller values, while those further away will have larger distance values. To avoid extreme weighting, smooth processing is required. The expression is as follows:

$$\begin{aligned} {{L}_{ij}}={{\log }_{2}}(L+2) \end{aligned}$$

(6)

where $L_{ij}$ represents the distance value at pixel position (i,j) , and this value is taken as the weight for the corresponding pixel point. The distance value inside the crack should be negative, thus: $-1\times L_{ij}$ . The distance value outside the crack should be positive, thus: $1\times L_{ij}$ . This way, when the model’s prediction is correct, the forward operation result inside the crack tends towards 1. When multiplied by the distance value inside the crack, it becomes a very small value. The forward operation result outside tends towards 0. When multiplied by the distance value outside, it becomes a very small value. Finally, taking the average of all pixels’ results yields the global minimum value. Due to the disproportionate ratio of foreground to background in the dataset, the distance transform values for the exterior region should be adjusted. Otherwise, the extensive background region may receive too much attention, which is detrimental to model convergence. Therefore, for $L_{ij}$ outside the mask, we need to set an upper limit. The expression is as follows:

$$\begin{aligned} {{L}_{ij}}=\max ({{L}_{\max }},{{L}_{ij}}) \end{aligned}$$

(7)

Additionally, it is important to note that the distance transform values near the edge also need to be smoothed. Since both the model’s prediction accuracy and the annotation accuracy are poor, forcibly applying distance transform values may lead to overfitting. In this paper, pixels at positions where the absolute value of the distance transform is less than $\beta$ are multiplied by a scaling factor of 0.5, ensuring that the resulting loss values are not too large. This is illustrated in Fig. 9.

Figure 9

$\beta$ schematic diagram.

The results of the accuracy of $\beta$ in setting different values are shown in Table 1, and the highest value is obtained in $\beta$ = 5 numerical indicators, and $\beta$ is set to 5 in this paper. Figure 10 shows the results of the model taking different $\beta$ identifications.

During the model training process, the cross-entropy function aids in model convergence, thus it is also included as part of the loss function. Additionally, the Weighted Edge Loss and cross-entropy functions are combined to form the final Weighted Edge CE Loss.

$$\begin{aligned} WE= & \sum \limits _{ij}{0.5\times \beta \times {{L}_{ij}}} \end{aligned}$$

(8)

$$\begin{aligned} WECEL= & W\times CE+(1-W)\times WE \end{aligned}$$

(9)

where CE represents the cross entropy function, WE represents the edge loss function, and W is the weight assigned to both loss functions. From Fig. 11, it can be observed that after incorporating WECEL, UNet exhibits finer boundary detection of cracks, demonstrating the effectiveness of WECEL.

Table 1 The effect of different $\beta$ values on the accuracy of the model.

Figure 10

Different $\beta$ recognition results of values.

Figure 11

Feature map visualization during training with or without WECEL addition. After adding WECEL, the boundaries of the feature map become noticeably more refined.

Experiments and results

Datesets

We evaluated the performance of CPCDNet on four benchmarks, including the Crack500, CFD, DeepCrack, and GAPs384 datasets, Table 2 demonstrates the division of the dataset:

Crack500⁴²: In this dataset, the authors collected road crack images using a smartphone with a size of approximately 2000$\times$1500 pixels, each image annotated at the pixel level. Due to the significant difference in dataset size compared to others, the images were cropped to 512$\times$480 in this study.

CFD⁸: This dataset is constructed from 118 images captured using smartphones to comprehensively reflect the urban road conditions in Beijing, China. Each image has a manually annotated ground truth contour, capturing noise such as shadows, oil stains, and water stains.

GAPs384⁴³: This dataset is constructed by selecting 384 crack images from the GAPs dataset and annotating them at the pixel level to create a new crack dataset called GAPs384.

Deepcrack537⁴⁴: Liu et al. established a dataset called DeepCrack537, comprising 537 images with annotation labels. All images and labels are sized at 544 $\times$ 384 pixels. DeepCrack537 is randomly partitioned, with 300 images used for training and 237 images used for testing, serving as the dataset for training and evaluating all models.

Table 2 Dataset splitting.

Training strategy

The parameters used for model training in this study are listed in Table 3. The training was conducted on a server with the following specifications: CPU: Intel(R) Core(TM) i7-9700 CPU, GPU: Nvidia GeForce RTX 3090. All models were implemented using the PyTorch framework. At the start of training, the weight W for the loss function is set to 1, indicating that only the cross-entropy loss function is utilized. With each epoch, the weight W for the cross-entropy function is gradually decreased, while the weight for the Weighted Edge Loss is increased. The weight for the cross-entropy loss is incremented by (epoch/300)$\times$0.1 , with each epoch, gradually increasing until reaching 0.1.

Table 3 Training parameters.

Evaluation metrics

In this study, precision, recall, mIoU, and F-score are used as metrics for crack identification accuracy. Here, TP represents the number of true positives, FP represents the number of false positives, and FN represents the number of false negatives. The calculation of these four metrics is as follows:

$$\begin{aligned} Precision= & \frac{TP}{TP+FP} \end{aligned}$$

(10)

$$\begin{aligned} Recall= & \frac{TP}{TP+FN} \end{aligned}$$

(11)

$$\begin{aligned} F= & \frac{2\times Precision\times Recall}{Precision+Recall} \end{aligned}$$

(12)

$$\begin{aligned} mIoU= & \frac{1}{2}(\frac{TP}{TP+FP+FN}+\frac{TN}{TN+FN+FP}) \end{aligned}$$

(13)

Comparison of different networks

In order to compare the performance of CPCDNet with other mainstream networks, this study trained U-Net⁴⁵, DeepLabv3+⁴⁶, HRNet⁴⁷, Segformer⁴⁸, DeepCrack⁴⁴, Crackseg⁴⁹ and CrackW-Net⁵⁰on the four datasets. CPCDNet outperforms other networks in all metrics averaged across the four datasets. Tables 4, 5, 6, and 7 show the model’s recognition accuracy across four public datasets,the recognition results are shown in Figs. 12 and 13.

Table 4 Summary of crack segmentation results from 8 networks on Crack500.

Table 5 Summary of crack segmentation results from 8 networks on Deepcrack537.

Table 6 Summary of crack segmentation results from 8 networks on Gaps384.

Table 7 Summary of crack segmentation results from 8 networks on CFD.

Figure 12

Each model identifies the results for each dataset, (a–c) are and Gaps384 (d–f) are Crack500.

Figure 13

Each model identifies the results for each dataset, (a–c) are and CFD (d–f) are DeepCrack537.

• (1) Crack500: This dataset contains clearer cracks compared to the other three datasets, with most cracks occupying a higher proportion of the images. However, we observed that the annotations are rougher compared to the actual cracks, and there are some annotation errors, possibly due to the subjective judgment and uncertainty during the annotation process, which increases the difficulty of the crack detection task, CPCDNet achieves an mIoU of 80.36% and an F-score of 87.12%. Compared to the original UNet, CPCDNet improves mIoU by 0.67%, Recall by 0.85%, Precision by 0.05%, and F-score by 0.54%.

• (2) CFD: This dataset primarily consists of asphalt road surfaces with complex background information and numerous interferences, making it easy for the model to misclassify some background information as cracks. Additionally, the crack structures in this dataset are highly complex, which makes it extremely prone to missing some cracks during detection. In column (c) of Fig. 13, we can observe that most models identify stains in the background as cracks. CPCDNet achieves an mIoU of 77.71% and an F-score of 85.57%. Compared to the original UNet, CPCDNet improves mIoU by 1.68%, Recall by 0.51%, Precision by 1.06%, and F-score by 0.86%.

• (3) Deepcrack537: This dataset mainly comprises cement road surfaces with relatively less background noise, resulting in the best performance among all models across the four datasets. Deepcrack537 contains numerous small cracks, often appearing alongside clear cracks, making it challenging for models to identify them. For instance, in column (d) of Fig. 13, small cracks are difficult to extract as they have similar contrast to the ground. Our model achieves a Recall of 90.98% and an F-score of 95.05% on this dataset. Compared to the original UNet, CPCDNet improves mIoU by 6.16%, Recall by 6.79%, Precision by 0.48%, and F-score by 4.03%.

• (4) GAPs384: This dataset presents significant challenges for crack identification. Firstly, the low contrast between cracks and the background makes it difficult to distinguish cracks, leading to the possibility of mistaking background clutter for cracks. Secondly, the cracks in this dataset are relatively small and sparse in the images, making them hard for models to capture. Consequently, the performance of all models on this dataset is the poorest among the four datasets. Our model achieves the best results with an mIoU of 71.16% and an F-score of 79.82%. Compared to the original UNet, CPCDNet improves mIoU by 7.73%, Recall by 11.62%, Precision by 0.1%, and F-score by 8.94%.

Figure 14

PR curves of each model on publicly available data.

Figure 15

Loss curves of each model on publicly available data.

Our model outperforms other mainstream models, especially in the extraction of fine cracks and crack boundaries, producing more refined and continuous results. Compared to other models, our algorithm more sensitively captures tiny cracks and extracts finer and more complete crack boundaries, capturing more details of crack boundaries. Visual results intuitively demonstrate our model’s better preservation of details and clarity of crack boundaries compared to other models. Figure 14 shows the PR curves of each model on different datasets. Figure 15 shows the loss curves of each model on different datasets.

Effectiveness analysis

We tested the model with several images outside the existing image database. Figure 16 shows images (a)–(e) with pavements featuring water seepage and various types of interference, while (f) and (g) are two negative samples. CPCDNet was able to accurately detect cracks even without training on similar samples and did not misidentify pavement stains or manhole covers as cracks, demonstrating the effectiveness of the model.

Figure 16

CPCDNet’s performance in detecting pavement cracks with interference.

At the same time, we performed a 10% zoom on the images from four datasets, and the model was still able to accurately detect pavement cracks, the recognition result is shown in Fig. 17.

Figure 17

CPCDNet’s performance on zoomed pavement images.

Ablation analyse

To validate the effectiveness of our model approach, we conducted five sets of ablation experiments on the Deepcrack537 dataset: (1) UNet, (2) UNet+DSC representing UNet with DSC convolution added to the first layer of the encoder, (3) UNet+CAM representing UNet with CAM added to the skip connections, (4) UNet+WECEL representing UNet with the loss function replaced by WECEL, and (5) CPCDNet proposed in this paper. Figure 18 presents the recognition results of different models added to the test set. In the first row, UNet fails to recognize the marked area, while with the addition of our algorithm, the recognition becomes more completed and detailed. In the second row, UNet exhibits misrecognition, which is substantially reduced after adding our algorithm. In the third row, UNet fails to detect the small cracks on the right side, but with the addition of our algorithm, the small cracks are effectively identified. Meanwhile, in the fourth row, UNet shows crack fragmentation, which is resolved by adding our algorithm. CPCDNet not only enhances the capability to extract small features but also addresses the issue of inaccurate boundaries. The analysis indicates the effectiveness and superiority of our algorithm.

Figure 18

Add different models to identify Deepcrack537 results.

From Table 8, it can be observed that adding DSC increased mIoU by 1.23%. This means that DSC can enhance the model’s ability to capture detailed information about crack pillars during the encoding phase, thus confirming the hypothesis that DSC can better fit the shape of road cracks. Adding CAM increased mIoU by 4.90%, indicating that the introduction of this module improved the positional accuracy of pixel recovery after upsampling. Adding WECEL resulted in an increase in mIoU by 3.73%, suggesting that WECEL, through weight adjustment, enabled the model to focus more on the edge regions of cracks, thereby improving the predictive performance of crack edges. This allows the model to more accurately capture and emphasize edge information in crack detection tasks.

Table 8 Prediction each model predicts the accuracy of Deepcrack537.

Conclusions

To address the issues of discontinuity in crack detection models, a pavement crack image segmentation algorithm called CPCDNet has been proposed. Extensive experiments on four crack datasets have demonstrated the superior segmentation performance of CPCDNet. The main contributions of this paper are as follows:

• (1) Introduced DSC to enhance the perception of elongated structures, thereby improving the capture of crack structures.

• (2) Designed the CAM module, which uses learned offset values to guide the pixel value recovery during the upsampling process, thereby enhancing the continuity of crack extraction.

• (3) Developed WECEL, which adjusts weights by applying different penalties based on the distance of each pixel to the crack edges, improving crack edge detection capability.

In the design of WECEL, the $\beta$ value was manually controlled using empirical methods. In the future, $\beta$ should be made a dynamically varying parameter based on crack width to improve the algorithm’s applicability and accuracy. Additionally, we observed that some cracks are overly smoothed during edge extraction. While this enhances the clarity and continuity of crack extraction, it can also lead to the loss or blurring of crack edges, resulting in the loss of some detailed information and impacting the algorithm’s precision. Therefore, further optimization of the crack edge extraction process is needed to balance smoothing with detail preservation. Finally, the current model’s parameter count still does not meet the requirements for real-time crack detection. Future work should focus on further simplifying the model’s complexity to better meet the needs of routine inspections.