Optimized dual-tree complex wavelet transform aided multimodal image fusion with adaptive weighted average fusion strategy

Abstract

Image fusion is generally utilized for retrieving significant data from a set of input images to provide useful informative data. Image fusion enhances the applicability and quality of data. Hence, the analysis of multimodal image fusion is a new to the research topic, which is designed by combining the images of multimodal into single image in order to preserveexact details. On the other hand, the existing approaches face challenges in the precise interpretation of source images, and also it have only captured local information without considering the wide range of information. To consider these weaknesses, a multimodal image fusion model is planned to develop according to the multi-resolution transform along with the optimization strategy. At first, the images are effectively analyzed from standard public datasets and further, the images given into the Optimized Dual-Tree Complex Wavelet Transform (ODTCWT) to acquire low frequency and high frequency coefficients. Here, certain parameters in DTCWT get tuned with the hybridized heuristic strategy with the Probability of Fitness-based Honey Badger Squirrel Search Optimization (PF-HBSSO) to enhance the decomposition quality. Then, the fusion of high-frequency coefficients is performed using adaptive weighted average fusion technique, whereas the weights are optimized using PF-HBSSOto achieve the optimal fused results. Similarly, the low-frequency coefficients are combined by average fusion. Finally, the fused images undergo image reconstruction using the inverse ODTCWT. The experimental evaluation of the designed multimodal image fusion illustratessuperioritythat distinguishes this work from others.

Introduction

Image fusion is a recently emerging concept owing to the amplifying requirements of diverse image processing applications especially in medical-aided diagnosis, video surveillance, remote sensing, and so on¹. Image fusion is rapidly growing with various imaging sensors and the accessibility of a huge range of imaging techniqueslikeComputed Tomography (CT), and Magnetic Resonance Images (MRI), etc. It has explored the healthcare community for efficient decision-making and treatment to patients². In addition, the major goal of image fusion also considers various factors like the fused image should be reliable and robust, inconsistencies or artifacts have to be eliminated, and salient information in any of the inputs must not be eradicated². On the other hand, the major issues of image fusion research are similarity across modalities as data formation can be statistically uncorrelated and completely different, the efficient feature illustration of every modality and image noise, etc.³. In addition to these requirements in real-time applications, image fusion-guided disease prognosis and diagnosis have been formulated to assist medical professionals in decision-making as there is a restriction on human interpretation of clinical images owing to their subjectivity⁴. The major reason of multimodal clinical image fusion is to get the information with superior quality by combining the complementary information from various source images⁵.

Image fusion can be performed in various ways including multi-focus, multi-temporal, multi-modal, and multi-view fusion techniques⁶. Among these approaches, multi-modal image fusion is more essential, and it is carried out on images gathered by different sensors. Moreover, it is more helpful in getting precise results, especially in the medical field⁷. Generally, multi-modal image fusion combines both complementary and supplementary information of source images⁸.The multimodal image fusion results in final fused images that is free from redundant and random information. It minimizes the storage space, and stores one final fused image instead of storing two individual images⁹. The amalgamation of two different modalities results in precise localization or detection of abnormalities.The fundamental features of multi-modal image fusion are listed here. It reduces the uncertainty as the joint information from various sensors minimizes the vagueness related to the decision or sensing process¹⁰. The temporal and spatial coverage is extended for better performance. Fusion requires condensed representations to give complete information on images¹¹. Multi-modal image fusion increases the system efficiency by reducing the redundancy in different measurements. It enhances reliability and reduces noise¹².

Generally, image fusion is conducted via different approaches like transform domain as well as spatial domain methods. The consideration of high pass filtering, Intensity and Hue Saturation (IHS), Brovey method etc., are performed in the spatial domain methods. Thus, there is a need of adopting transform domain approaches come into the picture. Some popular transforms used for image fusion process include Contourlet (CT)¹³, Curvelet (CVT)¹⁴, Stationary Wavelet (SWT)¹², Discrete Wavelet (DWT)¹¹, DTCWT¹⁵, and Non-Subsampled Contourlet Transform (NSCT)¹⁶. While estimating with spatial domain methods, transform domain techniques get higher efficiency in terms of image fusion.On the other hand, a reliable, accurate, and appropriate image fusion approach is needed for several classes of images in diverse domains that must be simply interpretable for getting superior image fusion performance¹⁷. Some challenges are inexpensive computation time, uncontrollable acquisition conditions, and errors found in fusing the images. Thus, there is a need of suggesting an innovative multi-modal image fusion approach with the integration of two medical images by adopting transform domain techniques.

The innovationssuggested in this paper are listed here.

• To recommend a new Multimodal Image Fusion with intelligent approaches like ODTCWT and adaptive weighted average fusion strategy along with the suggestion of hybrid nature-inspired approaches for performing medical image fusion for better localization of abnormalities and disease diagnosis through the gathered images.

• To propose a novel ODTCWT and adaptive weighted average fusion strategy for efficient image fusion using a new hybrid nature-inspired algorithm termed PF-HBSSO for obtaining the salient information from the input images and formulates the objective as the maximization of fusion mutual information.

• To implement the PF-HBSSO algorithm by the combination of Honey Badger Algorithm (HBA) as well as Squirrel Search Algorithm (SSA) for recommending ODTCWT by optimizing the filter coefficients and weights for adaptive weighted average fusion model for increasing the convergence rate that aids in maximizing the fused image quality.

Followed by introduction, the forthcoming section is shown.Part II specifiesthe discussion on existing works. Part III recommends an innovativemodel for multimodal image fusion. Part IV specifies the generation of low and high frequency coefficientsusingODTCWT. Part V derives the fusion of high frequency and low frequency by heuristic algorithm. Part VI estimates the results and Part VII completes this paper.

Study on existing works

Literature review

Research work based on deep learning models

In 2021, Zuoet al.¹⁸ has presented a new automated multi-modal medical image fusion strategy using classifier-based feature synthesis with a deep multi-fusion scheme. They have used a pre-trained autoencoder to analyze the fusion strategy by multi-cascade fusion decoder and a feature classifier. The public datasets were used for analyzing the image fusion results. TheParameter-Adaptive Pulse Coupled Neural Network (PAPCNN)was used in thelow and high-frequency coefficients. This image fusion was especially used for classifying brain diseases via the final fused images.

In 2022, Sun et al.¹⁹ have suggested a new deep MFNet using LiDAR data and multimodal VHR aerial images for performing medical image fusion. The multimodal learning and attention strategy was utilized for adaptively fusing the intramodal and intermodal features. A multilevel feature fusion module, pyramid dilation blocks, and a multimodal fusion strategy were implemented. This proposed network has adopted the adaptive fusion of multimodal features, enhanced the effects of global-to-local contextual fusion, and improved the receptive field. Moreover, this network was optimized using a multiscale supervision training strategy. The ablation studies and simulation outcomes have supreme performance of the recommended MFNet.

In 2021, Fu et al.²⁰ have proposed a novel multimodal biomedical image fusion approach through deep Convolutional Neural Network (CNN) and rolling guidance filter”. The VGG model was applied for enhancing the image details and edges. Here, the rolling guidance filter was intended for extracting the detail and base images. Here, the fusion was done on both perceptual, detail, and base images with three diverse fusion methods. They have then chosen the image decomposition constraints by simulation for getting the suitable structure and texture images. In addition, the normalization operation was used to the perceptual images to eradicate noise and feature variations. Finally, it has shown the superior fusion outcomes and achieved better performance in terms of various objective measures.

In 2022, Goyal et al.²¹ have collected the images from standard sources, where NSCT was used for extracting the features. Next, a Siamese Convolutional Neural Network (sCNN) was applied for getting the significant features by weighted fusion. In order to eradicate noise, a new method has beenenhanced rate. Finally, the combination of NSCT + sCNN + FOTGV strategies has helped in enhancing the image fusion and also exhibited higher performance on both quantitative and visual analysis.

In 2022, Venkatesan and Ragupathyan²² have suggested a medical image fusion approach for fusing both MRI and CT images for recommending a healthcare model. To get both spectral and spatial domain features, the hybrid technique by integrating Deep Neural Network and DWT was suggested for getting more accuracy rate while estimating with traditional approaches. The performance enhancement was noticed in terms of standard deviation and average entropy for the designed DWT-CNN fusion approach compared with other wavelet transform methods. The superior efficiency on image fusion was noticed and has achieved considerable fusion performance rate.

In 2018, Bernal et al.²³ have suggested a supervised deep multimodal fusion model for automated human activity and egocentric action recognition to monitor and assist patients. This model has collected video data using body-mounted or egocentric camera and motion data gathered with wearable sensors. The performance was estimated on multimodal public dataset and has analyzed the efficiency. They have used CNN-LSTM architecture for performing the multimodal fusion to get the results regarding automated human activity and egocentric action recognition.

Research work based on machine learning algorithms

In 2021, Duan et al.²⁴ have recommended a new regional medical multimodal image fusion by adopting Genetic Algorithm (GA)-derived optimized approach. A weighted averaging technique was recommended for averaging the images of the source clinical images. Next, a fast Linear Spectral Clustering (LSC) superpixel technique was used for getting the homogenous regions and preserved the detailed information of images, which has segmented the average images and obtained the superpixel labels. The most significant regions were chosen and produced a decision map. The efficiency of the designed fusion approach was estimated via various experimental evaluations. Finally, the performance estimation on GA-based image fusion has shown the superiority on final fused images over others.

Research work based on image processing techniques

In 2022, Kong et al.²⁵ have implemented a new medical image fusion approach via Side Window Filtering (SWF) and Gradient Domain-Guided Filter Random Walk (GDGFRW) in the Framelet Transform (FT) domain. Initially, FT was used on standard multimodal images for getting the residual and approximate illustrations. Then, a new GDGFRW was used for integrating the superiority of GD and GFRW that has built for interpreting the sub-bands, and the fusion was done by SWF. Next, inverse FT was performed for getting the residual models have fused images. The performance were addressed the fusion issues and outperformed the recent representative ones regarding objective estimation and subjective visual efficiency.

Comparative analysis of the existing techniques and proposed model

In 2023, Zhang et al.²⁶ have implemented the novel fusion approach using Infrared-To-Visible Object Mapping (IVOMFuse) for extracting the target region from the infrared image. Further, the Expectation–Maximization (EM) has evolved to tune the probabilities in the target region. The fused image was attained by combining PCA and average fusion strategy. Hence, the final validation was attained by considering the TNO, CVC14, and RoadScene to get the final outcomes. In 2022, Zhou et al.²⁷ have suggested the differential image registration model termed as robust image fusion to assist thermal anomaly detection (Re2FAD). The fusion strategy has been effectively done to enhance the accuracy. In 2023, Gu et al.²⁸ have implemented the improved end-to-end image fusion approach (FSGAN) model to enhance the image fusion approach. Here, the auxiliary network has been extracted to enhance performance with diverse experiments.

Due to the heterogeneous nature, the multimodal image fusion is challenging in accordance of misalignment and non-linear relationships between the input data²⁶. Also, the decomposition based methods are not highly preferred in the fusion model²⁷. However, there is a complexity of discovering better multimodal images with fusion quality estimation in the suggested image fusion approaches²⁸.To eradicate the drawbacks in the existing techniques, an effective deep learning method is implemented in the multimodal image fusion model. By considering the decomposition model, the multimodal image fusion gets enhanced by analyzing the texture details and smoothen the layers. It has the ability to maximize image quality to detect the performance effectively. The diverse implementation outcome is done whereas the recommended framework ensures to get better reliable outcomes.

Problem specification

In multimodal image fusion, it is very challenging to perform the multi-scale analysis that intends to analyze the feature maps extracted using shearlet domain. The analysis of the strengths and weakness of the existing models is given in Table 1. LSC and GA²⁴ are very efficient in both the objective evaluation and visual effects in the segmentation of medical images. However, when increasing the region count, the fusion efficiency may get reduced and increase the running time in the image fusion. PAPCNN¹⁸ provides accurate and detailed information present in the fusion results. On the other hand, it does not completely utilize the fusion layer and decoding layer, which is observed through the quantification evaluations. Deep MFNet¹⁹ attains better performance regarding the visualization and quantification when considering the quantitative and qualitative evaluations. Yet, it does not consider the multi-scale decomposition for encoding and decoding to get performance enhancement. VGG network²⁰ ensures the final fused images through the combination of three informative images like fused base image, detail image as well as perceptual image. Still, it has provided the results with increased color distortion and fusion noise without considering the fusion quality. sCNN²¹ are trained with the concatenated features for considering huge significance.But, it is time-consuming and cannot perform region-based medical image fusion. DWT-CNN²² is efficient on capturing the high-level association among the modalities and obtains the feature descriptors from the spatiotemporal regions. Yet, it may fail on preserving the shift-invariance. GDGFRW²⁵ has an ability to understand the temporal patterns of behavior over data modalities, which have been hidden through the overriding of individual modality. Still, it is unable to perform multi-focus image fusion. RNN²³ has efficiently utilized the location and hand presence as their significant cues for automatically classifying the images. Yet, it does not support the practical, feedback and in-device inference in the fusion. Hence, it is important to develop an enhanced multimodal image fusion model with superior optimization strategy.

Table 1 Strengths and weakness of existing multimodal image fusion models.

An intelligent model for multimodal image fusion

Collection of dataset

This multimodal image fusion approach gathers medical images for performing the fusion, which helps in healthcare systems regarding better treatment planning and decision making.It is available from https://www.med.harvard.edu/aanlib/home.htm. The proposed model considers the images of MRI and Single Photon/Positron Emission Computed Tomography (SPECT/PET). The resolution of theimageis taken as 256 × 256. In total, the 66 images are considered for the evaluation. The gathered images are known as $C_{a}$, where $a = 1,2,3, \cdots ,A$_, and the final number of obtained images is denoted as $A$.The sample images of MRI and SPECT/PET are visualized in Fig. 1.

Figure 1

Sample images in terms of MRI and SPECT/PET.

Proposed multimodal image fusion model

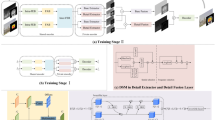
Imaging technology in the healthcare applications need a huge amount of information that helps to provide the additional requirement for medical image fusion. It is further split into single-modal and multimodal image fusion. Various researchers are focused on designing multi-modal image fusion with several complications in the information offered uisng single-modal fusion. The multimodal image fusion comprises both physiological and anatomical data, which makes disease detection easier. Various modalities in the medical field are SPECT, PET, MRI, CT, etc. It has offered medical information regarding the human body’s structural properties such as soft tissue, etc. Different imaging approaches preserve diverse characteristics regarding the similar part. Hence, the reason for image fusion is to get a superior perceived experience, fusion quality, and contrast. The better image fusion results must require to follow the below constraints like avoiding bad states like noise and misregistration from the images. In classical approaches, the issues presented in the fusion effects are enhanced but not addressed effectively including feature information extraction and color distortion. Thus, there is a need to utilize innovative and intelligent approaches for medical image fusion that remains a major complication in this research area. Finally, it is concluded that there is a huge requirement for medical image fusion with multimodal medical images for getting better functional and structural information about the same part and thus, the fused images will be high-quality information preserved images.Consequently,the multimodal image fusion model is designed with intelligent approaches in this paper, which promotes medical image fusion. The visual representation ofdevelopedmodel is depicted in Fig. 2.

Figure 2

Architectural representation of multimodal image fusion with developed framework.

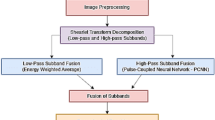
A new multimodal image fusion approach is recommended here, especially for the medical fieldwith the help of multi-resolution transform with the optimization strategy. Firstly, the source medical images are collected from benchmark sources. The next process is to decompose both images using the ODTCWTto acquire the frequency coefficient of low and high. Here, the filter coefficients of DTCWT are tuned using recommended PF-HBSSO algorithm.The decomposition helps in distinguishing the frequencies from the images to get the texture as well as smooth layer. The individual processing of both frequency parts helps in better preservation of images. Next, the fusion of high-frequency coefficients is performed bythe adaptive weighted average fusion technique, where the weights are optimized using the same PF-HBSSO algorithmto achieve the optimal fused results. Consequently, the low-frequency coefficients are fused usingstandard average fusion technique. At last, the fused image is retained using inverse ODTCWT to maximize thefused mutual information and ensure the quality of fused images.

Generating low and high “frequency coefficients” by optimized dual-tree complex wavelet transform

Optimization concept by PF-HBSSO

In this proposed multimodal image fusion approach, a new heuristic algorithm is recommended with the adoption of two recently familiar algorithms like SSA²⁹ and HBA³⁰. Here, the suggested model uses this new PF-HBSSO algorithm for maximizing the performance of image fusion regarding maximization of fused mutual information. PF-HBSSO algorithm optimizes the frequency coefficientsin DT-CWT and also the weights used for weighted average fusion for fusing the high frequency coefficients. This innovation increases the efficiency of the designed model while estimating with other approaches, which is detailed in result section. Here, HBA is chosen for performance enhancement owing to their vast range of features like skill towards sustaining the swapping among exploitation and exploration phases, good diversity, convergence speed, and provides statistical significanceto handle complex optimization problems, and utilization of the dynamic search schemes. Conversely, it faces complications in handling the local optima solutions. Henceforth, a SSA is adopted into this mechanism for giving better performance owing to their higher efficiency, capability towards producing the better solutions at faster manner even for critical and high dimensional optimization problems.

A new PF-HBSSO algorithm is recommended in this paper by modifying the random parameter $b$ used in HBA technique, where this random parameter $b$ is assigned in the range of [0, 1] in conventional HBA. On the other hand, this sameparameter $b$ is implemented in this PF-HBSSO by taking the probability of fitness-based solutions as shown in Eq. (1).

$$b = \frac{\sqrt P }{\alpha }$$

(1)

Here, the $P$ determines the number of population and $\alpha$ is specified as the capability of the individuals to reach food ($\alpha$ ≥ 1) as given in traditional HBA. Moreover, in this recommended PF-HBSSO,$\alpha$ is found by determininghow many number of fitness is less than mean fitness, which results in getting the better reach of optimal solutions at higher convergence rate.

Consequently, this new parameter $b$ is used for updating the solutions from either HBA or SSA with the following conditions. If $b < 0.5$ is verified, then the solution updating is carried out via digging phase of HBA or else the solution updating is performed using SSA. Here, the solution updating in SSA is carried out via formulating the case 1 with the condition of total flying squirrels. Hence, it produces higher convergence rate and free from local optimal with superior outcomes, which increases the efficiency of image fusion.

Initially, the population of search individual is created based on HBA, as derived in Eq. (2).

$$z_{j} = l_{j} + b_{1} \left( {u_{j} - l_{j} } \right)$$

(2)

The $j^{th}$ position of honey badger is specified in Eq. (4). In Eq. (2), a random number with limit of [0, 1] is specified as $b_{1}$, the upper and lower bounds of search range istermed as $u_{j}$ and $l_{j}$ and the $j^{th}$ position of individual referring candidate solution is derived as $z_{j}$.

$$z = \left[ \begin{gathered} \begin{array}{*{20}c} {z_{11} } & {z_{12} } & \cdots \\ {z_{21} } & {z_{22} } & \cdots \\ \vdots & \vdots & \cdots \\ \end{array} \,\,\,\,\,\begin{array}{*{20}c} {z_{1S} } \\ {z_{2S} } \\ \vdots \\ \end{array} \hfill \\ \begin{array}{*{20}c} {z_{p1} } & {z_{p2} } & { \cdots \,} & {z_{pS} } \\ \end{array} \hfill \\ \end{gathered} \right]$$

(3)

$$z_{j} = \left[ {z_{j}^{1} ,z_{j}^{2} , \cdots ,z_{j}^{S} } \right]$$

(4)

The size of the population is shown as $P$. In the next stage,the parameter $b$ is implemented by Eq. (1) and verifies $b < 0.5$. Then, the solution updating is started with HBA while satisfying the $b < 0.5$.

HBA has two phases for updating their solutions, which aredigging phase and honey phase. But, PF-HBSSO algorithm only formulates the digging as well as honey phase is replaced by SSA.

The digging phase is executed while honey badger performs in Cardioid shape as shown in Eq. (5).The position is updated by evaluating digging as well as the honey phase.Here, the position is updated by the several movement patterns that help to sort better solution during the optimization problem. The updated position is generally suited for the global optimization in which it maximizes or minimizes the multivariate function to find out the optimal solution. It helps to set the desired and reliable outcomes. The position update mechanism helps to avoid from the premature convergence to maximize the algorithms efficiency and effectiveness.

$$z_{new} = z_{prey} + D \times \alpha \times It \times z_{prey} + D \times b_{3} \times \delta \times h_{j} \times \left| {\cos \left( {2\pi b_{4} } \right) \times \left[ {1 - \cos \left( {2\pi b_{5} } \right)} \right]} \right|$$

(5)

$$D = \left\{ {\begin{array}{*{20}c} 1 & {if\,b_{6} \le 0.5} \\ { - 1} & {else} \\ \end{array} } \right.$$

(6)

$$It = b_{2} \times \frac{CS}{{4\pi \cdot h_{j}^{2} }}$$

(7)

$$CS = \left( {y_{j} - y_{j + 1} } \right)^{2}$$

(8)

$$h_{j} = z_{prey} - z_{j}$$

(9)

$$\delta = G \times \exp \left( {\frac{ - i}{{i_{\max } }}} \right)$$

(10)

The variables $b_{2}$,$b_{2}$,$b_{4}$,$b_{5}$,$b_{6}$ and $b_{7}$ is denoted as random numbers with a specific interval of [0, 1].Also,the global prey position is denoted as $z_{prey}$, the flag utilized for modifying the search direction is mentioned as $D$, and also the term $It$ specifies the smell intensity, distance among the individual and prey is known as $h_{j}$, the concentration strength is specified as $CS$, density factor is termed as $\delta$ and the constant term is derived as $G$, where the maximum number of iterations denotes the $i_{\max }$ and iteration number is specified as $i$.

Then, the proposed PF-HBSSO verifies the $b < 0.5$ factor, if it is not satisfied then; the solutions are executed by formulating the case 1 of SSA with the condition of total flying squirrels.

The location of the search individuals is updated while they move from the acorn treesto hickory nut tree as derived in Eq. (11).

$$z_{act}^{new} = \left\{ {\begin{array}{*{20}c} {z_{act}^{old} + r_{G} \times K_{C} \times \left( {z_{hit}^{i} - z_{act}^{i} } \right)} & {if\,v_{1} \ge \rho_{dg} } \\ {random\,position} & {or} \\ \end{array} } \right.$$

(11)

$$r_{G} = \frac{{y_{G} }}{\tan \left( \phi \right) \times o}$$

(12)

$$\tan \left( \phi \right) = \frac{Q}{X}$$

(13)

$$Q = \frac{1}{{2\chi e^{2} srCr_{dd} }}$$

(14)

$$X = \frac{1}{{2\chi e^{2} srCr_{ll} }}$$

(15)

In the afore mentioned equations, the constant terms are correspondingly derived as $\chi$,$o$,$y_{G}$,$e$,$sr$,$Cr_{ll}$ and $Cr_{dd}$, the and the lift force is represented by $X$, $Q$ specifies the drag force, and the gliding angle is known as $\tan \left( \phi \right)$, random gliding distance is indicated by $r_{G}$, the random function $v_{1}$ is computed at the interval of $\left[ {0,1} \right]$ and the gliding constant is derived by $K_{C}$ and the position of search individual that reached hickory nut tree is shown as $z_{hit}^{i}$, the position of search individual in acorn tree is derived as $z_{act}^{i}$. Moreover, the predator presence probability $\rho_{dg}$ is the essential role in updating position of individuals.

Finally, the search individuals are updated and the optimal solutions are attained for enhancing the efficiency of image fusion. Here, the new parameter updating for integrating two familiar algorithms gives the better efficiency and it is exhibited in results.

The pseudo-code of PF-HBSSOisshown in Algorithm 1.

Algorithm 1: PF-HBSSO

The hybrid heuristic algorithms exhibit better significance in recent days and thus, this paper also recommend one hybrid algorithm to increase efficiency of image fusion.The applications of the suggested PF-HBSSO model are solving unimodal, multimodal, and multi-dimensional optimization problems, system control, machine design and engineering planning. The flowchart of the designed PF-HBSSO is visualized in Fig. 3.

Figure 3

Flowchart of the designed PF-HBSSO algorithm.

Optimized DT-CWT-based image decomposition

In the recommended model, the decomposition of both MRI and SPECT/PET is done using ODT-CWT, where a newly recommended PF-HBSSO optimizes the filter coefficients of DTCWT for getting the better fusion effects that promotes the medical diagnosis approach.The gathered images $C_{a}$ are given to ODT-CWT, where the decomposition of images is done via ODT-CWT for getting low frequency and high frequency coefficients.

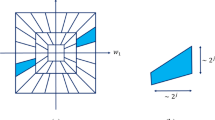
DT-CWT³¹ is the most eminent approach used in image fusion approaches, where the masks are used for extracting the information from the decomposed structure. It is the extended version of DWT, which is processed by executing two parallel trees. It is useful in eradicating the aliasing effects and achieved shift invariance.It helps reveal the visual sensitivity, which comprises of real and complex coefficients. The gathered images $C_{a}$ are given to ODT-CWT for getting frequencies of low $L$ and high $H$ in Eq. (16).

$$\left( {L,H} \right) = ODT - CWT\left( {C_{a} } \right)$$

(16)

$$L_{FU} = \phi_{L} \left( {L_{1} ,L_{2} } \right)$$

(17)

$$H_{FU} = \phi_{H} \left( {H_{1} ,H_{2} } \right)$$

(18)

Here, the fusion rules for high and low frequency coefficients are correspondingly known as $\phi_{H}$, and $\phi_{L}$, which are optimized by PF-HBSSO algorithm.

Finally,ODT-CWT offers ideal reconstruction over the traditional wavelet transform for getting better multimodal image fusion approach for medical images, which will be explained in upcoming sections.The gathered images $C_{a}$ are given to ODT-CWT, where decomposition of images is done via ODT-CWT for getting low and high frequency.

The framework of ODT-CWT for image decomposition using recommended PF-HBSSO algorithm is expressed in Fig. 4.

Figure 4

Illustration of ODT-CWT for image decomposition using recommended PF-HBSSO algorithm

High frequency and low frequency image fusion by proposed heuristic algorithm

Developed objective model

The implemented multimodal image fusion approach aims to improve the performance rate with the help of PF-HBSSO algorithm. Here, the PF-HBSSO algorithm is used for optimizing the frequency coefficients in DT-CWT and also the weights used for the weighted average fusion method for fusing the high frequency coefficients. This model considers the major goal as the maximization of fused mutual information as equated in Eq. (19).

$$OF = \mathop {\arg \max }\limits_{{\left\{ {\phi_{H} ,\phi_{L} ,W_{1} ,W_{2} } \right\}}} \left( {FMI} \right)$$

(19)

Here, the high and low frequency coefficientsare optimized using PF-HBSSO algorithm and the weights used for the weighted average fusion method is represented as $W_{1} ,W_{2}$ that is also optimized by PF-HBSSO algorithm. The range of $\phi_{H}$,$\phi_{L}$ are assigned among [-20, 20] and $W_{1} ,W_{2}$ are assigned among the range of [0, 1]. The optimal tuning of frequency coefficients results in better image decomposition whereas the weight optimization in weighted average fusion increases performance of high frequency fusion method. Term $FMI$ represents fused mutual information. The fused mutual information is determined among the fused image and the source image as derived here.

$$FMI = FMI_{IF} + FMI_{IS}$$

(20)

$$FMI_{IF} = \sum\limits_{ig = 0}^{Ys} {\sum\limits_{jg = 0}^{Qs} {gt_{{FiAi_{igjg} }} } } \log_{2} \left( {\frac{{gt_{{FiAi_{igjg} }} }}{{gt_{{Fi_{igjg} }} gt_{{Ai_{igjg} }} }}} \right)$$

(21)

$$FMI_{IS} = \sum\limits_{ig = 0}^{Ys} {\sum\limits_{jg = 0}^{Qs} {gt_{{GiAi_{igjg} }} } } \log_{2} \left( {\frac{{gt_{{GiAi_{igjg} }} }}{{gt_{{Gi_{igjg} }} gt_{{Ai_{igjg} }} }}} \right)$$

(22)

In the aforementioned equations, the joint histogram among source and fused images are correspondingly specified as $gt_{{GA_{igjg} }}$, and $gt_{{FA_{igjg} }}$, the column and row size of the image are correspondingly known as $Qs$ and $Ys$, and the normalized histogram of the source image 1 $Fi$, source image 2 $Ai$, and fused image $Bi$ are specified accordingly.The higher mutual information value represents the superior quality of fused images.

High frequency optimization by adaptive weighted average fusion

The recommended model gets the high frequency coefficients of two different imaging modalities using ODT-CWT.It is fused using adaptive weighted average fusion strategy. This scheme is modeled in Eq. (23).

$$HBi = W_{1} \times Fi_{H} + W_{2} \times Bi_{H}$$

(23)

Here, the fused images are known as $HBi$, the weights utilized for fusing the high frequency coefficients of images are correspondingly specified as $W_{1}$ and $W_{2}$, where the range of weights is assigned byPF-HBSSO algorithm in the range of [0, 1], the high frequency coefficients of two source images are given as $Fi_{H}$ and $Bi_{H}$, where the weights $W_{1}$ and $W_{2}$ are optimized using PF-HBSSO algorithm.The high frequency coefficients are fused via this recommended adaptive weighted average fusion scheme, which is carried out via optimizing the weights utilized for the fusion process.High frequency coefficients are fused for specifying the edge information to increase the image fusion quality. There is a need of maintaining the superiority of frequency information in the images for increasing the better contrast in the final fused images.

Finally, the final high frequency coefficients of two source images is attained as $HBi$, which is further given to the reconstruction process to get final fused images. The sample representation of adaptive weighted average fusion for fusing the high frequency images is given in Fig. 5.

Figure 5

Fusion process of high frequency by adaptive weighted fusionmodel.

Low frequency optimization by average fusion

In this suggested image fusion model, the average fusion is performed on low frequency coefficients of two source images, which is used for storing the local information in terms of increasing the image fusion. This process is derived in Eq. (24).

$$LBi = \frac{{\left( {Fi_{L} + Bi_{L} } \right)}}{2}$$

(24)

The average fusion method is performed via taking the averaging among two different modal source images. Averaging is the simplest technique in implementation, where the average of entire pixels from the input low-frequency coefficients of medical images is considered as the intensity of the output pixel. The averaging operation is useful in reducing the bad information and enhancing the good information from the images by taking a mean image. Although this approach is not eminent in image fusion, it is helpful in fusing the low-frequency coefficients.The final fused low frequency of two source images is attained as $LBi$. In Fig. 6, it represents the averaging fusion-based low frequency source image model.

Figure 6

Fusion process of low frequency by adaptive weighted fusion model.

Image reconstruction by inverse ODT-CWT

In this designed multimodal image fusion approach, the final fused images are attained using inverse ODT-CWT from both MRI and SPECT/PET images, which is derived in Eq. (25).

$$Fu_{a} = IODT - CWT\left( {HBi,LBi} \right)$$

(25)

Here, the final fused images $Fu_{a}$ are attained using inverse ODT-CWT via fusing both low frequency fused images $LBi$ and high frequency fused images $HBi$. At last, the final fused images are attained via the image reconstruction stage and ensured its higher quality regarding the maximization of fused mutual information.

Experimental analysis

Validation setting

There commended multimodal image fusion framework was implemented in MATLAB 2020a, with different quantitative measures. Some techniques like Dragon Algorithm (DA)³², Grey Wolf Optimizer (GWO)³³, HBA³⁰, SSA²⁹, and traditional transform approaches such as PCA³⁴, DWT³⁵, IHS³⁶, DCT³⁷, CWT³⁸, NSCT³⁹ and DT-CWT²⁸. The experimentation was done via measures like number of population as 10, chromosome length as 82, and the maximum Iteration was considered as 10.The recent methods like Spatial-Frequency Information Integration Network (SFINet)⁴⁰, Channel Attention dual adversarial Balancing network (CABnet)⁴¹, DUSMIF⁴² and Dense-ResNet⁴³ are compared using the developed model.

Validation metrics

• (a) SSIM: The SSIM measure helps to evaluate the local patterns of different pixel intensities. It is formulated in Eq. (26).

  $$\begin{gathered} SSIM\left( {RC_{a} ,Fu_{a} } \right) = \hfill \\ \frac{{\left( {2\mu_{{RC_{a} }} \mu_{{Fu_{a} }} + Vn_{1} } \right)\left( {2\sigma_{{RC_{a} Fu_{a} }} + Vn_{2} } \right)}}{{\left( {\mu_{{RC_{a} }}^{2} + \mu_{{Fu_{a} }}^{2} + Vn_{1} } \right)\left( {\sigma_{{RC_{a} }}^{2} + \sigma_{{Fu_{a} }}^{2} + Vn_{2} } \right)}} \hfill \\ \end{gathered}$$

  (26)

  Here, the constants are represented as $Vn_{1}$ and $Vn_{2}$, it is measured among two images $\left( {RC_{a} ,Fu_{a} } \right)$_, and the average of $Fu_{a}$ is termed as $\mu_{{Fu_{a} }}$,and the average of $RC_{a}$ is termed as $\mu_{{RC_{a} }}$. The covariance of $RC_{a}$ and $Fu_{a}$ is termed as $\sigma_{{RC_{a} Fu_{a} }}$ and the variance of $RC_{a}$ and $Fu_{a}$ are termed as $\sigma_{{RC_{a} }}$ and $\sigma_{{Fu_{a} }}$, respectively.

• (b) BRISQUE: The non-referenced image $Fu_{a}$ is calculated using score = Brisque ($Fu_{a}$).

• (c) Entropy: It is used to measure the information content of a fused image. The high entropy value indicates the fused image has rich information content and given in Eq. (27).

  $$Ent = - \sum\limits_{ig = 0}^{Ng} {hh_{{Fu_{a} }} } \left( {ig} \right)\log_{2} hh_{{Fu_{a} }} \left( {ig} \right)$$

  (27)

  Here, the term $hh_{{Fu_{a} }}$ is specified as the probability of the gray level of fused image.

• (d) PSNR: The PSNR is expressed in Eq. (28).

  $$PSNR = 20\log_{10} \left( {\frac{{Ng^{2} }}{{RMSE^{2} }}} \right)$$

  (28)

  Here, the number of gray levels is denoted as $Ng$.

• (e) RMSE: It is formulated in Eq. (29).

  $$RMSE = \sqrt {\frac{1}{Ys \times Qs}\sum\limits_{ig = 1}^{Ys} {\sum\limits_{jg = 1}^{Qs} {\left( {RC_{a} \left( {ig,jg} \right) - Fu_{a} \left( {ig,jg} \right)} \right)^{2} } } }$$

  (29)

  Here, $RC_{a}$ is the reference image,$Fu_{a}$ is the fused image and the intensity values of the reference and fused imageare accordingly represented as $RC_{a} \left( {ig,jg} \right)$ and $Fu_{a} \left( {ig,jg} \right)$.

• (f) Standard Deviation: It is used for measuring the fusion performance, where the larger standard deviation results show better fusion results. The STD is described in Eq. (30).

  $$STD = \left( {\frac{1}{Ys \times Qs}\sum\limits_{ig = 1}^{Ys} {\sum\limits_{jg = 1}^{Qs} {\left( {Fu_{a} \left( {ig,jg} \right) - \hat{\mu }} \right)^{2} } } } \right)^{\frac{1}{2}}$$

  (30)

  In Eq. (30), the mean value of the image is given as $\hat{\mu }$.

Experimental images

Some of the resultant images attained using different techniques and proposed model are shown in Fig. 7.The recent image fusion techniques like Unified and Unsupervised end-to-end image fusion network (U2Fusion)³⁷, Information Gate Network for multimodal medical image fusion (IGNFusion)³⁸ and Fast, Lightweight Image Fusion Network (FLFuse-Net) are compared in the image fusion model. This resultant analysis helps the developed model show effective outcomes.

Figure 7

Resultantimages attained using the existing method and proposed model.

Estimation over heuristic approaches

The effectiveness of the achieved fused images isanalyzed over various techniques as given in Fig. 8. From the evaluation, it is clearly shown that the designed model has exhibited its higher performance over traditional approaches. For example, while comparing with the recent heuristic algorithms, the recommended ODT-CWT-based PF-HBSSO algorithm specifies superior effectiveness over traditional methods.

Figure 8

Efficiency analysis on designed model over heuristic approaches for (a) Fused mutual information, (b) Standard deviation, (c) Entropy, (d) Brisque, (e) SSIM, (f) PSNR, (g) RMSE and (h) SNR.

Estimation over transform approaches

The effectiveness of the designed image fusion model is estimated over traditional transform domain approaches as listed in Fig. 9. The final fused images are compared over conventional approaches using standard statistical measures to illustrate the efficiency of the multi-modal image fusion approach.

Figure 9

Efficiency analysis on designed model over transform domain approaches for (a) Fused mutual information, (b) Standard deviation, (c) Entropy, (d) Brisque, (e) SSIM, (f) PSNR, (g) RMSE and (h) SNR.

Comparative estimationof image fusion over heuristic algorithms

The comparative estimation of the designed image fusion over various optimization algorithms is given in terms of various performance metrics from Tables 2, 3, 4, 5, 67, 8 and 9. The investigation clearly exhibited superior performance over both positive measures and error measures. The positive measures show the superior performance regarding image fusion quality whereas the negative measures specify the performance enhancement by getting lower error rates in image fusion. Hence, the designed model exhibit better performance and thus, it is more applicable for medical applications.

Table 2 Efficiency estimation on multi-modal image fusionover heuristic algorithms for fused mutual information.

Table 3 Efficiency estimation on multi-modal image fusion over heuristic algorithms for standard deviation.

Table 4 Efficiency estimation on multi-modal image fusion over heuristic algorithms for entropy.

Table 5 Efficiency estimation on multi-modal image fusion over heuristic algorithms for Brisque.

Table 6 Efficiency estimation on multi-modal image fusion over heuristic algorithms for SSIM.

Table 7 Efficiency estimation on multi-modal image fusion over heuristic algorithms for PSNR.

Table 8 Efficiency estimation on multi-modal image fusion over heuristic algorithms for RMSE.

Table 9 Efficiency estimation on multi-modal image fusion over heuristic algorithms for SNR.

Comparative estimation on image fusion over transform algorithms

The comparative analysis on the designed image fusion approach over various transform approaches for various performance metrics are given from Tables 10, 11, 12, 13, 14, 15, 16 and 17. By analyzing the values, the designed fusion model exhibits the better performance and clearly shows the superiority over the traditional methods.

Table 10 Efficiency estimation on multi-modal image fusion over transform algorithms for fused mutual information.

Table 11 Efficiency estimation on multi-modal image fusion over transform algorithms for standard deviation.

Table 12 Efficiency estimation on multi-modal image fusion over transform algorithms for entropy.

Table 13 Efficiency estimation on multi-modal image fusion over transform algorithms for Brique.

Table 14 Efficiency estimation on multi-modal image fusion over transform algorithms forSSIM.

Table 15 Efficiency estimation on multi-modal image fusion over transform algorithms for PSNR.

Table 16 Efficiency estimation on multi-modal image fusion over transform algorithms for RMSE.

Table 17 Efficiency estimation on multi-modal image fusion over transform algorithms for SNR.

Comparative analysis of the developed model with recent methods

The comparative analysis of the developed model is done using the recent methods in the multimodal image fusion approach shown in Table 18. This table analysis is performed by analyzing the entropy measure that helps to show the potential outcome in the designed framework. The recent methods like SFINet, CABnet, DUSMIF, and Dense-ResNet model is compared with different images. In this experimental evaluation, the developed PF-HBSSO-DT-CWT model shows 29.2, 29.13, 26.25, and 30.9% decreased than SFINet, CABnet, DUSMIF, and Dense-ResNet in terms of validating the image 6. The analysis of performance evaluation shows the developed model shows lower entropy value. Thus, it ensures to reduce the dimensionality problem that occur between the data points. Commonly, the developed model used to evaluate better data quality outcomes to make the possible predictions in the multimodal image fusion approach.

Table 18 Performance analysis of multimodal image fusion model with recent methods.

Conclusion

A multimodal image fusion model wasrecommendedin this paper via heuristic derived transform approaches. Initially, the medical source images wereacquired from the standard public datasets, and further, decomposed was done using the ODTCWT to acquire low frequency and high frequency coefficients. Here, frequency coefficients in DTCWT were tuned with the PF-HBSSO to enhance the better fusion quality. Then, the fusion of high-frequency coefficients was performed with the adaptive weighted average fusion technique, where the weights were optimized using the same PF-HBSSO algorithm to achieve the optimal fused results. Similarly, the low-frequency coefficients were fused by average fusion. Finally, the fused images were given to inverse ODTCWT for image reconstruction. The experiments have demonstrated that the recommended multimodal image fusion method has illustrated superior efficiency than the conventional image fusion approaches. For example, the SNR of the designed PF-HBSSO-DTCWT has achieved higher rate while estimating with traditional approaches for image 8, which was 35.2, 36.5, 72.9, 27.7, 51.6, 53, and 51% maximized than PCA, DWT, IHS, DCT, CWT, NSCT, and DT-CWT. However, the proposed model has to be improved in future in terms of statistical analysis to eradicate the performance overlap with the traditional heuristic algorithms.