Longitudinal splitting and grouting in deep buried rock layers based on the coupling effect between slurry and rock

Abstract

The coupling effect between slurry and a fractured rock layer controls the width of the fracturing channel and the grouting pressure. This effect is attenuated as the slurry diffusion front spreads from the grouting hole. This study examined the motion of slurry and the fracture expansion process, thereby establishing a longitudinal grout-splitting model of slurry-rock coupling by deriving a slurry-splitting diffusion motion equation that considers the time-varying viscosity of the slurry and attenuation of the fracture width. Research has demonstrated that in the initial stage of grouting, the plastic viscosity of the slurry is low, making grouting pressure and grouting rate the main determinants of the slurry’s splitting and diffusion range, as both factors can significantly expand the diffusion range of the slurry. However, once the viscosity of the slurry exceeds a certain threshold, viscosity becomes the primary factor that restricts the diffusion range of the slurry. Therefore, when using a slurry with time-varying viscosity, a higher initial grouting rate and grouting pressure should be selected in the early stages of grouting. As the grouting pressure stabilizes, the viscosity of the slurry should be appropriately increased to enable the slurry to quickly gel and seal the fractures.

Introduction

In recent years, the rapid advancement of mining engineering construction in China has increased the role of grouting technology in the sealing of subterranean water and the fortification of pliable rock layers^1,2,3. Nevertheless, escalating mining depths in China, coupled with the intricate and mutable nature of grouted rock strata, often result in undesirable grouting outcomes and occasionally hinder the safe extraction of deep-seated resources^4,5,6. To address the challenges of high ground pressure, high water pressure, and poor injectability in deep strata^7,8,9, high-pressure grout-splitting technology is commonly implemented in engineering endeavors to enhance grouting efficacy.

With the advancements in grouting technology, experts and scholars have delved into the intricacies of grouting theory. Yun et al.¹⁰ performed grout-splitting experiments on various sand samples and introduced a predictive model for fracture pressure, thereby forecasting the splitting grouting pressure of saturated weathered granite. Murdoch¹¹ obtained a qualitative conclusion about the geometric shape of cracks through indoor experiments, observing that the crack width gradually decreased. Hassle et al.¹² streamlined the concept of two-dimensional radial flow in equations that described grout movement. Houlsby¹³ conducted a single crack grouting test to explore and analyze the grouting rate, grouting pressure, and other parameters. The results showed that both the grouting rate and pressure can significantly increase the diffusion radius. Baker¹⁴ modeled a crack as a horizontal fissure and formulated a diffusion equation for a Newtonian fluid grout within rock fractures, thereby successfully applying it to tunnel settlement control. In China, Cheng et al.¹⁵ considered multiple factors, including the geo-stress characteristics of deeply buried rock layers, rock mechanics, and time-varying viscosity of the grout, to establish a single-crack circular lateral splitting diffusion model, with an accompanying diffusion equation, thereby analyzing the influence of rock elastic modulus, slurry viscosity, and grouting rate on the diffusion of rock splitting grouting. Kang et al.¹⁶ developed a high-pressure splitting grouting modification technology and conducted an industrial trial at the Kouzidong Mine of China Coal Xinji. They then used this model to improve the self-supporting capacity of the tunnel surrounding rock. Building on previous studies, Li et al.^17,18,19 developed a single-crack slurry transport equation considering the time-varying viscosity of the slurry. This equation was successfully applied to the grouting project in the fault fracture zone of the Yonglian Tunnel in Jiangxi Province. Xu²⁰ examined a permeation grouting model of fractured rock layers, leading to the derivation of the flow equation for plate cracks. The proposed study considers the coupling effect of grout and rock layers during the grouting process of deeply buried rock layers, to comprehensively analyze the expansion pattern of longitudinal cracks and motion behavior of the grout. A longitudinal splitting diffusion model was established to determine the longitudinal cracking pressure and splitting expansion conditions for grouting. The study derived and experimentally verified the longitudinal splitting diffusion equation, accounting for the dynamic change in the width of the splitting channel. Additionally, the influence of the mechanical parameters of the grouted rock layer and grouting parameters on the splitting diffusion of grout, was analyzed. This research provides a theoretical basis for the design of grout-splitting in deep rock layers.

Longitudinal grout-splitting diffusion model

Determination of splitting extension direction

The force on the grout hole is shown in Fig. 1. In this figure, the principal vertical stress is $\sigma_{V}$; the maximum and minimum principal horizontal stresses are denoted by $\sigma_{H}$ and $\sigma_{h}$, respectively. Theoretical analyses and indoor experiments showed that the grouting pressure required to overcome the strength of the grouted rock layer in the direction of the vertical minimum principal stress is smaller; therefore, splitting always occurs in the plane perpendicular to the minimum principal stress. Therefore, the direction of the minimum principal stress determines the direction and expansion pattern of rock-splitting.

Fig. 1

Split grouting process analysis model diagram.

The primary vertical stress predominantly originates from the gravitational force exerted by the overlying strata, whereas the horizontal stress primarily arises from lateral tectonic movement and vertical compression. Both forms of stress linearly increase with increasing depth. Statistical data indicate that in most regions, the two principal stresses are located within a horizontal or near-horizontal plane, typically at an angle not exceeding 30°. The maximum horizontal principal stress usually exceeds the vertical stress, with a ratio ranging from 0.7 to 5.5 and typically greater than two. In most instances, the vertical stress represents either the minimum or the intermediate principal stress²¹. When the vertical stress is the minimum principal stress, grout-splitting generally produces transverse cracks perpendicular to the vertical stress, whereas when the minimum horizontal principal stress is the minimum principal stress, grout-splitting generally produces longitudinal cracks perpendicular to it. In previous work, the focus was on analyzing single-fracture transverse cracking models¹⁵, whereas this study focused on longitudinal cracking grouting diffusion models.

Basic assumptions

A longitudinal split-extended model was established, as depicted in Fig. 1. The model assumes that $\sigma_{{\text{h}}} < \sigma_{V} < \sigma_{H}$ and the grout pipe is vertical to the horizontal plane. During the grouting process, the diffusion distance of the grout and the grout pressure at various locations continuously change. The grout is subjected to resistance from the walls on both sides of the fracture channel, which results in a decaying nonuniform load distribution of the grouting pressure inside the fracture channel because of the viscosity. Simultaneously, the width of the fracture channel gradually decreases from the grouting hole to the crack tip, and the crack width at the crack tip is zero, as shown in Fig. 1.

Based on the preceding analysis, the following are assumed for the theoretical model:

• 1. The slurry is an incompressible generalized Bingham fluid characterized by laminar flow.

• 2. The injected rock layer is an isotropic elastic body.

• 3. The boundary of the fracture channel exhibits no slippage.

• 4. The unit-time flow rate of the slurry diffusing through any expansion section inside the fissure is equal to the grouting rate at the grouting hole.

• 5. The slurry only exists inside the splitting channel, and its mass does not change with flow loss.

Longitudinal initial splitting pressure and expansion pressure for grouting

Initial splitting pressure

The plane force in the bare-hole section of the grouting hole is illustrated in Fig. 2. The radius of the bare grouting hole is $r$; grout-splitting pressure is $P_{0}$; and tensile strength is $\sigma_{t}$. When the maximum tensile stress around the hole exceeds the tensile strength of the rock layer, the grouting hole splits along the direction of the maximum principal stress, and the grouting pressure is the initial splitting pressure.

$$P_{0} = 3\sigma_{h} - \sigma_{H} + \sigma_{t}$$

(1)

Fig. 2

Longitudinal initial splitting analysis model diagram of the bare hole section.

Splitting extension pressure

After the rupture of the borehole wall, the grout enters the crevice, and under the action of the grouting pressure, the surface of the crevice is simultaneously subjected to the action of the stress field and grouting pressure, as shown in Fig. 1. According to solid-state mechanics²², when the grouting pressure reaches the threshold value, the crevice expands further and the expansion pressure is expressed by:

$$P_{k} = \frac{{K_{I} }}{{\sqrt {\pi L} }} + \sigma_{h}$$

(2)

where $K_{I}$ represents the stress intensity factor at the crack tip;$P_{K}$ denotes the expansion pressure of the splitting channel; $r$ is the radius of the grouting hole, which is negligible compared with the distance of the splitting extension; and $L$ is the half-length of the crack.

During the grout-splitting process, the expansion distance of the splitting channel can reach tens of meters; therefore, the term ${{K_{I} } \mathord{\left/ {\vphantom {{K_{I} } {\sqrt {\pi L} }}} \right. \kern-0pt} {\sqrt {\pi L} }}$ in Eq. (2) is negligible, and the expansion pressure of the fracture channel is considered to be equal to the minimum horizontal principal stress:

$$P_{k} = \sigma_{h}$$

(3)

Slurry constitutive equation

Theoretical research has been conducted on commonly used cement–water glass grouting. The viscosity changes directly affect the diffusion range of the slurry because of the yield shear force, and the slurry viscosity increases with time until it is completely gelatinated. Considering that the slurry must overcome shear force and time-varying plastic viscosity during movement, the rheological equation for the slurry is expressed as follows:

$$\tau = \tau_{0} + u(t)\dot{\gamma }$$

(4)

where $\tau$ represents the shear stress of the slurry; $\tau_{0}$ represents the yield shear force; $u(t)$ denotes the plastic viscosity of the slurry; $\dot{\gamma }$ corresponds to the shear rate, and t denotes the grouting duration.

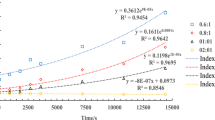
The viscosity-time function of the slurry was obtained by fitting the experimental data. The viscosity-time curves of slurries with different cement-to-water glass volume ratios are shown in Fig. 3, measured using a viscometer, according to¹⁵.

Fig. 3

Viscosity versus time curve.

The fitted equation for cement–water glass slurry viscosity $u(t)$ as a function of time is shown in Table 1.

Table 1 Relationship of the viscosity of different C–S slurries to time.

The change in the viscosity of the slurry displayed an exponential relation:

$$u(t) = kt^{2}$$

(5)

The formula represents m as the time-varying viscosity parameter, where $k = 8.57 \times 10^{ - 3} \sim 2.477 \times 10^{ - 2}$.

Slurry equation of motion

The flow pattern of the slurry was that of a generalized Bingham fluid. Ignoring the influence of the weight of the slurry and neglecting leakage, the force analysis of the slurry micro-unit is shown in Fig. 4.

Fig. 4

Micro unit balance analysis.

When the half-length of the fracture is L, under the action of grouting pressure, the micro-unit exhibits laminar flow of velocity v. in the x direction. The pressures at the two ends of the micro-unit are $P + dP$ and $P$, and the shear stresses $\tau$ on the two sides are opposite to the flow direction. The shear stress and constitutive equation of the slurry can be obtained according to the force balance of the micro-unit.

$$\tau = - y\frac{dP}{{dx}}$$

(6)

$$\tau = \tau_{0} + u(t)\left( {\frac{dv}{{dy}}} \right)$$

(7)

where v is the rate of slurry migration, and y is the distance perpendicular to the direction of migration.

By solving Eqs. (6) and (7) simultaneously, we obtain the following:

$$\frac{dv}{{dy}} = - \frac{y}{u(t)}\left( {\frac{dP}{{dx}} - \frac{{3\tau_{0} }}{w}} \right)$$

(8)

When $\tau < \tau_{0}$, there is a central flow core region with a width of 2 h, that is, when $- h \le y \le h$, $v = v(y = \pm h),$ and when $y = \pm {w \mathord{\left/ {\vphantom {w 2}} \right. \kern-0pt} 2}$, $v = 0$. Throughout the grouting process, the pressure gradient of the grout significantly exceeded its yield shear strength. Thus, the average flow velocity of the grout in the fracture cross-section can be simplified as follows:

$$\overline{v} = \frac{{ - w^{2} }}{12u(t)}\left( {{\raise0.7ex\hbox{${dP}$} \!\mathord{\left/ {\vphantom {{dP} {dx}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${dx}$}} - \frac{{3\tau_{0} }}{w}} \right)$$

(9)

where $dP/dx$ is the pressure gradient along the direction of slurry diffusion; w is the width of the splitting channel and is a function of the slurry diffusion distance.

During the grouting process, according to the law of conservation of mass, when the height of the grouting section is 2H, the grouting rate q is given expressed as follows:

$$q = 2\int_{ - H}^{H} {\int_{{ - {w \mathord{\left/ {\vphantom {w 2}} \right. \kern-0pt} 2}}}^{{{w \mathord{\left/ {\vphantom {w 2}} \right. \kern-0pt} 2}}} {\overline{v} } \,dy} dz$$

(10)

If the slurry flows only in the radial direction, then the splitting diffusion distance of the slurry at time t is x. Based on the conservation of mass, the corresponding time at x is $t = 4Hxw/q$.

When the grouting duration reaches time t, the equation that represents the spatial and temporal distributions of the viscosity within the diffusion zone at position x is as follows:

$$u(t,x) = u\left( \frac{4Hxw}{q} \right)$$

(11)

The grouting time t in Eq. (11) is eliminated because the spatial and temporal distributions of the slurry’s viscosity are determined by the spatial location and grouting time, which influences the slurry spreading distance when the grouting rate is constant.

Equations (4), (8) through (11) combined produce the following results:

$$\frac{dP}{{dx}} = - \frac{{3k\left( \frac{4Hxw}{q} \right)^{2} q}}{{Hw^{3} }} + \frac{{3\tau_{0} }}{w} = - \frac{{48kHx^{2} }}{qw} + \frac{{3\tau_{0} }}{w}$$

(12)

Equation (12) expresses the slurry pressure gradient inside the splitting channel.

Equation for controlling crack deformation

In the grout-splitting process, the grouting material applies pressure perpendicular to the fracture surface, which results in a displacement perpendicular to the fracture surface, and the increment of the fracture opening depends on the grout pressure at the fracture. The associated force of the grout pressure on the rock layers on both sides of the fracture channel has a small angle with the direction perpendicular to the grout diffusion direction. However, because the grout diffusion range is much larger than the fracture aperture, this angle can be ignored in stress calculations. The grout pressure is also attenuated in the diffusion direction, and the influence of this pressure on rock deformation results in a non-uniform force during the rock deformation process. However, the spatial attenuation of the grout pressure in the grout diffusion direction is very slow; therefore, within a small area, the rock deformation can be calculated using a uniform pressure. Therefore, the rock deformation process was simplified to a model that assumed uniform pressure acting in the direction of fracture extension, whereby the relationship between grout pressure and splitting channel width is obtained.

The additional stress $P^{ * }$ caused by the slurry pressure $P\left( x \right)$ directly acts as a uniform load on the rock layers on both sides of the crack; thus, a rectangular Cartesian coordinate system can be established, as shown in Fig. 5, where the displacements m and n in the x and z directions are both zero, and the displacement in the y direction is s. The displacement components are as follows:

$$m = n = 0,s = s\left( y \right)$$

(13)

and we have the following:

$$\varepsilon_{x} = \varepsilon_{z} = 0$$

(14)

Fig. 5

A force model for semi-infinite space bodies.

According to the elasticity equations, we have:

$$\begin{gathered} \varepsilon_{x} = \frac{1}{E}\left[ {\sigma_{x} - \nu \left( {\sigma_{y} + \sigma_{z} } \right)} \right] \hfill \\ \varepsilon_{y} = \frac{1}{E}\left[ {\sigma_{y} - \nu \left( {\sigma_{x} + \sigma_{z} } \right)} \right] \hfill \\ \varepsilon_{z} = \frac{1}{E}\left[ {\sigma_{z} - \nu \left( {\sigma_{x} + \sigma_{y} } \right)} \right] \hfill \\ \end{gathered}$$

(15)

where E is the elastic modulus of the rock layer, and ν is the Poisson’s ratio.

The strain in the y-direction of the rock layer is obtained by substituting Eq. (14) into Eq. (15).

$$\varepsilon_{y} = \frac{{\left( {1 - \nu - 2\nu^{2} } \right)\sigma_{y} }}{{\left( {1 - \nu } \right)E}}$$

(16)

The stress $\sigma_{y} = - P^{ * }$ in the y-direction inside the rock layer is obtained from a force analysis, and the displacement of the rock layer in the y-direction can be obtained according to Eq. (16) and the geometric equation $\varepsilon_{y} = {{\partial s} \mathord{\left/ {\vphantom {{\partial s} {\partial y}}} \right. \kern-0pt} {\partial y}}$:

$$s = - \frac{{\left( {1 - \nu - 2\nu^{2} } \right)\sigma_{y} }}{{\left( {1 - \nu } \right)E}}y + C$$

(17)

where C is a constant to be determined.

To determine C, the displacement boundary condition is utilized, setting the impact distance of the grout-splitting as D, and the displacement along the y-direction at y = D/2 as 0. By substituting this boundary condition into Eq. (17), the following displacement equation is obtained:

$$s = \frac{{\left( {D - y} \right)\left( {1 - \nu - 2\nu^{2} } \right)P^{ * } }}{{2\left( {1 - \nu } \right)E}}$$

(18)

The maximum vertical displacement at the slurry-rock interface was derived from the analysis.

$$s_{\max } = \frac{{D\left( {1 - \nu - 2\nu^{2} } \right)P^{ * } }}{{2\left( {1 - \nu } \right)E}}$$

(19)

Substituting w = 2s_max and $P^{*} = P(x) - \sigma_{h}$ into Eq. (19) yields the following splitting channel width control equation:

$$w = \frac{{D\left( {1 - \nu - 2\nu^{2} } \right)}}{{\left( {1 - \nu } \right)E}}\left( {P\left( x \right) - \sigma_{h} } \right)$$

(20)

Formulation of the spatial distribution equation for fracture channel width and slurry pressure.

From Eqs. (12) and (20), we obtain the following results:

$$\frac{dw}{{dx}} = \frac{{D\left( {1 - \nu - 2\nu^{2} } \right)}}{{\left( {1 - \nu } \right)E}}\left( { - \frac{{48kHx^{2} }}{qw} + \frac{{3\tau_{0} }}{w}} \right)$$

(21)

The width of the fracture channel progressively narrows as the slurry diffuses, and ultimately reduces to zero. By applying the boundary condition, where $x = L$ and $w = 0$ to Eq. (21), the governing equation for the fracture channel width can be derived.

$$w = \sqrt {\frac{{D\left( {1 - \nu - 2\nu^{2} } \right)}}{{\left( {1 - \nu } \right)E}}\left[ {\frac{32kH}{q}\left( {L^{3} - x^{3} } \right) - 6\tau_{0} \left( {L - x} \right)} \right]}$$

(22)

Substituting Eq. (22) into Eq. (20) yields the spatial distribution equation for the slurry pressure within the splitting channel.

$$P\left( x \right) = \sqrt {\frac{{\left( {1 - \nu } \right)E}}{{D\left( {1 - \nu - 2\nu^{2} } \right)}}\left[ {\frac{32kH}{q}\left( {L^{3} - x^{3} } \right) - 6\tau_{0} \left( {L - x} \right)} \right]} + \sigma_{h}$$

(23)

When $x=r$ and $P = P_{0}$, the radius of the grouting hole r is relatively small compared to the fracture extension distance and can be ignored. The grouting fracture diffusion equation is then given by:

$$P_{0} = \sqrt {\frac{{E\left( {1 - \nu } \right)}}{{D\left( {1 - \nu - 2\nu^{2} } \right)}}\left( {\frac{32kH}{q}L^{3} - 6\tau_{0} L} \right)} + \sigma_{h}$$

(24)

Equation (24) is the diffusion equation for grout fracturing. The grout-splitting of rock layers is controlled by the mechanical properties of the grouted rock layers, and the grout viscosity, rate, and pressure.

According to Eq. (24), disregarding the change of slurry viscosity with time, the equation governing the diffusion of grout fractures can be expressed as follows:

$$P_{0} = \sqrt[4]{{\frac{{12\mu_{0} qLE^{3} \left( {1 - \nu } \right)^{3} }}{{HD^{3} \left( {1 - \nu - 2\nu^{2} } \right)^{3} }}}} + \sigma_{h}$$

(25)

Verification analysis

An indoor experiment was conducted by Yushi et al.²³ to evaluate the proposed theory.

Yushi et al.²³ used a large true triaxial fracturing model test device to conduct fracturing experiments under true triaxial stress conditions. The specific experimental control parameters of specimen 2# are shown in Table 2. In the stress field loading simulations, $\sigma_{V}$ = 15 MPa, $\sigma_{H}$ = 15 MPa, and $\sigma_{h}$ = 10 MPa. According to the experimental results, the observed height of the splitting channel 2H = 0.02 m. For more details on the experimental model, please refer to²³.

Table 2 Test parameter values²³.

These parameters were substituted into Eq. (25) to solve for the pressure variation with time, thereby comparing the results to the test results of the 2^# specimens²³, as shown in Fig. 6.

Fig. 6

Variation curve of grouting pressure with time.

• 1. At the outset of the experiment, the pressure increased to approximately 20.8 MPa within the first 120 s, resulting in the emergence of fissures within the unlined segment of the borehole in the specimen. According to Eq. (1), the initial splitting pressure was calculated to be 17.4 MPa, and the calculated and measured values differed considerably. According to the experimental results in²⁴, under the triaxial hole pressure condition, the rock tensile strength value determined by the closed unlined borehole section grouting fracturing method was significantly higher, approximately 2.5 times the uniaxial tensile strength, and the rock tensile strength, which was determined based on the closed unlined borehole section grouting fracturing method was 6 MPa. Recalculation of the initial splitting pressure according to (1) yielded a value of 21 MPa, which is consistent with the measured value.

• 2. After the occurrence of splitting in the bare hole section, the formation of the splitting channel caused a rapid decrease in pressure, with a magnitude of approximately 10 MPa, at 180 s. Therefore, this moment was defined as the starting point of the theoretical calculations. As the fracturing fluid was continuously injected, the fracture continued to expand, and the pressure exhibited a see-saw fluctuation. At 950 s, the pressure reduced rapidly with the rapid diffusion of the fracture along the fault surface to the edge of the rock sample, thereby releasing pressure.

• 3. Based on a comparative analysis of the theoretical and experimental values shown in Fig. 6, the associated curves have a high degree of consistency; however, the theoretical curve is slightly higher than the experimental curve. This difference is mainly because in the theoretical derivation process, only two main resistances to the fracture propagation of the fracturing fluid are considered: the viscous force generated by the shear flow of the fracturing fluid and in situ stress acting on the fracture wall. Potential factors such as the fracturing fluid penetrating into both sides of the fracture were not considered. Nevertheless, the error obtained was still within the acceptable error range for engineering applications.

Grout-splitting diffusion law

According to the theoretical model mentioned in the previous section, the diffusion law and influencing factors of grout-splitting were analyzed under the influence of the mechanical parameters of the grouted rock layers and time-varying viscosity factors of the grout. The main parameter settings are as follows: the principal stresses ${\sigma }_{V}$ = 15 MPa, ${\sigma }_{H}$ = 20 MPa, ${\sigma }_{h}$ = 10 MPa; the sandy mudstone elastic modulus E = 4 GPa, Poisson’s ratio of the sandy mudstone ν = 0.2; grouting section height 2H = 1 m; grouting influence range D = 10 m; yield shear stress ${\tau }_{0}$ = 6 Pa; and grouting rate q = 120 L/min. The grouting material was taken as C:S = 1:1 for the cemented water glass slurry.

Time-varying viscosity of slurry

For the slurry material C:S = 1:1, 2:1, and 3:1 of the cement-sodium silicate slurry were considered for the analysis, and the time-varying viscosity parameters were substituted into the grout-splitting diffusion equation to obtain the $P_{0} - L$ relationship curve under the influence of the viscosity factor, as shown in Fig. 7.

Fig. 7

Influence of the slurry viscosity on diffusion distance of the slurry.

According to the analysis shown in this figure:

• 1. The grouting pressure increased exponentially with fracture propagation distance, first slowly and then rapidly. When the fracture propagation distance was relatively small, the pressure growth was slow because the grouting time was short. The viscosity growth rate of the time-varying viscosity slurry was small, and the fracture propagation distance for different slurry ratios was not sensitive to the grouting pressure changes. After the fracture extended to 2 m, the plastic viscosity of the slurry gradually increased with time, and the required pressure gradually increased. Therefore, the rheological properties of the slurry significantly influenced the grout-splitting pressure.

• 2. As fracture propagation progressed, when different proportions of slurry reached the same splitting propagation distance, there was a significant difference in the required grouting pressure. For example, when the grouting propagation distance L = 8 m, the required grouting pressures for the C:S ratios 1:1, 2:1, and 3:1 were 17.89 MPa, 20.08 MPa, and 23.43 MPa, respectively. It is evident that the higher the viscosity of the liquid, the greater is the viscous resistance encountered during grout-splitting, the more difficult the fracture extension, and the higher the grouting pressure required to reach the predetermined splitting propagation distance.

Elastic modulus

The analysis was conducted with elastic moduli of E = 4 GPa, 8 GPa, and 12 GPa for the sandy mudstone. By substituting the elastic modulus parameter into the splitting and grouting diffusion equations, the $P_{0} - L$ relationship curve was obtained under the influence of the strength factor, as shown in Fig. 8.

Fig. 8

Influence of the modulus of elasticity on diffusion distance of the slurry.

According to the analysis presented in this figure:

• 1. Under the same splitting diffusion distance conditions, the relationship of the grouting pressure to the elastic modulus of the rock mass is nonlinear. For example, when the grout diffusion distance is L = 8 m, the elastic modulus of the grouted rock mass increases from 4 to 12 GPa, and the corresponding grouting pressure increases from 17.89 to 23.67 MPa. Therefore, the larger the elastic modulus of the grouted rock layer, the higher is the resistance encountered by grout-splitting, the more difficult the crack extension process, and the greater the required grout-splitting pressure.

• 2. Although the strength of the grouted rock layer is a geological factor beyond human control, it has an important influence on the fracture grouting process. Therefore, before conducting grout-splitting engineering in deep rock layers, the strength of the grouted rock layer and its stress state should be accurately measured.

Grouting rate

The grouting rate was analyzed at q = 120 L/min, 180 L/min, and 240 L/min. By substituting the grouting rate parameter into the grout-splitting diffusion equation, the $P_{0} - L$ relationship curve was obtained under the influence of the injection grouting rate factor, as shown in Fig. 9.

Fig. 9

Influence of grouting rate on diffusion distance of slurry.

According to the analysis shown in this figure:

• 1. The grouting pressure is related to the distance of the fracture expansion in a positive nonlinear manner, and the slope increases with an increase in the splitting propagation distance. This indicates that once slurry cracking reaches the threshold distance, if the slurry continues to crack and spreads a small distance, it provides a higher grouting pressure. As such, after the injection pressure exceeds the threshold range, the impact on the slurry-splitting propagation distance gradually decreases.

• 2. When the grouting pressure is constant, the rate of grouting exhibited a nonlinear direct proportionality relationship to the distance of the splitting diffusion, but the increase gradually reduced with time. For example, when the grouting pressure P₀ = 14.55 MPa, the grouting rate increased from 120 L/min to 180 L/min, and the corresponding splitting diffusion distance increased from 5.54 m to 6.95 m, which is an increase of 1.34 m. When the grouting rate increased from 180 to 240 L/min, the corresponding splitting diffusion distance increased from 6.95 to 8 m; this increase of 1.05 m is less than 28%. Therefore, clearly both grouting pressure and grouting rate must be increased simultaneously to effectively increase the range of grout-splitting diffusion. Increasing the grouting pressure or rate alone cannot achieve the desired grouting effect.

The analysis indicates that the primary factors that influence grout-splitting include the rock’s elastic modulus, time-varying viscosity of the slurry, grouting pressure, and grouting rate. Initially, when the plastic viscosity of the slurry is minimal, the grouting pressure and grouting rate are the main factors that control the range of slurry splitting and diffusion. Increasing the grouting rate markedly enhanced diffusion. However, once the viscosity of the slurry surpasses a specific threshold, it becomes the principal factor determining the scope of diffusion. Consequently, the formulation and selection of grouting parameters, makes it imperative to consider geological factors holistically. In the nascent phase of grouting, opting for a higher initial grouting rate and pressure is advisable for penetrating cracks within the rock formations. Subsequently, as the grouting pressure stabilizes and the slurry thoroughly permeates the fractures, increasing the viscosity of the slurry accelerates the solidification reaction, thereby forming a gelatinous seal on the fissure face.

Conclusion

• 1. By combining the motion law of the slurry and the expansion form of cracks, and considering the mechanical characteristics of the injected rock mass and geo-stress factors, the longitudinal initial splitting pressure and expansion conditions of the splitting channel were obtained. A longitudinal grouting splitting model was established considering the slurry-rock coupling effect. A splitting diffusion equation was derived based on the time-varying viscosity of the slurry and attenuation of the crack width, and experimental verification was further performed.

• 2. The elastic modulus of the rock, time-varying slurry viscosity, and grouting rate are the principal determinants governing the grout-splitting process. The higher the elastic modulus of the rock mass, the greater is the viscosity of the slurry, resulting in increased resistance to splitting grouting. This makes it more difficult for cracks to propagate. Initially, when the plastic viscosity of the slurry is low, the grouting pressure and rate predominantly determine the extent of slurry fracture diffusion. As the slurry transitions into the high-plasticity phase, viscosity emerges as the primary determinant influencing the diffusion range of the slurry.

• 3. Given the fluid-solid coupling characteristics between the slurry and rock fractures, opting for a higher initial grouting rate and pressure at the onset of the grouting process is advisable to facilitate the creation or penetration of cracks within the rock formation. Once the grouting pressure reaches equilibrium, the slurry is allowed to permeate the fractures. Concurrently, enhancing the viscosity of the slurry and accelerating its solidification reaction rate expedite the gelatinization and sealing of fractures on the fracture surface.

Considering the challenges associated with the inability to visualize the grouting process and the intricate nature of the splitting expansion mechanism, the presented longitudinal splitting diffusion model of single cracks does not account for the filtration effect of slurry loss. This suggests that the flow rate per unit of time across any diffusion section within the crack is equivalent to the grouting rate at the injection point. These issues warrant further investigation.