Bilateral enhancement network with signal-to-noise ratio fusion for lightweight generalizable low-light image enhancement

Abstract

Low-light image enhancement aims to enhance the visibility and contrast of low-light images while eliminating complex degradation issues such as noise, artifacts, and color distortions. Most existing low-light image enhancement methods either focus on quality while neglecting computational efficiency or have limited learning and generalization capabilities. To address these issues, we propose a Bilateral Enhancement Network with signal-to-noise ratio fusion, called BiEnNet, for lightweight and generalizable low-light image enhancement. Specifically, we design a lightweight Bilateral enhancement module with SNR (Signal-to-Noise Ratio) Fusion (BSF), which serves the SNR map of the input low-light image as the interpolation weights to dynamically fuse global brightness features and local detail features extracted from a bilateral network and achieve differentiated enhancement across different regions. To improve the network’s generalization ability, we propose a Luminance Normalization (LNM) module for preprocessing and a Dual-Exposure Processing (DEP) module for post-processing. LNM divides the channels of input features into luminance-related channels and luminance independent channels, and reduces the inconsistency of the degradation distribution of input low-light images by only normalizing the luminance-related channels. DEP learns overexposure and underexposure corrections simultaneously by employing the ReLU activation function, inverting operation, and residual network, which can improve the robustness of enhancement effects under different exposure conditions while reducing network parameters. Experiments on the LOL-V1 dataset shows BiEnNet significantly increased PSNR by 8.6$\%$ and SSIM by 3.6$\%$ compared to FLW-Net, reduced parameters by 98.78$\%$, and improved computational speed by 52.64$\%$ compared to the classical KIND.

Introduction

Due to the influence of factors such as shooting environment and equipment limitations, images captured in low-light environments often exhibit various issues, including low brightness, low contrast, severe noise, and uneven color distribution. These image quality problems not only impair visual perception but also significantly impact subsequent downstream computer vision tasks, such as semantic segmentation^1,2and object detection^3,4. In recent years, numerous low-light image enhancement methods^{5,6,7,8,9,10,11,12,13,14} have been proposed. Although these methods have achieved impressive enhancement results, striking a balance between efficiency and quality remains challenging.

Low-light image enhancement methods can be broadly categorized into two categories: traditional methods (e.g., histogram equalization^15,16,17, Retinex model^{18,19,20,21,22}) and deep learning methods (e.g., MBLLEN⁸, SNR-Aware²³, and SKF²⁴). The evolution from traditional methods to deep learning approaches marks a significant advancement in low-light image enhancement. Traditional methods rely on physical modeling and optimization of image degradation, using hand-crafted algorithms to achieve enhancement. However, as data availability and computational power have grown, deep learning approaches have emerged, leveraging neural networks to learn mappings from input to output, resulting in more precise and efficient low-light enhancement.

Traditional methods, such as CLAHE¹⁵, improve the detection of fine structures in mammographic images through contrast-limited adaptive histogram equalization. However, these methods often encounter challenges in complex scenes, such as over-enhancement or noise amplification. Moreover, they require substantial manual prior information for parameter tuning, increasing complexity and limiting their flexibility and applicability in real-world scenarios.

Deep learning methods address some of these issues by training neural networks on large datasets, enabling automatic learning of the mapping from low-light to enhanced images. These methods offer notable improvements in accuracy, robustness, and speed. Nevertheless, they also have limitations. For instance, SKF²⁴ enhances low-light images using semantic-aware guidance but suffers from a complex network structure and large model parameters, leading to prolonged processing times and lower computational efficiency. Furthermore, because deep learning models inherently learn mappings between input and output domains, variations among samples make them heavily reliant on training data, reducing their generalization capabilities.

In this paper, we opt to normalize the degradation before low-light image enhancement to make the input images have a more consistent degradation distribution. For this, we designed a lightweight Luminance Normalization (LNM) module to normalize the luminance-related channels. The LNM consists of a normalization module for processing luminance information and a gating module for channel selection. Initially, the normalization module normalizes each channel separately, then the gating module filters out the luminance-related channels, and finally, the normalized channels are merged with the original channels. This method can reduce the differences between samples while reducing the loss of information due to normalization and improving the generalization of the model. Considering the variability of exposure conditions, we use a simple network to simultaneously learn the correction of two exposure attribute features. To achieve this, we design the Dual-Exposure Processing (DEP) module, which primarily comprises an exposure activation module and an exposure learning module. Initially, the exposure activation module extracts underexposed and overexposed features. Then, the exposure learning module concurrently learns to correct these features. Finally, we fuse the processed features to enhance the network’s robustness across various exposure conditions.

For the enhancement part of the network, considering that different regions of low-light images have varying degrees of brightness and noise degradation conditions, regions with very low brightness have more noise and cannot achieve effective enhancement by relying solely on local information. Conversely, regions with higher brightness achieve good enhancement using only local region information. Therefore, our solution for the enhancement part is to utilize both global and local features. To this end, we design the Bilateral Enhancement module with SNR Fusion (BSF). The global branch, taking the luminance channel and its histogram of the low-light image as inputs, captures global information. Meanwhile, the local branch, with a residual connection structure, captures local information. Then, guided by the SNR prior information of low-light images, it dynamically fuses global and local features to achieve better low-light image enhancement.

In our extensive experiments conducted on representative datasets (LOL-V1²⁵, LOL-V2²⁶), as well as a mixed dataset, the results show that our BiEnNet recovers more realistic color tones and better contrast and detail compared to other methods (see Fig. 1). Overall, our work makes the following key contributions:

• We propose an LNM module that selects luminance-related channels for normalization, thus enhancing the network’s generalization ability under unknown conditions. It is lightweight and can be easily integrated into other tasks.

• To further improve the network’s robustness, we devise a DEP module, which simultaneously learns both underexposure and overexposure features within a single network. It enhances the network’s ability to handle exposure variations, and like the LNM module, it is lightweight and adaptable for integration into other tasks.

• We design a lightweight BSF module, which is a dual-branch module. The two branches capture global and local features, respectively. By dynamically fusing these features based on SNR priors, we achieve better low-light image enhancement.

Related work

Low-light image enhancement

Researchers have focused on low-light enhancement for many years, mainly dividing it into two categories: traditional methods and deep learning methods. Among them, traditional methods mainly include histogram equalization^15,16,17and the Retinex model^{18,19,20,21,22}. Histogram equalization adjusts overall brightness by expanding the grayscale distribution of an image. Zuiderveld et al.¹⁶ proposed local region histogram equalization, which effectively reduces noise amplification by limiting the upper bound of contrast enhancement. Lee et al.¹⁷ introduced using a tree-structured hierarchical 2D histogram to represent grayscale differences in high-frequency regions. Based on color constancy, the Retinex theory decomposes the original image into an illumination map and reflectance map. Fu et al.²⁰ utilized a weighted variational model to preserve more detailed reflectance. Li et al.²¹ improved the performance of low-light enhancement by introducing noise mapping into the Retinex model. Although these methods have achieved excellent results in enhancing brightness and contrast, they still have significant limitations, such as unsatisfactory noise removal and color restoration.

With the rapid development of deep learning in the field of computer vision, these techniques have been successfully applied to the low-light enhancement field and have become mainstream methods. Lv et al.⁸ proposed a multi-branch enhancement network capable of extracting features at different levels and fusing them to generate output images. Jiang et al.²⁷ introduced the first unsupervised low-light image enhancement method, enabling training without paired data. Guo et al.⁶ proposed Zero-DCE, which designs deep networks to estimate dynamically adjustable pixels and curves to achieve brightness enhancement. The structure of URetinex-Net proposed by Wu et al.²⁸ consists of initialization, optimization, and illumination adjustment modules, which achieve noise suppression and detail preservation. Compared with traditional methods, deep learning methods can learn complex feature representations from massive data, resulting in clearer and more naturally enhanced results. However, due to these typically involving large-scale network structures, they requires substantial computational resources during both training and deployment, resulting in longer processing times and making them unsuitable for real-time response applications.

Model generalization

The generalization ability of a model refers to its performance on unseen datasets, specifically whether it can successfully transfer and apply the knowledge learned from training data to other scenarios. The strength of generalization ability is an important criterion for measuring whether a model has practical application value. Therefore, how to train models with better generalization ability using limited datasets is one of the important topics in deep learning research. In early machine learning algorithms, researchers proposed many methods to address this issue, such as regularization^29,30and cross-validation³¹.

However, with the increasing complexity and scale of models, previous generalization methods are no longer sufficient to meet practical application needs. Researchers have developed various methods to address this challenge, including domain generalization³², transfer learning³³, meta-learning³⁴, zero-shot learning³⁵, self-supervised learning^6,21,36, and adversarial training³⁷. Current methods mainly address this issue from the perspectives of datasets or optimization algorithms. Single-domain generalization³⁸ has also recently gained attention, aiming to train models from a single source domain that can generalize well to other unseen domains. However, these methods typically involve complex network structures, making them unsuitable for real-time application needs. They also do not solve the problem from the perspective of consistency in the degradation distribution of the input images.

Exposure correction

In the field of digital image processing, exposure correction is a crucial aspect. Traditional exposure correction methods mainly include histogram equalization³⁹, gamma correction⁴⁰, and the Retinex model^18,20. Reza et al.³⁹proposed CLAHE, which corrects exposure by adaptively adjusting the histograms of different regions. LIME¹⁸ uses the maximum intensity of the RGB channels as an initial rough illumination map and then refines it using prior structures. However, because these methods heavily rely on manual design and neglect the relationships between pixels, they often exhibit unnatural results.

In recent years, deep learning-based exposure correction methods have gradually emerged^{41,42,43,44,45}. Mertens et al.⁴¹ proposed a method that suggests blending well-exposed regions from a sequence of images with different exposure levels into a single high-quality image. However, it requires a multi-exposure image sequence as input, so it cannot apply directly to a single image. Zhang et al.⁴² first used sampled tone mapping curves to construct multi-exposure image sequences for each video frame. Then, they gradually fuse the image sequences in a spatiotemporal manner to obtain enhanced videos, thus applying the technique to exposure-deficient video enhancement. More recently, Afifi et al.⁴³ developed a pyramid-based network to correct exposure in a coarse-to-fine manner, initially restoring brightness and subsequently refining details. Although these methods have achieved good results, they do not fully utilize both overexposure and underexposure features simultaneously, resulting in suboptimal correction effects.

Methods

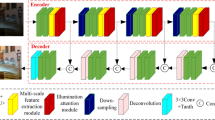
As shown in Fig. 2, BiEnNet primarily consists of three primary components: the Luminance Normalization (LNM) module, the Bilateral Enhancement module with SNR Fusion (BSF), and the Dual-Exposure Processing (DEP) module. Given a low-light image $\varvec{I}_{L}$, the network first expands the channel dimension of the low-light image using the encoder. Then, the LNM module normalizes the channels related to the luminance information of the features, and a decoder obtains the normalized low-light image $\varvec{I}_{N}$ to provide a low-light image with a more consistent luminance distribution for the subsequent enhancement. For the low-light enhancement part, the BSF module obtains global luminance features and local detail features of $\varvec{I}_{N}$ through the Global Brightness Adjustment (GBA) module and the Local Feature Extraction (LFE) module, respectively. Concurrently, the SNF module employs a non-learning method to obtain an SNR map of $\varvec{I}_{N}$, which guides the dynamic fusion of global and local features. Finally, the DEP module’s role is to learn feature representations under different exposure conditions simultaneously, enhancing the network’s robustness to various exposure conditions.

Luminance normalization module

Motivation

Due to different lighting conditions and camera parameters, the actual images obtained often exhibit different levels of degradation. This inconsistency among samples poses a challenge for a well-trained model, especially for images with degraded conditions that are not present in the training data. A common approach is to increase the diversity of the training dataset to expand its capacity. However, the high cost of data collection often makes this method impractical. Moreover, a more diverse dataset may increase the difficulty of model training, potentially leading to instability in the training process.

Normalization possesses the capability of reducing differences in image brightness, allowing for a more consistent brightness distribution across different images. This assists the model in effectively extracting information that is not related to brightness, mitigating the impact of brightness variations on model training, reducing the difficulty of subsequent operations, and improving the model’s generalization capabilities. Therefore, we choose to apply normalization methods to images with different brightness levels to achieve a more consistent brightness distribution and improve the model’s generalization performance.

Luminance normalization

As shown in Fig. 3, the LNM mainly consists of two parts: a normalization module that processes brightness information and a gating module for channel selection. Since Instance Normalization (IN)⁴⁶ is unaffected by the number of channels and batch size, and its computation is relatively simple, we use IN for channel normalization. Assume the input feature map $\varvec{F}_{x}\in {\mathbb {R}}^{C\times H\times W}$, where C is the number of channels, and H and W are the height and width of the feature map, respectively. For each channel feature in $\varvec{F}_{x}$, IN first calculates its mean $\mu (\varvec{F}_{x, c})$ and variance $\sigma (\varvec{F}_{x, c})$, then subtracts the mean $\mu (\varvec{F}_{x, c})$ and divides by the variance $\sigma (\varvec{F}_{x, c})$, and finally scales and shifts the result. We can represent this process as:

$$F_x^\prime=\textstyle \bigcup _{c} IN(F_{x,c})=\textstyle \bigcup _{c}\left(\alpha_c\frac{F_{x,c}-\mu(F_{x,c})}{\sqrt{\sigma^{2}(F_{x,c})+\ni}}+\eta_c\right)$$

(1)

where $\mu (\varvec{F}_{x, c})$ and $\sigma (\varvec{F}_{x, c})$ are computed for each channel, $\textstyle \bigcup _{c}$ represents the merging of all normalized channels, and ${\alpha }_{c}$ and ${\eta }_{c}$ are learnable scaling and shifting parameters, and ∋ is a very small constant used to prevent division by zero. This method ensures that each channel of every sample has its own mean and variance, thus maintaining the independence between samples. Therefore, this approach can effectively reduce the brightness differences between samples, thereby improving the model’s generalization ability.

Although the benefits of normalization in reducing sample variations and enhancing model stability, it inevitably leads to some information loss. For instance, it can affect the correlation between channels, potentially impacting the model’s accuracy to some extent. Therefore, to mitigate the information loss caused by normalization, we introduce a gating mechanism for channel selection. We expect the gating module to output values close to 0 or 1 to control which channels require normalization. This is specifically expressed as follows:

$$\begin{aligned} \varvec{F}_{y} = (1-\varvec{G}) \odot \varvec{F}_{x}+\varvec{G} \odot \varvec{F}_{x}^{\prime } \end{aligned}$$

(2)

where, $\varvec{G}$ represents the gating module, which outputs values of 0 or 1. And $\odot$ denotes channel-wise multiplication, which is used to selectively weights the normalized features $\varvec{F}_{x}^{\prime }$ and the original features $\varvec{F}_{x}$ based on the gating weights $\varvec{G}$. We expect $\varvec{G}$ to dynamically output 0 or 1 according to different features, thereby selecting the channels that truly require normalization. The Sigmoid activation function maps input values to the range [0, 1], making it suitable for representing probabilities or weights for normalizing data. Inspired by this property, we design $\varvec{G}$ as:

$$\begin{aligned} \varvec{G} = \frac{\beta ^{2}}{\beta ^{2} + \varepsilon } \end{aligned}$$

(3)

where $\beta$ is the output vector of feature $\varvec{F}_{x}$ through the convolution layer with activation function, and $\varepsilon$ is a very small constant to prevent division by zero. We control the value of $\varvec{G}$ using $\beta$, enabling $\varvec{G}$ to filter the channel effectively.

When $\beta = 0$, the normalized image is the same as the original low-light image, i.e., $\varvec{F}_{y} = \varvec{F}_{x}$. And when $\beta \ne 0$, then $\varvec{G} \approx 1$ and $\varvec{F}_{y} = \varvec{F}_{x}^{\prime }$. Since $\beta$ is generated by convolution operations, $\varvec{G}$ easily outputs as 1. To prevent the normalized image from being identical to the original image, we set the normalization operation as in Eq. 2, making $\varvec{G}$ more inclined towards normalized channels. As shown in Fig. 4, we plot the brightness distribution of images with the same content but different brightness distributions. After processing with the trained LNM, they exhibit similar brightness distributions, further demonstrating the effectiveness of our LNM module.

Bilateral enhancement module with SNR fusion

Low-light images exhibit varying characteristics such as brightness and noise across different regions. In the same low-light image, regions with lower brightness suffer more severe noise degradation, while regions with higher brightness experience less damage, resulting in relatively better visibility. Most existing methods primarily focus on capturing global information but overlook the imbalance in characteristics across different regions. This may lead to insufficient enhancement in lower brightness regions and over-enhancement in higher brightness regions.

For low-light regions heavily affected by noise, local features alone cannot achieve effective enhancement due to the limited amount of useful information available. In contrast, regions with less noise degradation can be effectively enhanced using only local features.

To address this issue, we employ a dynamic enhancement strategy to enhance pixels in different regions. For regions with high SNR, we enhance them primarily through local information, as they contain sufficient useful information. For regions with low SNR, where noise severely affects local information and useful details are scarce, we utilize global information to enhance them effectively.

Based on this idea, we propose a Bilateral Enhancement module with SNR Fusion (BSF), as shown in Fig. 2; it mainly consists of three parts: the Global Brightness Adjustment (GBA) branch, the Local Feature Extraction (LFE) branch, and the SNR Fusion (SNF) branch.

Global brightness adjustment

Zhang et al.⁴⁷ have demonstrated that enhancing the V channel of an image in the HSV space can represent the processes of contrast and brightness enhancement while also minimizing noise and color distortion. Additionally, Guo et al.⁶ prove that iterative application of the following enhancement curve equation effectively extracts enhancement information.

$$\begin{aligned} LE_{m}(x) = LE_{m-1}(x) + \omega _{m}LE_{m-1}(x)(1 - LE_{m-1}(x)) \end{aligned}$$

(4)

where, $m$ represents the number of iterations and controls the curvature. $LE_{m}(x)$ denotes the enhanced version of the input image, and $\omega _{m}$ is a parameter map of the same size as the image.

Inspired by this, our Global Brightness Adjustment module takes the V channel and its histogram from the low-light image as input. It extracts brightness information from the V channel’s histogram and then treats it as a trainable curve parameter $\omega _{0,1,...,n}$. Using an iterative method, we adjust the V channel features to generate the global brightness feature. As shown in Fig. 5 (a), the main component of this branch is a simple multi-layer perceptron with very few parameters. The adjustment process can be expressed as:

$$\begin{aligned} \begin{aligned}&\omega _{0,1,...,n} = g(h(V)) \\&V_{m+1} = V_{m} + \omega _{m}(V_{m} - V_{m}^{2}) \end{aligned} \end{aligned}$$

(5)

where, $g(\cdot )$ represents the multi-layer perceptron part, and $h(\cdot )$ represents the brightness histogram of the low-light image.

Local feature extraction

Transformer is first proposed in the field of natural language processing (NLP)⁴⁸, where its multi-head self-attention mechanism dynamically focuses on different parts of the input sequence in context, enabling outstanding performance in text understanding and generation. Following its success, transformer is gradually introduced to computer vision^49,50, demonstrating powerful feature extraction capabilities. However, its complex architecture and large parameter scale limit its application in lightweight models.

In the local feature extraction module, our primary goal is to extract features from regions heavily affected by noise. Inspired by the transformer model, we design a transformer-style Local Enhancement Block (LEB). To achieve the lightweight design, we replace the self-attention mechanism with depth-wise convolutions and substitute the transformer’s feed-forward network with an MLP composed of two 1 $\times$ 1 convolutions to enhance feature representation further.

As shown in Fig. 2, the normalized low-light image $\varvec{I}_{N}$ first passes through a 3 $\times$ 3 depth-wise convolution to expand the channel dimension, producing the input feature $\varvec{F}_{in}$. Subsequently, $\varvec{F}_{in}$ is processed by the local feature extraction (LFE) branch composed of two stacked LEBs. For the lightweight design of the LEB, as shown in Fig. 5 (b), the LEB uses a depth-wise convolution to encode positional information from $\varvec{F}_{in}$, which is then connected with $\varvec{F}_{in}$ via a residual connection to avoid information loss, resulting in $\varvec{F}_{em}$. The enhanced local detail feature $\varvec{F}_{pdp}$ is then extracted using a depth-wise separable convolution network comprising PWConv-DWConv-PWConv with layer normalization. Finally, we use an MLP with layer normalization to further strengthen the feature representation, producing $\varvec{F}_{leb}$.

We apply a skip connection between the output features $\varvec{F}_{leb, 2}$ of the stacked LEB and the input features $\varvec{F}_{in}$ to retain some fundamental information about the original image. The enhancement process can be expressed as:

$$\begin{aligned} \begin{aligned}&\varvec{F}_{in} = Conv_{3\times 3}(\varvec{I}_{N}) \\&\varvec{F}_{leb, 2} = \sum _{k=1}^{2}(PWP(Norm(Conv_{3\times 3}(\varvec{F}_{in, k}) + \varvec{F}_{in, k})) + MLP(Norm(\varvec{F}_{pdp, k}))) \\&\varvec{F}_{l} = \varvec{F}_{leb, 2} + \varvec{F}_{in} \end{aligned} \end{aligned}$$

(6)

where, $\varvec{F}_{in, k}$ represents the input features of the k-th LEB block, where $\varvec{F}_{in, 1}$ = $\varvec{F}_{in}$, and $\varvec{F}_{pdp, k}$ denotes the enhanced features obtained from the k-th PWConv-DWConv-PWConv operation. $\varvec{F}_{l}$ is the local detail features finally output by local feature extraction LFE.

SNR fusion

Estimating noise solely from the input image while simultaneously providing a corresponding clean image to estimate the SNR is challenging and significantly increases the model’s complexity. To achieve a lightweight design, we use a non-learning-based method to estimate the SNR of the low-light image. As shown in Fig. 2, given a low-light input image $\varvec{I}_{N}$, we first use a mean filtering method to obtain the denoised image $\varvec{I}_{d}$. We then apply a weighted averaging method to both $\varvec{I}_{N}$ and $\varvec{I}_{d}$ to get the corresponding grayscale images $\varvec{I}^{g}$ and $\varvec{I}_{d}^{g}$, respectively. By calculating the difference between $\varvec{I}^{g}$ and $\varvec{I}_{d}^{g}$, we obtain the noise image ${\varvec{N}}$. Finally, we apply element-wise division to $\varvec{I}_{d}^{g}$ and ${\varvec{N}}$ to get the final SNR map $\varvec{S}$. The calculation process is expressed as follows:

$$\begin{aligned} \begin{aligned}&\varvec{I}_{d} = blur(\varvec{I}_{N})\\&\varvec{I}^{g} = gray(\varvec{I}_{N}), \varvec{I}_{d}^{g} = gray(\varvec{I}_{d})\\&\varvec{N} = abs(\varvec{I}^{g} - \varvec{I}_{d}^{g}), \varvec{S} = \varvec{I}_{d}^{g} / \varvec{N}\\ \end{aligned} \end{aligned}$$

(7)

Next, we reshape the obtained SNR map to match the dimensions of the global brightness features and local features, and normalize its values to the range [0, 1]. Finally, we use the refined SNR map $\varvec{S}^{'}$ as interpolation weights to dynamically fuse global brightness features $\varvec{F}_{g}$ and local detail features $\varvec{F}_{l}$. The fusion process can be expressed as:

$$\begin{aligned} \varvec{F}_{en} = (1 - \varvec{S^{\prime }}) \times \varvec{F}_{g} + \varvec{S^{\prime }} \times \varvec{F}_{l} \end{aligned}$$

(8)

Dual-exposure processing module

Motivation

In the field of image processing, issues of underexposure and overexposure are prevalent and often affect image quality and subsequent computer vision tasks. Traditional image processing techniques typically rely on complex algorithms and parameter adjustments, making it challenging to adaptively handle diverse exposure conditions. With the development of deep learning technology in image processing, new solutions have emerged to address this issue. However, achieving robust handling of different exposure conditions while maintaining a lightweight network remains a challenging task.

In convolutional neural networks, activation functions play a role in activating certain features, helping the network capture complex characteristics. As shown in Fig. 6, when the network mainly focuses on features of underexposed regions, ReLU and NegReLU functions exhibit differential responses to the two exposure properties, where NegReLU represents the operation of inverting the input values and then applying the ReLU function. Specifically, ReLU tends to process underexposed features, while NegReLU responds more to overexposed features. Additionally, the activation of ReLU for underexposed images and the activation of NegReLU for overexposed images show similarities. Based on this observation, we design the Dual-Exposure Processing (DEP) module, as shown in Fig. 7. It mainly consists of an exposure activation module composed of ReLU and NegReLU activation functions and an exposure learning module with residual networks.

Dual-exposure processing

To further improve the robustness of the network under different exposure conditions, we introduce a DEP module after the augmented network. Specifically, for the input feature $\varvec{F}_{en}$, we first use ReLU and NegReLU activation functions to obtain features $\varvec{F}_{u}$ and $\varvec{F}_{o}$ representing underexposed and overexposed properties, respectively. Then, to learn these two features consistently, the exposure learning module processes these features through two residual blocks (RsBlock), resulting in $\varvec{F}_{u}^{'}$ and $\varvec{F}_{o}^{'}$. Since $\varvec{F}_{o}$ is obtained by inverting ReLU, we need to apply the same inversion process to it before proceeding to the next step to obtain the feature in its original format.

Additionally, to retain more important information from the input feature $\varvec{F}_{en}$, we use the LNM module to normalize it and obtain the feature $\varvec{F}_{c}$, which remains invariant to exposure attributes. We then concatenate the three features $\varvec{F}_{u}^{'}$, $\varvec{F}_{o}^{'}$, and $\varvec{F}_{c}$, so the final feature contains exposure information from both attributes. The whole process is as follows:

$$\begin{aligned} \begin{aligned}&\varvec{F}_{u}^{'} = {\mathcal {R}}(\varvec{F}_{u}), \varvec{F}_{o}^{'} = -{\mathcal {R}}(\varvec{F}_{o}), \varvec{F}_{c} = LNM(\varvec{F}_{en})\\&\varvec{F}_{u}^{''} = {\mathcal {P}}[\varvec{F}_{u}^{'},\varvec{F}_{c}], \varvec{F}_{o}^{''} = {\mathcal {P}}[\varvec{F}_{o}^{'},\varvec{F}_{c}], \varvec{F}_{out} = {\mathcal {P}}[\varvec{F}_{u}^{''}, \varvec{F}_{o}^{''}]\\ \end{aligned} \end{aligned}$$

(9)

where ${\mathcal {R}}$ represents the residual network block, $[\cdot ]$ denotes the concatenation operation, and ${\mathcal {P}}$ indicates the 1$\times$1 convolution layer. Through these operations, the final output features $\varvec{F}_{out}$ simultaneously contain information from both exposure attributes.

Loss function

To better enhance the network’s performance, this paper employs the loss function that includes not only the commonly used Charbonnier loss function $\varvec{L}_{char}$ and SSIM structural similarity loss $\varvec{L}_{ssim}$ but also a color similarity loss function $\varvec{L}_{color}$, a luminance similarity loss function $\varvec{L}_{bright}$, and a structural similarity loss function $\varvec{L}_{struct}$⁵¹.

Charbonnier loss function

The $\varvec{L}_{char}$ is a variant of the $\varvec{L}_{1}$ loss function, which, compared to $\varvec{L}_{1}$, includes an additional regularization term $\epsilon$. It enhances model performance by approximating the $\varvec{L}_{1}$ loss. The gradient near-zero values are prevented from becoming too small due to the presence of $\epsilon$, thus avoiding gradient vanishing. It can be expressed as:

$$\begin{aligned} \varvec{L}_{\text{ char }} = \sqrt{({\hat{y}} - y)^{2} + \epsilon ^{2}} \end{aligned}$$

(10)

where ${\hat{y}}$ represents the enhanced image, y represents the ground truth image, and $\epsilon$ is a small constant set to $10^{-3}$ to prevent division by zero.

Color similarity loss function

The $\varvec{L}_{color}$ utilizes cosine similarity to measure the hue and saturation differences between two pixels, ensuring that the enhanced image’s colors match the reference image more closely. It can be expressed as:

$$\begin{aligned} \varvec{L}_{color} = 1 - \sum \limits _{i=1, j=1}^{m,n} cos(\varvec{E(\varvec{I}_{i,j}),\varvec{Y}_{i,j}}) \end{aligned}$$

(11)

where $\varvec{E}$ and $\varvec{Y}$ represent the pixel values of the enhanced image and the reference image, respectively, and the $cos(\cdot )$ denotes the cosine similarity between the two vectors. By minimizing the $\varvec{L}_{color}$, the network generates enhanced images with hue and saturation closer to those of the ground truth image.

Brightness similarity loss function

It aims to ensure that the brightness order within each image block of the enhanced image remains consistent with that of the reference image¹⁹. Specifically, it requires the enhanced image to linearly transform from the noise-free reference image, significantly suppressing noise and improving the quality of the enhanced image. This loss function follows:

$$\begin{aligned} \begin{aligned} \varvec{L}_{bright} = 1 - \sum \limits _{c}^{r,g,b} \sum \limits _{i=1, j=1}^{m,n} cos(&b(\varvec{E}(\varvec{I}_{i,j}^{c})) - min(b(\varvec{E}(\varvec{I}_{i,j}^{c})),\\&b(\varvec{Y}(\varvec{I}_{i,j}^{c})) - min(b(\varvec{Y}(\varvec{I}_{i,j}^{c}))) \end{aligned} \end{aligned}$$

(12)

where, $b(\cdot )$ represents image patches centered on $\varvec{E}$ and $\varvec{Y}$. The brightness relationship between them can be expressed as $b(\varvec{E})=\lambda b(\varvec{Y})+\delta$. Different image patches have different $\lambda$ and $\delta$, and subtracting the minimum value removes the influence of the constant $\delta$.

Structural similarity loss function

It uses gradients to represent structural information, modifying Eq. 12 yields the expression for this loss function:

$$\begin{aligned} \begin{aligned} \varvec{L}_{struct} = 1 - \sum \limits _{c}^{r,g,b} \sum \limits _{i=1, j=1}^{m,n} cos(&b\nabla (\varvec{E}(\varvec{I}_{i,j}^{c})) - min(b\nabla (\varvec{E}(\varvec{I}_{i,j}^{c})),\\&b\nabla (\varvec{Y}(\varvec{I}_{i,j}^{c})) - min(b\nabla (\varvec{Y}(\varvec{I}_{i,j}^{c}))) \end{aligned} \end{aligned}$$

(13)

To better normalize the brightness distribution, we use the Charbonnier loss function $\varvec{{\mathcal {L}}}_{low}$ to constrain the normalized low-light image $\varvec{I}_{N}$ to be as close as possible to the original low-light image ${\varvec{I}}$. In the experiments, we set the same weight for all loss functions based on empirical observations. Therefore, the total loss is expressed as:

$$\begin{aligned} \varvec{L}_{total} = \varvec{L}_{char} + \varvec{L}_{ssim} + \varvec{L}_{color} + \varvec{L}_{bright} + \varvec{L}_{struct} + \varvec{L}_{low} \end{aligned}$$

(14)

Experiments

Dataset

In this section, we train our network on the LOL-V1²⁵and LOL-V2²⁶ training datasets and then test it on the corresponding test sets and a mixed dataset. The details of the training and test sets are as follows:

LOL-V1

It contains 500 image pairs, with 15 used for testing. To highlight the impact of data quantity on the network, we use only 343 image pairs for training. During training, we randomly crop each training image into patches of size 100$\times$100 and use data augmentation methods involving random rotation and random flipping to enhance the diversity of the training dataset, effectively reducing and preventing overfitting.

LOL-V2

This dataset contains 689 image pairs for training and 100 image pairs for testing. During training, we randomly crop each training image into patches of size 100$\times$100 and use data augmentation methods involving random rotation and random flipping to enhance the diversity of the training dataset, effectively reducing and preventing overfitting.

Mixed dataset

This dataset consists of LOL-V1 (15 images)²⁵, LIME (10 images)¹⁸, MF (10 images)¹¹, and VV (23 images). It does not have reference images and is used only for evaluating the no-reference metric NIQE⁵².

Implementation details

The experiment is conducted on a server running Ubuntu 20.04.6 operating system, equipped with an NVIDIA 4090 GPU and a configured PyTorch deep learning framework. During training, the input image size is set to 100 $\times$ 100, with a batch size of 128. To achieve better training results and prevent overfitting, the maximum number of epochs is set to 30,000, and an early stopping mechanism is employed. Through multiple tests, setting the patience value to around 2,000 and the error threshold delta to 0.001 achieves satisfactory training performance. To reduce the number of model parameters, the histogram bin value for the V channel of low-light images is set to 32, which is experimentally validated in the Ablation experiments section. We use the Adam optimization algorithm and find that applying a learning rate adjustment strategy leads to poorer training outcomes. Therefore, both the learning rate and weight decay are set to $10^{-4}$. To maintain model accuracy while improving training speed, we set the model saving frequency to every 20 epochs when epoch $\le$ 1,000, and every 100 epochs otherwise.

To better compare the low-light enhancement performance of different methods, we use PSNR, SSIM, CIEDE2000⁵³, and NIQE⁵² as objective evaluation metrics. The PSNR and SSIM measure the peak signal-to-noise ratio and structural similarity of the enhanced images, respectively. Higher values indicate better enhancement effects. The International Commission on Illumination (CIE) introduced CIEDE2000 in 2000 as an improved color difference evaluation metric based on the CIELAB color space. It accounts for the non-uniformity of human visual perception and addresses color perception issues more effectively. Lower values indicate smaller color differences. NIQE is a no-reference image quality assessment metric that measures the perceptual quality of images without needing a reference image. Lower values indicate better perceptual quality of the enhanced images.

Compared methods

To validate the effectiveness of our method, we compare it with several state-of-the-art low-light enhancement methods, including traditional methods (LIME¹⁸), unsupervised methods (ZeroDec++⁷, PairLIE⁵⁴), and supervised methods (RetinexNet²⁵, MBLLEN⁸, KIND⁹, KIND++⁵⁵, IAT⁵⁶, DecNet⁵⁷, FLW-Net⁵¹).

Objective evaluation

Tables 1 and 2 present the quantitative comparison of different models on the LOL-V1, LOL-V2, and mixed datasets. We observe that our BiEnNet achieves superior results over other methods in terms of PSNR, SSIM, and CIEDE2000 metrics on both the LOL-V1 and LOL-V2 datasets. Additionally, the number of training samples indeed affects model performance, with a more significant impact on PSNR compared to other metrics. For instance, compared to LOL-V1, training BiEnNet on the LOL-V2 dataset increases the PSNR by nearly 0.6dB (e.g., from 29.06 to 29.66), while the SSIM only increases by about 0.01dB (e.g., from 0.86 to 0.87). The improvements in NIQE and CIEDE2000 are also minimal, decreasing from 3.49 to 3.48 and from 6.16 to 6.10, respectively. Although our method does not achieve the best scores across the board in terms of NIQE, number of parameters, and testing time-for example, on the NIQE metric of the combined dataset, our method yields comparable results to MBLLEN, KIND, and KIND++-BiEnNet boasts a relatively low number of parameters (0.1M) and consumes less time during testing. In summary, our BiEnNet attains results that are close to or even better than other methods in overall metrics.

Visual comparison

In addition to objective evaluations, we conduct visual comparisons on the LOL-V1, LOL-V2, and mixed datasets to further affirm the effectiveness of our BiEnNet. Fig. 8 and 9provide the visual comparison results of various methods on the LOL-V1 and LOL-V2 datasets. It is apparent that the low-light images, once enhanced by BiEnNet, exhibit superior improvements in brightness, color, and detail, thus more closely resembling the reference images. As LIME is a traditional enhancement method, it cannot effectively perform targeted enhancements under different conditions, resulting in images with significant noise and darker colors. Moreover, the unsupervised methods ZeroDec++⁷and PairLIE⁵⁴, lacking guidance from reference images during training, do not achieve optimal enhancement effects, especially on the LOL-V1 test dataset. The RetinexNet²⁵and MBLLEN⁸ methods show severe color distortion issues after enhancing low-light images. Fig. 10 presents the visual comparison on the mixed dataset, where our BiEnNet achieves a better balance in detail preservation, color fidelity, and halo artifacts.

Ablation experiments

Determination of the bin Value

In this ablation study, we evaluate bin values of 8, 16, 32, 64, and 128. By comparing the changes in model parameters and the PSNR and SSIM performance on the LOL-V1 and LOL-V2 test dataset, we determine the optimal bin value, as shown in Fig. 11.

The results indicate that as the bin value increases, both PSNR and SSIM reach their highest values at bin = 32 on both the LOL-V1 and LOL-V2 test datasets. The overall trend shows an initial increase followed by a decline. This phenomenon may be due to the fact that although increasing the number of bins improves model precision, an excessive number of bins can lead to overfitting or parameter redundancy, which decreases accuracy. Moreover, the number of model parameters increases steadily with the bin value. Therefore, to balance model parameters and performance, we choose bin = 32 as the optimal value.

Demonstration of module effectiveness

We conduct ablation experiments by continuously adding and combining modules in different ways to demonstrate the effectiveness of each module in our proposed method. The entire ablation experiment trains and tests on the LOL-V1 dataset. As shown in Table 3, we use four metrics-PSNR, SSIM, CEIDE2000, and NIQE-in the quantitative comparison experiments.

In Table 3, “1” indicates that the entire network only has a simple Global Brightness Adjustment (GBA) branch. Although it has the lowest scores in all groups, it still achieves good results, demonstrating its effectiveness. “2”, “3”, and “4” add the Luminance Normalization (LNM) module, Dual-Exposure Processing (DEP) module, and the combination of Local Feature Extraction (LFE) and SNR Fusion (SNF) branches to the GBA, respectively. Since LNM and DEP mainly improve the network’s generalization ability, they show similar improvements in PSNR and SSIM metrics. The Bilateral Enhancement Module with SNR Fusion (BSF), composed of LFE, SNF, and GBA, is the main low-light enhancement part of the entire network. Therefore, “4”, “6”, and “7”, which include LFE and SNF, show significant improvements. The improvement effect of their combinations with LNM and DEP is also similar. Group “8” represents the complete BiEnNet. Due to its improved generalization ability for different degradations and better enhancement capability, this group achieves the best enhancement effect.

As shown in Fig. 12, we also present the visual comparison results of each setting. Group “1” restores overall brightness and contrast, but the enhanced image has unsaturated tones and more noise, especially in the red and green boxed areas. Groups “2” and “3”, which add LNM and DEP, show some improvement in tone restoration but still have significant gap compared to the reference image. Group “4”, “6”, and “7”, which add LFE and SNF, show further improvements in color and detail restoration, especially in the green boxed area. Finally, our complete BiEnNet network, containing all branches, has better enhancement capability. Therefore, “8” achieves an enhancement effect closest to the reference image.

Conclusion

In this paper, we propose a deep learning-based lightweight generalizable low-light enhancement scheme. Specifically, to eliminate the brightness differences in input images, we propose a channel normalization method to obtain a more consistent degradation distribution in the preprocessing stage. In the low-light enhancement stage, we acquire global and local features through a dual-branch enhancement network and effectively fuse the global and local features using the SNR map of low-light images to achieve a better enhancement effect. Finally, to further improve the model’s robustness, we design a dual-exposure processing module in the post-processing state that guides the network to learn features under different exposure conditions simultaneously. Experiments on three public datasets demonstrate the superiority of our method compared to other state-of-the-art methods. However, our method still has certain limitations. For extremely low-light non-synthetic images, most regions contain very little recoverable information, and since our LOL training dataset mainly consists of synthetic low-light images, BiEnNet may produce color distortions that affect overall image quality. In future research, we plan to optimize the network structure while incorporating real low-light image datasets to improve the network’s performance on extremely low-light real-world images. We also aim to explore its potential applications in downstream image processing tasks.

Fig. 1

Visual comparison with some other state-of-the-art methods. It can be observed that the enhanced images generated by our method closely resemble the reference images in terms of color and details.

Fig. 2

Detailed architecture of BiEnNet network. Before low-light enhancement, we use LNM to normalize brightness degradation, reducing inconsistencies between images. During enhancement, BSF employs signal-to-noise ratio fusion, using SNF to compute the SNR map S for low-light images, with DB and GB representing denoising and grayscale computation. GBA and LFE capture global brightness and local detail features, respectively, and then BSF dynamically fuses them through S. Finally, DEP learns the correction for two exposure conditions, enhancing network robustness.

Fig. 3

Detailed structure of the brightness normalization (LNM) module. LNM consists mainly of a per-channel IN normalization layer composed of multiple INs and a gating module for selecting luminance-relevant channels.

Fig. 4

Comparison of brightness distributions between low-light images and LNM-normalized results. The low-light images are from the LOL-V2²⁶ test dataset. The images on the left have the same content but different brightness distributions; the images on the right show the brightness distributions before and after LNM. The results show that the normalized images have similar brightness distributions after applying LNM.

Fig. 5

Detailed structure of parts in the bilateral enhancement module. (a) Global Brightness Adjustment Branch (GBA) mainly consists of an MLP network and high-order curve adjustment. (b) Local Enhancement Block (LEB), mainly comprises layer normalization, depth-wise separable convolution, and a simple MLP network.

Fig. 6

Comparison of activation feature heatmaps for underexposed and overexposed images using ReLU and NegReLU activation functions. When the network activates features of underexposed images, ReLU tends to activate the underexposed parts, whereas NegReLU, in contrast to ReLU, tends to activate the overexposed features. Furthermore, ReLU and NegReLU exhibit similar tendencies in activating features of both underexposed and overexposed images.

Fig. 7

Detailed structure of the Dual-Exposure Processing Module. It uses the ReLU activation function to extract features from two exposure properties and then learns these features through residual network blocks. Finally, it employs LNM to obtain exposure-invariant features, which merge with the previously extracted features to produce the final output features.

Fig. 8

Visual comparison of different methods on the LOL-V1²⁵dataset, including LIME¹⁸, ZeroDec++⁷, PairLIE⁵⁴, RetinexNet²⁵, MBLLEN⁸, KIND⁹, KIND++⁵⁵, IAT⁵⁶, DecNet⁵⁷, and FLW-Net⁵¹.

Fig. 9

Visual comparison of different methods on the LOL-V2²⁶dataset, including LIME¹⁸, ZeroDec++⁷, PairLIE⁵⁴, RetinexNet²⁵, MBLLEN⁸, KIND⁹, KIND++⁵⁵, IAT⁵⁶, DecNet⁵⁷, and FLW-Net⁵¹.

Fig. 10

Visual comparison of different methods on the mixed dataset. The methods include LIME¹⁸, ZeroDec++⁷, PairLIE⁵⁴, RetinexNet²⁵, MBLLEN⁸, KIND⁹, KIND++⁵⁵, IAT⁵⁶, DecNet⁵⁷, and FLW-Net⁵¹.

Fig. 11

Variations in PSNR and SSIM metrics of BiEnNet on the LOL-V1²⁵and LOL-V2²⁶ test datasets under different bin value settings, along with variations in the model’s parameter count.

Fig. 12

Visual comparison results on the LOL-V1²⁵ dataset under different settings. The main comparison focuses on the red and green boxed areas. The visual effect when using all branches together is the closest to the reference image.

Table 1 Quantitative comparison results on the LOL-V1²⁵, LOL-V2²⁶and mixed datasets. Bold indicates the best results, and italic indicates the second-best results. LIME¹⁸represents a traditional method, ZeroDec++⁷and PairLIE⁵⁴ represent unsupervised learning methods, and the others represent supervised learning methods.

Table 2 The comparison results of color difference metric CIEDE2000⁵³and running efficiency on the LOL-V1²⁵and LOL-V2²⁶ datasets. The best and second-best results are marked in Bold and italic, respectively.

Table 3 Visual comparison of different methods on the mixed dataset. The methods include LIME¹⁸, ZeroDec++⁷, PairLIE⁵⁴, RetinexNet²⁵, MBLLEN⁸, KIND⁹, KIND++⁵⁵, IAT⁵⁶, DecNet⁵⁷, and FLW-Net⁵¹.