Complex Diophantine interval-valued Pythagorean normal set for decision-making processes

Abstract

A novel method for solving the multiple-attribute decision-making problem is proposed using the complex Diophantine interval-valued Pythagorean normal set (CDIVPNS). This study aims to discuss aggregating operations and how they are interpreted. We discuss the concept of CDIVPN weighted averaging (CDIVPNWA), CDIVPN weighted geometric (CDIVPNWG), generalized CDIVPN weighted averaging (CGDIVPNWA) and generalized CGDIVPN weighted geometric (CGDIVPNWG). This study aimed to examine several aggregation operators using complex Diophantine interval-valued Pythagorean normal sets. We calculated the weighted average and geometric distance based on an aggregating model. We demonstrate that complex Diophantine interval-valued Pythagorean normal sets satisfy algebraic structures such as associative, distributive, idempotent, bounded, commutative and monotonic properties. In this study, we discuss the mathematical properties of the score and accuracy values. We provide an example of how enhanced score and accuracy values are used in the real world. Machine tool technology and computer science play essential roles in robots. To evaluate robotic systems, four factors must be considered such as tasks, precision, speed and completion of the work. Consequently, it is evident that the models are significantly influenced by the natural number $\nabla$. To further demonstrate the effectiveness of the suggested approach, flowchart based multi-criteria decision-making is provided and applied to a numerical example. Additionally, a comparative study has been carried out to demonstrate the better results that the proposed approach provides when compared to current approaches.

Introduction

Every day, intelligence collecting, machine learning, knowledge compilation, and other techniques are employed to resolve conflicts. Demonstrating the success of strategic planning is a huge task. Mathematical theory facilitates the use of proper decision-making procedures. The DM idea may be useful to businesses since it examines and ranks numerous points of view depending on their characteristics. We may select, categorize, develop, and assess our choices efficiently. MADM analyzes every possible feature and factor in order to arrive at an optimal solution. Historically, it was widely understood that weights and characteristics must be stated numerically. Multiple evaluations and DM challenges need the examination of a variety of criteria and indications. Assessing and collecting data for evaluation indicators can assist solve assessment and DM issues. The assessment information is confusing since MADM issues are common in real-world systems due to their complexity.

Motivation

Kaplan et al.¹ suggest that artificial intelligence (AI) has the potential for solving significant social problems in the future. Margetts et al.² propose that major economies fund AI research and development through considerable government efforts. Recent study by Cresswell et al.^3,4 identifies machine learning, neural networks, natural language processing (NLP), smart robots, knowledge graphs, and expert systems as significant technological subsystems in the current AI technology architecture. AI poses a risk to human civilization in addition to moral concerns due to its possible impact on politics and jobs. Multidisciplinary Technology assessment (TA) initiatives are necessary to identify these risks and opportunities. AI is a general-purpose technology that has the potential to impact every aspect of society and the economy, according to several studies. In addition to allowing online platforms to profit from the market, the advancement of deep learning technology will provide highly efficient social responsibility solutions. Furthermore, according to Klinger et al.^5,6, AI technology has the potential to alter societal structures as it becomes more prevalent in certain economic and financial domains. Thus, we wish to identify the key research issue for AI from a TA perspective in order to have a better understanding of the potential impacts and necessary governance. Because real-world systems are always changing, decision-makers may find it challenging to choose the best course of action. It is possible to reduce several goals to a single one, notwithstanding the difficulty. Restricting people’s goals, motivations, and perspectives proved difficult for a number of businesses. When making decisions, individuals or committees must consider many goals at once. Consequently, more logical and reliable methods have been created to assist decision makers in selecting the best option. Agostini et al.⁷ presented the concept of an efficient interactive decision-making (DM) framework for robotic applications.

Literature review

The complexity of real-world systems makes it increasingly difficult for decision-makers to identify the best solution. Although deciding between alternatives can be difficult, it is possible to select the best option. It is challenging for many firms to find opportunities, achieve goals, and consider viewpoint constraints. As a consequence, individual or group decision-makers should consider multiple objectives simultaneously. There are a wide range of multi-attribute decision-making (MADM) related issues that need to be addressed on a daily basis. Due to this, it is necessary to improve decision making (DM) abilities. Research has been done in this field using a variety of methods by several researchers. Almost every challenge in real life involves uncertainty. The uncertainties include fuzzy set (FS)⁸, intuitionistic set (IFS)⁹, Pythagorean set (PFS)¹⁰ and neutrosophic set (NS)¹¹. Each element of the universe is graded in the FS, based on its degree of membership in the set of elements. The membership degrees (MD) indicates the membership range in a set. Various fuzzy methods are available, including regression prediction using fuzzy time series¹² and clustering fuzzy c-numbers¹³. Atanassov⁹ introduced an IFS, classifying them based on whether the combined membership degree (MD) and non-membership degree (NMD) are more than one. When there is greater than one MD or NMD, decision making (DM) can become problematic. PFS concept was proposed by Yager¹⁰. The MD and NMD squared were used to generalize the IFS logic. The maximum value of can be obtained by combining these parameters. As discussed in^14,15,16, PFS can be used in various applications. Zhang et al.¹⁷ investigated geometric AOs in group DM using interval-valued PFS (IVPFS), extending their methodology. Using this method, preferences are ranked by proximity to the ideal solution, distances to the solution are calculated, and the preferred solution is then combined with the distance to the ideal solution. Khan developed an application that uses Einstein’s Choquet integral operators to facilitate MAGDM. The induced IVPFS uses the Einstein AO. Liu et al.¹⁸ discussed an AO-based q-rung picture FS. The IVPFS with a normal set was described by Yang¹⁹.

Peng et al.²⁰ explore NSS with MADM using the MABAC and TOPSIS approaches. Zhang et al.²¹ presented a generalization of PFS using TOPSIS. The MADM spherical vague normal operator is discussed in a recent study by Palanikumar et al.²². For the q-rung orthogonal pair FS (q-ROFS), both MG and NMG have power q, but their sum can never be greater than 1. PFSs and IFSs are generalized q-ROFSs, therefore they can be considered special cases of q-ROFSs. If q increases, there is a greater number of orthopairs that satisfy the bounding constraint, and if q increases, there is a larger number of orthopairs that satisfy the bounding constraint. The q-ROFSs can express fuzzy information over a broader range. Because parameter q can be adjusted, q-ROFSs are flexible and better suited to uncertain environments. An increase in q achieved as the ambiguity in the decision information increases. It is possible that some experts were influenced by their own desires and surroundings. Therefore, they may have an MDG of 0.75 and an NMG of 0.65 when evaluating certain decision-making things. The fuzzy information cannot be described by IFNs and PFNs, but q-ROFNs can be described if the parameter q is increased. Therefore, the q-ROFS is more flexible and suitable for describing uncertain data. A bipolar FS using TOPSIS was proposed by Akram et al.²³ in 2018. The MCGDM was proposed by Adeel et al.²⁴ based on m-polar fuzzy linguistic TOPSIS. A review of complex PFS in 2019 by Ullah et al.²⁵ discussed its applications in pattern recognition. Smarandache developed the NSS theory¹¹. Neutosophy is the knowledge of the neutral mind; FS and IFS differ in their neutrality. Truth grades (TD), indeterminacy grades (ID) and false grades (FD) range from 0 to 1. It is possible to generalize the FS and IVFS approach with the NSS approach. Several authors have recently discussed different types of aggregation operators^26,27,28. This involves obtaining a ranking of preferences based on proximity to the ideal solution, calculating distances to those solutions, and combining them. A generalization of the FS and IVFS is the NSS approach.

Yager²⁹ developed an q-rung orthopair FS (q-ROFS), in which the sum of the q-powers of the MD and NMD can only be [0, 1]. For this example, we have $0.67^{3} + 0.74{3} = 0.3008 + 0.4052 = 0.7060$. We can see that q-ROFS is a more general model than IFSs or PFSs. In the field of aggregation operators, similarity measures (SMs), hybrid aggregation operators, and so on, the q-ROFS is a fundamentally useful tool for processing troublesome fuzzy data. There has been considerable success in developing aggregation operators for the q-ROFS environment, according to the aggregation operators. As an example, Fei et al.³⁰ developed aggregation operators based on multi-criteria decision making in Pythagorean fuzzy environment. Multi-criteria group decision making based on ELECTRE-I method in Pythagorean fuzzy information was investigated by Garg et al.³¹. Zhou et al.³² proposed divergence measure of PFSs based on belief function and its application in medical diagnosis. Any two objects can be compared using the SM to determine the degree of similarity between them. There have been many applications of SMs in different contexts. Oztaysi et al.³³ discusse the concept of social open innovation platform design for science teaching by using Pythagorean fuzzy analytic hierarchy process. Song et al.³⁴ interacted the loan risk assessment based on Pythagorean fuzzy analytic hierarchy process. Liu³⁵ deals with the concept of some q-rung orthopair fuzzy aggregation operators and their applications to MADM. The nature of real-life situations entails a wide range of complicated circumstances, and data measures are helpful when dealing with uncertain data. For example, in acknowledgment of design, clinical determination, and bunching investigation, numerous data measures are used, such as similitude, separation, and entropy. The PFS and q-ROFS are two existing MADM methodologies with weaknesses for fuzzy information. As a result, complex q-ROFS can only be calculated if the sum of the real part (and imaginary part) of the complex MD and the real part (and imaginary part) of the complex NMD is between [0, 1]. There is a broader scope of information, and it can be expressed in a more general way. Zulqarnain et al. discussed the various AOs with the concept of Pythagorean fuzzy soft sets, T-spherical fuzzy sets and q-rung orthopair fuzzy soft set^{36,37,38,39,40,41}.

Complex FS (CFS) is an FS that extends MD from a real number to a complex number was introduced by Ramot et al.⁴². Based on Ramot et al.⁴³, the FS may be generalized to CFS, which is an FS with complex MDs. As the set of complex numbers is a generalization of the set of real numbers. Accordingly, a CFS is an extension of the FS, whose range is extended from closed interval [0, 1] to a disk of radius one in a complex plane. The membership function of CFS X is denoted as $\mu _{X}(u)$ and defined on the universal U as; for any $u \in U$ a complex value in the disk of radius one in a complex plane. Thus, all values of $\mu _{X}(u)$ lie inside a circle of radius one in complex plane and $\mu _{X}(u) = r_{X}(u)e^{i\omega _{X}(u)}$; where $i = \sqrt{-1}$. The term $r_{X}(u)$ is said to be amplitude term; $\omega _{X}(u)$ is said to be phase term. Both these terms are real valued with $r_{X}(u)\in [0,1]$. The CFS X is represented as $\{(u,\mu _{X}(u))|u\in U \}$. According to Yazdanbakhsh et al.⁴⁴, their analysis of CFSs is based on explaining their reasoning and logic. Alkouri et al.⁴⁵, NMD is incorporated into the complex IFS (CIFS). The MD and NMD can be generalized across the entire unit circle. Garg et al.⁴⁶ used the MADM method to deal with CIFSs. The CPFS concept was first presented in 2002 by Ullah et al.⁴⁷. Liu et al.⁴⁸ introduced complex root FS (CROFS). An AO found in CROFS that maps onto MacLaurin symmetric means was developed by Rong et al.⁴⁹. Akram et al.⁵⁰ proposed a new theory of complex picture FS including the Hamacher AOs. From CFSs, CIFSs, CPFSsand CROFSs, this theory follows from the components of complex picture FS. An amplitude term and a phase term are used to represent the truth, abstinence and falsehood degrees in a CPFS. Zhan et al.⁵¹ discussed the idea Fuzzy control model and simulation for nonlinear supply chain system with lead times. Zhan et al.⁵² interacted the concept of discrete switched model and fuzzy robust control of dynamic supply chain network. Zhan et al.⁵³ introduced the logic fuzzy emergency model and robust emergency strategy of supply chain system under random supply disruptions. Sarwar et al.⁵⁴ discussed the concept of fuzzy fixed point results and applications to ordinary fuzzy differential equations in complex valued metric spaces.

Xia et al.⁵⁵ deals that the idea fuzzy sampled-data stabilization of chaotic nonlinear systems. Edalatpanah et al.⁵⁶ presented a technique for averaging the fuzzy Einstein coefficients for complex q-rung pictures. Recently, many researchers discussed the new aggregation operators using FS, IVFS and CFS^{57,58,59,60,61}. Amin et al.⁶² discussed the new concept of generalized cubic Pythagorean fuzzy AOs and their application to MADM. Gao et al.⁶³ deals the concept of semi-Markov jump T-S fuzzy systems with time delay. Zhang et al.⁶⁴ introduced the concept of mitigation of bullwhip effect in closed?loop supply chain based on fuzzy robust control. Ge et al.⁶⁵ dicussed the concept of adaptive inventory control based on fuzzy neural network under uncertain environment. Rahim⁶⁶ introduced the MCDM based on frank AOs under Pythagorean cubic FSs. Recently, Ahmad et al.⁶⁷ deals with the development of p, q quasi-rung ortho-pair fuzzy Hamacher AOs and its application in DM problems. Rahim⁶⁸ deals that the GDM algorithm with sine trigonometric p, q quasi-rung ortho-pair AOs and their applications. Zulqarnain et al.^{69,70,71,72,73,74,75} deals that the various generalized fuzzy logical and its real life applications. Zhang et al.⁷⁶ deals that the concept of observer-based sliding mode control for fuzzy stochastic switching systems with deception attacks. Sun et al.⁷⁷ communicated the idea of sliding mode control of discrete-time interval type-2 fuzzy Markov jump systems with the preview target signal. Duan et al.⁷⁸ deals the concept of H control for continuous-discrete systems in TS fuzzy model with finite frequency specifications.

Hwang et al.⁷⁹ investigated a practical use of MADM. Using reference parameters, Riaz et al.⁸⁰ spoke about Linear Diophantine FS (LDFS). The LDFS is more flexible and effective than other methods as it uses reference parameters. Furthermore, LDFS classifies the data in MADM issues by altering the physical meaning of reference parameters. Kannan et al.⁸¹ have addressed the concept of the LDFS with CODAS approach for logistic specialist selection. Gazi et al.⁸² employ the Pentagonal fuzzy DEMATEL technique to identify the most important elements for women’s empowerment in the sports sector. Palanikumar et al.⁸³ have investigated the concept of a q-rung complex Diophatine neutrosophic normal set with an aggregation operation based on score and accuracy values. In this study, we introduce the concept of a complex Diophantine Pythagorean normal interval-valued set (CDIVPNS) that can be accessed through AOs. This method can be applied to DM problems using these operators. This study aimed to clarify the significance of CDIVPNS. Our aim was to extract data from the CDIVPNS using the AO. Consequently, these studies make the following contributions.

Objectives

• 1. The CDIVPNSs were given score values and accuracy values.

• 2. The CDIVPNNs satisfy the properties of associativity, distributivity, idempotence, boundedness, commutativity and monotonicity.

• 3. We applied the proposed operator to a problem to demonstrate its effectiveness and reliability.

• 4. DM is responsible for determining an outcome based on natural number $\nabla$.

This study is comprises of six sections. Section 2 presents the preliminaries. Section 3 discusses CDIVPNS with certain operations. The CDIVPNS concept using a few aggregating operators is discussed in section 4. The algorithm based on the CDIVPNS data is discussed in Section 5, along with a numerical example. Section 6 presents the conclusions and future directions of this work.

Basic concepts

In this section, we begin our research with an overview of fundamental terms.

Definition 2.1

¹⁰ Let $\Theta$ be a universe. The PFS $\mathcal {Z}$ in $\Theta$ is $\mathcal {Z}= \Big \{\theta , \big \langle R^{{T}}_{\mathcal {Z}}(\theta ), R^{{F}}_{\mathcal {Z}}(\theta )\big \rangle \big | \theta \in \Theta \Big \}$, where $R^{{T}}_{\mathcal {Z}}, R^{{F}}_{\mathcal {Z}}: \Theta \rightarrow [0,1]$ denote the MD and NMD of $\theta \in \Theta$ to $\mathcal {Z}$, respectively and $0 \preceq (R^{{T}}_{\mathcal {Z}}(\theta ))^{2}+(R^{{F}}_{\mathcal {Z}}(\theta ))^{2} \preceq 1$. For $\mathcal {Z} = \big \langle R^{{T}}_{\mathcal {Z}},R_{\mathcal {Z}}^{{F}} \big \rangle$ is represent a Pythagorean fuzzy number.

Definition 2.2

¹⁷ The PIVFS $\mathcal {Z}$ in $\Theta$ is $\widehat{\mathcal {Z}}= \Big \{\theta , \Big \langle \widehat{ R^{{T}}_{\mathcal {Z}}}(\theta ), \widehat{ R^{{F}}_{\mathcal {Z}}}(\theta )\Big \rangle \Big | \theta \in \Theta \Big \}$, where $\widehat{ R^{T}_{\mathcal {Z}}}, \widehat{ R^{F}_{\mathcal {Z}}}: \Theta \rightarrow Int([0,1])$ denote the MD and NMD of $\theta \in \Theta$ to $\mathcal {Z}$, respectively and $0 \preceq (R^{{T}u}_{\mathcal {Z}}(\theta ))^{2} +(R_{\mathcal {Z}}^{{F}u}(\theta ))^{2} \preceq 1$. For $\mathcal {Z}=\Big \langle \Big [ R^{{T}l}_{\mathcal {Z}}, R^{{T}u}_{\mathcal {Z}}\Big ],\Big [R_{\mathcal {Z}}^{{F}l},R_{\mathcal {Z}}^{{F}u}\Big ]\Big \rangle$ is called a Pythagorean interval-valued fuzzy number (PIVFN).

Definition 2.3

¹⁷ Let $\mathcal {Z}= \Big \langle [ R^{{T}l}, R^{{T}u}],[ R^{{F}l}, R^{{F}u}] \Big \rangle$, $\mathcal {Z}_{1}= \Big \langle [ R^{{T}l}_{1}, R^{{T}u}_{1}], [ R^{{F}l}_{1}, R^{{F}u}_{1}] \Big \rangle$ and

$\mathcal {Z}_{2}= \Big \langle [ R^{{T}l}_{2}, R^{{T}u}_{2}], [ R^{{F}l}_{2}, R^{{F}u}_{2}] \Big \rangle$ be any three PIVFNsand $q > 0$. Then

• 1. $\mathcal {Z}_{1}\bigoplus \mathcal {Z}_{2}= \begin{bmatrix} \Big [\sqrt{( R^{{T}l}_{1})^{2} + ( R^{{T}l}_{2})^{2} -( R^{{T}l}_{1})^{2} \cdot ( R^{{T}l}_{2})^{2}}, \sqrt{( R^{{T}u}_{1})^{2} + ( R^{{T}u}_{2})^{2} -( R^{{T}u}_{1})^{2} \cdot ( R^{{T}u}_{2})^{2}}\,\Big ],\\ \Big [ R^{{F}l}_{1}\cdot R^{{F}l}_{2}, \, R^{{F}u}_{1}\cdot R^{{F}u}_{2}\Big ] \end{bmatrix}$,

• 2. $\mathcal {Z}_{1} \bigotimes \mathcal {Z}_{2} = \begin{bmatrix} \Big [ R^{{T}l}_{1}\cdot R^{{T}l}_{2},\, R^{{T}u}_{1}\cdot R^{{T}u}_{2}\Big ],\\ \Big [\sqrt{( R^{{F}l}_{1})^{2} + ( R^{{F}l}_{2})^{2} -( R^{{F}l}_{1})^{2} \cdot ( R^{{F}l}_{2})^{2}}, \sqrt{( R^{{F}u}_{1})^{2} + ( R^{{F}u}_{2})^{2} -( R^{{F}u}_{1})^{2} \cdot ( R^{{F}u}_{2})^{2}}\,\Big ] \end{bmatrix}$,

• 3. $\nabla \cdot \mathcal {Z} = \begin{bmatrix} \Big [\sqrt{1-\big ( 1- ( R^{{T}l})^{2}\big )^{\nabla }}, \sqrt{1-\big ( 1- ( R^{{T}u})^{2}\big )^{\nabla }}\,\,\Big ], \Big [( R^{{F}l})^{\nabla }, ( R^{{F}u})^{\nabla }\Big ] \end{bmatrix},$

• 4. $\mathcal {Z}^{\nabla }= \begin{bmatrix} \Big [( R^{{T}l})^{\nabla }, ( R^{{T}u})^{\nabla }\Big ], \Big [\sqrt{1-\big ( 1- ( R^{{F}l})^{2}\big )^{\nabla }}, \sqrt{1-\big ( 1- ( R^{{F}u})^{2}\big )^{\nabla }}\,\,\Big ] \end{bmatrix}.$

Definition 2.4

For any PIVFN $\mathcal {Z}= \Big \langle [ R^{{T}l}, R^{{T}u}], [ R^{{F}l}, R^{{F}u}] \Big \rangle$, the score function of $\mathcal {Z}$ is defined as

$$\begin{aligned}S(\mathcal {Z})= \frac{1}{2} \Big ( ( R^{{T}l})^{2} + ( R^{{T}u})^{2}- ( R^{{F}l})^{2}-( R^{{F}u})^{2} \Big ),\,\, S(\mathcal {Z})\in [-1,1]\end{aligned}$$

Accuracy function of $\mathcal {Z}$ is

$$\begin{aligned}H(\mathcal {Z})= \frac{1}{2} \Big ( ( R^{{T}l})^{2} + ( R^{{T}u})^{2} +( R^{{F}l})^{2} + ( R^{{F}u})^{2} \Big ),\,\, H(\mathcal {Z})\in [0,1].\end{aligned}$$

Definition 2.5

^12,13

• (i) Let $M(\theta )= e^{-\big (\frac{\theta -\alpha }{\beta }\big )^{2}},(\beta >0)$ be called a fuzzy number (FN), where $M= (\alpha , \beta )$ is said to be normal FN (NFN) and $\widehat{N}$ represents a normal FS.

• (ii) Let $L=(\alpha _{1},\beta _{1})\in \widehat{N}$ and $M=(\alpha _{2},\beta _{2})\in \widehat{N}$, $(\beta _{1},\beta _{2}>0)$, then the distance is defined as $\mathbb {D}(L,M)= \sqrt{(\alpha _{1}-\alpha _{2})^{2} + \frac{1}{2}(\beta _{1}-\beta _{2})^{2}}$.

Basic operations using CDPNIVN

Based on the concepts of complex Diophantine Pythagorean interval-valued number (CDPIVN) and normal fuzzy number (NFN), we defined CDPNIVN and its operations.

Definition 3.1

The complex Diophantine Pythagorean interval-valued set (CDPIVS) $\widehat{\mathcal {Z}}$ in $\Theta$ is $\widehat{\mathcal {Z}}= \Big \{\theta , \Big \langle [\widehat{R^{{T}}_{\mathcal {Z}}}(\theta )e^{2i\pi \widehat{ I^{{T}}_{\mathcal {Z}}}(\theta )}, \widehat{ R^{{F}}_{\mathcal {Z}}}(\theta )e^{2i\pi \widehat{ I^{{F}}_{\mathcal {Z}}}(\theta )}],[\lambda (\theta ),\mu (\theta )]\Big \rangle \Big | \theta \in \Theta \Big \}$, where $\widehat{ R^{T}_{\mathcal {Z}}}, \widehat{ R^{F}_{\mathcal {Z}}}: \Theta \rightarrow Int([0,1])$ denote the amplitude truth degree, and amplitude false degree of $\theta \in \Theta$ to $\widehat{\mathcal {Z}}$, respectively. Also, $\widehat{ I^{T}_{\mathcal {Z}}}, \widehat{ I^{F}_{\mathcal {Z}}}: \Theta \rightarrow Int([0,1])$ denote the phase truth degree and phase false degree of $\theta \in \Theta$ to $\widehat{\mathcal {Z}}$, respectively. A CDPIVS is satisfy the following condition: $0 \preceq (\lambda R^{{T}u}_{\mathcal {Z}}(\theta ))^{2}+(\mu R_{\mathcal {Z}}^{{F}u}(\theta ))^{2} \preceq 1$ and $0 \preceq (\lambda I^{{T}u}_{\mathcal {Z}}(\theta ))^{2} +(\mu I_{\mathcal {Z}}^{{F}u}(\theta ))^{2} \preceq 1$. For $\widehat{\mathcal {Z}}= \Big \langle [ R^{{T}l}_{\mathcal {Z}}e^{i2\pi I^{{T}l}_{\mathcal {Z}}}, R^{{T}u}_{\mathcal {Z}}e^{i2\pi I^{{T}u}_{\mathcal {Z}}}], [ R^{{F}l}_{\mathcal {Z}}e^{i2\pi I^{{F}l}_{\mathcal {Z}}}, R^{{F}u}_{\mathcal {Z}}e^{i2\pi I^{{F}u}_{\mathcal {Z}}}],[\lambda ,\mu ] \Big \rangle$ is called a complex Pythagorean interval-valued number (CDPIVN), Here R means that real part and I means that imaginary part.

Definition 3.2

Let $(\alpha , \beta ) \in \widehat{N}$, $\widehat{\mathcal {Z}}= \Big \langle (\alpha , \beta ); [ R^{{T}l}e^{i2\pi I^{{T}l}}, R^{{T}u}e^{i2\pi I^{{T}u}}], [ R^{{F}l}e^{i2\pi I^{{F}l}}, R^{{F}u}e^{i2\pi I^{{F}u}}],[\lambda ,\mu ] \Big \rangle$ is a CDPNIVN, TD and FD are defined as $\big [ R^{{T}l}, R^{{T}u}\big ]= \Big [ R^{{T}l} e^{-\big (\frac{\theta -\alpha }{\beta }\big )^{2}}, R^{{T}u} e^{-\big (\frac{\theta -\alpha }{\beta }\big )^{2}}\Big ]$ and $\big [ R^{{F}l}, R^{{F}u}\big ]= \Big [1-\big (1- R^{{F}l}\big ) e^{-\big (\frac{\theta -\alpha }{\beta }\big )^{2}}, 1-\big (1- R^{{F}u}\big ) e^{-\big (\frac{\theta -\alpha }{\beta }\big )^{2}}\Big ]$, respectively. Also, $\big [ I^{{T}l}, I^{{T}u}\big ]= \Big [ I^{{T}l} e^{-\big (\frac{\theta -\alpha }{\beta }\big )^{2}}, I^{{T}u} e^{-\big (\frac{\theta -\alpha }{\beta }\big )^{2}}\Big ]$ and $\big [ I^{{F}l}, I^{{F}u}\big ]= \Big [1-\big (1- I^{{F}l}\big ) e^{-\big (\frac{\theta -\alpha }{\beta }\big )^{2}}, 1-\big (1- I^{{F}u}\big ) e^{-\big (\frac{\theta -\alpha }{\beta }\big )^{2}}\Big ]$, $\theta \in \Theta$ respectively, where $\Theta$ is a non-empty set and $\big [ R^{{T}l}, R^{{T}u}\big ], \big [ R^{{F}l}, R^{{F}u}\big ], \big [ I^{{T}l}, I^{{T}u}\big ]$, $\big [ I^{{F}l}, I^{{F}u}\big ]\in Int([0,1])$ and $0 \preceq \big (\lambda R^{{T}u}(\theta )\big )^{2}+ \big (\mu R^{{F}u}(\theta )\big )^{2} \preceq 1$ and $0 \preceq \big (\lambda I^{{T}u}(\theta )\big )^{2}+ \big (\mu I^{{F}u}(\theta )\big )^{2} \preceq 1$.

Definition 3.3

For any CDPIVN $\widehat{\mathcal {Z}}= \Big \langle [ R^{{T}l}_{\mathcal {Z}}e^{i2\pi I^{{T}l}_{\mathcal {Z}}}, R^{{T}u}_{\mathcal {Z}}e^{i2\pi I^{{T}u}_{\mathcal {Z}}}], [ R^{{F}l}_{\mathcal {Z}}e^{i2\pi I^{{F}l}_{\mathcal {Z}}}, R^{{F}u}_{\mathcal {Z}}e^{i2\pi I^{{F}u}_{\mathcal {Z}}}],[\lambda ,\mu ] \Big \rangle$, the score function of $\widehat{\mathcal {Z}}$ $S_{1}(\widehat{\mathcal {Z}})= \frac{\alpha }{2}\left( X + Y\right)$, $S_{2}(\widehat{\mathcal {Z}})= \frac{\beta }{2}\left( X + Y\right)$ and $S(\widehat{\mathcal {Z}})= \frac{S_{1}(\widehat{\mathcal {Z}})+S_{2}(\widehat{\mathcal {Z}})}{2}$. where

$$\begin{aligned} & X= \left( \frac{(\lambda R^{{T}l})^{2} + (\lambda R^{{T}u})^{2}}{2}+1 - \frac{(\mu R^{{F}l})^{2}+(\mu R^{{F}u})^{2}}{2} \right) \\ & Y= \left( \frac{(\lambda I^{{T}l})^{2} + (\lambda I^{{T}u})^{2}}{2} - \frac{(\mu I^{{F}l})^{2}+(\mu I^{{F}u})^{2}}{2} \right) ,\end{aligned}$$

where $\,\, S(\widehat{\mathcal {Z}})\in [-1,1]$.

The accuracy function $H_{1}(\widehat{\mathcal {Z}})= \frac{\alpha }{2}\left( X_{1} + Y_{1}\right)$, $H_{2}(\widehat{\mathcal {Z}})= \frac{\beta }{2}\left( X_{1} + Y_{1}\right)$ and $H(\widehat{\mathcal {Z}})= \frac{H_{1}(\widehat{\mathcal {Z}})+H_{2}(\widehat{\mathcal {Z}})}{2}$, where

$$\begin{aligned} & X_{1}= \left( \frac{(\lambda R^{{T}l})^{2} + (\lambda R^{{T}u})^{2}}{2}+ \frac{(\mu R^{{F}l})^{2}+(\mu R^{{F}u})^{2}}{2} \right) \\ & Y_{1}= \left( \frac{(\lambda I^{{T}l})^{2} + (\lambda I^{{T}u})^{2}}{2}+ \frac{(\mu I^{{F}l})^{2}+(\mu I^{{F}u})^{2}}{2} \right) ,\end{aligned}$$

where $\,\, H(\widehat{\mathcal {Z}})\in [0,1].$

Definition 3.4

Let $\widehat{\mathcal {Z}}= \Big \langle (\alpha , \beta ); [ R^{{T}l}e^{i2\pi I^{{T}l}}, R^{{T}u}e^{i2\pi I^{{T}u}}],$ $[ R^{{F}l}e^{i2\pi I^{{F}l}}, R^{{F}u}e^{i2\pi I^{{F}u}}],[\lambda ,\mu ] \Big \rangle,$

$\widehat{\mathcal {Z}}_{1}= \Big \langle (\alpha _{1}, \beta _{1}); [ R^{{T}l}_{1}e^{i2\pi I^{{T}l}_{1}}, R^{{T}u}_{1}e^{i2\pi I^{{T}u}_{1}}], [ R^{{F}l}_{1}e^{i2\pi I^{{F}l}_{1}}, R^{{F}u}_{1}e^{i2\pi I^{{F}u}_{1}}] ,[\lambda _{1},\mu _{1}] \Big \rangle$

and $\widehat{\mathcal {Z}}_{2}= \Big \langle (\alpha _{2}, \beta _{2}); [ R^{{T}l}_{2}e^{i2\pi I^{{T}l}_{2}}, R^{{T}u}_{2}e^{i2\pi I^{{T}u}_{2}}], [ R^{{F}l}_{2}e^{i2\pi I^{{F}l}_{2}}, R^{{F}u}_{2}e^{i2\pi I^{{F}u}_{2}}],[\lambda _{2},\mu _{2}] \Big \rangle$ be three CDPNIVNsand $\nabla > 0.$ Then

• 1.
  $$\begin{aligned} & \widehat{\mathcal {Z}}_{1}\bigoplus \widehat{\mathcal {Z}}_{2} \\ & \quad = \begin{bmatrix} (\alpha _{1} + \alpha _{2}, \beta _{1} + \beta _{2});\\ \begin{bmatrix} \root 2\nabla \of {(\lambda R^{{T}l}_{1})^{2\nabla } + (\lambda R^{{T}l}_{2})^{2\nabla } -(\lambda R^{{T}l}_{1})^{2\nabla } \cdot (\lambda R^{{T}l}_{2})^{2\nabla }} e^{i2\pi \root 2\nabla \of {(\lambda I^{{T}l}_{1})^{2\nabla } + (\lambda I^{{T}l}_{2})^{2\nabla } -(\lambda I^{{T}l}_{1})^{2\nabla } \cdot (\lambda I^{{T}l}_{2})^{2\nabla }}},\\ \root 2\nabla \of {(\lambda R^{{T}u}_{1})^{2\nabla } + (\lambda R^{{T}u}_{2})^{2\nabla } -(\lambda R^{{T}u}_{1})^{2\nabla } \cdot (\lambda R^{{T}u}_{2})^{2\nabla }} e^{i2\pi \root 2\nabla \of {(\lambda I^{{T}u}_{1})^{2\nabla } + (\lambda I^{{T}u}_{2})^{2\nabla } -(\lambda I^{{T}u}_{1})^{2\nabla } \cdot (\lambda I^{{T}u}_{2})^{2\nabla }}} \end{bmatrix},\\ \Big [\left( \mu R^{{F}l}_{1}\cdot \mu R^{{F}l}_{2}\right) e^{i2\pi (\mu I^{{F}l}_{1}\cdot \mu I^{{F}l}_{2})}, \left( \mu R^{{F}u}_{1}\cdot \mu R^{{F}u}_{2} \right) e^{i2\pi (\mu I^{{F}l}_{1}\cdot \mu I^{{F}l}_{2})}\Big ] \end{bmatrix}, \end{aligned}$$
• 2.
  $$\begin{aligned} & \widehat{\mathcal {Z}}_{1} \bigotimes \widehat{\mathcal {Z}}_{2} \\ & \quad = \begin{bmatrix} (\alpha _{1} \cdot \alpha _{2}, \beta _{1} \cdot \beta _{2});\\ \Big [\left( \lambda R^{{T}l}_{1}\cdot \lambda R^{{T}l}_{2}\right) e^{i2\pi (\lambda I^{{T}l}_{1}\cdot \lambda I^{{T}l}_{2})}, \left( \lambda R^{{T}u}_{1}\cdot \lambda R^{{T}u}_{2} \right) e^{i2\pi (\lambda I^{{T}l}_{1}\cdot \lambda I^{{T}l}_{2})}\Big ],\\ \begin{bmatrix} \root 2\nabla \of {(\mu R^{{F}l}_{1})^{2\nabla } + (\mu R^{{F}l}_{2})^{2\nabla } -(\mu R^{{F}l}_{1})^{2\nabla } \cdot (\mu R^{{F}l}_{2})^{2\nabla }}, e^{i2\pi \root 2\nabla \of {(\mu I^{{F}l}_{1})^{2\nabla } + (\mu I^{{F}l}_{2})^{2\nabla } -(\mu I^{{F}l}_{1})^{2\nabla } \cdot (\mu I^{{F}l}_{2})^{2\nabla }}},\\ \root 2\nabla \of {(\mu R^{{F}u}_{1})^{2\nabla } + (\mu R^{{F}u}_{2})^{2\nabla } -(\mu R^{{F}u}_{1})^{2\nabla } \cdot (\mu R^{{F}u}_{2})^{2\nabla }} e^{i2\pi \root 2\nabla \of {(\mu I^{{F}u}_{1})^{2\nabla } + (\mu I^{{F}u}_{2})^{2\nabla } -(\mu I^{{F}u}_{1})^{2\nabla } \cdot (\mu I^{{F}u}_{2})^{2\nabla }}} \end{bmatrix} \end{bmatrix}, \end{aligned}$$
• 3.
  $$\begin{aligned} \nabla \cdot \widehat{\mathcal {Z}} = \begin{bmatrix} (\nabla \cdot \alpha , \nabla \cdot \beta );\\ \begin{bmatrix} \root 2\nabla \of {1-\big ( 1- (\lambda R^{{T}l})^{2\nabla }\big )^{\nabla }}e^{i2\pi \root 2\nabla \of {1-\big ( 1- (\lambda I^{{T}l})^{2\nabla }\big )^{\nabla }}},\\ \root 2\nabla \of {1-\big ( 1- (\lambda R^{{T}u})^{2\nabla }\big )^{\nabla }} e^{i2\pi \root 2\nabla \of {1-\big ( 1- (\lambda I^{{T}u})^{2\nabla }\big )^{\nabla }}} \end{bmatrix}\\ \Big [(\mu R^{{F}l})^{\nabla } e^{i2\pi (\mu I^{{F}l})^{\nabla }}, (\mu R^{{F}u})^{\nabla } e^{i2\pi (\mu I^{{F}u})^{\nabla }}\Big ] \end{bmatrix}, \end{aligned}$$
• 4.
  $$\begin{aligned} \widehat{\mathcal {Z}}^{\nabla } = \begin{bmatrix} (\alpha ^{\nabla }, \beta ^{\nabla });\\ \Big [(\lambda R^{{T}l})^{\nabla } e^{i2\pi (\lambda I^{{T}l})^{\nabla }}, (\lambda R^{{T}u})^{\nabla } e^{i2\pi (\lambda I^{{T}u})^{\nabla }}\Big ],\\ \begin{bmatrix} \root 2\nabla \of {1-\big (1- (\mu R^{{F}l})^{2\nabla }\big )^{\nabla }}e^{i2\pi \root 2\nabla \of {1-\big ( 1- (\mu I^{{F}l})^{2\nabla }\big )^{\nabla }}},\\ \root 2\nabla \of {1-\big (1- (\mu R^{{F}u})^{2\nabla }\big )^{\nabla }} e^{i2\pi \root 2\nabla \of {1-\big ( 1- (\mu I^{{F}u})^{2\nabla }\big )^{\nabla }}} \end{bmatrix} \end{bmatrix}. \end{aligned}$$

Aggregation operators for CDPNIVNs

Aggregate operators can be used to bring together and process several kinds of data. A collection of current approaches in information analysis, engineering, economics, and other areas is represented by aggregate operators. The number of objects in a collection or their numerical properties can be summed up to find the lowest, maximum, average, or total value. An aggregate operator is used to combine a set of values. In this section, new CDPNIVS techniques are introduced and aggregate operators are defined. Linguistic growth, ambiguous numbers, score, and accuracy values may all be further investigated by looking at these fundamental characteristics. The main properties of a CDPNIVN with AO are associativity, commutativity, idempotency, boundedness and monotonicity. We present the operators for CDPNIVWA, CDPNIVWG, CDGPNIVWA, and CDGPNIVWG throughout this section.

CDPNIV weighted averaging (CDPNIVWA)

There are two basic types of operators for weighted averaging and geometric AO in CDPNIVNs.

Definition 4.1

Let $\widehat{\mathcal {Z}}_{k} = \Big \langle (\alpha _{k}, \beta _{k}); [ R^{{T}l}_{k}e^{i2\pi I^{{T}l}_{k}}, R^{{T}u}_{k}e^{i2\pi I^{{T}u}_{k}}], [ R^{{F}l}_{k}e^{i2\pi I^{{F}l}_{k}}, R^{{F}u}_{k}e^{i2\pi I^{{F}u}_{k}}],[\lambda _{k},\mu _{k}] \Big \rangle$ be the family of CDPNIVNs, $W= (\chi _{1},\chi _{2},...,\chi _{m})$ be the weight of $\widehat{\mathcal {Z}}_{k}$, $\chi _{k}\succeq 0$ and $\boxplus ^{m}_{k=1} \chi _{k}=1$. Then CDPNIVWA operator is defined as CDPNIVWA $(\widehat{\mathcal {Z}}_{1}, \widehat{\mathcal {Z}}_{2},..., \widehat{\mathcal {Z}}_{m})= \boxplus ^{m}_{k=1} \chi _{k}\widehat{\mathcal {Z}}_{k}$.

Theorem 4.1

Let $\widehat{\mathcal {Z}}_{k} = \Big \langle (\alpha _{k}, \beta _{k}); [ R^{{T}l}_{k}e^{i2\pi I^{{T}l}_{k}}, R^{{T}u}_{k}e^{i2\pi I^{{T}u}_{k}}], [ R^{{F}l}_{k}e^{i2\pi I^{{F}l}_{k}}, R^{{F}u}_{k}e^{i2\pi I^{{F}u}_{k}}],[\lambda _{k},\mu _{k}] \Big \rangle$ be a family of CDPNIVNs. Then

$$\begin{aligned}&\text{CDPNIVWA }(\widehat{\mathcal {Z}}_{1}, \widehat{\mathcal {Z}}_{2},..., \widehat{\mathcal {Z}}_{m})\\ &\quad =\begin{bmatrix} \Big (\boxplus ^{m}_{k=1} \chi _{k}\alpha _{k}, \boxplus ^{m}_{k=1} \chi _{k}\beta _{k} \Big );\\ \Bigg [ \root 2\nabla \of {1-\odot ^{m}_{k=1}\Big ( 1-(\lambda R^{{T}l}_{k})^{2\nabla } \Big )^{\chi _{k}}} e^{i2\pi \root 2\nabla \of {1-\odot ^{m}_{k=1}\Big ( 1-\left( \frac{\lambda I^{{T}l}_{k}}{2\pi }\right) ^{2\nabla } \Big )^{\psi _{k}}} }, \\ \root 2\nabla \of {1-\odot ^{m}_{k=1}\Big ( 1-(\lambda R^{{T}u}_{k})^{2\nabla } \Big )^{\chi _{k}}} e^{i2\pi \root 2\nabla \of {1-\odot ^{m}_{k=1}\Big ( 1-\left( \frac{\lambda I^{{T}u}_{k}}{2\pi }\right) ^{2\nabla } \Big )^{\psi _{k}}}}\Bigg ];\\ \Big [\odot ^{m}_{k=1} (\mu R^{{F}l}_{k})^{\chi _{k}} e^{i2\pi \odot ^{m}_{k=1} \left( \frac{\mu I^{{F}l}_{k}}{2\pi }\right) ^{\psi _{k}}},\odot ^{m}_{k=1}(\mu R^{{F}u}_{k})^{\chi _{k}} e^{i2\pi \odot ^{m}_{k=1}\left( \frac{\mu I^{{F}u}_{k}}{2\pi }\right) ^{\psi _{k}} }\Big ] \end{bmatrix}.\end{aligned}$$

Proof

The proof of the Theorem is given in appendix.$\square$

Theorem 4.2

If all $\widehat{\mathcal {Z}}_{k} = \Big \langle (\alpha _{k}, \beta _{k}); [ R^{{T}l}_{k}e^{i2\pi I^{{T}l}_{k}}, R^{{T}u}_{k}e^{i2\pi I^{{T}u}_{k}}], [ R^{{F}l}_{k}e^{i2\pi I^{{F}l}_{k}}, R^{{F}u}_{k}e^{i2\pi I^{{F}u}_{k}}],$ $[\lambda _{k},\mu _{k}] \Big \rangle (k=1,2,...,n)$ are equal with $\widehat{\mathcal {Z}}_{k} = \widehat{\mathcal {Z}},$ then CDPNIVWA$(\widehat{\mathcal {Z}}_{1}, \widehat{\mathcal {Z}}_{2},..., \widehat{\mathcal {Z}}_{m})= \widehat{\mathcal {Z}}$ (idempotency property).

Proof

The proof of the Theorem is given in appendix.$\square$

Theorem 4.3

Let $\widehat{\mathcal {Z}}_{k} = \Big \langle (\alpha _{kj}, \beta _{kj}); [ R^{{T}l}_{kj}e^{i2\pi I^{{T}l}_{kj}}, R^{{T}u}_{kj}e^{i2\pi I^{{T}u}_{kj}}], [ R^{{F}l}_{kj}e^{i2\pi I^{{F}l}_{kj}}, R^{{F}u}_{kj}e^{i2\pi I^{{F}u}_{kj}}]$, $[\lambda _{k},\mu _{k}] \Big \rangle (k=1,2,...,n)$; $(j= 1,2,...,k_{j})$ be a collection of CDPNIVWA, where $\overleftarrow{\alpha }= \min \alpha _{kj}$, $\overrightarrow{\alpha }= \max \alpha _{kj},$ $\overleftarrow{\beta }= \max \beta _{kj}$, $\overrightarrow{\beta }= \min \beta _{kj},$ $\overleftarrow{\lambda R^{{T}l}}= \min \lambda R^{{T}^{-}}_{kj},$ $\overrightarrow{\lambda R^{{T}l}}=\max \lambda R^{{T}^{-}}_{kj},$ $\overleftarrow{\lambda R^{{T}u}}=\min \lambda R^{{T}^{+}}_{kj}$, $\overrightarrow{\lambda R^{{T}u}}=\max \lambda R^{{T}^{+}}_{kj},$ $\overleftarrow{\mu R^{{F}l}}=\min \mu R^{{F}^{-}}_{kj}$, $\overrightarrow{\mu R^{{F}l}}=\max \mu R^{{F}^{-}}_{kj},$ $\overleftarrow{\mu R^{{F}u}}=\min \mu R^{{F}^{+}}_{kj}$, $\overrightarrow{\mu R^{{F}u}}=\max \mu R^{{F}^{+}}_{kj}$ and $\overleftarrow{\lambda I^{{T}l}}= \min \lambda I^{{T}^{-}}_{kj},$ $\overrightarrow{\lambda I^{{T}l}}=\max \lambda I^{{T}^{-}}_{kj},$ $\overleftarrow{\lambda I^{{T}u}}=\min \lambda I^{{T}^{+}}_{kj},$ $\overrightarrow{\lambda I^{{T}u}}=\max \lambda I^{{T}^{+}}_{kj},$ $\overleftarrow{\mu I^{{F}l}}=\min \mu I^{{F}^{-}}_{kj},$ $\overrightarrow{\mu I^{{F}l}}=\max \mu I^{{F}^{-}}_{kj},$ $\overleftarrow{\mu I^{{F}u}}=\min \mu I^{{F}^{+}}_{kj},$ $\overrightarrow{\mu I^{{F}u}}=\max \mu I^{{F}^{+}}_{kj}.$

Then,

$$\begin{aligned} & \Big \langle (\overleftarrow{\alpha }, \overleftarrow{\beta }); [\overleftarrow{\lambda R^{{T}l} e^{i2\pi (\lambda I^{{T}l})}},\overleftarrow{\lambda R^{{T}u}e^{i2\pi (\lambda I^{{T}u})}}], [\overrightarrow{\mu R^{{F}l} e^{i2\pi (\mu I^{{F}l})}},\overrightarrow{\mu R^{{F}u}e^{i2\pi (\mu I^{{F}u})}}]\Big \rangle \\ & \quad \preceq q-Rung CDPNIVWA (\widehat{\mathcal {Z}}_{1}, \widehat{\mathcal {Z}}_{2},..., \widehat{\mathcal {Z}}_{m})\\ & \quad \preceq \Big \langle (\overrightarrow{\alpha }, \overrightarrow{\beta }); [\overrightarrow{\lambda R^{{T}l} e^{i2\pi (\lambda I^{{T}l})}},\overrightarrow{\lambda R^{{T}u}e^{i2\pi (\lambda I^{{T}u})}}], [\overleftarrow{\mu R^{{F}l} e^{i2\pi (\mu I^{{F}l})}},\overleftarrow{\mu R^{{F}u}e^{i2\pi (\mu I^{{F}u})}}]\Big \rangle . \end{aligned}$$

(boundedness property).

Proof

The proof of the Theorem is given in appendix.$\square$

Theorem 4.4

Let $\widehat{\mathcal {Z}}_{k} = \Big \langle (\alpha _{t_{kj}}, \beta _{t_{kj}}); [ R^{{T}l}_{t_{kj}}e^{i2\pi I^{{T}l}_{t_{kj}}}, R^{{T}u}_{t_{kj}}e^{i2\pi I^{{T}u}_{t_{kj}}}], [ R^{{F}l}_{t_{kj}}e^{i2\pi I^{{F}l}_{t_{kj}}}, R^{{F}u}_{t_{kj}}e^{i2\pi I^{{F}u}_{t_{kj}}}]$, $[\lambda _{k},\mu _{k}] \Big \rangle$ and $\widehat{W}_{k} = \Big \langle (\alpha _{h_{kj}}, \beta _{h_{kj}});$ $[ R^{{T}l}_{h_{kj}}e^{i2\pi I^{{T}l}_{h_{kj}}}, R^{{T}u}_{h_{kj}}e^{i2\pi I^{{T}u}_{h_{kj}}}]$, $[ R^{{F}l}_{h_{kj}}e^{i2\pi I^{{F}l}_{h_{kj}}}, R^{{F}u}_{h_{kj}}e^{i2\pi I^{{F}u}_{h_{kj}}}],[\lambda _{k},\mu _{k}] \Big \rangle$ $(k=1,2,...,m); (j= 1,2,...,k_{j})$ be the families of CDPNIVWAs. For any i, $\alpha _{t_{kj}} \preceq \beta _{h_{kj}}$, $\left( \lambda R^{{T}l}_{t_{kj}}\right) ^{2} + \left( \lambda R^{{T}u}_{t_{kj}}\right) ^{2} \preceq \left( \lambda R^{{T}l}_{h_{kj}}\right) ^{2} + \left( \lambda R^{{T}u}_{h_{kj}}\right) ^{2}$ and $\left( \mu R^{{F}l}_{t_{kj}}\right) ^{2} + \left( \mu R^{{F}u}_{t_{kj}}\right) ^{2} \succeq \left( \mu R^{{F}l}_{h_{kj}}\right) ^{2} + \left( \mu R^{{F}u}_{h_{kj}}\right) ^{2}$ and $\left( \lambda I^{{T}l}_{t_{kj}}\right) ^{2} + \left( \lambda I^{{T}u}_{t_{kj}}\right) ^{2} \preceq \left( \lambda I^{{T}l}_{h_{kj}}\right) ^{2} + \left( \lambda I^{{T}u}_{h_{kj}}\right) ^{2}$ and $\left( \mu I^{{F}l}_{t_{kj}}\right) ^{2} + \left( \mu I^{{F}u}_{t_{kj}}\right) ^{2} \succeq \left( \mu I^{{F}l}_{h_{kj}}\right) ^{2} + \left( \mu I^{{F}u}_{h_{kj}}\right) ^{2}$ or $\widehat{\mathcal {Z}}_{k} \preceq \widehat{W}_{k}$. Then CDPNIVWA $\left( \widehat{\mathcal {Z}}_{1}, \widehat{\mathcal {Z}}_{2},..., \widehat{\mathcal {Z}}_{m} \right) \preceq q-Rung CDPNIVWA \left( \widehat{W}_{1}, \widehat{W}_{2},..., \widehat{W}_{m}\right)$ (monotonicity property).

Proof

The proof of the Theorem is given in appendix.$\square$

CDPNIV weighted geometric (CDPNIVWG)

Definition 4.2

Let $\widehat{\mathcal {Z}}_{k} = \Big \langle (\alpha _{k}, \beta _{k}); [ R^{{T}l}_{k}e^{i2\pi I^{{T}l}_{k}}, R^{{T}u}_{k}e^{i2\pi I^{{T}u}_{k}}], [ R^{{F}l}_{k}e^{i2\pi I^{{F}l}_{k}}, R^{{F}u}_{k}e^{i2\pi I^{{F}u}_{k}}],[\lambda _{k},\mu _{k}] \Big \rangle$ be a family of CDPNIVNs. The CDPNIVWG operator is defined as CDPNIVWG $(\widehat{\mathcal {Z}}_{1}, \widehat{\mathcal {Z}}_{2},..., \widehat{\mathcal {Z}}_{m})=\odot ^{m}_{k=1} \widehat{\mathcal {Z}}_{k}^{\chi _{k}}$.

Theorem 4.5

Let $\widehat{\mathcal {Z}}_{k} = \Big \langle (\alpha _{k}, \beta _{k}); [ R^{{T}l}_{k}e^{i2\pi I^{{T}l}_{k}}, R^{{T}u}_{k}e^{i2\pi I^{{T}u}_{k}}], [ R^{{F}l}_{k}e^{i2\pi I^{{F}l}_{k}}, R^{{F}u}_{k}e^{i2\pi I^{{F}u}_{k}}],[\lambda _{k},\mu _{k}] \Big \rangle$ be a family of CDPNIVNs. Then

$$\begin{aligned} &\text{CDPNIVWG }(\widehat{\mathcal {Z}}_{1}, \widehat{\mathcal {Z}}_{2},..., \widehat{\mathcal {Z}}_{m})\\ &\quad=\begin{bmatrix} \Big (\odot ^{m}_{k=1} \alpha _{k}^{\chi _{k}},\odot ^{m}_{k=1} \beta _{k}^{\chi _{k}} \Big );\\ \Big [\odot ^{m}_{k=1} (\lambda R^{{T}l}_{k})^{\chi _{k}} e^{i2\pi \odot ^{m}_{k=1} \left( \frac{\lambda I^{{T}l}_{k}}{2\pi }\right) ^{\psi _{k}}},\odot ^{m}_{k=1}(\lambda R^{{T}u}_{k})^{\chi _{k}}; e^{i2\pi \odot ^{m}_{k=1}\left( \frac{\lambda I^{{T}u}_{k}}{2\pi }\right) ^{\psi _{k}} }\Big ];\\ \Bigg [ \root 2\nabla \of {1-\odot ^{m}_{k=1}\Big ( 1-(\mu R^{{F}l}_{k})^{2\nabla } \Big )^{\chi _{k}}} e^{i2\pi \root 2\nabla \of {1-\odot ^{m}_{k=1}\Big ( 1-\left( \frac{\mu I^{{F}l}_{k}}{2\pi }\right) ^{2\nabla } \Big )^{\psi _{k}}} }, \\ \root 2\nabla \of {1-\odot ^{m}_{k=1}\Big ( 1-(\mu R^{{F}u}_{k})^{2\nabla } \Big )^{\chi _{k}}} e^{i2\pi \root 2\nabla \of {1-\odot ^{m}_{k=1}\Big ( 1-\left( \frac{\mu I^{{F}u}_{k}}{2\pi }\right) ^{2\nabla } \Big )^{\psi _{k}}}}\Bigg ];\\ \end{bmatrix}.\end{aligned}$$

Proof

There is a proof based on the Theorem 4.1 that follows.$\square$

Theorem 4.6

If all $\widehat{\mathcal {Z}}_{k} = \Big \langle (\alpha _{k}, \beta _{k}); [ R^{{T}l}_{k}e^{i2\pi I^{{T}l}_{k}}, R^{{T}u}_{k}e^{i2\pi I^{{T}u}_{k}}], [ R^{{F}l}_{k}e^{i2\pi I^{{F}l}_{k}}, R^{{F}u}_{k}e^{i2\pi I^{{F}u}_{k}}],$ $[\lambda _{k},\mu _{k}] \Big \rangle (k=1,2,...,n)$ are equal with $\widehat{\mathcal {Z}}_{k} = \widehat{\mathcal {Z}}$. Then CDPNIVWG$(\widehat{\mathcal {Z}}_{1}, \widehat{\mathcal {Z}}_{2},..., \widehat{\mathcal {Z}}_{m})=\widehat{\mathcal {Z}}$.

Proof

There is a proof based on the Theorem 4.2 that follows.$\square$

Remark 4.1

According to the CDPNIVWG operator, we can satisfy both boundedness property and monotonicity property.

Proof

Based on Theorems 4.3 and 4.4, the proof follows.$\square$

Generalized CDPNIVWA (CDGPNIVWA)

The CDPNIVNs were operated according to the following operational laws to compute the weighted averaging and geometric AOs.

Definition 4.3

Let $\widehat{\mathcal {Z}}_{k} = \Big \langle (\alpha _{k}, \beta _{k}); [ R^{{T}l}_{k}e^{i2\pi I^{{T}l}_{k}}, R^{{T}u}_{k}e^{i2\pi I^{{T}u}_{k}}], [ R^{{F}l}_{k}e^{i2\pi I^{{F}l}_{k}}, R^{{F}u}_{k}e^{i2\pi I^{{F}u}_{k}}],[\lambda _{k},\mu _{k}] \Big \rangle$ be a family of CDPNIVN. Then CDGPNIVWA $(\widehat{\mathcal {Z}}_{1} , \widehat{\mathcal {Z}}_{2},..., \widehat{\mathcal {Z}}_{m})= \Big (\boxplus ^{m}_{k=1} \chi _{k}\widehat{\mathcal {Z}}_{k}^{\nabla } \Big )^{1/\nabla }$ is called a CDGPNIVWA operator.

Theorem 4.7

Let $\widehat{\mathcal {Z}}_{k} = \Big \langle (\alpha _{k}, \beta _{k}); [ R^{{T}l}_{k}e^{i2\pi I^{{T}l}_{k}}, R^{{T}u}_{k}e^{i2\pi I^{{T}u}_{k}}], [ R^{{F}l}_{k}e^{i2\pi I^{{F}l}_{k}}, R^{{F}u}_{k}e^{i2\pi I^{{F}u}_{k}}],[\lambda _{k},\mu _{k}] \Big \rangle$ be a family of CDPNIVNs. Then

$$\begin{aligned}&\text{CDGPNIVWA }(\widehat{\mathcal {Z}}_{1}, \widehat{\mathcal {Z}}_{2},..., \widehat{\mathcal {Z}}_{m})\\ &\quad=\begin{bmatrix} \left( \left( \boxplus ^{m}_{k=1} \chi _{k}\alpha _{k}^{\nabla }\right) ^{1/\nabla }, \left( \boxplus ^{m}_{k=1} \chi _{k}\beta _{k}^{\nabla }\right) ^{1/\nabla }\right) ;\\ \begin{bmatrix} \Bigg (\root 2\nabla \of { \begin{aligned} 1-\odot ^{m}_{k=1} \Bigg ( 1-\Big ((\lambda R^{{T}l}_{k})^{\nabla }\Big )^{2\nabla }\Bigg )^{\chi _{k}}\\ \end{aligned}}\,\,\Bigg )^{1/\nabla } e^{i2\pi (\root 2\nabla \of { \begin{aligned} 1-\odot ^{m}_{k=1} \Bigg ( 1-\Big (\left( \frac{\lambda I^{{T}l}_{k}}{2\pi }\right) ^{\nabla }\Big )^{2\nabla }\Bigg )^{\psi _{k}}\\ \end{aligned}}\,\,\Bigg )^{1/\nabla },} \\ \Bigg (\root 2\nabla \of { \begin{aligned} 1-\odot ^{m}_{k=1} \Bigg ( 1-\Big ((\lambda R^{{T}u}_{k})^{\nabla }\Big )^{2\nabla }\Bigg )^{\chi _{k}}\\ \end{aligned}}\,\,\Bigg )^{1/\nabla } e^{i2\pi (\root 2\nabla \of { \begin{aligned} 1-\odot ^{m}_{k=1} \Bigg ( 1-\Big (\left( \frac{\lambda I^{{T}u}_{k}}{2\pi }\right) ^{\nabla }\Big )^{2\nabla }\Bigg )^{\psi _{k}}\\ \end{aligned}}\,\,\Bigg )^{1/\nabla }} \end{bmatrix},\\ \begin{bmatrix} \root 2\nabla \of {1-\Bigg ( \begin{aligned} 1-\Bigg (\odot ^{m}_{k=1} \Bigg ( \root 2\nabla \of {1-\Big (1-(\mu R^{{F}l}_{k})^{2\nabla }\Big )^{\nabla }}\Bigg )^{\chi _{k}}\\ \end{aligned}\,\,\Bigg )^{2\nabla }\Bigg )^{1/\nabla }} \\ e^{i2\pi \root 2\nabla \of {1-\Bigg ( \begin{aligned} 1-\Bigg (\odot ^{m}_{k=1} \Bigg ( \root 2\nabla \of {1-\Big (1-\left( \frac{\mu I^{{F}l}_{k}}{2\pi }\right) ^{2\nabla }\Big )^{\nabla }}\Bigg )^{\psi _{k}}\\ \end{aligned}\,\,\Bigg )^{2\nabla }\Bigg )^{1/\nabla }}, } \\ \root 2\nabla \of {1-\Bigg ( \begin{aligned} 1-\Bigg (\odot ^{m}_{k=1} \Bigg ( \root 2\nabla \of {1-\Big (1-(\mu R^{{F}u}_{k})^{2\nabla }\Big )^{\nabla }}\Bigg )^{\chi _{k}}\\ \end{aligned}\,\,\Bigg )^{2\nabla }\Bigg )^{1/\nabla }} \\ e^{i2\pi \root 2\nabla \of {1-\Bigg ( \begin{aligned} 1-\Bigg (\odot ^{m}_{k=1} \Bigg ( \root 2\nabla \of {1-\Big (1-\left( \frac{\mu I^{{F}u}_{k}}{2\pi }\right) ^{2\nabla }\Big )^{\nabla }}\Bigg )^{\psi _{k}}\\ \end{aligned}\,\,\Bigg )^{2\nabla }\Bigg )^{1/\nabla }}, } \end{bmatrix} \end{bmatrix}.\end{aligned}$$

Proof

The proof of the Theorem is given in appendix.$\square$

Remark 4.2

If $\nabla =1$, then CDGPNIVWA operator is modified to the CDPNIVWA operator.

Theorem 4.8

If all $\widehat{\mathcal {Z}}_{k} = \Big \langle (\alpha _{k}, \beta _{k}); [ R^{{T}l}_{k}e^{i2\pi I^{{T}l}_{k}}, R^{{T}u}_{k}e^{i2\pi I^{{T}u}_{k}}],\ [ R^{{F}l}_{k}e^{i2\pi I^{{F}l}_{k}}, R^{{F}u}_{k}e^{i2\pi I^{{F}u}_{k}}],$

$[\lambda _{k},\mu _{k}] \Big \rangle (k=1,2,...,n)$ are equal with $\widehat{\mathcal {Z}}_{k} = \widehat{\mathcal {Z}}$. Then CDGPNIVWA$(\widehat{\mathcal {Z}}_{1}, \widehat{\mathcal {Z}}_{2},..., \widehat{\mathcal {Z}}_{m})=\widehat{\mathcal {Z}}$.

Proof

Proof follows from Theorem 4.2.$\square$

Remark 4.3

Based on the CDGPNIVWA operator, we satisfy the boundedness property and monotonicity property.

Generalized CDPNIVWG (CDGPNIVWG)

Definition 4.4

Let $\widehat{\mathcal {Z}}_{k} = \Big \langle (\alpha _{k}, \beta _{k}); [ R^{{T}l}_{k}e^{i2\pi I^{{T}l}_{k}}, R^{{T}u}_{k}e^{i2\pi I^{{T}u}_{k}}], [ R^{{F}l}_{k}e^{i2\pi I^{{F}l}_{k}}, R^{{F}u}_{k}e^{i2\pi I^{{F}u}_{k}}],[\lambda _{k},\mu _{k}] \Big \rangle$ be a family of CDPNIVNs. Then CDGPNIVWG $(\widehat{\mathcal {Z}}_{1} , \widehat{\mathcal {Z}}_{2},..., \widehat{\mathcal {Z}}_{m})= \frac{1}{\nabla }\Big (\odot ^{m}_{k=1} (q\widehat{\mathcal {Z}}_{k})^{\chi _{k}} \Big )$ is said to be a CDGPNIVWG operator.

Theorem 4.9

Let $\widehat{\mathcal {Z}}_{k} = \Big \langle (\alpha _{k}, \beta _{k}); [ R^{{T}l}_{k}e^{i2\pi I^{{T}l}_{k}}, R^{{T}u}_{k}e^{i2\pi I^{{T}u}_{k}}], [ R^{{F}l}_{k}e^{i2\pi I^{{F}l}_{k}}, R^{{F}u}_{k}e^{i2\pi I^{{F}u}_{k}}],[\lambda _{k},\mu _{k}] \Big \rangle$ be a family of CDPNIVNs. Then the CDGPNIVWG$(\widehat{\mathcal {Z}}_{1}, \widehat{\mathcal {Z}}_{2},..., \widehat{\mathcal {Z}}_{m})$ is defined as follows:

$$\begin{aligned}\begin{bmatrix} \Bigg ( \frac{1}{\nabla }\odot ^{m}_{k=1} (q \alpha _{k})^{\chi _{k}}, \frac{1}{\nabla }\odot ^{m}_{k=1} (q \beta _{k})^{\chi _{k}}\Bigg );\\ \begin{bmatrix} \root 2\nabla \of {1-\Bigg ( \begin{aligned} 1-\Bigg (\odot ^{m}_{k=1} \Bigg ( \root 2\nabla \of {1-\Big (1-(\lambda R^{{T}l}_{k})^{2\nabla }\Big )^{\nabla }}\Bigg )^{\chi _{k}}\\ \end{aligned}\,\,\Bigg )^{2\nabla }\Bigg )^{1/\nabla }} \\ e^{i2\pi \root 2\nabla \of {1-\Bigg ( \begin{aligned} 1-\Bigg (\odot ^{m}_{k=1} \Bigg ( \root 2\nabla \of {1-\Big (1-\left( \frac{\lambda I^{{T}l}_{k}}{2\pi }\right) ^{2\nabla }\Big )^{\nabla }}\Bigg )^{\psi _{k}}\\ \end{aligned}\,\,\Bigg )^{2\nabla }\Bigg )^{1/\nabla }} }, \\ \root 2\nabla \of {1-\Bigg ( \begin{aligned} 1-\Bigg (\odot ^{m}_{k=1} \Bigg ( \root 2\nabla \of {1-\Big (1-(\lambda R^{{T}u}_{k})^{2\nabla }\Big )^{\nabla }}\Bigg )^{\chi _{k}}\\ \end{aligned}\,\,\Bigg )^{2\nabla }\Bigg )^{1/\nabla }} \\ e^{i2\pi \root 2\nabla \of {1-\Bigg ( \begin{aligned} 1-\Bigg (\odot ^{m}_{k=1} \Bigg ( \root 2\nabla \of {1-\Big (1-\left( \frac{\lambda I^{{T}u}_{k}}{2\pi }\right) ^{2\nabla }\Big )^{\nabla }}\Bigg )^{\psi _{k}}\\ \end{aligned}\,\,\Bigg )^{2\nabla }\Bigg )^{1/\nabla }} } \end{bmatrix},\\ \begin{bmatrix} \Bigg (\root 2\nabla \of { \begin{aligned} 1-\odot ^{m}_{k=1} \Bigg ( 1-\Big ((\mu R^{{F}l}_{k})^{\nabla }\Big )^{2\nabla }\Bigg )^{\chi _{k}}\\ \end{aligned}}\,\,\Bigg )^{1/\nabla } e^{i2\pi (\root 2\nabla \of { \begin{aligned} 1-\odot ^{m}_{k=1} \Bigg ( 1-\Big (\left( \frac{\mu I^{{F}l}_{k}}{2\pi }\right) ^{\nabla }\Big )^{2\nabla }\Bigg )^{\psi _{k}}\\ \end{aligned}}\,\,\Bigg )^{1/\nabla } }, \\ \Bigg (\root 2\nabla \of { \begin{aligned} 1-\odot ^{m}_{k=1} \Bigg ( 1-\Big ((\mu R^{{F}u}_{k})^{\nabla }\Big )^{2\nabla }\Bigg )^{\chi _{k}}\\ \end{aligned}}\,\,\Bigg )^{1/\nabla } e^{i2\pi \Bigg (\root 2\nabla \of { \begin{aligned} 1-\odot ^{m}_{k=1} \Bigg ( 1-\Big (\left( \frac{\mu I^{{F}u}_{k}}{2\pi }\right) ^{\nabla }\Big )^{2\nabla }\Bigg )^{\psi _{k}}\\ \end{aligned}}\,\,\Bigg )^{1/\nabla } } \,\, \end{bmatrix} \end{bmatrix}.\end{aligned}$$

Proof

Proof follows from Theorem 4.7.$\square$

Remark 4.4

If $\nabla =1$, then CDGPNIVWG operator is modified to the CDPNIVWG operator.

Remark 4.5

As a result of the CDGPNIVWG operator, the boundness and monotonicity properties are satisfied.

Proof

Theorems 4.3 and 4.4 provide the proof.$\square$

Theorem 4.10

If all $\widehat{\mathcal {Z}}_{k} = \Big \langle (\alpha _{k}, \beta _{k}); [ R^{{T}l}_{k}e^{i2\pi I^{{T}l}_{k}}, R^{{T}u}_{k}e^{i2\pi I^{{T}u}_{k}}], [ R^{{F}l}_{k}e^{i2\pi I^{{F}l}_{k}}, R^{{F}u}_{k}e^{i2\pi I^{{F}u}_{k}}],$

$[\lambda _{k},\mu _{k}] \Big \rangle (k=1,2,...,n)$ are equal with $\widehat{\mathcal {Z}}_{k} = \widehat{\mathcal {Z}}$. Then CDGPNIVWG$(\widehat{\mathcal {Z}}_{1}, \widehat{\mathcal {Z}}_{2},..., \widehat{\mathcal {Z}}_{m})=\widehat{\mathcal {Z}}$.

MADM approach using CDPNIV

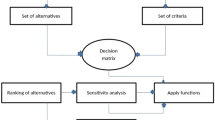
For determining the optimal choice in a MADM problem, a number of considerations must be taken into considerations. Applications for MADM include engineering design and finance, among other areas. The principle, classifications, and methods of the MADM application are explained in this paper. Additionally, a list of some of the main methods is provided in this section. The MADM technique uses a variety of different quantitative and/or qualitative criteria to assess an objects functionality. Instead of recommending decision-makers on what kind of action to take, these methods assist them in choosing the best alternative for their particular needs. The MADM approach does not include trial-and-error techniques, in contrast to traditional trial-and-error processes. The competitive and technologically evolving world is a complex one. They act as a basis for the priorities, structure, assessment, selection, and objectives. Important components of MADM included organizing and developing experiments as well as assessing and selecting the best methods. A decision maker contribution is combined with weighted skills in a MADM process to determine which options are best. Take a look at a MADM problem with m selections (attributes) and n attributes. Let $\mathcal {Z}= \{\mathcal {Z}_{A},\mathcal {Z}_{B},...,\mathcal {Z}_{n}\}$ be a discrete set of alternatives, and $C= \{\Gamma _{1},\Gamma _{2},...,\Gamma _{m}\}$ be the set of attributes. Ratings provide information about the performance of alternative $\mathcal {Z}_{n}\}$ against attribute $\Gamma _{m}$. Let us also assume that $w = \{\chi _{1},\chi _{2},...,\chi _{m}\}$ be the weight vector assigned for the attributes $C= \{\Gamma _{1},\Gamma _{2},...,\Gamma _{m}\}$ by the decision makers. The following decision matrix provides information about the values associated with MADM alternatives. This decision-making problem is solved using the proposed operators in the following steps. Let $\widehat{\mathcal {Z}}_{kj} = \Big \langle (\alpha _{kj}, \beta _{kj}); [ R^{{T}l}_{kj}e^{i2\pi I^{{T}l}_{kj}}, R^{{T}u}_{kj}e^{i2\pi I^{{T}u}_{kj}}], [ R^{{F}l}_{kj}e^{i2\pi I^{{F}l}_{kj}}, R^{{F}u}_{kj}e^{i2\pi I^{{F}u}_{kj}}],[\lambda _{k},\mu _{k}] \Big \rangle$ denote CDPNIVN of alternative $\mathcal {Z}_{k}$ in attribute $\Gamma _{j}$. Since $[ R^{{T}l}_{kj}e^{i2\pi I^{{T}l}_{kj}}, R^{{T}u}_{kj}e^{i2\pi I^{{T}u}_{kj}}],$ $[ R^{{F}l}_{kj}e^{i2\pi I^{{F}l}_{kj}}, R^{{F}u}_{kj}e^{i2\pi I^{{F}u}_{kj}}],\lambda _{k},\mu _{k} \in [0,1]$ and $0 \preceq (\lambda R^{{T}u}_{kj}(\theta ))^{2}+(\mu R_{kj}^{{F}u}(\theta ))^{2} \preceq 1$ and $0 \preceq (\lambda I^{{T}u}_{kj}(\theta ))^{2}+(\mu I_{kj}^{{F}u}(\theta ))^{2} \preceq 1$. The decision matrix $\mathscr {D}=(\widehat{\mathcal {Z}}_{kj})_{m \times p}$, where for $k=1,2,...,m$ and $j= 1,2,...,p$.

Figure 1 shows a flowchart of the algorithm for the MADM process using CDPNIVS.

Fig. 1

Flowchart of the algorithm for the MADM.

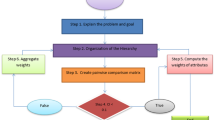
Algorithm for CDPNIV

Step-1: Enter the decision values for CDPNIVS.

Step-2: To determine the normalized decision values, we will use the following formula. The decision matrix $\mathscr {D}=(\widehat{\mathcal {Z}}_{kj})_{m \times p}$ is normalized into $\overrightarrow{\mathscr {D}}=(\overbrace{\mathcal {Z}_{kj}})_{m \times p}$; where

$\overbrace{\mathcal {Z}_{kj}}$= $\Big \langle (\overrightarrow{\alpha _{kj}}, \overrightarrow{\beta _{kj}})$; $[\overrightarrow{ R^{{T}l}_{kj}e^{ij2\pi I^{{T}l}_{kj}}},\overrightarrow{ R^{{T}u}_{kj}e^{ij2\pi I^{{T}u}_{kj}}}], [\overrightarrow{ R^{{F}l}_{kj}e^{ij2\pi I^{{F}l}_{kj}}},\overrightarrow{ R^{{F}u}_{kj}e^{ij2\pi I^{{F}u}_{kj}}}],[\lambda _{k},\mu _{k}] \Big \rangle$ and

$$\begin{aligned}\overrightarrow{\alpha _{kj}}= \frac{\alpha _{kj}}{\max _{k}(\alpha _{kj})}, \overrightarrow{\beta _{kj}}= \frac{\beta _{kj}}{\max _{k}(\beta _{kj})} \cdot \frac{\beta _{kj}}{\alpha _{kj}},\,\, \overrightarrow{\lambda R^{{T}l}_{kj}}= \lambda R^{{T}l}_{kj}, \overrightarrow{\lambda R^{{T}u}_{kj}}= \lambda R^{{T}u}_{kj}.\end{aligned}$$

Step-3: It is necessary to determine the aggregate values for each alternative are determined. It is based on CDPNIV information AOs, attribute $k_{j}$ in $\widehat{\mathcal {Z}}_{k}$,$\overbrace{\mathcal {Z}_{kj}}= \Big \langle (\overrightarrow{\alpha _{kj}}, \overrightarrow{\beta _{kj}})$; $[\overrightarrow{ R^{{T}l}_{kj}e^{ij2\pi I^{{T}l}_{kj}}},\overrightarrow{ R^{{T}u}_{kj}e^{ij2\pi I^{{T}u}_{kj}}}], [\overrightarrow{ R^{{F}l}_{kj}e^{ij2\pi I^{{F}l}_{kj}}},\overrightarrow{ R^{{F}u}_{kj}e^{ij2\pi I^{{F}u}_{kj}}}],[\lambda _{k},\mu _{k}] \Big \rangle$ is aggregated into $\overbrace{\mathcal {Z}_{k}}= \Big \langle (\overrightarrow{\alpha _{k}}, \overrightarrow{\beta _{k}})$; $[\overrightarrow{ R^{{T}l}_{k}e^{i2\pi I^{{T}l}_{k}}},\overrightarrow{ R^{{T}u}_{k}e^{i2\pi I^{{T}u}_{k}}}], [\overrightarrow{ R^{{F}l}_{k}e^{i2\pi I^{{F}l}_{k}}},\overrightarrow{ R^{{F}u}_{k}e^{i2\pi I^{{F}u}_{k}}}],[\lambda _{k},\mu _{k}] \Big \rangle$.

Step-4: Calculate the scores of each alternative using the following steps: $S_{1}(\widehat{\mathcal {Z}})= \frac{\alpha }{2}\left( X + Y\right)$, $S_{2}(\widehat{\mathcal {Z}})= \frac{\beta }{2}\left( X + Y\right)$ and ${\mathbb {S}}(\widehat{\mathcal {Z}})= \frac{S_{1}(\widehat{\mathcal {Z}})+S_{2}(\widehat{\mathcal {Z}})}{2}$. where

$$\begin{aligned}X= & \left( \frac{(\lambda R^{{T}l}_{k})^{2} + (\lambda R^{{T}u}_{k})^{2}}{2}+1- \frac{(\mu R^{{F}l}_{k})^{2}+(\mu R^{{F}u}_{k})^{2}}{2} \right) \\ Y= & \left( \frac{(\lambda I^{{T}l}_{k})^{2} + (\lambda I^{{T}u}_{k})^{2}}{2}- \frac{(\mu I^{{F}l}_{k})^{2}+(\mu I^{{F}u}_{k})^{2}}{2} \right) ,\end{aligned}$$

where $\,\, {\mathbb {S}}(\widehat{\mathcal {Z}})\in [-1,1]$.

Compute the accuracy values of each alternatives are as follows: $H_{1}(\widehat{\mathcal {Z}})= \frac{\alpha }{2}\left( X_{1} + Y_{1}\right)$, $H_{2}(\widehat{\mathcal {Z}})= \frac{\beta }{2}\left( X_{1} + Y_{1}\right)$ and ${\mathbb {H}}(\widehat{\mathcal {Z}})= \frac{H_{1}(\widehat{\mathcal {Z}})+H_{2}(\widehat{\mathcal {Z}})}{2}$. where

$$\begin{aligned}X_{1}= \left( \frac{(\lambda R^{{T}l}_{k})^{2} + (\lambda R^{{T}u}_{k})^{2}}{2}+ \frac{(\mu R^{{F}l}_{k})^{2}+(\mu R^{{F}u}_{k})^{2}}{2} \right) \end{aligned}$$

$$\begin{aligned}Y_{1}= \left( \frac{(\lambda I^{{T}l}_{k})^{2} + (\lambda I^{{T}u}_{k})^{2}}{2}+ \frac{(\mu I^{{F}l}_{k})^{2}+(\mu I^{{F}u}_{k})^{2}}{2} \right) ,\end{aligned}$$

where $\,\, {\mathbb {H}}(\widehat{\mathcal {Z}})\in [0,1]$.

Step-5: Hence the output indicates that the optimal value is $\max \mathscr {D}^{*}_{k}$, the decision must be made as to which one is the best. Therefore, is the optimal value based on the output, so the decision must be made as to which one is the best.

Real life applications

Computer science is an interdisciplinary field of study. Robotics deals with the design, construction, operation, and use of robots. It is agreed that robots are primarily used in place of humans to replace them. Software can be used in many fields, including mechanics, electronics, computer science, graphics, and software engineering. Humans can be replaced in several ways. Aircraft Manufacturing: According to scientists, robots are used in most aircraft manufacturing processes. Artificial intelligence is a growing field in robotics. Human assistance is not necessary for most tasks. In aircraft manufacturing, the ultimate robot is employed first. Cafes and Hotels: The majority of hotels in China and other countries are now serving as servers. The most fascinating thing is that they are capable of speaking to people. According to Kern Capek, a robot is derived from an etymological robot. For example, the hot industry requires extensive research from scientists. Army: The development of robots has made them useful to the army. Owing to their use in a variety of non-functional areas in critical situations, they are considered soldiers. The use of robots in the army can save a human lives. With robots, one can avoid many emotional and technical fireworks encountered by humans. The army can benefit greatly from them. Agriculture: A growing number of crops are being cultivated with the help of robots. The agricultural field is thriving with robots. Lethice robots, Merlin robots, milking robots, rospheres, orange harvesters, and rospheres are among the robots that are used. Farming uses robotics extensively. For example, it is particularly appropriate to use milk bots. A first of its kind agricultural robot, Dubble Viro, can pick tomatoes without causing any damage. The development of robotics has been greatly influenced by the Cambridge University. Vegebots are robots that eat vegetables. Humanoid bot: The first humanoid robot in the world is WABLT-1, which uses the latest robotic technology. Developed at Waseda University in 1967 and 1972, it has been used since then. This project was called WABLT. An intelligent humanoid system at full scale. In 1961, the first robot to work at factor was a general motor. Five different uses of robotics (alternatives) such as Aircraft Manufacturing $\mathcal {Z}_{1}$, Cafes and Hotels $\mathcal {Z}_{2}$, Army $\mathcal {Z}_{3}$, Agriculture $\mathcal {Z}_{4}$, Humanoid bot $\mathcal {Z}_{5}$ with four attributes are considered as tasks $(\Gamma _1)$, precision $(\Gamma _2)$, speed $(\Gamma _3)$ and completion of work $(\Gamma _4)$ and their corresponding weights are $(\psi ,\beta ) = \{0.4, 0.3, 0.2, 0.1\}$. Robotic systems that perform well in the real world exhibit the best performance. Considering the following factors helps us make decisions.

Step:1 In Tables 1, 2, 3 and 4 shows that decision information as follows:

Table 1 Decision data.

Table 2 Decision data.

Table 3 Decision data.

Table 4 Decision data.

Step:2 Tables 5, 6, 7 and 8 shows that the normalized decision values as follows:

Table 5 Normalized decision data.

Table 6 Normalized decision data.

Table 7 Normalized decision data.

Table 8 Normalized decision data.

The CDPNIVWA operator is listed in Table 9.

Table 9 CDPNIVWA operator  (q = 1).

The score values are calculated as follows: ${\mathbb {S}}_{1}=0.3792$, ${\mathbb {S}}_{2}=0.3431$, ${\mathbb {S}}_{3}=0.4138$, ${\mathbb {S}}_{4}=0.3656$ and ${\mathbb {S}}_{5}=0.3657$. The following is a list of alternatives and their respective ranks: $\mathcal {Z}_{3} \succeq \mathcal {Z}_{1} \succeq \mathcal {Z}_{5} \succeq \mathcal {Z}_{4} \succeq \mathcal {Z}_{2}.$ Therefore, robotic $\mathcal {Z}_{3}$ is the best option.

Comparison for proposed and existing methods

Our method is thoroughly examined using two methods of comparative analysis to determine its availability and significance. This section aims to validate the results of the proposed approach against other approaches and illustrate its most crucial characteristics through a comparative analysis. In this paper, we propose a decision-making method that can be applied to solving MADM problems using attribute weights based on the results. In the MADM process, the importance of the score values cannot be emphasized. However, only a few studies have been conducted on the MADM. These studies used score values as selection criteria for alternatives such as NSs, IVNSs or vague NSs. In this study, we intend to analyze alternative techniques for calculating score values to determine whether the proposed DM approach can be implemented in practice. Yang et al.¹⁹ constructed an NIVWA from the AOs. The MADM spherical vague normal operator is discussed in a recent study by Palanikumar et al.²². It illustrates the usefulness and benefits that can be obtained by employing it. Using CDPNIVWG, CDGPNIVWA and CDGPNIVWG, this work employs score values techniques. The following are some examples of different types of distance.

The various types of score and accuracy values for proposed and existing approaches as shown in Table 10.

Table 10 Proposed approach.

The benefits of the suggested algorithm are shown by contrasting its features with those of a number of other algorithms that are currently in use. If the operator’s property is satisfied, it indicates it using the symbols $\checkmark$ and $\times$. Furthermore, current methods do not address GDM concerns; instead, they exclusively address MADM problems. Tables 11 and 12 provide score and accuracy numbers that allow us to compare the proposed and current models.

The score values can be compared between the existing and proposed models in Table 11 to determine whether they are applicable and valid.

Table 11 Validity of the aggregating operator.

The accuracy values can be compared the between existing and proposed models in Table 12 to determine whether they are applicable and valid.

Table 12 Validity of the aggregating operator.

Figure 2 shows that existing and proposed approach for score values were calculated using weighted averaging operators.

Fig. 2

Score values facilitate the comparison of proposed and existing models.

Figure 3 shows that existing and proposed approach for accuracy values were calculated using weighted averaging operators.

Fig. 3

Accuracy values facilitate the comparison of proposed and existing models.

The aggregation information provided by the CDPNIVWA operator for each alternative as in the Tables 13 and 14.

Table 13 CDPNIVWA operator  $(\nabla = 2)$.

The score values are calculated as follows: ${\mathbb {S}}_{1}=0.3425$, ${\mathbb {S}}_{2}=0.326$, ${\mathbb {S}}_{3}=0.3855$, ${\mathbb {S}}_{4}=0.3365$, ${\mathbb {S}}_{5}=0.3296$.

Table 14 CDPNIVWA operator  $(\nabla = 3)$.

The score values are calculated as follows: ${\mathbb {S}}_{1}=0.3404$, ${\mathbb {S}}_{2}=0.3255$, ${\mathbb {S}}_{3}=0.3843$, ${\mathbb {S}}_{4}=0.3351$, ${\mathbb {S}}_{5}=0.3274$. If $1\le \nabla \le 2$, then $\mathcal {Z}_{3}\succeq \mathcal {Z}_{1}\succeq \mathcal {Z}_{5} \succeq \mathcal {Z}_{4} \succeq \mathcal {Z}_{2}$. If $\nabla =3$, then new ranking is $\mathcal {Z}_{3} \succeq \mathcal {Z}_{1} \succeq \mathcal {Z}_{4} \succeq \mathcal {Z}_{5} \succeq \mathcal {Z}_{2}$. Consequently, it is optimal to switch from $\mathcal {Z}_{4}$ to $\mathcal {Z}_{5}$ as an alternative. Similarly, alternative rankings are based on the value of $\nabla$, which is derived from CDPNIVWG, CDGPNIVWA and CDGPNIVWG operators.

Limitations of the proposed work

A key factor in choosing the best options is distance. The strategy with the highest value yielded the best results ultimately. The recommended aggregating methodologies were tested for validity and superiority using current methods. The proposed aggregating operators are more accurate and reliable than current methods. This approach is effective because it takes into consideration the relationships among the several qualities. Consequently, the suggested methodology provided superior ranking outcomes. By using the above-mentioned results, we can observe that our technique provided exactly the same ranking results by Palanikumar et al.²² and Zaoli et al.¹⁹ using the current aggregating method. This work computes the accuracy and score for CDPNIVNs. It has benefits for real-world calculations. As a result, a numerical example demonstrated that taking these two elements into consideration improved the score and accuracy. A real-world example demonstrates how accuracy and score values are used in practical applications. We suggest using these aggregation operators to find the optimal solution to the MADM problem. This example allows for the comparison of options and alternatives by exposing multiple options and alternatives based on an ideal set of qualities. The fundamental elements of this approach are weighted operators, which are developed from the weighted aggregating model. This methods primary goal is to handle a larger variety of complex problems. Weighted operators introduce score values and accuracy values, allowing an optimal set of preferences to be evaluated compared towards alternative and option choices.

Advantages

This article is a discussion of the benefits and advantages of the suggested idea. The operators CDPNIVWA, CDPNIVWG, CDGPNIVWA, and CDGPNIVWG are introduced. One of this method’s primary benefits is that it allows multiple specialists to evaluate DM procedures both objectively and subjectively. It is intriguing to analyze robotics selections as an unpredictable sequence of rules and processes. As an example, a number of alternatives and possibilities that rely on the complex attitudes of decision-makers among an ideal set of attributes will be displayed, enabling comparison of the available options. The main component of this approach is the generalized weighted operator, which is based on the weighted aggregation model. As a result, they display similar traits. Apart from emphasizing complicated problems as the main driving force, its attributes have been expanded to encompass a wider variety of problems. Weighted operators, which incorporate accuracy and score values, allow one to compare an ideal set of preferences with alternatives or options selected by decision-makers.

Conclusion

This article presents a new scoring and accuracy technique for MADM in a CIVPNS. A CIVPNN represents the overall score of each alternative with respect to each attribute throughout the evaluation process. A CIVPNS with aggregation approach is used to aggregate the opinions of all decision makers. The objective of this work is to further develop the aggregating approach, a widely used DM method, with respect to neural network MADM problems. CIVPNSs are more useful than accurate data in resolving unclear variables in DM problems. An evaluation process is most appropriate when consideration is given to the decision maker’s weight, criteria have been combined, and alternatives are evaluated while reviewing the criteria. CIVPNNs were used to express in language the scores of each alternative based on each criterion. For the CIVPNSs, the ideas of score and accuracy values were presented. As the numerical example illustrates, the score and accuracy numbers were consequently larger. To illustrate their usefulness, a real-world application is given. A few characteristics of the suggested AO rules for CIVPNWA, CIVPNWG, CGIVPNWA, and CGIVPNWG are covered in this article. It also offers illustrations of how these operators have been developed using a variety of techniques. By choosing the best option from a wide range of options available in the context of the approach, people can make informed decisions while establishing CIVPNS with the MADM method, even in the face of unclear and contradictory information. In this work, a MADM problem with natural number $\nabla$ is solved using the CGIVPNWA, CGIVPNWG, CIVPNWA, and CGIVPNWG operators. It has been shown that one can utilize CIVPNWA, CIVPNWG, CGIVPNWA, and CGIVPNWG to distinguish between alternatives. It could possibly be significant for the decision-makers to possess $\nabla$ in order to develop a rating of the options that is acceptable. The decision maker can estimate how much of DM needed to calculate the conclusion based on the values of $\nabla$.

The following subjects are covered in further detail: A Pythagorean hesitant form connects vague sets and IVPFSs. Normal Pythagorean and normal spherical vague sets are studied in terms of q-rung vague sets, Fermatean q-rung vague sets, complex fuzzy sets, and q-rung vague sets in order solve the problem. Decision of lead-time compression and stable operation of supply chain. Optimization of management mode of small- and medium-sized enterprises based on decision tree model. A vetoed multi-objective grey target decision model with application in supplier choice.