Introduction

Single image super-resolution (SISR) constitutes a longstanding challenge within the domains of computer vision and image processing. Its primary objective resides in the reconstruction of a high-resolution image based on a provided low-resolution input. Since deep learning has been successfully applied to the SR task1, numerous methods based on the convolutional neural network (CNN)2,3,4,5,6,7,8,9 have been proposed and almost dominate this field in the past few years. Nevertheless, owing to the parameter-dependent receptive field scaling and content-independent local interactions of convolutions employed, the CNN is constrained in its ability to capture long-range dependencies10.

To overcome this constraint, several Transformer-based image super-resolution (SR) networks10,11,12,13 have been introduced, aiming to model long-range dependencies and enhance SR performance. For instance, the Image Processing Transformer (IPT)11 was intentionally pre-trained on the ImageNet14 dataset to thoroughly exploit the capabilities of the Transformer architecture, thereby attaining optimal performance in image SR. SwinIR10 was proposed, leveraging the Swin Transformer architecture15, with the primary aim of substantially enhancing SR performance. In addition, HAT13 was proposed based on SwinIR10 delving deeper into the potential of the Transformer architecture and achieved state-of-the-art results on the image SR task.

Despite the performance improvements achieved by these Transformer-based methods in image SR tasks, they still encounter certain challenges. One of the challenges faced by Transformers in the field of image SR is the escalating computational complexity of the self-attention module with the increase in sequence length or image resolution. Furthermore, with the augmentation of image resolution or sequence length, there is a corresponding increase in model size, the quantity of floating-point operations per second (FLOPS), and the inference time of the model. These factors necessitate meticulous consideration and resolution to ensure the efficient and scalable deployment of image SR Transformer models in real-world applications. In addressing the challenges, we have embarked on exploratory investigations. Our objective is to identify an approach that, while ensuring the performance of image SR models, concurrently reduces the computational complexity and parameter amount of the model. This pursuit aims to propel the deployment and practical application of image SR models.

Recently, Scattering Vision Transformer has shown great promise in image classification and instance segmentation tasks with a significant reduction in a number of parameters and FLOPS. On the one hand, it uses a spectral scattering network to address the attention complexity and Dual-time Complex Wavelet Transforms (DTCWT) to capture the fine-grained information using spectral decomposition into low-frequency and high-frequency components of an image. On the other hand, it uses attention layers that focus on extracting semantic features and addressing long-range dependencies present in the image. A Hybrid Attention Transformer is proposed for SR tasks that combines self-attention, channel attention and an overlapping cross-attention to activate more pixels for better reconstruction13.

In this paper, we propose a Scattering Vision Transformer for Super-Resolution, namely SVTSR. SVTSR consists of three modules: shallow feature extraction, deep feature extraction and image reconstruction. Diverging from the conventional approach, to mitigate the computational complexity and reduce the parameter amount of the model, we introduced a scatter layer in the deep feature extraction component, concurrently reducing the number of RHAG (residual hybrid attention groups) layers. Ultimately, our SR model surpassed the baseline in terms of PSNR and SSIM metrics on classic SR datasets such as Set516 and Set1417, achieving satisfied results. Moreover, the model exhibited a reduction in parameter amount by over tenfold compared to the baseline.

Overall, the main contributions of our work are as follows:

  • We introduce an invertible spectral network based on DTCWT transformation into vision transformers for image SR tasks to decompose image features into low-frequency and high-frequency features;

  • We design a novel vision transformer for image super-resolution tasks;

  • Detailed performance analysis shows that our method achieves state-of-the-art performance. In addition, the model’s parameter count reduces by more than tenfold compared to the baseline model;

Related work

Vision transformer

Recently, Transformer18 has attracted the attention of computer vision community due to its success in the field of natural language processing. A series of Transformer-based methods15,19,20,21,22,23,24,25,26,27,28,29,30,31 have been developed for high-level vision tasks, including image classification15,20,25,32,33,34,35, object detection15,30,36,37,38, segmentation28,34,39,40, etc. Despite the demonstrated superiority of the vision Transformer in modeling long-range dependencies20,41, numerous studies have highlighted the potential of convolution to enhance the visual representation of Transformer22,24,31,42,43. Because of its outstanding performance, the Transformer has also been implemented for tasks related to low-level vision10,11,12,13,44,45,46,47,48. Specifically, IPT11 devises a ViT-style network and incorporates multi-task pre-training for image processing purposes. SwinIR10introduces an image restoration Transformer model inspired by15. VRT45presents Transformer-based architectures for video restoration tasks. EDT12 incorporates a self-attention mechanism and a strategy of pre-training across multiple related tasks. HAT13 integrates self-attention, channel attention, and a novel overlapping cross-attention mechanism to activate a greater number of pixels, thereby enhancing the quality of reconstruction and further advancing the state-of-the-art in SR. Although Transformer-based methods in the field of super-resolution have made significant progress in performance metrics such as PSNR and SSIM, challenges still exist in terms of model computational complexity and parameter quantity, which hinders the practical deployment and application of super-resolution models. We use spectral transform block based on an invertibility spectral network instead of the standard self-attention network and reduce the number of transformer layers, thus achieving a reduction in model computational complexity and number of model parameters while maintaining model performance metrics (Fig. 1).

Figure 1
figure 1

PSNR results compared to the total number of parameters of classical methods for image super-resolution (\(\times 4\)) on the Set5 dataset.

Full size image

Frequency learning

Numerous studies have been conducted focusing on the frequency domain in low-level restoration tasks49,50,51,52,53,54. Several methodologies50,51,52 were examined for decomposing features into distinct frequency bands using a multi-branch CNN to enhance the level of detail. Typically, the omni-frequency region-adaptive network51 employed a multi-branch CNN to segregate diverse frequency components and enhance these attributes using the proposed frequency enhancement unit. Frequency-specific convolutional neural networks52 segregated the input images into three sub-frequency clusters and conducted training for the convolutional neural network individually for each sub-frequency cluster. The ultimate SR image was synthesized by amalgamating the multi-SR images generated from various networks. Moreover, the frequency aggregation network50 extracted distinct frequencies from the low resolution (LR) image and forwarded them individually to a channel attention-grouped residual dense network to produce corresponding features. Next, these residual dense features are adaptively aggregated to reconstruct the high resolution (HR) image with improved details and textures. Other approaches49,53,54 converted images into the frequency domain. For instance, D349 devises a dual-domain restoration network to eliminate artifacts present in compressed images. The wavelet-based dual recursive network54 was introduced to decompose the LR image into a sequence of wavelet coefficients and predict the corresponding sequence of HR wavelet coefficients using networks, thereby generating the final HR image. SwinFIR53 extends SwinIR10 through the substitution of fast Fourier convolution, aiming to investigate the image-wide receptive field to enhance the SR performance. Our method introduces a DTCWT-based STB block to decompose image features into low frequency and high frequency features.

Figure 2
figure 2

The overall architecture of SVTSR and the structure of STB and RHAG.

Full size image

Method

Network architecture

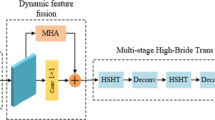
As shown in Fig. 2, SVTSR consists of three modules: shallow feature extraction, deep feature extraction and high quality (HQ) image reconstruction module. The architecture design is widely used in previous works8,10,13.

Shallow feature extraction

Given a low-quality (LQ) input \(I_{LQ} \in R^{H\times W\times C_{in} }\) (H, W and are the image height, \(C_{in}\) width and input channel number, respectively), we use a \(3\times 3\) convolutional layer \(H_{CONV} (\cdot )\) to extract shallow feature \(F_{0} = R^{H\times W\times C}\) as

$$\begin{aligned} F_{0}= H_{CONV} (I_{LQ} ), \end{aligned}$$
(1)

where C is the feature channel number. The convolution layer is good at early visual processing, leading to more stable optimization and better results42. It also provides a simple way to map the input image space to a higher dimensional feature space.

Deep feature extraction

we extract deep feature \(F_{DF} \in R^{H\times W\times C }\) from \(F_{0}\) as

$$\begin{aligned} F_{DF} = H_{DF} (F_{0} ), \end{aligned}$$
(2)

where \(H_{DF} (\cdot )\) is the deep feature extraction module and it contains K layers, comprising m Spectral Transform blocks (STB) and (K - m) residual hybrid attention groups (RHAG), where K denotes the network’s depth, and one \(3\times 3\) convolution layer \(H_{CONV3}\). More specifically, intermediate features \(F_{1},F_{2},...,F_{m},F_{m+1},...,F_{K}\) and the output deep feature \(F_{DF}\) are extracted block by block as

$$\begin{aligned} \begin{aligned}&F_{i} = H_{STB} (F_{i-1} ),i=1,2,...,m,\\&F_{j} = H_{RHAG} (F_{j-1} ),j= m+1,m+2,...,K,\\&F_{DF} =H_{CONV} (F_{K} ) \end{aligned} \end{aligned}$$
(3)

where \(H_{STB} (\cdot )\) denotes the i-th STB, \(H_{RHAG} (\cdot )\) denotes the j-th RHAG and \(H_{CONV}\) is the last convolutional layer. The Spectral Transform block (STB), being invertible, adeptly capture both the global and the fine-grain information in the image effectively via low-pass and high-pass filters, while residual hybrid attention group (RHAG) focus on extracting semantic features and addressing long-range dependencies present in the image. The STB structure is described in detail in Sect. 3.2. Applying a convolutional layer at the end of feature extraction can incorporate the inductive bias of the convolution operation into the Transformer-based network, providing a more robust foundation for subsequently aggregating shallow and deep features.

High quality image reconstruction

We reconstruct the high-quality image \(I_{SR}\) by aggregating shallow and deep features as

$$\begin{aligned} I_{SR} = H_{IR}(F_{0}+ F_{DF} ), \end{aligned}$$
(4)

where \(H_{IR} (\cdot )\)is the function of the HQ image reconstruction module. The pixel-shuffle method55 is adopted to up-sample the fused feature.

Loss function

We optimize the parameters of SVTSR by minimizing the L1 pixel loss as

$$\begin{aligned} LOSS= \left\| I_{IR}- I_{HQ} \right\| _{1}, \end{aligned}$$
(5)

where \(I_{IR}\) is obtained by taking \(I_{LQ}\) as the input of SVTSR, and \(I_{HQ}\)is the corresponding ground-truth HQ image.

Spectral transform block (STB)

Overview of DTCWT

Discrete Wavelet Transform (DWT) substitutes the infinite oscillating sinusoidal functions with a collection of locally oscillating basis functions, commonly referred to as wavelets56,57. A wavelet is formed by combining a low pass scaling function \(\phi (t)\) with a shifted version of a band-pass wavelet function, denoted as \(\psi (t)\). Mathematically, it can be represented as follows:

$$\begin{aligned} x(t)= \sum _{n=-\infty }^{\infty } c(n)\phi (t-n)+\sum _{j=0}^{\infty } \sum _{n=-\infty }^{\infty } d(j,n) ^{j/2} \psi (2^{j}t-n ), \end{aligned}$$
(6)

Where c(n) represents the scaling coefficients, and d(j,n) represents the wavelet coefficients. These coefficients are calculated through the inner product of the scaling function \(\phi (t)\) and the wavelet function \(\psi (t)\) with input x(t).

$$\begin{aligned} c(n)= \int _{-\infty }^{\infty } x(t)\phi (t-n)dt,d(j,n)= 2^{j/2} \int _{-\infty }^{\infty } x(t)\psi (2^{j} t-n)dt. \end{aligned}$$
(7)

The Discrete Wavelet Transform (DWT) encounters the following challenges: oscillations, shift variance, aliasing, and a deficiency in directionality. One solution to address the above problems involves employing the Complex Wavelet Transform (CWT), which utilizes complex-valued scaling and wavelet functions. The DTCWT tackles the challenges encountered by the CWT. The DT-CWT57,58,59 closely approaches mirroring the desirable characteristics of the Fourier transform, such as a smooth, non-oscillating magnitude, nearly shift-invariant magnitude with a simple near-linear phase encoding of signal shifts, significantly reduced aliasing, and improved directional selectivity of wavelets in higher dimensions. This facilitates the detection of edges and orientational features within images. The wavelet transformation consists of six orientations: \(15^{\circ } ?45^{\circ }?75^{\circ }?105^{\circ }?135^{\circ }\) and \(165^{\circ }\). The dual-tree CWT utilizes two real DWTs: the first DWT produces the real part of the transform, while the second DWT produces the imaginary part. The two real DWTs utilize distinct sets of filters, which are collaboratively designed to provide an approximation of the overall complex wavelet transform and meet the perfect reconstruction (PR) criteria. Let \(h_{0} (n),h_{1} (n)\) represent the low-pass and high-pass filter pair in the upper band, while \(g_{0} (n),g_{1} (n)\) represent the same for the lower band. Two real wavelets, denoted as \(\psi _{h} (t)\) and \(\psi _{g} (t)\), are linked with each of the two real wavelet transforms. The complex wavelet \(\psi _{h} (t):=\psi _{h} (t)+ \psi _{g} (t)\)can be approximated using the Half-Sample Delay condition60, where \(\psi _{h} (t)\) is approximately the Hilbert transform of \(\psi _{g} (t)\) like

$$\begin{aligned} \begin{aligned}&g_{0} (n)\approx h_{0} (n-0.5)\Rightarrow \psi _{g} (t)\approx H\left\{ \psi _{h}(t) \right\} \psi _{h}(t)= \sqrt{2} \sum _{n} h_{1} (n)\phi _{h} (t),\\&\phi _{h} (t)= \sqrt{2} \sum _{n} h_{0} (n)\phi _{h} (t),\\ \end{aligned} \end{aligned}$$
(8)

Similarly, we can define \(\psi _{g} (t),\phi _{g} (t)\), and \(g_{1} (n)\). As the filters are real, implementing DTCWT does not necessitate complex arithmetic. In 1D, it is merely two times more expansive because the total output data rate is precisely twice the input data rate. It is also straightforward to invert since the two separate DWTs can be inverted. Comparing DTCWT with the Fourier Transform, obtaining the low pass and high pass components of an image is challenging with the Fourier Transform, and it is less invertible (Loss is high when performing Fourier and inverse Fourier transforms) compared to DTCWT. Moreover, it cannot address time and frequency simultaneously.

The structure of STB

Figure 2 illustrates the distinct components of the STB Structure in detail. The Spectral Transform Block consists of three components: Spectral Transformation, Spectral Gating Network, and Spectral Channel and Token Mixing.

Spectral transformation

The input image I undergoes shallow feature extraction to acquire feature \(F_{0} \in R^{C\times H\times W}\) , with a spatial resolution of \(H\times W\) and C channels. To further extract the features of \(F_{0}\), we input \(F_{0}\) into a sequence of transformer layers. Instead of the standard self-attention network, we utilize a spectral transform based on an invertible spectral network. This enables us to capture both fine-grained and global information in the image. The fine-grain information comprises texture, patterns, and small features encoded by the high-frequency components of the spectral transform. The global information includes overall brightness, contrast, edges, and contours encoded by the low-frequency components of the spectral transform. Given feature \(F_{0} \in R^{C\times H\times W}\), we employ spectral transform using DTCWT61, as discussed in Sect. 3.2.1, to obtain the corresponding frequency representations \(X_{F}\) by \(X_{F} = F_{spectral} (F_{0} )\). The frequency domain transformation \(X_{F}\) yields two components: one low-frequency component, i.e., the scaling component \(X_{\phi }\), and one high-frequency component, i.e., the wavelet component \(X_{\psi }\). The simplified formulation for the real component of \(F_{DTCWT} (\cdot )\) is as follows:

$$\begin{aligned} X_{F} (u,v)= X_{\phi } (u,v)+X_{\psi } (u,v)= \sum _{0}^{H-1} \sum _{w=0}^{W-1} c_{M,h,w} \phi _{M,h,w} +\sum _{m=0}^{M-1} \sum _{h=0}^{H-1} \sum _{w=0}^{W-1} \sum _{k=1}^{6} d_{m,h,w}^{k} \psi _{m,h,w}^{k} \end{aligned}$$
(9)

M denotes resolution, and k denotes directional selectivity. Similarly, we compute the transformation for the imaginary component of \(F_{DTCWT} (\cdot )\).

Spectral gating network

We introduce a technique called Spectral Gating Network (SGN) to extract spectral features from both low and high-frequency components of the scattering transform. Figure 2 illustrates the structure of the method. We employ learnable weight parameters to blend each frequency component, employing distinct blending methods for low and high frequencies. For the low-frequency component \(X_{\phi } \in R^{C\times H\times W}\), we utilize the Tensor Blending Method (TBM), a novel technique. TBM combines \(X_{\phi }\) with \(W_{\phi }\) through element-wise tensor multiplication, also recognized as the Hadamard tensor product.

$$\begin{aligned} M_{\phi } = [X_{\phi } \odot W_{\phi } ], \end{aligned}$$
(10)

where \((X_{\phi },W_{\phi } )\in R^{C\times H\times W}\), and \(M_{\phi } \in R^{C\times H\times W}\), \(W_{\phi }\) having same dimension as in \(X_{\phi }\). \(M_{\phi }\) represents the low-frequency image representation, capturing the global information of the image. Acquiring effective features in the high-frequency components \(X_{\phi } \in R^{k\times C\times H\times W\times 2}\) poses a significant challenge due to their complex-valued nature and ’k’ times more dimensions compared to the low-frequency components. Hence, applying the Tensor Blending Method to the high-frequency components \(X_{\psi }\) would amplify the parameter count by 2k times and escalate the computational cost (GFLOPS), where k denotes directional selectivity, and the factor of 2 denotes the complex value comprising real and imaginary parts. To tackle this challenge, we introduce a novel approach called the Einstein Blending Method (EBM) to efficiently and effectively blend the high-frequency components \(X_{\psi }\) with the learnable weight parameters \(W_{\psi }\) within the Spectral Gating Network proposed in this paper. By employing EBM, we can capture fine-grain details in the image, including texture, patterns, and small features. To perform EBM, we initially reshape a tensor A from \(R^{H\times W\times C}\) to \(R^{H\times W\times C_{b} \times C_{d} }\), where \(C= C_{b} \times C_{d}\), and \(b>> d\). We then define a weight matrix of size \(W_{\psi _{c} } \in R^{C_{b}\times C_{d} \times C_{d} }\). We then conduct Einstein multiplication between A and W along the last two dimensions, resulting in a blended feature tensor \(Y\in R^{H\times W\times C_{b}\times C_{d} }\). The formula for EBM is:

$$\begin{aligned} Y^{H\times W\times C_{b} \times C_{d} } = A^{H\times W\times C_{b}\times C_{d} } \otimes W^{C_{b}\times C_{d}\times C_{d} }, \end{aligned}$$
(11)
Spectral channel and token mixing

We execute EBM in the channel dimension of the high-frequency component, termed Spectral Channel Mixing, and subsequently in the token dimension of the high-frequency component, referred to as Spectral Token Mixing. To perform EBM in the channel dimension, we first reshape the high frequency component \(X_{\psi }\) from \(R^{2\times k\times H\times W\times C}\) to \(R^{2\times k\times H\times W\times C_{b}\times C_{d} }\), where \(C= C_{b} \times C_{d}\), and \(b>>d\). We then define a weight matrix of size \(W_{\psi _{c} } \in R^{C_{b}\times C_{d}\times C_{d} }\). We then conduct Einstein multiplication between \(X_{\psi }\) and W along the last two dimensions, yielding a blended feature tensor \(S_{\psi _{c} } \in R^{2\times k\times H\times W\times C_{b}\times C_{d} }\). The formula for EBM in Channel mixing is:

$$\begin{aligned} S_{\psi _{c} }^{2\times k\times H\times W\times C_{b}\times C_{d} } = X_{\psi }^{2\times k\times H\times W\times C_{b}\times C_{d} } \otimes W_{\psi _{c} }^{C_{b}\times C_{d} \times C_{d} } + b_{\psi _{c} }, \end{aligned}$$
(12)

To perform EBM in the Token dimension, we first reshape the high frequency component \(S_{\psi _{c} }\) from \(R^{2\times k\times H\times W\times C}\) to \(R^{2\times k\times C\times W\times H}\), where \(H=W\). We then define a weight matrix of size \(W_{\psi _{t} } \in R^{W\times H\times H}\). We then execute Einstein multiplication between \(X_{\psi }\) and W along the last two dimensions, producing a blended feature tensor \(S_{\psi _{t} } \in R^{2\times k\times C\times W\times H}\). The formula for EBM in Token mixing is:

$$\begin{aligned} S_{\psi _{t} }^{2\times k\times C\times W\times H} = S_{\psi _{c} }^{2\times k\times C\times W\times H}\otimes W_{\psi _{t} }^{W\times H\times H} + b_{\psi _{t} }, \end{aligned}$$
(13)

where \(\otimes\) represents an Einstein multiplication, the bias terms \(b_{\psi _{c} } \in R^{C_{b} \times C_{d} }\), \(b_{\psi _{t} } \in R^{H \times H }\). Now, the total number of weight parameters in the high-frequency gating network is \((C_{b} \times C_{d}\times C_{d} )+ (W\times H\times H)\) instead of \((C\times H\times W\times k\times 2)\) where \(C>>H\) and bias is \((C_{b}\times C_{d} )+ (H\times W)\). This decreases the number of parameters and multiplications during high-frequency gating operations in an image. We utilize the standard torch package62 for performing Einstein multiplication. Ultimately, we execute inverse spectral transform using both low-frequency and high-frequency representations to revert the spectral domain back to the physical domain.

Figure 3
figure 3

Visual quality comparisons of \(\times 4\) image SR on Set14, BSDS100 and Manga109 test datasets.

Full size image

Experiments

Experimental setup

Like the HAT13work, we use DF2K (DIV2K7+ Flicker2K63) dataset as the training dataset. The model is trained on four NVIDIA GeForce GTX 1080 Ti blocks. For the structure of SVTSR, the STB number and RHAG number are both set to 3. The channel number is set to 96. Both (S)W-MSA and OCA are configured with an attention head number of 6 and a window size of 16. Five benchmark datasets, specifically Set516, Set1417, BSD10064, Urban10065, and Manga10966, are employed to assess the methodologies. To evaluate the effectiveness of the proposed method, we utilize PSNR, SSIM, model size and parameters as the metrics.

Quantitative results

Table 1illustrates the quantitative indicators (PSNR and SSIM) comparison between our approach and the state-of-the-art methods, including CNN-based approaches (EDSR7, RCAN8, SAN2, IGNN61, HAN67, NLSN68, RCAN-it69) and Transformer-based SR methods (SwinIR10, EDT12, HAT13). As shown in Table 1, our SVTSR achieves the best performance on all five benchmark datasets. Concretely, SVTSR surpasses HAT by 0.07dB-0.12dB on Set14 and 0.06dB-0.13dB on BSD100. At the same time, it can be seen from Table 2 that the biggest advantage of our method is that the number of parameters of the model is only 2.3M-2.5M, and the size of the model is only 21.16MB-22.56MB, which is much lower than the baseline HAT 20.6-20.80M and 161.27–162.40MB. These data show that the size and number of parameters of our model decreased significantly while keeping PSNR and SSIM metrics slightly above SOTA. All these results show the effectiveness of our method.

Table 1 Comparison of quantitative indicators (PSNR and SSIM) with state-of-the-art methods on benchmark datasets.
Full size table

Qualitative results

We present several challenging examples for visual comparison (at \(\times\)4 magnification) across three test datasets in Fig. 3, including “MukoukizuNoChonbo” in Manga109, “210088” in BSDS100, “monarch” in Set14. The SVTSR successfully recovered clear image texture information. Conversely, all the other approaches exhibit severe blurry effects. Similar behaviors are also observable in “MukoukizuNoChonbo” within Manga109. During the process of character recovery, SVTSR achieves notably clearer textures compared to other methods. The visual outcomes additionally illustrate the superiority of our approach.

Table 2 Comparison of quantitative indicators (Model Size and Params) with several classical methods. The best results are marked in bold.
Full size table
Table 3 The STB model consists of a low-frequency component and a high-frequency component facilitated by a scattering network using the Dual Tree Complex Wavelet Transform. Every frequency component is governed by a parameterized weight matrix employing Patch mixing and/or Channel Mixing. This table provides details regarding all combinations, and \(STB_{TTEE}\) emerges as the best-performing option among them. The PSNR, SSIM indicators in the table were measured on the Set5 test set.
Full size table

Ablation study

STB employs a spectral network to partition the signal into low-frequency and high-frequency components. We utilize a gating operator to acquire effective learnable features for spectral decomposition. The gating operator involves the multiplication of the weight parameter in both high and low frequencies. We have performed experiments employing both tensor and Einstein mixing techniques. Tensor mixing operates as a straightforward multiplication operator, whereas Einstein mixing employs an Einstein matrix multiplication operator. Observationally, in low-frequency components, Tensor mixing exhibits superior performance compared to Einstein mixing. As demonstrated in Table-3, we begin with \(STB_{TTTT}\), incorporating tensor mixing in both high and low-frequency components. We observe that it may not achieve optimal performance. Subsequently, we reverse the approach and employ Einstein mixing in both low and high-frequency components, however, this also does not yield optimal performance. Subsequently, we devised the alternative method \(STB_{TTEE}\), which utilizes tensor mixing in low frequency and Einstein mixing in high frequency. In the high-frequency domain, further decomposition involves token and channel mixing, while in the low-frequency domain, we simply apply tensor multiplication, given its representation as an energy or amplitude component.

Conclusion

In this paper, we present a novel vision transformer model, SVTSR, for SISR tasks. We introduce an invertible spectral network founded on DTCWT transformation into vision transformers designed for image SR tasks to partition image features into low-frequency and high-frequency components. Extensive experiments show the effectiveness of the proposed model. Our method not only outperforms SOTA method in PSNR and SSIM indexes, but also has significant advantages over other methods in model size and number of parameters.