Introduction

Large amplitude Internal Solitary Waves (ISWs hereafter) propagate in stratified waters over long distances. They are specific internal waves achieving a balance between non-linear steepening and non-hydrostatic dispersion. ISWs can be generated by tide-topography interactions at shelf break or sills1,2,3,4, by upwelling front oscillations5, at river plume fronts6,7 and even by eddies8. In addition they can result from the non-linear steepening of internal tides as in the South China Sea9. ISWs are of great importance for vertical mixing10,11, sediment transport on shelves1,12,13,14 and threaten the safety of underwater infrastructures.

The Strait of Gibraltar (SoG hereafter) is the only dynamical connection between the Atlantic Ocean and the semi-enclosed Mediterranean Sea. The density difference between the relatively cold and salty Mediterranean waters and the warm and fresh Atlantic waters drives a baroclinic two-layer flow15. The Mediterranean waters flow westward in the Mediterranean Outflow while the Atlantic waters flow eastwards as a jet in the upper layer. The exchange flow maintains a strong pycnocline between both water masses which deepens westward in the SoG16. This permanent pycnocline plays the role of an internal-wave guide. The strong barotropic tide17,18,19 and the complex bathymetry of the SoG favors the generation of internal tides and Internal Solitary Waves (ISWs). Large amplitude ISWs have long been described in the SoG, from in-situ measurements20,21,22,23,24,25,26,27,28,29,30, satellite or airborne observations31,32,33,34,35,36 and more recently with numerical modeling30,37,38,39,40,41. They are generated at Camarinal Sill (CS hereafter), the main topographic feature, by the release of a hydraulic jump created during sufficiently strong tidal outflows (westward tidal current during the flood) and they propagate eastward to the Alboran Sea.

Apart from these impressive eastward propagating ISWs, other ISWs develop in the SoG. Watson et al.31 observed northward propagating wave off the coast of Ceuta, Brandt et al.35 identified westward propagating wave west of CS, Richez et al.32 reported cross-strait ISWs. Recently, Roustan et al.29 (RBGL23 hereafter) evidenced the existence of reflected wave propagating northwestward from the Moroccan shelf-break towards the Spanish shelf associated to the well-known eastward propagating ISWs. They named these waves R-waves and the corresponding incident waves I-waves, names that we retain in this study. The authors suggested that these R-waves have a signature in the sea level measurements at the Tarifa tide gauge.

In-situ measurements of ISWs are scarce and short in time as they generally require the deployment of Acoustic Doppler Current Profilers (ADCPs) or Conductivity-Temperature-Depth (CTD) mooring lines sampling at relatively high frequency involving very high energy supply. This complexity is enhanced in the SoG characterized by heavy maritime traffic and harsh environment. We present here a unique opportunity to obtain a continuous time series of nearly 10 years of in-situ measurements. In this study, we propose to lean on the results of RBGL23 in order to address the question of the ISWs emission at longer time-scale. First we confirm that R-waves leave a signature in the sea level at Tarifa, then we build an algorithm to automatically detect their signature. We assess how this signature in the sea level at Tarifa is a good proxy of the presence of I-waves. From the long time-series of sea level measurements of Tarifa tide gauge (2015-2023), we investigate the variability of the generation of ISWs in the SoG from tidal to seasonal scales. Finally we discuss the physical mechanisms able to drive this variability.

Data

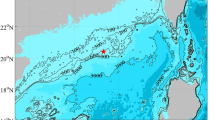
The study is based on multiple data sources : high frequency tide gauge, in-situ measurements, satellite data and atmospheric hindcasts. The high frequency (1min) Tarifa tide gauge record from 2015 to 2023 is extensively used. The tide gauge is located in the Tarifa harbor, protected from surface waves perturbations (green dot on Fig. 1).

We analysed the Synthetic Aperture Radar (SAR hereafter) Sentinel-1 images from 2018 to 2023 provided by Ocean Data lab (https://ovl.oceandatalab.com/). The SAR signal is impacted by small-scale sea-surface rugosity, which allows to visualize front of convergence/divergence currents associated with ISWs as bright and dark bands42. It has been widely used to infer ISWs information in the SoG and elsewhere.32,33,34,35,36,43 The Sentinel-1 constellation used here provides 4 images per week over the SoG.

The field experiment, PROTEVS GIB20, was performed in October 2020 on the French R/V L’Atalante. The campaign was designed to sample the flow at very high frequency (up to 0.1Hz frequency) during part of a fortnightly cycle between the \(8^{th}\) and the \(18^{th}\) of October 202028. In this study, we use three moorings : two ADCPs moorings MO2 and MO4, and one array of CTD probes MO5 (Fig. 1). MO2 consists in a Nortek CONTINENTAL at 190kHz upward looking ADCP moored at the bottom near CS (\(35.93^\circ\)N, \(-5.768^\circ\)W) providing current every 30s in 5m thick bins. MO4 consists in an upward-looking 75kHz RDI ADCP moored 5km east of CS (\(35.933^\circ\)N, \(-5.678^\circ\)W) 100m over the bottom providing current every minute in 8m thick bins. MO5 consists in an array of CTD-SBE37 probes spaced by 50m and inter-spaced every 10m with T-SBE56 probes sampling at 10s frequency. Near the equinox, the variations of the tidal amplitude are very important leading to intense tidal current up to \(-2\)m/s at MO2 in spring tides which tilts the mooring lines. The density profiles are interpolated at constant depth from SBE37/SBE56 probes. In addition one Argo float (number 6903016) was deployed in the Alboran gyre where it remained trapped for a few months.

Figure 1
figure 1

Inset: Strait of Gibraltar and adjacent basins. Red box frames the zoom area. Map: Strait of Gibraltar. Blue/red diamonds indicate the location of the PROTEVS GIB20 ADCP/CTD mooring lines, blue star indicates the location of the INGRES ADCP and green circle plots the position of the Tarifa Tide Gauge.

Full size image

To access longer current measurement over CS, we used the INGRES data set. It consists in two ADCPs, a RDI 75kHz upward looking and a Norterk 500kHz downward looking located in the southern channel of Camarinal Sill (Fig. 1). The mooring was deployed from August 2020 to May 2021 sampling at 30min frequency from the near bottom to 10m below the surface. We use this mooring to infer the tidal current from 2015 to 2023 from an harmonic decomposition of the zonal component, which dominates the signal.

For complementary analysis, we investigate hindcast atmospheric data from the ARPEGE model of Meteo-France (1h-5km fields) in the Strait of Gibralar during the period 2015-2023.

Methods

Froude number

The internal Froude number, Fr, indicates the local criticality of the flow i.e. the ability of internal waves to propagate upstream of the background current. It is computed as the ratio between the mean flow velocity and the phase speed of long internal gravity waves. When \(Fr >1\), the flow is supercritical meaning that internal waves can not propagate upstream. A bore propagates when the flow changes from supercritical to subcritical with slackening current.

The definition of the Froude number, in the complex baroclinic and fully stratified flow characteristic of the SoG, is debated in the literature16,22,28,44. But, the latter authors (see appendix A of Roustan et al.28) show that criticality of the flow slightly depends on the calculation method used over CS. To account more realistically for the stratification, we compute the Froude number as the ratio between the total barotropic zonal current \(\bar{U}\) and the phase speed, \(c_\phi =\omega /k\) of the first mode internal wave solution of the Sturm-Liouville problem45:

$$\begin{aligned} \frac{\textrm{d}^2\phi }{\textrm{d}z^2} + k^2\frac{N^2-\omega ^2}{\omega ^2-f^2}\phi = 0 \end{aligned}$$
(1)

with \(N^2\) the squared Brunt-Väisälä frequency, f the Coriolis parameter, \(\omega\) the wave frequency, k the horizontal wavenumber, and \(\phi\) the modal structure of the vertical velocity \(W = \phi (z)e^{i(kx-\omega t)}\). Equation (1) results from the linearized Navier–Stokes equations in the non-viscous, incompressible, Boussinesq limits. We solve equation 1 with the constant depth, H, and rigid-lid approximation, leading to \(\phi (0) = \phi (H) = 0\). Equation (1) does not account for the sheared flow that happens in the Strait of Gibraltar. Including the shear term in the equation changes slightly the phase speed, but it does not change its seasonal pattern, which is driven by the seasonality of the stratification through term \(N^2\). Since the study mainly focus on the seasonal variation of ISWs detection, the inclusion of the shear does not modify the results and, therefore, it has not been considered in Eq. (1).

Tidal current reconstruction

We use the vertically average zonal current measured at the INGRES mooring for nine months to compute the harmonic constituents of the tidal current at this point from the utide python-package (https://github.com/wesleybowman/UTide/tree/master/utide). The algorithm resolves 59 harmonic constituents of which only 25 have an amplitude greater than 1cm/s. The RMSE, computed as the root mean squared difference between the measured current observations and reconstructed current during the INGRES period, is 14 cm/s. This result suffices to quantify the strength of the tidal current at each tidal cycle. Based on these harmonics, we reconstruct the zonal tidal current for the period 2015-2023.

Detection of internal solitary wave signature in tide gauge data

Recently, RBGL23 evidenced the signature of ISWs, in the high frequency measurements of sea level from Tarifa tide gauge. They showed that it is the signature of R-waves which are reflected waves from the well-known eastward propagating I-waves emitted at CS. In this first part, we propose an algorithm to automatically detect the signature of such waves in the sea level sampled at 1min. The algorithm is based on a wavelet analysis of the high-pass signal carefully investigated for three typical days where R-waves were clearly distinguishable on SAR images (Fig. 2). Then we calibrate our algorithm on the GIB20 field experiment data set and the SAR images featuring R-waves in 2020. Finally, we address the ability to detect I-waves - which are incident waves emitted at CS—through the observations of sea level at Tarifa in a 5-year SAR images database (2018–2023).

R-waves signature

Figure 2 shows R-wave signature on the Sentinel-1 SAR images at three dates : 2019-06-04, 2022-08-11 and 2023-01-20. The dates are chosen to have different stratification conditions through the year. The associated high frequency (orange curve) and smoothed (with a 60min sliding window, blue curve) sea level signals are presented for each situation (middle row). RBGL23 found that R-waves arrive at Tarifa near Low Water (LW hereafter). For this reason we restrict the analysis \(\pm 90\)’ around LW. At the three dates, the sea level signal presents high frequency fluctuations (15min to 30min) of few centimeters around LW (middle row Fig. 2). The elevation signal is consistent with the surface signature of ISW of depression of few tens of meters29,38,46,47. We analyse the high pass (\(8^{th}\)-order Butterworth filter at 1 hour cut-off frequency) surge signal with a Morlet continuous wavelet decomposition. It suggests that these HF signature observed around LW are in the band 30min-45min (supplementary Fig. S1) which is consistent with the 30min-60min band reported by RBGL23. Note that we tested several mother wavelet for the decomposition with only slightly changes (Supplementary Fig. S1). We use the wavelet signal at 40min period for the peak detection (purple dots in lower panels) as its corresponds to the maximum associated with the signal (see black circle in Fig. S1). The last two cases in Fig. 2, 2022-08-11 and 2023-01-20, show that these high-frequency oscillations are effectively phased with the R-waves when they reach Tarifa harbor. Indeed, the waves are respectively detected at 06:20 and 18:08 while the SAR images were taken at 06:28 and 18:18. This result confirms that the high frequency signature corresponds to the residual signal of the R-wave propagating shoreward as suggested by RBGL23.

Figure 2
figure 2

Upper panels : Synthetic Aperture Radar (SAR) images from Sentinel-1 depicting R-wave signatures. Green dots show the location of the Tarifa tide gauge Middle panels : hourly (blue curve) and 1 min sea level (SL in the legend) (orange curve) at Tarifa at the dates of the SAR images. R-waves detections are depicted with red dots. Vertical black dotted line shows the time of the SAR image. Blue dot show the low water (LW in the legend). Lower panels : Morlet wavelet decomposition of the 1min sea level signal, using a 40min period. R-waves detections are plotted in purple dots. See text for complementary information about the threshold used for detection.

Full size image

Automatic detection

The second task was to develop an automatic algorithm to detect the R-wave events in the sea level measured at Tarifa tide gauge. To define a threshold for the detection on the wavelet signal, we used the in-situ observations of I-waves/R-waves during the PROTEVS GIB20 field experiment reported by RBGL23 and SAR images depicting R-waves in 2020. From the in situ observations we identify tidal periods without ISW observations. The threshold of peak detection is selected such that no detection is reported whenever no ISW is observed, giving a minimal value of \(6\times 10^{-4}\). Then, from 13 SAR images depicting R-waves in 2020, we check if the threshold was not too restrictive. In all the 13 images, we were able to detect a signature at Tarifa, increasing the confidence in our choice.

Figure 3a shows the detected ISWs during the field experiment (8–18th of October 2020). The green curve superimposed shows the barotropic current over CS (at MO2) computed as the vertically-averaged zonal current. Figure 3b shows the high frequency sea level signal (blue curve) and the squared Morlet wavelet at 40 min period used for the detection. The threshold is evidenced as a black dashed line. An ISW event corresponds to a LW where the squared Morlet wavelet at 40 min period is greater than the threshold at least once within 90 min around LW.

Figure 3
figure 3

(a) Sea level at Tarifa : (orange curve) at 1min frequency, (blue curve) smoothed with a 1 h running average. Red dots show the peak detection. Black stars depict LW when ISWs are identified. Green line shows the zonal barotropic current at MO2 (right y-axis) computed as the depth-averaged zonal current. (b) High frequency surge (8th order 1 h cutoff frequency high-pass Butterworth filter, blue curve left y-axis) and squared Morlet wavelet coefficient at 40min period (orange curve right y-axis lighted \(\pm 90\)min around LW). (c) Zoom between the 12\(^{th}\) of October at 18:00 and the 13th at 22:00 (indicated in (a)) showing the vertical velocity at MO4 and few isopycnal surfaces at MO5. Barotropic current at MO2 is superimposed (green curve, right axis). R-waves and I-waves are highlighted respectively with solid and dashed boxes. The Froude number over CS is indicated at the top with black arrows.

Full size image

Figure 3c shows the vertical velocity at MO4 superimposed with a few isopycnals at MO5 (black lines) and the barotropic current at MO2 (green line, right y-axis) on a short period (\(12\textrm{th}-13\textrm{th}\) of October). This period is especially interesting as the algorithm detects an event during the first tidal period but not during the second. This is consistent with the in-situ observations at MO4/MO5. During the first tidal period the flow is hydraulically controlled over CS (\(Fr>1\)) leading to a rapid rise of the pynocline at MO5 in the early outflow (\(\sim 19:00\)). This is a feature expected upstream when control occurs over CS48,49. At the end of the outflow (\(\sim 23:00\)) a rapid plunge of the isopycnal surfaces is followed by 10min oscillations consistent with the high frequency inversion observed in the vertical velocity at MO4. This signature corresponds to the propagation of I-waves generated at CS. Later, another group of ISWs is observed at the end of the tidal inflow (\(\sim 04:00\)); it corresponds to the reflected R-waves (RBGL23). At the same time, the algorithm detects ISWs at Tarifa. Conversely, during the second tidal period, neither the I-wave nor the R-waves are observed (and the isopycnals do not rise in the early outflow) suggesting that no hydraulic control (\(Fr<1\)) occurred at this tide. Then, the algorithm does not detect any ISW.

This analysis was repeated for the whole period of in-situ measurements and is presented in Fig. 4 during neap tides. It shows consistent results : whenever neither the I-wave, R-wave, nor control signature was observed, the algorithm did not detect any ISW at Tarifa. This gives us a great confidence in our ability to discriminate between ISWs emission and no ISWs emission. Note that the case of the 11th night is quite surprising as the isopycnal shows a bore (30’ after HW) but no peak is detected. Possibly the isopycnal is not steep enough to degenerate into ISWs early enough for reflection to happen. We checked whether this discrepancy was an artifact of our method, but it is in fact a physical difference in the high-frequency sea level data (supplementary Fig. S2).

Figure 4
figure 4

Isopycnal elevation (blue curve) and squared Morlet walet at 40 min period (orange curve) \(\pm 3\) h around respectively high/low water during neap tides of PROTEVS GIB20 field experiment. Red dots mark the peak detection of the Algorithm. The black dashed curve shows the sea level at Tarifa. Numbers on the right are the time (day hour:min of October, 2020) of high water. The vertical dotted lines frame the time interval scrutinized for detection.

Full size image

I-waves signature

Large amplitude, eastward propagating ISWs (I-waves) are emitted at CS around the end of the tidal outflow and propagate up to 100km in the Alboran Sea23. RBGL23 attributed R-waves to the reflection of I-waves on the Moroccan shelf-break during their eastward journey in the SoG. Their observations and their theoretical analysis suggested that a reflected R-wave was emitted whenever an I-wave exists, but the GIB20 dataset spans too short a time window to draw any final conclusion.

Therefore, we use complementary data to assess if R-wave signature at Tarifa is a reliable proxy of I-wave propagation in the SoG. Sea level at 1min frequency is sampled since 2013, and the Sentinel-1 SAR images have been available since 2015. We perform the analysis for the period 2018-2023 which gives about 500 SAR images with ISWs signature: 78 R-wave images and 415 I-wave images, which we characterize according to the position of the leading ISW : west of Tarifa (Zone1), between Tarifa and Ceuta (Zone2) and in the Alboran Sea (Zone3) in Fig. 1. Note that the detections of I-waves and R-waves have been performed manually for each image, retaining only those images clearly showing the ISW signature.

Table 1 Percentage of detection at Tarifa tide gauge of ISWs identified in Sentinel-1 SAR images.
Full size table

On the date of the R-wave images, an ISW event is detected in \(99\%\) of the cases, which gives confidence in the methods (Table 1). For I-wave images, we check the next LW when the signature falls in Zone1, the nearest LW when it falls in zone2, and the two previous LW when it falls in zone3. These choices are based on the dynamical knowledge of I-waves. West of Tarifa (Zone1) the I-wave is near the generation zone (late flood/early ebb) and the reflected R-wave is not yet formed, thus its signature is expected at the next LW as shown in RBGL23. The I-wave are observed between Tarifa and Ceuta (Zone2) during the ebb of the next flood26,30 with expected R-wave signature at the nearest LW. For the ISWs observed in the Alboran Sea (Zone3), it is more complicated to accurately find the LW that bears their signature at Tarifa. Previous studies highlighted the important variability in the propagation speed of the eastward propagating ISWs due to tidal and subinertial variations of the total current26,30,31. To prevent false non-detection, we compare with the two previous LWs. An ISW event is detected at about \(95\%\) of I-wave SAR images (Table 1). It suggests that a large part of the I-waves are effectively reflected and their reflection propagate up to Tarifa tide gauge even in those cases when the expected R-waves do not show up in SAR images.

Based on these findings, we assert that the signature of a R-wave at Tarifa tide gauge is a reliable proxy to study the variability in the emission of I-waves at CS, which is the topic of the rest of the paper.

Multi-scale variability of ISW emission in the SoG

The emission of large amplitude ISWs in the SoG has long been known to result from the formation of a large internal hydraulic jump released as a bore when the westward-tidal current slackens by the end of the flood. The formation and amplification of the hydraulic jump is caused by a change in the nature of the flow, which becomes supercritical over CS with increasing current while it remains subcritical on the deeper lee-side22,24,28,39,40,50,51. The hydraulic nature of the flow is characterized by the Froude number \(Fr = \bar{U}/c_\phi\), therefore any change in currents and/or stratification should impact the generation of ISWs at CS. The long series of high frequency sea-level measurements at Tarifa allows us to investigate the variability of ISWs emission from tidal, to seasonal scales.

Variability at the tidal periods

Because of the standing-wave pattern of the semi-diurnal tide in the area, the barotropic tidal flow heads west between low and high water (flood or tidal-outflow) and east from high to low water (ebb or tidal-inflow)17,18,19. Since we do not have direct measurements of the barotropic current U at CS for the whole period, we use harmonic predictions over the 8 years based on the nine months of data at mooring INGRES (see methods). We characterize the strength of one tidal outflow as the maximum predicted current (westward heading) during each tidal outflow. The harmonic predictions are sufficiently accurate to reproduce the diurnal cycle of the tidal current, which is quite strong in the SoG18.

Figure 5a illustrates the distribution of the maximum tidal current at each outflow colored according to whether an ISW is detected or not, for the period 2015-2023 (6265 LWs). The strongest the tidal current, the greater the proportion of ISW events detected, in agreement with the theoretical framework. Indeed, for a constant \(c_\phi\), the Froude number is driven by the strength of the tidal current. Moreover, previous studies showed that hydraulic control is achieved in spring tides but not always during neap tides22,28,39.

Figure 5
figure 5

(a) Histogram of maximum tidal current during outflow, \(U_{max}\), colored by the ISW detection. See text for detailed definition of \(U_{max}\). (b) Monthly distribution of maximum tidal current during outflow, \(U_{max}\), in case of (orange boxes) ISW detection and (blue boxes) no ISW detection. Boxplots represent the first (Q1) and third (Q3) quartiles, outliers are defined as values out of the \([Q1-1.5IQ,Q3+1.5IQ]\) with \(IQ = Q3-Q1\).

Full size image

For \(U_{max}\) larger than 1.2m/s, ISW are emitted more than \(90\%\) of the time whereas for \(U_{max}\) smaller than 0.6m/s, ISW events are detected less than half of the tidal cycles. This result confirms that ISW emission in the SoG is largely driven by tidal variations and is controlled by the amplitude of these variations. The result is unchanged at the monthly scale with the tidal strength significantly impacting the ISW emission (Fig. 5b). Other physical processes occurring in the SoG might explain the variability of the emission at low tidal amplitude, one being the change in stratification over CS, which is discussed in the following sections.

This result highlights the predominant role of the tidal current in the emission of internal solitary wave. Over a certain tidal strength, ISWs are emitted at almost each tidal outflow. In the following, we focus on the neap/intermediate tides when the emission of ISWs might be influenced by others mechanisms.

Seasonal variability

The strong baroclinic density-driven two-layer flow is associated with a permanent pycnocline at about 100m depth, due to the halocline in the SoG between the salty Mediterranean and fresh Atlantic waters. This pycnocline allows the formation of ISWs at all seasons29,34. In summer and fall, the Atlantic layer presents a seasonal thermocline at about 30m depth increasing the density difference between the Atlantic and the Mediterranean waters. The impact of this seasonal thermocline in the ISWs dynamics in the SoG has been poorly investigated. We address this question here.

Figure 6 presents monthly stratification in the Alboran Sea computed from 2005 to 2015 MEDATLAS climatology (panel a) and an Argo float deployed in the Alboran gyre during the field experiment and remained trapped for a few months (panel b). We compute the phase speed of the first mode for long internal gravity waves for each monthly-averaged profile. It ranges from 1.3m/s in late winter (February and March) to 1.6m/s in late summer and fall (August to November) when the seasonal thermocline is fully developed. The seasonal variations of the stratification modify the internal wave phase speed by around \(20\%\). Based on the phase speed, months can be sorted in two extreme groups, weak-thermocline period (January to March) and strong-thermocline period (August to November). The Argo float shows that the seasonal thermocline is still relatively developed in December 2020, which illustrates possible late destratification for certain years. When the seasonal thermocline is strongly developed, the associated mode 1 phase speed is high, thus stronger currents are needed to achieve hydraulic control over CS compared with winter weak-stratification, which suggests a reduction of the ISW emission near neap tides in summer conditions.

Figure 6
figure 6

(a) Monthly climatology stratification in the Alboran Sea (MEDATLAS 2015) and associated phase speed of the first mode of long internal gravity wave45. (b) Stratification profile based on Argo float (number 6903016) data in October-January 2020/2021 which was trapped in the Alboran Gyre. Monthly averaged profiles are showed in bold with associated phase speed. The inset map shows the trajectory of the float during this period.

Full size image

Figure 7a shows the seasonal variations of the percentage of detected ISW events. Figure 7b/c shows the seasonal variations of the percentage of detected ISW events near spring/neap tides. The percentage of ISW detection is around \(85\%\) with a very slight monthly variability. The minimal percentage happens in May/June/July along with the lower occurrence of low tidal amplitudes (not shown), suggesting that the decrease of the percentage of ISW events is attributable to stratification variations rather than to lower tidal amplitudes. Near spring tides, there is no clear seasonal variations, the variability looks more chaotic from one month to another (Fig. 7b). Near neap tides, Fig. 7c shows a slight seasonal cycle with minimum detection in May to July and a maximum in January. To better account for the variability of the tidal range which impact the number of neap tide event, we computed the probability to detect an ISW conditioned by \(U_{max} \le U_0\), where \(U_0\) represents a certain threshold for the two extreme thermocline conditions (Fig. 8).

Figure 7
figure 7

(a) Monthly percentage of LW with detected ISW events. (b) Monthly percentage of detected ISWs near spring tides (\(U_{max} \ge p_{U_{max}, 90}\) as a threshold). (c) Monthly percentage of detected ISWs near neap tides (\(U_{max} \le p_{U_{max}, 10}\) as a threshold).

Full size image
Figure 8
figure 8

Probability of ISW detection conditioned by a relatively small maximum tidal current, \(U_0\), function of this threshold for (blue) weak and (orange) strong thermocline conditions. Weak thermocline includes January to March, while strong thermocline includes August to November. The size of the point scales with the number of low water that verify the condition.

Full size image

Figure 8 highlights the seasonal variability much more clearly; from weak to strong thermocline conditions the probability of detecting ISWs at low tidal strength decreases by a few percents. At first order, the seasonal cycle of ISW emission matches the seasonal cycle of the internal gravity wave phase speed (Fig. 6). Thus, the seasonal stratification, which progressively develops in summer, increases the tidal energy required to achieve hydraulic control over CS leading to a sensitive decrease of the probability of detecting ISW events at low tidal amplitude. In addition, Fig. 8 confirms that the tidal strength is the main driver of the ISW emission: increasing \(U_0\) linearly increases the probability of ISW emission. Note that the probability difference between the two extreme conditions varies with the threshold. This suggests that other processes might influence the ISWs emission at intermediate tides. As far as we know, the dynamics of sill with double pycnocline–halocline and thermocline in this case—have been poorly studied until now.

Discussion

ISWs are known to have a very weak surface signature as the ratio between the surface anomaly and the wave amplitude is proportional to the density jump46,47, which is certainly why coastal detection of ISW signatures has been poorly investigated in the literature. Giese et al.52 showed that coastal seiches in Puerto Rico harbor can be triggered by large amplitude ISWs shoaling at the shelf-break. With a simple two-layer model, Chapman and Giese53 evidenced a mechanism of baroclinic to barotropic energy transfer depending on the incident ISW amplitude, shelf depth and stratification. The maximum sea level elevation expected from this simple model is expressed as :

$$\begin{aligned} \eta _{max} = A_{isw} \frac{2\epsilon h_2}{d^{1/2}(1+\epsilon ^{1/2}h_2^{3/2}h_1^{-1/2})} \end{aligned}$$
(2)

where \(\epsilon = \frac{\rho _2-\rho _1}{\rho _1}\), with \(\rho _i\) the density in layer i, d the shelf depth, \(h_i\) the thickness of layer i and \(A_{isw}\) the amplitude of the incident ISW. RBGL23 showed that R-waves are of typical amplitude of 60 m at MO5. The Spanish shelf is about 50m deep in front of Tarifa, and the pycnocline depth is typically 100 m. The summer stratification is characterised by \(\rho _1 = 1026 \text {kg \, m}^{-3}\) and \(\rho _2 = 1029 \text {kg\, m}^{-3}\) while in winter the upper layer density decreases to \(\rho _1 = 1027 \text {kg\,m}^{-3}\). This leads to \(\eta _{max}^{winter} = 33\) cm and \(\eta _{max}^{summer} = 40\) cm, an order of magnitude higher the observed sea level oscillations (Fig. 2). It should be noted that there is still some uncertainty about the amplitude of the R-wave, which was measured in the SoG, quite a long way from the shoaling zone. In addition, this simple model does not account for frictional effects, which are important in shallow water dynamics and might explain the discrepancies between the model and our observations. Considering a typical decrease of \(\exp (-C_D\frac{L}{c_\phi })\) due to frictional effect during a typical time \(T=\frac{L}{c_\phi }\), \(\eta\) is reduced by one order of magnitude (factor 0.14) and falls in the range of our observations. The computation has been performed with \(C_D = 0.05\), \(c_\phi = 30\) m/s (typical surface gravity wave speed at 100m depth) and L=1km the distance between the shelf-break and the Spanish coast. In addition, this simple model reveals that R-wave surface signature should be higher in summer than in winter. Consequently, the seasonal cycle highlighted in this study, with fewer ISW events in summer/autumn at low tidal amplitude (Fig. 7b), would not be an artefact of detection due to the decrease of the ISW signature in sea level in summer.

The variability of ISWs generation in the SoG has previously been addressed at smaller time-scale from in situ observations23,25. The former authors exhibited the role of the subinertial flow in the triggering of ISWs at CS. The subinertial flow in the SoG is related to the fluctuation of the atmospheric pressure over the western Mediterranean basin. High pressure systems over the Mediterranean Sea leading to westward subinertial flow are favorable to the emission of ISWs at CS54,55. Vazquez et al.25 showed the influence of the meteorological forcing in the emission of ISWs. From past observations, they evidenced inhibition of ISWs generation when atmospheric conditions favors subinertial barotropic inflow i.e. low pressure over western Mediterranean Sea54.

We assess the possible contribution of the subinertial current in the seasonal cycle highlighted in this study. We use the local wind at Tarifa as a proxy of the sea level pressure over the Mediterranean Basin. Easterlies (eastward coming wind) are associated with anticyclonic circulation (high pressure) over the Mediterranean basin17,55,56. Therefore, strong easterlies correlate with enhanced westward subinertial barotropic current favorable to ISWs emission. Figure 9 compares the monthly distribution of the zonal wind according to whether or not an ISW event was detected in neap tides (panel a) and spring tides (panel b). It does not reveal a clear trend in neap tides which supports the hypothesis that the reduction of the ISW emission in summer is mainly due to a change in stratification.

Figure 9
figure 9

Monthly distribution of the zonal wind in the SoG in neap tide for ISW events (orange) and non-ISW events (blue).

Full size image

We highlighted the role of the stratification changes for the emission of ISWs in the SoG based on the occurrence of R-waves observed at Tarifa. However, it opens the question of the impact of such a double pycnocline on the reflection mechanism along the Moroccan shelf-break. From a two-dimensional vertical non-hydrostatic model RBGL23 evidenced that the I-waves reflect on the Moroccan shelf-break in a simple pycnocline configuration. Recently, Lamb57 showed that double pynocline systems lead to complex interactions of the ISWs. As far as we know, the shoaling and breaking of ISW in double pynocline environment have not been studied and could be a topic of interest especially for the R-wave formation in the SoG in summer stratification conditions.

These findings rest on the ability to infer I-waves emission from R-waves coastal detection. We evidence that R-waves is a relevant proxy for I-waves. However, we can not exclude some cases where I-waves do not reflect or when reflection does not sign in Tarifa sea level. This represents at most \(5\%\) of the cases, in comparison with Sentinel-1 SAR images. In addition, note that we tested different algorithms to detect ISW events in the sea level, based on the detection of high frequency peaks for example. They all yielded the same conclusions on the variability of the emission of ISWs at the different scales.

Conclusion

This research emphasizes the untapped potential of tide gauges in detecting ISW events and the opportunity they offer to access long, typically expensive-to-collect derived from ADCP/CTD, series of in-situ observations. It provides opportunities to better characterize and understand the complex variability of ISWs propagating towards the coast worldwide as many tide gauges at high frequency are now available58. In the case of Tarifa tide gauge, reflected R-waves sign because the tide gauge is located on the pathway of these waves, but any ISWs shoaling near a coastal tide gauge station might be observed using this approach with few adjustments to the detection threshold. For example the tide gauge of Messina (Sicily, Italy) has sampled the sea level at 1min frequency since 2017; it is perfectly located to observe large ISWs emitted in the Messina Strait33.

Thanks to this method, we provide the first multi-time-scale analysis of the variability in the emission of ISWs in the SoG. The analysis confirms that tide is the main driver in the triggering of such waves, which are emitted at almost every tidal cycle during spring tides.

We exhibit the role of the seasonal stratification in the ISWs dynamics (summer thermocline), still little investigated in the SoG. The seasonal cycle in the ISWs emission during neap tides strongly suggests that stratification variability is a key ingredient of the ISWs dynamics in the SoG. Therefore, quantifying the impact of seasonal stratification changes over physical processes involved in the SoG, will be necessary.