Introduction

Construction activities have increased all over India in response to the country’s recent rapid growth and development. The amount of waste generated from construction and demolition has increased significantly as a result; estimates place the annual production at about 3 billion metric tons1,2,3. Increased waste production is a contributing factor to a number of environmental issues, including depletion of finite natural resources, dust and carbon emissions, noise pollution, land damage, excessive energy use, and the creation of hazardous waste4,5. Because there is a constant stream of new research, the amount of information on managing this waste can become overwhelming. To address the growing problem of construction and demolition waste, India must, it is evident, move quickly to adopt improved waste management techniques and promote more sustainable practices6,7,8,9,10.

In the construction sector, mortar is widely used for its affordability, accessibility, and frequent application. However, the creation of paver blocks, illustrated in Fig. 6, significantly depends on natural materials such as sand and gravel, constituting around 60 to 75 percent of the overall volume11,12,13,14. Utilizing waste materials from various industries in the manufacturing of paver blocks presents a practical approach to enhancing sustainability within the construction sector. Utilizing recycled aggregates in mortar can lead to a decrease in the need for new raw materials, a reduction in waste generation, and a significant reduction in the environmental impact of construction practices15,16,17.

The potential use of construction and demolition waste (CDW) as a substitute for fine aggregate has been evaluated at different proportions, specifically 0%, 20%, 40% and 60%. Investigations indicate that as the CDW content rises, there is a significant enhancement in the properties of the material. The compressive strength of the mix shows an increase of up to 40% with CDW replacement, indicating more strength compared to conventional materials. Beyond this level, the strength will decline, but utilizing CDW up to 40% presents a sustainable and effective option in construction, minimizing the reliance on natural resources while effectively handling waste18,19,20,21,22.

Coconut fibers and other alternative natural fibers play an important role in enhancing building material properties and advancing sustainable engineering innovations. These fibers can significantly improve the performance of composites, making them useful across various construction applications. Coconut fibers strengthen the mechanical properties of building materials while promoting environmental sustainability. Their use contributes to more durable, eco-friendly building solutions that support the shift toward greener construction practices 20,23,24.

Coconut shell fibres have been used in this study to improve the mechanical strength of the paver block. Coconut shell fibres possess exceptional strength and resilience, resulting in an ideal choice for enhancing the strength of cementitious composites25,26. The study focuses on enhancing the tensile and compressive strengths of the mortar mix by incorporating these fibres. Additionally, it aims to enhance the overall durability and crack resistance of the mortar. This strategy highlights the benefits of using coconut shells as a sustainable and cost-effective option for creating building components that are both strong and environmentally friendly27,28.

On other hand, focused on enhancing mechanical properties by employing a range of machine learning methods, such as Response Surface Methodology (RSM), Support Vector Machine (SVM), Gradient Boosting (GB), Artificial Neural Networks (ANN), and Random Forest (RF)26,29,30. All these techniques were employed to simulate and forecast the mechanical properties of the materials being studied, capitalizing on their unique strengths in managing intricate datasets. The incorporation of these complex algorithms significantly improved the precision of the forecasts while also offering important insights into the connections among input variables and the resulting mechanical properties, resulting in improved decisions in material design and utilization31,32.

This mortar composition is innovative due to its incorporation of Construction and Demolition Waste (CDW) alongside coconut fibre, which contributes to improved early compressive strength. Evaluations conducted at 7 and 14 days show a significant enhancement in compressive strength at 14 days relative to 7 days, highlighting the positive impact of CDW in enhancing the matrix as time progresses. Furthermore, the addition of coconut fibre is essential in decreasing brittleness and avoiding failure, leading to a more ductile fracture behaviour when subjected to load. This investigation further incorporates advanced AI methodologies for forecasting compressive strength values, providing an accurate instrument to assess performance attributes.

This study found that substituting 60% of the fine aggregate with construction and demolition waste (CDW) and incorporating 1% coconut fiber led to notable enhancements in both the strength and sustainability of the paver blocks. When compared to conventional paver blocks, noticed for their superior strength and cost-effectiveness, the modified blocks provide similar performance and promote environmental sustainability through the use of recycled materials. This approach is innovative due to its effective incorporation of waste materials while maintaining the high quality of the paver blocks, presenting an attractive choice for sustainable construction practices.

Materials and methods

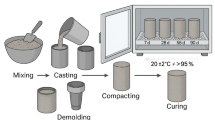
This Fig. 1 shows a methodical examination of the application of alternative aggregate materials. The procedure begins with the combination of cement, fine aggregate, and construction and demolition waste (CDW) to create an aggregate mixture. This formulation is designed with a 1:2 ratio, indicating one kg of cement combined with two kgs of fine aggregate. The mechanical properties of this mix are subsequently assessed through experimental work. After that, techniques from machine learning are employed, particularly response surface methodology, to improve the mechanical properties of the mix informed by experimental results and to forecast values.

Fig. 1
figure 1

Methodology for this investigation.

Full size image

An investigation is underway to investigate the potential of utilizing recycled construction and demolition waste (CDW) from landfills in Madanapalle, Andhra Pradesh, India, as an alternative to natural fine aggregates in construction projects. The CDW experiences ball milling to produce fine particles that conform to designated size ranges, passing through a 4.75 mm sieve while being retained on a 2.36 mm sieve. The study centres on tackling the depletion of natural resources caused by the construction sector’s rising need for aggregates, which further leads to elevated CO2 emissions. The study explores the use of CDW as a substitute for conventional fine aggregates, with the goal of developing building materials that are environmentally friendly and economically practical, while also minimizing landfill waste and promoting sustainable practices in construction. The chemical properties of CDW similarly to natural fine aggregates show in the Table 1.

Table 1 Properties of natural aggregate and construction and demolition waste.
Full size table

Cement plays a vital role in construction materials, helping to bind aggregates together in mortar. In Table 2 represent when combined with water, a chemical reaction occurs that results in the formation of a solid, long-lasting structure. This process helps to strengthen and preserve buildings and infrastructure over time.

Table 2 Properties of cement.
Full size table

Coconut fibres offer significant benefits because of to their lightweight composition and impressive strength-to-weight ratio, making them a perfect choice for enhancing composite materials. Show in the Table 3 and Fig. 2 these materials possess impressive compressive strength and durability, related to their high cellulose content. Additionally, their natural sustainability and eco-friendly attributes make them a preferred option for a wide range of uses. Furthermore, their ability to be used in various structural and non-structural composites is evidence to their flexibility in aspect ratio lengths. Table 4 demonstrate the mix design ratio for finding the compressive strength.

Table 3 Properties of coconut fibres.
Full size table
Fig. 2
figure 2

Equal Length of Coconut Fiber.

Full size image
Table 4 Mix ID and mixing percentages.
Full size table

The chosen proportions of CDW and coconut fibres in this study aim to optimise mechanical properties and promote sustainability. Proportions are determined to achieve a balance between compressive strength and durability, utilising industry standards and previous findings that highlight ideal ranges for recycled aggregates and natural fibres in mortar. This combination seeks to meet or exceed current requirements, forming a composite that utilises the reinforcing characteristics of waste materials while maintaining performance integrity.

Methods

Response surface methodology (RSM)

The model’s statistical significance was assessed using R2, adjusted R2, and predicted R2 values with the Response Surface Methodology (RSM) approach. The considered F-value provides insight into the impact of variables on the response33. Higher F-values indicate a stronger influence of the corresponding factor on the findings from the experiment. The statistical relevance of the model’s results can be assessed using the P-value. If the P-value is less than 0.05, it indicates that the model parameters are significant31. The RSM modelling was conducted using Design-Expert software, which allows for the input of databases of any size, removing the requirement for a pre-defined experimental approach. The flexibility of the Historical Data Design (HDD) approach is a major benefit34,35,36.

$$\text{Y}={\upbeta }_{0}+{\upbeta }_{1}\text{A}+{\upbeta }_{2}\text{B}+{\upbeta }_{12}\text{AB}+{\upbeta }_{11}{\text{A}}^{2}+{\upbeta }_{22}{\text{B}}^{2}$$
(1)

where;

  • Y: Response variable (dependent variable).

  • β0: Intercept term.

  • β1, β2Linear coefficients for variables AAA and BBB.

  • β12: Interaction coefficient between AAA and BBB.

  • β11, β22: Quadratic coefficients for AAA and BBB.

  • A, B: Independent variables or predictors.

Support vector machine (SVM)

After being developed by Vapnik and Chervonenkis in 1963, the SVM algorithm was first presented at Boser’s Computational Learning Theory (COLT) conference in 1992 by Guyon and Vapnik37. For many years, statisticians have relied on the SVM algorithm, a state-of-the-art regression technique in ML, to address complex data classification and regression issues. Many studies using the SVM method have also been completed with great success in the field of structural engineering38,39.

This optimization issue can be reformulated as the dual problem shown below, the solution to which can then be found.

$$f\left(x\right)=\omega .\varnothing \left(x\right)+b$$
(2)

where;

  • f(x): Predicted output of a function.

  • ω: Weight vector.

  • Φ: Feature transformation of xxx.

  • B: Bias term.

Subjected to

$$\left\{\begin{array}{c}{d}_{1}{-\omega .\varnothing \left(x\right)-b\le \delta }\\ {\omega .\varnothing \left(x\right)+b-d}_{1}\le \delta \end{array}\right.$$
(3)

where;

  • d1: Target value for the output.

  • δ: Tolerance level.

  • Constraints indicating that the difference between the model prediction and the target is within tolerance δ.

Where \(\delta\) is the max

$$c\frac{1}{n}\sum_{i=1}^{n}\left({\varepsilon }_{1}{+\varepsilon }_{i}^{*}\right)\frac{1}{2}{\Vert \omega \Vert }^{2}$$
(4)

where;

  • c: Regularization parameter.

  • n: Number of data points.

  • \({\varepsilon }_{1}{, \varepsilon }_{i}^{*}\): Slack variables representing errors.

  • ∥ω∥: Norm of the weight vector, related to regularization

Subjected to

$$\left\{ {\begin{array}{*{20}c} {d_{1} - \omega \emptyset \left( {x_{i} } \right) - b_{t} \le \varepsilon + \varepsilon_{1} } \\ {\omega \emptyset \left( {x_{i} } \right) + b_{t} d_{t} \le \varepsilon + \varepsilon_{i}^{*} } \\ {\varepsilon_{t} \varepsilon_{i}^{*} \ge 0} \\ \end{array} } \right.$$
(5)

where;

  • xi: Input data point.

  • Bi: Bias term at time t.

  • ε, ε1, εi∗: Error tolerances and slack variables, ensuring constraints on the prediction error.

    $$f\left(x,{a}_{i}+{a}_{i}^{*}\right)=\sum_{i=1}^{n}\left({a}_{i}-{a}_{i}^{*}\right)k\left(x-{x}_{i}\right)+b$$
    (6)

Where;

  • ai, ai∗: Lagrange multipliers.

  • k(x − xi): Kernel function, representing similarity between x and xi​.

    $$R\left({a}_{i}+{a}_{i}^{*}\right)=\sum_{i=1}^{n}{d}_{i}\left({a}_{i}-{a}_{i}^{*}\right)-\varepsilon \left({a}_{t}-{a}_{t}^{*}\right)-\frac{1}{2} \sum_{t=1}^{n}\sum_{j=1}^{n}\left({a}_{t}{-a}_{t}^{*}\right) \left({a}_{j}-{a}_{j}^{*}\right) k\left(x,{x}_{i}\right)$$
    (7)

Where;

  • R: Objective function to be maximized or minimized.

  • di: Target values.

  • Represents optimization over Lagrange multipliers with kernel evaluations.

Subjected to

$$\sum_{i=1}^{n}\left({a}_{t}{-a}_{t}^{*}\right)={0}_{0\le {a}_{t}^{*}\le c i=\text{1,2},3,\dots ..n}^{0\le {a}_{t}\le c i=\text{1,2},3,\dots \dots n}$$
(8)

where;

  • c: Regularization parameter.

  • at, at∗: Constraints on Lagrange multipliers, ensuring bounded values.

$$k\left({x}_{i}*{x}_{j}\right)=\text{exp}(-\delta {\left({x}_{i},{x}_{j}\right)}^{2 })$$
(9)

  • The solutions are (-αi + αi ∗) and b, where K (xi, x) is a kernel function.

Gradient boosting (GB)

Gradient boosting is an advanced machine learning method that uses pseudo-residuals instead of regular residuals and boosts inside a functional space. Using a collection of weak models—usually straightforward decision trees—this technique creates a prediction model with little assumptions about the data40,41. When decision trees are used as weak learners, a model known as gradient-boosted trees is produced, which is frequently more effective than random forests. Gradient-boosted trees are constructed step-by-step, just like other boosting techniques. What sets them apart, though, is that they allow for the optimization of any differentiable loss function, providing more versatility in terms of model improvement42,43.

This Fig. 3 shows the procedure involved in gradient boosting within the realm of machine learning. It presents various iterations, with different input trees examining unique datasets. Every tree produces forecasts, which are then combined using a voting process to create a final model that estimates mechanical properties. This collective method improves prediction precision by leveraging the advantages of each individual tree.

Fig. 3
figure 3

Topographical structure of GB.

Full size image

The standard approach to calculating the regularized loose objective function f(L) for L is as follows:

$$f\left( L \right) = \mathop \sum \limits_{i = 1}^{n} l \left( {y^{\left( i \right)} ,\hat{y}_{L}^{\left( i \right)} } \right)\mathop \sum \limits_{j = 1}^{L} \Omega \left( {f_{j} } \right)$$
(10)

where;

  • \(f\left(L\right)\): Objective function in boosting.

  • \(l ({y}^{(i)} ,{\widehat{y}}_{L}^{(i)})\): Loss function comparing true and predicted values.

  • w(fj): Weight function for model fj.

where n denotes the number of samples, \(l()\) the function for loss \({y}^{\left(i\right)}\) represents the actual value of sample I, while \({\widehat{y}}_{L}^{\left(i\right)}\) denotes the predicted value of sample I at iteration L. The term \({f}_{j}\) refers to the tree model utilized in the ith prediction, and Ὡ serves as the formalization indication, which can be determined using the formula provided below:

$$\Omega \left( f \right) = \gamma N + \frac{1}{2} \lambda \mathop \sum \limits_{J = 1}^{N} w_{j}^{2}$$
(11)

where;

  • w(f): Regularization term for weights.

  • γ, λ: Regularization parameters.

  • Ensures penalty for model complexity through weight regularization.

In this context, N represents the number of leaves in the nodes, while γ and ʎ serve as constants used for overseeing the regularization process. Additionally, \({w}_{j}^{2}\) denotes the score normalization within each leaf node.

The ideal quantity of trees in the XGBoost model \({f}_{L}\left({x}^{\left(i\right)}\right)\) can be determined through the subsequent regression formula.

$$f\left( L \right) = \mathop \sum \limits_{i = 1}^{n} l\left( {y^{\left( i \right)} ,\hat{y}_{L - 1}^{\left( i \right)} + f_{L} \left( {x^{\left( i \right)} } \right)} \right) + \Omega \left( {f_{L} } \right)\mathop \sum \limits_{j = 1}^{L - 1} \Omega \left( {f_{j} } \right)$$
(12)

where;

  • f(L): Boosted function.

  • \({f}_{L}({x}^{(i)})\): New model added to the ensemble.

Artificial neural networks (ANN)

Artificial neural networks (ANNs), also known as neural networks, are well-liked ML techniques for performing data analysis through a hierarchical structure of nodes that make judgments. The ANN system is a layered architecture with input, output, and hidden layers that work together to process data and produce actionable results in the output layer general ANN structure show in Fig. 4. A neuron is a process that a mathematical equation can represent in terms of the weighted sum of its inputs.

Fig. 4
figure 4

(a) General ANN structure (b) Typical artificial neuron.

Full size image

Random forest (RF)

The decision tree is the fundamental building block of random forest (RF), an ensemble learning technique. The decision trees’ foundational principles information, and information gain form the basis for selecting features in the order of their use for classification. This study used Bootstrap sampling, which entails selecting a subset of the population at random to train with repeated replacement before either voting or averaging the findings. For the training set, a new Bootstrap sample is utilised for every tree construction44,45. Consequently, in the case of the k-th tree in particular, we refer to the non-participants in the production of this tree as the "out-of-bag samples" since they make up around one-third of the training examples. The selection of RF features is based on the computed out-of-bag error rate, which is also a parameter for RF establishment. Also, by randomly interfering with all features in the out-of-bag data sample with noise and then determining the out-of-bag data error of each decision tree, we can get the relevance of features46,47,48. The field of civil engineering has made extensive use of this technique for handling classification and regression problems. As seen in Fig. 5, the framework for the FDM parameter models based on random forests is displayed.

Fig. 5
figure 5

Topographical structure of Random Forest.

Full size image

Results and discussions

Compressive strength (CS)

The increase of compressive strength in different mortar mixes (M1 to M36) assessed at 7 and 14 days. Show in the Fig. 10, The study noticeable development indicates a rise in strength over time, which matches expectations as the curing process progresses. For example, Mix M1 demonstrates a rise from 27 MPa at 7 days to 28.96 MPa at 14 days, indicating the continuous hydration of cement. Mixes like M2 and M5 show modest increases, with M2 rising from 25 MPa to 26.011 MPa and M5 increasing from 26.75 MPa to 26.89 MPa. These minor adjustments may suggest reduced hydration rates or differences in the mixture’s substance that influence the pace of strength progression. Conversely, mixes such as M31 and M33 indicate significant increases in strength, with M31 improving from 35.17 MPa to 38.55 MPa and M33 advancing from 38.55 MPa to 39.12 MPa, indicating that these mixes may be more suitable for high-strength applications.

As the mix IDs advance, the data indicates that specific mixes with elevated initial strength, like M32 to M36, persist in achieving considerable strength gains over time. The M32 value rises from 36.977 MPa to 38.9 MPa, whereas M34 shifts from 37.52 MPa to 38.92 MPa. This pattern indicates that these mixes are intended for extended durability and may excel in structural applications that demand greater load-bearing capacity. Notably, Mix M33 reaches its peak strength at 7 days with a measurement of 38.55 MPa, which then rises to 39.12 MPa after 14 days, emphasising its swift early strength development (Fig. 6).

Fig. 6
figure 6

C&D Waste as final product of paver block.

Full size image

The usual characteristics of cement-based materials, showing that strength improves over time because of ongoing hydration. The differences in strength development among various mixes highlight the impact of mix proportions, encompassing elements such as cement content, water-cement ratio, and the inclusion of supplementary materials like fly ash or fibres. This information can be crucial for refining the mix designs tailored to the unique needs of various construction projects, ensuring a balance between initial strength growth and enduring durability. In Figs. 7, 8 and 9 are representing a material inside the paver block visualization.

Fig. 7
figure 7

Header Failure of The Paver Block by Using of Compressive Machine.

Full size image
Fig. 8
figure 8

Pores of the failed component’s structure.

Full size image
Fig. 9
figure 9

Arranged of the materials in the paver blocks.

Full size image

A comparison with current literature is included to highlight the uniqueness of the findings. This study separates its products by uniquely integrating CDW with coconut fibres to improve early compressive strength. Testing conducted at 7 and 14 days indicates important enhancements. This method showcases the practicality of incorporating sustainable materials while uncovering particular interaction effects that enhance existing understanding of improving mortar characteristics, offering an innovative solution for environmentally conscious construction materials (Fig. 10).

Fig. 10
figure 10

Compressive Strength Each Mix Design Ratio of The Paver Blocks And Compared 7Days And 28Days.

Full size image

The 28-day strength is generally regarded as the benchmark for standard paver blocks, ensuring that the cement has fully hydrated. In certain instances, particularly with innovative or altered paver blocks, the development of strength might happen more rapidly owing to the inclusion of alternatives or additives. Consequently, the strengths at 7 and 14 days has been tested to determine the performance at an early stage, serving as a more dependable measure for particular applications or materials that set quickly. This method is frequently applied when substances demonstrate initial strength development.

Optimization using RSM

Table 5 shows an overview of the design factors associated with the RSM approach. A total of 36 distinct experiments have been conducted to ascertain the type of design, utilizing standard evaluation criteria. The quadratic model has been utilized for the design process.

Table 5 Design of RSM.
Full size table

Table 6 represented the F-value assesses how well the model accounts for variance in relation to residuals, where greater values suggest a higher level of significance. The overall model demonstrates an F-value of 198.33, indicating a substantial explanation of the variance. The p-value evaluates the probability of the results happening randomly; lower p-values suggest higher statistical significance. Elements such as CDW (%) and coconut fibres exhibit notably low p-values (0.0058 and 0.0007, respectively), indicating their substantial influence. In contrast, the interaction between these elements (AB) and other components like A2 and B2 display differing levels of significance as reflected in their p-values.

$$\begin{aligned} {\text{Compressive}}\,{\text{Strength}} & = 25.79311 + 0.041338{\text{CDW}}\,(\% ) - 5.26128\,{\text{Coconut}}\,{\text{Fibres}}\,(\% ) \, \\ & \quad + 0.014338{\text{CDW}}\,(\% )*{\text{Coconut}}\,{\text{Fibres}}\,(\% ) - 0.000403{\text{CDW}}\,(\% )^{2} \, \\ & \quad + \, 14.92798\,{\text{Coconut}}\,{\text{Fibres}}\,(\% )^{2} \, \\ \end{aligned}$$
(13)
Table 6 Results from ANOVA.
Full size table

The statistical data provided emphasizes the essential metrics utilized to evaluate the effectiveness and dependability of a model. The standard deviation (Std. Dev.) is 0.7396, suggesting a modest level of variability within the dataset. A mean value of 29.59 indicates a consistent central tendency within the data. The coefficient of variation (C.V. %) of 2.50% further substantiates this, indicating a minor dispersion in relation to the mean. The model exhibits a R2 value of 0.9706 and an adjusted R2 of 0.9657, indicating a robust alignment between the predicted and actual values, with the adjusted R2 reflecting the number of predictors involved. The anticipated R2 of 0.9510 reflects strong predictability, and an Adeq Precision value of 39.7883 indicates a satisfactory signal-to-noise ratio, implying that the model is suitable for optimization applications.

The Fig. 11 presents the analysis using Response Surface Methodology (RSM), featuring both two-dimensional and three-dimensional surface plots. These plots demonstrate how variables interact and influence the outcome. The visual depiction enhances comprehension of how various elements affect the result.

Fig. 11
figure 11

RSM analysis surface of the plots (A) 7Days and (B) 14Days.

Full size image

The results obtained from experiments and estimations for the CS are displayed in Table 7. The models of forecast outcomes aligned well with the outcomes derived from the experiments. Figure 5 presents a graphical representation of data points that demonstrates the correlation among the predictions and the actual measurements. The precision of the findings from the assessment in estimating the compressive strength has been emphasized once more.

Table 7 Multiple machine learning response.
Full size table

Machine learning

The Fig. 12 below shows the test results and scores from this study, featuring machine learning models including SVM, Gradient Boosting (GB), Random Forest (RF), Neural Networks (NN), along with a scatter plot shown in pink. The anticipated data is marked in blue, offering a visual contrast between the machine learning forecasts and the real values. This figure was created with the orange tool, a popular choice for visualizing and analyzing data in machine learning processes.

Fig. 12
figure 12

Process of Machine Learning.

Full size image

The criteria for selecting AI models, such as RSM, SVM, GB, ANN, and RF, are dictated by each model’s ability to manage complicated, non-linear relationships among variables when forecasting mortar properties. RSM was selected for its ability to enhance material proportions, whereas SVM and RF are recognised for their precision and reliability in complex datasets. GB and ANN have been identified for their ability to capture complex patterns and flexibly learn from data. Every model function based on particular assumptions, including data distribution and independence, and was completely evaluated to reduce partiality and improve the trustworthiness of the predictive results.

This study predicted material mechanical properties using AI machine learning methods SVM, RF, and GB. Performance of each model is shown in Fig. 13 the frequency distribution of predicted mechanical properties in Fig. 13. The SVM model predicted a gradual increase in frequency with a mean of 28.88 and a standard deviation of 2.53. However, the Random Forest model had a higher mean of 29.74 and a standard deviation of 3.78, indicating greater prediction variation. Gradient Boosting had the most diverse predictions with a mean of 29.84 and a standard deviation of 4.00. While all models accurately predict mechanical properties, Gradient Boosting and Random Forest outperform SVM in accuracy and variability, revealing their potential for mechanical behaviour prediction.

Fig. 13
figure 13

Frequence of the mechanical properties…… (A) SVM, (B) RF, (C) GB, (D) ANN.

Full size image

The graph collection Fig. 14 shows the relationship between (A) SVM, RF, and GB machine learning models and NN predictions, (B) RF & NN, (C) Frequency and Coconut Fiber (%), (D) NN and GB, (E) NN & NN, (F) NN & SVM (G) RF &Coconut Fiber (%), (H) SVM & GB, (I) GB & Coconut Fiber (%), (J) RF & GB, as well as how coconut fibres affect mechanical properties, particularly strength. Each graph shows a positive correlation, as shown by high R-squared (r) values, indicating that coconut fibre percentage increases strength. The strong alignment of data points with the regression line across models shows that machine learning can predict construction material performance, especially with coconut fibres to improve strength.

Fig. 14
figure 14figure 14

The hyperlink among multiple machine learning models.

Full size image

The matrix plot Fig. 15 demonstrates the connections between compressive strength (CS) and the ratios of fine aggregates (F.A), construction and demolition waste (CDW), and coconut fibers in concrete mixtures. The percentages of F.A and CDW exhibit stable trends with slight variations in CS, while the rise in coconut fibers is associated with an increase in compressive strength. The trend lines, likely obtained through advanced analytical techniques, suggest that coconut fibers contribute more substantially to improving the mechanical properties of concrete than the other factors considered.

Fig. 15
figure 15

Matrix plots.

Full size image

This heat map in Fig. 16 shows the relationship between the percentage of construction and demolition waste (CDW) and coconut fibers, highlighting their joint impact on the mean compressive strength (CS) of concrete. The colour gradient, transitioning from blue (indicating lower compressive strength) to red (indicating higher compressive strength), demonstrates that increased amounts of coconut fibers, particularly at 1%, markedly improve compressive strength irrespective of CDW content. Conversely, mixtures that contain smaller percentages of coconut fiber generally exhibit reduced compressive strength, regardless of the amounts of CDW present. This examination, possibly informed by advanced computational techniques, underscores the beneficial effects of coconut fibers on mechanical characteristics, while CDW appears to exert a comparatively minor influence.

Fig. 16
figure 16

Heat map.

Full size image

The heat map has been updated to feature correlation values shown within each cell, improving the clarity of the findings. Currently, every cell in the heat map illustrates the average compressive strength (CS) value linked to particular percentages of CDW and coconut fibres, facilitating a quick evaluation of how these factors influence CS. This adjustment enhances clarity and precision in understanding the interaction effects and alignment.

CDW improves paver block strength and as a fine aggregate substitute. CDW reduces landfill waste and improves compressive strength and durability when used in the right proportions. Particle size and mineral composition can optimise its performance, making it a useful construction material alternative.

The matrix plot in Fig. 17 shows the correlation between CS and the proportions of coconut fibers, CDW, and fine aggregates (F.A) in concrete mixtures. The initial plot, showcasing the relationship between CS and coconut fibers, reveals a positive correlation, demonstrating that as the percentage of coconut fibers increases, the compressive strength also rises. The plots for CDW and F.A percentages exhibit a more dispersed distribution, lacking a distinct trend of enhancement in compressive strength. This indicates that although coconut fibers greatly improve the mechanical characteristics of paver block, the effects of CDW and F.A on compressive strength are less consistent. This examination could contribute to a machine learning strategy aimed at comprehending the impact of these materials on paver block performance.

Fig. 17
figure 17

Matrix plot.

Full size image

The research applied AI to forecast outcomes, accompanied by an examination of the anticipated and observed results. The anticipated values typically surpassed the actual results, with Support Vector Machine (SVM) models producing lower estimates, whereas Gradient Boosting (GB) models showcased enhanced accuracy in predictions relative to other machine learning methods. In the Fig. 18 assessment of the mechanical characteristics across various mix designs, it was noted that the strength exhibited an increase from M5 to M9, a decline from M10 to M13, stability from M14 to M16, a resurgence from M17 to M22, and a subsequent decrease between M22 and M23. There was an enhancement in strength observed from M24 to M28, followed by a steady rise from M29 to M36. The incorporation of AI has notably streamlined processes and improved results within the construction industry. When individuals possess a strong understanding of machine learning, it can significantly aid engineers in enhancing material properties and design.

Fig. 18
figure 18

Actual Value VS Predicted Value by using SVM, RF, GB and NN.

Full size image

Performance evaluation

The reliability of the study is strengthened by meticulous methodological selections and strong model validation approaches. The choice of model was driven by the necessity to effectively forecast intricate connections in mortar characteristics, employing cross-validation to mitigate overfitting and enhance generalisability. Metrics like Mean Squared Error (MSE) and R-squared (R2) were employed to evaluate predictive accuracy, confirming the reliability of each model. Furthermore, the validation using experimental data affirmed the alignment of AI predictions with real-world results, showcasing the efficacy of the selected models in reflecting the impact of CDW and coconut fibres on mortar performance.

The accuracy and quantity of errors made by the system have been assessed using performance metrics.

Sum of Squares Error stands for SSE.

$$SSE=\sum_{i=1}^{N}{\left({a}_{PREDICT}-\overline{a }\right)}^{2}$$

N is number of data a PREDICT is actual value \(\overline{a }\) is predicted value.

Equation provides the formula, which is MAE.

$$MAE=\left(\frac{1}{N}\right)*\left(\sum_{i=1}^{N}\left({a}_{PREDICT}{-a}_{PREDICT}\right)\right)$$

The predicted value for the jth neuron is denoted as a PREDICT, the experiment yielded the value a TARGET, and N is the total number of trials.

MSE mean squared error

$$MSE=\left(\frac{1}{N}\right)\sum_{i=1}^{N}{\left({a}_{PREDICT}-{\widehat{a}}_{PREDICT}\right)}^{2}$$

N is number of data a PREDICT is actual value \(\widehat{a}\) PREDICT is predicted value.

A data point’s (targeted) average deviation from the model’s (expected) forecast value is known as RMSE. The effectiveness of the approach is improved when the RMSE Equation is lower.

$$RMSE=\sqrt{\left(\frac{1}{N}\right)*\left(\sum_{i=1}^{N}{\left({a}_{PREDICT}{-a}_{PREDICT}\right)}^{2}\right)}$$

R2 is the initial parameter; it is the complete fraction of a variation of a parameter.

$${R}^{2}=1-\left(\frac{\sum_{i=1}^{N}{\left({a}_{PREDICT}-{a}_{TARGET}\right)}^{2}}{{\sum }_{i=1}^{N}{\left({a}_{PREDICT}\right)}^{2}}\right)$$

The R2 (R-squared) values Table 8 shown in the table are generally calculated for the testing dataset, reflecting the model’s capacity to extend its applicability to data that has not been encountered before. The coefficient of determination indicates the degree to which the predictions generated by the model align with the real results observed in the test set. When values are obtained from the training dataset, it reflects the model’s alignment with the data it has been exposed to. However, for the purpose of evaluation, results from the testing dataset are more pertinent for gauging the model’s effectiveness on novel, unobserved data.

Table 8 Several algorithms evaluated MSE, RMSE, MAE and R2.
Full size table

Conclusion

Several types of AI machine learning applications, including prediction-making, are regularly employed. The aim of this research is to estimate the mechanical strength of paver blocks by examining different machine learning techniques. This study investigates the effects on the strength and functionality of these blocks when fine aggregate is replaced with CDW, which is used as an additive in coconut fiber. Here is a short summary of the results.

  • The highest compressive strength was achieved with a mix comprising 40% fine aggregate, 60% CDW, and an optimal addition of 1% coconut fiber, utilizing a verified machine learning approach.

  • RSM examinations indicated that the R2 value for the compressive strength was 0.9706. The simulations estimate the compressive strength at a rate of 39.7883% based on this value.

  • Random Forest demonstrated the greatest prediction accuracy with a R2 of 0.935, trailed by Gradient Boosting at 0.905, Neural Network at 0.768, and SVM at 0.692. The effectiveness of each model is evident in its capacity to forecast mechanical properties, with ensemble techniques (RF and GB) demonstrating superior performance compared to others.

  • The conclusions of the studies assessing the mechanical strength have been thoroughly examined through RSM analysis techniques, providing accurate calculation of impacts.

Moreover, the program could significantly improve the combinations that are mainly employed in civil engineering projects. In engineering claims, the documented models can provide a structured approach to minimize the time invested in multiple tests. In the future, specialists can investigate the different frameworks of SVM, decision tree (DT), Gaussian process regression, and extreme gradient boosting tree (XGBoost) algorithms for a broader spectrum of civil engineering applications.