Precision measurement for effective pollution mitigation by evaluating air quality monitoring systems in linguistic Pythagorean fuzzy dombi environment

Abstract

Air quality is a major concern for human health, with pollutants linked to respiratory problems and chronic illnesses. Air quality monitoring systems are essential for measuring and tracking pollutants in indoor and outdoor environments. In the various disciplines of fuzzy environments, the aggregation operators are indispensable components of the decision-making process and possess a significant capacity to manage unpredictable and ambiguous data. This study utilizes the linguistic Pythagorean fuzzy set to address the aforementioned environmental scenarios, which improve comprehension of air quality through the application of AOs. This work introduces two new aggregation operators: the linguistic Pythagorean fuzzy Dombi ordered weighted averaging (LPFDOWA) and the language Pythagorean fuzzy Dombi ordered weighted geometric (LPFDOWG), and examines their structural properties. Furthermore, we develop a novel scoring function for multiple attribute decision-making (MADM) issues within the context of linguistic Pythagorean fuzzy knowledge. We provide a systematic mathematical procedure to address MADM issues within the context of the linguistic Pythagorean fuzzy Dombi framework. Furthermore, we effectively employ these approaches to address the MADM issue of selecting an efficient Air quality monitoring systems for air pollution monitoring. Additionally, we present a thorough comparative analysis to demonstrate the effectiveness of the proposed methodology relative to conventional techniques.

Introduction

Background

Extensive research and a systematic process of decision-making have shown that effective MADM involves assessing and choosing the most optimal choice from a diverse collection of possibilities while considering a broad range of characteristics. Before reaching the end result, decision-makers carefully analyze many conflicting factors in order to resolve the real-world scenario. The approach includes weighting qualities depending on their importance, structuring evaluations with a decision matrix, and combining attribute scores using appropriate techniques. The optimal solution is then identified using decision rules.

Decision-makers express the characteristics according to different types of assessments (crisp numbers, intervals, and fuzzy numbers), respectively. Decision-makers sometimes struggle to effectively articulate their findings using exact numerical values due to the growing ambiguity of data and cognitive limitations. In acknowledging the limitations associated with simulating the complexities of real-world decision-making scenarios using only exact numerical data. In his landmark work, Zadeh¹ first proposed the idea of fuzzy sets. Kahne² presented a decision-making procedure that takes into account the properties in terms of multiple features that have different degrees of relevance. Jain³ invented a decision-making technique in which he found an inferior alternative instead of an optimal alternative. Dubois and Prade⁴ studied some properties concerning a class of fuzzy variables in 1978. Yager⁵ introduced several aggregation operators (AOs) that have their basis in fuzzy sets.

Taking into consideration Zadeh’s work, Atanassov⁶ developed the idea of intuitionistic fuzzy sets (IFS) to overcome the lack of an explicit specification of reluctance in fuzzy sets. This extension entails assigning the elements of a membership degree (MD) and a non-membership degree (NMD) to meet the specified conditions associated with hesitancy. Vague set theory is employed in the development of a MADM technique in⁷. Szmidt and Kacprzyk⁸ established IFS theory that is used to address the difficulties encountered in group decision-making. Li⁹ presented MADM models and techniques utilizing IFS. Xu and Yager¹⁰ created a few geometric AOs on IFS. Xu¹¹ influenced aggregation processes in the IFS environment. A solution to the MADM problem was proposed by Zhao et al.¹² using generalized aggregation operations on IFS in 2010. In the field of group decision-making, Wang and Xu¹³ explored the concept of induced generalized AOs for IFS. Garg^14,15 developed advanced interactive averaging and geometric aggregation methods that employ Einstein t-norm procedures. In¹⁶, an evaluation of solar panels was conducted using a MADM technique based on IF Aczel Alsina Heronian mean operators. Furthermore, academics have prioritized the FS and IFS examinations. These investigations can address uncertainty that is quantitatively defined. However, in practical scenarios, several decision-making problems frequently necessitate the qualitative presentation of ambiguity and imprecise data. When assessing an individual, decision-makers often favor using phrases such as “very low, low, medium, high, very high” to define their intellectual capacity. In this setting, the decision-makers can express their viewpoint on the matter using linguistic terms. Zhang¹⁷ introduced the concept of a LIFS, which was derived from the concept of an IFS. The LIFS utilizes intuitionistic fuzzy numbers (IFNs) to accurately represent the levels of MD and NMD of a linguistic variable. In 2016, Ju et al.¹⁸ introduced a MADM technique that utilizes linguistic intuitionistic Maclaurin symmetric mean AOs. The concept of the linguistic intuitionistic fuzzy-weighted Bonferroni mean operators was developed by Liu et al.¹⁹. Liu²⁰ introduced the linguistic interval intuitionistic geometric aggregation (LIGA) operator. Furthermore, Liu and Wang²¹ developed enhanced linguistic intuitionistic fuzzy AOs and utilized them for solving MADM problems.

The implementation of IFS theory has proven to be successful in various decision-making processes. Nevertheless, under certain circumstances, it is conceivable that the sum of the membership and non-membership degrees exceeds one. Yager²² thoroughly analyzed this shortcoming and proposed a method to expand the notion of IFSs, known as Pythagorean fuzzy sets (PFSs). The concept of PFS fulfils the specified criterion $\:{\left({\mu\:}_{P}\left(x\right)\right)}^{2}+{\left({\vartheta\:}_{P}\left(x\right)\right)}^{2}\le\:1$. The analysis of IFS and PFS concludes that PFS is more efficient than IFS in handling uncertain information in MADM challenges. Research on the theory and practice of PFS has advanced in three main areas since its proposal: the establishment of fundamental theories such as operational laws, the use of comparative analysis, and the utilization of enlarged MADM techniques for PFS. Yager and Abbasov²³ examined the correlation between PFS and complex numbers in their analysis. Zhang and Xu²⁴ extended the utilization of the TOPSIS technique to the PF environment, whereas Yager²⁵ proposed a Pythagorean membership grade in the MADM problem. Garg^26,27 introduced generalized averaging and geometric aggregation techniques for Pythagorean fuzzy numbers (PFNs), including Einstein t-norm procedures. Ma and Xu²⁸ presented symmetrical PF-weighted averaging and geometric operators for implementation in MADM.

If a decision-maker has a preference for an item represented by a linguistic intuitionistic fuzzy number $\:\left({u}_{5},\:{u}_{3}\right)$, where the linguistic term is represented by $\:{u}_{t}$ with $\:t\in\:\left[\text{0,6}\right]$, then the LIFS method is unable to resolve this preference for the linguistic variable as $\:5+3\nleqq\:6$. In 2018, Garg²⁹ examined the concept of a linguistic Pythagorean fuzzy set, which is characterized by MD and NMD that squared sum less than or equal to the cardinality of the set. Peng and Yang³⁰ influenced the application of Pythagorean fuzzy linguistic terms (PFLT) in MAGDM scenarios, taking inspiration from linguistic variables and PFSs. Lin. et al.³¹ established the LPF interaction Boneferroni mean AO and utilized it for MAGDM problems. Du et al.³² proposed a new MADM technique that employs linguistic interval-valued Pythagorean fuzzy information. Ahmad³³ introduced innovative entropy measurements within the framework of q-rung orthopair fuzzy soft sets. Khan et al.³⁴ presented a MADM method utilizing T-spherical fuzzy AOs with unknown attribute weight information.

In 1982, Dombi³⁵ suggested the integration of novel operators, referred to as Dombi t-norm and Dombi t-conorm. These operators exhibit a desirable degree of variability when assessing the influence of parameters. Researchers can effectively handle MADM difficulties by utilizing Dombi AOs. In addition, in 2021, Seikh and Mandal³⁶ created the IFS Dombi AOs. Liu et al.³⁷ applied the Dombi-Bonferroni technique to IFS. In 2019, Akram et al.³⁸ presented the PF Dombi AOs. Later on, q-rung orthopair fuzzy Dombi³⁹, bipolar fuzzy Dombi⁴⁰, and picture fuzzy Dombi⁴¹ AOs were developed. In 2020, Ashraf et al.⁴² explored the incorporation of spherical fuzzy Dombi AOs. In 2020, Liu et al.⁴³ introduced the application of interval-valued fuzzy Dombi AOs to evaluate information security risk with greater precision. Jaleel⁴⁴ developed the WAPSA technique employed in an agricultural robotic system utilizing Dombi AOs in the purview of bipolar complex fuzzy soft information. In 2023, Masmali et al.⁴⁵ proposed an optimization strategy that employs a complex Intuitionistic Fuzzy Dombi environment to determine the most effective method for purifying water. Qiyas et al.⁴⁶ examined the linguistic picture fuzzy Dombi AOs and their application in the MADM problem. Moreover, Seikh and Mandal^47,48 established the Dombi AOs in the context of interval-valued Fermateen and interval-valued spherical fuzzy environments. Karaaslan and Husseinawi⁴⁹ examined the application of hesitant T-spherical fuzzy Dombi AOs and demonstrated their practical use.

Research gap, motivations, and objectives of the current study

PFS has an advantage over IFS because it does not have a constraint on the sum of membership and non-membership degrees. However, PFS does not have the capacity to organically include human perception. The linguistic Pythagorean fuzzy set (LPFS) overcomes this constraint by merging the advantages of PFS with linguistic expressions. LPFS enables professionals to articulate their assessments by utilizing phrases such as “low,” “medium,” or “high” when combined with the associated numerical levels. This facilitates the connection between numerical representation and human comprehension, hence simplifying the management of the ambiguity and subjectivity that are inherent in decision-making processes. LPFS offers a more authentic and comprehensible method of expressing ambiguous data, especially when working with human specialists. Furthermore, AOs are essential for simplifying large datasets and merging information into a single meaningful value, enabling deeper analysis of trends, patterns, and key statistics. Dombi AOs are particularly effective in decision-making, handling implicit information with adjustable parameters to suit varying risk preferences. Their versatility makes them valuable for many fuzzy decision-making scenarios. However, in PF contexts, they can be limiting, as they rely on a specific dimension and may oversimplify complex situations with multiple variables of varying importance. Additionally, the mathematical complexity of the Dombi parameter can hinder accessibility for non-experts. To address these limitations, LPF Dombi AOs have been introduced as a more adaptable alternative. The combination of linguistic expressions with the Dombi parameter allows experts to express their preferences in natural language sentences. This improves comprehension and simplifies the integration of subjective and qualitative aspects that are frequently involved in decision-making. At their fundamental level, they act as a link between the mathematical framework of Dombi operators and the linguistic proficiency of human specialists. Information aggregation within the LPF environment appears more reliable and user-friendly as a result of this connection. The above discussion motivates us to introduce two innovative Dombi AOs in the framework of LPF settings in this article.

Air is a crucial natural resource on our world. However, air quality has substantially declined in recent years, particularly in urban areas of developing countries. Consequently, individuals are seeking improved methods to assess air quality in their surroundings to implement suitable measures, such as using masks or being indoors. To mitigate air pollution, an air quality monitoring system is essential. Air quality monitoring entails the assessment of various pollutants in the atmosphere. This is a crucial resource for enhancing air quality, safeguarding public health, and maintaining regulatory compliance. It can also be utilized to identify sources of pollution, monitor climate change, or facilitate research and development. The novelty of this article is to present a solution to the decision-making problem of selecting an efficient Air quality monitoring systems (AQMS) for monitoring air pollution through the application of newly defined Dombi AOs in the context of LPF settings.

The primary contributions of this study are briefly delineated in the subsequent five points:

• 1. An innovative score function is introduced for MADM scenarios in LPF settings. This function provides an effective ranking system for selecting alternatives.

• 2. Two novel Dombi AOs are delineated within the framework of LPF knowledge, and their fundamental structural characteristics are examined.

• 3. A novel approach that effectively resolves MADM difficulties is devised by the application of recently proposed LPF Dombi AOs.

• 4. The effectiveness of the presented methodologies is demonstrated by offering a solution to the MADM challenge of selecting an efficient AQMS for monitoring air pollution.

• 5. The efficacy and applicability of the proposed LPF Dombi AOs is assessed through a comprehensive comparative study with existing techniques. This comparative analysis offers valuable insights into the effectiveness of the proposed approaches, highlighting their suitability for practical applications.

This research article has been organized as follows: Sect. 2 offers fundamental concepts and definitions aimed at improving understanding of the main findings. Section 3 introduces the formulation of the novel score function to address MADM challenges within the context of the LPF Dombi environment. Section 4 defines two Dombi OWA operators to aggregate LPFNs and analyzes their structural properties. Section 5 contains a strategy based on recently defined AOs for solving MADM problems. It also shows the relevance of these operators by solving a MADM problem for selecting an efficient AQMS for monitoring air pollution and presents a comparative analysis of proposed strategies with existing strategies. Section 6 concludes the study and outlines recommendations for future research.

Preliminaries

This section presents essential concepts and definitions to improve understanding of the major results.

Definition 1

³⁸. A PFS is defined on a universe as:

$$\:P=\left\{\left(x,{\mu\:}_{P}\left(x\right),{\vartheta\:}_{P}\left(x\right)\right)|\:x\in\:X\right\},$$

where $\:{\mu\:}_{P}:\:X\to\:\left[\text{0,1}\right]\:$and $\:{\vartheta\:}_{P}:\:X\to\:\left[\text{0,1}\right]\:$are functions, representing the MD and NMD of each element $\:x\in\:X$ in the set $\:P$, satisfying the restricted condition $\:{\left({\mu\:}_{P}\left(x\right)\right)}^{2}+{\left({\vartheta\:}_{P}\left(x\right)\right)}^{2}\le\:1$. The hesitancy degree of the element $\:x\in\:X$ in the set $\:P$ is defined as $\:{\:\pi\:}_{p}\left(x\right)=\sqrt{1-{\mu\:}_{p}^{2}\left(x\right)-{\vartheta\:}_{p}^{2}\left(x\right)}$.

Definition 2

⁵⁰. Let be a finite set of linguistic terms having odd cardinality. Let and be any two linguistic terms of then they must adhere to the following properties:

• a) Set $\:U$ is structured as an ordered set: $\:i<j\iff\:{u}_{i}<{u}_{j}$,

• b) The operators, such as negation, maximum, and minimum, must exist in the ordered set $\:U$ as follows:

  • 1. $\:Neg\left({u}_{i}\right)={u}_{j}$where $\:j=t-i$,

  • 2. $\:Max({u}_{i},{u}_{j})={u}_{j}\iff\:i<j,$

  • 3. $\:Min({u}_{i},{u}_{j})={u}_{i}\iff\:i<j.$

Definition 3

⁵⁰. Let be a finite set of linguistic terms having odd cardinality. A continuous linguistic term set is defined as. If, it is categorized as an original linguistic term; if, it is categorized as a virtual linguistic term.

Definition 4

²⁹. Consider a nonempty, finite universe of discourse and a continuous linguistic term set, then a LPFS is defined as:

$$\:A=\left\{\right(x,{u}_{\mu\:}\left(x\right),{u}_{\vartheta\:}\left(x\right)|x\in\:X\},$$

where $\:{u}_{\mu\:}\left(x\right),\:{u}_{\vartheta\:}\left(x\right)\in\:\:\overline{U}$ denote the linguistic MD and linguistic NMD, respectively, of the element $\:x\in\:X$ in the set $\:A$. For convenience, we write $\:\left({u}_{\mu\:}\left(x\right),{u}_{\vartheta\:}\left(x\right)\right)\:$as $\:\alpha\:=\left({u}_{\mu\:},{u}_{\vartheta\:}\right).$ This representation is called LPFN and it satisfies the restricted condition $\:0\le\:\mu\:\le\:\:t,\:0\le\:\vartheta\:\le\:t$ and $\:{\mu\:}^{2}+{\vartheta\:}^{2}\le\:{t}^{2}$ for any $\:x\in\:X$ in the set $\:A$. The degree of LPF indeterminacy of $\:x\in\:X$ in $\:A$ is defined as: $\:{\pi\:}_{A}\left(x\right)={u}_{\sqrt{{t}^{2}-{\mu\:}^{2}-{\vartheta\:}^{2}}}$.

Definition 5

²⁹. Consider the three LPFNs, and. These LPFNs satisfy the subsequent fundamental laws:

• 1. $\:{\alpha\:}_{1}={\alpha\:}_{2}$ iff $\:{u}_{{\mu\:}_{1}}={u}_{{\mu\:}_{2}}$ and $\:{u}_{{\vartheta\:}_{1}}={u}_{{\vartheta\:}_{2}}$,

• 2. $\:{\alpha\:}_{1}<{\alpha\:}_{2}\:$iff $\:{u}_{{\mu\:}_{1}}<{u}_{{\mu\:}_{2}}\:$and $\:{u}_{{\vartheta\:}_{1}}>{u}_{{\vartheta\:}_{2}}$,

• 3. $\:{\alpha\:}^{c}=({u}_{\vartheta\:},{u}_{\mu\:}),$

• 4. $\:{\alpha\:}_{1}\vee\:{\alpha\:}_{2}=({max}({u}_{{\mu\:}_{1}},{u}_{{\mu\:}_{2}}),{min}({u}_{{\vartheta\:}_{1}},{u}_{{\vartheta\:}_{2}}\left)\right),$

• 5. $\:{\alpha\:}_{1}\wedge\:{\alpha\:}_{2}=({min}({u}_{{\mu\:}_{1}},{u}_{{\mu\:}_{2}}),{max}({u}_{{\vartheta\:}_{1}},{u}_{{\vartheta\:}_{2}}\left)\right).$

We examine the following operational laws for LPFNs based on t-norm and s-norm.

Definition 6

²⁹. Consider the three LPFNs, , and, then

$$1.\quad\:{\alpha\:}_{1}\oplus\:{\alpha\:}_{2}=\left({u}_{t\left(\sqrt{{\mu\:}_{1}^{2}/{t}^{2}+{\mu\:}_{2}^{2}/{t}^{2}-{\mu\:}_{1}^{2}{\mu\:}_{2}^{2}/{t}^{4}}\right)},{u}_{t\left({\vartheta\:}_{1}{\vartheta\:}_{2}/{t}^{2}\right)}\right);$$

$$2.\quad\:{\alpha\:}_{1}\otimes\:{\alpha\:}_{2}=\left({u}_{t\left({\mu\:}_{1}{\mu\:}_{2}/{t}^{2}\right)},{u}_{t\left(\sqrt{{\vartheta\:}_{1}^{2}/{t}^{2}+{\vartheta\:}_{2}^{2}/{t}^{2}-{\vartheta\:}_{1}^{2}{\vartheta\:}_{2}^{2}/{t}^{4}}\right)}\right);$$

$$3.\quad\:\lambda\:\alpha\:=\left({u}_{t\left(\sqrt{1-(1-{\mu\:}^{2}/{t}^{2}{)}^{\lambda\:}}\right)},{u}_{t(\vartheta\:/t{)}^{\lambda\:}}\right);$$

$$4.\quad\:{\alpha\:}^{\lambda\:}=\left({u}_{t(\mu\:/t{)}^{\lambda\:}},{u}_{t\left(\sqrt{1-(1-{\vartheta\:}^{2}/{t}^{2}{)}^{\lambda\:}}\right)}\right).$$

Definition 7

³⁸. For any real numbers and, Dombi’s t-norm and s-norm are expressed as follows:

$$1.\quad\:T(a,b)=\frac{1}{1+{\left[{\left(\frac{1-a}{a}\right)}^{k}+{\left(\frac{1-b}{b}\right)}^{k}\right]}^{\frac{1}{k}}},$$

(2.1)

$$2.\quad\:S(a,b)=1-\frac{1}{1+{\left[{\left(\frac{a}{1-a}\right)}^{k}+{\left(\frac{b}{1-b}\right)}^{k}\right]}^{\frac{1}{k}}}$$

(2.2)

Where $\:k\ge\:1$ and $\:\left(a,b\right)\in\:{\left[\text{0,1}\right]}^{2}$. In the above expressions (2.1) and (2.2), respectively, they are named the Dombi product and the Dombi sum.

Formulation of an innovative score function for LPFNs

In addressing the complexities of MADM problems, this section proposes a novel score function specifically designed for LPFNs.

Definition 8

Consider a LPFN with The score function for LPFN is expressed in the following way:

$$\:S\left(\alpha\:\right)={u}_{\left(\frac{{t}^{2}{e}^{\left(\frac{{\mu\:}_{\alpha\:}^{2}}{{t}^{2}}-\frac{{\vartheta\:}_{\alpha\:}^{2}}{{t}^{2}}\right)}}{2{t}^{2}-{\mu\:}_{\alpha\:}^{2}-{\vartheta\:}_{\alpha\:}^{2}}\right)},\:\left(\frac{{t}^{2}{e}^{\left(\frac{{\mu\:}_{\alpha\:}^{2}}{{t}^{2}}-\frac{{\vartheta\:}_{\alpha\:}^{2}}{{t}^{2}}\right)}}{2{t}^{2}-{\mu\:}_{\alpha\:}^{2}-{\vartheta\:}_{\alpha\:}^{2}}\right)\in\:\left[\frac{1}{e},e\right]$$

Where $\:e=2.71828$.

The ranking criteria for two LPFNs $\:\alpha\:$ and $\:\beta\:$ based on the preceding definition, is determined as follows:

• 1. ${\rm If} S\left(\alpha\:\right)>S\left(\beta\:\right), then \alpha\:>\beta {\rm means} \alpha\: {\rm is stronger than} \beta\:$

• 2. If $\:S\left(\alpha\:\right)<S\left(\beta\:\right)$, then $\:\alpha\:<\beta\:$ means $\:\alpha\:$ is weaker than $\:\beta\:$;

• 3. If$\:\:S\left(\alpha\:\right)=S\left(\beta\:\right)$, then $\:\alpha\:\sim\:\beta\:$.

To demonstrate the effectiveness of our suggested score function $\:S$ for LPFNs, we present the following illustrative example:

Example 1

Let and be any two LPFNs defined on. By applying Definition 8 to LPFNs and results in and. Therefore, the above property 2 in Definition 8 suggests that. This observation suggests that is weaker than .

Formulation of LPF Dombi ordered weighted AOs for LPFNs and their characteristics

In this section, we initiate the study of two novel AOs, namely, LPFDOWA and LPFDOWG operators and explore their fundamental structural characteristics.

Definition 9

For any three LPFNs, and defined on with, Within this framework, the Dombi operational laws for LPFNs are described in the following manner:

$$1. \quad\:{\alpha\:}_{1}\oplus\:{\alpha\:}_{2}=\left({u}_{t\left(\sqrt{1-\frac{1}{1+{\left\{{\left(\frac{{\mu\:}_{1}^{2}}{{t}^{2}-{\mu\:}_{1}^{2}}\right)}^{k}+{\left(\frac{{\mu\:}_{2}^{2}}{{t}^{2}-{\mu\:}_{2}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)},{u}_{t\left(\sqrt{\frac{1}{1+{\left\{{\left(\frac{{t}^{2}-{\vartheta\:}_{1}^{2}}{{\vartheta\:}_{1}^{2}}\right)}^{k}+{\left(\frac{{t}^{2}-{\vartheta\:}_{2}^{2}}{{\vartheta\:}_{2}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)}\right);$$

$$2. \quad\:{\alpha\:}_{1}\otimes\:{\alpha\:}_{2}=\left({u}_{t\left(\sqrt{\frac{1}{1+{\left\{{\left(\frac{{t}^{2}-{\mu\:}_{1}^{2}}{{\mu\:}_{1}^{2}}\right)}^{k}+{\left(\frac{{t}^{2}-{\mu\:}_{2}^{2}}{{\mu\:}_{2}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)},{u}_{t\left(\sqrt{1-\frac{1}{1+{\left\{{\left(\frac{{\vartheta\:}_{1}^{2}}{{t}^{2}-{\vartheta\:}_{1}^{2}}\right)}^{k}+{\left(\frac{{\vartheta\:}_{2}^{2}}{{t}^{2}-{\vartheta\:}_{2}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)}\right);$$

$$3. \quad\:\lambda\:\alpha\:=\left({u}_{t\left(\sqrt{1-\frac{1}{1+{\left\{\lambda\:{\left(\frac{{\mu\:}^{2}}{{t}^{2}-{\mu\:}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)},{u}_{t\left(\sqrt{\frac{1}{1+{\left\{\lambda\:{\left(\frac{{t}^{2}-{\vartheta\:}^{2}}{{\vartheta\:}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)}\right);$$

$$4.\quad \:{\alpha\:}^{\lambda\:}=\left({u}_{t\left(\sqrt{\frac{1}{1+{\left\{\lambda\:{\left(\frac{{t}^{2}-{\mu\:}^{2}}{{\mu\:}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)},{u}_{t\left(\sqrt{1-\frac{1}{1+{\left\{\lambda\:{\left(\frac{{\vartheta\:}^{2}}{{t}^{2}-{\vartheta\:}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)}\right).$$

Fundamental aspects of the Dombi ordered weighted averaging operator for LPFNs

This subsection serves to introduce the LPFDOWA operator. This operator is specifically designed to simplify the process of aggregating LPFNs, thus offering a comprehensive solution to aggregate the LPF environment.

Definition 10

Consider a collection of n LPFNs, denoted as defined on, and be the associated weight vector (WV) of, where such that and the operational parameter is. Additionally, is a permutation of such that. The LPFDOWA operator is defined as a mapping : defined as:

$$\:LPFDOWA\left({\alpha\:}_{1},{\alpha\:}_{2},\ldots,{\alpha\:}_{n}\right)={\oplus\:}_{i=1}^{n}{w}_{i}{\alpha\:}_{\gimel\:\left(i\right)}$$

$$\:=\left({u}_{t\left(\sqrt{1-\frac{1}{1+{\left\{{\sum\:}_{i=1}^{n}{w}_{i}{\left(\frac{{\mu\:}_{\gimel\:\left(i\right)}^{2}}{{t}^{2}-{\mu\:}_{\gimel\:\left(i\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)},{u}_{t\left(\sqrt{\frac{1}{1+{\left\{{\sum\:}_{i=1}^{n}{w}_{i}{\left(\frac{{t}^{2}-{\vartheta\:}_{\gimel\:\left(i\right)}^{2}}{{\vartheta\:}_{\gimel\:\left(i\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)}\right).$$

Theorem 1

Consider number of LPFNs denoted as for defined on and be the corresponding WV of, where such that and operational parameter is. Moreover, is a permutation of such that. The LPFDOWA operator yields an aggregated value as an LPFN, and can be written as:

$$\:LPFDOWA\left({\alpha\:}_{1},{\alpha\:}_{2},\ldots,{\alpha\:}_{n}\right)={\oplus\:}_{i=1}^{n}{w}_{i}{\alpha\:}_{\gimel\:\left(i\right)}$$

$$\:=\left({u}_{t\left(\sqrt{1-\frac{1}{1+{\left\{{\sum\:}_{i=1}^{n}{w}_{i}{\left(\frac{{\mu\:}_{\gimel\:\left(i\right)}^{2}}{{t}^{2}-{\mu\:}_{\gimel\:\left(i\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)},{u}_{t\left(\sqrt{\frac{1}{1+{\left\{{\sum\:}_{i=1}^{n}{w}_{i}{\left(\frac{{t}^{2}-{\vartheta\:}_{\gimel\:\left(i\right)}^{2}}{{\vartheta\:}_{\gimel\:\left(i\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)}\right).$$

Proof

To prove the validity of Theorem 1, we use mathematical induction with regard to variables .

Consider the initial case scenario when $\:n=2$, we have $\:{\alpha\:}_{1}=({u}_{{\mu\:}_{1}},{u}_{{\vartheta\:}_{1}})$ and $\:{\alpha\:}_{2}=({u}_{{\mu\:}_{2}},{u}_{{\vartheta\:}_{2}})$, by applying the Dombi operational laws on LPFNs, as specified in Definition 9, we obtained the following outcomes:

$$\:{w}_{1}{\alpha\:}_{\gimel\:\left(1\right)}=\left({u}_{t\left(\sqrt{1-\frac{1}{1+{\left\{{w}_{1}{\left(\frac{{\mu\:}_{\gimel\:\left(1\right)}^{2}}{{t}^{2}-{\mu\:}_{\gimel\:\left(1\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)},{u}_{t\left(\sqrt{\frac{1}{1+{\left\{{w}_{1}{\left(\frac{{t}^{2}-{\vartheta\:}_{\gimel\:\left(1\right)}^{2}}{{\vartheta\:}_{\gimel\:\left(1\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)}\right);$$

$$\:{w}_{2}{\alpha\:}_{\gimel\:\left(2\right)}=\left({u}_{t\left(\sqrt{1-\frac{1}{1+{\left\{{w}_{2}{\left(\frac{{\mu\:}_{\gimel\:\left(2\right)}^{2}}{{t}^{2}-{\mu\:}_{\gimel\:\left(2\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)},{u}_{t\left(\sqrt{\frac{1}{1+{\left\{{w}_{2}{\left(\frac{{t}^{2}-{\vartheta\:}_{\gimel\:\left(2\right)}^{2}}{{\vartheta\:}_{\gimel\:\left(2\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)}\right);$$

Employing Definition 10 results in the following:

$$\:LPFDOWA\left({\alpha\:}_{1},{\alpha\:}_{2}\right)={w}_{1}{\alpha\:}_{\gimel\:\left(1\right)}\oplus\:{w}_{2}{\alpha\:}_{\gimel\:\left(2\right)}$$

$$\:=\left({u}_{t\left(\sqrt{1-\frac{1}{1+{\left\{{w}_{1}{\left(\frac{{\mu\:}_{\gimel\:\left(1\right)}^{2}}{{t}^{2}-{\mu\:}_{\gimel\:\left(1\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)},{u}_{t\left(\sqrt{\frac{1}{1+{\left\{{w}_{1}{\left(\frac{{t}^{2}-{\vartheta\:}_{\gimel\:\left(1\right)}^{2}}{{\vartheta\:}_{\gimel\:\left(1\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)}\right)\oplus\:\left({u}_{t\left(\sqrt{1-\frac{1}{1+{\left\{{w}_{2}{\left(\frac{{\mu\:}_{\gimel\:\left(2\right)}^{2}}{{t}^{2}-{\mu\:}_{\gimel\:\left(2\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)},{u}_{t\left(\sqrt{\frac{1}{1+{\left\{{w}_{2}{\left(\frac{{t}^{2}-{\vartheta\:}_{\gimel\:\left(2\right)}^{2}}{{\vartheta\:}_{\gimel\:\left(2\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)}\right)$$

Then

$$\:{w}_{1}{\alpha\:}_{\gimel\:\left(1\right)}\oplus\:{w}_{2}{\alpha\:}_{\gimel\:\left(2\right)}=\left({u}_{t\left(\sqrt{1-\frac{1}{1+{\left\{{w}_{1}{\left(\frac{{\mu\:}_{\gimel\:\left(1\right)}^{2}}{{t}^{2}-{\mu\:}_{\gimel\:\left(1\right)}^{2}}\right)}^{k}+{w}_{2}{\left(\frac{{\mu\:}_{\gimel\:\left(2\right)}^{2}}{{t}^{2}-{\mu\:}_{\gimel\:\left(2\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)},{u}_{t\left(\sqrt{\frac{1}{1+{\left\{{w}_{1}{\left(\frac{{t}^{2}-{\vartheta\:}_{\gimel\:\left(1\right)}^{2}}{{\vartheta\:}_{\gimel\:\left(1\right)}^{2}}\right)}^{k}+{w}_{2}{\left(\frac{{t}^{2}-{\vartheta\:}_{\gimel\:\left(2\right)}^{2}}{{\vartheta\:}_{\gimel\:\left(2\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)}\right);$$

Consequently,

$$\:LPFDOWA\left({\alpha\:}_{1},{\alpha\:}_{2}\right)=\left({u}_{t\left(\sqrt{1-\frac{1}{1+{\left\{{\sum\:}_{i=1}^{2}{w}_{i}{\left(\frac{{\mu\:}_{\gimel\:\left(i\right)}^{2}}{{t}^{2}-{\mu\:}_{\gimel\:\left(i\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)},{u}_{t\left(\sqrt{\frac{1}{1+{\left\{{\sum\:}_{i=1}^{2}{w}_{i}{\left(\frac{{t}^{2}-{\vartheta\:}_{\gimel\:\left(i\right)}^{2}}{{\vartheta\:}_{\gimel\:\left(i\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)}\right).$$

Therefore, we see that the result is true for $\:n=2$.

Next, we assume that the assertion is true for $\:n=r$, that is

$$\:LPFDOWA\left({\alpha\:}_{1},{\alpha\:}_{2},\ldots,{\alpha\:}_{r}\right)={\oplus\:}_{i=1}^{r}{w}_{i}{\alpha\:}_{\gimel\:\left(i\right)}$$

$$\:=\left({u}_{t\left(\sqrt{1-\frac{1}{1+{\left\{{\sum\:}_{i=1}^{r}{w}_{i}{\left(\frac{{\mu\:}_{\gimel\:\left(i\right)}^{2}}{{t}^{2}-{\mu\:}_{\gimel\:\left(i\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)},{u}_{t\left(\sqrt{\frac{1}{1+{\left\{{\sum\:}_{i=1}^{r}{w}_{i}{\left(\frac{{t}^{2}-{\vartheta\:}_{\gimel\:\left(i\right)}^{2}}{{\vartheta\:}_{\gimel\:\left(i\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)}\right).$$

Then,

$$\:LPFDOWA\left({\alpha\:}_{1},{\alpha\:}_{2},\ldots,{\alpha\:}_{r},{\alpha\:}_{r+1}\right)={\oplus\:}_{i=1}^{r}{w}_{i}{\alpha\:}_{\gimel\:\left(i\right)}\oplus\:{w}_{r+1}{\alpha\:}_{\gimel\:\left(r+1\right)}$$

$$\:=\left({u}_{t\left(\sqrt{1-\frac{1}{1+{\left\{{\sum\:}_{i=1}^{r}{w}_{i}{\left(\frac{{\mu\:}_{\gimel\:\left(i\right)}^{2}}{{t}^{2}-{\mu\:}_{\gimel\:\left(i\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)},{u}_{t\left(\sqrt{\frac{1}{1+{\left\{{\sum\:}_{i=1}^{r}{w}_{i}{\left(\frac{{t}^{2}-{\vartheta\:}_{\gimel\:\left(i\right)}^{2}}{{\vartheta\:}_{\gimel\:\left(i\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)}\right)\oplus\:\left({u}_{t\left(\sqrt{1-\frac{1}{1+{\left\{{w}_{r+1}{\left(\frac{{\mu\:}_{\gimel\:\left(r+1\right)}^{2}}{{t}^{2}-{\mu\:}_{\gimel\:\left(r+1\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)},{u}_{t\left(\sqrt{\frac{1}{1+{\left\{{w}_{r+1}{\left(\frac{{t}^{2}-{\vartheta\:}_{\gimel\:\left(r+1\right)}^{2}}{{\vartheta\:}_{\gimel\:\left(r+1\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)}\right).$$

Consequently,

$$\:LPFDOWA\left({\alpha\:}_{1},{\alpha\:}_{2},\dots\:,{\alpha\:}_{r+1}\right)=\left({u}_{t\left(\sqrt{1-\frac{1}{1+{\left\{{\sum\:}_{i=1}^{r+1}{w}_{i}{\left(\frac{{\mu\:}_{\gimel\:\left(i\right)}^{2}}{{t}^{2}-{\mu\:}_{\gimel\:\left(i\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)},{u}_{t\left(\sqrt{\frac{1}{1+{\left\{{\sum\:}_{i=1}^{r+1}{w}_{i}{\left(\frac{{t}^{2}-{\vartheta\:}_{\gimel\:\left(i\right)}^{2}}{{\vartheta\:}_{\gimel\:\left(i\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)}\right).$$

Therefore, the result is valid for $\:n=r+1$. Thus, Theorem 1 is valid for each $\:n\in\:\mathbb{N}$.

Example 2

Assume that there are five friends who decide to embark on a shopping adventure. According to these individual preferences, the quality of clothes is categorized in the form of LPFNs as follows, and defined on continuous linguistic terms set with the corresponding WVs of LPFNs and the operational parameter In order to aggregate these values using the LPFDOWA operator, we initially permute LPFNs by using Definition 8 as follows:

$$\:S\left({\alpha\:}_{1}\right)={u}_{1.4775},\:S\left({\alpha\:}_{2}\right)={u}_{1.5002},\:S\left({\alpha\:}_{3}\right)={u}_{2.7193},\:S\left({\alpha\:}_{4}\right)={u}_{0.9303},\:S\left({\alpha\:}_{5}\right)={u}_{0.7251}.\:$$

According to Definition 10, the permuted values of LPFNs are arranged in descending order as follows:

$$\:{\alpha\:}_{\gimel\:\left(1\right)}=\left({u}_{6},{u}_{1}\right)\:,\:\:{\alpha\:}_{\gimel\:\left(2\right)}=\left({u}_{5},{u}_{2}\right),\:{\:\alpha\:}_{\gimel\:\left(3\right)}=\left({u}_{5},{u}_{3}\right),\:{\alpha\:}_{\gimel\:\left(4\right)}=\left({u}_{4},{u}_{3}\right)\:\text{a}\text{n}\text{d}\:{\alpha\:}_{\gimel\:\left(5\right)}=\left({u}_{3},{u}_{1}\right).\:$$

Employing Definition 10 results in the following:

$$\:LPFDOWA\left({\alpha\:}_{1},{\alpha\:}_{2},{\alpha\:}_{3},{\alpha\:}_{4},{\alpha\:}_{5}\right)={\oplus\:}_{i=1}^{5}{w}_{i}{\alpha\:}_{\gimel\:\left(i\right)}$$

$$\:=\left({u}_{8\left(\sqrt{1-\frac{1}{1+{\left\{{\sum\:}_{i=1}^{5}{w}_{i}{\left(\frac{{\mu\:}_{\gimel\:\left(i\right)}^{2}}{{8}^{2}-{\mu\:}_{\gimel\:\left(i\right)}^{2}}\right)}^{2}\right\}}^{\frac{1}{2}}}}\right)},{u}_{8\left(\sqrt{\frac{1}{1+{\left\{{\sum\:}_{i=1}^{5}{w}_{i}{\left(\frac{{8}^{2}-{\vartheta\:}_{\gimel\:\left(i\right)}^{2}}{{\vartheta\:}_{\gimel\:\left(i\right)}^{2}}\right)}^{2}\right\}}^{\frac{1}{2}}}}\right)}\right)$$

$$\:=\left({u}_{8\left(\sqrt{1-\frac{1}{1+{\left\{0.21{\left(\frac{{6}^{2}}{{8}^{2}-{6}^{2}}\right)}^{2}+0.24{\left(\frac{{5}^{2}}{{8}^{2}-{5}^{2}}\right)}^{2}+0.3{\left(\frac{{5}^{2}}{{8}^{2}-{5}^{2}}\right)}^{2}+0.13{\left(\frac{{4}^{2}}{{8}^{2}-{4}^{2}}\right)}^{2}+0.12{\left(\frac{{3}^{2}}{{8}^{2}-{3}^{2}}\right)}^{2}\right\}}^{\frac{1}{2}}}}\right)},\:\:{u}_{8\left(\sqrt{\frac{1}{1+{\left\{0.21{\left(\frac{{8}^{2}-{1}^{2}}{{1}^{2}}\right)}^{2}+0.24{\left(\frac{{8}^{2}-{2}^{2}}{{2}^{2}}\right)}^{2}+0.3{\left(\frac{{8}^{2}-{3}^{2}}{{3}^{2}}\right)}^{2}+0.13{\left(\frac{{8}^{2}-{3}^{2}}{{3}^{2}}\right)}^{2}+0.12{\left(\frac{{8}^{2}-{1}^{2}}{{1}^{2}}\right)}^{2}\right\}}^{\frac{1}{2}}}}\right)}\right);$$

Thus,

$$\:LPFDOWA\left({\alpha\:}_{1},{\alpha\:}_{2},{\alpha\:}_{3},{\alpha\:}_{4},{\alpha\:}_{5}\right)=\left({u}_{5.2687},{u}_{1.2953}\right).$$

This validates Theorem 1.

Within the LPFDOWA operator, it appears that a finite number of LPFNs exhibit the property of Idempotency. This assertion is substantiated by the subsequent result.

Theorem 2

Consider number of LPFNs denoted as for defined on and be the corresponding WV of, where such that and operational parameter is. Moreover, is a permutation of such that. If for all then

$$\:LPFDOWA\left({\alpha\:}_{1},{\alpha\:}_{2},\ldots,{\alpha\:}_{n}\right)=\alpha\:$$

Proof

Considering the provided settings, we obtain and ,

$$\:LPFDOWA\left({\alpha\:}_{1},{\alpha\:}_{2},\ldots,{\alpha\:}_{n}\right)={\oplus\:}_{i=1}^{n}{w}_{i}\alpha\:$$

$$\:=\left({u}_{t\left(\sqrt{1-\frac{1}{1+\left(\frac{{\mu\:}^{2}}{{t}^{2}-{\mu\:}^{2}}\right){\left\{{\sum\:}_{i=1}^{n}{w}_{i}\right\}}^{\frac{1}{k}}}}\right)},{u}_{t\left(\sqrt{\frac{1}{1+\left(\frac{{t}^{2}-{\vartheta\:}^{2}}{{\vartheta\:}^{2}}\right){\left\{{\sum\:}_{i=1}^{n}{w}_{i}\right\}}^{\frac{1}{k}}}}\right)}\right)$$

Consequently,

$$\:LPFDOWA\left({\alpha\:}_{1},{\alpha\:}_{2},\dots\:,{\alpha\:}_{n}\right)=\left({u}_{t\left(\sqrt{1-\frac{1}{1+\left(\frac{{\mu\:}^{2}}{{t}^{2}-{\mu\:}^{2}}\right)}}\right)},{u}_{t\left(\sqrt{\frac{1}{1+\left(\frac{{t}^{2}-{\vartheta\:}^{2}}{{\vartheta\:}^{2}}\right)}}\right)}\right)$$

$$\:=\left({u}_{\mu\:},{u}_{\vartheta\:}\right)=\alpha\:$$

.

Theorem 3

(Monotonicity) Consider any two collections of number of LPFNs represented as and for defined on a continuous linguistic term set and is the associated WV of these LPFNs,, where such that and operational parameter is. Additionally, is a permutation of such that. If and. Then,

$$\:LPFDOWA\left({\alpha\:}_{1},{\alpha\:}_{2},\ldots,{\alpha\:}_{n}\right)\le\:LPFDOWA\left({\beta\:}_{1},{\beta\:}_{2},\ldots,{\beta\:}_{n}\right).$$

Proof

Considering the provided settings, we obtain for all

$$\:\Rightarrow\:{u}_{{\left(\frac{{\mu\:}_{\gimel\:\left(\text{i}\right)}^{2}}{{t}^{2}-{\mu\:}_{\gimel\:\left(\text{i}\right)}^{2}}\right)}^{k}}\le\:{u}_{{\left(\frac{{\mu\:}_{\gimel\:\left(\text{i}\right)}^{{\prime\:}2}}{{t}^{2}-{\mu\:}_{\gimel\:\left(\text{i}\right)}^{{\prime\:}2}}\right)}^{k}}$$

$$\:\Rightarrow\:{u}_{{\left\{{\sum\:}_{i=1}^{n}{w}_{i}{\left(\frac{{\mu\:}_{\gimel\:\left(\text{i}\right)}^{2}}{{t}^{2}-{\mu\:}_{\gimel\:\left(\text{i}\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}\le\:{u}_{{\left\{{\sum\:}_{i=1}^{n}{w}_{i}{\left(\frac{{\mu\:}_{\gimel\:\left(\text{i}\right)}^{{\prime\:}2}}{{t}^{2}-{\mu\:}_{\gimel\:\left(\text{i}\right)}^{{\prime\:}2}}\right)}^{k}\right\}}^{\frac{1}{k}}}$$

$$\:\Rightarrow\:{u}_{\left(1+{\left\{{\sum\:}_{i=1}^{n}{w}_{i}{\left(\frac{{\mu\:}_{\gimel\:\left(\text{i}\right)}^{2}}{{t}^{2}-{\mu\:}_{\gimel\:\left(\text{i}\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}\right)}\le\:{u}_{\left(1+{\left\{{\sum\:}_{i=1}^{n}{w}_{i}{\left(\frac{{\mu\:}_{\gimel\:\left(\text{i}\right)}^{{\prime\:}2}}{{t}^{2}-{\mu\:}_{\gimel\:\left(\text{i}\right)}^{{\prime\:}2}}\right)}^{k}\right\}}^{\frac{1}{k}}\right)}$$

$$\:\Rightarrow\:{u}_{\left(\frac{1}{1+{\left\{{\sum\:}_{i=1}^{n}{w}_{i}{\left(\frac{{\mu\:}_{\gimel\:\left(\text{i}\right)}^{2}}{{t}^{2}-{\mu\:}_{\gimel\:\left(\text{i}\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}\right)}\ge\:{u}_{\left(\frac{1}{1+{\left\{{\sum\:}_{i=1}^{n}{w}_{i}{\left(\frac{{\mu\:}_{\gimel\:\left(\text{i}\right)}^{{\prime\:}2}}{{t}^{2}-{\mu\:}_{\gimel\:\left(\text{i}\right)}^{{\prime\:}2}}\right)}^{k}\right\}}^{\frac{1}{k}}}\right)}$$

$$\:\Rightarrow\:{u}_{\left(1-\frac{1}{1+{\left\{{\sum\:}_{i=1}^{n}{w}_{i}{\left(\frac{{\mu\:}_{\gimel\:\left(\text{i}\right)}^{2}}{{t}^{2}-{\mu\:}_{\gimel\:\left(\text{i}\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}\right)}\le\:{u}_{\left(1-\frac{1}{1+{\left\{{\sum\:}_{i=1}^{n}{w}_{i}{\left(\frac{{\mu\:}_{\gimel\:\left(\text{i}\right)}^{{\prime\:}2}}{{t}^{2}-{\mu\:}_{\gimel\:\left(\text{i}\right)}^{{\prime\:}2}}\right)}^{k}\right\}}^{\frac{1}{k}}}\right)}$$

$$\:\Rightarrow\:{u}_{\sqrt{1-\frac{1}{1+{\left\{{\sum\:}_{i=1}^{n}{w}_{i}{\left(\frac{{\mu\:}_{\gimel\:\left(\text{i}\right)}^{2}}{{t}^{2}-{\mu\:}_{\gimel\:\left(\text{i}\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}}\le\:{u}_{\sqrt{1-\frac{1}{1+{\left\{{\sum\:}_{i=1}^{n}{w}_{i}{\left(\frac{{\mu\:}_{\gimel\:\left(\text{i}\right)}^{{\prime\:}2}}{{t}^{2}-{\mu\:}_{\gimel\:\left(\text{i}\right)}^{{\prime\:}2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}}$$

$$\:\Rightarrow\:{u}_{t\left(\sqrt{1-\frac{1}{1+{\left\{{\sum\:}_{i=1}^{n}{w}_{i}{\left(\frac{{\mu\:}_{\gimel\:\left(\text{i}\right)}^{2}}{{t}^{2}-{\mu\:}_{\gimel\:\left(\text{i}\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)}\le\:{u}_{t\left(\sqrt{1-\frac{1}{1+{\left\{{\sum\:}_{i=1}^{n}{w}_{i}{\left(\frac{{\mu\:}_{\gimel\:\left(\text{i}\right)}^{{\prime\:}2}}{{t}^{2}-{\mu\:}_{\gimel\:\left(\text{i}\right)}^{{\prime\:}2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)}$$

(4.1)

Moreover, by applying the above mathematical procedure to the relation $\:{u}_{{\vartheta\:}_{\gimel\:\left(\text{i}\right)}}\ge\:{u}_{{\vartheta\:}_{\gimel\:\left(\text{i}\right)}^{{\prime\:}}}\:\text{f}\text{o}\text{r}\:\text{a}\text{l}\text{l}\:i$, we obtain

$$\:{u}_{t\left(\sqrt{\frac{1}{1+{\left\{{\sum\:}_{i=1}^{n}{w}_{i}{\left(\frac{{t}^{2}-{\vartheta\:}_{\gimel\:\left(i\right)}^{2}}{{\vartheta\:}_{\gimel\:\left(i\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)}\ge\:{u}_{t\left(\sqrt{\frac{1}{1+{\left\{{\sum\:}_{i=1}^{n}{w}_{i}{\left(\frac{{t}^{2}-{\vartheta\:}_{\gimel\:\left(i\right)}^{{\prime\:}2}}{{\vartheta\:}_{\gimel\:\left(i\right)}^{{\prime\:}2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)}$$

(4.2)

By comparing the relations 4.1, 4.2 and using Definition 5, we get

$$\:LPFDOWA\left({\alpha\:}_{1},{\alpha\:}_{2},\ldots,{\alpha\:}_{n}\right)\le\:LPFDOWA\left({\beta\:}_{1},{\beta\:}_{2},\ldots,{\beta\:}_{n}\right).$$

Theorem 4

(Boundedness) Consider number of LPFNs denoted as for defined on and be the corresponding WV of, where such that and operational parameter is. Moreover, is a permutation of such that. Let and. Then,

$$\:{\alpha\:}^{-}\le\:LPFDOWA\left({\alpha\:}_{1},{\alpha\:}_{2},\ldots,{\alpha\:}_{n}\right)\le\:{\alpha\:}^{+}.$$

Proof

Consider the result achieved by applying the LPFDOWA operator to the collection of LPFNs, denoted as. Considering the provided settings, we obtain and .

So, for each LPFN, $\:\begin{array}{c}{min}\\\:i\end{array}\left({u}_{{\mu\:}_{\gimel\:\left(i\right)}}\right)\le\:{u}_{{\mu\:}_{\gimel\:\left(i\right)}}\le\:\begin{array}{c}{max}\\\:i\end{array}\left({u}_{{\mu\:}_{\gimel\:\left(i\right)}}\right)$

$$\:\Rightarrow\:\begin{array}{c}{min}\\\:i\end{array}\left({u}_{{\left(\frac{{\mu\:}_{\gimel\:\left(i\right)}^{2}}{{t}^{2}-{\mu\:}_{\gimel\:\left(i\right)}^{2}}\right)}^{k}}\right)\le\:{u}_{{\left(\frac{{\mu\:}_{\gimel\:\left(i\right)}^{2}}{{t}^{2}-{\mu\:}_{\gimel\:\left(i\right)}^{2}}\right)}^{k}}\le\:\begin{array}{c}{max}\\\:i\end{array}\left({u}_{{\left(\frac{{\mu\:}_{\gimel\:\left(i\right)}^{2}}{{t}^{2}-{\mu\:}_{\gimel\:\left(i\right)}^{2}}\right)}^{k}}\right)$$

$$\:\Rightarrow\:\begin{array}{c}{min}\\\:i\end{array}\left({u}_{{\left\{{\sum\:}_{i=1}^{n}{w}_{i}{\left(\frac{{\mu\:}_{\gimel\:\left(i\right)}^{2}}{{t}^{2}-{\mu\:}_{\gimel\:\left(i\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}\right)\le\:{u}_{{\left\{{\sum\:}_{i=1}^{n}{w}_{i}{\left(\frac{{\mu\:}_{\gimel\:\left(i\right)}^{2}}{{t}^{2}-{\mu\:}_{\gimel\:\left(i\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}\le\:\begin{array}{c}{max}\\\:i\end{array}\left({u}_{{\left\{{\sum\:}_{i=1}^{n}{w}_{i}{\left(\frac{{\mu\:}_{\gimel\:\left(i\right)}^{2}}{{t}^{2}-{\mu\:}_{\gimel\:\left(i\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}\right)$$

$$\:\Rightarrow\:\begin{array}{c}{max}\\\:i\end{array}\left({u}_{\left(\frac{1}{1+{\left\{{\sum\:}_{i=1}^{n}{w}_{i}{\left(\frac{{\mu\:}_{\gimel\:\left(i\right)}^{2}}{{t}^{2}-{\mu\:}_{\gimel\:\left(i\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}\right)}\right)\le\:{u}_{\left(\frac{1}{1+{\left\{{\sum\:}_{i=1}^{n}{w}_{i}{\left(\frac{{\mu\:}_{\gimel\:\left(i\right)}^{2}}{{t}^{2}-{\mu\:}_{\gimel\:\left(i\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}\right)}\le\:\begin{array}{c}{min}\\\:i\end{array}\left({u}_{\left(\frac{1}{1+{\left\{{\sum\:}_{i=1}^{n}{w}_{i}{\left(\frac{{\mu\:}_{\gimel\:\left(i\right)}^{2}}{{t}^{2}-{\mu\:}_{\gimel\:\left(i\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}\right)}\right)$$

$$\:\Rightarrow\:\begin{array}{c}{min}\\\:i\end{array}\left({u}_{t\left(\sqrt{1-\frac{1}{1+{\left\{{\sum\:}_{i=1}^{n}{w}_{i}{\left(\frac{{\mu\:}_{\gimel\:\left(i\right)}^{2}}{{t}^{2}-{\mu\:}_{\gimel\:\left(i\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)}\right)\le\:{u}_{t\left(\sqrt{1-\frac{1}{1+{\left\{{\sum\:}_{i=1}^{n}{w}_{i}{\left(\frac{{\mu\:}_{\gimel\:\left(i\right)}^{2}}{{t}^{2}-{\mu\:}_{\gimel\:\left(i\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)}\le\:\begin{array}{c}{max}\\\:i\end{array}\left({u}_{t\left(\sqrt{1-\frac{1}{1+{\left\{{\sum\:}_{i=1}^{n}{w}_{i}{\left(\frac{{\mu\:}_{\gimel\:\left(i\right)}^{2}}{{t}^{2}-{\mu\:}_{\gimel\:\left(i\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)}\right)$$

(4.3)

Moreover, by adapting the above mathematical procedure for the relation, $\:\begin{array}{c}{max}\\\:i\end{array}\left({u}_{{\vartheta\:}_{\gimel\:\left(i\right)}}\right)\le\:{u}_{{\vartheta\:}_{\gimel\:\left(i\right)}}\le\:\begin{array}{c}{min}\\\:i\end{array}\left({u}_{{\vartheta\:}_{\gimel\:\left(i\right)}}\right)$, we obtain the following outcome,

$$\:\begin{array}{c}{max}\\\:i\end{array}\left({u}_{t\left(\sqrt{\frac{1}{1+{\left\{{\sum\:}_{i=1}^{n}{w}_{i}{\left(\frac{{t}^{2}-{\vartheta\:}_{\gimel\:\left(i\right)}^{2}}{{\vartheta\:}_{\gimel\:\left(i\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)}\right)\le\:{u}_{t\left(\sqrt{\frac{1}{1+{\left\{{\sum\:}_{i=1}^{n}{w}_{i}{\left(\frac{{t}^{2}-{\vartheta\:}_{\gimel\:\left(i\right)}^{2}}{{\vartheta\:}_{\gimel\:\left(i\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)}\le\:\begin{array}{c}{min}\\\:i\end{array}\left({u}_{t\left(\sqrt{\frac{1}{1+{\left\{{\sum\:}_{i=1}^{n}{w}_{i}{\left(\frac{{t}^{2}-{\vartheta\:}_{\gimel\:\left(i\right)}^{2}}{{\vartheta\:}_{\gimel\:\left(i\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)}\right)$$

(4.4)

By comparing the relations 4.3 and 4.4, we get

$$\:{\alpha\:}^{-}\le\:LPFDOWA\left({\alpha\:}_{1},{\alpha\:}_{2},\ldots,{\alpha\:}_{n}\right)\le\:{\alpha\:}^{+}.$$

Fundamental aspects of Dombi ordered weighted geometric operator for LPFNs

This subsection serves to introduce the LPFDOWG operator. This operator is specifically designed to simplify the process of aggregating LPFNs, thus offering a comprehensive solution to aggregate the LPF environment.

Definition 11

Consider a collection of n LPFNs, denoted as defined on and be the associated WV of, where such that and the operational parameter is. Additionally, is a permutation of such that. The LPFDOWG operator is defined by a mapping such that : defined as:

$$\:LPFDOWG\left({\alpha\:}_{1},{\alpha\:}_{2},\ldots,{\alpha\:}_{n}\right)={\otimes\:}_{i=1}^{n}{{\alpha\:}_{\gimel\:\left(i\right)}}^{{w}_{i}}$$

$$\:{\otimes\:}_{i=1}^{n}{{\alpha\:}_{\gimel\:\left(i\right)}}^{{w}_{i}}=\left({u}_{t\left(\sqrt{\frac{1}{1+{\left\{{\sum\:}_{i=1}^{n}{w}_{i}{\left(\frac{{t}^{2}-{\mu\:}_{\gimel\:\left(i\right)}^{2}}{{\mu\:}_{\gimel\:\left(i\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)},{u}_{t\left(\sqrt{1-\frac{1}{1+{\left\{{\sum\:}_{i=1}^{n}{w}_{i}{\left(\frac{{\vartheta\:}_{\gimel\:\left(i\right)}^{2}}{{t}^{2}-{\vartheta\:}_{\gimel\:\left(i\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)}\right)$$

.

Theorem 5

Consider number of LPFNs denoted as for defined on and be the corresponding WV of, where such that and operational parameter is. Moreover, is a permutation of such that. The LPFDOWG operator yields an aggregated value as an LPFN, and can be written as:

$$\:LPFDOWG\left({\alpha\:}_{1},{\alpha\:}_{2},\ldots,{\alpha\:}_{n}\right)={\otimes\:}_{i=1}^{n}{{\alpha\:}_{\gimel\:\left(\text{i}\right)}}^{{w}_{i}}$$

$$\:=\left({u}_{t\left(\sqrt{\frac{1}{1+{\left\{{\sum\:}_{i=1}^{n}{w}_{i}{\left(\frac{{t}^{2}-{\mu\:}_{\gimel\:\left(\text{i}\right)}^{2}}{{\mu\:}_{\gimel\:\left(\text{i}\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)},{u}_{t\left(\sqrt{1-\frac{1}{1+{\left\{{\sum\:}_{i=1}^{n}{w}_{i}{\left(\frac{{\vartheta\:}_{\gimel\:\left(\text{i}\right)}^{2}}{{t}^{2}-{\vartheta\:}_{\gimel\:\left(\text{i}\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)}\right).$$

Proof

To prove the validity of Theorem 5, we use mathematical induction with regard to variables.

Consider the initial case scenario when $\:n=2$, we have$\:\:{\alpha\:}_{1}=({u}_{{\mu\:}_{1}},{u}_{{\vartheta\:}_{1}})$ and $\:{\alpha\:}_{2}=({u}_{{\mu\:}_{2}},{u}_{{\vartheta\:}_{2}})$, applying the Dombi operational law on LPFNs, as specified in Definition 9, we obtain the following outcomes:

$$\:{\alpha\:}_{\gimel\:\left(1\right)}^{{w}_{1}}=\left({u}_{t\left(\sqrt{\frac{1}{1+{\left\{{w}_{1}{\left(\frac{{t}^{2}-{\mu\:}_{\gimel\:\left(1\right)}^{2}}{{\mu\:}_{\gimel\:\left(1\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)},{u}_{t\left(\sqrt{1-\frac{1}{1+{\left\{{w}_{1}{\left(\frac{{\vartheta\:}_{\gimel\:\left(1\right)}^{2}}{{t}^{2}-{\vartheta\:}_{\gimel\:\left(1\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)}\right);$$

$$\:{\alpha\:}_{\gimel\:\left(2\right)}^{{w}_{2}}=\left({u}_{t\left(\sqrt{\frac{1}{1+{\left\{{w}_{2}{\left(\frac{{t}^{2}-{\mu\:}_{\gimel\:\left(2\right)}^{2}}{{\mu\:}_{\gimel\:\left(2\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)},{u}_{t\left(\sqrt{1-\frac{1}{1+{\left\{{w}_{2}{\left(\frac{{\vartheta\:}_{\gimel\:\left(2\right)}^{2}}{{t}^{2}-{\vartheta\:}_{\gimel\:\left(2\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)}\right);$$

Employing Definition 11 results in the following:

$$\:LPFDOWG\left({\alpha\:}_{1},{\alpha\:}_{2}\right)={\alpha\:}_{\gimel\:\left(1\right)}^{{w}_{1}}\otimes\:{\alpha\:}_{\gimel\:\left(2\right)}^{{w}_{2}}$$

$$\:=\left({u}_{t\left(\sqrt{\frac{1}{1+{\left\{{w}_{1}{\left(\frac{{t}^{2}-{\mu\:}_{\gimel\:\left(1\right)}^{2}}{{\mu\:}_{\gimel\:\left(1\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)},{u}_{t\left(\sqrt{1-\frac{1}{1+{\left\{{w}_{1}{\left(\frac{{\vartheta\:}_{\gimel\:\left(1\right)}^{2}}{{t}^{2}-{\vartheta\:}_{\gimel\:\left(1\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)}\right)\otimes\:\left({u}_{t\left(\sqrt{\frac{1}{1+{\left\{{w}_{2}{\left(\frac{{t}^{2}-{\mu\:}_{\gimel\:\left(2\right)}^{2}}{{\mu\:}_{\gimel\:\left(2\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)},{u}_{t\left(\sqrt{1-\frac{1}{1+{\left\{{w}_{2}{\left(\frac{{\vartheta\:}_{\gimel\:\left(2\right)}^{2}}{{t}^{2}-{\vartheta\:}_{\gimel\:\left(2\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)}\right);$$

So,

$$\:{\alpha\:}_{\gimel\:\left(1\right)}^{{w}_{1}}\otimes\:{\alpha\:}_{\gimel\:\left(2\right)}^{{w}_{2}}=\left({u}_{t\left(\sqrt{\frac{1}{1+{\left\{{w}_{1}{\left(\frac{{t}^{2}-{\mu\:}_{\gimel\:\left(1\right)}^{2}}{{\mu\:}_{\gimel\:\left(1\right)}^{2}}\right)}^{k}+{w}_{2}{\left(\frac{{t}^{2}-{\mu\:}_{\gimel\:\left(2\right)}^{2}}{{\mu\:}_{\gimel\:\left(2\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)},{u}_{t\left(\sqrt{1-\frac{1}{1+{\left\{{w}_{1}{\left(\frac{{\vartheta\:}_{\gimel\:\left(1\right)}^{2}}{{t}^{2}-{\vartheta\:}_{\gimel\:\left(1\right)}^{2}}\right)}^{k}+{w}_{2}{\left(\frac{{\vartheta\:}_{\gimel\:\left(2\right)}^{2}}{{t}^{2}-{\vartheta\:}_{\gimel\:\left(2\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)}\right);$$

Consequently,

$$\:LPFDOWG\left({\alpha\:}_{1},{\alpha\:}_{2}\right)=\left({u}_{t\left(\sqrt{\frac{1}{1+{\left\{{\sum\:}_{i=1}^{2}{w}_{i}{\left(\frac{{t}^{2}-{\mu\:}_{\gimel\:\left(i\right)}^{2}}{{\mu\:}_{\gimel\:\left(i\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)},{u}_{t\left(\sqrt{1-\frac{1}{1+{\left\{{\sum\:}_{i=1}^{2}{w}_{i}{\left(\frac{{\vartheta\:}_{\gimel\:\left(i\right)}^{2}}{{t}^{2}-{\vartheta\:}_{\gimel\:\left(i\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)}\right)$$

Hence, it is valid for$\:\:n=2$.

Next, we assume that the assertion is true for $\:n=r$, that is

$$\:LPFDOWG\left({\alpha\:}_{1},{\alpha\:}_{2},\ldots,{\alpha\:}_{r}\right)={\otimes\:}_{i=1}^{r}{{\alpha\:}_{\gimel\:\left(i\right)}}^{{w}_{i}}$$

$$\:=\left({u}_{t\left(\sqrt{\frac{1}{1+{\left\{{\sum\:}_{i=1}^{r}{w}_{i}{\left(\frac{{t}^{2}-{\mu\:}_{\gimel\:\left(i\right)}^{2}}{{\mu\:}_{\gimel\:\left(i\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)},{u}_{t\left(\sqrt{1-\frac{1}{1+{\left\{{\sum\:}_{i=1}^{r}{w}_{i}{\left(\frac{{\vartheta\:}_{\gimel\:\left(i\right)}^{2}}{{t}^{2}-{\vartheta\:}_{\gimel\:\left(i\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)}\right)$$

Then,

$$\:LPFDOWG\left({\alpha\:}_{1},{\alpha\:}_{2},\ldots,{\alpha\:}_{r},{\alpha\:}_{r+1}\right)={\otimes\:}_{i=1}^{r}{{\alpha\:}_{\gimel\:\left(i\right)}}^{{w}_{i}}\otimes\:{{\alpha\:}_{\gimel\:\left(r+1\right)}}^{{w}_{r+1}}$$

$$\:=\left({u}_{t\left(\sqrt{\frac{1}{1+{\left\{{\sum\:}_{i=1}^{r}{w}_{i}{\left(\frac{{t}^{2}-{\mu\:}_{\gimel\:\left(i\right)}^{2}}{{\mu\:}_{\gimel\:\left(i\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)},{u}_{t\left(\sqrt{1-\frac{1}{1+{\left\{{\sum\:}_{i=1}^{r}{w}_{i}{\left(\frac{{\vartheta\:}_{\gimel\:\left(i\right)}^{2}}{{t}^{2}-{\vartheta\:}_{\gimel\:\left(i\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)}\right)\otimes\:\left({u}_{t\left(\sqrt{\frac{1}{1+{\left\{{w}_{r+1}{\left(\frac{{t}^{2}-{\mu\:}_{\gimel\:\left(r+1\right)}^{2}}{{\mu\:}_{\gimel\:\left(r+1\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)},{u}_{t\left(\sqrt{1-\frac{1}{1+{\left\{{w}_{r+1}{\left(\frac{{\vartheta\:}_{\gimel\:\left(r+1\right)}^{2}}{{t}^{2}-{\vartheta\:}_{\gimel\:\left(r+1\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)}\right);$$

Consequently,

$$\:LPFDOWG\left({\alpha\:}_{1},{\alpha\:}_{2},\ldots,{\alpha\:}_{r+1}\right)=\left({u}_{t\left(\sqrt{\frac{1}{1+{\left\{{\sum\:}_{i=1}^{r+1}{w}_{i}{\left(\frac{{t}^{2}-{\mu\:}_{\gimel\:\left(i\right)}^{2}}{{\mu\:}_{\gimel\:\left(i\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)},{u}_{t\left(\sqrt{1-\frac{1}{1+{\left\{{\sum\:}_{i=1}^{r+1}{w}_{i}{\left(\frac{{\vartheta\:}_{\gimel\:\left(i\right)}^{2}}{{t}^{2}-{\vartheta\:}_{\gimel\:\left(i\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)}\right).$$

Therefore, the result is valid for $\:n=r+1$. Thus, Theorem 5 is valid for each $\:n\in\:\mathbb{N}$.

Example 3

By utilizing the LPFDOWG operator on the data provided in Example 2, we acquired

$$\:LPFDOWG\left({\alpha\:}_{1},{\alpha\:}_{2},{\alpha\:}_{3},{\alpha\:}_{4},{\alpha\:}_{5}\right)={\otimes\:}_{i=1}^{5}{{\alpha\:}_{\gimel\:\left(i\right)}}^{{w}_{i}}\:$$

$$\:=\left({u}_{8\left(\sqrt{\frac{1}{1+{\left\{{\sum\:}_{i=1}^{5}{w}_{i}{\left(\frac{{8}^{2}-{\mu\:}_{\gimel\:\left(i\right)}^{2}}{{\mu\:}_{\gimel\:\left(i\right)}^{2}}\right)}^{2}\right\}}^{\frac{1}{2}}}}\right)},{u}_{8\left(\sqrt{1-\frac{1}{1+{\left\{{\sum\:}_{i=1}^{5}{w}_{i}{\left(\frac{{\vartheta\:}_{\gimel\:\left(i\right)}^{2}}{{8}^{2}-{\vartheta\:}_{\gimel\:\left(i\right)}^{2}}\right)}^{2}\right\}}^{\frac{1}{2}}}}\right)}\right);$$

$$\:=\left({u}_{8\left(\sqrt{\frac{1}{1+{\left\{0.21{\left(\frac{{8}^{2}-{6}^{2}}{{6}^{2}}\right)}^{2}+0.24{\left(\frac{{8}^{2}-{5}^{2}}{{5}^{2}}\right)}^{2}+0.3{\left(\frac{{8}^{2}-{5}^{2}}{{5}^{2}}\right)}^{2}+0.13{\left(\frac{{8}^{2}-{4}^{2}}{{4}^{2}}\right)}^{2}+0.12{\left(\frac{{8}^{2}-{3}^{2}}{{3}^{2}}\right)}^{2}\right\}}^{\frac{1}{2}}}}\right)},\:\:{u}_{8\left(\sqrt{1-\frac{1}{1+{\left\{0.21{\left(\frac{{1}^{2}}{{8}^{2}-{1}^{2}}\right)}^{2}+0.24{\left(\frac{{2}^{2}}{{8}^{2}-{2}^{2}}\right)}^{2}+0.3{\left(\frac{{3}^{2}}{{8}^{2}-{3}^{2}}\right)}^{2}+0.13{\left(\frac{{3}^{2}}{{8}^{2}-{3}^{2}}\right)}^{2}+0.12{\left(\frac{{1}^{2}}{{8}^{2}-{1}^{2}}\right)}^{2}\right\}}^{\frac{1}{2}}}}\right)}\right)$$

$$\:=\left({u}_{4.1798},{u}_{2.5443}\right).$$

Similar to the LPFDOWA operator, the LPFDOWG operator also possesses the following properties:

Theorem 6

(Idempotency) Consider number of LPFNs denoted as for defined on and be the corresponding WV of, where such that and operational parameter is. Moreover, is a permutation of such that. If for all then

$$\:LPFDOWG\left({\alpha\:}_{1},{\alpha\:}_{2},\ldots,{\alpha\:}_{n}\right)=\alpha\:$$

Proof

This Theorem’s proof is demonstrated in a straightforward manner, as shown in Theorem 2.

Theorem 7

(Monotonicity) Consider any two collections of number of LPFNs represented as and for defined on a continuous linguistic term set and is the associated WV of these LPFNs,, where such that and operational parameter is. Additionally, is a permutation of such that. If and. Then,

$$\:LPFDOWG\left({\alpha\:}_{1},{\alpha\:}_{2},\ldots,{\alpha\:}_{n}\right)\le\:LPFDOWG\left({\beta\:}_{1},{\beta\:}_{2},\ldots,{\beta\:}_{n}\right).$$

Proof

This Theorem’s proof is similar to that of Theorem 3.

Theorem 8

(Boundedness) Consider number of LPFNs denoted as for defined on and be the corresponding WV of, where such that and operational parameter is. Moreover, is a permutation of such that. Let and. Then,

$$\:{\alpha\:}^{-}\le\:LPFDOWG\left({\alpha\:}_{1},{\alpha\:}_{2},\ldots,{\alpha\:}_{n}\right)\le\:{\alpha\:}^{+}.$$

Proof

The proof of this Theorem can be executed similarly, as in the case of Theorem 4. Therefore, we exclude the repetition here.

Application of the proposed LPF Dombi AOs in MADM problems

In this section, we propose a decision-making process for a scenario by using the Dombi ordered weighted AOs on the information provided in the form of LPFNs to solve MADM problems.

Consider $\:\chi\:=\left\{{\chi\:}_{1},{\chi\:}_{2},\ldots,{\chi\:}_{m}\right\}$ be the set of alternatives and $\:Y=\left\{{Y}_{1},{Y}_{2},\ldots,{Y}_{n}\right\}$ be the set of attributes each associated with the WV $\:w={\left\{{w}_{1},{w}_{2},\ldots,{w}_{n}\right\}}^{T}$, where $\:{w}_{j}>0$, for all $\:j=\text{1,2},\ldots,n$ such that $\:{\sum\:}_{j=1}^{n}{w}_{j}=1$. Additionally, $\:\left(\gimel\:\left(1\right),\:\gimel\:\left(2\right),\:\gimel\:\left(3\right),\dots\:,\gimel\:\left(n\right)\right)$ is a permutation of $\:\left\{\text{1,2},\ldots,n\right\}.$ Consider a LPF decision matrix $\:D={\left[\left({\alpha\:}_{ij}\right)\right]}_{m\times\:n}$$\:={\left[\left({u}_{{\mu\:}_{ij}},{u}_{{\vartheta\:}_{ij}}\right)\right]}_{m\times\:n}$where $\:{u}_{{\mu\:}_{ij}},{u}_{{\vartheta\:}_{ij}}\in\:\:\overline{U}=\left\{{u}_{q}|{u}_{0}\le\:{u}_{q}\le\:{u}_{t},q\in\:[0,t]\right\}$ are the linguistic membership and linguistic non-membership degrees of the element $\:x\in\:X$ to the LPF decision matrix $\:D$ assigned by an expert under which an alternative $\:{\chi\:}_{i}$ fulfilled the attribute$\:\:{Y}_{j}$.

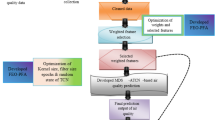
To effectively solve the MADM problem utilizing the proposed LPF Dombi ordered weighted AOs, the algorithm is structured in the following way:

Step 1 Create the LPF decision matrix using LPFNs related to the provided alternatives corresponding to attributes .

Step 2 To acquire the LPF permuted decision matrix, we follow the subsequent two stages.

• 1. Calculate the score values of all attributes $\:{Y}_{j}$, corresponding to each alternative $\:{\chi\:}_{i}\:$of the LPF decision matrix $\:D$, using Definition 8.

• 2. Arrange the calculated values from the previous stage in descending order to obtain the LPF permuted decision matrix $\:{D}_{\gimel\:\left(ij\right)}$.

Step 3 Calculate the aggregated value, of each alternative by applying the LPFDOWA operator as follows:

$$\:{\phi\:}_{i}=LPFDOWA\left({\alpha\:}_{i1},{\alpha\:}_{i2},\ldots,{\alpha\:}_{in}\right)$$

$$\:=\left({u}_{t\left(\sqrt{1-\frac{1}{1+{\left\{{\sum\:}_{j=1}^{n}{w}_{j}{\left(\frac{{\mu\:}_{\gimel\:\left(ij\right)}^{2}}{{t}^{2}-{\mu\:}_{\gimel\:\left(ij\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)},{u}_{t\left(\sqrt{\frac{1}{1+{\left\{{\sum\:}_{j=1}^{n}{w}_{j}{\left(\frac{{t}^{2}-{\vartheta\:}_{\gimel\:\left(ij\right)}^{2}}{{\vartheta\:}_{\gimel\:\left(ij\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)}\right)$$

Similarly, compute the aggregated value$\:{\:\phi\:}_{i}$ of each alternative $\:{\chi\:}_{i}$ within the context of the LPFDOWG operator in the following manner:

$$\:{\phi\:}_{i}=LPFDOWG\left({\alpha\:}_{i1},{\alpha\:}_{i2},\ldots,{\alpha\:}_{in}\right)$$

$$\:=\left({u}_{t\left(\sqrt{\frac{1}{1+{\left\{{\sum\:}_{j=1}^{n}{w}_{j}{\left(\frac{{t}^{2}-{\mu\:}_{\gimel\:\left(ij\right)}^{2}}{{\mu\:}_{\gimel\:\left(ij\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)},{u}_{t\left(\sqrt{1-\frac{1}{1+{\left\{{\sum\:}_{j=1}^{n}{w}_{j}{\left(\frac{{\vartheta\:}_{\gimel\:\left(ij\right)}^{2}}{{t}^{2}-{\vartheta\:}_{\gimel\:\left(ij\right)}^{2}}\right)}^{k}\right\}}^{\frac{1}{k}}}}\right)}\right)$$

Step 4 Calculate the score value for each $\:{\alpha\:}_{i}$, utilizing the formula provided in Definition 8.

Step 5 Analyze each alternative according to its score value in order to choose the most suitable alternative.

The grammatical view of the above algorithm is presented in Fig. 1.

Fig. 1

Pictorial depiction of Algorithm using LPF Dombi OWA\OWG operators.

Numerical illustration: a case study (Selection of an efficient AQMS to monitor air pollution)

As the world becomes ever more urbanized and industrialized, the significance of air quality has risen. The air we breathe has a profound impact on human health, environmental sustainability, and the well-being of all living beings. The introduction of air quality monitoring systems (AQMSs) are indispensable tools for characterizing atmospheric composition in the quest for healthier living conditions and understanding the air’s influence on human activities. AQMS, with its systematic measurement and evaluation of pollutants existing in the environment, such as carbon monoxide and sulfur dioxide gases, along with particle-size fractionated and volatile organic compounds, holds the potential to significantly improve human health and environmental sustainability. The data in this monitoring system is used to diagnose health risks and helps set up regulations, policy decisions, and public awareness. Therefore, robust AQMSs are vital for cities facing issues of rapid urbanization and industrial expansion to further encourage sustainable development and protect public health.

There is scientific evidence that long-term exposure to air pollution increases the probability of serious respiratory illnesses. The increase in these health issues underscores the need for considerable reductions in air pollution. Pollution-associated health problems may cost governments a lot, leading to serious public health issues as well as a dent in the economy. It is therefore important to focus on the development of reliable AQMS as a preventive measure.

Regular air quality monitoring should be carried out to identify rapidly deteriorating atmospheric conditions. These AQMSs give real time, accurate reports on pollution levels to help authorities detect new trends and quickly react to minimize health risks. The awareness provided by each particular tool inhibits the collective economic costs that would otherwise result if respiratory difficulties became ever more common^51,52,53. Historically, classical AQMSs have been characterized by their inherent massive physical size and the large costs incurred by pre-deployment (and post-deployment) stakeholders. Now, in large cities, these relatively small and expensive installations have limited their use most of the time. Moreover, while they might achieve results in terms of accuracy measurement through these traditional channels, the processes for them to operate offline are pretty laborious. This operational aspect limits the transmission of air quality data in real-time, which is a major downside. Recognizing the constraints, there is now a growing understanding of paradigmatic change in AQMS. The data’s validity in this case study is corroborated by reliable sources, as^54,55,56, which offer a solid foundation for the use of the numerical approach. The importance of monitoring strategies that are able to offer more detailed spatial and temporal resolutions that may provide a wider perspective on air quality trends is further highlighted by this evolution. This calls for an immediate solution that will generate the specific, current, and high-resolution air quality data necessary to respond adequately and in a timely way, both from decision-making support and environmental control viewpoints. In present-era requirements, we can see the strong demand for air quality data, and thus, a call to action comes that is beyond the traditional monitoring systems.

Challenges

• Technological complexities: Choosing AQMS with appropriate technological parameters can be difficult because of the constantly changing monitoring technologies.

• Budget constraints: Ensuring cost-effective solutions necessitates careful consideration of how to balance precise monitoring with financial limits.

• Continuous Monitoring: Implementing a monitoring system in changing metropolitan settings presents logistical difficulties, such as the requirement for consistent maintenance and data organization.

• Consistent Geographic Coverage: To provide consistent coverage in various geographic regions, strategic placement of monitoring equipment is necessary due to logistical challenges.

• Data Integration: For current systems to function smoothly, integrating data from air quality sensors may present technical challenges.

Conclusion: The case study shows that strategic planning is critical when selecting and installing AQMSs in metropolitan settings. A solid basis enables the development of robust monitoring systems that can adapt to changing environmental conditions. The findings of this case study serve to improve existing practices and provide guidance for future projects that aim to promote sustainable urban development and improved community health.

Implementation of numerical methods

This section provides an overview of the MADM approach used to select an effective AQMS for the purpose of mitigating air pollution. This can be achieved by applying the suggested Dombi-ordered weighted AOs in LPF settings.

In a densely populated metropolitan environment characterized by tall skyscrapers and busy streets, the quality of the air has been a persistent cause for concern. Eventually, the escalation of pollution prompts individuals to respond. The administration points an expert to undertake a thorough evaluation of the city’s requirements for monitoring air quality and meticulously review the various technologies, including factors such as accuracy, dependability, and scalability.

The expert selects the four AQMS $\:\left\{{\chi\:}_{1},{\chi\:}_{2},{\chi\:}_{3},{\chi\:}_{4}\right\}$ as a set of alternatives, where

• 1. $\:{\chi\:}_{1}=$ IQAir: Known for scientific accuracy, IQAir is widely used in hospitals, labs, and government projects for reliable air quality measurements in both professional and home settings.

• 2. $\:{\chi\:}_{2}=$ Airthings view plus: This monitor stands out for its radon detection and air quality metrics like CO₂ and particulate matter. It’s trusted due to industry certifications and consistent sensor performance.

• 3. $\:{\chi\:}_{3}=$ Yvelines: Designed for home use, Yvelines provides accurate air quality monitoring, especially for common pollutants like CO₂ and volatile organic compounds (VOCs), raising awareness about indoor air quality.

• 4. $\:{\chi\:}_{4}=$ uHoo smart air monitor: Offering comprehensive air quality readings, including humidity and VOCs, uHoo uses advanced algorithms for accuracy and integrates with smart home systems for proactive air control.

The expert investigates the efficiency and reliability of these alternatives on the basis of certain attributes $\:\left\{{Y}_{1}=Uptime\:and\:reliability\:,{Y}_{2}=Accuracy,\:{Y}_{3}=scalability,{Y}_{4}=Data\:Accessibility\:and\:Transparency\right\}$, and these attributes are further interpreted in the form of the following linguistic terms set $\:U=\left\{{u}_{0}=extremely\:inefficient,{u}_{1}=very\:inefficient,{u}_{2}=inefficient,{u}_{3}=slightly\:einfficient,{u}_{4}=neutral,{u}_{5}=slightly\:efficient,{u}_{6}=efficient,{u}_{7}=very\:efficient,{u}_{8}=extremely\:efficient\right\}.\:\:$

Step 1 Summarize the expert’s assessments for each alternative $\:{\chi\:}_{i}$ corresponding to each attribute $\:{Y}_{j}$ in the form of a LPF decision matrix, with entries as LPFNs in the following Table 1.

Table 1 LPF decision matrix.

The associated WV of four attributes suggested by the expert is$\:\:w={\left(\text{0.1,0.3,0.4,0.2}\right)}^{T}$ where $\:{\sum\:}_{i=1}^{4}{w}_{i}=1$.

$\:\varvec{S}\varvec{t}\varvec{e}\varvec{p}\:2$ In order to acquire the LPF permuted decision matrix, we follow the subsequent two stages:

• 1. Calculate the score values of all attributes $\:{Y}_{j}$, corresponding to each alternative $\:{\chi\:}_{i}\:$of the above LPF decision matrix using Definition 8.

For $\:{\chi\:}_{1}$

$$\:S\left({\:\alpha\:}_{11}\right)=1.1990,\:S\left({\:\alpha\:}_{12}\right)=0.6931,\:S\left({\:\alpha\:}_{13}\right)=0.9129,\:S\left({\:\alpha\:}_{14}\right)=1.7370$$

For $\:{\chi\:}_{2}$

$$\:S\left({\:\alpha\:}_{21}\right)=1.2151,\:S\left({\:\alpha\:}_{22}\right)=0.6145,\:S\left({\:\alpha\:}_{23}\right)=0.5818,\:S\left({\:\alpha\:}_{24}\right)=0.4070;$$

For $\:{\chi\:}_{3}$

$$\:S\left({\:\alpha\:}_{31}\right)=0.8975,\:S\left({\:\alpha\:}_{32}\right)=0.5453,\:S\left({\:\alpha\:}_{33}\right)=0.5570,\:S\left({\:\alpha\:}_{34}\right)=0.4656;$$

For $\:{\chi\:}_{4}$

$$\:S\left({\:\alpha\:}_{41}\right)=0.8975,\:S\left({\:\alpha\:}_{42}\right)=0.5818,\:S\left({\:\alpha\:}_{43}\right)=0.8742,\:S\left({\:\alpha\:}_{44}\right)=0.7288.$$

• 2. Arrange the calculated values from the previous stage in decreasing sequence to obtain the LPF permuted decision matrix.

The data is presented in Table 2.

Table 2 LPF permuted decision matrix.

Step 3:

• Obtained the aggregated value $\:{\phi\:}_{i}$, for each alternative $\:{\chi\:}_{i}$ by utilizing the LPFDOWA operator to Table 2, with the specific value of $\:k$ set to $\:2$. The outcomes of this procedure are presented in Table 3.

• Obtained the aggregated value $\:{\phi\:}_{i}$, for each alternative $\:{\chi\:}_{i}$ by utilizing the LPFDOWG operator to Table 2, with the specific value of $\:k$ set to $\:2$. The outcomes of this procedure are presented in Table 4.

Table 3 Computed aggregated values for each alternative based on the LPFDOWA operator.

Table 4 Computed aggregated values for each alternative based on the LPFDOWG operator.

Step 4

• Calculate the score value for each $\:{\phi\:}_{i}$ from Table 3 by applying Definition 8.

$$\:S\left({\phi\:}_{1}\right)={u}_{1.1746},\:S\left({\phi\:}_{2}\right)={u}_{0.7864},\:S\left({\phi\:}_{3}\right)={u}_{0.6561}\:\text{a}\text{n}\text{d}\:S\left({\phi\:}_{4}\right)={u}_{0.8070}$$

• Calculate the score value for each $\:{\phi\:}_{i}$ from Table 4 by applying Definition 8.

$$\:S\left({\phi\:}_{1}\right)={u}_{0.8597},\:S\left({\phi\:}_{2}\right)={u}_{0.4477},\:S\left({\phi\:}_{3}\right)={u}_{0.5014}\text{a}\text{n}\text{d}\:S\left({\phi\:}_{4}\right)={u}_{0.6736}$$

Step 5

• Since$\:\:S\left({\phi\:}_{1}\right)>S\left({\phi\:}_{4}\right)>S\left({\phi\:}_{2}\right)>S\left({\phi\:}_{3}\right)$, based on calculated score values for $\:{\phi\:}_{i}$, the alternatives are prioritized in the following hierarchical sequence:

$$\:{\chi\:}_{1}>{\chi\:}_{4}>{\chi\:}_{2}>{\chi\:}_{3}.$$

• Since $\:S\left({\phi\:}_{1}\right)>S\left({\phi\:}_{4}\right)>S\left({\phi\:}_{3}\right)>S\left({\phi\:}_{1}\right)$, based on calculated score values for $\:{\phi\:}_{i}$, the alternatives are prioritized in the following hierarchical sequence:

$$\:{\chi\:}_{1}>{\chi\:}_{4}>{\chi\:}_{3}>{\chi\:}_{2}$$

Hence, IQAir emerges as an efficient AQMS alternative to monitor air pollution.

Comparative analysis

This analysis is conducted by comparing the proposed approaches with the existing methodologies, namely, LIF ordered-weighted averaging (ordered-weighted geometric) operators¹⁷ and LPF ordered-weighted averaging (ordered-weighted geometric) operators²⁹. The results produced by the implementation of these operators are described in Table 5 and are sequentially ranked in Table 6.

Table 5 Aggregated values of the alternatives using the existing and newly proposed methods.

Table 6 Score value and corresponding ranking of alternatives under both existing and newly proposed methods.

Comparison 1. Zhang’s model, as stated in reference¹⁷, has shortcomings in accurately depicting the connection between linguistic membership and linguistic non-membership in a unified manner because the sum of linguistic MD and linguistic NMD exceeds a certain interval. The LPF environment studied in this article addresses this limitation. This is accomplished by squaring both terms and maintaining that the sum of their squares is less than or equal to the squared cardinality of the set. We use the LPF Dombi AOs in those situations where more advanced handling of uncertainty is needed beyond what the traditional LIF environment can offer. Moreover, the dynamic properties of these techniques would be of great help in decision-making processes impeded by complex and uncertain information. Furthermore, the methods proposed in¹⁷ are versatile enough to handle the MADM problem mentioned above, but their effectiveness is low because they cannot entertain extended parameter values. On the other hand, our developed Dombi-ordered weighted aggregation mechanism in the LPF knowledge framework is significantly interesting, particularly for solving MADM problems by considering a parameter-driven approach rather than a valuated fusion method that makes it flexible during transitions and gives more control on the aggregation process with better reliable results as compared to others. Consequently, this also allows for better combination over complicated linguistic previsions, providing more accurate and adjustable decision-making outcomes compared to the LIFOW AOs.

Comparison 2. The techniques outlined in reference²⁹ are limited in their capacity to effectively handle imprecise decision-making scenarios because they cannot accurately reflect nuanced uncertainty using parametric values. The suggested models are adaptable and provide a highly customizable approach. They are unique in their ability to accurately quantify complexity-induced uncertainty with parameter values. This uniqueness makes the proposed models more flexible and allows for a higher level of customization. Parameterizing these strategies can adjust many aspects of the aggregation process, which makes managing uncertainty a more accurate experience. Flexibility is crucial, particularly when a more accurate handling of uncertainty is required beyond the capabilities of any significant aggregate operators. The models²⁹ cannot effectively solve the previously mentioned MADM problem because they are not flexible enough for variable parameter adaptation. However, Dombi-ordered weighted AOs in the LPF framework proposed in this article are unique because they can offer adjustable regularization depending on parameters. This facilitates the handling of complex linguistic assessments that can be analyzed and combined at a much more reliable level in decision outcomes compared with LPFOW AOs.

Comparison 3. The strategies delineated in³⁸ neglect to consider scenarios where human-centered interpretation and qualitative aspects are crucial, whereas the newly introduced techniques offer a method for addressing the variations between Pythagorean fuzzy numbers and linguistically comprehensible expressions.

Comparison 4. The LPFDOW AOs, based on the order in which data points are ranked, can take into consideration simultaneously both the relative importance and position of a rating among data points, which may give a more accurate estimation of air quality when compared to the last distinct pairwise fuzzy preference relations. They also monitor when the pollution starts to increase or decrease during the day. The LPFDOW operator retains the data sequence by employing identical fundamental operations and assigns higher importance to more recent measurements by assigning them greater weight. It is very convenient for controlling the regeneration of pollution by a factory, as it can demonstrate leakage or growth problems. It is capable of considering different phase processes (sensor orders, which refer to the sequence in which different sensors detect pollution) to find the underlying cause using the LPFDOW operators.

The graphical illustration of the discussion presented in Tables 5 and 6 is depicted in Fig. 2.

Fig. 2

Graphical illustration of ranking of alternatives using different methodologies.

The above discussion shows how these methods are more useful than the traditional ones, which have already been presented in existing methodologies. Consequently, the LPF Dombi-ordered weighted AOs consider preference changes and thereby reduce the information loss encountered by conventional LPF operators. The parameters are used to highlight the flexibility of the recently proposed operators. Compared with LPFS and LIFS, LPF Dombi-ordered weighted AOs provide a better approach. They are good frameworks to deal with linguistic expressions and Pythagorean uncertainty simultaneously, so they can be used for a wide range of possible problems.

Conclusions

In this paper, the concepts of the LPFDOWA and LPFDOWG operators have been established by integrating the LPFS and Dombi AOs. A novel score function has been formulated, facilitating the ranking and selection of the most optimally suitable choice. Moreover, many important fundamental LPF Dombi aggregation laws have been explored, and various structural properties of LPFDOWA and LPFDOWG operators have been established. A systematic mathematical mechanism has been devised for MADM problems by implementing the suggested techniques in the framework of LPF information. Furthermore, the effectiveness of these new methods has been verified by presenting a solution to the MADM problem of selecting an efficient AQMS to monitor air pollution. In addition, a comparative analysis has been conducted to demonstrate the efficiency and applicability of newly defined methodologies in comparison to existing knowledge.

Limitations of the current study

Upon assessing the suggested operators in comparison to alternative methods, it is clear that they produce aggregate results that are both understandable and satisfactory to the decision-maker. Although the approaches delineated in this article offer numerous advantages, they are subject to certain limitations:

• These strategies are not capable of handling circumstances in which the sum of the squared linguistic MD and linguistic NMD exceeds $\:t$, where $\:t$ represents the cardinality of the linguistic terms set.

• This research may not be appropriate for scenarios involving data gathering at varied time intervals due to the lack of an inherent dynamic adjustment mechanism to address MADM concerns.

Potential goals of future studies

• The techniques developed in this article will be applied to more generalized environments, specifically linguistic Fermatean fuzzy, linguistic interval-valued Fermatean fuzzy, and linguistic Pythagorean fuzzy dynamic settings to rectify the above-mentioned limitations.

• We will investigate the superiority and applicability of the proposed methodologies by successfully applying them to many important decision-making scenarios in various fields like environmental modeling, medical diagnostics, artificial intelligence, etc. We will further broaden the scope of the newly proposed methodologies to the strategies developed in^57,58,59.