Introduction

The internal structure of the breast, which includes the adipose and glandular tissues, Cooper’s ligaments, and blood vessels, plays a crucial role in breast support and health1. However, frequent exercise can increase breast displacement, potentially causing breast pain which poses a risk of damaging the internal breast tissues, a problem that is challenging to observe objectively. Therefore, understanding the biomechanics of the breast and its response to physical activities is essential in designing suitable sports bras that provide unique support and protection for women.

Studies have shown that exercise-induced breast discomfort is related to the vertical displacement of the breasts2,3, and the strain caused by nipple movement that exceeds the static strain limitation4. In terms of internal structure, breast pain is also concerned with tension in the fine structure (skin and Cooper’s ligaments) that help to support the breast5. These findings reveal the importance of characterising the mechanical behaviour and properties of the internal structure of the breast. However, studies that focus on the mechanical properties of the Cooper’s ligaments and their interaction with the adipose tissues remain scarce6.

In breast motion research, infrared cameras7 or motion capture systems4 have been broadly adopted to obtain breast motion with the use of reflective markers on the body of the subjects. These techniques can help researchers obtain the movement displacement and acceleration of the breast under different motion conditions. In these studies, running is the most important activity for studying breast motion. The literature7,8,9,10 has reported relative breast displacement, the movement of breast tissues in relation to the trunk, in the vertical (4.2–11 cm), medial lateral (1.8–6.2 cm), and anterior posterior (2.2–5.9 cm) directions during running on a treadmill without bra support. The vertical acceleration is about 2.8–4.87 g4,8,10. Comparatively speaking, running causes greater breast displacement than walking9. However, studies have been done that show breast displacement during other activities. For example, Risius et al.11 studied multiplanar breast kinematics during running, jumping and agility tasks. Langenderfer and Ustinova12 studied the nonlinear properties of breast, thorax and upper-arm movements during jumping jacks. Ocran et al.13 specifically examined breast movement during golfing with emphasis on the upper-body twisting. Furthermore, Zhou et al.14 used a mixed model to study breast deformation and predict nipple movement in older women during yoga. Even though these studies provide valuable insights into breast motion across a variety of sports and emphasise the significance of sport-specific movements, the changes in the internal structure of the breasts during movement have been largely neglected.

The finite element (FE) method is a commonly used approach in the field of biomechanics for simulation purposes15,16. Current studies have used the FE method to simulate breast behaviour in a variety of activities, such as walking, running, jumping or specific physical activities. Chen et al.17 constructed a 3D dynamic FE model composed of the torso, breast and three layers of skin. A hyper-elastic Neo-Hookean material model is used to simulate the large nonlinear deformation of the breast tissues, and yields accurate predictions of breast displacement during running. Cai et al.18 used a theoretical mathematical model to study the viscoelastic behaviour of the breasts during free vibration and running. A 3D FE model that includes the torso and breast was constructed to predict nipple displacement. Liu et al.19 utilised the FE method to predict breast deformation during jumping, and incorporated the torso and breasts into their model. The material coefficient of the Mooney-Rivlin hyperelastic model of the breast is a direct reference to research work by Abbas Samani20. However, the direct utilisation of breast coefficients in previous studies may result in a large difference between the set material coefficient in the model and the actual material properties, thus potentially affecting the accuracy of the model. An iterative search of the material coefficient is still necessary. Liang et al.21 conducted an FE analysis to simulate breast displacement under static and dynamic running conditions. Their FE model included a rigid torso, breast, and subcutaneous tissues. The Mooney-Rivlin material coefficient of the breast was determined by iteratively examining the discrepancies between the FE modelled results and experimental data. Similarly, Zhang et al.22 employed a nonlinear biomechanical FE model to simulate breast deformation of older women with arm abduction during yoga. The FE model consisted of the trunk, breast, pectoral major muscles and bones. Among them, the Moony-Rivlin coefficient of the breast was determined by using a forward-leaning method specifically developed for the elderly23. These studies serve as valuable sources of information for the development of a dynamic biomechanical model of the breasts with the FE method.

Nevertheless, these studies all have certain limitations. First, they focused solely on the FE modelling of the breast and torso. The biomechanical behaviour of the internal structure of the breast, such as the adipose and glandular tissues, and Cooper’s ligaments, has been somewhat overlooked24. Given the importance of the internal structure of the breast, medical research typically constructs static breast models that incorporate the internal components based on magnetic resonance imaging (MRI) data. For instance, Del Palomar et al.25 proposed an FE model for breast biomechanics, which includes the fatty and fibroglandular components, to predict the position and shape of the breast under the influence of gravity. Similarly, Dufaye et al.26 presented a hyperelastic model of the static behaviour of the breast based on FE simulations, which also took into account fat and roughly glandular components. Sturgeon et al.27 took another approach and constructed an FE model of the breast based on a template. This model utilised voxel-based segmentation that automatically adjusted to the geometry of the breast and body models. Material properties were assigned based on the segmented voxels, thus allowing for a more accurate representation26. Mira et al.28 also developed and evaluated a biomechanical FE model of the breast that considers the adipose tissues, muscles, skin, suspension ligaments, and thoracic fascial muscles. However, it is worth noting that their model utilised a linear unit structure for the Cooper’s ligaments, which deviates from the anatomical reality of the breast. More importantly, these medical studies have only examined the breast in the static state and neglected the crucial aspect of simulating the motion of breast tissues under significant strains, thus revealing a research gap in this domain. Secondly, existing breast kinematics research, which have used various methodologies, primarily emphasises breast motion during running, but neglects the fact that women participate in a wide range of sports and exercises, many of which have varying intensities of motion, particularly those that involve similar motion patterns.

An advanced nonlinear large strain FE model that considers multiple components of the breast could provide a clear picture of the intricate biomechanical behaviours of the breast tissues under different types of movements and at different activity intensities. This advanced model is a vital tool for describing the nuanced effects of various exercises and their respective intensities on the internal structure of the breast, thus facilitating accurate quantification of activity level and exertion intensity. This model is of paramount importance, as it paves the way for a better understanding of breast dynamics across a range of different physical activities and varying degrees of exerted force. The findings of this study have valuable contribution to the field of sports medicine and sports bra design, thus offering a critical lens to examine the physiological response and support of the breast tissues during exercise.

The objective of this study is to develop a dynamic FE model of multiple components of the breast to study the impact of different types of activities at different intensities. Dynamic data of subjects who engage in different types of movements and their intensities are acquired by using 4D scanning technology and motion capture systems. Geometric modelling is used to construct an FE model of the biomechanics of the different breast components. The optimal material parameters are determined through a stepwise grid search method. Following the validation of the FE model, a comparison is made to evaluate the biological responses of the internal components of the breast during different types of activities and their intensities.

Materials and methods

Subjects

In this study, three subjects who are between 24 and 28 years old with a bra size of 80 C (metric bra sizing system) participated in the experiment. These subjects, designated as subject 1, 2, and 3, are 160–162 cm height, 58–60 kg weight, and 22.5–23.4 body mass index (BMI). These subjects gave signed informed consent before taking part in the experiment, which was approved by the Human Subjects Ethics Sub-committee of the Hong Kong Polytechnic University (Approval No. HSEARS20211012001). All methods were performed in accordance with the relevant guidelines and regulations.

Data collection

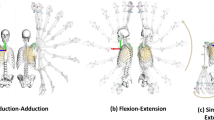
The experiment aimed to compare breast motion during different activities (running, jumping rope, high knee skipping) at different intensities, as outlined in Fig. 1a. These activities use common daily movements with regular and comparable patterns of movement. Specifically, the selected activities for the experiment included running on a treadmill at speeds of 4, 6, and 8 km/h, and jumping rope at a rate of 100, 120, and 140 skips/min29,30. High knee skipping is a good warm-up exercise31; and its rate was set at 120, 140, and 160 skips/min32. The rate of jumping rope and high knee skipping was controlled by using a metronome. As shown in Fig. 1b, the subjects are braless and flat markers are used as markers (outer diameter: 6 mm, inner diameter: 3 mm) on their body. The marker placement is based on8,21,33. The X, Y and Z directions represent the mediolateral, vertical directions, and anteroposterior directions respectively. A 4D scanning system (3dMD system, US) was used to scan the subjects to obtain the surface data during movement. The subjects were asked to stand as a standard standing position, which is the standard posture for 3D body scanning, and then initiate and maintain the prescribed movements for 30 s. The 4D scanning system has 30 machine vision cameras that can capture 120 frames per second. A motion capture system (VICON Vero, Nexus 2.15, UK), which has 12 digital cameras and can capture 120 frames per second, was employed to capture the trajectories of the markers on the body.

Fig. 1
figure 1

Experimental setting: (a) type of activity; (b) position of markers.

Full size image

3D image processing

The motion data of the clavicle from the motion capture system were used as input for the dynamic FE model, and denoised by using a low-pass filter (zero lag 4th order Butterworth filter, cut off frequency fc = 6 Hz)34. Subsequently, the 3D static data of a standard standing position derived from the 4D scanning were imported into Geomagic Design X software (US) to generate the initial geometric model. The model underwent preprocessing steps including removing the head and limbs, filling the holes, and smoothing the torso. The initial model consisted of a rigid torso and a layer of subcutaneous soft tissues. The thickness of the layer of subcutaneous soft tissues was determined based on the BMI of the subjects and the relevant literature35,36. The breast region was extracted from the soft tissue model based on the breast contours.

Construction of gravity-free breast model

During the 4D scanning process, the breasts naturally deformed due to gravity. In this study, it is necessary to first obtain a gravity-free breast model before simulating breast motion under the effect of gravity. The gravity-free breast model served as the initial geometric configuration for the FE modelling of multiple components of the breast. An inverse algorithm24,37 was employed by using MSC Marc 2020 software (US) with Python 3.9.16 to construct the gravity-free breast model. The objective function of the iterative inverse algorithm used in this study aimed to minimise the discrepancy of the surface shape error between the computed model and the measured geometry under gravity. The algorithm iteratively adjusted the external force parameters of the model until convergence was achieved. The process was to apply upward gravity on the breast and then downward gravity. Finally, the initial shape of the gravity-free breast was obtained through successive iterations by comparing the shape of the breast under gravity with that obtained through 4D scanning.

Geometric model construction

After obtaining the gravity-free model, the geometric model of the multiple components of the breast was constructed based on breast anatomy. This geometric model of the breast has seven components, including a rigid torso, an outer layer of soft tissues, skin, pectoralis major muscles, Cooper’s ligaments, and glandular and breast adipose tissues, as shown in Fig. 2. The process and details of this geometric model are based on38. Then, all solid sub-models were built by using a Boolean operation. Boolean operations enable the combination and manipulation of shapes to create complex models. In this context, operations such as union, intersection, and difference were employed to accurately represent the breast’s intricate anatomy. Each component was modelled to reflect its unique characteristics and spatial relationships. For example, the intersection operation defined precise boundaries between the skin and underlying tissues, while the difference operation carved out space for the pectoralis major muscles. All of the solid sub-models were meshed by using four-node tetrahedron elements in MSC Apex Software (US), and the skin was meshed by thin triangular shell elements. The mesh size of each breast component was determined by using a grid convergence analysis, which obtained the mesh sizes of outer layer of soft tissues (8 mm), skin (8 mm), pectoralis major muscles (4 mm), Cooper’s ligaments (4 mm), and glandular (6 mm) and breast adipose tissues (6 mm). Seed points for common nodes were set on the contact surface to ensure that the force transfer was continuous during the simulation.

Fig. 2
figure 2

Geometric model of the multiple components of breast. MSC Apex software (MSC Apex 2020, US, https://hexagon.com/products/msc-apex-modeler ) used for geometric modelling and meshing.

Full size image

Material properties

In this study, all of the soft tissues were considered to be a homogenous isotropic hyper-elastic material with nonlinear behaviour. Considering the quasi-incompressibility of the material, a Poisson’s ratio (ν) of 0.49 was assigned to these soft tissue materials22,28. The material of the breast adipose tissues is referred to as a fifth-order Mooney-Rivlin material with 5 coefficients, which are defined to represent their nonlinear behaviour with larger deformations. Table 1 shows the density and the initial material coefficients of the adipose tissues (C10, C01, C11, C20, and C02) refer to the ex-vivo breast properties in Samani’s study20. To manage the computational complexity, other breast components, including the skin, layer of soft tissues, pectoralis major muscles, Cooper’s ligaments and glandular tissues, were characterised by using a Neo-Hookean model39. The Young’s modulus (E) and the density of the soft breast tissues, modelled by using the Neo-Hookean constitutive model, were determined based on relevant published studies, which are listed in Table 1. The existing studies suggest that normal glandular tissues are 1 to 6.7 times stiffer than adipose tissues40.

Table 1 Material properties of components using Mooney-Rivlin and Neo-Hookean models.
Full size table

To optimise material coefficient of determination, a stepwise grid search method was employed to obtain the optimal approximate solution of the Mooney-Rivlin coefficients of the breast adipose tissues. In the coefficients of the fifth-order Mooney-Rivlin constitutive model, since \(E=6({C_{10}}+{C_{01}})\)20 and Young’s modulus E are highly correlated with material stiffness46, it can be inferred that C10 and C01 play a crucial role in determining the material stiffness. Material stiffness is the main factor that affects nonlinear biomechanical behaviour. Consequently, the initial parameter values of C11, C20, and C02 were initially held constant. Given that\(E=6({C_{10}}+{C_{01}})\), then:

$${E_1} \leqslant 6({C_{10}}+{C_{01}}) \leqslant {E_u}$$
(1)

Where E1 (0.5 kPa) and Eu (25 kPa) are the minimum and maximum boundaries of the Young’s modulus E of the breast adipose tissues, respectively45,47, and 1/6 of E1 and Eu are recorded as a and b, respectively. Besides, to meet the positive definiteness requirements of the parameters, the constraints of C10 and C01 are shown in Fig. 3. The search scope is shown in Fig. 4 (shaded in gray). The objective function f(Cij) is the relative mean absolute error (RMAE) value (see Eq. 2) between the FE simulation results and experimental data from the motion capture system during running at 6 km/h. The average RMAE of all directions was calculated for each marker. The average RMAE of all of the markers was calculated to obtain the objective function f(Cij).

The stepwise grid search method is shown in Figs. 3 and 4. p is the search step size, which can be adjusted according to the accuracy requirements. The steps are:

Step 1 First-level search: Let C10 and C01 denote independent variables x and y, respectively. Assume that C10 is equal to C01, which implies x = y. Using a step size of p1, the function f is calculated through the traversal, which is shown in blue in Fig. 4. Subsequently, the independent variables (x1, y1) which corresponds to the minimum value of function f of the first-level search are obtained.

Step 2 Second-level search: aims to improve accuracy and further find the optimal value of the Young’s modulus E. Again, assume C10 = C01, which means that x = y. Using a step size of p2, the function f is calculated through the traversal to obtain the independent variables (x2, y2) that correspond to the minimum value of function f of the second-level search, which is shown in purple in Fig. 4.

Step 3 - Third-level search: done under the premise that the optimal Em value has been found, specifically 6(x2 + y2) = Em. The third level search aims to find the optimal values for the components C10 and C01, denoted as x and y, respectively. By utilising a step size of p3, the function f is calculated ergodically, and shown in orange in Fig. 4. Finally, the independent variable (x3, y3) of the minimum value of function f of the third-level search is obtained.

Step 4 Fourth-level search: Given that the optimal values for C10 and C01 have been determined, the fourth-level search is conducted to identify the suitable components C11, C20 and C02. The scaling factor is 2p4, which uses a step size of p4, and function f is iteratively calculated. Consequently, the independent variables (C10, C01, C11, C20, C02) that correspond to the minimum value of the function f of the fourth-level search are obtained.

The search process for the optimal approximate solution involves a total of 26 iterations which ensures that Cij represents the optimal approximate solution within the given limited computational resources.

Fig. 3
figure 3

Optimal material parameters flow.

Full size image
Fig. 4
figure 4

Search scope and process.

Full size image

Boundary conditions and simulation

For computational efficiency, the left half of the model was utilised for the FE simulation. Using MSC Marc 2020 software (US), symmetrical boundary conditions were applied to establish the sagittal plane as symmetrical. The upper body model comprised a rigid torso and six deformable soft tissue components, with these components contact modelled through glued interaction. A downward gravity field with an acceleration of 9800 mm/s2 was applied onto the breast components, including the adipose and glandular tissues and Cooper’s ligaments. Motion boundary conditions were set based on experimental data. Among them, running and high knee skipping are motion boundary conditions in the X and Y directions. Jumping rope has only the motion boundary condition in the Y direction. During simulation, a static structural analysis was conducted to simulate the effects of gravity loading. Subsequently, dynamic simulation of the multiple components of the breast was performed by using a transient dynamic analysis with the implicit dynamic method. The full Newton-Raphson method was used as the iterative solution method.

Validation method

Previous studies21,22,37 have compared FE simulation results and experimental data and focused on specific landmarks of the body, including the clavicle, shoulders, and nipple points. In this study, more markers are used (20) for comparison and verification. The assessment criterion for evaluating the differences between the simulated and experimental results is the relative mean absolute error (RMAE)48:

$$RMAE=\frac{1}{N}\sum\limits_{{i=1}}^{n} {\left| {\frac{{{D_{EXP}} - {D_{FEM}}}}{{{D_{EXP}}}}} \right|}$$
(2)

where \({D_{EXP}}\) and \({D_{FEM}}\) are the displacement of the key points obtained from the experimental and simulation data, respectively. N represents the total number of sample data points in one motion trajectory. The average RMAE is obtained within these markers.

Results and discussion

Search results of optimal material parameters

The optimal material parameters for the three subjects are shown in Fig. 5. Figure 5a, b and c show that when the objective function f, defined as the average RMAE value of every marker point, reaches its minimum, the optimal Mooney-Rivlin coefficients C10 and C01 for the breast of each subject are obtained through a three-level iterative search. As shown in Fig. 5d, the fourth-level search results indicate when p4 is set to 0, which leads to the scaling factor remaining at 1 (20=1), the objective function f reaches its minimum. The objective function f converges to 8.8681%, 7.0026% and 5.3133% for Subjects 1, 2 and 3, respectively. Given that all values are less than 10%, the accuracy is acceptable28,37. The optimal Mooney-Rivlin coefficients Cij for the breast of the three subjects are also shown in Fig. 5.

Fig. 5
figure 5

Optimal material parameters for subjects with stepwise grid search method: (a) Subject 1; (b) Subject 2; (c) Subject 3; (d) Fourth-level search results.

Full size image

Validity of FE simulation of motion

The effectiveness of the model was assessed by comparing the Euclidean distance between the experimental data and the nodes of the FE simulation, measured as the RMAE. The verification results are shown in Table 2. The table shows the average RMAE of marker points obtained from the nine motion conditions of the three subjects in the X, Y, and Z directions. The majority of average RMAEs are less than 6%, with only a small minority exceeding 8%, which shows validity49.

Table 2 RMAE results of subjects from nine motion conditions.
Full size table

Effect of type of activity on biomechanical behaviour of internal components of breast

According to the data obtained from the motion capture system, the vertical displacement and acceleration of the breast peak at moment ta when the foot is in full contact with the ground. The FE simulation also obtained similar results; the vertical displacement and acceleration of the breast components peak at the time of maximum impact (time ta). During the motion cycle, the maximum impact occurs at time ta, so the maximum stress of each breast component also occurs at time ta. Figure 6a shows the maximum equivalent von Mises stress of the breast internal components under different types of movement at time ta. A running speed of 6 km/h and jumping rope and high knee skipping rate of 120 skips/min are used to compare the impact of these different types of movement on the breast. Running, jumping rope and high knee skipping are denoted as R, J and H, respectively. Figure 6b shows the equivalent von Mises stress nephogram of the breast internal components of Subject 1 during these three tasks at time ta.

Fig. 6
figure 6

Maximum equivalent von Mises stress of breast internal components during different activities at time ta: (a) Different movements of subjects; (b) Stress nephogram of Subject 1. MSC Marc software (MSC Marc 2020, US, https://hexagon.com/products/marc ) used for finite element analysis (FEA) simulations.

Full size image

Figure 6 show the interactions between the breast components. The maximum equivalent von Mises stress of the breast internal components in ascending order is the glandular tissues, pectoralis major muscles, adipose tissues, and Cooper’s ligaments. The Cooper’s ligaments are the main supporting structure of the breast tissues2,8,50,51, which are elastic connective tissues, and have higher extensibility and contraction during exercise, so they are most susceptible to stress. The adipose tissues are second most susceptible to stress, primarily in the regions that come in contact with the glandular tissues and Cooper’s ligaments. As they have a larger mass and fluidity, the adipose tissues tend to vibrate more vigorously as the body moves. This increase in motion may contribute to greater breast swing or oscillation, potentially leading to elevated stress levels within the adipose tissues. The pectoralis major muscles support the breast by concentrating stress at the point of contact with the Cooper’s ligaments. The glandular tissues are subjected to the least amount of stress, and the stress is primarily located in the posterior region. This is because the tissues are located deep within the breast, surrounded by protective fat and other tissues, which reduce direct impact and vibration during exercise.

Figure 6a shows that among the three different types of activities analysed, jumping rope results in the highest stress levels on the internal components of the breast, followed by high knee skipping, while running incurs the lowest stress levels. Subject 1 shows a maximum stress of 29.58 kPa in her Cooper’s ligaments during jumping rope, whereas high knee skipping and running result in maximum stresses of 23.88 kPa and 18.98 kPa, respectively. Similarly, Subject 2 demonstrates a maximum stress of 27.61 kPa in her Cooper’s ligaments during rope jumping, with high knee skipping and running resulting in maximum stresses of 20.27 kPa and 17.73 kPa, respectively. Subject 3 follows a similar trend. This may be because of the different landing methods. When jumping rope, the entire body is lifted off the ground and hovers briefly before hitting the ground again. The impact of this vertical jump is usually greater than running or high knee skipping. Every time the feet hit the ground, the breast tissues are subjected to a downward force, which may lead to higher tension and vibration of the Cooper’s ligaments and adipose tissues in the breast, thus resulting in the highest amount of stress. Running and high knee skipping require alternately landing on one foot, and the impact force is distributed on both feet, so the vertical impact force is relatively smaller when landing. However, compared to running, the vertical range of motion of the lower limbs during high knee skipping is greater which is harder on the body. Therefore, there is more stress on the breast tissues during high knee skipping than running. In a previous study, Gefen and Dilmoney45 conducted analytical approximations to quantify the forces exerted on the breasts during routine activities. They calculated the corresponding internal forces supported by the Cooper’s ligaments, pectoral fascia, and ribs. Their findings indicate that during walking, running, and jumping, the forces on the Cooper’s ligaments increase to approximately 15 N, 50 N, and 60 N, respectively.

Effect of intensity of activity on biomechanical behaviour of breast internal components

Figure 7a, b, and c shows the maximum equivalent von Mises stress of the breast internal components during different activity intensities (speed/rate) during running, jumping rope exercises and high knee skipping, respectively. It compares the simulated stress on each breast component, relationship between stress and intensity, and significant effect of intensity on the stress on the breast components.

Fig. 7
figure 7

Breast internal components during different intensities (speed/rate) during different activities: (a) Running; (b) Jumping rope; (c) High knee skipping.

Full size image

During running (see Fig. 7a), the internal breast components experience stress in the following ascending order: the glandular tissues, pectoralis major muscles, adipose tissues, and Cooper’s ligaments. Taking Subject 1 as an example, at a running speed of 8 km/h, the stress experienced of the glandular tissues, pectoralis major muscles, adipose tissues, and Cooper’s ligaments can reach 3.89 kPa, 6.12 kPa, 10.56 kPa, and 27.11 kPa, respectively. Running speed is directly proportional to the stress on the Cooper’s ligaments; as the speed increases, so does the stress on the Cooper’s ligaments. Similarly, the stress on the adipose tissues increases with increase in running speed, which can be attributed to its large volume and close connections to the ligaments. Running speed is also proportional to the stress on the pectoralis major muscles as the muscles provide additional support. When the running speed increases, the inertia of the breast tissues also increases, thus allowing the breast to maintain motion at higher speeds. This results in greater inertial force, and consequently, increased stress on the supporting structures (including the Cooper’s ligaments and pectoralis major muscles), and adipose tissues. However, the stress on the glandular tissues is the lowest and therefore, these tissues are the least affected. Despite changes in speed, the proportional relationship between speed and stress on the glandular tissues is relatively small. By using linear fitting between the speed and equivalent von Mises stress, slope k quantifies the significance of running speed on stress. Among the breast components, slope k, in descending order, is: the glandular tissues, pectoralis major muscles, adipose tissues, and Cooper’s ligaments. The k value of the Cooper’s ligaments is higher than that of the adipose tissues, which indicates that speed has a more significant effect on the Cooper’s ligaments. For example, Subject 1 shows that the equivalent von Mises stress for the Cooper’s ligaments at a running speed of 8 km/h is 8.13 kPa higher than that at 6 km/h. However, the stress on the adipose tissues when running at 8 km/h is only 5.25 kPa higher than that at 6 km/h. This shows that running speed has a relatively large effect on the stress experienced by the Cooper’s ligaments. In contrast, the k values for the glandular tissues of Subjects 1, 2 and 3 are only 0.1, 0.083 and 0.17, respectively, which are significantly lower than those for the other breast components. This indicates that running speed has little effect on the stress on the glandular tissues.

During the jumping rope exercises (see Fig. 7b), the breast components are subjected to different levels of stress. The ascending order of stress to the breast components is: the glandular tissues, pectoralis major muscles, adipose tissues, and Cooper’s ligaments. That is, the Cooper’s ligaments are subjected to the most stress. For example, at a rate of 140 skips/min, the stress on the Cooper’s ligaments of Subject 1 reaches as high as 35.59 kPa, while the adipose tissues reach 16.24 kPa. The stress on the glandular tissues and pectoralis major muscles is 4.22 kPa and 10.65 kPa, respectively. The rate of jumping rope is proportional to the stress on the breast components. As the rate is increased, the vertical speed and inertia force also increase, thus resulting in greater stress on the breast tissues. The value of the slope k, obtained through linear fitting of the rate and stress, indicates the degree of correlation between these variables. Among the breast components analysed, the slope (k) values follow the order: glandular tissues < pectoral major muscles < adipose tissues < Cooper’s ligaments. This indicates that the positive correlation between rate and stress is the most significant for the Cooper’s ligaments because higher rates of jumping lead to more intensive stretching and contracting of the Cooper’s ligaments, thus enhancing their supportive effect. The second most significant effect of the rate of jumping rope is on the adipose tissues, where a high rate of jumping can lead to higher vibration amplitude of the fluid-like adipose tissues, thus affecting stress levels. However, an increase in rate of jumping has a minimal effect on the glandular tissues because these tissues are small in volume and located deeper within the adipose tissues, thus making them less susceptible to vibration.

During high knee skipping (Fig. 7c), the stress experienced by the breast components follows the order of glandular tissues < pectoral major muscles < adipose tissues < Cooper’s ligaments, from lowest to highest stress levels. For instance, at a rate of 160 skips/min, the Cooper’s ligaments of Subject 1 are subjected to the highest stress, which reach 32.29 kPa. The stress on the pectoralis major muscles and adipose tissues can reach 5.59 kPa and 13.99 kPa, respectively. The stress on the glandular tissues is the lowest at 3.75 kPa. The slope k value, obtained by linear fitting the rate and stress, indicates correlation between these variables. There is a significantly positive correlation between rate of skipping and stress on the Cooper’s ligaments for Subject 1, with a k value of 0.21. But the R square value obtained by linear fitting is too scattered for other subjects. A second-order (quadratic) polynomial fitting was applied to fit the changing trend. Then it could obtain the fitting equations between rates (x) and stress (y) of Subject 1 (-0.001 x2 + 0.36 x -11.89 = y, R2 = 1), Subject 2 (0.006 x2-1.67 x + 139.50 = y, R2 = 1), and Subject 3 (0.021 x2 -5.71 x + 397.05 = y, R2 = 1). It indicates that the stress of the Cooper’s ligaments reaches the minimum at the rate of 140 skips/min for subjects 2 and 3. Next, the correlation between the rate of skipping and stress on the adipose tissues is less significant (k = 0.1). For adipose tissue, when the rate increases from 120 skips/min to 140 skips/min, the change in stress is 3.82 kPa. However, when the rate of skipping increases from 140 skips/min to 160 skips/min, the change in stress is only 0.26 kPa. A similar pattern is observed for the other breast components, where the change in stress is relatively small when the rate in skipping increases from 140 skips/min to 160 skips/min. It can be inferred that as the rate of high knee skipping increases, the stress on the breast tissues proportionally increases. However, beyond a certain threshold, the influence of rate of skipping on the breast component diminishes. This could be due to the balance of forces exerted on the breast tissues during the alternating leg movement with high knee skipping. Consequently, regardless of the increase in rate of skipping, the impact on the breast components remains minimal. Moreover, the influence of the rate of skipping on the pectoralis major muscles and glandular tissues appears to be insignificant.

Potential application and limitation

The findings provide valuable guidelines for further research into the relationships among activities types, exercise intensity, and stress on the breasts, and potentially lead to new insights into breast health and injury prevention. Sports bra manufacturers can utilise these findings to design bras that offer targeted support for high-impact activities, such as jumping rope and high knee skipping, by focusing on materials and features that reduce stress on the Cooper’s ligaments and accommodate different exercise intensities and rates, thus ensuring optimal wear comfort and protection. In postoperative nursing care for individuals who are recovering from breast augmentation, breast reduction, or a mastectomy, understanding the impact of stress from exercise on the breast components is crucial. This knowledge guides the type of exercise carried out and changes made to its intensity or format, thus minimising stress on the breast tissues and surgical incisions. Considering the effect of speed and rate of exercising on the internal breast components can contribute to appropriate exercise recommendations, thus protecting sensitive areas, including the Cooper’s ligaments and more vulnerable tissues, during the healing process. Moreover, these studies can translate into valuable suggestions for personalised training, thus enabling coaches to offer tailored advice to their clients regarding the impact of exercise on breast health. By helping individuals select suitable activities and intensities, coaches can minimise the risk of discomfort or injury, which is particularly important for those with larger breasts and prone to stress-related issues.

Several limitations are found in this study. First, the type of activity is limited, which warrant the inclusion of different types of activities in future research. Secondly, the study sample size and representation of population groups are limited. Future work will incorporate and examine diverse groups and populations in terms of age and physique. Lastly, the accuracy of the material search method could be improved given better computational resources. These limitations are areas for future investigation and refinement.

Conclusions

This study evaluated the biological responses of the internal components of the breast when carrying out different types of activities at different intensities. Among the three tasks examined, jumping rope imposes the highest level of stress on the internal components of the breast. Following closely behind is high knee skipping, while running causes the least amount of stress. In running and jumping rope, the speed and rate of exercise respectively show a positive correlation with the stress experienced by the internal components of the breast. The rate of high knee skipping has a positive correlation with stress, and when it reaches a constant rate, the influence of the rate of skipping declines. In each type of exercise, the effect of their intensity on the stress imposed on the internal components of the breast, is (in ascending order): the glandular tissues, pectoralis major muscles, adipose tissues, and Cooper's ligaments. The magnitude of the stress on the internal components of the breast also follows this order. The current work may provide valuable biomechanical knowledge for the future design of sports bras, post-surgical care protocols, and personalised training for improved support and reduced injury risks.