Model-free current control solution employing intelligent control for enhanced motor drive performance

Abstract

The study presents an intelligent, model-free current control strategy that eliminates the need for explicit plant models while efficiently reducing the effect of plant parameter perturbation. By employing a data-driven approach with fewer input features, the proposed scheme reduces the computational burden during training while maintaining high control performance. Unlike conventional model predictive current control (MPCC), which is computationally expensive because of solving optimization problems at each sample time, and requires precise plant models, the proposed method enhances system performance by addressing plant model discrepancies through data-driven techniques. Additionally, adaptive particle swarm optimization (APSO) is used to optimize the gain parameters of the outer speed control loop for improved dynamic performance. To verify the effectiveness of the data-driven control scheme, a comparative study with a conventional control scheme is presented. We verify that the switching states obtained from the model-based control design are learned with an accuracy of 94.8% using the proposed model-free data-driven approach. Test results show that the proposed approach outperforms traditional methods, offering superior steady-state performance, lower harmonic distortion, and increased robustness.

Introduction

Motor drive control has been a popular area of research in the industry for several decades. Several control algorithms have been implemented to enhance the control performance. Among these, model predictive control (MPC) has received considerable attention because of the simple control design, convenience of implementation, rapid dynamic response, absence of the need for pulse width modulation (PWM) modulation techniques, incorporation of system nonlinearities and constraints, and feasibility of applying multivariable control^1,2. Conventional linear controllers such as PID and LQR are well-suited for systems with linear dynamics but face challenges in handling nonlinearities and constraints effectively. In contrast, Model Predictive Control (MPC) excels in addressing these complexities by incorporating system constraints and nonlinearities providing better performance in real-time, making it a more suitable benchmark for advanced control strategies^3,4. In addition, MPC explicitly utilizes a system model to predict the future behavior of controlled state variables over a given time horizon. Subsequently, the MPC selects the best control action (i.e., the best switching signals and optimal voltage vector) by minimizing the cost function representing the desired behavior of the system. Many approaches have been proposed to lower the total harmonic distortion (THD) and increase the steady and dynamic performance^5,6. MPC with a long horizon provides tremendous performance improvements. However, a significant disadvantage is that it increases the computational load of online optimization problems. To address this problem, a one-step prediction horizon was proposed to track the reference current effectively and reduce the computational complexity^7,8.

The focus of researchers on the application of artificial intelligence (AI) in the field of electric motor control has surged recently. This is because neural networks can potentially display rapid dynamic responses and remarkable performance compared with other control schemes. Various identification strategies such as fuzzy logic, reinforcement learning, and local linear regression have been proposed. Local linearization (local linear regression) and complex calculations are the common disadvantages of these approaches^9,10,11. Recently, AI has been implemented to solve complex tasks such as artificial neural network (ANN)-based current control, AI-based motor parameter identification, ANN-torque observers, and ANN-based sensorless speed control^12,13,14. To achieve a lower THD and enhance the steady-state and dynamic performances of the control system, a model-free predictive current control based on an ANN with an LC filter was proposed for both linear and nonlinear loads¹⁵. In addition, model-free neural networks with long prediction horizons have been employed widely for the identification and estimation of power converters with an accuracy of 86.9% is presented in the literature^16,17. A state-of-the-art feedforward neural network architecture with a multilayer perceptron was designed to predict reference voltage commands. It displayed a remarkable performance compared with linear current control under system disturbance^18,19. Furthermore, learning-based model-free predictive control (MFPC) techniques have shown promising results in enhancing the performance of power converters. A predictor-based data-driven model-free adaptive predictive control (MFAPC) for power converters using machine learning is proposed²⁰ . While this approach demonstrates robustness, it requires a substantial amount of data for training and may suffer from slow convergence, particularly in real-time applications. Similarly, Ref.²¹ introduced a supervised imitation learning approach for finite-set model predictive control (FCS-MPCC) systems, aiming to mimic the traditional FCS-MPCC response. However, this approach primarily focuses on replicating the traditional control strategy rather than improving dynamic performance, which limits its ability to adapt to varying system conditions. Thus, the main goal of proposed work is to design a data-driven controller which eliminates the need for a priori knowledge of control plant model and weighting factors, addressing the key limitations of both the MFAPC and imitation learning methods with higher prediction accuracy. By employing a data-driven framework, the propsoed approach adapts to system dynamics without relying on predefined models or extensive datasets, making it more flexible and applicable to a wide range of power converter systems.

Data-driven controllers have several advantages over conventional control schemes: (a) the mathematical model of the system to be controlled is not required, (b) the performance of the system is improved if the network is trained effectively, and (c) the network can be trained conveniently based on data acquired from the system prior to expert knowledge. Furthermore, by lowering the training input feature, this study presents an optimal approach as compared to conventional methods. The reduction in training input features helps to reduce the computational burden during training while maintaining a better overall control performance with high prediction accuracy compared to conventional methods. The growing demand for real-time motor control systems necessitates solutions that can operate efficiently with minimal computational complexity while maintaining robustness. This work addresses these needs by leveraging a model-free, data-driven approach that offers enhanced control accuracy and faster computation.

The key concept of this study is to handle the switching pulses of a two-level three-phase inverter (2L3P VSI) with a data-driven control solution employing AI. A model predictive controller with a single prediction horizon is employed for offline data generation during the training phase. This strategy ensures that the neural network is trained with high-quality optimal control actions. Thereby, it leverages the robustness and performance of model predictive current control (MPCC). By providing realistic and representative data that address a wide range of operating conditions, this approach enhances the ANN’s capability to achieve high performance and generalization while minimizing its dependency on an accurate system model during training. Moreover, by incorporating MPCC in the training phase, we ensured that the proposed ANN-based controller inherits the strengths of MPCC. This has yielded a robust, high-performance control solution while transitioning to a model-free methodology.

The MPC applied to the VSI is considered as a classification problem because it involves finite switching states applied at each instant. This reduces a predefined cost function. Utilizing the generated dataset, a supervised learning process was used to train the neural network. This enabled it to map the input data to the corresponding output switching pulses based on input–output data pairs. Adaptive PSO was employed in a speed control loop to obtain the optimal gain parameters by reducing the objective function. Based on model-free neural network predictive control, the system input values were mapped to the output during training. Then, the network was employed online to eliminate MPC that would help eliminate the effect of model mismatch. The results demonstrate the efficacy of the proposed control design.

The following are the unique contributions of this study:

• (1) The paper presents a model-free data-driven current control approach that employs function approximators. The proposed data-driven design employs fewer input/output training features. Unlike existing methods that focus primarily on general system performance, the proposed data-driven approach achieves a higher accuracy 94.8% in learning the switching states compared to the results presented in literature.

• (2) Unlike traditional finite control-set model predictive control, the proposed data-driven approach does not rely on prior knowledge of the control plant model enabling its application to a wide range of power converter systems.

• (3) Traditional MPCs are computationally expensive due to optimization at each sample time. In contrast, the proposed data-driven approach provides an efficient, data-driven solution that reduces the computational complexity while maintaining excellent control performance.

• (4) This study emphasizes the effectiveness of feature selection for optimizing closed-loop control.

• (5) Utilization of an adaptive metaheuristic optimization algorithm based on the algorithm performance to tune the controller gains of the speed control loop to enhance closed loop dynamic performance

• (6) A comprehensive study and performance analysis (including a model-based control design) are provided to demonstrate the superiority of the proposed data-driven current control approach.

The remainder of this paper is organized as follows. First, a detailed discussion of the proposed control design is presented in “Proposed control design” section. The data collection, network training, and test results are discussed in “Test results and discussion” section. Finally, “Conclusion” section concludes the study.

Fig. 1

Voltage source inverter (VSI)-connected surface-mounted permanent-magnet synchronous motor (SPMSM).

Proposed control design

This section discusses a 2L3P voltage source inverter (VSI) connected to a surface-mounted permanent-magnet synchronous motor (SPMSM) drive. It is illustrated in Fig. 1. A mathematical model of the control system was defined. Then, the proposed control strategy for tuning the speed control and designing a data-driven current control solution was investigated.

Mathematical model of the inverter and SPMSM

Using a discrete-time model of the system, the MPC approach predicts the future value of the phase current for each feasible voltage vector (VV). The mathematical model of the SPMSM was discretized to determine the necessary conditions for model prediction. Over the sample period Ts, an internal discrete-time model of the motor drive was used to anticipate the future state of the output state variable for input control. To identify the best output VV, MPC examines a 2L3P inverter model. The inverter output obtained by modulating the input DC voltage through the switch gate pulse is expressed as follows:

$$\begin{aligned} S=\frac{2}{3}{({S_{1}+e^{{j}\frac{2\pi }{3}}S_{3}+e^{{j}\frac{4\pi }{3}}S_{5}})}. \end{aligned}$$

(1)

The three-phase motor voltage is then transformed into a rotating reference frame by employing Park’s transformation as follows:

$$\begin{aligned} \left[ {\begin{array}{c} {{v}_{d}^e}\\ {{v}_{q}^e}\\ {v}_{0}^e \end{array}} \right] = \frac{2V_{dc}}{9}\left[ { \begin{array}{ccc} ~{\cos\theta _{r}} & {\cos(\theta _{r}-\frac{2\pi }{3})} & {\cos(\theta _{r}+\frac{2\pi }{3})} \\ {\sin\theta _{r}} & {\sin(\theta _{r}-\frac{2\pi }{3})} & {\sin(\theta _{r}+\frac{2\pi }{3})} \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} \end{array}} \right] \left[ { \begin{array}{ccc} ~{2} & {-1} & {-1} \\ {-1} & ~{2} & {-1} \\ {-1} & {-1} & ~{2} \end{array}} \right] \left[ {\begin{array}{c} {S}_{1} \\ {S}_{3} \\ S_{5} \end{array}} \right] . \end{aligned}$$

(2)

2L VSI has eight feasible VVs: $V_{0}\, and\, V_{7}$ are zero voltage vectors, and the remaining $V_{1}...V_{6}$ are active voltage vectors. One of the zero vectors was considered to reduce the computational load of MPC. The discrete-time model of SPMSM was derived utilizing Eular forward approximation. It is given as

$$\begin{aligned} i^{k+1}_{d} = i^{k}_{d} + \frac{T_{s}}{L_{s}}(-r_{s}i_{d}^k + \omega _{r}^{k}L_{s}i_{q}^{k}+v_{d}^k), \end{aligned}$$

(3)

$$\begin{aligned} i^{k+1}_{q} = i^{k}_{q} + \frac{T_{s}}{L_{s}}(-r_{s}i_{q}^k-\omega _{r}^{k}L_{s}i_{d}^{k} - \omega _{r}^{k}\lambda _{m}+v_{q}^k), \end{aligned}$$

(4)

where the currents are the control outputs and the voltages are the control inputs derived from the gate pulse of the inverter switches. The electromagnetic torque required to drive the SPMSM is derived as follows:

$$\begin{aligned} {T_{e}}={\frac{3P}{2}}[{\lambda _{m}}{i^{e}_{q}}]. \end{aligned}$$

(5)

Evolutionary algorithm for speed loop gain tuning

In this study, the APSO algorithm was implemented in the proposed closed-loop control design to tune the outer speed loop. Control parameter configurations are pivotal in optimizing algorithms. These ensure the efficient exploration of problem spaces without diverging paths. These parameters are the inertia weight $\omega$, cognitive acceleration coefficient $c_1$, and social acceleration coefficient $c_2$. Although constant values such as $\omega = 0.729844$, $c_1 = 2$, and $c_2 = 2$ are common, dynamic parameter adaptation has been advocated for enhanced solutions²².

An adaptive technique dynamically adjusts $c_1$ and $c_2$ based on the current time step $k$ and maximum time steps $n_k$. Initially, $c_1$ is large and $c_2$ is small to promote exploration. As time advances, $c_1$ decreases and $c_2$ increases. This promotes a shift toward exploitation. This ensures extensive exploration early followed by the focused exploitation of better solutions. In this study, the adaptive inertia weight method was used to maintain a balance between exploration and exploitation within the swarm (a departure from the conventional constant inertia weight). In this approach, the selection of the inertia weight is contingent on the performance of the algorithm. If the algorithm exhibits rapid improvement, a faster decrease in the inertial weight is selected. Meanwhile, in the case of sluggish progress, a slower reduction or even a temporary increase is considered to induce exploration. The pseudocode for Algorithm 1 describes the main steps in the gain selection process. The particle velocity was updated using (7)²³. The process of optimal gain selection was performed offline. The optimal gain values were selected based on the minimization of the objective function in this study, which was selected as the integral time absolute error (ITAE). In this study, the ITAE was selected as the error performance index because it focuses on a more accurate steady-state error-free control. Hence, we anticipated a good overall optimization of the speed control loop. It was calculated over a time interval as given in Eq. (6). We considered the residual difference between the reference and actual speeds at each data point.

$$\begin{aligned} \text {ITAE} = \int \limits_{0}^{\infty } t |\omega _{i}^{ref} - \omega _{i}^{act}| dt. \end{aligned}$$

(6)

The obtained optimal gain values, as shown in Fig. 2, were used online in the outer speed control loop. Algorithm 1 is described as follows: (a) The swarm size is initialized from line 2–4 by assigning the global best values. (b) The For loop is run for a predefined number of iterations from line 5–15. (c) The particle position, best velocity, and global best values are updated from line 5–14, and the best particle position searched by a swarm is stored in $g_{best}$.

$$\begin{aligned} v_{i,d}(k+1) = wv_{i,d}(k) + c_{1}r_{1}(p_{i} - x_{i,d}(k)) + c_{2}r_{2}(p_{g} - x_{i,d}(k)). \end{aligned}$$

(7)

The expression provides the update rule for the velocity component $v_{i,d}$ of a particle in an APSO algorithm at iteration $k+1$. Here, $w$ is the inertia weight. $c_{1}$ and $c_{2}$ are the cognitive and social coefficients, respectively. $r_{1}$ and $r_{2}$ are random numbers distributed uniformly between zero and one. $p_{i}$ represents the best position achieved by the $i$-th particle tll the present time. $p_{g}$ is the global best position identified by any particle in the swarm. $x_{i,d}$ denotes the $d$-th dimension of the current position of the $i$-th particle at iteration $k$. This equation governs how the velocity of each particle is updated based on its previous velocity, personal best position, and best position identified by any particle in the swarm.

The inertia weight $w$ is dynamically adjusted based on the swarm’s performance. The algorithm monitors stagnation using a counter, $Stag_{Cnt}$, which is updated as follows:

$$\begin{aligned} \textit{Stag}_{\text {Cnt}} = {\left\{ \begin{array}{ll} \textit{Stag}_{\text {Cnt}} + 1, & \text {if } gBest_{1, \text {errCol}} \ge P^{\text {Best}}_{\text {Err}} \\ 0, & \text {otherwise} \end{array}\right.}. \end{aligned}$$

(8)

Here, $gBest_{1, \text {errCol}}$ represents the global best error in the current iteration, and $P^{\text {Best}}_{\text {Err}}$ is the previous global best error. If there is no improvement in the global best solution, the stagnation counter ${Stag-{Cnt}}$ is incremented; otherwise, it is reset to zero.

The inertia weight $w$ is then updated based on the value of ${Stag_{Cnt}}$:

$$\begin{aligned} w = {\left\{ \begin{array}{ll} \min (w + w_{\text {inc}}, w_{\text {max}}), & \text {if } \textit{Stag}_{\text {Cnt}} \ge \textit{Stag}_{\text {Thersh}} \\ w, & \text {otherwise} \end{array}\right.}, \end{aligned}$$

(9)

where $w_{\text {inc}}$ is the increment value for the inertia weight. $w_{\text {max}}$ is the maximum allowable inertia weight. ${Stag_{Thersh}}$ is the threshold for the stagnation counter. When the stagnation counter ${Stag_{Cnt}}$ exceeds the predefined threshold $Stag_{Thersh}$, the inertia weight $w$ is increased by $w_{\text {inc}}$, ensuring it does not exceed $w_{\text {max}}$. This mechanism helps the swarm to explore new areas of the search space when it gets stuck, thereby enhancing diversity and improving the algorithm’s performance in finding the global optimum.

The position update for PSO is governed by the following equation:

$$\begin{aligned} \textbf{x}_{i}(k+1) = \textbf{x}_{i}(k) + \textbf{v}_{i}(k+1), \end{aligned}$$

(10)

where $\textbf{x}_{i}(k+1)$ is the updated position of particle $i$ at iteration $k+1$, $\textbf{x}_{i}(k)$ is the current position of particle $i$ at iteration $k$, $\textbf{v}_{i}(k+1)$ is the velocity of particle $i$ at iteration $k+1$.

Fig. 2

Selection of optimal gain values with the minimum objective function.

Algorithm 1

Adaptive particle swarm optimization.

Predictive current control

Model-based predictive current control

MPC methods have gained popularity in industrial applications owing to their rapid dynamic responses and effective control capabilities. Figure 3 illustrates the working strategy of MPCC. The load currents $i_\alpha$ and $i_\beta$, in conjunction with their references, are illustrated for $T_s$. The optimal voltage vector for the next sample instant is predicted by employing the measured current and all switching states. $i_\alpha ^{p}(v2,5)$ corresponds to when the voltage vector minimizes $i_\alpha$. Meanwhile, the voltage vectors $v_6$ and $v_5$ correspond to the minimization of $i_\beta$. Therefore, the voltage vector that minimizes the cost function is $v_5$.

Fig. 3

Working principle of MPCC technique.

In the current control mechanism, the inverter is the most important consideration for tracking the reference currents to measure the current accurately. The phase currents are controlled directly in FCS-MPCC. The cost function is selected as

$$\begin{aligned} g = {(i_{d}^{*k}-i_{d}^{*(k+1)})^2} + {(i_{q}^{*k}-i_{q}^{*(k+1)})^2}, \end{aligned}$$

(11)

where $\textbf{i}_{dq}^{*k}$ is the reference current in the rotor reference frame.

MPCC has a simple principle and is convenient to implement. However, a significant drawback is that it requires a large number of online calculations to solve optimization problems. This increases the computational complexity of the control system. Moreover, these are highly dependent on the system model. Various methods have been proposed to address this problem^24,25,26. This paper presents a feed-forward ANN-based controller for optimal current control performance by utilizing MPC’s flexibility for data generation to train a network offline. The goal was to achieve a lower THD and good performance in various working environments.

Fig. 4

Three-layer feedforward neural network with measured and reference currents $(I_{\alpha \beta }^{[k,k-1]})$ and switching states $(S_{1,3,5}^{[k-1]})$ as inputs. Meanwhile, the output constitute the optimal voltage vector $V_{i}$.

Proposed model-free predictive current control

Various data-driven techniques, particularly AI-based control designs, have emerged in the field of power conversion systems. A well-designed ANN can significantly improve the performance of a learning system. Nodes, weights, and layers are the components of various ANN models. The general expression for defining a neuron in an NN is as follows:

$$\begin{aligned} N=\left( \sum _{i=1}^{k} w_{i} x_{i}\right) +b, \end{aligned}$$

(12)

k is the number of elements, $x_{i}$ is the input vector, $w_{i}$ is the interconnected weight, and b is the bias factor. N is a process that utilizes an activation function (which is generally a nonlinear function) to ensure a universal approximation property²⁷. It is given as follows:

$$\begin{aligned} f(N)=f\bigg[\left( \sum _{i=1}^{k} w_{i} x_{i}\right) +b\bigg]. \end{aligned}$$

(13)

Considering the fixed number of switching states for VSI, the states can be considered as classes. Therefore, the optimal voltage vector challenge can be considered a multi-class classification problem at each time step, with the optimum switching states considered as the patterns to be learned using an FNN.

In this paper, A feedforward NN (FNN) with seven input neurons was structured. It is responsible for mapping the network output. A neural network was designed to specify the switching states of the inverter as shown in Fig. 4a. All the inputs were separated into layers without links between the layers. The information was processed using a one-way connection. Model-based predictive current control provides optimal voltage vectors by minimizing the cost function to track the reference trajectories by providing finite switching pulses. The set of switching states is finite for each optimal voltage vector. We considered the prediction of the switching states of a two-level three-phase inverter to be a classification problem. A large number of voltage vectors results in more precise gridding in the stationary reference frame. This can significantly enhance the prediction accuracy of the learning algorithm. Employing a smaller grid structure, the algorithm performs better and provides more accurate predictions. This results in an improved accuracy of the trained network. The reference and measured currents obtained from the FCS-MPCC in a rotating reference frame are transformed into a stationary reference frame by inverse Park’s transformation as follows:

$$\begin{aligned} \left\{ \begin{array}{l} i_\alpha =i_d \cos \left( \theta _r\right) -i_q \sin \left( \theta _r\right) \\ i_\beta =i_d \sin \left( \theta _r\right) +i_q \cos \left( \theta _r\right) \end{array}\right.\end{aligned}.$$

(14)

The currents in the stationary plane are utilized as training data to enhance the prediction accuracy of the network. The input layer contains seven neurons. Here, four input neurons represent the error between the measured and reference phase currents in the stationary reference frame at the previous and present time instants $[k-1,k]$, as given in Ref.¹⁵. The other three represent the optimal gate pulses for the previous instant $[k-1]$. The representation of an FNN is shown in Fig. 4b. Here, a is the total input connection; $x_{j}$ represents the input; $w_{h,j}$, and $b_{h,j}$ represent the weight and bias of the hidden layer, respectively; and $\varphi _{h}$ is the hidden layer activation function.

$$\begin{aligned} \Delta {I_{\alpha \beta }^{[k]}} = I^{[k]}_{\alpha \beta } - I^{*[k]}_{\alpha \beta }, \\ \Delta {I_{\alpha \beta }^{[k-1]}} = I^{[k-1]}_{\alpha \beta } - I^{*[k-1]}_{\alpha \beta }. \end{aligned}$$

(15)

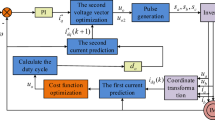
The activation function $(\varphi )$ is the core of the ANN. It is based on the layer locations of the input, hidden, or output layers. Different activation functions have been demonstrated to be advantageous. The mathematical definitions and derivatives of the most commonly used activation functions such as sigmoid, tangent hyperbolic, rectified linear unit, and softmax functions are listed in Table 1. A flowchart of the proposed data-driven control solution is shown in Fig. 5.

Table 1 Non-linear activation functions.

Fig. 5

An overview of a proposed solution.

In this study, the hyperbolic tangent (tanh) function was used as the activation function with 20 neurons in the hidden layer. In the output layer, the softmax function is used as an activation function. This yields a probability between 0 and 1. Moreover, the sum of the probabilities is 1 at each instant. The voltage vector across the output with the maximum probability is active for each sampling instant. The working mechanism of the Softmax activation function at the output node is illustrated in Fig. 6. The voltage vector across the output with the maximum probability is active for each sampling instant.

Fig. 6

Visualization of Softmax output in a trained network.

It is important to note that the two-level inverter can have only eight switching states. This results in six active VVs and two identical zero VVs at the origin of the coordinates, namely, V0 or V7. Given the difficulties in distinguishing between the two output voltages for zero VVs, selecting any switching state can significantly minimize the implementation difficulty. For simplicity and further reduction in the utilized VV, only V0 is defined as zero VV within the scope of this work and is used in conjunction with the active VVs. This ensures an additional ripple reduction.

Without requiring a mathematical model of the inverter or a pre-defined cost function to be reduced at each sample time Ts, the proposed neural network provides an optimal voltage vector that should be applied across the inverter as shown in Table 2. Moreover, compared with model-based current control approach, the proposed solution has a low computational complexity due to its ability to generate control signals through a single forward pass of the pre-trained network. Furthermore, the ability of neural networks to approximate complex functions makes them attractive candidates for controlling PMSM systems without requiring precise mathematical models.

Table 2 Inverter switching configuration.

Model training and preparation of dataset

The proposed neural network was trained offline using a dataset generated by MPCC. MPCC ensures high-quality optimal control actions across a wide range of working conditions. The dataset includes a diverse set of operating points to accurately capture the dynamics of the system (including steady-state and transient scenarios, different load conditions, external disturbances, variations in sampling time, and step and sinusoidal reference inputs) to enable the NN to generalize effectively to the actual working conditions. In addition, to address non-ideal practical solutions, we included noise and parameter variations in the training dataset to replicate real-world conditions and improve the NN robustness. The dataset consists of input-output pairs. Here, the inputs are the current states and reference signals, and the outputs are the optimal switching signals generated by MPCC. Through supervised learning, the NN effectively maps input features such as current states and reference signals to the optimal voltage vector that provides optimal gating pulses to the inverter. The training-based appraoch simplifies the controller design process by eliminating the need for detailed system modelling and solving optimization problem. Unlike MPCC, which require exact motor parameters for excellent dynamic performance under varied operating conditions. Additionally, the proposed data-driven approach ensures adaptability and provides optimal control performance under system parameter variations, which enhances usability during deployment.

Training input feature selection and process

The selection of the optimal set of input features is crucial for designing an effective ANN-based control strategy. Depending on the type of inverter and specific goals of the study, various features can enhance both training and testing phases. These phases accurately evaluate the system’s capability to learn and control the system dynamics. For the 2L3P VSI, we evaluated combinations of measured variables (including current errors in both stationary and rotating reference frames) using transformations, current errors in the abc coordinate system, and switching states. Initially, various combinations of input features were tested empirically to identify the best mapping from the raw data to the desired outputs. Each feature set was tested using a range of training samples representing different operating conditions. These samples were acquired via MPC as a benchmark and used to train the ANN, assess the THD of the output current, and evaluate the overall accuracy of the network by analyzing the confusion matrix.

From the evaluation, the optimal switching state $S_{opt}$ at instant $(k-1)$ and the current error in the stationary reference frame were identified as the optimal set of input features because of their superior performance in reducing THD and achieving a higher accuracy in matching the predictive class to the true class during training. In addition, the use of a large number of voltage vectors resulted in more precise gridding in the stationary reference frame. This significantly enhanced the prediction accuracy of the learning algorithm. Employing a smaller grid structure enables the algorithm to perform better and provide more accurate predictions. This, in turn, yields an improved accuracy of the trained network. Notably, the selected input features significantly improved the performance of the control strategy during online implementation, thereby replacing conventional MPC control.

Error metrics

Throughout the training process, we used the mean squared error (MSE) to assess the performance of the neural network. We calculated the error by comparing the NN’s predicted output with the true value. It was then used to adjust the weights of each neuron to minimize this error. This iterative process was repeated over multiple training cycles until the error between the predicted and true values was minimized. These metrics provide effective insights into how effectively a neural network learns to replicate the optimal control actions produced by the MPCC algorithm.

Fig. 7

Model-free intelligent controller fed by 2L3P VSI.

Table 3 Performance analysis of trained NN under different numbers of hidden layers and test cases.

Test results and discussion

This section thoroughly analyzes and evaluates the two proposed control strategies considering various loads and operating conditions.

Testing platform

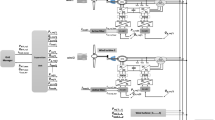
To demonstrate the efficacy of FNN-based model-free current control and compare its performance with that of model-based current control, we utilized Matlab software (2022a) to implement the models (as shown in Fig. 7) and performed training on the generated data-sets. First, training was performed offline by employing MPC as a baseline model. Then, the trained neural network was employed online to acquire the optimal voltage vector using the proposed and conventional schemes via a laptop with an Intel® Core i7-1195G7 2.90 GHz CPU, 16 GB RAM, and NVIDIA Geforce® RTX laptop GPU 3050, and running Windows 10 64 bit.

Table 4 SPMSM parameter values.

Training procedure

The training process consisted of three main steps:

• (a) Data generation employing MPC as the baseline model for both training and testing

• (b) Post- and pre-processing of the generated data for the training and testing phases utilized offline and online in the control system.

• (c) Setting up of the FNN hyperparameters.

The measured and reference variables of the phase current in the stationary reference frame and one-step delay-switching signals were fed into the FNN. Seven signals were considered as input features to the neural network, i.e., k = 7. The optimal voltage vector $V_{FNN}|_i (i=0,...6)$ applied at each sampling moment was the FNN output. The Softmax activation function at the output layer squashed the output between zero and one. This indicates the optimal VV to be applied in each sampling period Ts. The output layer is a seven-dimensional array that contains the indices of the seven voltage vectors, Vi, that the inverter generates. NN Output is one-hot encoding. This implies that for each sampling period, only the index of the optimal VV would be active (i.e., having a higher probability among all the classes, as given in Table 2).

The dataset and number of hidden layers were selected based on a higher training accuracy, as given in Table 3. The dataset was divided into three parts: 70% of the data were randomly selected for training, and 15% were randomly selected for each of testing and validation. Training was performed using a scaled conjugate gradient scheme that utilizes the remarkable convergence property of conjugate gradient optimization and involves less computational complexity²⁸.

Test results

To verify the performance of the proposed model-free current control, we evaluated the dynamic performance of SPMSM with the control parameters listed in Table 4 by employing the conventional and proposed control designs under various operating conditions. To analyze the prediction accuracy of the proposed NN, a confusion matrix is presented in Fig. 8. The overall prediction accuracy of the trained network was 94.8%. This indicated how well the network predicted the classes, as listed in Table 2. At each sampling instant, the single voltage vector with the highest probability was activated following predetermined switching configurations.

Fig. 8

Performance matrix.

Fig. 9

Motor drive speed response in the wide operating range under 0 load condition.

The motor performance under no-load condition is shown in Fig. 9. The motor started from standstill and accelerated to 200 rad/s with 0 load torque applied. The speed was increased to 600 rad/s at 0.98 s. The test results indicated that the overshoot and settling time of the conventional approach were larger than those of the proposed control design.

The shaft speed was maintained constant to demonstrate the current controller performance. The motor response was evaluated while tracking the reference currents. In Fig. 10, the dynamic performance of the model-free control design is evaluated under various load-torque conditions. The motor was operated at 800 rad/s during the loading step. The transient torque performance was also tested. It can be observed that the proposed design replicated the responses of the model-based design with less overshoot, less steady-state error, and faster settling. The model-free control approach improved the dynamic performance of the load torque under transient conditions.

Figure 11 shows the dynamic performance of the zoomed-in motor drive under various load-torque steps. The motor-drive phase current in the stationary and rotating reference frames demonstrates the effectiveness of the model-free control approach. The transient response, steady-state errors, overshoot, settling time, and tracking rate were enhanced remarkably in the proposed design compared with those in the conventional scheme.

Fig. 10

Motor dynamic response under varied load conditions at 800 rad/s.

Fig. 11

Motor dynamic response under varied load conditions.

The motor-speed control performance over a wide operating range with an applied load torque is shown in Fig. 12. The motor accelerated linearly from 0 to 700 rad/s at 0.65 s with a step variation of 100 rad/s and then, decelerated to 0 rad/s at 0.7 s. The motor decelerated further to − 500 rad/s with a step variation of − 100 rad/s until 1.5 s, and to − 700 rad/s at 1.7 s. It then linearly accelerated back to 0 rad/s at 1.9 s. Figure 13 shows the zoomed-in speed, reference current track in the stationary reference frame, and motor torque response during the speed transient. Both model-based and model-free control designs effectively tracked the reference shaft speed. However, for each reference speed of acceleration or deceleration, the proposed control design exhibited less overshoot and settling time and responded faster than the conventional control design. Moreover, the torque and current oscillations were higher when the conventional control design was employed. It can also be observed that the motor exhibited robustness during the speed reversal transient. This implies that the proposed control design is more reliable, more stable, and faster than the conventional control scheme, which makes it superior.

Fig. 12

Dynamic performance over a wide speed operation range under load conditions.

Fig. 13

Expanded result of Fig. 12, wide speed operating range under load torque.

The motor resistance and inductance may significantly fluctuate from their nominal values in real-world applications. In the model-based control design, the inner current control loop is highly dependent on the motor parameters. This degrades the control performance in the case of parametric uncertainty.

Figure 14 shows the test results. These demonstrate the robustness of the proposed model-free control scheme for a parametric model variation. Initially, 12 N m was applied to a motor operating at 1200 rad/s. At 0.5 s, the load torque was reduced to 0 N. m and then, increased to 10 N m at 0.7 s with an equal rotor speed. The transient torque performance was analyzed with a 50 % increase and decrease in stator resistance and inductance, respectively. It can be observed that the model-free control design showed a good transient response with less steady-state error, undershoot, and fast convergence. It is more reliable and stable than the model-based control design. The torque transient performance was less affected by parametric variations in the proposed control design compared with a model-based control scheme having a large undershoot, high steady-state error, and low convergence to the reference values. A comparative analysis is presented in Table 5.

Table 5 Comparative analysis of model-based and model-free control design.

Finally, the performance evaluation under normal conditions, parameter mismatch scenarios, and variations in sampling time are illustrated in Fig. 15. The THD of output currents in the state-of-the-art MPCC were 4.72%, 4.97%, and 5.39%, respectively. Meanwhile, the proposed control scheme achieved significantly lower THD values of 2.55%, 2.63%, and 3.57% for identical scenarios. Furthermore, the tracking error in the proposed control design outperformed that of the conventional MPCC scheme, thereby evidencing superior control performance. Additionally, the results revealed exceptional control and tracking performance even under parameter mismatches and unknown perturbations. Moreover, it maintained a highly dynamic transient similar to that of the standard MPCC approach.

Fig. 14

Test results, electromagnetic torque response under parametric variations at shaft speed of 800 rad/s.

Fig. 15

Performance evaluation of proposed and conventional control approaches in steady-state and transient-state under normal condition, parameter mismatch $(L_s = 5.5\,\mathrm{{mH}})$, and variation in sample time (left to right).

Conclusion

A model-free neural-network-based current controller with an optimal gain-tuning approach for the speed regulator is presented in this paper. The network was trained offline by conventional MPC as a baseline control to generate the input and output dataset. The trained network was employed online as an intelligent current control that exhibited good steady-state and dynamic performance without affecting the model mismatch or parametric variations. The primary contribution of this study lies in its ability to train a network to learn the optimal voltage vector directly from a predefined VSI gating signal. This approach achieves a performance accuracy of 94.8%, outperforming existing networks in the literature while utilizing fewer training features for both output targets and predictions. This reduction in training complexity leads to a more effective and computationally cheap solution, ensuring robust drive performance across varied operating conditions. Unlike conventional predictive control, the proposed data-driven strategy eliminates the need for iterative optimization at each sample interval, enabling faster execution and significantly reducing computational burden. In addition, using an adaptive optimization strategy, the closed-loop control performance was enhanced. Moreover, the test results verified the capability of the proposed controller to generate optimal voltage vectors, which enhanced the dynamic performance with reduced computational complexity through a single forward pass of pre-trained network. The results show that the data-driven control approach achieves good steady-state and transient performances with reduced ripples and lower harmonic distortion under various operating conditions (i.e., varied speed reference, varied load step, and parametric uncertainty). The proposed approach satisfies the drive-control performance requirements with a remarkable dynamic response.