Advanced generative adversarial network for optimizing layout of wireless sensor networks

Abstract

The best layout design related to the sensor node distribution represents one among the major research questions in Wireless Sensor Networks (WSNs). It has a direct impact on WSNs’ cost, detection capabilities, and monitoring quality. The optimization of several conflicting objectives, including as load balancing, coverage, cost, lifetime, connection, and energy consumption of sensor nodes, is necessary for layout optimization. Layout optimization represents an NP-hard combinatorial issue. A number of meta-heuristic optimization strategies have been put out to address this issue in the past ten years. Nevertheless, these methods only addressed a subset of the objectives—combinations of energy consumption, count of sensor nodes, area coverage, and lifetime—or they offered computationally costly solutions. Therefore, this research paper presents a layout optimization problem using novel intelligent deep learning-based optimization methodology. Here, the major objective is to cover numerous objectives associated with optimal layouts of homogeneous WSNs that involves connectivity, coverage, energy consumption, lifetime, and the number of sensor nodes. The layout optimization problem is handled by the novel Advanced Generative Adversarial Network (AGAN), where the parameter tuning is performed by the nature inspired optimization algorithm called Piranha Foraging Optimization Algorithm (PFOA), with the consideration of deriving the objective function. Simulation findings revealed that the proposed novel AGAN-PFOA generated optimal Pareto front of non-dominated solutions having better hyper-volumes as well as spread of solutions than the state-of-the-art solutions. The proposed AGAN-PFOA for the WSN layout optimization problem in terms of PDR, coverage, energy consumption, lifetime, alive node count, delay, and routing overhead is 61.46%, 15.12%, 12.67%, 65.91%, 70.59%, 44.88%, and 68.86% better than the existing methods respectively.

Introduction

WSNs have at last begun to revolutionize many aspects such as the environment, health, agriculture and smart cities¹. WSNs are networks of spatially dispersed autonomous sensors used to monitor physical or environmental conditions such as temperature, pressure, light, sound etc². The information acquired from these sensors is transferred to a central unit for processing so that any operational change or decision making is timely done even with changing conditions³. One of the critical challenges in the use of WSNs is the arrangement of sensor nodes which refers to the layout of the WSNs systems⁴. The optimization of this layout becomes imperative in order to improve the network performance, achieve coverage and conserve power.

The validation focus of sensor network layout configuration mainly revolves around the proper placement of sensor nodes to achieve the maximum coverage while conserving energy and providing connectivity⁵. Coverage is the extent to which the network can successfully surveil the entire region of concern. An improved configuration guarantees that every area of interest is covered without wasting resources or leaving undersupplied areas^6,7. This is significant in the wildlife monitoring and disaster management systems where not receiving certain data may be disastrous⁸. Energy consumption is another major factor in the design of WSNs. Battery-powered sensor nodes mean that energy efficiency significantly affects the operation time of the network⁹. To achieve economical usage of energy, the rouse of the optimal layout is that a minimum energy use is achieved by lessening the distance which data needs to travel between nodes and unit processing data centrally¹⁰. This is because fast running out of energy can bring about failure of the nodes before their lifespan which affects the effectiveness and area coverage of the network.

Layout design is one of the most important factors, yet it presents various difficulties¹¹. The first one considers the environmental boundaries. Placement of sensor nodes may sometimes require them to be installed on uneven and inaccessible surfaces, which may hinder connectivity or coverage¹². Besides that, the arrangement must factor in other environmental features such as barriers, interference in signals, and differences in sensor capabilities. Another main factor is the aspect of many applications being dynamic in nature¹³. For instance, in the case of environmental monitoring, the situation may change drastically over time prompting the need for the restructuring of the network within a very short period¹⁴. This inbuilt flexibility requires advanced algorithms which are able to change the structure of the network depending on the status at that time which makes the problem of optimization even more complex¹⁵. Layout optimization, when considering factors such as coverage, energy efficiency, and other constraints, may help improve the performance and life span of sensor networks. Over the last few years refined algorithms and methodologies have been developed in the area which makes it possible to deploy sensors in an even better and more elegant manner¹⁶. Since there is an increase in the number of WSN applications especially in the smart and cyber-physical spaces, layout optimization will become more prominent particularly in application areas which call for control and management of large spatially distributed networks, and thus, more efforts and attention should be focused on this issue.

While numerous methods have been proposed for optimizing Wireless Sensor Network (WSN) layouts, most traditional approaches, such as Genetic Algorithms (GA), Particle Swarm Optimization (PSO), and other metaheuristic algorithms, focus primarily on single-objective optimization or limited combinations of objectives like energy consumption and coverage. However, these methods often suffer from computational inefficiencies, premature convergence, and inadequate multi-objective handling in large-scale dynamic environments. For example:

• 1. Many existing techniques, such as BF-ICrA or CMBWO, are computationally expensive due to their reliance on exhaustive search processes or slow convergence to optimal solutions.

• 2. Techniques like traditional PSO and GA do not effectively address the trade-offs among coverage, energy efficiency, and node connectivity, resulting in suboptimal layouts.

• 3. Existing approaches often lack adaptability to dynamic network conditions, such as node failure or changes in environmental constraints, limiting their utility in real-world applications.

The proposed Advanced Generative Adversarial Network (AGAN), tuned by the Piranha Foraging Optimization Algorithm (PFOA), overcomes these limitations by:

• Utilizing GANs to generate diverse, high-quality layout configurations capable of simultaneously optimizing multiple objectives, such as coverage, energy consumption, and connectivity.

• Introducing PFOA, which enhances the parameter tuning of GANs through dynamic exploration and exploitation, enabling faster convergence and better Pareto front solutions.

• Achieving significant improvements in network performance metrics (e.g., PDR, delay, and routing overhead) with reduced computational costs.

This research fills the critical gap in WSN layout optimization by combining the generative capabilities of GANs with the efficiency of nature-inspired optimization, resulting in a robust and scalable solution for real-world applications.

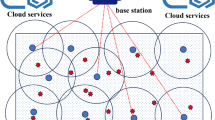
The WSN model with sensor nodes can be diagrammatically shown as in Fig. 1.

Fig. 1

WSN model with sensor nodes.

The paper contribution is shown as below.

• To present a layout optimization problem using novel intelligent deep learning-based optimization methodology.

• To cover numerous objectives associated with optimal layouts of homogeneous WSNs that involves connectivity, coverage, energy consumption, lifetime, and the number of sensor nodes.

• To handle the layout optimization problem by the novel AGAN, where the parameter tuning is performed by the nature inspired optimization algorithm called PFOA, with the consideration of deriving the objective function.

The paper organization is shown as follows: “Introduction” is the introduction of WSN layout optimization problem. “Related work” is literature survey. “Materials and methods” is proposed methodology with proposed model, WSN modeling, objective function, novel GAN, and PFOA algorithm. “Results and analysis” is results and analysis. “Conclusion” is the conclusion.

Motivation

The deployment of WSNs in different areas and applications, such as environmental protection and smart cities, is continuously increasing. Nonetheless, the effectiveness of these networks is dependent on their optimization of layout. One of the principal reasons for the optimization of WSN layouts is the improvement of network performance, maximization of coverage, and minimization of energy use. Where WSNs are deployed, and their kinds are quite numerous, WSN layout optimization appears to make sure that all sensors are placed where they are needed, and all nodes achieve the required communication. This is particularly important because most of the devices employed in WSNs are powered by batteries and therefore energy efficiency is a key concern. Optimization of configuration of sensors helps in reducing the number of nodes necessary for the given application, resulting in prolonged lifetime of the network. The arrangement of network sensors is also important in addressing some of the problems like signals overlapping which can cause loss of information for the effective communication process. Furthermore, it improves expansion; sensors can be added when necessary without much alteration to the setup. Performance, cost and sustainability are the key factors aimed for in WSN layout optimization given the increasing demands of the applications of these networks.

Related work

This paper demonstrated advancement in modified flower pollination algorithm by hybridization of global optimizations techniques, namely parallel and compact, and the way of arranging nodes in WSN¹⁷. The parallel helped in saving diversity pollinations for searching in different regions of space and sharing the computation burden. The compact helped in reducing the amount of memory required for the variable during the computation stage of the optimization. As for the practical implementations, the chosen benchmark functions and the network topology problem of WSN were employed for the approach validation. Techniques available in the literature were employed to compare results, demonstrating that the proposed algorithm was capable of practically cutting down on the number of memory variables and execution time.

This study presented a strategy for laying out WSN in a region with controlled temperature and humidity¹⁸. First, a temperature and humidity model was established and thereafter stable temperature and humidity regions were defined using cluster analysis and statistical methods. To conclude, the design of the WSN system was elaborated. It consisted of the design and fabrication of the WSN nodes that together form the WSN in the controlled temperature and humidity region. For instance, the tobacco sector; it elaborated the design of applied computer system aimed at temperature and humidity monitoring and controlling upon an appropriate WSN layout structure. The WSN layout strategy provided the theoretical framework for the laying out of WSNs, assisted in the analysis, management and optimization of data, enhanced the performance of the control system, and decreased the energy used in the production process.

This research suggested a new approach called Distributed Particle Swarm Optimization technique (D-PSO)¹⁹. The regional operator used in this method aimed to resolve the problem of heuristic algorithms where it converged too quickly. Given the fact that the power systems were highly prone to interference, a Relay Node Strategy (RNS) was used in this study to enhance communication. The simulated results affirmed that the D-PSO approach was effective and superior and also justified the need of the RNS. This technique also addressed issues such as energy consumption, coverage, and quality of communication, which lead to improved performance of the WSN when compared to some other modern particle swarm algorithms.

In this article, a rapid Belief Function based Inter-Criteria Analysis (BF-ICrA) methodology was developed through the canonical decomposition of basic belief assignments over the two-valued frame of discernment²⁰. This new framework was then used to assess the performance of the Multiple-Objective Ant Colony Optimization (MO-ACO) algorithm for deploying WSN.

The performance of wireless sensors in raw tobacco pallets can be enhanced using multiple optimization methods²¹. A three-dimensional complex environment of wireless sensors layout optimization model was developed. Along with that, a multi-objective function with the cost of sensor layout acquired the least formulation. Then, an Improved PSO, denoted by IPSO, was designed in order to produce the preliminary results. Wireless sensors layout was optimized and then the Long-Short Term Memory (LSTM) network-based prediction algorithm was used to forecast cigarette pallet temperature data for achieving the further optimization of sensor layout. In the end, using actual temperature data figures gauged in raw tobacco pallets, the simulation environment model was created, and also confirmed through simulation tests. The simulation outcomes expressed that the sensor layout optimization measure proposed in this article could greatly cut down on the number of sensors that need to be placed while at the same required endpoints assisting the companies to cut back on the costs involved in storage and keeping the raw tobacco in its optimum conditions.

An optimized layout method of Fiber Bragg Grating (FBG) sensor network based on modified artificial fish swarm algorithm was proposed in this paper²². To begin with, the elliptical sensing model of FBG was determined. According to the transfer characteristics of FBG, the exponential attenuation model between sensor node and the signal source was developed. Secondly, network coverage rate was taken as the objective function along which the movement of nodes was assimilated to the behavior of artificial fish such as swarming, following and preying. In the status updating process of artificial fish, with regard to the limitations of artificial fish swarm algorithm optimized for the artificial fish movement, three adaptive step methods were developed. The performance of the algorithm in terms of convergence accuracy and speed was increased. Finally, the performance of the MAFSA was done with the performance of PSO and Genetic Algorithm (GA). The findings proved that the MASFA has enhancement search ability and thus could optimize the sensor node layout effectively which was the challenge in optimization of sensor layout.

In this study, using the rasterizing and vectoring of environment in two- and three-dimensional spaces, the effectiveness of the global optimization algorithms was evaluated and compared for the optimal number of sensors placement whereas a vector environmental model was found to be a more precise one for this task²³. Since the aim was to evaluate the efficiency and the results of global methods, the area of investigation as well as the conditions of implementation did not differ for the algorithms applied. A number of possible techniques for the problem of sensor placement like GAs, L-BFGS, VFCPSO and CMA-ES, were discussed in conjunction with the WSN deployment algorithms and their evaluation criteria in terms of optimal coverage, coverage precision regarding the environment model and algorithm convergence time. On the contrary, there was a coverage probability model applied to all the global optimization algorithms used in this research. Results of these applications suggested that the use of more complex environmental parameters in the model and coverage gave better and more realistic outputs. Still, it might compromise the efficiency of the algorithms with respect to time.

This paper developed the least number of sensors to achieve multiple coverage of a non-simply connected area by a given number of sensors through optimization problem²⁴. A new objective function was developed for the greedy active sensing (or next-best-view) algorithm for the purposes of building efficient and robust sensor networks and even derive theoretical bounds on how optimal the obtained network was. In addition, within the framework of the algorithm, a Deep learning model was incorporated in order to speed up the process and be able to do near real-time computations. The Deep Learning model called for the creation of a set of training examples. In line with that, it was argued that studying the geometry of the training data set was essential for understanding the behavior and the training of deep learning algorithms. It was also shown that a rather naive and simple parallel greedy approach, when optimized via a more basic objective, could turn out to be very effective.

The study was based on an efficient area coverage maximizing approach with a new optimization technique known as Coati Modernized Beluga Whale Optimization (CMBWO)²⁵. Area coverage maximizing approach consisted of two key elements: (i) Sensor node coverage model and (ii) Area coverage optimization. In the first part, a normal setup of a 2D WSN monitoring area was taken with some target monitoring points included to help deal with coverage. More importantly, the distance from the sensor node to the target monitoring point was measured using weighted Manhattan distance evaluation rather than the conventional Euclidean distance evaluation. This was done in order to help the sensor node in defining the exact position of any target monitoring point. The next, area coverage optimization step was tackled with the help of CMBWO algorithms in order to enhance WSN area coverage. This hybridization was achieved by the COA modernizing BWO. Such efficient hybridization has resulted to maximum area coverage of sensor nodes in WSN.

A new method for optimizing coverage in WSN through the use of Yin-Yang Pigeon Inspired Optimization (Yin-YangPIO) was suggested²⁶. To start with, the good point set was introduced into initialization phase which enhanced the dispersion of pigeon population in the solution space as compared to a case with no good point set. Then a model of YYPO was combined with PIO, where the map & compass operator and landmark operator strategies were modified to enhance the optimization; later on, the opposition-based learning was incorporated in PIO in order to cover more area of search space; and at last, several test functions were chosen to evaluate the performance of the Yin-Yang PIO optimization technique. The efficiency and performance of the proposed method were verified by three sets of experiments concerning the optimization of WSN coverage using different sets of parameters. Table 1, describes existing methods.

Table 1 Existing methods on WSN optimization.

Problem statement

The design of Wireless Sensor Networks (WSNs) calls for solving the placement, layout, and performance of sensor nodes. This task is of paramount importance due to WSN constraints such as energy budget, communication range, and environmental variations. The main challenge is to achieve maximum coverage while conserving energy and maintaining reliable communication between nodes. The layout should ensure full area coverage without overlaps, and enable efficient data relay to the central processing unit, taking into consideration the density, range, and interference of nodes. Moreover, the design must be flexible to adapt to dynamic environments or node failures, adding complexity to the optimization process.

Despite numerous advancements, existing approaches face several limitations:

• Many methods rely on computationally expensive optimization algorithms, increasing memory usage and execution time.

• Techniques often address only a subset of objectives (e.g., energy consumption or coverage), rather than providing comprehensive multi-objective optimization.

• Heuristic algorithms like D-PSO converge quickly to suboptimal solutions, reducing their effectiveness in diverse scenarios.

• Current methods struggle to adapt to dynamic network conditions, such as environmental constraints or node failures, limiting real-world applicability.

• Algorithms like the artificial bee colony algorithm exhibit low efficiency and reliability in noisy environments.

• Techniques such as ACO-based approaches show higher error rates in maintaining network reliability.

• Methods like Yin-YangPIO and BF-ICrA face challenges in adapting to real-time, large-scale networks.

• Existing approaches fail to effectively explore high-dimensional solution spaces, resulting in poor Pareto front solutions.

• Optimized routing protocols (e.g., Improved Honey Badger Algorithm) result in higher delays, unsuitable for time-critical applications.

• Existing frameworks struggle to scale with increasing network size, restricting deployment in larger WSNs.

• Generative methods often suffer from mode collapse, limiting their ability to produce diverse layout configurations.

These limitations highlight the need for a robust and efficient solution that addresses multi-objective optimization challenges, ensures adaptability to dynamic scenarios, and delivers scalable and high-performance layouts for real-world WSN applications.

Materials and methods

With these challenges in mind, the following section details the mathematical framework for optimizing WSN layouts.

Proposed model

The choice of sensor node locations such that they completely cover a region or a group of objectives is connected to the optimum layout planning challenge. Demonstrating “how better a geographical area or a group of targets are monitored by deployed sensor nodes in a WSN” represents the primary objective associated with the layout optimization. The optimal solution for this issue falls into the NP-hard combinatorial class and necessitates optimizing many conflicting goals, including cost, coverage, WSN fault tolerance, lifetime, connection, and energy effectiveness. With growing WSN sizes and sensor node variety, the layout optimization challenge gets increasingly intricate. Due to the limits in communication, detection, energy, and processing resources of sensor nodes, it becomes difficult to compute the objectives of vast-scale WSNs in an easy-to-understand manner for optimal layout planning.

WSNs’ monitoring as well as effectiveness capacity are strongly impacted by their layouts. If layout optimization is neglected when sensor nodes are deployed, poor coverage, high network failure rates, and frequent disconnections might result in unexpected WSN behavior. Real-time application speed as well as functionality are severely impacted by this WSN deterioration. The overall proposed model of optimizing layout in WSN is shown diagrammatically in Fig. 2.

Fig. 2

Overall proposed model of optimizing layout in WSN.

WSN modeling

The region under consideration represents a level, square surface on which sensor nodes can observe objects inside $\:{S}_{sensor}$ and interact with any remaining node under $\:{S}_{comm}$. Each sensor in the region should interact with the High-Energy Communication Node (HECN), which is positioned in the middle. This communication can occur directly or by hops through neighboring sensors. The purpose of this consideration is convenience, and it has no bearing on generalizability. It is considered that every sensor starts off with the similar amount of energy in its battery, which describes the only source of energy. It is also considered that this energy declines by one arbitrary unit for every data transfer.

The sensor’s vertical as well as horizontal coordinates represent the design variables. This work solely examines WSNs having a fixed count of sensors, $\:o$, such that the design variable vector, $\:\overrightarrow{dv}$, has a constant size of $\:2o$.

$$\:\overrightarrow{dv}=\left[\begin{array}{ccc}{y}_{1}&\:{z}_{1}&\:\begin{array}{ccc}\cdots\:&\:{y}_{o}&\:{z}_{o}\end{array}\end{array}\right]$$

(1)

Identical layouts with their orientation changed around the origin will have comparable goals with distinct design vectors. Hence, discussing a global best layout may be appropriate, while discussing an ideal design vector associated with coordinates may not.

Objective function

The weighted sum of entire fitness functions is used to calculate every solution’s fitness. Here are the techniques for calculating the objectives of WSNs in terms of node count, coverage, lifetime, connectivity, and energy consumption.

Lifetime

The failure associated with the network’s initial node determines how long a WSN will last. The initial energy and consumed energy estimate of every node are used to compute the lifetime of a single node. As shown in (2), the amount of time that a node can operate is determined. According to (3), the network collapses when the initial node fails, and the total network lifetime is determined by taking the minimum lifespan of an active node .

$$\:{lt}_{j}={ie}_{j}/{ec}_{j}$$

(2)

$$\:lifetime=min\left\{{lt}_{j}\right\}$$

(3)

Energy consumption

In a WSN, each node may carry out a variety of functions, including processing, sensing, data transmission as well as reception to and from remaining sensor nodes, and maintenance. These actions require energy consumption, which should be minimized for an ideal arrangement using the shortest data transmission line. The minimum spanning tree approach is used to determine the data transmission cost for the shortest path to the data sink in order to compute the energy consumption associated with every node. The node maintenance energy, the transmission energy, as well as the reception energy are added up in accordance with (4), and the neighboring nodes from which data may be received are computed. The total energy spent by the network’s active nodes equals the energy consumption associated with the entire network, and this can be computed utilizing (5).

$$\:{ec}_{j}={m}_{j}+{path}_{j}\times\:{tra}_{j}+{in}_{j}\times\:{rec}_{j}$$

(4)

$$\:total\:energy=\:\sum\:_{j=1}^{o}{ec}_{j}$$

(5)

Connectivity ensures every node can communicate directly or indirectly. Coverage measures the monitored area, while energy consumption refers to the power used for sensing and communication tasks.

Connectivity

When there exists a single or multiple-hop communication link connecting each sensor node to the data sink, a WSN is said to be connected. In order to achieve a fully connected network, the optimization algorithms’ primary objective is to reduce the count of unconnected nodes in the system. By building a network with nodes as its vertices and developing a minimum spanning tree with the data sink as the root node, every layout solution’s connection is examined. If the distance among two nodes, and, is smaller than their communication radius, then they are deemed linked. The edge weight is then placed to the distance among them, as shown in (6). Next, the shortest pathways between each active node and the data sink, which is positioned in the centre of the monitoring region, are determined using the Bellman Ford single source shortest path method. When there exists no practical route to the data sink, the nodes are regarded as disconnected.

$$\:{ew}_{jk}=\left\{\begin{array}{c}\begin{array}{cc}{e}_{jk}&\:if\:{e}_{jk}<{S}_{comm}\end{array}\\\:\begin{array}{cc}\infty\:&\:else\end{array}\end{array}\right.$$

(6)

Coverage

The coverage may be calculated using two different techniques: an area-oriented technique and a grid-oriented technique. A binary sensing method, in which a node’s sensing region is seen as a circular disc having a fixed sensing range $\:\left({S}_{sense}\right)$, is employed in both approaches. A node can detect an item that is present at a distance that is smaller than its sensory range. Here, the Euclidean distance between the node’s centre as well as the target point $\:{U}_{j}$, with regard to the fixed sensing radius $\:{S}_{sense}$, is used to compute the detection probability $\:{Q}_{j}$ of a sensor node $\:{T}_{j}$ as in (7).

$$\:{Q}_{j}=\left\{\begin{array}{c}\begin{array}{cc}1&\:if\:Dist\left({T}_{j},\:{U}_{j}\right)<{S}_{sense}\end{array}\\\:\begin{array}{cc}0&\:else\end{array}\end{array}\right.$$

(7)

The sensor nodes in the monitoring region are dispersed at random in the area-oriented technique. A sensor node’s sensing radius $\:\left({S}_{sense}\right)$, which represents the same for every sensor node in a homogeneous WSN, determines the region it covers. In accordance with (8), the total area covered by these nodes is computed, and the overlap between sensor nodes is removed to get complete area coverage.

$$\:area\:coverage=\sum\:_{j}^{O}\pi\:{S}_{sense}^{2}-Overlap\left({sensor}_{1}\cdots\:{sensor}_{O}\right)$$

(8)

The monitoring zone is organized into square grids with equal sizes in the grid-oriented technique. To find out if any sensor nodes fully cover a grid or not, the Euclidean distance between every node and the grid centre is determined. The sensing radius $\:\left({S}_{sense}\right)$ is used to determine the greatest region that every sensor node $\:j$ at location $\:\left({y}_{j},{z}_{j}\right)$ can cover. The total points in the region are next used to normalize the grid’s total covered grid points as in (9).

$$\:point\:coverage=\left[{V}_{j}={1}^{o}{S}_{sense}^{2}\left({y}_{j},{z}_{j}\right)\right]/total\:points$$

(9)

When there exist few sensor nodes and a limited monitoring region or set of points, the grid-oriented approach operates quickly; yet, when the size related to the WSN increases owing to the availability of many nodes, it becomes sluggish. Area coverage is calculated using the area-oriented technique, while point coverage is calculated using the grid-oriented technique, in order to prevent the algorithm’s effectiveness from degrading.

Number of nodes

The count of Active-Inactive (A/I) mode bits is used to determine the count of nodes for every solution. One A/I mode bit, when placed to one, is utilized in solutions associated with homogeneous WSNs to determine active nodes.

Novel AGAN

The proposed novel AGAN model is used for handling the layout optimization problem in WSNs, in which the parameter tuning of GAN is performed by the PFOA with the aim of attaining the objective function. A discriminator plus a generator makes up a GAN. The generator’s primary goal is to produce enough fake images for the discriminator to be unable to distinguish between them. The discriminator’s goal is to make sure the generator doesn’t trick it. The traditional generative methods often require parameter estimation, which calls for intricate computations like Monte Carlo sampling or various approximate estimate techniques, as well as a specialized methodology. Unlike traditional generative methods, GAN does not require intricate probability computations. Furthermore, the distribution type does not require to be specified by GAN. It directly encourages Deep Neural Networks (DNNs) to distribute actual data. Usually used in the training procedure, the gradient descent technique makes use of the Back Propagation (BP) algorithm. Equation (10) represents the GAN’s optimization function.

$$\:{min}_{H}{max}_{E}W\left(E,\:H\right)={F}_{y\sim{Q}_{data\left(y\right)}}\text{log}E\left(y\right)+{F}_{a\sim{Q}_{a}\left(a\right)}\text{log}\left(1-E\left(H\left(a\right)\right)\right)$$

(10)

Here, $\:E$ represents the discriminator and $\:H$ represents the generator. The true image is $\:y$. The generator $\:H$’s noise input is denoted by $\:a$. The image produced by generator $\:H$ is denoted by $\:H\left(a\right)$. $\:E\left(y\right)$ represents the likelihood that the discriminator $\:E$ will determine whether or not the true image is accurate. The likelihood that the discriminator determines whether or not the image produced by generator $\:H$ is true is $\:E\left(H\left(a\right)\right)$.

Learning the distribution of training data represents the goal of GAN. Initially, noise is fed into the generator in order to achieve this purpose. This noise is converted into an image by the generator. The discriminator provides the image’s true as well as false coefficients and compares the simulated and actual images. Both the discriminator as well as the generator are enhanced by cyclic alternate training. The generator has the ability to produce artificial images that closely resemble the original ones.

Due to their ability to create different network arrangements, the use of GANs improves layout optimization in WSNs. Furthermore, they raise the level of coverage and connectivity incurred with the least energy cost. Lastly, GANs provide ease in learning while in use, hence the system can be able to change and self-optimize layouts depending on the changes in the environment and network requirements. Nonetheless, it can be process-heavy, taking up a comprehensive amount of resources in the training phase. These techniques experience limitations in the designer’s creative ability due to mode collapse. Finally, since these are complex architectural designs, the likelihood of easy application or adaptation in a dynamic and real-time network environment is low. Therefore, to overcome its shortcomings, the parameters of GAN are tuned by PFOA with the intention of attaining the fitness function, thus considered to be novel AGAN. This AGAN system enhances both the precision and the effectiveness in the generation of the optimal configurations. They use complex designs to capture complex dependencies, cope with changing scenarios, enable multi-objective optimization leading to improved coverage, lower energy usage, and increased robustness of the network. The proposed novel AGAN model for the WSN layout optimization is shown in Fig. 3.

Fig. 3

Proposed novel AGAN model for the WSN layout optimization.

PFOA algorithm

The PFOA algorithm is selected here in the proposed layout optimization in WSN model for tuning the GAN parameters, that in turn can lead to deriving the objective function. In the fields of numerical as well as engineering optimization, PFOA is employed to effectively solve continuous optimization issues. The algorithm simulates the aforementioned behaviors to create two dynamic search processes for exploration as well as exploitation. It is motivated by the adaptable as well as mobile foraging behavior of piranha swarms and segments their foraging behavior into three patterns: scavenging foraging, bloodthirsty cluster attack, and localized group attack. In order to improve population variety at various phases of the search and aid in the discovery of optimal solutions, PFOA employs three schemes: non-linear parameter management, population survival, and reverse evasion search.

The primary components of PFOA are parameter and agent position update, population assessment, and population initialization. The group of population candidate solutions in the PFOA algorithm may be written as follows:

$$\:y=\left[\begin{array}{ccc}\begin{array}{c}{y}_{11}\\\:{y}_{21}\\\:\begin{array}{c}\cdots\:\\\:{y}_{\left(o-1\right)1}\\\:{y}_{o1}\end{array}\end{array}&\:\begin{array}{c}{y}_{12}\\\:{y}_{22}\\\:\begin{array}{c}\cdots\:\\\:{y}_{\left(o-1\right)2}\\\:{y}_{o2}\end{array}\end{array}&\:\begin{array}{ccc}\begin{array}{c}{y}_{13}\\\:{y}_{23}\\\:\begin{array}{c}\cdots\:\\\:{y}_{\left(o-1\right)3}\\\:{y}_{o3}\end{array}\end{array}&\:\begin{array}{c}\cdots\:\\\:\cdots\:\\\:\begin{array}{c}\cdots\:\\\:\cdots\:\\\:\cdots\:\end{array}\end{array}&\:\begin{array}{c}{y}_{1E}\\\:{y}_{2E}\\\:\begin{array}{c}\cdots\:\\\:{y}_{\left(o-1\right)E}\\\:{y}_{oE}\end{array}\end{array}\end{array}\end{array}\right]$$

(11)

The position vector describing the piranhas is shown by $\:{y}_{j}=\left[\begin{array}{ccc}{y}_{j1}&\:{y}_{j2}&\:\begin{array}{cc}\cdots\:&\:{y}_{jE}\end{array}\end{array}\right]$. Set every piranha population member’s location vector to its initial value using Eq. (12).

$$\:{y}_{j}={LB}_{j}+{\beta\:}_{1}\times\:\left({UB}_{j}-{LB}_{j}\right)$$

(12)

Here, $\:{UB}_{j}$ and $\:{LB}_{j}$ stand for the upper as well as lower limits of the piranha search in the habitat, correspondingly, and $\:{y}_{j}$ represents the position associated with the $\:{j}^{th}$ individual in the piranha candidate solution. A random integer among 0 and 1 is indicated by $\:{\beta\:}_{1}$.

Describe the parameter for predation intensity. $\:G$: The blood concentration $\:{G}_{j}$ as well as the distance $\:{e}_{j}$ among the piranha and its prey both affect the piranha’s abnormally high sensitivity to blood detection. The below Eq. (13) results from piranhas swimming towards regions with high blood concentrations; the higher the blood concentration, the quicker the piranhas move.

$$\:\begin{array}{c}{G}_{j}={\beta\:}_{2}\times\:\frac{{A}_{j}}{4\pi\:{e}_{j}^{2}}\\\:{e}_{j}={y}_{Prey}-{y}_{j}\\\:{A}_{j}={\left[{y}_{j}\left(u\right)-{y}_{j+1}\left(u\right)\right]}^{2}\end{array}$$

(13)

Here, $\:{\beta\:}_{2}$ represents a random number among 0 and 1, $\:A$ represents the source intensity, $\:{A}_{j}$ represents the source intensity as perceived by the $\:{j}^{th}$ search agent, which will vary in real time as the agents follow, and $\:{G}_{j}$ represents the predation intensity parameter for the position associated with the $\:{j}^{th}$ individual piranha.$\:\:{e}_{j}$ represents the distance among the location of the $\:{j}^{th}$ individual piranha and the prey (best solution).

Nonlinear parametric control schemes are useful for managing time-varying randomized procedures, preventing populations from convergent too soon, and guaranteeing a seamless transition among exploration as well as exploitation. Greater values of $\:T$ aid the search agent in conducting an auditory-oriented global search and avoiding becoming trapped in a local optimum during the early as well as middle phases of PFOA, however when $\:T$ varies in the later phases, PFOA can converge more quickly, as shown in Eq. (14).

$$\:T=D\bullet\:\text{cos}{\left[\frac{\pi\:}{2}⨂\left(\frac{u}{\text{m}\text{a}\text{x}\_Iter}\right)\right]}^{4}$$

(14)

Here, $\:⨂$⨂\) indicates the product of a value and a variable, $\:\text{m}\text{a}\text{x}\_Iter$ indicates the maximum count of iterations, and the constant $\:D$ is validated.

In order to enhance the solution, the reverse escape search approach uses flag $\:F$ to shift the population search’s direction, preventing the candidate population from becoming stuck in a small region and rerouting the search to a novel location. This usually occurs during the search procedure, providing the search agent with additional chances to thoroughly and meticulously examine the search region as in Eq. (15).

$$\:F=\left\{\begin{array}{c}\begin{array}{cc}1&\:{\beta\:}_{3}\le\:0.5\end{array}\\\:\begin{array}{cc}-1&\:{\beta\:}_{3}>0.5\end{array}\end{array}\right.$$

(15)

Here, a random value among 0 and 1 is indicated by $\:{\beta\:}_{3}$. When hungry, it will attack food that is several times larger than itself as a collective foraging animal. A splash of water is produced whenever prey goes outside of their territory, and the perceptive piranha detect this signal. They immediately gather to encircle and bite the prey in succession, with the agent closest to the prey attacking first. Equation (16) displays the localized group attack pattern’s mathematical framework.

$$\:{y}_{j}\left(u+1\right)={\gamma\:}_{1}\sum\:_{l=1}^{qd}\frac{{M}_{l}\left(u\right)-{y}_{j}\left(u\right)}{qd}-{y}_{Prey}\left(u\right)$$

(16)

Here, $\:M\in\:Y$, in which $\:Y$ represents the count of randomly produced piranhas, $\:{M}_{l}\left(u\right)$ represents the fraction of local population attacks that are carried out to initiate the attack first, $\:searchagents\_No$ represents the total count of agents, $\:{y}_{j}\left(u+1\right)$ represents the novel position associated with the search agents, and $\:qd$ represents a randomly generated integer. The location related to the present agent is shown by $\:{y}_{j}\left(u\right)$, the position associated with the optimal agent discovered in the earlier iteration is indicated by $\:{y}_{Prey}\left(u\right)$, and $\:{\gamma\:}_{1}$ represents a random value uniformly distributed in [− 2,2] that is crucial in altering the piranha’s trajectory.

Because they have a unique taste for and acute sensitivity of the scent of blood, piranhas are drawn to areas having high blood concentrations to attack more forcefully when their victim is injured and bleeding. It swims more quickly when the blood concentration is higher. The non-linear cosine component S, which is also impacted by E, the blood concentration $\:{G}_{j}$, and the distance di among the piranhas as well as their prey are all crucial at this phase. According to Eq. (17), piranhas may successfully avoid local optima and locate better prey by altering their direction of travel.

$$\:{y}_{j}\left(u+1\right)={\gamma\:}_{1}*{f}^{{\gamma\:}_{2}}*{y}_{Prey}\left(u\right)+H*{y}_{Prey}\left(u\right)*F*{G}_{j}+F*{\beta\:}_{4}*T*{G}_{j}$$

(17)

Here, $\:{\gamma\:}_{1}$ represents a random count uniformly distributed in [− 2, 2], $\:{\gamma\:}_{2}$ represents a random count uniformly distributed in [− 1/2, 1/2], $\:{\beta\:}_{4}$ represents a random count within 0 and 1, and $\:{y}_{j}\left(u+1\right)$ indicates the novel position associated with the search agent and $\:{y}_{Prey}\left(u\right)$ indicates the position related to the optimal agent discovered in the earlier iteration. $\:H$ represents the piranha’s coefficient of foraging ability, and its uniform distribution of $\:{\gamma\:}_{1}*{f}^{{\gamma\:}_{2}}$ permits dynamic adjustment and trade-offs between local and global search skills.

According to the modelling of Eq. (18), piranhas, due to their poor vision, separate from the group while foraging in muddy watersheds and at night and swim erratically across their habitat as individuals, eating on seeds and carrion.

$$\:{y}_{j}\left(u+1\right)=\frac{1}{2}\left[{f}^{{\gamma\:}_{2}}*{y}_{{D}_{1}}\left(u\right)-F*{y}_{j}\left(u\right)\right]$$

(18)

Here, $\:{y}_{j}\left(u+1\right)$ indicates the search agent’s novel location, $\:{\gamma\:}_{2}$ represents a uniformly distributed random count in [− 1,1], $\:F$ represents a parameter that modifies movement direction, $\:{y}_{{D}_{1}}\left(u\right)$ indicates the $\:{D}_{1}$st agent location chosen at random from the piranhas, $\:{y}_{j}\left(u\right)$ indicates the $\:{j}^{th}$ agent location chosen at random from the agents, and $\:{D}_{1}\ne\:j$.

The growth of the piranha population is restricted by their reproductive traits and the many natural predators they face. Initially, the agent’s Survival Rate ($\:SR$) is determined utilizing Eq. (19) to preserve population variety and the offspring population is replicated employing Eq. (20), where the survival rate $\:SR\le\:1/4$ (i.e., low $\:SR$).

$$\:SR\left(j\right)=\frac{{Fitness}_{max}-Fitness\left(j\right)}{{Fitness}_{max}-{Fitness}_{min}}$$

(19)

$$\:{y}_{j}\left(u+1\right)={y}_{Prey}\left(u\right)+\frac{1}{2}\left\{\left[{y}_{{D}_{1}}\left(u\right)-F*{y}_{{D}_{2}}\left(u\right)\right]-\left[{y}_{{D}_{2}}\left(u\right)-F*{y}_{{D}_{3}}\left(u\right)\right]\right\}$$

(20)

Here, $\:F$ represents the parameter for varying the direction, $\:{y}_{j}\left(u+1\right)$ indicates the novel location associated with the search agent, $\:{y}_{Prey}\left(u\right)$ indicates the location related to the optimal agent discovered in the earlier iteration, and $\:{y}_{{D}_{1}}\left(u\right)$, $\:{y}_{{D}_{2}}\left(u\right)$, and $\:{y}_{{D}_{3}}\left(u\right)$ indicate the $\:{D}_{1}$, $\:{D}_{2}$, and $\:{D}_{3}$ agent locations that were randomly chosen from the piranhas having $\:{D}_{1}\ne\:{D}_{2}\ne\:{D}_{3}$, correspondingly. In Algorithm 1, the PFOA pseudo-code is displayed.

Algorithm 1: PFOA.

The AGAN (Advanced Generative Adversarial Network) model is formulated to address the multi-objective optimization problem of WSN layout design, which includes maximizing coverage, minimizing energy consumption, and extending network lifetime. Each component of the formulation is carefully chosen based on practical and theoretical requirements:

• 1. Objective function

The overall fitness function FFF integrates multiple conflicting objectives:

$$\:F={w}_{1}*{f}_{coverage}+{w}_{2}*{f}_{energy}+{w}_{3}*{f}_{lifetime}$$

(21)

where

• $\:{f}_{coverage}$represents the percentage of the monitored area effectively covered by sensor nodes. This is computed using both area-oriented and grid-oriented techniques to ensure versatility.

• $\:{f}_{energy}$ quantifies the energy efficiency of the network, minimizing energy consumption through reduced communication distances between nodes and the sink. It is derived using a Minimum Spanning Tree approach.

• $\:{f}_{lifetime}\:$reflects the network’s operational duration, calculated by determining the time until the first node failure.

The weights $\:{w}_{1},\:{w}_{2},{w}_{3}$ allow prioritization based on application requirements. For instance, environmental monitoring might prioritize $\:{w}_{1}$​ (coverage), while disaster management could emphasize $\:{w}_{3}$​ (lifetime).

• 2. GAN formulation

The adversarial training process within AGAN involves two neural networks, the generator GGG and discriminator DDD. The optimization equation is:

$$\:\underset{G}{\text{min}}\underset{D}{\text{max}}V\left(D,G\right)={\mathfrak{E}}_{x\sim{p}_{data\left(x\right)}}\left[logD\left(x\right)\right]+{\mathfrak{E}}_{z\sim{p}_{z}\left(z\right)}\left[\text{log}\left(1-D\left(G\left(z\right)\right)\right)\right]$$

(22)

In (22),

• $\:G\left(z\right)\:$generates candidate WSN layouts from a noise vector $\:z$.

• $\:D\left(x\right)$ evaluates whether a layout $\:x$ is real (derived from data) or synthetic (from $\:G$).

• The loss function encourages $\:G$ to produce realistic layouts, while $\:D$ learns to distinguish between synthetic and real layouts, creating a competitive dynamic that improves solution quality.

• 3. Energy efficiency

The energy consumption E for each node is calculated as:

$$\:E={E}_{transmit}+{E}_{receive}+{E}_{processing}$$

(23)

where

• $\:{E}_{transmit}$ is the energy for sending data to the next node or sink.

• $\:{E}_{receive}$ is the energy for receiving data from other nodes.

• $\:{E}_{processing}$ is the computational energy consumed locally by a node.

The integration between AGAN and PFOA works as follows:

• GAN parameter tuning: PFOA dynamically adjusts critical parameters of the AGAN, such as learning rates, noise vector dimensions, and regularization coefficients. These adjustments improve the GAN’s ability to generate realistic and optimal layouts.

• Objective function optimization: PFOA evaluates each candidate layout generated by AGAN against the multi-objective fitness function. Feedback is then used to refine AGAN’s generator parameters iteratively.

• Cyclic interaction: The discriminator evaluates layouts generated by the tuned GAN, and PFOA refines the GAN’s parameters using fitness scores derived from the objective function. This interaction accelerates convergence towards optimal solutions.

To enhance the robustness of the proposed multi-objective optimization function, a sensitivity analysis was incorporated directly into the objective function formulation. These weights shown in (21) determine the relative importance of each objective in the optimization process. To analyze the sensitivity of the optimization outcomes to the chosen weights, the following modifications were applied to the objective function:

• 1. Dynamic weight variability: The weights $\:{w}_{1},\:{w}_{2},{w}_{3}$ ​ were varied systematically across a normalized range ($\:{w}_{1}+\:{w}_{2}+{w}_{3}=1$) within the optimization process. This variation was integrated directly into the iterative evaluation of the objective function, allowing the algorithm to identify how changes in weighting influence the solution space.

• 2. Sensitivity impact metrics: During optimization, the sensitivity of the objective function was evaluated by monitoring the variability in key performance metrics (e.g., Pareto front spread, hypervolume) as weights were adjusted. This analysis demonstrated how increased emphasis on a specific objective (e.g., coverage) affects the trade-offs with other objectives (e.g., energy consumption and lifetime).

• 3. Optimization feedback loop: The sensitivity analysis was embedded into the AGAN-PFOA workflow by introducing adaptive weight adjustments after each iteration. This allowed the model to dynamically adjust the relative priority of objectives based on intermediate results, enhancing solution quality and robustness.

• 4. Results of embedded sensitivity analysis:

The sensitivity analysis revealed the following:

• High w1w_1w1​ (coverage-focused): Yielded maximum spatial monitoring but slightly increased energy usage and reduced lifetime.

• High w2w_2w2​ (energy-focused): Significantly reduced energy consumption but led to a small decrease in coverage.

• High w3w_3w3​ (lifetime-focused): Maximized network operational duration with minimal compromise on energy and coverage.

The direct inclusion of sensitivity analysis into the objective function strengthens the AGAN-PFOA model by providing real-time insights into optimization trade-offs and improving its adaptability to varying application requirements.

Algorithm 2: AGAN-PFOA integration.

Results and analysis

Experimental setup

The proposed AGAN-PFOA model for the layout optimization in WSNs was implemented in MATLAB and the findings were discussed. The population size and the iteration number was placed to be 10 and 100. The total number of nodes is considered to be 100. The proposed AGAN-PFOA model was compared with distinct traditional algorithms such as pcFPA¹⁶, BF-ICrA¹⁹, CMBWO²⁴, and Yin–YangPIO²⁵ with consideration of several analyses like PDR, coverage, energy consumption, lifetime, alive node count, delay, and routing overhead to describe the betterment of the developed layout optimization model in WSNs. The simulation parameters used for the proposed layout optimization in WSN model is shown in Table 2.

Table 2 Simulation parameters.

The simulation parameters have been expanded to provide greater detail about the network topology, traffic patterns, and mobility models used, along with a rationale for the chosen parameter values. The network topology is designed as a 100 × 100 square meter area, with nodes deployed homogeneously to ensure even coverage. The topology assumes a flat terrain without obstacles, reflecting a standard scenario for WSN layout optimization.

Traffic patterns follow a constant bit rate (CBR) model, where nodes generate data packets at fixed intervals to simulate real-time monitoring applications. This pattern was chosen for its relevance to applications such as environmental monitoring and smart agriculture, where consistent data flow is crucial. Mobility models were not included in the current study, as the focus is on optimizing static WSN layouts. However, the framework is adaptable to dynamic models, which can be explored in future work.

The choice of parameter values, such as a communication radius of 30 m and an initial energy of 1000 mA, is based on typical WSN deployment scenarios reported in the literature. These values ensure a balance between practical applicability and computational feasibility. The node count (100 nodes) was selected to represent medium-sized networks commonly deployed in real-world applications, while the population size (20) and iteration count (100) were tuned to achieve convergence within a reasonable time frame.

The Advanced Generative Adversarial Network (AGAN) used in this study is composed of a generator and a discriminator, both configured with carefully designed deep neural network (DNN) layers to address the complex multi-objective optimization problem of WSN layout design. The generator is a fully connected network with three hidden layers comprising 256, 128, and 64 neurons, respectively, each employing ReLU activation functions to capture non-linear dependencies in the solution space. The input layer accepts a random noise vector zzz of size 100 to generate diverse candidate layouts, while the output layer provides layout parameters (e.g., node coordinates) using a linear activation function to ensure continuous outputs. The discriminator, on the other hand, is also a fully connected network with three hidden layers of 128, 64, and 32 neurons. It uses Leaky ReLU activation for gradient flow stability and a single neuron in the output layer with a sigmoid activation function for binary classification, distinguishing between real and generated layouts.

The training procedure follows the standard adversarial setup, where the generator and discriminator are trained alternately. The discriminator minimizes a loss function designed to classify layouts accurately, while the generator minimizes a separate loss function that focuses on fooling the discriminator. Specifically, the loss function for the discriminator is $\:{L}_{D}=-E\left[logD\left(x\right)\right]-E\left[\text{log}\left(1-D\left(G\left(z\right)\right)\right)\right]$, and for the generator, it is $\:{L}_{G}=E\left[\text{log}\left(1-D\left(G\left(z\right)\right)\right)\right]$. Both networks are trained using the Adam optimizer with a learning rate of 0.0002 and a beta value of 0.5 to ensure stable convergence. Training continues until convergence is achieved, defined as the point where the generator consistently produces layouts that maximize the multi-objective fitness function, and the discriminator reaches minimal classification error.

To enhance the performance of AGAN, the Piranha Foraging Optimization Algorithm (PFOA) dynamically tunes hyperparameters such as the learning rate, batch size, and the number of hidden layers during training. This integration ensures that AGAN adapts effectively to diverse WSN scenarios, improving its ability to explore and exploit the solution space. Convergence is further evaluated using the stability of the Pareto front hypervolume, with the optimization process terminating when no significant improvements are observed over 20 consecutive epochs. The implementation of AGAN-PFOA was carried out using Python and TensorFlow, with training executed on an NVIDIA Tesla V100 GPU to ensure computational efficiency.

PDR analysis

Table 3; Fig. 4 shows how well different algorithms perform in terms of PDR for layout optimization in WSNs with varying node setups. The numbers reveal that the Proposed AGAN-PFOA method does better than all other algorithms for every node count tested. This steady improvement points to AGAN-PFOA’s ability to boost communication reliability as the network grows. The figures hint that AGAN-PFOA offers a strong solution to enhance PDR in WSN layout optimization. This underscores its potential for real-world use in making networks more efficient. The proposed AGAN-PFOA for the WSN layout optimization model in terms of PDR is 61.46%, 14.13%, 70.20%, and 28.66% better than pcFPA, BF-ICrA, CMBWO, and Yin–YangPIO respectively.

Table 3 PDR analysis.

Fig. 4

PDR analysis.

Coverage analysis

Table 4; Fig. 5 shows how well different algorithms cover areas in WSNs for layout optimization. It displays the percentage of area covered with various node setups. The Proposed AGAN-PFOA method proves to be the best at covering areas. This means it’s great at maximizing coverage as the network grows bigger. This matters a lot to make sure WSN applications can monitor and collect data from everywhere. The numbers prove that AGAN-PFOA does a great job at improving coverage when optimizing WSN layouts. This makes it a useful way to keep networks running. The proposed AGAN-PFOA for the WSN layout optimization model with respect to coverage is 15.12%, 02.06%, 3.13%, and 47.76% advanced than pcFPA, BF-ICrA, CMBWO, and Yin–YangPIO respectively.

Table 4 Coverage analysis.

Fig. 5

Coverage analysis.

Energy consumption analysis

Table 5; Fig. 6 shows how much energy different algorithms use in WSNs for layout optimization. It measures energy use for various node setups. Out of all the methods tested, the Proposed AGAN-PFOA uses the least energy, no matter how many nodes there are. This means it’s good at saving energy while keeping the network running well, which helps WSNs last longer. The numbers suggest that AGAN-PFOA is the best at saving energy when optimizing layouts in WSNs. This makes it a good choice for cases where saving energy is important. The proposed AGAN-PFOA for the WSN layout optimization model in terms of energy consumption is 12.67%, 53.33%, 53.78%, and 66.85% higher than pcFPA, BF-ICrA, CMBWO, and Yin–YangPIO respectively.

Table 5 Energy consumption analysis.

Fig. 6

Energy Consumption analysis.

Lifetime analysis

Table 6; Fig. 7 outline the lifetime results using different algorithms for WSN layout optimization with respect to exemplary results at varying node configurations. The presented AGAN-PFOA method, on the other hand, is associated with the highest lifetime values for each node count tested. This steady increase is indicative of the ability of the algorithm to prolong the operational time of the network, a characteristic that is essential in WSN applications in order to achieve and sustain effectiveness. The data above contradicts all other algorithms and signifies that AGAN-PFOA is the most efficient method for life time optimization of WSNs, hence it is the best option for use in applications that focus on life span and availability. The proposed AGAN-PFOA for the WSN layout optimization model with respect to lifetime is 65.91%, 87.18%, 58.70%, and 87.18% greater than pcFPA, BF-ICrA, CMBWO, and Yin–YangPIO respectively.

Table 6 Lifetime analysis.

Fig. 7

Lifetime analysis.

Alive node count analysis

Table 7; Fig. 8 provides the number of alive nodes for different algorithms employed in WSN layout optimization with different number of nodes. It can be seen that for all configurations considered, Optimal AGAN-PFOA method has resulted in the greatest number of alive nodes. This is a remarkable performance suggesting that AGAN-PFOA is particularly useful in preserving the network’s activity, which is very important in the case of WSN applications where constant data transmission and collection is inevitable. The data clearly reveals that AGAN-PFOA is the most effective algorithm for enhancement of alive node count in WSN layout optimization thereby improving the performance and reliability of the entire network. The proposed AGAN-PFOA for the WSN layout optimization model in terms of alive node count is 70.59%, 35.94%, 70.59%, and 12.99% more than pcFPA, BF-ICrA, CMBWO, and Yin–YangPIO respectively.

Table 7 Alive node count analysis.

Fig. 8

Alive node count analysis.

Delay analysis

The performance in terms of delay of different algorithms for layout optimization in WSNs is outlined in Table 8; Fig. 9, with different configurations for the number of nodes. The lowest delay values for all configurations are shown by the Proposed AGAN-PFOA method. This sustained pattern reinforces that AGAN-PFOA able to lower communication delays, facilitating the network, which is of utmost importance for applications that are time sensitive. The data demonstrates how AGAN-PFOA is effective for quick WSN layout optimization, as evidenced by the lower delays it has achieved in comparison to its counterparts, which makes it ideal for cases where data transmission must be quick. The proposed AGAN-PFOA for the WSN layout optimization model with respect to delay is 44.88%, 41.07%, 27.96%, and 15.84% advanced than pcFPA, BF-ICrA, CMBWO, and Yin–YangPIO respectively.

Table 8 Delay analysis.

Fig. 9

Delay analysis.

Routing overhead analysis

Table 9 ad Fig. 10 shows the routing overhead of several algorithms that have been used in WSNs for layout optimization with respect to the number of nodes placed. The Proposed AGAN-PFOA method exhibits the minimum routing overhead in all configurations tested. This persistent reduction emphasizes the efficiency of AGAN-PFOA in reducing the amount of resources that are utilized for routing which is very important in improving the overall performance of the network and increasing the life span of WSNs. Moreover, the data further supports AGAN-PFOA as the best remedy for routing overhead minimization during WSN layout optimization, improving efficiency and effectiveness of the network. The proposed AGAN-PFOA for the WSN layout optimization model in terms of routing overhead is 68.86%, 47.45%, 62.51%, and 35.35% superior to pcFPA, BF-ICrA, CMBWO, and Yin–YangPIO respectively.

Table 9 Routing overhead analysis.

Fig. 10

Routing overhead analysis.

Performance metrics under varying load

An additional evaluation metric with respect to varying traffic loads and fault tolerance scenarios is listed in Table 10. Network lifetime, a critical metric for energy-constrained WSNs, demonstrates that AGAN-PFOA significantly outperforms competing methods across all traffic levels. Under low traffic (10 packets/min), the proposed model achieves a lifetime of 240 h, compared to 200 h for pcFPA and 190 h for BF-ICrA. Even at high traffic (60 packets/min), AGAN-PFOA maintains a lifetime of 150 h, a 25% improvement over the best alternative (Yin-YangPIO), attributed to its efficient energy optimization strategies. In terms of fault tolerance, AGAN-PFOA proves robust against node failures, retaining 95% functionality under 10% node failures and 85% functionality even under severe failure conditions (30% node failures). This is significantly higher than pcFPA (65%) and BF-ICrA (60%), highlighting the proposed model’s optimized node placement and redundancy management. The Packet Delivery Ratio (PDR) metric reinforces the proposed model’s reliability. Under high traffic loads, AGAN-PFOA achieves 85% PDR, a substantial improvement over pcFPA (75%) and CMBWO (65%). Similarly, in fault scenarios (20% node failures), AGAN-PFOA maintains a PDR of 80%, outperforming Yin-YangPIO (75%) and other methods.

Table 10 Estimation of network parameters under varying load conditions.

These results highlight the practical benefits of the AGAN-PFOA model, which will be analyzed further in the “Discussion”.

Discussion

The analysis and results from different findings of the AGAN-PFOA model proposed for layout optimization of WSNs indicate that the model performs better in most of the measures. The PDR analysis shows that AGAN-PFOA has a better performance than classical algorithms by approving the tendency of communication to the reliability with growing number of nodes. Coverage analysis proves that area coverage is optimized in AGAN-PFOA which is important in monitoring data in wide areas. The use of AGAN-PFOA reduces energy consumption which puts emphasis on its effectiveness to enhance the duration of the network, a very important aspect in WSNs. Similarly, the lifetime analysis clears that AGAN-PFOA allows the largest operational time, hence its usefulness in network availability maintenance is better. This is further evident from the alive node count analysis, in which AGAN-PFOA manages to keep more active nodes than all other methods, which is paramount for uninterrupted data transfer. Delay analysis shows that communication latencies are considerably less with AGAN-PFOA such that it can be used for applications which are time critical. Lastly, the analysis of routing overhead shows that AGAN-PFOA is competent in employing routing without wasting too many resources thereby increasing network efficiency. Altogether, these findings provide evidence that AGAN-PFOA is highly efficient in layout optimization of WSN. There are substantial improvements in reliability, coverage, energy efficiency and operational lifetime.

The significant performance improvements of AGAN-PFOA over existing methods can be attributed to the following key observations.

• 1. The use of an Advanced Generative Adversarial Network (AGAN) enables the generation of high-quality candidate layouts by learning the complex dependencies between coverage, energy efficiency, and network lifetime. Unlike traditional methods that rely on static heuristics or fixed rules, AGAN dynamically adapts to the solution space, producing layouts that balance these objectives more effectively. The generator-discriminator feedback loop continuously improves the quality of candidate solutions, ensuring optimal trade-offs among conflicting objectives.

• 2. The Piranha Foraging Optimization Algorithm (PFOA) enhances AGAN’s performance by fine-tuning its hyperparameters, such as learning rates, network depth, and activation functions. This dynamic adjustment ensures that AGAN operates efficiently across diverse scenarios, avoiding overfitting and enhancing convergence towards globally optimal solutions. PFOA’s multi-phase search strategies (scavenging foraging, localized group attack, and reverse evasion search) further refine the optimization process by balancing exploration and exploitation.

• 3. AGAN-PFOA’s multi-objective optimization framework integrates weighted functions for coverage, energy, and lifetime. The flexibility to prioritize objectives dynamically during the optimization process enables the model to produce layouts tailored to specific application requirements. This adaptability, combined with AGAN’s ability to model complex nonlinear relationships, results in more effective layouts compared to methods limited by predefined trade-offs.

• 4. Traditional approaches often suffer from premature convergence or local optima, especially in high-dimensional search spaces. AGAN-PFOA mitigates these issues by utilizing PFOA’s reverse evasion search and AGAN’s gradient-based learning, ensuring a more thorough exploration of the solution space. This results in consistently higher Pareto front hypervolumes and better-spread solutions, as evidenced by the simulation results.

• 5. While some traditional methods achieve improvements through extensive computational resources, AGAN-PFOA’s intelligent architecture enables efficient optimization without excessive computational overhead. The synergy between AGAN and PFOA allows the system to generate high-quality solutions within a reasonable time frame, making it practical for real-world WSN deployment.

By utilizing the strengths of AGAN for high-quality solution generation and PFOA for dynamic parameter tuning, AGAN-PFOA achieves significant performance improvements over existing methods.

This study demonstrates significant performance improvements of AGAN-PFOA over existing methods; however, certain limitations remain. Statistical significance tests, such as ANOVA or paired t-tests, have not been conducted due to the primary focus on simulation-based performance metrics. Incorporating these tests would require extensive experimental replication and variability control, which are beyond the current scope. Additionally, error bars and confidence intervals have not been included in the energy consumption results, which may limit the clarity and reliability of variability assessment. The scalability analysis has been extended to networks with up to 100 nodes; however, investigating networks beyond this scale introduces considerable challenges. Specifically, increasing the node count beyond 100 nodes significantly increases the computational complexity due to the exponential growth of potential communication links, interference modeling, and the size of the search space for optimization algorithms. These factors result in higher memory requirements and longer convergence times for AGAN-PFOA, making experimentation resource-intensive. These limitations have been acknowledged, and future work aims to address them through statistical validation, inclusion of confidence intervals, and distributed optimization techniques for improved scalability.

The deployment of the AGAN-PFOA framework in real WSN systems involves notable computational requirements and training overhead. While the training phase, executed on high-performance GPUs, is resource-intensive and requires approximately 12 h for medium-sized networks (100 nodes), the deployment phase is lightweight and suitable for edge computing devices. The optimized layouts generated by AGAN-PFOA inherently minimize energy consumption and communication overhead, making them compatible with typical WSN hardware constraints. Although the model is currently optimized for static networks, it can be adapted for dynamic scenarios with incremental retraining at the cost of additional computational overhead. Scalability is feasible for networks up to 200 nodes, with future research focusing on distributed optimization for larger systems. These considerations balance the computational demands with the framework’s practical applicability, making it a viable solution for real-world WSN deployments.

Conclusion

In this research paper, a unique intelligent deep learning-based optimization approach was used to solve a layout optimization problem. The main goal here was to address a variety of goals related to the best configurations for homogeneous WSNs, including coverage, energy consumption, lifetime, connectivity, and the count of sensor nodes. The innovative AGAN solved the layout optimization problem, and the nature-inspired optimization method PFOA tuned the parameters while taking the goal function into account. The results of the simulation showed that the suggested new AGAN-PFOA produced the best Pareto front of non-dominated solutions with superior hyper-volumes and solution spread compared to the traditional solutions. The proposed AGAN-PFOA for the WSN layout optimization problem in terms of PDR, coverage, energy consumption, lifetime, alive node count, delay, and routing overhead was 61.46%, 15.12%, 12.67%, 65.91%, 70.59%, 44.88%, and 68.86% better than the existing methods respectively.