Introduction

Insect herbivory can impact the surrounding ecosystem at various scales, affecting the development rate and survival of host plant populations1,2,3,4,5. Likewise, the characteristics of the plant resource (physical and chemical traits, abundance, and distribution) also impact insect population dynamics1,6,7,8,9,10. An abundant high-quality resource could increase insect fitness, survival, and dispersal capacity, affecting their abundance, performance and potentially driving insect outbreaks across the landscape7,11,12.

In northern Patagonia Argentina, the steppe ecoregion (around 730,000 km2) is characterised by vegetation dominated by grassland and forbs, with no trees except near rivers and lakes. In this region, wetlands are important ecosystems due to their environmental and ecological functions, including providing food resources for different wild and domestic herbivore species13,14,15. Additionally, the increasing frequency of extreme weather events exposes humid environments to drought, affecting primary production and leading to competition between herbivores for the limited food resource15,16,17. Historically, these environments have suffered degradation caused by overgrazing, resulting in changes in the quality, abundance, and composition of grassland plant species, which can promote outbreaks of herbivorous insects14,18,19,20,21,22.

One of the most well-represented groups of herbivorous insects inhabiting the steppe wetlands of northern Patagonia is grasshoppers23,24. In this study, we focused on two native species: Dichroplus elongatus and Dichroplus vittigerum. These grasshoppers, commonly named as “tucuras”, have a generalist diet consisting mainly of grasses and dicotyledons, enabling them to attack both grasslands and crops5,8,17,24,25,26,27,28. Currently, most studies on their diet refer to the Pampas area in central Argentina, which has different environmental and climatic conditions compared to the Patagonian region, where information on grasshoppers’ diets is limited. There is little information about the feeding patterns of the Patagonian grasshopper on plants in the region. In the study carried out by Amadio and collaborators29 they demonstrated that in Patagonian wetlands, D. maculipennis prefer and consume some plant species more than others depending on the nutritional foliar traits (i.e. amount of protein). The most consumed plant was Taraxacum officinale (Asterales: Asteraceae), followed by Holcus lanatus (Poales: Poaceae) and Juncus balticus (Poales: Poaceae). These plants represent the main forage resource for livestock in these environments30.

Dichroplus elongatus is found in both natural pastures and different crops across South America (Argentina, Brazil, Chile, and Uruguay)23,24 and is considered a pest of economic importance26,31 when the densities exceed 10 indiv/m2, whereas D. vittigerum is distributed across northern Patagonia32,33. A study by Mariottini et al.5 showed that densities between 8 and 30 individuals/m2 of D. maculipennis, a grasshopper species considered pest, significantly reduced productivity in the wetlands compared to controls. Specifically, it was observed that a density of 30 individuals/m2 caused the most significant losses, resulting in a 55% decrease in grass cover within just one month. Several factors condition grasshoppers’ distribution, such as temperatures, precipitation and humidity34, as well as the presence of natural enemies and intra- and interspecific competition35,36. When favourable conditions are provided for the presence of species considered pests, the risk of outbreaks increases considerably. To determine the impact caused by herbivorous insect pests in both natural and agricultural environments, it is essential to achieve proper environmental management, to minimise economic losses and damage to ecosystem services. Therefore, it is important to estimate insect population densities from which they begin to cause damage to wetlands at early stages. This is one of the many challenges faced by research in ecology, which can be addressed with the help of mathematical models.

Mathematical models are suitable as pest management tools due to their predictive capability when appropriately validated with field data37. This allows for evaluating realistic scenarios that could not be carried out in the field. Their utility lies in their ability to integrate different factors, both biotic and environmental38. In the specific case we aim to address here, the information provided by this type of model could be used to prevent potential threats and damages that producers might face in the presence of grasshoppers, considering the forage resources available for their livestock.

One possible approach, which we used in this study, is to develop ad-hoc models that represent simplified versions of the ecosystems under investigation. This has several advantages: one is having a relatively low number of parameters, which provides a suitable mathematical framework for understanding the basic behaviour of the system; the other is the possibility of carrying out extensive numerical simulations and thus studying different possible ecological scenarios that can be contrasted with real data.

Certainly, a model is, by definition, a simplification of reality, and therefore there are aspects that must be handled with care. One is the risk of oversimplifying the processes and variables involved. Another is the ecological interpretation of the results obtained as outputs from the mathematical model. Finally, a very common challenge is the lack of sufficient quantity and quality of data to validate the model. To prevent all these potential complications, interdisciplinary collaboration is essential in constructing the model. This ensures detailed and precise information about the relevant aspects of the system under study, allows for asking the right questions to focus the study and minimise the number of parameters, and provides data for parameter fitting and subsequent validation against real scenarios. The model presented in this work is a result of an interdisciplinary collaboration between physicists and biologists and is strongly based on field data, observations, and laboratory experiments.

Out of the many possible approaches, we chose to build an stochastic individual-based model39. These models can be thought of as collections of individuals interacting with each other, either directly or indirectly, for example, through the consumption of a common resource. Higher-level ecosystem properties emerge from these individual-based rules. Capturing this emergence and interpreting it in ecological terms is the central objective of this work.

Finally, another relevant aspect to consider is that a realistic model must necessarily include spatially dependent biological processes, such as dispersal and invasion, and must be able to account for the role of population fluctuations40. This approach involves constructing a spatially explicit version of the model, where processes are incorporated as specific dynamic rules within a spatial grid.

The aim of this study was to evaluate the possible impact of grasshoppers population densities under different scenarios characterised by the density of D. elongatus and the amount of wetland biomass. Our specific research question was: What is the threshold density of D. elongatus that the environment can tolerate, considering the damage caused by the species’ primary plant consumption? To accomplish this, we developed a spatially explicit stochastic model based on individuals with dynamic resources associated with consumption and recovery, and simulated different scenarios for both insect species and resources. The level of description of our model is suitable for studying the ecosystem of interest, considering various grasshopper densities and wetland conditions. These scenarios allow for assessing the damage to the forage resource that could affect availability for other herbivores by establishing environmental damage thresholds, which serve as useful guidelines for implementing pest management strategies.

Materials and methods

Field data and experimental procedures

In the present study, we employed three different methodologies to reach our main objective. First, we characterised the study site to determine the plant cover of the most representative species included in the diet of grasshoppers in Patagonian wetlands (e.g. Taraxacum officinale, Holcus lanatus and Juncus balticus, see the paper by Amadio et al.29). Secondly, to determine which plants and in what amounts are consumed by grasshoppers under natural conditions, we performed microhistological faecal analysis and feeding experiments to determine consumption rate. Finally, we developed a mathematical model that integrates this information. Below, we describe these methodologies in more detail.

Characterization of the site of study

To carry out our study, we selected a wetland located 40 km from the city of San Carlos de Bariloche, Río Negro, Argentina (− 41.0253, − 71.0457) for host plant and insect collection during the summer season (see below). Both orthoptera species cohabit in this wetland grazed by cattle. The climate in this area is cold-temperate, with snowfall in winter. Rainfall is scarce (oscillating between 100 and 700 mm per year) and concentrated mainly from April to September. The central zone of a wetland is the most humid and flood-prone, with hydrophilic herbaceous vegetation, a higher topographic level with highest forage production by grasses, and a peripheral zone with a greater predominance of steppe vegetation16. Bonvissuto et al.’s grassland elaborated a classification guide41, which considers relative floristic composition, soil coverage, and forage production (measured as dry forage). According to that, the wetlands can be categorised as: (A) in good condition, with higher forage production (ranging from 600 to 800 g/m2) and diversity of forage plants; (B) in moderate condition, an intermediate condition with annual forage production between 400 and 600 g/m2; (C) in poor condition, resulting in the worst condition with a forage production between 200 and 300 g/m2, where plants still allow environmental recovery with appropriate management. This classification indicates the extent of environmental degradation and provides guidance for managing and utilising the area. We will use this classification to characterise the wetland and define scenarios accordingly.

Wetland vegetation cover

We determined the percentage of vegetation cover in the wetland using the transect method42. We established four transects of 100 m (from the periphery to the centre of the wetland), setting a frame of 1 m2 every 10 m at each transect. Classification and plant cover were determined in the field during the summer season, and material was collected and transferred to the laboratory. Plants were selected according to the criteria of presence in transects or in the diet in a percentage greater than 10%. If more than one plant from each group (i.e. grasses, graminoids, herbs) was eligible, a single plant was selected to represent the group. It should be noted that these plant samples were used in the feeding experiments, and that experimental insects were collected at the same location.

Insect diet

We randomly selected 60 adult insects of each species of grasshoppers (30 females and 30 males) from the wetland with an entomological net. Each individual was placed in a plastic container with cotton soaked in water (no food) and kept under semi-controlled conditions (20 ± 2 °C, 40% ± 10% RH; 12 h light/dark cycle) for 24 h. We then collected and analysed faeces using the microhistological method established by Borrelli and Sbriller43 (Supplementary Material, Sect. 1). This technique allows us to determine the plant species consumed by the insects by observing plant tissues under a microscope and identifying them against reference samples.

Feeding behaviour

We collected adult individuals of D. elongatus (n = 133) and D. vittigerum (n = 140) at the wetland and maintained them under the same laboratory conditions as mentioned above. To evaluate feeding behaviour, we performed two experiments: a no-choice experiment to determine consumption rate and a two-choice experiment to evaluate if there is a consumption preference between offered plants.

No choice experiment

This experiment consisted of placing one adult individual in a plastic container (250 ml) with a food ration of one gram (fresh weight) of a plant species. To avoid dehydration, plants were placed in an oasis sponge with 5 ml of water. To determine the amount of food consumed (in mg/day), food plants were weighed at the beginning and end of the experiment (24 h later), with weight difference used as the variable. To control for the effect of drying on the plant, we performed simultaneous tests without any grasshopper and measured the proportion of weight loss. After this, leaves were reweighed and percentage weight loss through desiccation was estimated. A total of 71 individuals of D. elongatus were used for these experiments, and 84 individuals for D. vittigerum.

Two-choice experiment

The experimental arena for the paired experiments consisted of a rectangular plastic container (36 × 28.5 × 16 cm) which was segmented to form a T-shaped labyrinth. One gram of each stimulus was offered at either end of the labyrinth, i.e. J. balticus, T. repens, and Taraxacum officinale. Despite not being identified in the diet analysis of both species, we chose to include T. officinale based on prior research indicating it is favoured by Dichroplus sp.8,33. Grasshoppers were placed in the arena with both stimuli for 24 h (a different individual was used each time). Three combinations of stimuli per grasshopper species were established: J. balticus vs. T. repens, J. balticus vs. T. officinale and T. repens vs. T. officinale. For D. elongatus, 68 repetitions were carried out, whilst for D. vittigerum, a total of 65 repetitions were performed. To determine plant consumption after 24 h we followed the same procedure as in the no choice experiment.

Data analysis

To analyse the consumption rate of both plant species by grasshoppers and to detect differences in their consumption pattern, the no-choice experiments were analysed using a Mann–Whitney–Wilcoxon test as the data were non-parametric. The two-choice experiment was analysed with a non-parametric Wilcoxon Signed Rank test.

Mathematical model

Overview

With the purpose of providing a complementary tool for studying the effect of the herbivory caused by the two grasshopper species on wetland resources, we build a spatially explicit stochastic individual-based model where resources in each patch can be consumed and recovered. The dynamic rules of the species, as well as the variables and parameters of the model, are inspired by the results obtained through field observations and laboratory experiments. We developed a stochastic implementation of the model and performed extensive numerical simulations to explore the parameter space and analyse different scenarios of interest.

Among all the animal and plant species that make up this food web, we focus on two species of native grasshoppers, D. vittigerum and D. elongatus (which, at high densities, is considered a pest) and three plant resources present in that wetland.

The criteria used to choose these plants among all those available was twofold: the percentage of vegetation cover in wetland and the percentage of the species present in the diet of both species of grasshoppers (see Table 1). Model parameters such as food preference, consumption rate, density and dynamic species behaviour, as well as information about their life cycle, were taken from known data of these species and those collected for this study.

Table 1 Abundance of plants expressed as percentage plant cover (%) in the wetland and percentage (%) of plant presence in the diet of insects.
Full size table

According to the observations throughout ten years of monitoring orthoptera populations by our group, D. vittigerum emerges in late December, while D. elongatus during late January (pers. obs.). This allows us to initially assume that direct interspecific competition between these two species is not significant during most of their coexistence in the wetland. The same applies to intraspecific competition, as observations indicate that they can coexist in the same patch at high densities. However, there is indirect competition at high densities of individuals that cannot be overlooked, as in such situations, the high consumption of resources in a patch can limit the access of new individuals. This indirect competition is included in our model by establishing that grasshoppers only visit sites that have at least one available resource.

Although interspecific competition can affect the distribution of insect species in the wetland, we chose not to include additional species in the model for two main reasons. Firstly, it is essential to keep the number of parameters to a minimum to focus on answering our primary question regarding the impact of grasshopper invasion on the wetland. Secondly, personal observations at the study site indicate that this wetland experiences cattle rotation, meaning that the presence of grasshoppers does not overlap with that of cattle. This justifies not including cattle or other herbivore species in the model.

Another consequence of cattle inhabiting the wetland at different times of the year compared to grasshoppers is that we can assume that the distribution and abundance of patches containing each type of resource, as well as the initial vegetation biomass, reflect the conditions left by the cattle before they departed the wetland. Furthermore, we will assume that the grasshoppers are unable to completely desertify the patches and that the plants have the ability to recover over a period of time specific to each species.

Although insect predation, mainly by birds, can cause a decrease in grasshopper density, it was not considered in the model. Nonetheless, it is important to note that the pest threshold values found in this study are approximate bounds rather than precise values, which are beyond the capabilities of the model.

We focus on the stage where grasshoppers move from the peripheral zone towards the centre of the wetland, where food resources are more abundant. This movement occurs because during this period their consumption is maximal. Towards the end of their lives, they return to the dry edges of the wetland to oviposit and their consumption decreases. Since our interest lies in assessing the damage to the wetland rather than the detailed behaviour of grasshoppers, we do not model this last stage of species behaviour. Instead, we evaluate the state of resources after they have reached the central area of the wetland.

In Fig. 1 we present a schematic representation of the concepts and components of the model discussed below.

Fig. 1
figure 1

Schematic representation of the main components of the model. Components marked with an asterisk indicate that their values, distribution or behaviour were derived from the data presented in this work or from other bibliographic references (as indicated in the paper). The black-bordered boxes enclose the parameters that were varied in the simulations presented in this work and that gave rise to the scenarios proposed.

Full size image

Data used to build the model

In this section, we summarise the information from the ecosystem under study that was used to construct the model.

The spatial distribution and abundance of resources were determined through field experiments conducted specifically for the studied wetland. The data presented in the first column of Table 1 were used to quantify the number of patches occupied by each plant species. Additionally, information from Bonvissuto et al.41 was utilised to assess the wetland’s condition and estimate its vegetation biomass.

Regarding the grasshopper species, we used specific life cycle information to define the period when individuals of these species are present in the wetland, focusing particularly on the timing of egg hatching and the average lifespan of each species. Additionally, monitoring these species provided insights into their dynamic behaviour during periods of peak resource consumption, when they migrate towards areas with the highest resource concentration. Finally, we gathered information on the food preferences of each grasshopper species from previous studies8,29,33. The consumption rates obtained in our study (Tables 2, 3) also served as an indicator of their food preferences.

Table 2 Rate of consumption of plants by Dichroplus elongatus and D. vittigerum in no-choice experiments (Wilcoxon Mann–Whitney U analysis).
Full size table
Table 3 Comparisons and consumption (mg/day) for the two-choice experiments.
Full size table

Model implementation

The information presented in the previous section was included in the computational code developed specifically to model this wetland. The code was implemented in the Fortran 90 programming language. In our simulations, time advances discreetly, and at each time step the state of the system is governed by the ecological processes described above: migration of individuals from the two grasshopper species, resource consumption, and resource recovery. Below we provide details of the numerical implementation.

Design of the wetland and resource distribution

The wetland we studied has an area of approximately 83,000 m2 and a fairly regular (square) geometry, so it was modelled as a square with a side of 300 m, made up of 90,000 patches with a surface area of 1 m2. Both the density and the inhomogeneity of the different plant species observed in the wetland were replicated in the model, including patches that have none, one, two, or all three plant species depending on their location (see Fig. S1 of the Supplementary Material).

Dynamic behaviour of grasshoppers

The model specifically targeted individuals from both grasshopper species capable of movement and feeding within the wetland. The simulations cover a 150-day period, during which D. vittigerum individuals are the initial invaders of the wetland, followed one month later by D. elongatus. Based on observations of their movement, it was determined that their activity covers an area of approximately six square metres per day. During their peak consumption stage, they preferentially move from the edges towards the centre of the wetland. In our model, these behaviours translate to each grasshopper being able to move a maximum of six patches per day. This defines the time scale of our model: one day corresponds to 6 time steps of the model.

The conditions for an individual of either species to occupy a patch are twofold: (1) there must be at least one resource in the new patch, and (2) it must be closer to the centre than the current patch, i.e., the individual will move from patch j to patch i if d(i,0) < d(j,0), where d represents the distance relationship to the central patch 0.

Then, the probability of occupation O(i) of a given patch i by an individual is expressed mathematically as:

$$O\left( i \right) = \, 1 \, - \, \left[ {1 \, - \, r\left( i \right)} \right]^{\eta},$$

where r(i) = 1 if patch i have at least one resource or 0 in any other case, and η is the number of neighbouring patches that are occupied at the time and are farther from the centre than patch i. It is worth clarifying that, since the movement of the insects is limited to first- and second-order neighbors and the grid is square, the possible range of values for η is [0, 8]. Moreover, the condition that these sites must be farther from the center than patch i further restricts the value of η. However, any value of η > 0 will yield the same result in terms of the occupation of patch i.

Consumption

At each site they visit, grasshoppers consume a fixed amount of one of the available resources. Although experimental data shows that different species consume varying amounts of certain resources, to reduce the number of model parameters, we set the consumption of the three resources equally for both grasshopper species in a value close to the average from the data in Table 2. Furthermore, they prioritise resources based on preferences identified in two-choice experiments outlined in Table 3. This indicates that when encountering multiple resources within a patch, they are more inclined to consume their preferred choice.

As a result of consumption, resources within the patch diminish. We modelled fractional consumption in “portions”, meaning that if a grasshopper or group of grasshoppers remains in the patch for a sufficient period, the resources are depleted. This time scale depends on both the daily consumption rate of each grasshopper (fixed at 60 mg/day) and the initial patch biomass. This parameter is one of those varied in the simulations presented here, corresponding to scenarios A, B, and C summarised in Fig. 1. Given that each grasshopper visits around six patches per day, we assume that it consumes 10 mg of resources each time it enters a patch. To illustrate the mechanism, let’s assume the initial biomass of a patch is 210 g. The resource portions of that patch are calculated as Np = 210 g/0.01 g = 21,000. Consequently, each time a grasshopper enters a patch, it consumes one of these 21,000 portions.

The consumption preferences depend on the species and were derived from Table 3, focusing on the results with significant differences. Specifically, since the consumption difference between T. repens and T. officinale is not significant for D. elongatus, our model assigns an equal probability of being consumed first, with J. balticus being the last option. On the other hand, D. vittigerum consumes T. repens first, and then with equal probability, either T. officinale and J. balticus.

Resources recovery

The resources can regrow because we assume that the grasshoppers do not consume them to the extent of desertifying the patch. Based on personal observations, our model assumes that T. repens and T. officinale would regenerate within 2 weeks, while J. balticus would recover within three weeks. In terms of the dynamic proposed in the model, this means that the first two plant will recover in Nr = 14 days × 6 = 84 time steps, whereas J. balticus would need Nr = 21 days × 6 = 126 time steps. The implementation in our simulations consisted of defining the ratio between the portions of a given resource, Np, and the number of steps in the dynamics required for its recovery, Nr. At each time step, the resources of each patch are evaluated. If a given resource was present at the initial time and has depleted at the current time, it is replenished by an amount Np/Nr.

Values of the model parameters

  • Size of the grid: 300 ⨉ 300 = 90,000 patches.

  • Area of a patch: 1 m2.

  • Patches with T. repens: 4–7% (distributed throughout the grid but with variable density in different regions; see Sect. 2.2 of the Supplementary Material).

  • Patches with T. officinale: 2% (uniform throughout the wetland).

  • Patches with J. balticus: 35% (almost exclusively limited to the central area).

  • Patches with at least one resource: 40%

  • Vegetal biomass of the wetland: variable, from 180 to 1500 g/m2.

  • Number of grasshoppers of the species D. elongatus: variable, from 1 to 30 individuals/m2.

  • Number of grasshoppers of the species D. vittigerum: fixed at 1 individual/m2 (results with other densities of this species are presented in the Supplementary Material, Sect. 2.4).

  • Individuals of both species can move a maximum of six patches per day, to cells that are first or second neighbours, provided there is at least one resource in the new patch.

  • Daily consumption of both species of grasshoppers: 60 mg/day (close to the average values from Table 2).

  • Preference of consumptions of D. elongatus: T. repens = T. officinale > J. balticus (Table 3).

  • Preference of consumptions of D. vittigerum: T. repens > T. officinale = J. balticus (Table 3).

  • In all the simulations, day 1 corresponds to the moment in which the first group of grasshoppers of the species D. vittigerum begins its movement towards the interior of the wetland. A month later D. elongatus started the same process. For both species we considered an average lifespan of 120 days, after which they disappear from the wetland.

  • Recovery period for T. repens and T. officinale = 14 days. For J. balticus, 21 days (results without resource recovery are presented in the Supplementary Material, Sect. 2.5).

More information about the code implementation can be found in the Supplementary Material (Sect. 3), where a simple flowchart is provided. Additionally, the code developed can be accessed in Ref.44.

Scenarios studied

Different scenarios were studied by varying two parameters of the model: the density of D. elongatus (measured in individuals/m2) and different conditions of the wetland related to resource abundance (measured in g/m2).

  1. I.

    Low density: < 5 indiv/m2.

  2. II.

    Medium density: 5–10 indiv/m2.

  3. III.

    High density: > 10 indiv/m2.

  4. A.

    Good wetland condition: 600 g/m2 of initial vegetal biomass.

  5. B.

    Moderate wetland condition: 450 g/m2 of initial vegetal biomass.

  6. C.

    Poor wetland condition: 210 g/m2 of initial vegetal biomass.

The density of D. vittigerum was set at 1 indiv/m2, unless otherwise indicated.

Results

Field data and experimental results

Wetland vegetation cover and insect diet composition

Measurements of vegetation cover carried out in the field indicate that Juncus balticus (39.8%) is the dominant graminoid species, followed by the herbs Trifolium repens (4.02%) and Taraxacum officinale (1.36%). Based on these observations—Juncus balticus falling within the 30–50% range, Trifolium repens below 5%, and other grasses between 50 and 70%—the area meets the criteria for classification as a wetland in moderate condition according to the relative floristic composition proposed by Bonvissuto et al.41. Although both grasshopper species’ diet composition was the same, composed of T. repens and J. balticus, the proportions were different. Specifically, we showed that D. elongatus eats similar proportions of both plants, while D. vittigerum consumes more T. repens (Table 1).

Feeding behaviour

No-choice

A total of 63 adult D. elongatus and 74 adult D. vittigerum were used for this experiment to determine rate of consumption (Table 2). Analysis indicated a significant difference between T. repens and J. balticus for D. vittigerum (p = 0.04, W = 1494, n = 74), with T. repens being the most consumed. No differences were found in consumption by D. elongatus (p = 0.55, W = 842, n = 63).

Two-choice

Results obtained indicated that both species of insects can feed on the three species of plants offered (Table 3). However, consumption was not the same for all species. Particularly, when we offered leaves of J. balticus versus T. officinale to D. elongatus, we registered a significant difference (p = 0.04, V = 57, 19.10 and 34.36 mg/day, respectively). This could indicate that although T. officinale does not appear in the diet analysis of the grasshoppers, possibly because of limited presence at the study site, it represents a resource of interest for these insects. Remaining consumption comparisons were not significant. Meanwhile, we registered significant differences in the rate of consumption by D. vittigerum in the comparison J. balticus versus T. repens (p = 0.02; V = 82, 50.48 and 64.48 mg/day, respectively) and also for the pair T. repens and control T. officinale (p = 0.01; V = 61, 50.31 and 32.65 mg/day, respectively).

Numerical simulations

The main results of the numerical implementation of the mathematical model are presented below. The simulated scenarios correspond to different densities of D. elongatus and different conditions of the wetland, determined by the initial vegetal biomass of the patches with resources.

Temporal evolution of the system

An adequate way to analyse the impact that grasshoppers have on the resources they consume is through their evolution over time. In the following figures we show how the resources abundance and the fraction of patches with resources changed during the invasion by the two species of grasshoppers, which move from the edges to the centre of it.

In Fig. 2 we show the temporal evolution of a wetland under the condition identified as moderate, with a biomass of 450 g/m2. In both panels, the three curves correspond to different densities of D. elongatus. In Fig. 2A we plot the temporal evolution of the percentage of patches that have at least one of the three resources, whereas Fig. 2B indicates the evolution of the total biomass of the wetland. It is worth noting that the value 100% indicates the state of the wetland at day 1. It should not be confused with a situation where the wetland has complete vegetation cover; instead, it refers to the condition it was in when the grasshopper invasion began.

Fig. 2
figure 2

Temporal evolution of the state of a wetland for different densities of D. elongatus. (A) Percentage of patches with at least one resource. (B) Percentage of biomass of the wetland. The wetland is in a moderate condition, with an initial vegetal biomass of 450 g/m2. In both figures, the value 100% indicates the state of the wetland on day 1 (before the introduction of the grasshoppers). In all the cases, the density of D. vittigerum is 1 indiv/m2.

Full size image

The behaviour of the patch’s occupancy indicates that, for low grasshopper densities, the wetland is able to recover rapidly, even in the presence of the insects in the area. Higher grasshopper densities do not allow for recovery within the time window of the invasion. But regardless of the above, it is interesting to note that in all cases, the fraction of occupied patches decreases very little: after 150 days, more than 97% of the patches still have resources. However, during the same period, the total biomass of the wetland experienced a significant decrease for a sufficiently high grasshopper density. The effect of the grasshopper invasion on the wetland varies with the density of D. elongatus and the vegetal biomass present in the wetland, as will be clear below.

Another observation is that the structure of the curves of Fig. 2A reflects the way in which individuals of both species are incorporated into the wetland. The model mimics what was observed in the field: D. vittigerum begins its life cycle 1 month before D. elongatus. The first stage of the simulation corresponds to the gradual incorporation of D. vittigerum individuals in a low density, allowing resources to remain within initial levels. After 30 days, the incorporation of D. elongatus produces a marked decrease in resources. It is worth noting that the fluctuations of the curves observed when D. elongatus is introduced is a consequence of the dynamics imposed on the resources, that is, the consumption and recovery times assigned to each plant species.

To further illustrate the temporal evolution of resources, in Fig. 3 we show the behaviour of each resource separately for a wetland under the same conditions as the previous case, i.e. with an initial vegetal biomass of 450 g/m2, and for a density of D. elongatus of 20 indiv/m2. As in the previous figure, in Fig. 3A we plot the percentage of patches with available resources as a function of time, where 100% indicate the initial situation, just before the grasshoppers invasion. In Fig. 3B we depict the percentage of biomass in the wetland. As anticipated in the previous figure, the behaviour of patch occupancy differs from that of the total wetland biomass.

Fig. 3
figure 3

Temporal evolution of the resources in a wetland in a moderate condition. (A) Percentage of patches with resources. (B) Percentage of biomass for each plant in the wetland. Parameters: D. vittigerum = 1 indiv/m2, D. elongatus = 20 indiv/m2, Initial vegetal biomass = 450 g/m2. In both figures, the value 100% indicates the state of the wetland on day 1 (just before the grasshoppers invasion).

Full size image

Depending on the resource, patch occupancy after the grasshopper invasion varies between 96 and 99%. In contrast, the biomass of each plant type shows a much more significant decrease. The most affected plant seems to be T. officinale (40% of loss), followed by J. balticus (36%), whereas T. repens was the least affected, with a 23% of biomass loss.

In the Supplementary Material, Sect. 2.2, we illustrate the dynamic behaviour of grasshoppers, depicting different stages of the advance of both species.

Wetland deterioration

The main objective of the model is to propose different scenarios and analyse the long-term consequences of interactions between the species involved. It is relevant then to analyse the state of the wetland after the passage of the grasshoppers from the peripheries towards the centre. In Fig. 4 we show the effect of the grasshopper invasion on the biomass of the wetland and on the patch’s occupancy. We calculated degradation as the difference between the initial (day 1) and final (day 150) values of the variables defining the wetland’s condition. Following the classification made by Bonvissuto et al.41, the three panels represent wetlands in three different conditions: good, moderate, and poor. As in previous figures, we differentiate the system’s behaviour regarding patch occupancy (blue curve with squares) and biomass loss (red curve with circles). For the three scenarios, wetland degradation measured in biomass loss, increases with the increase in grasshopper density, up to a value where the degradation saturates. The worse the wetland condition, the fewer grasshoppers are needed to drive the system to total degradation. In the figure, the three scenarios depicting different densities of D. elongatus are separated by dashed vertical lines. We will use these findings to propose outbreak threshold values, above which the species can be considered a pest26,31.

Fig. 4
figure 4

Degradation of a wetland. Percentage of patch and biomass degradation after 150 days for several densities of D. elongatus and three wetland conditions: (A) good, corresponding to 600 g/m2 of initial vegetal biomass, (B) moderate, with 450 g/m2, and (C) poor, with 210 g/m2. Blue curves indicate the percentage of patches that lose all their resources. Red ones indicate the percentage of biomass reduction. Note that the scale on the vertical axis is different for each curve (as indicated by the corresponding coloured horizontal arrows). The three scenarios for the density of D. elongatus are separated by vertical dashed lines. The case presented in Fig. 3 is indicated here with black squares.

Full size image

On the other hand, the blue curves measure the decline in patch occupancy. In the worst scenario (maximum density of D. elongatus and poor condition for the wetland), nearly 10% of patches are completely degraded. This number, although it may seem low, should not be underestimated, as it signifies that all the biomass in a given patch has disappeared. Therefore, a 10% degradation in this variable should be interpreted as a 10% desertification of the wetland.

From the curves of Fig. 4 it becomes evident that the measurement of biomass loss is more sensitive to the different scenarios proposed, and it also suggests threshold pest values close to those recorded in the field.

In Table 4 we summarise the level of degradation of the wetland for the different scenarios studied, calculated as the percentage of biomass loss. The wetland studied was described as being in moderate condition. For this scenario, an intermediate density of D. elongatus can lead to deterioration close to 50%. These values are notably similar to the pest threshold of 10 individuals/m2 proposed by Cigliano and Otte31.

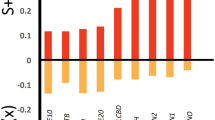
Table 4 Degradation of the wetland (in % of biomass loss) for the different scenarios studied, which correspond to various densities of D. elongatus (scenarios I, II and II) and different wetland conditions (scenarios A, B and C). The data were obtained from the simulations presented in Fig. 4.
Full size table

Inspired by a previous study that quantifies the loss of vegetal biomass caused by the presence of grasshoppers, which considers a degradation of nearly 50% as an extreme value5, in Fig. 5 we present the pest thresholds calculated with this criterion for several values of initial biomass of the wetland. This result allows us to estimate the pest threshold for arbitrary initial biomass values, which could be used to characterise other wetlands or regions with resources similar to those included in this model. In the Supplementary Material (Sect. 2.3) we present different options for defining the pest threshold with our mathematical model.

Fig. 5
figure 5

Pest threshold as a function of initial vegetal biomass. The threshold is defined as the value above which degradation exceeds 50% of the initial wetland biomass. Each point is the average over 10 realisations of the dynamics (standard deviation shown as error bars). The three wetland condition scenarios (labelled A–C) are separated by dashed lines.

Full size image

An additional interesting result is obtained by relaxing the fixed values chosen for each scenario and calculating an average pest threshold by averaging multiple biomass values within each scenario. These results are presented in Table 5 and correspond to initial biomass values ranging from 180 to 330 g/m2 for wetlands in poor condition, 390 to 570 g/m2 for wetlands in moderate conditions, and 600 to 800 g/m2 for wetlands in good conditions. In all cases, crossing the pest threshold implies a low patch desertification, close to 2%, but a biomass loss nearing 56%, even exceeding the 50% condition set to define the threshold.

Table 5 Pest thresholds for D. elongatus, defined as the value above which degradation exceeds 50% of the initial biomass of the wetland.
Full size table

Finally, a couple of comments regarding the generality of the model presented here.

The results shown correspond to simulations where the possibility of resource recovery in patches was considered. Since there is no clear data on the time and conditions of recovery of the plants studied in this work, we present in the Supplementary Material (Sect. 2.5) some results obtained with a version of the computational code where the consumed resources do not recover within the time window of the numerical simulation. The results without resource recovery yields similar values of biomass loss but differs in the levels of patch desertification.

Besides, it should be noted that all the results presented in this paper correspond to a fixed (and low) density of D. vittigerum, based on observed values in the wetland under study. The system’s dependence on this parameter is qualitatively similar to what is shown here with D. elongatus, although their presence in the wetland generates different effects for each resource. This is related to feeding preferences of the two grasshopper species, which are also included in the model. The reason why a study of the system’s dependence on D. vittigerum density was not presented here is because the field data available to us never exceed 2 individuals per square metre. Nevertheless, for completeness, we present some results with higher density values of D. vittigerum in the Supplementary Material (Sect. 2.4).

Discussion

In this paper, we present the main results of an interdisciplinary study involving field and laboratory experiments, along with the development of a mathematical model. The study aims to evaluate the potential impact of grasshopper population outbreaks under various scenarios, based on their feeding behaviour and resource availability.

Field data and experiments provide evidence that two species of polyphagous grasshoppers cohabiting in the patagonian wetlands present a similar diet composition (Table 1) but they consume the resources in different proportions (Table 2). Different consumption rates and preferences shown by D. elongatus and D. vittigerum (Table 3) suggest that these polyphagous insects may select food according to palatability and nutritional requirements. Specifically, we showed that D. elongatus eats similar proportions of both plants, while D. vittigerum consumes more T. repens. In our experiments, the absence of preferences displayed by D. elongatus between the two plant species present in their diet could indicate that the grasshopper perceives their nutrient value as similar. When T. officinale is offered, it is consumed in a significantly higher proportion than J. balticus. The low percentage plant cover of T. officinale at the site may explain why it is imperceptible in the microhistology analysis. On the other hand, D. vittigerum exhibits a higher consumption rate and preference of T. repens when offered with other plants, implying that the plant is its first choice to fulfil its main nutritional needs.

Despite the fact that the diets of both coexisting species of generalist herbivores overlap, data presented in Table 3 indicates that the amount and ratios of consumption vary. This type of behavioural difference suggests that nutritional needs and/or the ability to overcome the physicochemical defences of plants may also differ between the two insect species. These plants are also highly represented in livestock diet as part of the main forage resource in these environments30. Studying the composition of the diet plays a fundamental role to understand the potential impact of the herbivory on the environment, its effect on the feeding behaviour of other coexisting herbivores, and also in their ability to recover. From an ecosystem perspective, this nutritional niche diversification plus the slightly asynchronous life cycles could occur as a mechanism to avoid competition45,46. In future studies, it would be interesting to carry out more exhaustive experiments in order to determine if the diet varies with the stage of development and also to evaluate if consumption depends on the nutritional traits of plants or the amount of available food resources using a broader range of plant resources.

The developed mathematical model realistically imitated the dynamic behaviour of grasshoppers during the stage of greatest food consumption, which corresponds to the moment of highest resource damage. The study of the system’s temporal evolution clearly shows that low grasshopper densities allow the wetland to recover, even with the grasshoppers present. In contrast, higher insect densities prevent biomass recovery within the simulation time scale (see Figs. 3, 4). Although this is an expected result, it is less expected that a better indicator of damage would be the loss of vegetal biomass and not the fraction of desertified patches. It is important to note that the model does not incorporate information about the behavioral changes of D. elongatus under high-density conditions, such as swarm formation or changes in their feeding preferences. This omission is due to the lack of scientific reports addressing these aspects to date.

The numerical simulations conducted with the model also enabled us to identify insect density values at which the level of environmental degradation is significant. But the effect of the grasshopper invasion on the wetland not only depends on their densities but also on the vegetal biomass present in the wetland, as was clear in Fig. 4. This information has been summarised in Tables 4 and 5, facilitating comparison with previous field data. Studies on the damage caused by D. elongatus on forage crops in the central region of Argentina considering a pest threshold density of 10 indiv/m2 resulted in losses of up to 5% in alfalfa yield26. Densities above this threshold, ranging from 20 to 40 indiv/m2, caused decreases of up to 38% in soybean yield27. Besides, the damage in the crops in pampas estimated a forage loss of 50% when densities are higher than 30 indiv/m2 (see Ref.5). A threshold value close to 10 indiv/m2 was obtained with our model for a scenario in which the wetland is in a poor or moderate condition (see Table 4), with levels of degradation between 50 and 70% (measured as vegetal biomass loss). Remarkably, the wetland biomass conditions recorded in situ align with the information provided by the model. This allows us to be optimistic about the predictive capability of the model, while keeping in mind that it is just a basic and initial version that needs to incorporate several ecosystem-specific elements. Notably, even in its present form, the model enables us to extrapolate its results and propose pest thresholds for wetland conditions different from those studied in this work, as shown in Fig. 5 and Table 5.

Although our results are qualitative, this model shows sensitivity to the parameter that regulates the density of insects present in the system. To quantify the extent of damage, the model requires data obtained from a thorough exploration of the resources available in the wetland. These environments are considered of a high productivity and present spatial and temporal heterogeneity, including soil, hydrological and precipitation gradients among others, that condition vegetation distribution30,47,48. The forage production is influenced by this heterogeneity, the phenological stage of plants during the growing season and on the degree of disturbances and modifications in the system49. Grasshoppers’ herbivory can modify the nutrient cycling and the primary production in the environment by consuming plants with different decomposing rates, changing the abundances of grasses and forbs50,51.

One of the strengths of our model lies in its easy generalizability; thus, our goal is to utilise it as a cornerstone for increasingly complex systems that approximate real-world levels of complexity38,52,53. Moreover, its application extends beyond identifying the impact of a pest on a specific ecosystem; it could also function as a tool to enhance management strategies aimed at mitigating the effects of insect outbreaks in wetlands.

However, it is essential to recognize the limitations of this model and articulate our expectations for its improvement in future research. A necessary improvement is the inclusion of the interaction between biotic factors (such as insect herbivory, predation, and intra- and interspecific interactions) and abiotic factors (such as water dynamics, temperature, and soil quality). Incorporating these factors is particularly relevant in this context because inadequate management can alter soil characteristics and floristic composition, thereby increasing system vulnerability14. It is also important to consider the impact of climate change and the climate effect on the insect populations, including alterations in the emergency, growth, fecundity, and distribution54,55,56,57. The relationship between drought conditions and increased grasshopper damage can be attributed to different mechanisms. Drought conditions often create an optimal environment for egg hatching and the early developmental stages of grasshoppers, thereby promoting higher population densities. Additionally, during droughts, the reduction in forage availability not only intensifies the impact of grasshoppers feeding activity but also the competition with other herbivores. Studies investigating the effect of climate variables on D. elongatus densities in the pampas, showed that rainy days and thermal amplitude affect the variation observed in the species density58. All these factors contribute to the agricultural pest impacts, by favouring outbreaks and possibly affecting the threshold sensitivity. On the other hand, the impact that large herbivores grazing has over these environments is significant as well, modifying the floristic composition, the plant production, the soil composition, and ultimately the grasshopper’s response59,60,61. The developed model does not include the herbivory by large herbivores, but further exploration should be considered to have a more complete and long-term perspective. All these proposed improvements are left for future studies.

The significance of this study lies in its potential as a tool to assess the economic and environmental implications of damage caused by grasshoppers in a specific wetland. Among the former is the loss of forage resources, which can affect availability for other herbivores and consequently impact producers by reducing feed for their livestock. Regarding the latter, this model offers valuable insights for the conservation and responsible management of wetlands globally, with applicability to other environments vulnerable to potential pest insect attacks.