Task offloading optimization in mobile edge computing based on a deep reinforcement learning algorithm using density clustering and ensemble learning

Abstract

Mobile edge computing offloads compute-intensive tasks generated on mobile wireless devices (WD) to edge servers (ES), which provides mobile users with low-latency computing services. Opportunistic computing offloading is effective to enhance computing performance in dynamic edge network environments; however, careless offloading of tasks to ESs can lead to WDs preempting network computing resources with limited bandwidth, thereby resulting in inefficient allocation of computing resources. To address these challenges, this paper proposes the density clustering and ensemble learning training–based deep reinforcement learning (DCEDRL) method for task offloading decision-making in mobile edge computing (MEC). Firstly, DCEDRL utilizes multiple deep neural networks to explore the environment. It trains multiple models using ensemble learning methods to obtain a combination of prediction results. Secondly, DCEDRL utilizes an optimized density clustering method to identify and classify computing tasks with similar characteristics to improve subsequent task scheduling and resource allocation efficiency. Finally, according to the stored priority information, DCEDRL utilizes the priority weight to resample the samples, adjust the sampling strategy in real time, and improve the adaptability and robustness of the system. Simulation results demonstrate that the proposed DCEDRL method can reduce the backlog of tasks by greater than over 21% compared to the baseline algorithms.

Introduction

With the recent rapid development of the Internet of Things (IoT) and 5G communication technologies, mobile wireless devices (WD) are now being used to handle a series of computing tasks¹. However, limited battery capacity and energy requirements limit the ability to run computationally intensive applications on WDs². A suitable solution is to offload the tasks on the WD to a cloud server; however, offloading many tasks to the cloud will place enormous load pressure on the cloud server. Thus, mobile computing has seen a significant shift from centralized cloud computing to mobile edge computing (MEC)¹. Compared with centralized cloud server deployment, MEC deploys edge servers (ES) at the network’s edge; thus, they are closer to mobile users, which reduces computing delay and improves computing efficiency. However, if a WD blindly offloads computing tasks to an ES, the load in the resource-limited network environment will increase, resulting in computing delay, increased energy consumption, and uneven allocation of resources.

Compared with other computation offloading schemes, opportunistic offloading has demonstrated significant performance improvements in time-varying networks and scenarios involving unknown data arrival. Through the experimental evaluation of wireless channel gain³, energy harvesting level⁴, task input and output dependency⁵, and edge cache availability⁶, researchers have found that opportunistic computation offloading can offload tasks strategically, thereby improving the overall performance of the system and reducing device energy consumption. In the MEC environment, the decision process is typically modeled by a mixed integer nonlinear programming (MINLP) model, which determines binary offloading decisions and communication and computation resource allocation decisions simultaneously. Due to the high computational complexity of solving the MINLP problem, especially in large networks, it is frequently difficult to satisfy the requirements of time-sensitive tasks. Thus, efficient and low-complexity suboptimal algorithms are urgently required to solve the MINLP problem in MEC environments.

Recently, deep reinforcement learning (DRL) has emerged as an effective tool to solve various problems and challenges in communication and networks⁷, providing a practical scheme to address the problem of online computation offloading in MEC. DRL allows an agent to observe its state and make corresponding action decisions through interactions with the environment. The agent receives rewards from the environment based on the actions performed and improves its decision process continuously through reward feedback. DRL employs deep neural networks (DNN) to handle high-dimensional state information and complex environments to overcome the problem of insufficient generalizability of traditional heuristic algorithms, which makes agents perform better in complex and dynamic environments. It is particularly beneficial for online implementation because it eliminates complex MINLP computations and can learn from past experiences automatically in real time without labeling training data samples manually. Many previous studies have applied DRL techniques to the design of online offloading algorithms for MEC networks⁸.

To solve the above problems, this paper proposes enhanced DRL-based online offloading algorithm with density clustering. The proposed algorithm is designed to make corresponding optimization decisions while following strict energy constraints and random data arrival conditions, minimize the backlog of data queues, maintain long-term data queue stability, and maximize network data processing capacity to reduce network latency. The primary contributions of this study are as summarized as follows.

• 1. We designed a model to minimize the backlog task queue length, reduce energy consumption, and maximize the computing rate under strict energy constraints. This model makes optimal offload and resource allocation decisions within each time frame, which enables the system to maintain long-term stability and maximize performance indicators in demanding mobile edge networks.

• 2. For the unloading decision problem in MEC networks, we propose the density clustering and ensemble learning training–based DRL (DCEDRL) algorithm. DCEDRL utilizes density-based spatial clustering of applications with noise (DBSCAN)^9,10 to categorize each task based on the input environmental parameters. In addition, the grid search (GS) method is employed to determine the optimal combination of parameters for DBSCAN clustering within the specified parameter space. Thus, the offloading decision can be adjusted dynamically to enhance adaptability to various network environments.

• 3. A simulation model evaluates several performance indicators, e.g., task queue length, energy consumption, and network delay. The experimental results demonstrate that the proposed method is superior to existing benchmark models, and the performance of the proposed method exhibits an improvement of over 21%.

Related work

Recently, computation offloading has gained increasing importance in MEC², enabling wireless devices to offload compute-intensive tasks to edge servers to reduce latency and energy consumption offloading decision paradigm, which determines whether a task is executed locally or offloaded to an edge server, has been widely studied in MEC environments. Various algorithms have been proposed to tackle the binary computation offloading problem from different perspectives, focusing on reducing computational complexity.

Early research addressed offloading strategies using heuristic and optimization techniques. Lee et al.¹¹ investigated the offloading of tasks from WDs to neighboring nodes that arrive and depart randomly. They focused on scheduling computing tasks in dynamic environments and proposed an optimization strategy that enables each WD to independently select the optimal set of adjacent nodes, thus significantly improving computing efficiency. However, this method is unsuitable for optimizing long-term average objectives in other studies, particularly in scenarios requiring stable, consistent decision-making. Beck et al.¹² proposed a coordinate descent algorithm that incrementally approximates the local optimal solution by adjusting a single user’s binary offloading decision. The approach utilizes convex relaxation techniques for handling binary variables but encounters challenges in balancing performance and complexity. Similarly, Yan et al.⁵ employed Gibbs sampling to explore the decision space stochastically. In an attempt to simplify the search process, Bi et al.¹³ introduced the alternating direction method of multipliers to decompose the original combinatorial optimization problem into parallel one-dimensional subproblems. These optimization methods, including linear relaxation¹⁴ and quadratic approximation¹⁵, have been applied to manage binary variables. However, these approaches often need help avoiding tradeoffs between performance and complexity when dealing with integer variables. Therefore, they struggle to consistently provide high-quality solutions in rapidly changing environments, limiting their applicability for online decision-making.

To overcome the above problems, many studies have contributed to the binary offloading decision problem using heuristic optimization algorithms. Zhang et al.¹⁶ applied a simulated annealing algorithm to satisfy the latency, energy, and quality requirements of vehicular networks. Lu et al.¹⁷ focused on optimizing wireless energy transfer for uncrewed aerial vehicles using a block coordinate descent method. Long et al.¹⁸ approximated the offloading decision problem using reformed linearization, relaxation, and convex optimization methods. Zaman et al.^19,20 proposed a method to predict user locations using neural networks to assist the selection of target servers using a multi-objective genetic algorithm and a fitness function. Although heuristics are easy to implement and offer low computational complexity, they often fail to adapt optimally in complex and dynamically changing network conditions. When the network state fluctuates frequently or tasks exhibit high dynamics, these methods may yield suboptimal decisions, resulting in performance degradation.

To address the limitations of traditional heuristic methods, DRL approaches have been explored to optimize offloading decisions in MEC. DRL leverages the powerful representation capability of Deep Neural Networks (DNNs) to adapt to dynamic environments and achieve better performance. Value-based DRL methods, such as Deep Q-Network (DQN)²¹, Double DQN²², and Dueling DQN²³, train DNNs to estimate state-action value functions. Liu et al.⁸ and Zhao et al.²⁴ applied DQN to onboard edge computing. Li et al.²⁵ used DQN to optimize MEC network offloading by minimizing total costs. Chen et al.²⁶ proposed a model integrating DNN with K-Nearest Neighbors (KNN) to solve offloading, communication, and resource allocation problems in MEC networks. Yun et al.²⁷ and Yu et al.²⁸ further explored multi-user and multi-ES environments using DQN-based methods. Chen et al.²⁹ proposed a Parallel Exploration with Asynchronous Training-based Deep Reinforcement Learning (PEATDRL) algorithm to enhance task offloading efficiency. This method employs two independent DNNs for parallel exploration to generate diverse offloading strategies, enhancing adaptability and addressing convergence issues associated with traditional reinforcement learning approaches. Experimental results indicate that PEATDRL significantly improves task queue convergence speed by over 20% compared to baseline algorithms. Additionally, recent research introduced a multi-agent deep reinforcement learning (MA-DRL) framework³⁰ for optimizing task offloading in vehicular networks, which improves resource allocation by considering network state and task priorities. However, as the number of discrete offloading actions increases—especially when the number of WDs grows exponentially—these approaches become computationally expensive and complex.

Some researchers introduce policy-based methods, like the actor-critic algorithms, to improve the scalability of DRL approaches. Policy-based methods map input states directly to actions using DNNs, optimizing offloading strategies through continuous adaptation. The authors in³¹ focused on discrete offload decisions while considering uncertainties in transmit power and offloading rates, employing Q-learning to optimize state-action mappings. The DROO framework³² used Generative Adversarial Networks (GANs) to generate a reduced set of binary offload decisions, then applied linear programming for optimal resource allocation. DROO’s accurate estimation of operation results allowed for rapid convergence to near-optimal solutions. Expanding upon this, the authors in³³ proposed independent learning modules for discrete decision-making and continuous resource allocation. The authors in³⁴ employed DDPG to enhance the anti-interference characteristics of MEC network offloading decisions. Wei et al.³⁵ designed a DRL method that utilizes natural strategy gradient training to obtain offload decisions. Fang et al.³⁶ proposed a DRL-aided task offloading and resource allocation scheme to minimize power consumption in cloud-edge cooperation environments by jointly optimizing task offloading and resource allocation while adapting to network changes. Additionally, DDPG was employed in^37,38 to enhance offloading decisions’ anti-interference capabilities in vehicular and MEC networks. Nevertheless, these methods still face limitations in highly dynamic network environments, where frequent changes can impair decision accuracy.

Some studies combine Lyapunov optimization with DRL to enhance long-term stability. Bi et al.³⁹ integrated Lyapunov optimization with DRL to achieve long-term system stability, though the approach struggled with resource constraints when WDs or task arrival rates increased. To build upon these ideas, the ETHC framework⁴⁰ employed Lyapunov optimization-assisted DRL for hybrid cloud environments, decomposing long-term optimization into time-segmented subproblems to balance offloading decisions under energy consumption and cost constraints. While ETHC achieved efficient queue stability and resource utilization, its adaptability in highly dynamic environments was limited due to the rapid decision changes required.

Table 1 summarizes the description of the papers reviewed and compares their approach, key advantages, and limitations.

Table 1 Related work.

To reduce the computational complexity based on the binary offloading model and address its shortcomings in rapidly changing network environments, we propose the DBSCAN algorithm to identify tasks and nodes with abnormal performance in the computational offloading process using the density clustering method, which reduces computational complexity and improves decision accuracy. The advantages of the DBSCAN algorithm in detecting high-density areas and outliers make it particularly suitable for use in rapidly changing network environments and make up for the shortcomings of the traditional binary offloading model in terms of real-time performance and accuracy. In order to improve the robustness and accuracy of unloading decisions in multi-user and multi-task scenarios and overcome the limitations of a single model in complex and dynamically changing network environments, we introduce an ensemble learning method⁴¹ based on isomorphism to improve the robustness and accuracy of the unloading decisions by combining the advantages of multiple base learners. Ensemble learning can effectively overcome the limitations of a single model in complex and dynamic network environments and improve the overall performance of the unloading strategy through the collaboration of multiple models. This collaborative approach enables DCEDRL to accommodate environmental changes better, providing a more resilient and efficient solution for task offloading in MEC networks than existing methods like ETHC, especially in dynamic edge computing environments.

System model and optimization objective

This section discusses the system model and the corresponding optimization objective. Table 2 lists the meanings of the notations used in this paper.

Table 2 Notations and symbols.

System model

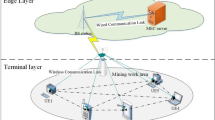
In this paper, we consider a system with n WDs that offload their computational tasks to an ES over continuous time frames of equal duration T, as shown in Fig. 1. In each time frame T, the data queue of the i-th WD receives an incoming data bitstream ${\text{A}}_{i}^{t}$, and the arrival of data ${\text{A}}_{i}^{t}$ follows an independent and identically distributed process with a bounded second moment, denoted ${\text{E}}[{({\text{A}}_{i}^{t})}^{2}]={\eta }_{i}<\infty$. The value of ${\eta }_{i}$ is known and can be estimated through past observations.

Fig. 1

System model of an MEC network with multiple WDs and multiple tasks considered within a labeled time frame.

The channel gain between the i-th WD and the ES in the t-th time frame is denoted ${h}_{i}^{t}$. Under the block fading assumption, ${h}_{i}^{t}$ remains constant within a time frame but varies independently across different frames. The i-th WD processes ${\text{D}}_{i}^{t}$ bits of data in the t-th time frame and produces computational output by the end of the frame. We assume a binary computation offloading policy where each WD processes the data locally or offloads it to the ES.

The system employs a time-division multiple access scheme for the WDs to share the common bandwidth to transmit task data to the ES. The binary variable ${x}_{i}^{t}$ indicates the offloading decision, where ${x}_{i}^{t}=1$ represents offloading to the ES, and ${x}_{i}^{t}=0$ represents local processing.

• 1. Local processing. The locally bits processed ${\text{D}}_{i,L}^{t}$ and the energy consumed ${\text{E}}_{i,L}^{t}$ in a time frame are given by Eqs. (1) and (2),

  $${D}_{i,L}^{t}=\frac{{f}_{i}^{t}T}{\varphi }$$

  (1)
  $${E}_{i,L}^{t}=\kappa ({f}_{i}^{t}{)}^{3}T$$

  (2)

  where ${f}_{i}^{t}$ is the local CPU frequency of the i-th WD, which is bounded by a maximum value ${f}_{i}^{\text{max}}$, $\varphi >0$ is the number of CPU cycles required to process one bit of data, and $\kappa >0$ is the computational efficiency parameter.

• 2. Offloading to ES. The bits offloaded and processed by the ES ${\text{D}}_{i,O}^{t}$ and the corresponding energy consumption ${\text{E}}_{i,O}^{t}$ are given by Eqs. (3) and (4),

  $$D_{i,O}^t=\frac{W\tau_i^tT}{\nu_\mu}\log_2\left(1+\frac{P_i^th_i^t}{N_0}\right)$$

  (3)
  $${E}_{i,O}^{t}={P}_{i}^{t}{\tau }_{i}^{t}T$$

  (4)

  where ${P}_{i}^{t}\le {P}_{i}^{\text{max}}$ is the transmit power of the i-th WD, ${\tau }_{i}^{t}$ is the fraction of time allocated for offloading (satisfying $0\le {\tau }_{i}^{t}\le 1$ and $\sum_{i=1}^{N} {\tau }_{i}^{t}\le 1$), ${\upsilon }_{\mu }>1$ represents the communication overhead, and ${N}_{0}$ denotes the noise power.

The overall processed bits ${\text{D}}_{i}^{t}$ and the energy consumption ${E}_{i}^{t}$ in the t-th time frame are given by Eqs. (5) and (6).

$${\text{D}}_{i}^{t} \triangleq (1-{x}_{i}^{t}{\text{)D}}_{i,L}^{t}+{x}_{i}^{t}{\text{D}}_{i,O}^{t}$$

(5)

$${E}_{i}^{t}\triangleq (1-{x}_{i}^{t}){E}_{i,L}^{t}+{x}_{i}^{t}{E}_{i,O}^{t}$$

(6)

Queue dynamics and stability

We use ${Q}_{i}(t)$ to describe the length of the data queue of the i-th WD at the beginning of the t-th time frame. The queue dynamics are modeled according to Eq. (7).

$${Q}_{i}(t+1)=\text{max}\{{Q}_{i}(t)-{\widetilde{D}}_{i}^{t}+{A}_{i}^{t},0\}, i=\text{1,2},\ldots$$

(7)

We assume an infinite queue capacity for analytical tractability. Data causality constraints ${D}_{i}^{t}<{Q}_{i}(t)$ ensure that queue lengths ${Q}_{i}(t)\ge 0$. Thus, we simplify the queue dynamics as shown in Eq. (8).

$${Q}_{i}(t+1)={Q}_{i}(t)-{D}_{i}^{t}+{A}_{i}^{t}, i=\text{1,2},\ldots$$

(8)

To ensure the stability of the data queue, we add a bounded expected value constraint to the average queue length, as shown in Eq. (9),

$$\text{lim}_{K\to \infty }\frac{1}{K}\sum _{t=1}^{K}E[{Q}_{i}(t)]<\infty$$

(9)

where the expected value $E$ is related to random events in the system⁴². Equation (9) guarantees that the expected value of the average length of the queue remains finite as the time K approaches infinity. Note that highly stability data queues result in finite processing delays for each task.

To better understand and manage this constraint, we introduce the concept of energy queue $\{{Y}_{i}(t){\}}_{i=1}^{N}$ to describe the average power constraint for each WD. The initial value of the energy queue is ${Y}_{i}(1)=0$, and its update process is given in Eq. (10),

$${Y}_{i}(t+1)=max\left({Y}_{i}(t)+\nu {e}_{i}^{t}-\nu {\gamma }_{i},0\right), i=1,\ldots ,N; t=1,\ldots ,K$$

(10)

where $\nu$ is a positive factor, ${e}_{i}^{t}$ represents random energy arrivals, and ${\gamma }_{i}$ is the power threshold. The energy threshold ${\gamma }_{i}$ is set to maximize the energy output while limiting energy consumption. Specifically, when the energy consumption of a WD is less than the energy threshold ${\gamma }_{i}$ and the energy queue ${Y}_{i}\left(t\right)=0$, the resource allocation strategy will adopt the maximum value of the transmitted power ${P}_{i}^{t}$ and the calculated frequency ${f}_{i}^{t}$, i.e., ${P}_{i}^{t}={P}_{i}^{max}$ and ${f}_{i}^{t}={f}_{i}^{max}$. The energy queue ${Y}_{i}(t)$ is affected by the arrival of random energy to $v{e}_{i}^{t}$ and the fixed power consumption of $v{\gamma }_{i}$. Thus, the energy queue describes the average power consumption of a WD.

Optimization objective

The main objective of optimization is to maximize the long-term average weighted computation rate of all computing devices while ensuring the stability of the data queue and the average power limit. Specifically, we optimize task offloading and resource allocation decisions within each time frame without prior knowledge of future channel status and data arrival.

We set $x={\{{x}^{t}\}}_{t=1}^{K}$, $\tau ={\{{\tau }^{t}\}}_{t=1}^{K}$, $f={\{{f}^{t}\}}_{t=1}^{K}$, and ${\mathbf{E}}_{O}=\{{E}_{i,O}^{t}{\}}_{t=1}^{K}$. The problem is formulated as a multistage stochastic MINLP problem, as given in Eqs. (11) and (12),

$${\text{maximize}}\underset{\mathbf{x},\tau ,\mathbf{f},{\mathbf{E}}_{O}}{lim} \frac{1}{K}\sum_{t=1}^{K} \sum_{i=1}^{N} {c}_{i}{\mathbb{E}}[{r}_{i}^{t}]$$

(11)

subject to

$$\left\{\begin{array}{l} \sum_{i=1}^{N} {\tau }_{i}^{t}\le 1,\forall t\\(1-x_i^t)\frac{f_i^tT}{\varphi}+x_i^t\frac{W\tau_i^tT}{\nu_\mu}\log_2\left(1+\frac{P_i^th_i^t}{N_0}\right)\leq D_i^t,\forall t\\ \underset{K\to \infty }{lim} \frac{1}{K}\sum_{t=1}^{K} E\left[(1-{x}_{i}^{t})\kappa ({f}_{i}^{t}{)}^{3}T+{x}_{i}^{t}{P}_{i}^{t}{\tau }_{i}^{t}T\right]\le {\gamma }_{i},\forall i\\ E[{Q}_{i}(t)]<\infty ,\forall i\\ {x}_{i}^{t}\in \{\text{0,1}\},{\tau }_{i}^{t}\ge 0\\ 0\le {f}_{i}^{t}\le {f}_{i}^{max},0\le {P}_{i}^{t}\le {P}_{i}^{max}.\end{array}\right.$$

(12)

Where ${c}_{i}$ denotes the weight for the i-th WD, ${\gamma }_{i}$ represents the power threshold, and ${r}_{i}^{t}$ is the computation rate. The constraints include the offloading time limit, data causality, average power consumption, and data queue stability.

To address the challenge of making real-time decisions under unknown channel and data arrival conditions, we propose the DBSCAN density clustering plus punishment and ensemble learning optimization framework, which is described in detail in subsequent chapters. The proposed framework ensures robust and efficient problem-solving for system models and objectives.

DCEDRL-based offloading strategy for MEC

Overview of the DCEDRL-based offloading strategy in MEC

The DCEDRL-based offloading strategy aims to optimize offloading decisions in Mobile Edge Computing (MEC) environments using Deep Reinforcement Learning (DRL). The strategy integrates environmental information through an iterative and systematic approach involving five main modules: density-based clustering (DBSCAN), actor-network, critic network, policy update, and queuing. These modules work in coordination to enhance the robustness and efficiency of task-offloading decisions.

The DBSCAN algorithm clusters incoming tasks based on their characteristics, such as size, priority, or resource requirements. This density clustering is applied before the ensemble learning process, serving as a preprocessing step to group similar tasks together. Clustering helps recognize patterns and inform subsequent decision-making, leading to more efficient offloading by reducing the complexity of the task space and identifying tasks with similar resource needs.

After clustering, the DRL-based decision-making process begins. In DRL, a single-agent approach often faces challenges balancing exploration (searching for better solutions) and exploitation (using known information to make decisions), which can hinder convergence and stability. Additionally, inaccuracies in estimating target values for the Q-function can introduce significant errors, causing unstable training.

Ensemble learning is integrated into the DCEDRL framework to address these issues. This approach uses multiple Deep Neural Networks (DNNs) rather than relying on a single agent. Each network in the ensemble is trained on different subsets or aspects of the data, thereby diversifying the exploration process. This helps reduce uncertainty when encountering new samples and enhances the stability and efficiency of convergence by providing a consensus over multiple predictions. By leveraging the combined output of several DNNs, ensemble learning improves the overall accuracy and robustness of the decision-making process, as it mitigates the impact of outliers and reduces the error propagation associated with a single-agent system.

The sequence of operations in the DCEDRL-based offloading strategy is as follows:

• 1. DBSCAN Clustering: Tasks are clustered based on their features, facilitating the identification of patterns and more effective task grouping.

• 2. Ensemble Learning with DRL: Multiple DNNs process the clustered tasks within the ensemble learning framework to explore various offloading strategies. This multi-agent approach enhances stability and accelerates convergence by collectively improving decision accuracy.

• 3. Policy Update: The DRL policy is iteratively refined based on feedback from the actor and critic networks.

• 4. Queueing and Task Execution: Optimized offloading decisions are implemented, managing the task queues for execution.

Figure 2 shows the structure of the overall decision-making process. By interacting with the environment iteratively and updating the policy, the DCEDRL-based algorithm optimizes offloading decisions effectively, and it realizes robust and efficient performance in dynamic environments.

Fig. 2

Architecture of edge computing task offloading decision system based on actor-critic–based density cluster ensemble learning.

DBSCAN algorithm in task offloading

Incorporating the DBSCAN algorithm into edge computing task offloading decisions allows for periodic updating of the task clusters to adapt to changing environments. An improved description and the mathematical formulation of this process is given in the following.

First, we represent the features of each task as a feature vector ${{F}}$, as given in Eq. (13),

$$F=[{A}_{i}^{t},{x}_{i}^{t},{h}_{i}^{t},W,{Q}_{i}(t),{Y}_{i}(t),L]$$

(13)

where ${\text{A}}_{i}^{t}$ is the data size (in bits) arriving from the i-th device in the t-th time frame, ${x}_{i}^{t}$ is the offloading decision of the i-th device at the t-th time frame, ${h}_{i}^{t}$ is the channel gain of the i-th device in the t-th time frame, $W$ is the weight of the WDs, ${Q}_{i}(t)$ is the task queue, ${Y}_{i}(t)$ is the energy queue, and $L$ is the Lyapunov control parameter.

We then perform a GS to determine the optimal parameters ${\epsilon }_{\text{best}}$ and ${\text{MinPts}}_{\text{best}}$ for the DBSCAN algorithm. The goal of the GS is to minimize the overall queue length. These parameters help define the density threshold for the clustering process.

Utilizing the best parameters, we apply the DBSCAN algorithm to cluster the tasks based on their feature vectors. For each task i, we identify the $\epsilon$-neighborhood (all tasks within a distance ${\epsilon }_{\text{best}}$). A task i is considered a core point if there are at least ${\text{MinPts}}_{\text{best}}$ tasks (including i) within its $\epsilon$-neighborhood, and tasks that are not core points but are within the $\epsilon$-neighborhood of a core point are considered border points. In addition, tasks that are neither core points nor border points are considered noise. Mathematically, this can be expressed as given in Eq. (14),

$${\text{Cluster}}(i)=\left\{\begin{array}{l}{\text{core}} \, {\text{point}} \, {\text{cluster}}\,\,\,\,if |\{ j\mid d({F}_{i},{F}_{j})\le {\epsilon }_{\text{best}}\}|\ge {\text{MinPts}}_{\text{best}}\\ {\text{border}} \, {\text{point}} \, {\text{cluster}}\,\,\,\,if \exists j s.t.d({F}_{i},{F}_{j})\le {\epsilon }_{\text{best}}~ and~ j \, {\text{is}} \, {\text{a}} \, {\text{core}} \, {\text{point}}\\ {\text{noise}}\,\,\,\,otherwise\end{array}\right.$$

(14)

where $\text{Cluster}(i)$ represents the cluster assignment for task i, $d({F}_{i},{F}_{j})$ is the distance between the feature vectors of tasks i and j, ${\epsilon }_{\text{best}}$ is the optimal distance threshold for clustering, and ${\text{MinPts}}_{\text{best}}$​ is the optimal minimum number of points required to form a dense region.

Then, the task clusters are updated periodically based on new data samples, which ensures that the clustering adapts to the changing environment, thereby maintaining relevance and accuracy.

Finally, the readout function $R(\cdot )$ is employed to aggregate the hidden state ${h}_{k}$ of all task clusters and obtain the Q-value, which represents the readiness of each task cluster for offloading. The Q-value is expressed as given in Eq. (15),

$$Q(s,a,\theta )=R\left(\sum_{k\in E} aggr({h}_{k})\right)$$

(15)

where $Q(s,a,\theta )$ is the Q-value representing the readiness of the task clusters for offloading, $R(\cdot )$ is the readout function used to aggregate the hidden states, $\sum_{k\in E}$ is the summation over all task clusters ${\text{E}}$, and $aggr({h}_{k})$ is the aggregation function applied to the hidden state ${h}_{k}$ of each task cluster k. ${\text{E}}$ represents the set of all task clusters, and ${h}_{k}$ represents the hidden state of each task cluster.

The integration of DBSCAN enhances the task offloading decision-making process by providing a structured approach to clustering tasks based on their features, which yields more informed offloading decisions.

Actor module

The actor module generates candidate routing actions based on the current environmental observations. This module utilizes a DNN parameterized by ${\theta }^{t}$ to output a relaxed offloading decision ${\widehat{\mathbf{x}}}^{t}\in [\text{0,1}{]}^{N}$, which is later quantized into feasible binary actions. This process is summarized as follows.

• 1. Input observation. The input to the DNN is ${\xi }^{t}\triangleq \{{h}_{i}^{t},{Q}_{i}(t),{Y}_{i}(t){\}}_{i=1}^{N}$, which includes channel gains, task queues, and energy queues.

• 2. DNN output. The DNN outputs a relaxed decision ${\widehat{\mathbf{x}}}^{t}$ expressed as shown in Eq. (16).

  $${\Pi }_{{\theta }^{t}}:{{\varvec{\xi}}}^{t}\mapsto {\widehat{\mathbf{x}}}^{t}=\{{\widehat{x}}_{i}^{t}\in [\text{0,1}], i=1,\ldots ,N\}$$

  (16)

• 3. Quantization. The relaxed decision ${\widehat{\mathbf{x}}}^{t}$ is quantized into ${M}_{t}$ feasible binary actions using a quantization function, as given in Eq. (17).

  $${\Upsilon }_{{M}_{t}}:{\widehat{\mathbf{x}}}^{t}\mapsto {\Omega }^{t}=\{{\mathbf{x}}_{j}^{t}|{\mathbf{x}}_{j}^{t}\in \{\text{0,1}{\}}^{N}, j=1,\ldots ,{M}_{t}\}$$

  (17)

In addition, the noisy order-preserving (NOP) quantization method is employed to ensure the candidate actions are close to ${\widehat{\mathbf{x}}}^{t}$.

Ensemble learning

In the unloading decision of edge computing tasks, a single DNN model faces challenges balancing exploration and utilization, which frequently leads to unstable convergence. If errors in the DNN result in an inaccurate estimate of the Q-value, the agent may select a suboptimal action. Due to the presence of errors, the agent may evaluate the value of specific actions incorrectly, thereby favoring certain actions or states. This bias will destroy the balance between exploration and utilization, making the agent unable to explore the state space and affecting convergence entirely. This incorrect decision can further affect the subsequent learning process and the final policy performance. To solve these problems, we employ ensemble learning to improve algorithm performance. Ensemble learning leverages extended exploration capabilities and explores the environment’s results by combining multiple DNN models to reduce the uncertainty of new samples. In this framework, ensemble learning enhances the environment’s exploration capabilities by setting up multiple homogeneous actor models.

Here, assume there are ${N}_{a}$ actor models, each controlled by parameters ${\theta }_{i}^{t}$ (where $i=1,\ldots ,{N}_{a}$ represents the model index), and each model generates a decision ${\widehat{x}}_{i}^{t}\in [\text{0,1}{]}^{N}$. These decisions are integrated into the final decision ${x}^{t}$, and the integration process is described as follows.

First, multiple model decision generation occurs. Each actor model i generates a decision ${\widehat{x}}_{i}^{t}$ based on the same environmental observation ${\xi }^{t}$ (including the channel gains, task queues, and energy queues), as given in Eq. (18).

$${\widehat{x}}_{i}^{t}={\Pi }_{{\theta }_{i}^{t}}({\xi }^{t}), i=1,\ldots ,{N}_{a}$$

(18)

Next, the decisions from all models are integrated into the final decision ${x}^{t}$ through a weighted average, as shown in Eq. (19).

$${x}^{t}=\frac{1}{{N}_{a}}\sum_{i=1}^{{N}_{a}} {\widehat{x}}_{i}^{t}$$

(19)

Then, the weighted average is applied. The weighted average considers the exploration results of each model and can be represented by weights ${w}_{i}$ to indicate the importance of each model. Typically, uniform weighting is employed, i.e., ${w}_{i}=\frac{1}{{N}_{a}}$, thereby ensuring that each model contributes equally to the final decision.

Mathematically, the integrated final decision ${x}^{t}$ can be expressed as given in Eq. (20).

$${x}^{t}=\frac{1}{{N}_{a}}\sum_{i=1}^{{N}_{a}} {\Pi }_{{\theta }_{i}^{t}}({\xi }^{t})$$

(20)

Finally, the sampling mode is employed. Here, rather than averaging the decisions directly, the final decision ${x}^{t}$ is sampled from the set of decisions generated by the ${N}_{a}$ actor models. This can be achieved by selecting one of the ${\widehat{x}}_{i}^{t}$ based on a probability distribution derived from the models’ performance or other criteria. A simple uniform sampling process is expressed in Eq. (21).

$${x}^{t}={\widehat{x}}_{k}^{t}\text{ where }k\sim \text{Uniform}(1,{N}_{a})$$

(21)

The sampling process can be adapted to use other probability distributions if some models are determined to be more reliable or accurate than other models.

Critic module

The critic module evaluates the candidate routing actions generated by the actor module and selects the optimal action. This module leverages model information to solve the resource allocation problem analytically by obtaining an optimal solution that maximizes the reward function $G({\mathbf{x}}^{t},{{\varvec{\xi}}}^{t})$. The evaluation process is summarized as follows.

• 1. Action evaluation. Each candidate action ${\mathbf{x}}_{j}^{t}$ is evaluated by solving the resource allocation problem, as shown in Eq. (22).

  $$G({\mathbf{x}}_{j}^{t},{{\varvec{\xi}}}^{t})=\underset{\tau ,f,{\epsilon }_{O},{r}_{O}}{max} \sum_{i\in {M}_{1}} \frac{({Q}_{i}(t)+V{{\varvec{c}}}_{i}){{\varvec{r}}}_{i,O}}{{\text{log}}_{2}({Y}_{j}(t){{\varvec{e}}}_{i,O}+C)+C}+\sum_{j\in {M}_{0}} \frac{({Q}_{j}(t)+V{{\varvec{c}}}_{j}){f}_{j}\frac{1}{\phi }}{{\text{log}}_{2}({Y}_{j}(t)\kappa {f}_{j}^{3}+C)+C}$$

  (22)

• 2. Action selection. The best action ${\mathbf{x}}^{t}$ is selected according to Eq. (23).

  $${{\varvec{x}}}^{t}=arg\underset{{{\varvec{x}}}_{j}^{t}\in {\Omega }_{t}}{max} G({{\varvec{x}}}_{j}^{t},{{\varvec{\xi}}}^{t})$$

  (23)

Policy update module

The policy update module refines the policy of the actor module through training. The DNN is updated using replay memory that stores recent data samples, and training commences after collecting sufficient samples. The update process involves minimizing a loss function over a batch of data samples using the Adam optimization algorithm.

• 1. Replay memory. The most recent ${\text{q}}$ data samples are stored in replay memory.

• 2. Training. The DNN is trained by minimizing the average cross-entropy loss, as shown in Eq. (24).

  $${L}_{S}({\theta }^{t})=-\frac{1}{|{\mathcal{S}}^{t}|}\sum_{\tau \in {\mathcal{S}}^{t}} [({{\varvec{x}}}^{\tau }{)}^{\intercal }log{\Pi }_{{\theta }^{t}}({\xi }^{\tau })+(1-{{\varvec{x}}}^{\tau }{)}^{\intercal }log(1-{\Pi }_{{\theta }^{t}}({\xi }^{\tau }))]$$

  (24)

• 3. Parameter update. After training, the parameters of the actor module are updated for the next time frame.

Queueing module

The queueing module updates the data and energy queues based on the executed actions. This module ensures that the system’s state is ready for the next time frame by performing the following steps.

• 1. Resource allocation execution. Execute the joint computation offloading and resource allocation action $\{{x}^{t},{y}^{t}\}$, processing data $\{{D}_{i}^{t}{\}}_{i=1}^{N}$, and consuming energy $\{{e}_{i}^{t}{\}}_{i=1}^{N}$​.

• 2. Queue updates. The data and energy queues $\{{Q}_{i}(t+1),{Y}_{i}(t+1){\}}_{i=1}^{N}$ are updated using the observed data arrivals and resource consumption.

Working process of DCEDRL algorithm

The DCEDRL algorithm’s working process for computation offloading and module training in each iteration is described in Algorithm 1. Here, we first initialize the DNN with random parameters and set up empty replay memory (Line 1). We also initialize the data and energy queues (Line 2). Then, for each time step $t$ from 1 to $K$ (Line 3), we observe the environment state (Line 4). If the time step $t$ is a multiple of the update interval ${\delta }_{u}$ (Line 5), we update ${M}_{t}$. We then determine the optimal parameters ${\epsilon }_{\text{best}}$ and ${\text{MinPts}}_{\text{best}}$ (Line 6). Using these parameters, we apply DBSCAN to cluster the tasks based on their feature vectors (Line 7). We then generate a relaxed offloading policy using the DNN (Line 8), and based on the relaxed offloading policy, we generate candidate offloading strategies using the NOP method (Line 9). From multiple actor models, we generate decisions and integrate them into a final decision using a weighted average (Lines 10–11). In addition, ensemble learning is employed to integrate decisions from multiple actor models into the final decision (Line 12). For each candidate offloading strategy, we compute the utility function $G({x}_{j}^{t},{\xi }^{t})$ by optimizing resource allocation (Line 13). Then, we select the optimal offloading strategy and obtain the corresponding joint decision control (Line 14). This joint decision is executed (Line 15), and we store the decisions and states in the replay buffer (Line 16). If the time step $t$ is a multiple of the first training interval ${\delta }_{u}$​ (Line 17), we sample a batch of data from the replay buffer and train the DNN using these data (Line 18–19). We then update the DNN parameters using the Adam algorithm (Line 20). The time step is incremented (Line 22), and the task and energy queues are updated based on the previous joint decision and new arrival observations (Line 23). This process continues until all iterations are completed (Line 24).

Algorithm 1

DCEDRL algorithm for computation offloading and module training

Performance

Experimental environment and parameter settings

We evaluate the performance of the proposed DCEDRL algorithm through simulation. We use the PyTorch framework to implement the RL algorithm and conducted the tests on an Intel i5 13600KF processor operating at 3.50 GHz with a 1 TB hard drive and 16 GB of memory. In terms of the network environment parameters, we took the experimental parameters reported in³⁶ as the benchmark and referred to the corresponding communication parameter settings. The average channel gain is expressed as ${\overline{h} }_{i}={A}_{d}{(\frac{3\times {10}^{8}}{4\pi {f}_{c}{d}_{i}})}^{{d}_{\text{e}}},i=1,\ldots ,N,$ where ${A}_{d}=3$ denotes the antenna gain, ${f}_{c}=915 {\text{MHz}}$ is the carrier frequency, ${d}_{e}=3$ is the path loss exponent, and ${d}_{i}$ denotes the distance (in meters) between the i-th WD and ES. The Rician distribution was used to model the line-of-sight wireless transmission, with an equivalent value of $0.3 {\overline{h} }_{i}.$ The noise power was set to ${N}_{0}=w{\upsilon }_{0},$ and the noise power spectral density was set to ${\upsilon }_{0}=-174 \text{dBm/Hz}.$ The weights of the WDs alternated between 1.5 and 1, and the maximum distance between the ES and WD was dependent on the number of WDs, which was set at 15 units apart, with the initial distance between the WD and ES was selected as 120, yielding ${d}_{i}=120+15(i-1),i=1,\ldots ,N$. The arrival rate of the tasks for all WDs followed an exponential distribution with $E[{A}_{i}^{t}]={\lambda }_{i},\,i=1,\ldots ,N$. These parameter settings were selected to ensure efficient modeling of the network environment, thereby facilitating effective analysis and optimization of the data queues and energy consumption in wireless communication systems.

Figure 3 shows the influence of the ${\epsilon }$ and ${\text{MinPts}}$ parameters in the DBSCAN algorithm on the task unloading decision performance. The parameter ${\epsilon }$ serves as the neighborhood radius, and its value affects the boundaries of the task clusters and the formation of clusters, where a small ${\epsilon }$ value results in a smaller neighborhood; thus, only tasks with similar features are clustered together. In this case, the clustering results will be more refined; however, it may also cause many tasks to be considered noise, which cannot be clustered efficiently. In contrast, large ${\epsilon }$ values expand the neighborhood, thereby allowing more tasks to form larger clusters. In this case, the clustering results may be rough. The ${\text{MinPts}}$ parameter is the minimum field point, which affects the threshold at which a task becomes a core point. Small ${\text{MinPts}}$ values cause more tasks to become core points, thereby forming more clusters. In this case, the clustering results will be more dispersed; however, this it may increase the number of noise points and affect the accuracy of the unloading decision. In contrast, large ${\text{MinPts}}$ values raise the threshold for becoming a core point, and only very feature-dense tasks can form clusters. In this case, the clustering results will be more compact; however, more tasks will be considered noise, which cannot be clustered efficiently.

Fig. 3

Performance under different density cluster values when N = 20 and ${\lambda }_{i}=2.6$ Mbps/WD: a different densities can reach a range; b minimum number of samples for different core point domains.

Figure 3a shows the influence of different ${\epsilon }$ values’ on performance using datasets with various values, e.g., (0.1, 1, 10), (0.1, 1, 20), (0.1, 1, 30), and (0.1, 1, 40). When the density detection was set to 10, a large number of tasks were considered noise because the neighborhood was too small; thus, the length of the data queue was relatively large. When it is increased to 20, the queue length was reduced considerably, and the performance was improved by approximately 42.41% due to the precise task partitioning for offloading decisions. When the density radius was increased to 30, the convergence rate was much slower than 20, and the performance was worse than 2. When the density radius increased to 40, the clustering results became rough, thereby making the unloading decision less rigorous. At this point, the performance improved by approximately 45.66% compared to 20.

Similarly, Fig. 3b shows the impact of different ${\text{MinPts}}$ settings on performance, with datasets including sample values of (1, 10, 2), (1, 20, 2), (1, 30, 2), and (1, 40, 2). As can be seen, optimal performance was observed at ${\text{MinPts}}$ values of 1 and 20 with a step size of 2, which is characterized by shorter data queue length and minimal task backlog. A ${\text{MinPts}}$ value of approximately 20 resulted in significantly lower data queue lengths compared to a setting of 10, and the performance was improved by 34.99%. However, increasing the ${\text{MinPts}}$ value resulted in a significant queue length and backlog increase beyond a ${\text{MinPts}}$ value of 10. The final queue lengths obtained with ${\text{MinPts}}$ values of 20 and 10 are similar; however, setting ${\text{MinPts}}$ to 20 enabled faster convergence and lower time overhead, thereby making this configuration more efficient.

Performance trends align with DBSCAN principles, where the $\epsilon$ parameter determines the neighborhood search radius, and the ${\text{MinPts}}$ parameter defines the minimum number of points required to form a cluster. Optimized ${\epsilon }$ and ${\text{MinPts}}$ values ensure efficient clustering, thereby reducing task queue length and energy consumption. However, excessively high values may cause over-clustering, thereby increasing processing time and queue length, and overly low values may result in insufficient clustering, thereby increasing individual processing time. Through the above experiments, we selected (0.1, 1, 20) and (1, 20, 2) as the optimal experimental parameters for ${\epsilon }$ and ${\text{MinPts}}$, respectively.

Figure 4 shows the training loss function of the system model across various learning rates. As can be seen, when the learning rate was 0.01, the loss function value was only approximately 0.23, which is much smaller than the loss value under other learning rates, thereby indicating the best degree of model fitting. The system was the most stable under this learning rate, and it converged to stability after approximately 1,000 training iterations. When the learning rate was increased to 0.05, the loss value was as high as 0.57, and the effect was the worst. When the learning rate was reduced to 0.005, the training loss value was approximately 0.35, which is inferior to the learning rate of 0.01. When the learning rate was decreased to 0.001, the loss value increased to approximately 0.54. These results indicate that excessive increases or decreases in the learning rate reduce the fitting effect of the model. After careful consideration, we selected 0.01 as the optimal learning rate.

Fig. 4

Training loss under different learning rates for ${\lambda }_{i}=2.6$ and $N=20$.

Figure 5 compares the performance effects of the size setting for model integration learning. A few models may result in an integrated system that must be more complex to capture the complexity and diversity of data and task offload decisions adequately. This may lead to underfitting, thereby resulting in insufficient predictive power of the model and lower efficiency of task offload decisions. However, too many models can cause the integrated system to be overly complex and prone to overfitting. Even if the performance is good on training data, the generalizability on unknown data may require improvement, which can result in instability and unreliability of task unloading decisions. Each additional model increases the required computing resources and communication overhead. However, resources are frequently limited in edge computing environments, and too many models can degrade system performance, which increases delay and the cost of the task-offloading decisions. As shown in Fig. 5, when the number of models used in the ensemble was one, two, three, four, five, and six, the corresponding time costs were 0.0845 s, 0.1802s, 0.2403 s, 0.2769 s, 0.3155 s, and 0.3838 s, respectively. The experimental results demonstrate that when the number of models increases from one to two, the system performance increases by 53.04%, and the time consumption increases by 113.25%, which is much greater than the corresponding performance improvement. When the number of models increased from two to three, the system performance was improved by 56.55%, and the corresponding time consumption was increased by 33.35%. In addition, when the number of models was increased from three to four and four to five, the performance of the system increased by 29.12% and 21.65%, respectively, and the corresponding time consumption increased by 15.23% and 13.94%, respectively Here, the performance improved by more than 20%, and the degree of time consumption increase was less than the degree of performance improvement. However, when the number of models was increased from five to six, the performance of the system decreased by 10.21%, and the time consumption increased by 21.65%. Thus, based on this analysis, five models were selected for optimal ensemble learning.

Fig. 5

Effect of scale selection on performance of ensemble learning for ${\lambda }_{i}=2.6$ and $N=20$.

The parameter settings of the simulation experiment are shown in Table 3.

Table 3 Simulation parameter settings.

Evaluation of computing offload performance

We evaluated the performance of different computing offloading methods experimentally under different N settings and different average data arrival rates.

We implemented other computing offloading solutions to facilitate an effective performance comparison with the DCEDRL algorithms, e.g., the LyDROO³⁹, ETHC⁴⁰, Enum, DCB + DRL, and ENS + DRL methods. The LyDROO, ETHC, and Enum methods are the baseline algorithms used for comparison in this experiment. The DCB + DRL and ENS + DRL methods were considered in ablation experiments to compare the performance of the DCEDRL model without ensemble learning and DCEDRL without density clustering, respectively. The LyDROO method uses the DRL method to make task-offloading decisions within a finite time, and it combines this with the Lyapunov drift method to address the challenge of maximizing computational performance while meeting the average power constraint and ensuring sufficient queue stability. The ETHC method is an online offloading algorithm based on the M/M/K queueing model that utilizes the DDPG method for decision-making. In addition, Enum is an enumeration method that performs computational offloading by enumerating all possible offloading decisions exhaustively within a given timeframe.

Figure 6 shows the case where the number of WDs was set to $N=10$. As shown in Fig. 6, the WD and MEC servers could support the load; thus, the data queue converged quickly and remains stable at average data arrival rates ${\lambda }_{i}$ of 2.2, 2.4, and 2.6. The DDPG-based ETHC approach relies on the critic network to guide the execution of actor network updates; thus, this method exhibits apparent disadvantages compared with updating directly based on the environment state and the task clustering. Note that enumeration methods perform better in less burdensome environments. The results show that the proposed DCEDRL method realizes better system performance than the compared algorithms due to its density clustering and ensemble learning training processes. In the initial phase, the DRL algorithm interacts with the environment to accumulate experience samples for training. At this time, the queue length increased, and after a certain training period, the queue length tended to stabilize. Density clustering plays a crucial role in DCEDRL, which enables the algorithm to make unloading decisions more efficiently by identifying high-density regions in the data distribution. In addition, ensemble learning improves the overall performance and stability by combining the advantages of multiple models. The results of the ablation experiments with the DBC + DRL and ESN + DRL method did not show significant comparative advantages due to the small environmental burden. However, random strategies perform well in less computationally taxing environments but become unstable as the rigor of the work environment increases. Generally, the DCEDRL improved the efficiency and effect of the algorithm through the combination of density clustering and ensemble learning, and it exhibits better adaptability and stability under different workload conditions.

Fig. 6

Performance of different methods under different average data arrival rates for N = 10: a ${\lambda }_{i}=2.2$ Mbps/WD; b ${\lambda }_{i}=2.4$ Mbps/WD; c ${\lambda }_{i}=2.6$ Mbps/WD.

Figure 7 shows the case where the number of WDs was set to $N=20$. As shown in Fig. 7a, all algorithms maintained a stable queue with an average data arrival rate of ${\lambda }_{i}=2.2$. However, as the number of WDs increased, the environmental space that needs to be explored and the complexity of random tasks also increased. Due to the density clustering and ensemble learning training methods, DCEDRL can explore the policy space more effectively and make more efficient decisions than the compared models, with a performance improvement of approximately 25.25% compared to the LyDROO method. Although the performance of the enumeration method was similar to that of DCEDRL, computational offloading decisions were not explored; thus, it cannot be compared in terms of energy consumption and lacks comparison characteristics. As shown in Fig. 7b, for ${\lambda }_{i}=2.4$, several methods maintained the stability of the data queue. Here, the performance of DCEDRL method improved by 44.73% compared with the LyDROO method. Figure 7c shows that the difficulty associated with exploring the best decision increased further when ${\lambda }_{i}=2.6$. Here, the data arrival rate exceeded the processing capacity, and the DCEDRL method made the optimal decision for the environment by optimizing the density clustering and ensemble learning such that the queue could converge and remain stable. In addition, the ENS + DRL method maintained the convergence and stability of the queue due to the advantages provided by ensemble learning; however, the effect was worse than DBSCAN, and other methods were unable to achieve convergence.

Fig. 7

Performance of different methods with different average data arrival rates for N = 20: a  ${\lambda }_{i}=2.2$ Mbps/WD; b  ${\lambda }_{i}=2.4$ Mbps/WD; c  ${\lambda }_{i}=2.6$ Mbps/WD.

Figure 8 shows the algorithm performance when the number of WDs was set to $N=30$ under three different data arrival rates. For ${\lambda }_{i}=2.2$ (Fig. 8a), all of the compared methods maintained the stability of the queue, and the performance of the DCEDRL method improved by approximately 17.91% compared with that of the LyDROO method. For ${\lambda }_{i}=2.4$, as shown in Fig. 8b, none of the methods maintained a stable task queue length except the DCEDRL method. In addition, as shown in Fig. 8c, none of the methods found a suitable strategy to maintain a stable data queue with ${\lambda }_{i}=2.6$. However, due to the density clustering and ensemble learning strategies, the proposed DCEDRL outperformed the compared methods in this case. These results demonstrate that the proposed DCEDRL method can maintain good performance in the face of strict constraints.

Fig. 8

Performance of different methods with different average data arrival rates for N = 30: a ${\lambda }_{i}=2.2$ Mbps/WD; b ${\lambda }_{i}=2.4$ Mbps/WD; c ${\lambda }_{i}=2.6$ Mbps/WD.

Figure 9 shows the throughput performance of each algorithm under the condition that task arrival rates are ${\lambda }_{i}=2.2$, 2.4, and 2.6, respectively, when $N=20$. In this paper, throughput is primarily determined by the average task arrival rate λ, representing the average data arrival rate per device. Since λ is defined at the individual device level, the number of devices N has little or no effect on throughput performance. Therefore, we choose $N=20$ as the representative scene of the experiment. With the increase of time, the throughput of the five algorithms gradually becomes stable. For ${\lambda }_{i}=2.2$, as shown in Fig. 9a, all comparison methods showed a good throughput growth trend and high queue stability. Among them, the throughput of DCEDRL increased by about 15.54% compared with LyDROO, and the throughput increased by about 23.20% compared with the ETHC method. For ${\lambda }_{i}=2.4$, as shown in Fig. 9b, with the increase of task arrival rate, the queue stability begins to decline, but the DCEDRL method still maintains the optimal performance, and its throughput is improved by about 17.96% compared with the LyDROO method and about 23.35% compared with the ETHC method. For ${\lambda }_{i}=2.6$, as shown in Fig. 9c, the queue stability of all methods is further decreased under high load, but DCEDRL is still significantly superior to other methods by means of density clustering and ensemble learning strategies, and its throughput is improved by about 19.46% compared with the LyDROO method. Compared with the ETHC method, the improvement is about 25.12%. These results show that the proposed DCEDRL method not only has excellent performance under low and medium load conditions but also significantly outperforms other methods under high load conditions, demonstrating its strong advantages in dealing with strict constraints and high-load tasks.

Fig. 9

Throughput of different methods with different average data arrival rates for $N=20$: a ${\lambda }_{i}=2.2$ Mbps/WD; b ${\lambda }_{i}=2.4$ Mbps/WD; c ${\lambda }_{i}=2.6$ Mbps/WD.

Performance of different clustering methods

To investigate the influence of different clustering algorithms on the task unloading decision performance, we employed the K-means clustering⁴³, hierarchical clustering⁴⁴, Gaussian mixture model (GMM)⁴⁵, and MeanShift⁴⁶ algorithms for comparison.

Figure 10 compares the DBSCAN, hierarchical, K-means, GMM, and MeanShift clustering methods. As shown, the GMM method performed well initially; however, over time, it may be affected by the data distribution and lead to a decline in efficiency because GMM may be affected by the data distribution when handling task unloading, resulting in a decrease in efficiency when handling long experiments. In addition, the performance of the hierarchical clustering method was relatively stable during the initial stage of the task unloading task; however, with increased task quantity and complexity, its processing time increases gradually, resulting in a task processing delay. The K-means method appeared to perform well in the medium term; however, it lagged progressively behind the other methods when processing tasks over longer periods, thereby resulting in a faster increase in the length of the data queue. The MeanShift method also performed well in the initial phase; however, when handling large-scale tasks, instability occurred, which resulted in performance degradation. This analysis shows that the performance of the DBSCAN method is improved by 40.02%, 29.41%, 20.49%, and 17.72% compared with the hierarchical, MeanShift, K-means, and GMM methods, respectively.

Fig. 10

Performance comparison of different clustering algorithms for ${\lambda }_{i}=2.6$ and $N=20$.

Comparison of energy consumption

The energy consumption characteristics of different unloading methods were also compared. As shown in Fig. 11a, for $N=10$, the average energy consumption of the DCEDRL method was less than that of the compared methods for ${\lambda }_{i}=2.2$. This is because the DCEDRL method increases the exploration of the environment, which allows it to discover realize better offload decisions. For ${\lambda }_{i}=2.4$, the energy consumption of the DCEDRL method was slightly higher than that of the ENS + DRL method because DBSCAN consumes part of the energy when performing density clustering of tasks. In addition, for ${\lambda }_{i}=2.6$, the energy consumption of DBSCAN was slightly higher than that of the LyDROO method due to the implemented density clustering and ensemble learning techniques. For $N=10$, the average energy consumption of all methods was less than the threshold of 0.08 W, which explains why all methods compared in Figs. 6 and 7a,b maintained a stable queue. These results indicate that the system has sufficient redundancy to handle the current workload, as shown in Fig. 8a.

Fig. 11

Average energy consumption: a N = 10; b N = 20; c N = 30.

As shown in Fig. 11b, for $N=20$ and ${\lambda }_{i}=2.4$, the DCEDRL method exhibits similar average energy consumption values as the LyDROO method. For example, when the data arrival rate was 2.6, the energy consumption approached the threshold of 0.08 W, which explains the difference in the task queue length growth shown in Fig. 7c. In addition, for ${\lambda }_{i}=2.6$, all methods exceeded the energy threshold, with the DCEDRL method exhibiting lower energy consumption than the compared methods. These findings demonstrate that the proposed DCEDRL method fully explored the policy space during the training phase to converge to a better solution. A similar observation is shown in Fig. 8c for a data arrival rate of ${\lambda }_{i}=2.6$.

As shown in Fig. 11c, for $N=30$, ${\lambda }_{i}=2.4$, and ${\lambda }_{i}=2.6$, the proposed DCEDRL achieved lower energy consumption compared to the other methods. This highlights the proposed method’s efficiency in terms of energy consumption due to its comprehensive exploration and optimized offloading decisions.

Time consumption comparison

This section compares the average time taken by different methods to update the policy in each time frame, with results summarized in Table 4. As the number of tasks (N) increases, the time overhead also rises across all methods. The ETHC, DBC + DRL, and LyDROO algorithms exhibit similar time costs, while DCEDRL incurs a higher time overhead due to its integrated learning approach, which actively enhances the exploration of the environment. The DBSCAN density clustering method in DBC + DRL also increases time consumption when processing unknown, randomly arriving data tasks. Similarly, ENS + DRL shows a higher time overhead than LyDROO and ETHC but remains lower than DCEDRL. Although DCERL’s average time consumption is higher than that of all baseline algorithms, as N increases, the baseline algorithms need to make efforts to cope with task backlog, resulting in a significant increase in average time consumption as the data queue grows. In contrast, DCERL can quickly process data, stabilize task queues, and maintain average time consumption at a manageable level.

Table 4 Average time consumption (unit: sec).

In Fig. 12, we can observe the changing trend of the time delay of different methods in completing the task with the data arrival rates. DCEDRL consistently exhibits the lowest latency, regardless of ${\lambda }_{i}=2.2$, 2.4, or 2.6 Mbit/s, indicating high efficiency and stability under different load conditions. In contrast, ENS + DRL is slightly inferior to DCEDRL, but its delay is always maintained at low, showing strong competitiveness. The performance of the two methods is better than that of other methods, especially in the case of increasing the data transmission rate, and can effectively avoid apparent delays in growth. On the other hand, the delay of DBC + DRL and LyDROO under each Lambda value is significantly higher than that of the previous two methods, and gradually increases with the increase of data transmission rate, showing relatively low efficiency under high load conditions. LyDROO, in particular, has a more obvious delay increase, indicating that its adaptability to high loads is not as good as DCEDRL and ENS + DRL. However, ETHC’s performance is the worst. No matter how ${\lambda }_{i}$ changes, its delay is always at the highest level, and its delay increases the most with the increase in data transmission rate, which reflects its low efficiency in task processing, especially in high-load scenarios, which may face performance bottlenecks.

Fig. 12

Average task latency of different methods in completing the task with the data arrival rates.

Rural and Urban settings of MEC

In this section, we extend our model to a real-world mobile edge computing (MEC) environment, where multiple factors such as device density, transmission power, bandwidth availability, and task arrival rate can significantly affect the performance of compute offloads. Specifically, we tested the model in two different scenarios: urban and rural environments, each representing unique resource and infrastructure conditions.

The parameter Settings for these two scenarios, shown in Table 5, reflect their actual characteristics. Urban environments with higher population density and heavy device use have a higher number of users, faster task arrival rates, and better network infrastructure. These conditions make the bandwidth between the user and the server higher, the transmission distance shorter, and the maximum power of data transmission higher. In contrast, rural environments are characterized by low population density, fewer task requests, and underdeveloped network infrastructure, resulting in lower bandwidth and longer transmission distances. The lower maximum transmission power in these Settings also reflects actual power limits in remote areas. These parameter choices reflect the differences between urban and rural environments and their impact on MEC performance.

Table 5 Parameter settings for urban and rural scenarios.

As shown in Fig. 13, the performance comparison between urban and rural scenarios highlights significant differences in average data queue length, system power consumption, and average throughput at different task arrival rates (λ values).

Fig. 13

Performance comparison of urban and rural scenarios under different ${\lambda }_{i}$: a average data queue length; b Energy consumption in MEC systems; c Average throughput.

In Fig. 13a, for all λ values, the average data queue length in the urban scenario is significantly shorter than in the rural scenario. This is due to higher bandwidth in urban environments and shorter transmission distances, allowing data to be processed and offloaded more quickly. Conversely, in rural environments, limited bandwidth and longer distances result in longer queue times, significantly when λ increases. This suggests that rural MEC systems may struggle to handle high task arrival rates efficiently, resulting in higher queue delays.

Figure 13b further highlights the difference in energy consumption between the two scenarios. Due to shorter transmission distances and stronger network infrastructure, urban environments consistently exhibit lower energy consumption. In rural situations, the need for long-distance communication and the limited availability of resources leads to increased energy demand, especially at higher λ values. This highlights the challenge of maintaining energy efficiency in rural MEC systems, where hardware and network limitations exacerbate resource use.

Finally, Fig. 13c shows that average throughput in urban environments is significantly higher than in rural environments. In urban scenarios, larger bandwidth supports more efficient task offloading, resulting in higher throughput even as λ increases. In rural environments, limited bandwidth and increased transmission distances limit throughput, especially at higher task arrival rates. This performance gap underscores the critical role of network infrastructure in determining the efficiency of MEC systems.

These results highlight the adaptability of our model in dealing with different MEC scenarios, providing insights into how to optimize resource allocation and task-offloading strategies for both urban and rural environments. The flexibility of the model allows for robust performance under different real-world MEC conditions, ensuring stable system performance even in challenging network environments.

Conclusion

This paper has proposed the DCEDRL method to compute task offloading decisions in mobile edge networks. The proposed method considers the long-term performance stability of the system while maximizing system performance. By using multiple DNN models for ensemble learning of the prediction results, the proposed DCEDRL method can effectively identify optimal offloading decisions. In addition, the density clustering method enhances the dynamic adaptability of the system such that optimal offloading decisions can be obtained for different network environments. Experimental results demonstrate that the proposed DCEDRL method realized effective offloading decisions under strict environmental constraints and is superior to other algorithms in terms of system performance, stability, and model fitting accuracy.

The proposed DRL method for selecting optimal unloading decisions shows significant potential for further development. However, the current study simplified the experiments by ignoring task upload delays, task computation, result download times, and uncertainties in real-world environments. These factors are crucial in practical applications, as they can significantly impact decision-making and system performance. Therefore, future work will enhance the robustness and practicality of the DRL method by simulating more complex network conditions and introducing random variables to better assess its deployment on real-world devices. Additionally, techniques like model pruning or distributed learning could be explored to optimize computational efficiency, especially considering the reliance on multiple DNNs and ensemble learning, which present opportunities to reduce the computational burden while maintaining or improving system performance.