Quantum implementation of the classical guided image filtering algorithm

Abstract

Image filtering involves the application of window operations that perform valuable functions, such as noise removal, image enhancement, high dynamic range (HDR) compression, and so on. Guided image filtering is a new type of explicit image filter with multiple advantages. It can effectively remove noise while preserving edge details, and can be used in a variety of scenarios. Here, we report a quantum implementation of guided image filtering algorithm, based on the novel enhanced quantum representation (NEQR) model, and the corresponding quantum circuit has been designed. We find that the speed and quality of filtering are improved significantly due to the quantization, and the time complexity is reduced exponentially from $O(2^{2q})$ to $O(q^2)$.

Introduction

Image filtering is widely used in computer vision and image processing to suppress or obtain the corresponding content in an image. Weighted least squares (WLS) filtering, bilateral filtering, and guided image filtering are three edge-preserving filtering algorithms, which can smooth the image while preserving the edge details, and thus have received wide attention¹. The core idea of WLS filtering² is to use the filtered input as guide information and optimize the quadratic function to achieve non-uniform diffusion, similar to anisotropic diffusion³. Bilateral filtering⁴ is an explicit filtering method by weighted averaging adjacent pixels in the filter output, where the weight depends on the intensity in the guidance image. Although bilateral filtering is effective in many cases, it can cause unwanted gradient inversion near the edge^2,5. Guided image filtering is a new type of explicit image filter, which has multiple advantages¹. First, similar to bilateral filtering, it has the smoothing property of preserving edge, but can avoid the phenomenon of gradient inversion and pseudo-edge. Secondly, guided image filtering is not limited to smooth operation, it can also make the filter output more structured and less smooth by guiding the image. Finally, guided image filtering performs well in a variety of applications, including image smoothing/enhancement, high dynamic range (HDR) compression, flash/no-flash imaging, matting/feathering, dehazing and joint upsampling. More importantly, guided image filtering is an efficient algorithm with a complexity of O(N) regardless of filter core size and intensity range, making it wide used in practical applications.

Currently, guided image filtering is still a classical algorithm running on classical computers. Although, it owns an excellent complexity of O(N), but when used for high-quality images, it will lead to sharp increases in computational time and memory usage. If used for real-time processing in digital images, the increases are undoubtedly formidable, like other classical algorithms. Thus, quantum image processing is emerging as an interdisciplinary field, and garnering widespread attention and in-depth exploration^6,7. Because of the parallelism and entanglement inherent in quantum computing, computational speed in quantum image processing can experience an exponential increase compared to classical image processing. Hence, it is very necessary to explore the quantum implementation of the classical guided image filtering algorithm.

Quantum image processing can be divided into three stages: preparation of quantum images, quantum image processing algorithms, and quantum image retrievals.

Quantum image preparation involves representing digital images as quantum image models. There exist various quantum image representation models, such as the qubit lattice representation⁸, the real ket representation⁹, the entangled images representation¹⁰, the flexible representation of quantum image (FRQI)¹¹, the quantum probability image encoding representation (QPIE)¹², the novel enhanced quantum representation (NEQR)¹³, and the novel quantum representation for color quantum image (NCQI)¹⁴, etc. Specially, the NEQR model stores image information in the basic state and encodes grayscale values using individual sequences of qubits. When the image is retrieved, the grayscale values of each pixel can be accurately recovered through measurement. Thus, it is the widely adopted mainstream quantum image representation model in current. In this paper, the NEQR model is used as the quantum image representation model.

A large quantity of quantum image processing algorithms have also emerged, including the geometrical transformation of quantum image^15,16,17,18, the feature extraction of quantum image¹⁹, the quantum image watermarking^{20,21,22,23,24}, the quantum image bilinear interpolation²⁵, the quantum image segmentation^26,27, the quantum image steganography^28,29, the quantum image edge detection^30,31,32, etc^33,34,35. Guided image filtering as one of the three edge-preserving filtering algorithms, has been widely used in classical image processing. In this paper, we combine guided image filtering with quantum image processing based on the NEQR model, and the corresponding quantum circuit has also been designed. We find that the speed and quality of filtering are largely improved, and the time complexity is significantly reduced from $O(2^{2q})$ to $O(q^2)$.

The rest of this work is organized as follows. Section “Classical guided image filtering” introduces the definition and principle derivation of classical guided filtering algorithm. Section “Quantum circuit module design” introduces the quantum circuit design of some operational modules used in this work, and their time complexity analysis. In sections “Quantum guided image filtering algorithm”, “Results”, the circuit design of the quantum guided image filter is described in detail from the design of the submodule, the overall time complexity is analyzed, and the circuit is simulated on a classical computer. In section “Conclusion”, we make a summary of the full work.

Classical guided image filtering

We first define the general linear variables of a filtering process that involves the guidance image G, the input image I, and the output image Q. Both G and I are given in advance according to the application, and they are generally the same, i.e. $G=I$. The main idea of the guided image filtering⁵ is to filter the input image I under the guidance of the guidance image G. In each filter window $\omega _k$ (centered on pixel k), the output image Q is considered as a linear representation of the guidance image based on local linear model:

$$\begin{aligned} Q_i=a_k\cdot G_i+b_k, \quad \forall ~ i\in \omega _k . \end{aligned}$$

(1)

where $a_k, b_k$ are linear coefficients assumed to be constant in $\omega _k$. This local linear model ensures that Q has an edge only if G has an edge, and the gradient of the filter output Q is as consistent as possible with the guidance image G, because $\nabla Q=a\nabla G$. It is understandable that the guided image filter performs low-pass filtering on the filter window $\omega _k$, retains the DC (Direct Current) component $b_k$ of the original window, and introduces the guidance image information through the coefficient $a_k$ to compensate the detail loss.

To determine the linear coefficient $a_k$, $b_k$, we need a constraint from the filter input I. We model the output Q as input I by removing some unwanted noise/texture equal component n in Eq. (2).

$$\begin{aligned} Q_i=I_i-n_i . \end{aligned}$$

(2)

To make the filter output Q roughly consistent with (in the filter window $\omega _k$) the filter input I, there is an optimization objective in Eq. (3).

$$\begin{aligned} min\sum \limits _{i \in \omega _{k}}\left( Q_{i} - I_{i} \right) ^{2} = min\sum \limits _{i \in \omega _{k}}\left( a_{k} \cdot G_{i} + b_{k} - I_{i} \right) ^{2} . \end{aligned}$$

(3)

By importing the regularization parameter $\varepsilon$ to control the size of $a_k$, we get:

$$\begin{aligned} min\sum \limits _{i \in \omega _{k}}\left( Q_{i} - I_{i} \right) ^{2} = min\sum \limits _{i \in \omega _{k}}\left( \left( {a_{k} \cdot G_{i} + b_{k} - I_{i}} \right) ^{2} + \varepsilon \cdot {a_{k}}^{2} \right) . \end{aligned}$$

(4)

Equation (4) is the linear ridge regression model³⁶.

The solution can be obtained easily, it can be described by Eqs. (5, 6).

$$\begin{aligned} a_k&=\frac{\frac{1}{|\omega |}\sum _{i\in \omega _k}G_iI_i-\mu _k{\bar{I}}_k}{\sigma _k^2+\varepsilon }, \end{aligned}$$

(5)

$$\begin{aligned} b_k&={\bar{I}}_k-a_k\mu _k. \end{aligned}$$

(6)

where, $\mu _k$ and $\sigma _k^2$ are the mean and variance of G in $\omega _k$, respectively, $|\omega |$ is the number of pixels in $\omega _k$, and ${\bar{I}}_k=\frac{1}{|\omega |}\sum _{i\in \omega _k}I_i$ is the mean of I in $\omega _k$. Thus, one can represent them as in Eqs. (7, 8).

$$\begin{aligned} a_k&=\frac{{Cov(G,I)}^{\omega _k}}{{Var(G)}^{\omega _k}+\varepsilon }, \end{aligned}$$

(7)

$$\begin{aligned} b_k&={Mean(I)}^{\omega _k}-a_k\cdot {Mean(G)}^{\omega _k}. \end{aligned}$$

(8)

When the $a_k$ and $b_k$ are obtained, one can get the Q according to the local linear model as described in Eq. (1).

The whole process of guided image filtering is shown in Fig. 1. It should be noted that the pixel i does not only appear in one filter window, but also be covered by several different filter windows. Because the $a_k$ and $b_k$ of different filter windows are diverse, any filter window covering pixel i can get a corresponding $Q_i$, so one needs to determine the unique $Q_i$. A simple method is to average the $Q_i$ of all filter windows. Therefore, after calculating the $a_k$, $b_k$ of all filter windows and obtaining the $Q_i$, one determines the filtering output according to Eq. (9).

Fig. 1

The guided image filtering process.

$$\begin{aligned} Q_i=\frac{1}{|\omega |}\sum _{k|i\in \omega _k}(a_kG_i+b_k) . \end{aligned}$$

(9)

Another method is that according to the symmetry of the filter window, the center pixels k of all windows $\omega _k$ covering pixel i are covered by the window $\omega _i$ centered on pixel i, that is, $\sum _{k|i\in \omega _k}a_k=\sum _{k\in \omega _i}a_k$. One can convert the average all $Q_i$ to the average all $a_k$ and $b_k$, and the filter output $Q_i$ can be reexpressed as in Eq. (10).

$$\begin{aligned} Q_i={\bar{a_i}}G_i+{\bar{b_i}} . \end{aligned}$$

(10)

where ${\bar{a}}_i$ and ${\bar{b}}_i$ are the average coefficients of all filter windows covering pixel i, which are given in Eqs. (11, 12).

$$\begin{aligned} {\bar{a}}_i&=\frac{1}{|\omega |}\sum _{k\in \omega _i}{a_k}, \end{aligned}$$

(11)

$$\begin{aligned} {\bar{b}}_i&=\frac{1}{|\omega |}\sum _{k\in \omega _i}{b_k}. \end{aligned}$$

(12)

In the above content, we give the definition, principle and formula derivation of guided image filtering. Next, we determine the edge-preserving filtering characteristics when $G\equiv I$. In this case, according to Eqs. (7, 8), $a_k$ and $b_k$ can be expressed as:

$$\begin{aligned} a_k&=\frac{{Var(I)}^{\omega _k}}{{Var(I)}^{\omega _k}+\varepsilon }, \end{aligned}$$

(13)

$$\begin{aligned} b_k&=(1-a_k){Mean(I)}^{\omega _k}. \end{aligned}$$

(14)

one can see that when $\varepsilon =0$, there $a_k=1$, $b_k=0$, and $Q=I$. When $\varepsilon \ne 0$, we consider two extreme conditions based on the relationship of ${Var(I)}^{\omega _k}$ and $\varepsilon$. In the first case, when the variance within the window $\omega _k$ is high (usually the edge area of the image), ${Var(I)}^{\omega _k}\gg \varepsilon$, we have $a_k\approx 1$, and thus we get $b_k\approx 0$, $Q_i\approx I_i$. The edge information of the image is preserved. In the second case, when the variance in the window $\omega _k$ is low (flat area of the image), ${Var(I)}^{\omega _k}\ll \varepsilon$, we have $a_k\approx 0$ and $b_k\approx {Mean(I)}^{\omega _k}$, the output image is slightly similar to the mean filtering of the guidance image.

Therefore, when the $a_k$ and $b_k$ are averaged to get ${\bar{a_i}}$ and ${\bar{b_i}}$, the final filtering output $Q_i$ is obtained according to Eq. (10). The output of the edge area is unchanged ($Q_i\approx I_i$), but the output of the flat area is equivalent to the mean filtering, $Q_i\approx \frac{1}{|\omega |}\sum _{k\in \omega _i}I_k$. The regularization parameter $\varepsilon$ determines the size of $a_k$ and is the standard to judge the variance. We can adjust the filtering effect by changing the size of the filter window and $\varepsilon$.

Quantum circuit module design

In this section, we introduce a series of specific quantum circuit modules to realize the function of the characteristic and briefly analyze its time complexity, including copy module, left shift/right shift module, ${+}1$/${-}1$ module, inverse number module, adder module, multiplier module, and divider module.

Definition of binary complement

Considering that the image needs to be normalized in the pre-processing stage, the gray value of pixels in the algorithm involves decimals. In order to facilitate calculation, we use binary complement to represent the gray value, which is defined as follows.

Assume that x is an $(n+1)$-bit binary number, it contains 1 sign bit, $x_m$, which 0 means positive and 1 means negative, m integer bits, $x_{m-1}, x_{m-2}, \ldots , x_0$, and $n-m$ fractional bits, $x_{-1}, x_{-2}, \ldots , x_{m-n}$. The complement $[x]_{c}$ of $x=x_m,x_{m-1}\cdots x_0.x_{-1}\cdots x_{m-n}$ can be expressed as³⁷:

$$\begin{aligned} \left. [x]_c=\left\{ \begin{array}{ll}0,x_{m-1}x_{m-2}\cdots x_0.x_{-1}\cdots x_{m-n},& \quad x_m=0,\\ 1,2^m-x_{m-1}x_{m-2}\cdots x_0.x_{-1}\cdots x_{m-n},& \quad x_m=1.\end{array}\right. \right. \end{aligned}$$

(15)

According to the definition of complement in Eq. (15), if we know $[x]_{c}$, we can get the value of x from Eq. (16).

$$\begin{aligned} x=\left\{ \begin{array}{ll}\sum _{k=m-n}^{m-1}x_k2^k,& \quad x_m=0,\\ -2^m+\sum _{k=m-n}^{m-1}x_k2^k,& \quad x_m=1.\end{array}\right. \end{aligned}$$

(16)

The advantage of complement is that subtraction, multiplication and division can be achieved by addition, and sign bit can be directly used as numerical value to participate in the operation, making the operation unified.

Copy module

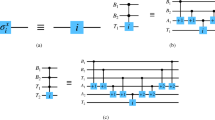
The copy module consists of q controlled-NOT gates, it can copy q-length qubit sequence information to another q-length auxiliary qubit sequence ${|{0}\rangle }^{\otimes \ q}$, the quantum circuit is shown in Fig. 2.

Fig. 2

The quantum circuit of Copy module.

In quantum image processing, the time complexity of a quantum circuit depends mainly on the number of basic quantum gates used in the circuit, and the basic quantum gates include NOT gate, Hadamard gate, controlled-NOT gate, and any $2\times 2$ unitary operator, whose complexity is considered uniform. The time complexity of copy module is only related to the number of controlled-NOT gates, for a replication module consisting of q controlled-NOT gates, the time complexity is O(q).

Left shift and right shift modules

Shift left is a qubit operation that is usually used to move all the bits of a binary number to the left by a specified number of bits. In a binary shift left, each bit is moved to the left, and the least significant bit is filled with zero.

The left shift module achieves shift by using a series of SWAP gates and sets the lowest position to zero by using controlled-NOT gates. Eq. (17) shows the result of the left shift, and the quantum circuit is shown in Fig. 3. Because in the algorithm we increase the numeric bit width to prevent overflow, the left shift module actually implements the binary multiplication operation ‘$\times 2$’ as well.

$$\begin{aligned} x&= x_m,x_{m-1}\cdots x_0.x_{-1}x_{-2}\cdots x_{m-n}\nonumber \\&\quad \rightarrow x_{m-1},x_{m-2}\cdots x_{0}x_{-1}.x_{-2}\cdots x_{m-n}0=x_l=2x . \end{aligned}$$

(17)

Fig. 3

The quantum circuit of Left Shift module.

Similarly, the right shift of binary numbers is to move each bit to the right in turn, and supplement the corresponding value of the signal bit in the most significant bit, so that the $n+1$ qubits of binary complement becomes $n+2$ qubits. Equation (18) shows the result of the right shift of binary complement, and the quantum circuit is shown in Fig. 4, it can also implement binary division operation ‘$\div 2$’.

$$\begin{aligned} x&= x_m,x_{m-1}\cdots x_{1}x_{0}.x_{-1}\cdots x_{m-n}0\nonumber \\&\quad \rightarrow x_m,x_{m}x_{m-1}\cdots x_{1}.x_{0}x_{-1}\cdots x_{m-n}=x_r=\frac{x}{2} . \end{aligned}$$

(18)

Fig. 4

The quantum circuit of Right Shift module.

Since a SWAP gate can be decomposed into 3 controlled-NOT gates, the time complexity of the left shift module is $O(3n+2)\approx O(n)$, and the time complexity of the right shift module is $O(3n+1)\approx O(n)$.

${+}1$ and ${-}1$ modules

These modules are operated on the least significant bit ${+}1$ and ${-}1$. For a binary complement x of $n+1$ qubits, the ${+}1$ module performs $x+2^{m-n}$ and the ${-}1$ module performs $x-2^{m-n}$, the corresponding quantum circuits are shown in Figs. 5 and 6.

Fig. 5

The quantum circuit of ${+}1$ module.

Fig. 6

The quantum circuit of ${-}1$ module.

According to the discussion of the time complexity in¹⁵, the time complexity of both ${+}1$ module and ${-}1$ module do not exceed $O(n^2)$ for an $(n+1)$-length qubit sequence.

Inverse number module

The process of taking the opposite of a binary complement is to first flip the complement value and then ‘${+}1$’ at the least significant bit. The inverse number module implements this operation, and its quantum circuit is shown in the Fig. 7.

Fig. 7

The quantum circuit of Inverse number module.

For a binary complement represented by $n+1$ qubits, the time complexity of inverse number module is $O(n+1+(n+1)^2)\approx O(n^2)$.

Adder module

Islam et al. proposed a reversible full adder based on Peres Gate³⁸. In this subsection, the reversible half adder module, reversible full adder module and adder module are given.

Reversible half adder module

The reversible half adder is used to add two separate qubits $x_i$ and $y_i$, and get a sum bit $s_i$ and a carry bit $c_i$. Its quantum circuit is shown in Fig. 8.

Fig. 8

The quantum circuit of Reversible half adder module.

The matrix v and $v^{+}$ are given in Eq. (19).

$$\begin{aligned} V&= \begin{bmatrix} \frac{1 + i}{2} & \quad \frac{1 - i}{2} \\ \frac{1 - i}{2} & \quad \frac{1 + i}{2} \end{bmatrix},\nonumber \\ V^{+}&= \begin{bmatrix} \frac{1 - i}{2} & \quad \frac{1 + i}{2} \\ \frac{1 + i}{2} & \quad \frac{1 - i}{2} \end{bmatrix}. \end{aligned}$$

(19)

Reversible full adder module

The reversible full adder is used to add two qubits $x_i$ and $y_i$ and a carry bit input $c_{i-1}$ together, get a sum bit $s_i$ and a carry bit output $c_i$. Its quantum circuit is shown in Fig. 9.

Fig. 9

The quantum circuit of Reversible full adder module.

Adder module

The adder module is used to add two qubit sequences together. For two qubit sequences representing $n+1$ bits of binary complement $x=x_m,x_{m-1}\cdots x_0.x_{-1}\cdots x_{m-n}$ and $y=y_m,y_{m-1}\cdots y_0.y_{-1}\cdots y_{m-n}$, the adder consists of a reversible half adder (RHA) and n reversible full adders (RFA). The quantum circuit of adder module is shown in Fig. 10, where the output of the qubit sequence representing x is $x+y$ and the auxiliary qubit ${|{0}\rangle }$ is to store the carry bit. To prevent overflow, $|x|<2^{m-1}$, $|y|<2^{m-1}$.

Fig. 10

The quantum circuit of Adder module.

The reversible half adder module consists of 4 controlled gates, and the reversible full adder module consists of 8 controlled gates. The time complexity of the adder module is $O(8n+4)\approx O(n)$.

Multiplier module

According to the Booth method on complement multiplication in the principle of computer composition³⁹, we give the quantum circuit of multiplier module, as shown in Fig. 11. For the multiplier ${|{x}\rangle }$, ${|{y}\rangle }$ of $n+1$ qubits, we use a sequence of $2n+1$ qubits to store the product ${|{xy}\rangle }$.

Fig. 11

The quantum circuit of Multiplier module.

According to Fig. 11, the multiplier module is composed of $2(n+1)$ adder modules, $2n+1$ inverse number modules and n right shift modules, so its time complexity is $O(2(n+1)n+(2n+1)n^2+n^2)\approx O(n^3)$.

Divider module

We present the divider module according to the complementary division method in the principle of computer composition³⁹. The divider module mainly consists of three modules: preprocess module, decimal divider module and post-process module.

Preprocess module

Because pixel values involve binary integer and decimal, we need to preprocess the dividend $x = x_m,x_{m-1}\cdots x_{0}.x_{-1}\cdots x_{m-n}$ and divisor $y = y_m,y_{m-1}\cdots y_{0}.y_{-1}\cdots y_{m-n}$ to convert them to decimals ${\hat{x}}=2^{p_x}\times x$, ${\hat{y}}=2^{p_y}\times y$, while ensuring that $0.25\le |x|<0.5$, $0.5\le |y|<1$ and $|x|<|y|$ to avoid quotient overflows (${\hat{x}}$ shift one more bit to the right and $p_x$ minus 1). The quantum circuit of preprocess module is shown in Fig. 12, where ${\hat{n}}=[\log _{2}n]$.

Fig. 12

The quantum circuit of Preprocess module.

The preprocess module is composed of inverse number module, left shift module, right shift module and ${+}1/{-}1$ modules, whose time complexity is about $O(n^2)$.

Decimal divider module

The decimal divider module uses addition and subtraction to calculate the division of two binary decimals, its quantum circuit is shown in Fig. 13.

Fig. 13

The quantum circuit of Decimal divider module.

According to Fig. 13, the time complexity of decimal divider module is $O(4(n+1)+2n^2(n+1)+n(n+1)+n^2)\approx O(n^3)$.

Post-process module

After running the division of decimals, the quotient is not the final result. We need to multiply the factors extracted during the preprocessing to the quotient, as given in Eq. (20). The quantum circuit of the designed post-process module is shown in Fig. 14.

$$\begin{aligned} \frac{x}{y}=\frac{{{\hat{x}}}_r}{{\hat{y}}}\times 2^{p_y-p_x+1} . \end{aligned}$$

(20)

Fig. 14

The quantum circuit of Post-process module.

According to Fig. 14, the time complexity of post-process module does not exceed $O(n^3)$.

Divider module

Finally, we combine the above modules to get a divider module that can realize the combination of integer and decimal complement division, the complete divider module is shown in Fig. 15.

Fig. 15

The quantum circuit of Divider module.

In short, the time complexity of divider module is about $O(n^3)$.

Quantum guided image filtering algorithm

In this section, we explain the design flow of quantum guided image filtering algorithm in detail, analyze its time complexity, and finally give the simulation results.

Design of quantum guided image filter

From the introduction of the principle in Section 2, the classical guided image filtering algorithm involves the calculation of mean, variance, $a_k, b_k$ and ${\bar{a_i}}, {\bar{b_i}}$. In this subsection, we design these calculations and present the circuit of quantum guided image filtering algorithm.

Cyclic shift operation

In the implementation of quantum guided image filtering, some operations need to use all the pixels in the filter window. In the quantum guided image filtering algorithm, we can get all the pixels by translation and superposition^30,31. Figure 16 takes a $3\times 3$ filter window image as an example to explain the process of cyclic shift, and Fig. 17 shows the quantum circuit of cyclic shift operation.

Fig. 16

Cyclic shift process of $3\times 3$ filter window image.

Fig. 17

The quantum circuit of Cyclic Shift operation.

Mean calculation

Equation (21) gives the formula for calculating the mean of matrix, we design the mean calculation module by using the adder and multiplier modules, as shown in Fig. 18.

$$\begin{aligned} Mean=\frac{1}{|\omega |}\sum _{i\in \omega _k}C_i . \end{aligned}$$

(21)

Fig. 18

The quantum circuit of Mean calculation operation.

Variance calculation

Equation (22) shows the calculation formula of matrix variance. According to Eq. (22), we need to design the square module first, and the quantum circuit is shown in Fig. 19. Then, we use the mean calculation operation, adder module, square module, inverse number module and so on to achieve the operation of variance calculation, the quantum circuit of variance calculation operation is shown in Fig. 20.

$$\begin{aligned} Var=\frac{1}{|\omega |}\sum _{i\in \omega _k}(C_i-Mean)^2 . \end{aligned}$$

(22)

Fig. 19

The quantum circuit of Square module.

Fig. 20

The quantum circuit of Variance calculation operation.

$a_k$ calculation

Assuming that the guidance image is the input image itself, i.e., $G=I$. According to Eq. (13), we use the above modules to design the $a_k$ calculation operation, and the quantum circuit is shown in Fig. 21.

Fig. 21

The quantum circuit of $a_k$ calculation operation.

$b_k$ calculation

After calculating $a_k$, we can follow Eq. (14) to design the quantum circuit for calculating $b_k$, as shown in Fig. 22.

Fig. 22

The quantum circuit of $b_k$ calculation operation.

${\bar{a_i}}, {\bar{b_i}}$ calculation

Due to the fact that different filter windows can cover the same pixel, there exist multiple sets of coefficients $a_k$ and $b_k$. In order to determine the unique parameters $a_i$ and $b_i$, we calculate the means of these $a_k$, $b_k$ based on the symmetry of the filter windows, and obtain the values of ${\bar{a_i}}$ and ${\bar{b_i}}$, which are given in Eqs. (11, 12). We use the method of cyclic shift again to design the quantum circuit, which is shown in Fig. 23.

Fig. 23

The quantum circuit of ${\bar{a_i}}$ and ${\bar{b_i}}$ calculation operation.

Quantum circuit of guided image filtering algorithm

In summary, the overall framework of the quantum circuit of guided image filtering algorithm proposed in this paper is shown in Fig. 24, including cyclic shift operation, calculation of $a_k$, calculation of $b_k$, calculation of ${\bar{a_i}}$ and ${\bar{b_i}}$, and finally the output image.

Fig. 24

The quantum circuit of guided image filtering algorithm.

Analysis of time complexity

Next, we take a $2^q\times 2^q$ gray-scale quantum image represented by $2q+n+1$ qubits as an example, start with the complexity analysis of each sub-module, and gradually get the complexity of the entire guided image filtering circuit. Among them, 2q qubits represent the position of pixel, and $n+1$ qubits represent the binary complement of pixel’s gray value.

• According to Fig. 17, for a $3\times 3$ filter window, the cyclic shift operation contains 10 ${+}1/{-}1$ modules and 8 copy modules, its time complexity is $O(10q^2+8(n+1))\approx O(q^2+n)$.

• From Fig. 18, the mean calculation operator consists of 8 adder modules and a multiplier module, whose time complexity is $O(8n+n^3)\approx O(n^3)$.

• As can be seen from Fig. 20, the variance calculation operator uses a series of adder modules, copy modules, square modules, etc., and its time complexity is about $O(n^3)$.

• The $a_k$ operator is composed of a variance calculation operator, an adder module and a divider module, its time complexity is $O(n^3+n+n^3)\approx O(n^3)$.

• After calculating $a_k$, the $b_k$ operator is designed according to Eqs. (13, 14) using a copy module, an inverse number module, an adder module and a multiplier module, whose time complexity is $O(n^3)$.

• Figure 23 shows that the quantum circuit for calculating ${\bar{a_i}}, {\bar{b_i}}$ contains ${+}1/{-}1$ module, adder module and multiplier module, so its time complexity does not exceed $O(q^2+n^3)$.

In summary, the complexity of quantum guided image filter designed in this paper is

$$\begin{aligned} O((q^2+n)+n^3+n^3+(q^2+n^3)+n^3+n)\approx O(q^2+n^3) . \end{aligned}$$

(23)

As can be seen, the most time-consuming sub-modules are the cyclic shift module and the ${\bar{a_i}}, {\bar{b_i}}$ calculation module. Among these modules, the ${+}1/{-}1$ modules play a decisive role. Because there are a large number of controlled-NOT gates in the ${+}1/{-}1$ modules, they have a high time complexity, which in turn leads to time-consuming submodules. Here, we can consider replacing this modules with other modules with the same function to further reduce the time complexity. For example, we can use an adder instead of ${+}1/{-}1$ modules to achieve the same function, reducing the operation time by increasing qubits, exchanging space for time.

For a large image, $n\ll q$, the complexity of quantum guided image filter is actually about $O(q^2)$. Compared with the classical guided image filter whose time complexity is $O(2^{2q})$, the quantum guided image filter achieves exponential acceleration.

Results

Due to the limited prevalence of quantum computer, we conduct simulation of the quantum guided image filtering algorithm on classical computer (simulation experiments are based on array computation packages NumPy and python³³). We selected a set of grayscale images with size of $512\times 512$ and color depth of 8 (as shown in Fig. 25) for testing, when the guidance image is the input image itself, the experimental results of different parameters of test image (a) are shown in Fig. 26.

Fig. 25

Test images. (a) Dog. (b) Castle. (c) Stone. (d) Lighthouse.

Fig. 26

Simulation results of different parameters in quantum guided image filter. (a) Test results of quantum guided image filter. (b) The PSNR of output images. (c) The SSIM of output images.

It can be seen that the edge-preserving filtering effect of quantum guided image filter is obvious, and it is determined by the filter window size and regularization parameter $\varepsilon$.

The analysis of this result is:

Since the regularization parameter $\varepsilon$ controls the size of $a_k$, $\varepsilon$ determines the smoothness of guided image filter to the original image. As $\varepsilon$ increases, $a_k=\frac{{Var(G)}^{\omega _k}}{{Var(G)}^{\omega _k}+\varepsilon }$ will gradually decrease and $b_k=(1-a_k){Mean(G)}^{\omega _k}$ will increase, that is to say, the closer it is to the mean filtering of I in the filter window $\omega _k$, the smoother it will be, while the easier to lose details. The filter size determines the neighborhood range that the guided image filter takes into account when filtering. Larger filter size can capture a larger range of structural information, but can lead to excessive smoothing. Smaller filter size allows for better detail retention, but may be sensitive to noise. Therefore, we need to constantly adjust the regularization parameter $\varepsilon$ and filter size to get the best results.

We performed the same experiment using classical guided image filtering and compared the filter details of the edge region of the two filters, the results are shown in Figs. 27, 28. It can be seen from the comparison that although both classical guided image filtering and quantum guided image filtering can retain edge information while smoothing the image, the filtering efficiency of quantum algorithm has been improved exponentially compared with that of classical algorithm. Meanwhile, the peak signal-to-noise ratio (PSNR) and structural similarity (SSIM) of quantum algorithm are slightly better than those of classical algorithm. In fact, we pay more attention to the exponential acceleration of filtering speed based on quantum superposition and entanglement characteristics.

Fig. 27

Simulation results of different parameters in classical guided image filter. (a) Test results of classical guided image filter. (b) The PSNR of output images. (c) The SSIM of output images.

Fig. 28

Comparison of the filtering effects for two filters. (a) Edge details. (b) Classical guided image filtering. (c) Quantum guided image filtering.

Then we simulate quantum Gaussian filtering, quantum mean filtering and quantum guided image filtering respectively, and select the edge parts for comparison, the results are shown in Fig. 29. Although the time complexity of these algorithms is roughly the same, in terms of filtering effect and scalability, the quantum guided image filtering algorithm can achieve better edge preserving filtering effect for different types of images, and its excellent robustness and generalization capabilities make it a broad application prospect.

Fig. 29

Comparison of the filtering effects for three filters. (a) Test images and edge details. (b) Quantum Gaussian filtering. (c) Quantum mean filtering. (d) Quantum guided image filtering.

It is worth discussing that, as can be seen from the circuit in Fig. 24, the proposed algorithm requires the use of a large number of qubits. Although our current quantum computers are good enough to implement this algorithm, there are still problems with processing images of larger sizes or higher dimensions due to the limitations of finite qubit counting and gate fidelity. In the future, we also need to optimize the qubit of the quantum guided image filtering algorithm and find simpler quantum circuit modules to replace them, so that the circuit can be simplified and show better performance on existing quantum computers.

Conclusion

In this paper, we propose a quantum guided image filtering algorithm. Firstly, we give a series of quantum circuit modules for operation, then we design the circuit of quantum guided image filter based on the novel enhanced quantum representation (NEQR) model, and analyze the overall time complexity of the algorithm. For an image whose size is $2^q\times 2^q$ and the binary complement of gray value is represented by $n+1$ qubits, the time complexity of quantum guided image filtering algorithm is $O(q^2)$, which basically achieves exponential acceleration compared with the time complexity $O(2^{2q})$ of classical guided image filtering algorithm. Finally, we simulate on the classical computer, and find that the edge-preserving filtering effect of quantum guided image filtering algorithm is more significant than that of other quantum filtering algorithms.