Introduction

Floods are one of the most common and severe natural hazards worldwide, resulting in one-fifth of losses in the whole disaster. Floods have a significant effect on the economy and society, including health, safety, and the environment1,2. Over the previous 20 years, the overall cost of damages associated with natural hazards has exceeded USD 2,440 billion, with water contributing approximately 74% of the total. Floods and storms are estimated to have caused 69% of financial losses, affecting over three billion people3,4. Furthermore, climate change may lead to more catastrophic floods, posing significant risks to society and infrastructure in the future5,6,7. Changes in temperature and precipitation can affect flood characteristics and impact different water resource sections, including reservoirs, flood protection, among others8,9. Numerous research has demonstrated that climate change can cause extreme hydrological events to occur more frequently and severely in the future10,11. Hence, it is important to analyze the flood characteristics and flood frequency based on climate change models and scenarios to provide effective management strategies for the future12. In general, the return period, or the mean recurrence interval of events that are at least as extreme as a given threshold, is computed by frequency analysis. In many situations, including the design and planning of structures and infrastructure, the traditional univariate flood frequency analyses might be insufficient because flood is a multidimensional phenomenon. Univariate frequency analysis is insufficient for fully assessing the flood as it ignores the interdependence of each event’s characteristics while the method of multivariate analysis, takes into account multiple factors, leading to a more comprehensive insight into flood behavior13,14. In a multivariate analysis, there exists a cross-dependence among the variables, as well as a sequential interdependence among the observations. So when considering all variables, the probability of the joint return period of multivariate analyses would be different than univariate ones. Multiple studies advocated the adoption of the multivariate flood frequency analysis instead of the univariate framework, particularly for a more accurate risk assessment15,16. To characterize flood events, it is important to investigate the interaction between two or more flood characteristics using a compound framework17,18,19,20. In recent decades, copula-based methods have gained popularity in assessing multivariate flood frequency analysis21. These methods offer a flexible approach to modeling the relationship between random variables without restrictions on marginal distributions22. By utilizing a variety of copula functions, different dependence structures between hydrologic variables can be captured23,24. This method enables the assessment of the combined dependent variables, allowing for a more robust assessment of flood event probabilities. For this purpose, it is essential to consider the key aspects of floods, including flood peak, flood volume, and flood duration, and their relationships25,26,27.

The three main copula families are Marshall-Olkin copulas, Elliptical copulas, and Archimedean copulas. The Archimedean copulas are commonly applied in hydrological cases and are specified regarding simple mathematical formulations which make them easy to implement and interpret28,29The hierarchical Archimedean copula is a specific type of copula which indicates that the copulas are organized like a tree with branches and each level of the hierarchy shows a different relationship between variables. In other words, in a hierarchical Archimedean copula, dependency is organized hierarchically, with stronger dependencies in lower branches, which may be more appropriate for complex datasets with hierarchical dependencies30,31,32. This class of copula can be categorized as symmetric or asymmetric according to their characteristics. Symmetric copulas make modeling simpler by assuming symmetry in the dependence structure. This implies that the strength and interdependence of variables remain constant regardless of whether the “first” or “second” variable is considered. Asymmetric copulas provide greater modeling flexibility by supporting alternative dependence structures for the lower and upper tails of the joint distribution. This is especially beneficial when the data contains signs of asymmetry, which symmetric copulas may not capture. Homogeneous and heterogeneous hierarchical Archimedean copulas are another category of Archimedean copulas that are employed in the modeling of multivariate dependence. Homogeneous asymmetric copulas assume that all variables or dimensions follow a similar Archimedean copula function. This indicates that the dependency between variables is constant across all dimensions. Such copulas are appropriate when there is consistency in the interdependence patterns across variables. On the other hand, Heterogeneous asymmetric copulas assume that different variables or dimensions follow a different copula function. These copulas offer the flexibility to capture varying degrees of asymmetry across different parts of the distribution3,33,34,35,36.

Over the past decades, only a few studies have investigated the changes in flood frequency under climate change. Most of these studies have focused on univariate and bivariate flood frequency analysis. Jeong et al.37 assessed the effects of climate change on three aspects of flooding: flood peak, volume, and duration. This assessment was conducted using a bivariate copula-based framework and focused on 21 basins in Canada. The results of projected changes generally point to future increases in the joint occurrence probabilities P1 (the probability of any one characteristic in a pair exceeding its threshold) and P2 (the probability of both characteristics in a pair exceeding their respective thresholds at the same time), as well as the marginal values, or return levels of flood characteristics. Duan et al.38 assessed the changes in flood frequency in the Huai River basin under various climate change scenarios, including A2, A1B, and B1, utilizing bivariate copula functions. The analysis of univariate and bivariate return periods demonstrates that flood characteristics are sensitive to various General Circulation Models (GCMs) and emission scenarios. Yin et al.12 assessed the implications of two climate change models on bivariate joint return periods of flood peak and volume. The results demonstrated that flood frequency may increase considerably under the RCP8.5 scenario, especially for the higher return periods. Goodarzi et al.39examined the impact of climate change on flood peak and volume variables in the Azarshahr Chay watershed. The Gumbel-Hougaard copula function was used to analyze bivariate joint return periods using the CanESM2 climate change model under three Representative Concentration Pathways (RCPs) for both the baseline (1976–2005) and the future (2030–2059) periods. The results indicate that the joint return periods of severe floods will decrease in the future, particularly under the RCP8.5 scenario. Manekar and Ramadas40 conducted a bivariate copula-based flood frequency analysis to evaluate the impact of climate change models (BCC-CSM2-MR, MPI-ESM1-2-HR) under SSP5-8.5 scenario on flood characteristics in baseline and future periods in eastern India. The results indicate that flood occurrences are expected to intensify in the near future. Specifically, the flood peak value is projected to increase by over 90%, but the length is anticipated to decrease. Also, the flood volume is expected to double in the future, which highlights the importance of preventive mitigation and decreasing the flood risk in the watershed.

This study aims to apply a trivariate copula-based framework to analyze the flood frequency based on two emission scenarios using eight General Circulation Models (GCMs) in three time horizons, including the historical period (1980–2012), the mid-term future (2040–2070), and the far future (2070–2100) considering various types of hierarchical Archimedean copula structures. In this study, Random Forest (RF) was utilized as the machine learning model for flood forecasting using precipitation, maximum, and minimum temperature as predictors. Flood projection was performed by driving the ML model using gridded observations and downscaled and bias-adjusted GCMs based on two climate change scenarios, including shared socio-economic pathways (SSP2-4.5 and SSP5-8.5) in three time horizons. Then, the flood characteristics, including volume, duration, and flood peak, were extracted based on the annual maximum series (AMS) approach. The correlation of three flood characteristics was evident in the data series for projected historical and future flood events and strengthened the necessity of trivariate flood frequency analysis. To analyze trivariate flood frequency, the hierarchical Archimedean copula framework was used in three structures including symmetric, heterogeneous asymmetric, and homogeneous asymmetric copula. For this, the best-fitted marginal distributions of flood volume, duration, and peak are selected for each model. Then, various copula structures were utilized to obtain the best-fitted trivariate copula for estimating the joint return periods in the conjunction case (a flood occurs only when all variables simultaneously surpass their thresholds) and disjunction case (a flood occurs only when at least one variable continues to be greater than the threshold). In addition to symmetric and homogeneous asymmetric structures, a new innovative Archimedean copula structure in heterogeneous asymmetric form has been used in this study. In the review of previous flood studies using the copula theory, it was found that such a structure is yet to be explored in hydrologic applications. By using this approach, it can be ensured that the correlation structure in the upper and lower tail dependency of each combination of variables in the copula structure is modeled appropriately.

Finally, to decrease the uncertainty of the climate change model’s projections, the ensemble results of joint return periods of all models were obtained. This study addresses the following objectives:

  • Assessing the multivariate behavior of flood characteristics and flood frequency analysis under different climate change models and scenarios in historical, mid-term future, and far future periods.

  • Performance evaluation of different structures of hierarchical Archimedean copulas, including symmetric, heterogeneous asymmetric, and homogeneous asymmetric copula.

Materials and methods

Case study

The suggested framework is applied to the Kan River basin (N35° 46′ − 35° 58′, E51° − 10–51° 23′) in Iran as a case study which experienced catastrophic flood events in the past. Figure 1shows the case study’s location and the basin’s climograph. This case study is located upstream of Tehran city (Iran’s capital) which is recognized as a crucial basin for flood management. Floods occur frequently in this area, causing significant destruction and losses throughout the historical periods because of lots of tourist and recreational centers near the main river. For example, on July 28, 2022, a devastating flood disaster occurred in this area. At least twenty-three individuals lost their lives in this flood, which was caused by precipitation with an average intensity of 79 mm/h for twenty minutes, or about 26 mm66. While there has been a noticeable increase in the frequency of floods over the past few decades in this basin, studies on the multivariate flood frequency analysis under climate change are lacking. It is critical to analyze flood frequency under climate change scenarios in this area to consider as a future mitigation implementation guideline. Table 1 provides the basic details of meteorological and hydrometric stations in the Kan River basin.

Fig. 1
figure 1

The case study’s location, the climograph, and the hydrometric and meteorological stations.

Full size image
Table 1 Information on meteorological and hydrometric stations in the Kan River basin.
Full size table

Methodology

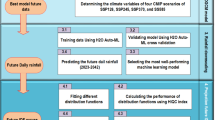
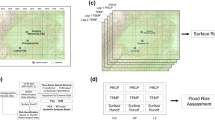
The methodological flowchart of this study is shown in Fig. 2, which consists of four major sections. The climate change projection section provides future climate scenarios based on downscaled and bias-adjusted precipitation, minimum and maximum temperatures of eight GCMs. Then Random Forest, as a machine learning approach, simulates the streamflow for three time horizons, including the historical (1980–2012), the mid-term future (2040–2070), and the far future (2070–2100) periods. Subsequently, flood characteristics, including volume, duration, and peak of the floods, are extracted based on the annual maximum series for each time frame. Finally, the trivariate copula-based flood frequency analysis projections compare the far future, mid-term future, and historical periods in conjunction and disjunction cases. The details are discussed in the following sub-sections.

Climate change datasets

Coupled Model Intercomparison Project Phase 6 (CMIP6) presents scenarios as the Shared Socioeconomic Pathways (SSPs) that illustrate possible societal development for attaining the target of radiative forcing by the end of the century. SSP1-1.9 represents the most optimistic scenario to provide a radiative forcing of 1.9 W/m2by 2100. SSP1-2.6 promotes growing sustainability by global emissions reduction to reach net zero after 2050. SSP2-4.5 proposes a scenario with emissions remaining at present levels until mid-century, but do not reach a state of net zero by 2100. SSP3-7.0 envisions a scenario in which countries become more competitive and emissions continue to rise, almost doubling from present levels by 2100. Eventually, SSP5-8.5 visualizes a future centered on accelerated exploitation of fossil fuel resources and shows the worst scenario for the future41,42.

Fig. 2
figure 2

The conceptual model schematic of the research.

Full size image

The scenario-based approach is utilized to describe the possible range of climatic futures and demonstrate the consequences of various pathways. In this study, we consider precipitation, minimum, and maximum temperature from eight climate change models based on two scenarios, including SSP2-4.5 and SSP5-8.5 in three-time horizons, including 1982–2012 as the baseline, 2040–2070 as the mid-term future, and 2070–2100 as the far future. The list of climate change models is shown in Table 2. All GCMs are downscaled and bias corrected based on gridded observations at 0.125° resolution using an empirical statistical method, namely multivariate bias correction based on N-dimensional probability density function transform (MBCn). The performance of this method for bias correction of precipitation is presented in Table 3.

Table 2 A. List of downscaled and bias-adjusted GCMs used in this study, sourced from Western University’s HydroClimEX Lab.
Full size table
Table 3 B. Performance of bias-adjusted GCMs used in this study.
Full size table

Streamflow simulation

Streamflow simulation and projection are crucial steps for flood frequency analysis. They obtain projections based on different climate change models and scenarios in which flood characteristics can be extracted. Flood forecasting models are classified into two types: hydrological models, also known as knowledge-based models and data-driven models43,44. Following Khajehali et al.45, we used random forest (RF) as a flood forecasting model that showed high performance in simulating daily streamflow in the Kan River basin. This machine-learning model was originally introduced by46and since that time, this model has been used in many hydrological applications. The combination technique of binary classification or regression trees is one of the capabilities of this model. RF is based on decision trees, which, for regression purposes, each tree predicts independently, then the response is defined as the mean of all decision tree predictions47,48,49,50. In this study, a series of daily meteorological and hydrological data from 2000 to 2020 were utilized for the model’s calibration (training) and validation (test). Two meteorological factors that have a significant impact on streamflow are temperature and precipitation. For this reason, daily precipitation and maximum and minimum temperatures with lags are chosen as predictors for daily streamflow simulation models in four sub-basins. The common practice to split all data into 70% for training and 30% for testing is applied in this step. This research utilized the CMIP6 database consisting of eight GCMs under two scenarios, including SSP2-4.5 and SSP5-8.5 to drive the ML model and project streamflow for historical and future periods.

Flood characteristics

The initial steps in flood frequency analysis include identifying flood events, separating flood events of baseflow, and identifying flood characteristics, such as the dates when the flood starts and ends, the flood duration, volume, and the maximum discharge. To do this, we employed the annual maximum series (AMS) approach for flood sampling. This technique selects the flood event in a specific period (one year) with the greatest peak of the flood. This approach enables the calculation of return periods for different flood magnitudes, allowing stakeholders to understand the likelihood of certain flood events occurring within a specific timeframe. We utilized the SFE_IFC toolbox in MATLAB51, which is based on the master recession curve (MRC) that aims to capture the general pattern of how water levels decline after peak flow and determine flood characteristics. This approach explains the relationship between discharge-storage in watersheds with various functional models like linear, power function, and so on. This method is a graphical representation of the discharge-storage relationship in watersheds utilized for hydrograph separation. This approach aims to mitigate the problem of unpredictability related to individual recession periods by extracting numerous curves across longer periods of time. The MRC was calculated using the matching strip approach, a graphical technique that involves overlapping curves to construct a single recession curve for a long data series by adjusting and combining separate recessions52,53. Baseflow separation is also essential in hydrology for distinguishing between baseflow (slow, sustained flow from groundwater) and surface runoff (rapid flow from precipitation or other surface sources) in a hydrograph. During the annual dry season, baseflow constitutes the entirety of the streamflow discharge. Current methodologies define the discharge’s static mean value during a single year’s dry season as deep baseflow. The deep baseflow can be calculated from the daily streamflow data by averaging the minimum of a 60-day moving window throughout an annual period52,54.

Flood frequency framework

Framework of Copula

According to Sklar (1959) it is possible to uniquely decompose any continuous d-variate distribution function H into its copula and its continuous univariate margins F1, …, Fd, as shown in Eq. 155.

$$H(x_1,\cdots,x_d )=C( F_1 (x_1),\cdots,F_d (x_d) ),\quad( x_1,\cdots, x_d )^T\in R^d$$
(1)

In this equation, H, C, xi, Fi(xi), are the joint cumulative distribution, copula function, random variable, and the cumulative distribution function of the ithvariable, respectively56. One advantage of this approach is that it enables the investigation of multivariate distribution functions with different marginal distributions, which is highly relevant in the context of statistical applications. The three main copula families are Marshall-Olkin copulas, Elliptical copulas, and Archimedean copulas, which are the most popular in hydrological studies. The most important advantage is the capacity to identify diverse forms of tail dependencies, including dependency solely on the upper tail without any dependence on the lower tail, or dependencies on both the lower and upper tails57,58. Table 4displays the copula list utilized in this study. The initial five families represent the well-known Ali-Mikhail-Haq, Frank, Clayton, Joe, and Gumbel families. The remaining four families are specific instances of the BB1 (12 and 14) and BB2 (19 and 20) families. These families were selected because not all families can be hierarchically nested to achieve an appropriate hierarchical Archimedean copula structure59,60. One of the requirements for modeling asymmetric structures is the Sufficient Nesting Condition (SNC). This condition states that the family fitted to the combination of variables in asymmetric copula structures must have the condition of θi ≤ θj and any combination of variables must also have the condition of τi ≤ τj, in which θ is the copula parameter and τ is the correlation coefficient corresponding to the variable’s combinations, and i and jare the upper and lower branch’s counter in the copula structure, respectively56. To fulfill the mentioned condition, the asymmetric heterogeneous copula structure can only be used by combining the following families.

  • Clayton families and families 12, 14, 19, and 20 in the form of C12141920.

  • Ali-Mikael-Haq and Clayton families and 19 and 20 families in the form of AC1920.

It should be mentioned that the Ali-Mikhail-Haq and Frank families cannot model the correlation between the variables of the upper and lower tail dependency. The 19, 20, and Clayton families can only model correlation in the lower tail dependency, and Gumbel and Joe’s families only can model correlation in the upper tail dependency. In addition, families 12 and 14 can model correlation in both lower and upper tail dependency60. Figure 3 shows three hierarchical Archimedean copula structures that were used in this study, including symmetric, heterogeneous asymmetric copula, and homogeneous asymmetric copula for three variables. The bivariate CDFs of copulas are summarized in Table 4 In this table, u and v are the cumulative distribution function of each variable and θ is the copula parameter.

Based on the Bayesian information criterion61, Akaike information criterion62, Root Mean Square Error (RMSE), and Nash–Sutcliffe Efficiency (NSE), the best-fitted copula is selected for the flood frequency analysis. The BIC and AIC criteria penalize complexity based on the number of parameters and quantify goodness-of-fit. Both BIC and AIC aim to make a trade-off between the complexity of a model and its goodness of fit. The main difference between BIC and AIC relates to the penalty terms that they use for model complexity. BIC tends to penalize complex models more severely than AIC, which can lead to a more conservative model selection63. The model with the highest value of NSE and lowest value of RMSE, AIC, BIC, or a combination of these criteria is selected as the optimal model. These criteria are expressed as follows:

$$RMSE=\:{\left(\frac{\text{1}}{\text{n}}{\sum\:}_{\text{i=1}}^{\text{n}}{\left({\text{c}}_{\text{p}}\left(\text{i}\right)\text{-}{\text{c}}_{\text{e}}\left(\text{i}\right)\right)}^{\text{2}}\right)}^{\text{0.5}}$$
(2)
$$AIC=N\,ln\,(MSE)+2k$$
(3)
$$BIC=N\,ln\,(MSE)+2k\,ln(n)$$
(4)
$$NSE= 1- \frac{\sum_1^n(c_p(i)-c_e(i))^{2}}{\sum_1^n(c_p(i)-\overline{c}_e)^{2}}$$
(5)

Where cp and ce are parametrical and empirical copula, N is the number of observations, the MSE stands for mean square error, or the squared value of RMSE, and k is the number of parameters.

Table 4 List of copula functions.
Full size table
Fig. 3
figure 3

Three structures of hierarchical Archimedean copulas (a) Symmetric, (b) Heterogeneous asymmetric copula, and (c) Homogeneous asymmetric copula for three variables.

Full size image
Joint return period

The average time between occurrences of events at or above a certain intensity, based on probability, rather than an actual measure of consecutive time intervals between events, such as floods, is referred to as the return period. The copula-based framework of flood characteristics for determining their joint return periods can be utilized to figure out critical information that is essential for flood management. This approach offers quantitative insights into the statistical relationships among multiple variables. Based on the copula theory, given d continuous dependent variables represented as x1, x2, …, xd, each with cumulative distribution functions F1, F2, ., Fd, the joint cumulative distribution function for these variables can be expressed by copula as Eq. 160. Based on this approach, a multivariate joint return period can be defined in several ways, including (a) the “AND” scenario, in which every variable exceeds an extreme threshold, (b) the “OR” scenario, in which only one of the variables exceeds the threshold64,65. The “AND” and “OR” trivariate joint return periods, assuming a stationary assumption, are expressed as follows based on the copula theory:

$$\:{\text{T}}_{\text{DVQ}}^{\text{AND}}=\:\frac{\text{1}}{{\text{P}}_{\text{DVQ}}^{\text{AND}}}$$
(6)

\(\:{\text{P}}_{\text{DVQ}}^{\text{AND}}\)= 1- Fd (D) - Fv (V) - Fp (P)+C (Fv (V), Fd (D)) +C (Fd (D), Fp (P)) + C (Fv (V), Fp (P))- C(Fv (V), Fd (D), Fp (P))

$$\:{\text{T}}_{\text{DVQ}}^{\text{OR}}\:=\:\frac{\text{1}}{\text{1-}\text{C}\text{(}{\text{F}}_{\text{d}}\:\left(\text{D}\right)\text{,}{\text{F}}_{\text{v}}\left(\text{V}\right)\text{,}{\text{F}}_{\text{q}}\left(\text{Q}\right)\text{)}}$$
(7)

It is evident that the conjunction case (AND) is more stringent than the disjunction case (OR) because all variables must surpass their respective thresholds; consequently, greater time is expected for the joint return periods in the conjunction than in the disjunction case.

Results and discussion

Projections of flood characteristics using a random forest model and climate change scenarios

In the flood projection step, a Random Forest model was developed utilizing historical data for daily flood simulation. The RMSE, R2, RSR and NSE criteria were used to evaluate discharge simulations. The performance of the model based on these criteria is displayed in Table 5 for each station.

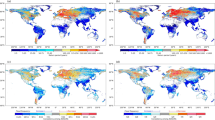
Table 5 Performance of Random Forest model in each station.
Full size table

After calibration and validation, this model was used to project daily streamflow in each hydrometric station for three-time horizons, incorporating bias-adjusted climate change data (precipitation, minimum, and maximum temperature) as the model’s inputs. The output of the model consists of daily streamflow for historical, mid-term future, and far future periods. We evaluated the impact of these three parameters on streamflow and analyzed how their changes under climate change would change streamflow response. As previously mentioned, each water year’s daily flow hydrograph is utilized to determine the features of the floods. For this purpose, a peak flood is selected based on the annual maximum series approach each year. In this way, 48 series of flood characteristics (duration, volume, and peak) were determined for each hydrometric station based on three-time horizons and eight climate change models under two scenarios. The results show that each flood characteristic will change differently under various climate change models and different climate change scenarios. Figure 4 shows the mean of annual flood peak, volume, and duration of eight GCM for historical, mid-term, and far future under SSP2-4.5 and SSP5-8.5 as boxplots in the basin’s outlet. A comparison of the results of three time horizons shows that all flood characteristics in the future are expected to increase relative to the historical period. In addition, according to the figure, climate change models show a range of possibilities for the duration, volume, and peak of discharge. Due to this uncertainty, it is necessary to utilize a combined approach for flood frequency analysis after using copulas.

Fig. 4
figure 4

Mean of annual flood peak, volume, and duration of eight GCMs for historical, mid-term future, and far future under SSP2-4.5 and SSP5-8.5 in the basin’s outlet [Color printing].

Full size image

In the next step, it is necessary to evaluate the dependency between flood characteristics in each time series of data. The Kendall correlation coefficients were calculated to assess the relationship between the flood’s duration, volume, and peak in baseline and future periods. The mean of this coefficient based on all climate models is displayed in Table 6 for the outlet of the basin. Kendall’s tau (τ) is the popular nonparametric criterion of correlation for random variables and the dependence measure range of this coefficient is between − 1 and 1. As shown in the table, the correlation between duration, volume, and peak of the flood for historical and future periods is obvious and supports the need for trivariate flood frequency analysis. Moreover, compared to the correlations between flood peak and volume or duration and flood peak, the correlation between duration and flood volume is more robust. The comparison of tail dependency of Soleghan station in three time horizons based on the first GCM and scenario SSP2-4.5 is shown in Fig. 5. The results show in the context of climate change models and climate emission scenarios, the behavior of these characteristics and their dependencies may evolve over time. Given these considerations, we propose that utilizing asymmetric heterogeneous copula is advantageous, as it allows for the integration of different functions at various levels within the copula structure. This approach is particularly beneficial in situations where dependencies fluctuate in response to changing climatic conditions. For example, the upper tail dependency between duration and peak of the flood is more rubust in the far future rather than in the mid-term future and historical and this behavior is completely reverse in lower tail dependency.

Table 6 Kendall’s tau (τ) between flood variables in three-time horizons.
Full size table
Fig. 5
figure 5

Comparison of tail dependency of Soleghan station in three time horizons based on first GCM and scenario SSP2-4.5.

Full size image

Fitting trivariate hierarchical archimedean copula model

After determining volume, duration, and flood peak, ten marginal distributions, including gamma, weibull, lognormal, logistic, log-logistic, generalized pareto, normal, extreme value, generalized extreme value, and exponential were used to describe these flood characteristics in each time horizon. Anderson-darling (AD), Kolmogorov-Smirnov (K-S), and Chi-squared tests were calculated to test the validation of each marginal distribution, and AIC was used to select the best-fitted marginal distribution for each variable in three-time horizons based on two scenarios of eight climate change models. Since the main objective of this study was to model trivariate copula-based flood frequency, three introduced copula structures were calculated for each climate change model and scenario in three-time horizons and four subbasins. After assessing each copula’s performance according to the criteria including BIC, AIC, NSE, RMSE, and Maximum Likelihood, the best-fitted copula function and structure were finally selected. Table 7 indicates the best trivariate fitted copula and goodness test results for Soleghan station in different time horizons and climate change models. As previously indicated, estimation accuracy increases with decreasing AIC, BIC, and RMSE, while model accuracy increases with increasing NSE and Maximum Likelihood criteria. After evaluating the efficacy of various copula functions and structures in fitting marginal distributions, it was shown that the optimal trivariate copula for the relationship between volume, flood peak, and duration varies depending on the climate models and scenarios. Figure 6 illustrates the performance of three copula structures used in this study. When evaluating hierarchical Archimedean copulas, it has been found that heterogeneous asymmetric copulas perform better than homogeneous asymmetric and symmetric copulas in most cases. Heterogeneous asymmetric copula offers the flexibility to capture varying degrees of asymmetry across different parts of the distribution, leading to more accurate modeling results compared to homogeneous asymmetric and symmetric copulas. The asymmetric copulas allow for different dependence levels in the lower and upper tails of the distribution, capturing asymmetry in tail dependency. Additionally, heterogeneous asymmetric copulas, specifically, offer even more flexibility by allowing for different forms of asymmetry in different parts of the distribution. This improved our data series of flood characteristics of different climate change models and scenarios following complex dependence structures.

Fig. 6
figure 6

Comparison of the best-fitted copula structure in each subbasin [Color printing].

Full size image
Table 7 Best trivariate fitted copula and goodness test results for Soleghan station.
Full size table

Trivariate joint return periods in conjunction and disjunction cases

Once the fittest copula structure was selected based on the goodness-of-fit criteria, trivariate joint return periods were derived in conjunction and disjunction cases. Figure 7 presents the outcomes of trivariate joint return periods in these cases in four sub-basins. The conjunction case offers valuable insights into how these joint return periods change over time under climate change and differ across regions. In comparison to the mid-term future and historical periods, there is a noticeable decrease in the joint return periods in the far future for each of the four sub-basins. The results show that the differences in the results become more noticeable as the threshold for analysis rises. In particular, the differences between historical, far future, and mid-term future outcomes are minimal when a lower threshold is used. But when the threshold is raised, the differences in the outcomes become more noticeable and pronounced. Moreover, the disjunction case shows minimal differences between the historical period, mid-term future, and far future when trivariate joint return periods are analyzed. Across all climate change scenarios and sub-basins, the historical period results remain relatively consistent and applicable in disjunction cases for both the mid-term and far future.

Fig. 7
figure 7

Trivariate joint return period in conjunction and disjunction cases in which T_DVQ_2 indicates trivariate joint return period of duration, volume, and flood peak for the threshold of 2 years univariate return period, T_DVQ_5 indicates trivariate joint return period of duration, volume, and flood peak for the threshold of 5 years univariate return period, and T_DVQ_10 indicates trivariate joint return period of duration, volume, and flood peak for the threshold of 10 years univariate return period [Color printing].

Full size image

In the situation of disjunction, when considering the “OR” scenario, there appears to be no notable distinction between historical and future climate change scenarios where at least one of the three variables must exceed the threshold. However, when considering the conjunction situation, the scenario when the “AND” condition is met, the differences between historical and future scenarios are more considerable. In the case of disjunction, a flood occurs if at least one of the three variables exceeds the threshold. Therefore, if climate change causes alterations in one or two variables, as long as at least one variable continues to be greater than the threshold, the outcome will stay in the historical period. However, in the case of conjunction, a flood occurs only when all three variables simultaneously surpass their thresholds. In this scenario, the effects of climate change on one or more variables can have a heightened influence since all factors must surpass their thresholds for a flood to transpire. Even small changes in a single variable can significantly impact the outcomes, resulting in more pronounced differences between past and future scenarios. Figure 8 demonstrates the outcomes of bivariate joint return periods in conjunction and disjunction cases in four sub-basins for duration-volume, duration-peak, and volume-peak. The results indicate that in the Keshar and Kiga sub-basin, bivariate flood frequency analysis based on duration and volume shows more noticeable changes when comparing the historical, mid-term future, and far future. The statement highlights that in this specific sub-basin, the volume and duration play a more significant role in flood frequency changes compared to other regions. Conversely, in Soleghan and Rendan stations, where flood peaks are more significant, the analysis highlights the importance of duration-peak and volume-peak. This explains that in these sub-basins, the changes in flood frequency are more dependent on changes in flood peak when comparing three-time horizons. Also, in bivariate joint return periods of disjunction cases, the difference between historical, mid-term future, and far future is negligible as the results of trivariate joint return periods.

Fig. 8
figure 8

Bivariate joint return period in conjunction cases (left side) and disjunction cases (right side) [Color printing].

Full size image

Conclusions

The occurrence of floods in recent decades has resulted in significant human and financial casualties, as well as irreparable destruction. Since the flood includes multiple characteristics that are regarded as influential variables, including flood peak, flood volume, and flood duration, applying a univariate flood frequency analysis can lead to certain inaccuracies. As a result, trivariate flood frequency analysis ought to be contemplated as a technique for comprehensively characterizing flood events and their occurrence probabilities. Also, because of nonstationary flood characteristics under climate change, flood frequency analysis based on historical data can’t be considered an accurate analysis. So, in this study, copula-based trivariate frequency analyses are used to assess the effects of climate change on flood frequency for a flood exposure basin over three-time horizons, covering the historical (1982–2012), mid-term future (2040–2070), and far future (2070–2100) years. The need for trivariate flood frequency analysis is supported by the correlation of the three flood characteristics (duration, volume, and flood peak), which is evident in the data series from both historical and projected future flood events. For this purpose, the hierarchical Archimedean copula framework was used in three structures, including symmetric, heterogeneous asymmetric, and homogeneous asymmetric copula and the best-fitted copula functions and structure are used to derive the trivariate flood frequency analysis under various JRP levels for historical and future periods in conjunction and disjunction cases. The accomplishments of this study are outlined here:

  • The correlation between volume, duration, and peak of the flood for historical and future periods was obvious and supported the need for trivariate flood frequency analysis. Furthermore, the nonstationary flood characteristics under climate change supported the need for flood frequency analysis based on various climate change models on different time horizons.

  • The use of new heterogeneous asymmetric copula structures for trivariate flood frequency analysis is considered superior to other copula structures, including homogeneous asymmetric and symmetric ones. Using these new copula structures ensures effective modeling of both upper and lower tail dependencies in the joint structure and mitigates uncertainty in flood frequency analysis. The advantage of modeling with these structures is considering different copula families that have different features of correlation modeling in the lower or upper tail dependency. It can be ensured that they can model the various correlation behaviors in each branch accurately. In other words, heterogeneous asymmetric copula offers the flexibility to capture varying degrees of asymmetry across different parts of the distribution, leading to more accurate modeling results compared to symmetric and homogeneous asymmetric copulas.

  • In the comparison between the results of the trivariate joint return periods in conjunction case based on the copula theory, it was found that the return period in this case compared to the univariate or bivariate joint return periods may lead to higher results. Additionally, comparison results based on three-time frames under climate change show that flood frequency is expected to increase in the far future compared to the mid-term future and historical period which proves the nonstationary of flood characteristics in the future.

  • The findings of this study, like those of prior studies, validate the severity of climate change as a pressing concern. It is crucial to acknowledge that these results depict possible futures based on the ensemble outcomes of eight climate change models that have their roots in varying assumptions. The actual projection will be influenced by a range of factors, such as societal reactions to climate change and localized factors like topography, geography, and land use, which impact floods in specific regions. Regional differences in precipitation, temperature, and land use changes are expected to have an impact on changes in flood patterns. Increased precipitation in certain regions may cause floods to occur more frequently or to be more severe, while differences in patterns of snowmelt may increase the risk of flooding in other areas.