Double diffusive MHD stagnation point flow of second grade fluid in non-Darcy porous media under radiation effects

Abstract

Non-Newtonian fluids are also widely used in a variety of scientific, engineering, and industrial domains, including the petroleum sector and polymer technologies. They are vital in the development of drag-reducing agents, damping and braking systems, food manufacturing, personal protective equipment, and the printing industry. Fluid movement and transport via porous materials draw a lot of attention; they are important in science and technology. Porous media appear in a variety of high-speed phenomena and devices, including catalytic converters, condensers, and gas turbines. Due to above physical significance, the influence of solar radiation and Lorentz forces on the behavior of non-Newtonian second-grade fluids in a Darcy-Forchheimer porous medium at a stagnation point is tackled in this study on both assisting and opposing flow regimes. A study on thermal diffusion or the Soret effect and diffusion-thermo or the Dufour effects are included in the research. Mathematical models are developed for the current situation and translated into a set of ordinary differential equations that are solved using MATLAB’s bvp4c. The data reveal that raising the second-grade fluid reduces the velocity profile while increasing the temperature and concentration profiles in both assisting and opposing flows. In both flowing regimes, increasing the porous medium parameter increases velocity while decreasing temperature. The descending trends in the velocity profiles with respect to the Forchheimer and Prandtl numbers occurs for both assisting and opposing flows. The assisting flow shows higher profiles, values compared to the opposing flow. Results show that increasing second- grade fluid parameter causes the increase in skin friction, Nusselt number and Sherwood number. The results of the current modeled problems are compared with already published results and it has been concluded that there is sufficient agreement between both of them, indicating the validity and accuracy of the present results.

Introduction

Non-Newtonian fluids that obey the viscosity law are classified into three categories: integral, differential, and rate-dependent. Aside from the differences, the differential variation defines a sub-model, such as viscoelastic second-grade fluids. Unlike Newton liquids, such fluids have a stress–strain tensor with just two derivative options, whereas Newtonian liquids have only one. Differential fluids of this sort are utilized in a range of applications, including aerospace, fiber and wire technology, food processing, and chemical synthesis. In particular, in engineering and manufacturing, they help in processing polymers, forming artificial film, extruding polymers, and making glass fibers, paper making, producing foods, condensation processes, and growing crystals. In addition, the joint account of heat and mass transfer plays an essential role in many processes since it is crucial, for instance, for cooling electronic devices and systems, air conditioning, desalination, heat transfer in humans and biological tissues, refrigeration in nuclear plants, power generation, preventing crop freezing, and various food processing operations. Therefore, the processes, theoretical foundations, and practical applications of flow generals of non-Newtonian second-grade fluids are of great interest to scientists and engineers interested in the optimal operation of important technological processes.

Hayat et al.¹ used a second-grade fluid model to analyze convective heat transmission at the stagnation point past a vertical plate. They employed homotopy analysis to solve the governing model. The results concluded that the opposed flow zone was produced in the opposing flow region by using a Newtonian scenario, which resulted in dual solutions. Balci et al.² addressed viscoelastic second-grade fluid and concluded that it is easy to apply in numerical simulation, which gave an advantage in accuracy and stability. Majeed et al.³ performed an investigation on ferromagnetic viscoelastic fluid flow past the stretching surface and encountered magnetic dipole and suction effects in their study. In this study, it was predicted that profiles of pressure and skin friction rise by mounting ferromagnetic parameters. Malaspinas et al.⁴ focused attention on the simulation of the viscoelastic fluid model by the Boltzmann method. Basically, their study, it was a new methodology suitable for the solution of non-trivial viscoelastic fluid flow. An analysis of a viscoelastic fluid model on an extending sheet was carried out by Prasad et al.⁵. It had been perceived that magnetic parameters and variable viscosity influences were considered. Abbas et al.⁶ addressed the mechanisms of heat and mass transfer with the impact of magnetic field past the inclined porous plate in the using the second-grade viscoelastic fluid model quidded with nanofluid filled in porous media. Nanomaterial flow and heat transportation in Walter-B fluid around a disk is examined by Shao et al.⁷. In this study, the influences of slip conditions, solar rays, energy source/sink, Joule heating, homogenous and heterogeneous were considered too. Tani and Roux⁸ determined the numerical solutions of the second-grade fluid flow under general Naiver slip conditions in Holder space. Baranovskii⁹ disclosed the study of found the numerical solutions for the regularized second-grade fluid under non-linear slip conditions. Baranovskii¹⁰ put forth the idea of weakly solvable equations for second-grade fluid steady-state flows. Ragupathi et al.¹¹ carried out the investigations on the mechanism of second grade fluid with nanofluif model. They took into account the effects of second-order slip, thermal jump, and magnetic field past the stretching sheet.

In many scientific and technical domains, fluid flow and transport processes through porous structures are of tremendous interest. In particular, fluid flow through porous media in the high-velocity regime becomes relevant in engineering applications like catalytic converters. Gaining a thorough grasp of non-isothermal flow and associated heat-transfer processes is essential for applications involving heating, cooling, and high-velocity flow. Porous media possess enormous practical applications in science, industry sector, and engineering. Due to its significance, the research community has paid attention to problems that are dealt with in porous media. Porous media consists of interconnected voids and a solid matrix. Porosity is defined as the ratio between volume of pores in the representative elementary volume and the volume of the representative elementary volume. The intrinsic permeability of a porous medium represents its ability to allow the fluid to flow through. It is a macro-scale property.

A French scientist Henry Darcy, performed an experiment on steady and one directional flow in his research work focusing on hydrological systems for water supply in the city of Dijon in a uniform sand column¹². Muskat¹³ discussed in detail the hydrodynamics flow process of fluids using porous medium inclusion in his study. He argued that this porosity effects can be considered even the slow motion of the fluid. Muskat¹⁴ proposed the analysis on flow of homogenous fluid through the porous medium. Teng and Zhao¹⁵ extended the work of Darcy’s law to the phenomena of non-Stokes flow in porous media. Forchheimer¹⁶ examined the fluid flow mechanism in porous media in high velocity regime. Ergun and Orning¹⁷ performed the investigations on fluid flow process through the packed beds saturated fluids. Ahmad and Pop¹⁸ focused on the research of convection via nanofluid past a normal surface implanted in porous space. Abbas et al.¹⁹ attended to non-Newtonian third-grade fluid under magnetic parameters and chemical reaction effects in Darcy-Forchheimer theory under porosity effects. Abbas et al.²⁰ discussed the effect of dissipating magnetohydrodynamics on the flow of third-grade fluid through a sheet that stretches exponentially in Darcy-Forchheimer porous media under Ohmic heating.

The diffusion-thermo effect (Dufour effect) is heat transfer caused by a concentration gradient. On the other hand, the thermal diffusion (Soret) effect refers to mass transfer caused by a temperature differential. These issues have piqued the interest of scholars due to their vast use in various fields of science. Kafousesias and Williams²¹ disclosed Soret and Dufour convective heat and mass transportation on vertical under viscosity that is temperature dependent. In²² Soret and Dufour heat transfer through three-dimensional flows with transpiration, solar rays, and magnetic force were disclosed. Axially symmetric fluid flow and Soret and Dufour heat transfer were studied by Hayat and his research fellows²³. The process of fluid flow and Sore tans Dufour heat transfer between two expanding and contracting walls was examined by Srinivas et al.²⁴. Afify²⁵ accomplished the research work on Soret and Dufour heat transfer in magnetohydrodynamic fluid flow under transpiration control along an extending surface. Seddeek²⁶ explored Soret and Dufour heat transfer under viscosity-dependent temperature, solar rays, and transpiration control along the extending surface. Eldabe et al.²⁷ focused on Soret and Dufour bio heat transportation in Eyring-Powell nanofluid fluid flow under solar radiation control.

Numerous academics are interested in heat transportation in stagnation points because of its significance in technical and industrial sectors. It includes material casting, cooling systems, ice chiller, glass blowing, air conditioning systems, etc. The mixed convection stagnation-point flow of an incompressible non-Newtonian fluid over a stretching sheet under convective boundary conditions is studied by Ishak et al.²⁸. The steady stagnation point flow towards a permeable vertical surface is investigated by Ishak et al.²⁹. Yolk et al.³⁰ investigated the unstable mixed convection boundary-layer flow of a micropolar fluid approaching its stagnation point on a double-infinite vertical flat plate. Roşca et al.³¹ examined the steady mixed convection stagnation point flow via a vertical flat plate with a second order slip when the plate is kept at a varied heat flux. Naganthran et al.³² investigated the behavior of steady mixed convection flow approaching a stagnation point along a permeable vertical stretching/shrinking flat plate in a Powell-Eyring fluid.

According to the literature review, many studies have been conducted on non-Newtonian fluids in porous mediums, as well as other distinct fluid features, due to various applications in science, engineering, and industry. However, to the best of our knowledge, no attempt has been made to examine heat and mass transfer in second-grade fluid along the vertical surface with stagnation point in Darcy-Forchheimer porous medium with solar radiation. Furthermore, the current analysis incorporates magnetohydrodynamics and thermal-diffusion (Soret effect) and diffusion-thermo (Dufour effect) phenomena that aid and oppose flow regimes. In the current investigation, the surface is fixed immobile in a Darcy-Forchheimer porous medium and maintained at a constant temperature in the flow of a viscous, incompressible fluid. The proposed problem is given a mathematical shape and then solved using the suitable numerical approach to obtain graphical and tabular representations of the numerical results. The following sections focus on the modeling, methodology, and discussion of the results using physical reasoning.

The mathematical modeling presented in this study addresses critical engineering applications where the control of heat and mass transfer in complex fluid systems is essential. Non-Newtonian viscoelastic fluids, such as the second-grade fluid analyzed here, are commonly used in industries including polymer manufacturing, chemical processing, and thermal management systems due to their unique flow characteristics and stress responses. By considering MHD effects, Darcy-Forchheimer porous media, and radiative and thermal diffusion phenomena, this study models conditions found in catalytic converters, cooling systems, and other high-performance thermal applications. The inclusion of both assisting and opposing flow regimes, along with Soret and Dufour effects, extends the model’s relevance to real-world scenarios, where fine control of thermal and concentration gradients can optimize efficiency and safety in industrial processes. This mathematical framework thus not only advances theoretical understanding but also offers a foundation for practical applications in engineering fields that rely on efficient thermal-fluid management.

Statement of the problem

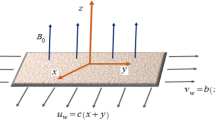
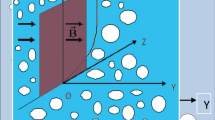
In this study, we explore the behavior of non-Newtonian second-grade fluid flow in the presence of various physical phenomena, including magnetohydrodynamics (MHD), radiation, and the Soret and Dufour effects, within a porous medium governed by Darcy-Forchheimer principles. The problem is formulated to model the dynamics of such fluids under two distinct flow regimes—assisting and opposing flows—around a stagnation point on a vertical surface. This setup is relevant for applications in engineering and industrial processes, where control over heat and mass transfer in complex fluid systems is crucial. We outline the assumptions, boundary conditions, and mathematical expressions that form the foundation of the present model, translating these complex interactions into a solvable framework of ordinary differential equations. By constructing a model that captures these multifaceted interactions, this section sets the groundwork for understanding the combined effects of thermal, solutal, and magnetic forces on non-Newtonian fluid behavior in porous structures.

The following assumptions and characteristics are considered in the current problem:

• Fluid is a viscous, incompressible, and second-grade non-Newtonian.

• Fluid flow is two-dimensional in stagnation point on the vertical surface.

• Buoyancy-driven flow is considered.

• The Darcy-Forchheimer porous medium is considered.

• Solar radiation effects are considered to give optically dense gray fluid.

• The magnetohydrodynamics effects with magnetic field of strength $B_{o}$ applied to the normal direction of fluid flow are assumed.

• The thermal-diffusion (Soret effect) and diffusion-thermo(Dufour effect) are accomplish.

• Two types of flow regimes named as assisting flow and opposing flow regimes are incorporated.

• The stagnation point flow is considered.

• The vertical surface with stagnation point is kep at constant temperature $T_{w} \left( x \right)$ with $T_{w} \left( x \right)$>$T_{\infty } \left( x \right)$.

• The mass concentration at the surface is $C_{W} \left( x \right)$ with $C_{w} \left( x \right)$>$C_{\infty } \left( x \right)$.

• Here, free stream temperature $T_{\infty }$ and free stream concentration $C_{\infty }$, are assumed.

• The vertical surface is immersed in fluid that has free stream velocity $U_{\infty }$ at a large distance from plate.

• Flow structure is given in Fig. 1.

Fig. 1

Flow configuration.

The constitutive expressions in a second-grade fluid are

$${\mathbf{T}} = - {\text{p}}{\mathbf{I}} +\upmu {\mathbf{A}}_{1} + \upalpha _{1} {\mathbf{A}}_{2} + \upalpha _{2} {\mathbf{A}}_{1}^{2} ,$$

(1)

$${\mathbf{A}}_{1} = \left( {\nabla {\mathbf{V}}} \right) + \left( {\nabla {\mathbf{V}}} \right)^{{\text{T}}},$$

(2)

$${\mathbf{A}}_{2} = \frac{{{\text{d}}{\mathbf{A}}_{1} }}{{{\text{dt}}}} + {\mathbf{A}}_{1} \left( {\nabla {\mathbf{V}}} \right) + \left( {\nabla {\mathbf{V}}} \right)^{{\text{T}}} {\mathbf{A}}_{1}.$$

(3)

where ${\text{p}}$ is pressure, ${\mathbf{V}}$ is velocity vector field, $\nabla$ is gradient operator, and ${\mathbf{I}}$ is unit tensor. The symbols ${\varvec{\mu}}$ is dynamic viscosity, $\upalpha _{1}$ is viscoelasticity, and $\frac{{\text{d}}}{{{\text{dt}}}}$ is material derivative. Moreover, $\mu , \alpha_{1} , \alpha_{2}$ satisfies the following condition;

$$\mu \ge 0, \alpha_{1} \ge 0, \alpha_{1} + \alpha_{2} = 0,$$

(4)

Following¹ the flow equations are as below:

$$\frac{\partial u}{{\partial x}} + \frac{\partial \nu }{{\partial y}} = 0,$$

(5)

$$u\frac{\partial u}{{\partial x}} + v\frac{\partial u}{{\partial y}} = U_{\infty } \frac{{dU_{\infty } }}{dx} + \nu \frac{{\partial^{2} u}}{{\partial y^{2} }} + k_{o} \left( {u\frac{{\partial^{3} u}}{{\partial x\partial y^{2} }} + \frac{\partial u}{{\partial x}}\frac{{\partial^{2} u}}{{\partial y^{2} }} + \frac{\partial u}{{\partial y}}\frac{{\partial^{2} v}}{{\partial y^{2} }} + \nu \frac{{\partial^{3} u}}{{\partial y^{3} }}} \right) \pm g\beta_{T} \left( {T - T_{\infty } } \right) \pm g\beta_{C} \left( {C - C_{\infty } } \right) - \frac{{\sigma B_{0}^{2} }}{\rho }u - \frac{\nu }{{K_{o} }}\left( {u - U_{\infty } } \right) - F_{1} \left( {u - U_{\infty } } \right)^{2},$$

(6)

$$u\frac{\partial T}{{\partial x}} + v\frac{\partial T}{{\partial y}} = \frac{k}{{\rho C_{P} }}\frac{{\partial^{2} T}}{{\partial y^{2} }} - \frac{1}{{\rho C_{P} }}\frac{{\partial q_{r} }}{\partial y} + \frac{{D_{m} k_{T} }}{{C_{s} C_{p} }}\frac{{\partial^{2} C}}{{\partial y^{2} }},$$

(7)

$$u\frac{\partial C}{{\partial x}} + v\frac{\partial C}{{\partial y}} = D_{m} \frac{{\partial^{2} C}}{{\partial y^{2} }} + \frac{{D_{m} k_{T} }}{{T_{m} }}\frac{{\partial^{2} T}}{{\partial y^{2} }}.$$

(8)

Boundary conditions:

$$\left. {\begin{array}{*{20}c} {u = 0 , v = 0 ,T = T_{w} \left( x \right), C = C_{w} \left( x \right) at y = 0,} \\ {u \to U_{\infty } \left( x \right)_{ , } \frac{\partial u}{{\partial y}} \to 0 , T \to T_{\infty } ,C \to C_{\infty } as y \to \infty .} \\ \end{array} } \right\}$$

(9)

Here, $x$ and $y$ horizontal and normal Cartesian coordinates, respectively. Here, along $x$ and $y$ axes, components of velocity are the $u$ and $v$, respectively. The notations g,$\nu ,k_{0}$, and $\alpha_{m} = \frac{k}{{\rho C_{P} }}$ are the gravitational acceleration, kinematic viscosity, relaxation parameter and thermal diffusivity, respectively. Where $T$ and $C$ are temperature and concentration, respectively. The symbols $T_{\infty }$ and $C_{\infty }$ are free stream temperature and concentration respectively. The representations $T_{m} , D_{m}$,$\beta_{C}$,and $k_{T}$ are mean fluid temperature, mass diffusivity, concentration expansion coefficient, and thermal diffusion ratio, respectively. Parameters $F_{1} = \frac{{C_{E} }}{{\sqrt {K_{o} } }}$,$\beta_{T} , K_{o} , C_{s} ,C_{p} , B_{o} ,\sigma$ are coefficient of inertia with $C_{E}$ the drag coefficient/ Ergun constant, thermal expansion coefficient, permeability of porous medium, concentration susceptibility, specific heat at constant pressure, magnetic field strength, and electrical conductivity, respectively. Moreover, $+$ sign with buoyancy term in Eq. (14) corresponds to assisting flow and $-$ sign with buoyancy term in Eq. (14) corresponds to opposing flow. Here, $U_{\infty } \left( x \right) = ax$, with $a$ is positive constant. It has been assumed that there is linear variation in $T_{w} \left( x \right)$ and $C_{w} \left( x \right)$ with coordinate $x$.It is assumed that $T_{W} \left( x \right) = T_{\infty } + bx$, and $C_{W} \left( x \right) = C_{\infty } + cx$ with $b$ and $c$ are positive constants.

In the light of Roseland approximation, the radiative heat flux $q_{r}$ is given below:

$$q_{r} = - \frac{{4\sigma^{*} }}{{3{\text{K}}^{*} }}\frac{{\partial T^{4} }}{\partial y},$$

(10)

where, ${\text{K}}^{*}$ is mean absorption coefficient, and $\sigma^{*}$ Stefan-Boltzmann constant is represented. Using Taylor series ${\text{T}}^{4}$ has the following form:

$${\text{T}}^{4} \approx 4{\text{T}}_{\infty }^{3} {\text{T}} - 3{\text{T}}_{\infty }^{4} .{ }$$

(11)

Neglecting the higher terms in Eq. (11), the radiative heat flux in Eq. (10) takes the following form:

$$q_{r} = - \frac{{16T_{\infty }^{3} \sigma^{*} }}{{3K^{*} }}\frac{\partial T}{{\partial y}}.$$

(12)

Solution methodology

This section is fully confined to the methodology that is adopted for the simulation of the current model. In this section detail the procedure of the conversion of the partial differential equations to ordinary differential equations with the help of an appropriate similarity variables transformation. Then the further this obtained set of ordinary differential equations are solved with suitable solutions technique. In the following subsections, the whole procedure is explained.

Similarity transformation

Exact solution of coupled and non-linear partial differential equations is difficult directly by solving them. Therefore, for the approximate solutions are computed and so the equations (Eqs. (5–8) with boundary condition given in Eq. (9) are converted to ODEs using the following variables shown in Eq. (13). These variables are used by¹ for a similar solution.

$$\eta = \sqrt {\frac{a}{\nu }} y,u = axf^{\prime}\left( \eta \right),v = - \sqrt {a\nu } f\left( \eta \right),\theta \left( \eta \right) = \frac{{T - T_{w} }}{{T_{w} - T_{\infty } }},\phi \left( \eta \right) = \frac{{C - C_{\infty } }}{{C_{w} - C_{\infty } }}$$

(13)

Using Eq. (13) into Eq. (5), then the equation of continuity is satisfied automatically. Using variables given in Eq. (13) into Eqs. (6–8) with boundary condition given in Eq. (9) the following form of equations are obtained.

$$f^{{\prime \prime \prime }} + ff^{{\prime \prime }} - f^{{\prime 2}} + 1 - K\left( {f^{{\prime \prime 2}} {\text{ }} - 2f^{\prime } f^{{\prime \prime \prime }} + ff^{{\prime \prime \prime \prime }} } \right) \pm \lambda _{T} \theta \left( \eta \right) \pm \lambda _{C} \phi \left( \eta \right) - M\left( {f^{\prime } - 1} \right) - K_{1} f^{\prime } - F\left( {f^{\prime } - 1} \right)^{2} = 0$$

(14)

$$f^{\prime}\theta - f\theta^{\prime} - \frac{\theta ^{\prime\prime}}{{Pr}}\left[ {1 + \frac{4}{3}Rd} \right] = Du\phi^{\prime\prime}\left( \eta \right)$$

(15)

$$f^{\prime}\phi - f\phi^{\prime} - \frac{1}{{S_{C} }}\phi^{^{\prime\prime}} = Sr\theta ^{\prime\prime}\left( \eta \right)$$

(16)

Subject to the flow conditions.

$f = 0,f^{\prime} = 0 , \theta = 1, \phi = 1$ at $\eta = 0$

$$f^{\prime} \to 1,f^{\prime\prime} \to 0 , \theta \to 0, \phi \to 0\quad {\text{as}}\;\eta \to \infty$$

(17)

where, ${\text{K}} = \frac{{k_{0} a}}{\rho }$, ${\text{Pr}} = \frac{\upsilon }{\alpha }$, ${\text{Du}} = \frac{{D_{m} k_{T} \left( {C_{w} - C_{\infty } } \right)}}{{C_{s} C_{p} \nu \left( {T_{w} - T_{\infty } } \right)}},{\uplambda }_{{\text{T}}} = \frac{{Gr_{T} }}{{Re_{x}^{2} }}$, ${\uplambda }_{{\text{C}}} = \frac{{Gr_{C} }}{{Re_{x}^{2} }}$, M $= \sigma B_{o}^{2} a/\rho$,${\text{K}}_{1} = \frac{\nu a}{{K_{o} U_{o} }}, {\text{F}} = \frac{{C_{E} x}}{{\sqrt {K_{o} } }}$, ${\text{Sr}} = \frac{{D_{m} k_{T} \left( {T_{w} - T_{\infty } } \right)}}{{T_{m} \nu \left( {C_{w} - C_{\infty } } \right)}},{\text{Rd}} = \frac{{4 T_{\infty }^{3} \sigma^{*} }}{{\rho C_{P} 3{\text{kK}}^{*} }}$, ${\text{Sc}} = \frac{\upsilon }{{D_{m} }}$, ${\text{Gr}}_{{\text{T}}} = g\beta_{T} \Delta Tx^{3} /\nu^{2}$,${\text{Gr}}_{{\text{C}}} = g\beta_{T} \Delta Cx^{3} /\nu^{2}$, ${\text{Re}} = U_{\infty } x/\nu$ are second grade fluid parameter, Prandtl number, Dufour number, mixed convection parameter, the modified mixed convection, magnetic field parameter, porosity parameter, the inertia coefficient, Soret number, radiation parameter, Schmidt number, Grashof number, modified Grashof number, and Reynolds number, respectively. The prime notation denotes the differentiation w.r.t $\eta$.

Physical quantities of interest are skin friction coefficient, Nusselt number and Sherwood number, respectively. These quantities are given in¹.where

$${\text{C}}_{{\text{f}}} = \frac{{\tau_{w} }}{{\rho U_{w}^{2} }}$$

$$\tau_{w} = \mu \left( {\frac{\partial u}{{\partial y}}} \right)_{y = 0}$$

(18)

$${\text{Nu}} = \frac{{q_{w} x}}{{k\left( {T - T_{\infty } } \right)}} + x\left( {q_{r} } \right)_{y = 0},$$

Where

$$q_{w} = - k\left( {\frac{\partial T}{{\partial y}}} \right)_{y = 0}.$$

(19)

$${\text{Sh}} = \frac{{q_{m} x}}{{D_{m} \left( {C - C_{\infty } } \right)}},$$

Where

$$q_{m} = - D_{m} \left( {\frac{\partial C}{{\partial y}}} \right)_{y = 0}$$

(20)

Using similarity variables given in Eq. (13), into Eqs. (18–20), the following transformed form is obtained:

$$\sqrt {{\text{Re}}_{{\text{L}}} } {\text{C}}_{{\text{f}}} = f^{\prime\prime}\left( 0 \right)$$

(21)

$$Re_{L}^{{ - \frac{1}{2}}} Nu_{x} = - \left( {1 + \frac{4}{3}Rd} \right)\theta^{\prime}\left( 0 \right).$$

(22)

$$Re_{L}^{{ - \frac{1}{2}}} Sh_{x} = - \phi ^{\prime}\left( 0 \right).$$

(23)

The solution technique utilized to solve the above mentions equations is elaborated in the next sections. The results will be computed and discussed in later sections.

Solution technique

The numerical outcomes are obtained by solving the Eqs. (14–16) with boundary conditions given in (17). Numerical solutions Eqs. Equations (14–16) are also given in tabular forms. A numerical simulation is performed by means of solver bvp4c. In simulation of numerical solutions $\eta_{\infty } = 8$ and bvp4c is based on finite difference method that uses three-stage Lobatoo formula. The continuous solutions decided the mesh selection and error control. In this technique of collocation mesh interval is divide the interval into subintervals. The initial mesh and initial approximation are provided to the mesh points for final solution of the equations. Equations (14–16) subject to the boundary conditions (17) are in higher order, so firstly they are converted to set of first order differential equations. Equations are as follow:

$$f = \Gamma \left( 1 \right), f^{\prime} = \Gamma \left( 2 \right),f^{\prime\prime} = \Gamma \left( 3 \right), f^{\prime\prime\prime} = \Gamma \left( 4 \right),\theta = \Gamma \left( 5 \right), \theta^{\prime} = \Gamma \left( 6 \right), \phi = \Gamma \left( 7 \right),\phi^{\prime} = \Gamma \left( 8 \right)$$

(24)

$$f^{{\left( {iv} \right)}} = \Gamma \Gamma 1 = \frac{1}{K*\Gamma \left( 1 \right)}(\Gamma \left( 4 \right) + \Gamma \left( 1 \right)*\Gamma \left( 3 \right) - \Gamma \left( 2 \right)^{2} + 1 - K\left( {\Gamma \left( 3 \right)^{2} - 2*\Gamma \left( 2 \right)*\Gamma \left( 4 \right)} \right) \pm \lambda_{T} \Gamma \left( 5 \right), \pm \lambda_{C} \Gamma \left( 7 \right) - M*\left( {\Gamma \left( 2 \right) - 1} \right) - K_{1} *\Gamma \left( 2 \right) - F*(\Gamma \left( 2 \right) - 1)^{2}$$

(25)

$$\theta^{\prime\prime} = \Gamma \Gamma 2 = - Pr*\left( {\left( {\frac{1}{{1 + \frac{4}{3}*Rd}}} \right)*\Gamma \left( 2 \right)*\Gamma \left( 5 \right) - \Gamma \left( 1 \right)*\Gamma \left( 6 \right) } \right) +{\prime} Du*\Gamma \Gamma 3$$

(26)

$$\phi^{\prime\prime} = \Gamma \Gamma 2 = - Sc*\left( {\Gamma \left( 2 \right)*\Gamma \left( 7 \right) - \Gamma \left( 1 \right)*\Gamma \left( 8 \right)} \right) + Sr*\Gamma \Gamma 2$$

(27)

Subject to the boundary conditions.

$$\Gamma \left( 1 \right), = \Gamma \left( 2 \right), = 0 , \Gamma \left( 5 \right), = 1, \Gamma \left( 7 \right), = 1\quad {\text{at}}\;\eta = 0$$

$$\Gamma \left( 2 \right) \to 1,\Gamma \left( 3 \right) \to 0 , \Gamma \left( 5 \right) \to 0, \Gamma \left( 7 \right) \to 0\quad {\text{as}}\;\eta \to \infty$$

(28)

The Eqs. (24–28) are put into the algorithm of bvp4c solver and then required solutions for an appropriate choice parameter involved in the problem are obtained. These solutions in graphical and tabular form are presented in the next sections.

Results and discussion

The numerical framework developed in this study offers a versatile tool for analyzing engineering problems involving non-Newtonian fluid flows in porous media under magnetic and thermal influences. The use of MATLAB’s bvp4c solver allows for precise solutions to the governing equations, which are adaptable to various parameter settings encountered in engineering applications. By adjusting parameters such as Prandtl number, Soret and Dufour numbers, and porosity, the model can simulate specific industrial conditions, making it a practical asset for engineers and researchers seeking to predict fluid behavior under complex forces. The results presented here demonstrate the framework’s potential to inform the design and optimization of processes requiring controlled thermal and concentration distributions, such as in enhanced oil recovery, polymer extrusion, and electronic cooling. This framework thus provides both a scientific contribution and a practical resource for addressing real-world engineering challenges.

This section focusses on the behaviors of the key variables, which are profile $f{^{\prime}}$, temperature profile $\theta$, and mass concentration profile $\phi$, as well as their derivatives, the skin friction coefficient, $f^{\prime\prime}\left( 0 \right)$,, the Nusselt number, $\theta^{\prime}\left( 0 \right)$, and the Sherwood number, ϕ $\phi^{\prime}\left( 0 \right)$. For this purpose, they were scrutinized with a series of controlling parameters, which indeed drives the considered phenomenon. Mainly, the effect of a series of physical parameters on the velocity, temperature, and concentration profiles were examined. This includes the mixed convection parameter, $\lambda_{T}$​, the modified mixed convection parameter, $\lambda_{C}$, the second-grade fluid parameter, $K$, the Soret number, Sr, the Schmidt number Sc magnetic field parameter ${\text{M}}$, Dufour number Du, Porous medium parameter $K_{1}$, inertia coefficient/Forchheimer number ${\text{F}}$, radiation parameter $Rd$, and Prandtl number $Pr$. The effects on these parameters are also displayed using various graphs, and tables, to indicate how each parameter effects the fluid behavior. In this analysis, it is aimed to understand the physical behavior involved and this study will indeed be helpful to optimize the system when it is applicable for practical use. It is organized in a step-by-step manner, and each step indicates the balance and tuning nature of these forces once the physique is tuned against a system parameter.

Figures 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 and 13 present a series of plots spanning a variety of parametric ranges for the velocity, temperature, and mass concentration profiles. These graphs showcase the effect of several specified parameters simultaneously on the velocity field, temperature distribution, and concentration profile, while the skin friction coefficient, Nusselt number, and Sherwood number across the boundary layer thickness parameter, are plotted distinctly. Also, these effects have been plotted using these specified parameters separately for assisting and opposing flow conditions. Each of these plots is meticulously designed to show how a specified set of parameter variations influence flow dynamic and thermal aspects. Such a conceptual representation would enable the precise natural interpretation of how a change in one parameter contributes to the fluid behavior in the assisting and opposing flow cases. Reading these figures would help demystify the complex interaction between fluid flow dynamics and thermal phenomenon in various conditions.

Fig. 2

Influence of ${\text{K}}$ on $f^{\prime}$.

Fig. 3

Influence of ${\text{K}}$ on $\theta$.

Fig. 4

Influence of ${\text{K}}$ on $\phi$.

Fig. 5

Influence of ${\text{K}}_{1}$ on $f^{\prime}$.

Fig. 6

Influence of ${\text{K}}_{1}$ on $\theta$.

Fig. 7

Influence of ${\text{F}}$ on $f^{\prime}$.

Fig. 8

Influence of ${\text{Pr}}$ on $f^{\prime}$.

Fig. 9

Influence of ${\text{Pr}}$ on $\theta$.

Fig. 10

Influence of ${\text{Rd}}$ on $\theta$.

Fig. 11

Influence of ${\text{M}}$ on $\theta$.

Fig. 12

Influence of ${\text{Sr}}$ on $\theta$.

Fig. 13

Influence of ${\text{Du}}$ on $\theta$.

As presented in Figs. 2, 3, 4, in both the assisting and opposing flows, the second-grade fluid parameter K significantly affects the velocity, temperature, and mass concentration fields. In Fig. 2, the velocity f′(η) decreases steeply with an increase in K in both kinds of flow, whereby the curves in opposing flow have lower peaks than those for the assisting flow since the opposite stream slows the fluid more effectively. In Fig. 3, the temperature θ(η) increases with K for both flows, although the curves for opposing flow exceed those of the assisting flow, this is due to the higher frictional heating effect in the opposing flow due to the reduction of the fluid density that leads the temperature to rise. Similarly, in Fig. 4, the mass concentration ϕ(η) also increases with K in both flows, though it is more pronounced in opposing flow. As the fluid density decreases, the mass transfer time is extended, and hence the temperature and concentration magnitudes are enhanced. It implies the increased interactions within the fluid as K is heightened since it influences the flow and thermal properties of the fluid.

Figures 5 and 6 show the effects of the porosity parameter K1 on the dimensionless velocity gradient f′(η) and the temperature profile θ(η) for both assisting and opposing flow. Under the influence of porosity K1, as proven in Fig. 5, f′(η) decreases for both assisting and opposing flow as K1 increases from 0.1 to 0.9. This is a clear indication of reduced viscous resistance offered by porous media, thereby facilitating the horizontal movement of the fluid. Additionally, Fig. 6 suggests that f′(η) also decreases with increasing K1, meaning that higher porosity lowers the temperature gradient, promoting heat transport efficiency. These results indicate the importance of porosity in determining the magnitude of fluid and thermal dynamics since higher porosity promotes the movement of fluid and the dissipation of heat, especially in MHD flows. Lastly, assisting flow has a more profound effect on opposing flow regarding temperature field since the it promotes more efficient dissipation of heat as the flow aids its dissipation. The opposing flow was found to be more resistant to the natural thermal gradients.

Figure 7 is showing the influence of F on f′(η)f for the two types of flow—assisted and unassisted. regardless of the flow type, f′(η) decreased with the increase in F. This indicates that the increased magnitude of drag due to a high Forchheimer number leads the liquid phase to experience more resistance offered by the porous media. This is attributed to an increased drag coefficient and a reduced porosity that collectively resists fluid flow. As can be observed, assisted flow has a consistently higher f′(η) values with increasing F compared to opposing flow, which has a smoother curve and is relatively more resistant to causing a rapid change in flow direction and resisting the convective flow that leads to change in velocity. Moreover, the assisted flow has higher f′(η) values with the increase in F compared to the opposing flow due to the minimal resistance caused by the lower change in the flow direction, which leads to a rapid increase in flow velocity. This evidence supports the process as earlier described of how flow dynamics altered by inertial effects within porous media will occur with an MHD context affected by magnetic fields and liquid viscosity.

Figures 8 and 9 shows the influence of the Prandtl number (Pr) on both the dimensionless velocity f′(η) and the temperature profile θ(η) under assisting and opposing flows. Figure 8 shows that with increasing Prandtl numbers (Pr = 1.0, 7.0, 10.0), the velocity gradient f′(η) decreases slightly for both assisting and opposing flows. The reduction of f′(η) is more important for the opposing flow case, indicating a stronger influence of viscosity. The decrease in velocity with Pr is due to the higher viscosity that dampens the velocity of the fluid. In fact, higher viscosity leads to reduced momentum transfer, thus flattening the velocity profile. The temperature profiles in Fig. 9, show that as Pr increases, the thermal boundary layer thickness decreases, especially close to the surface. This effect is similar for both assisting and opposing flows but is more pronounced in assisting flows. Higher Pr means lower thermal diffusivity; thus, heat is less effectively diffused. Thus, a thinner thermal boundary layer occurs. The trends presented in Figs. 8 and 9 show the importance of Prandtl number, on effecting the MHD flow and thermal characteristics in porous media. The more important effects shown in assisting flow case compared to opposing one highlight the influence of flow condition in enhancing momentum and heat transfer.

The impact of Rd on the temperature profile is presented in Fig. 10 for both assisting and opposing flows. As Rd increases, the temperature decreases for both assisting and opposing flow conditions. This is due to the fact that for higher Rd, the fluid becomes more able to transfer heat, thus the temperature across the boundary layer decreases. For both flow types, the curves have similar trends, but the temperature reduction is slightly more effective for the opposing flow case. This means that the opposing flow is more effective in dissipating heat. At higher Rd values a more efficient heat dissipation mechanism occurs through radiation.

Figure 11 presents the effects of the magnetic parameter (M) on the temperature profile θ(η) for the assisting and opposing flow conditions. The Magnetic Parameter (M) quantifies the influence of a magnetic field on the flow. When M increases, the temperature values decrease across the boundary layer for both types of flows (especially for the assisting flow). The increase of M mean stronger magnetic field and thus stronger Lorentz force. This force opposes the convective motions and reduce the mixing within the flow. Thus, the heat transfer efficiency decreases and lower temperatures across the flow occurs. The decrease in temperature is clearer for the assisting flow as compared to the opposing flow. In fact, in this case the flow direction and the magnetic field are in the same direction, causing a more important magnetic damping effect.

Figure 12 illustrates the effects of the Soret number (Sr) on the temperature profile θ(η) for both the assisting and opposing flows. The Soret number Sr evaluates the effect of temperature gradients on mass diffusion. When Sr is increased, the temperature values decrease for both flow types. This behavior indicates a more pronounced effect of thermal diffusion on mass transfer. Practically , it means that as the fluid heats up the temperature gradients drive the movement of species within the fluid more efficiently, and the mass transfer is improved due to thermal effects. This leads to a more efficient heat as mass transfer. The two flow conditions have similar trends, but the decrease in temperatures is more pronounced in the case of assisting flow.

Figure 13 present the impacts of the Dufour number (Du) on the temperature distribution (η) for the assisting and opposing flows conditions Dufour Number evaluates the effect of mass flux due to concentration gradients. When Du is increased, the temperature decreases for both flow conditions. Higher Du indicate a stronger coupling between mass and heat transfer due to concentration gradients. The increase of Du enhances the conversion of the energy from mass diffusion into thermal energy and cause a lowering of the temperature gradient. Assisting and opposing flows exhibit the same behaviour, but the Assisting flow shows a more pronounced decrease in θ(η) with increasing Du.

Figure 14, 15, 16 present the effects of the second-grade fluid parameter ${\text{K}}$ the skin friction coefficient $Re^{1/2} C_{f}$, the Nusselt number ${\text{Re}}^{ - 1/2} {\text{Nu}}$, and the Sherwood number ${\text{Re}}^{ - 1/2} {\text{Sh}}$, respectively. It is noted that as when $K$ increases then $Re^{1/2} C_{f}$ rises rapidly for both assisting and opposing flow. But worth noticing is that for opposing flow curves are higher than assisting flow. This whole phenomenon is shown in Fig. 14. Now if we look on the physical behavior of Nusselt number ${\text{Re}}^{ - 1/2} {\text{Nu}}$ and ${\text{Re}}^{ - 1/2} {\text{Sh}}$ with the increasing values of ${\text{K}}$ the similar increasing trend is noted as depicted in Figs. 15, 16, respectively. The physical impact porosity parameter $K_{1}$ on skin friction coefficient $Re^{1/2} C_{f}$, the Nusselt number ${\text{Re}}^{ - 1/2} {\text{Nu}}$, and the Sherwood number ${\text{Re}}^{ - 1/2} {\text{Sh}}$, respectively, has been displayed in Figs. 17, 18, 19. It was concluded that when $K_{1}$ increases then $Re^{1/2} C_{f}$ increases for both of the cases that is assisting flow and opposing flow accordingly, but , the Nusselt number ${\text{Re}}^{ - 1/2} {\text{Nu}}$, and the Sherwood number ${\text{Re}}^{ - 1/2} {\text{Sh}}$ decrease remarkably as illustrated in Figs. 18, 19. It is noteworthy, that curves for physical quantities are lower than assisting flow.

Fig. 14

Influence of $K$ on $Re^{1/2} C_{f}$.

Fig. 15

Influence of $K$ on $Re^{ - 1/2} {\text{Nu}}$.

Fig. 16

Influence of $K$ on $Re^{ - 1/2} {\text{Sh}}$.

Fig. 17

Influence of $K_{1}$ on $Re^{1/2} {\text{C}}_{{\text{f}}}$.

Fig. 18

Influence of $K_{1}$ on $Re^{ - 1/2} {\text{Nu}}$.

Fig. 19

Influence of $K_{1}$ on $Re^{ - 1/2} {\text{Sh}}$.

Table 1 provides a comparison of skin friction coefficient results for both assisting and opposing flows for different porosity parameter values K. The Table compare the results given by Hayat et al.¹ with current. The results are in concordance with the findings of Hayat et al.¹, indicating consistency and reliability of the numerical model.

Table 1 Comparison of results for skin friction $f^{\prime\prime}\left( 0 \right)$ when $\lambda_{T} = 0.2,Pr = 0.2,\lambda_{C} = 0.0,M = 0.0,Sr = 0.0, Du = 0.0,Sc = 0.0,F = 0.0,K_{1} = 0.0, Rd = 0.0$.

Conclusion

The current study presents a numerical investigation of the dynamics of heat and mass transfer in non-Newtonian viscoelastic second-grade fluid flow in a Darcy-Forchheimer porous medium under MHD effects, thermal radiation, and the influence of Soret and Dufour effects. The study investigated the complex interactions of these factors under both assisting and opposing flow conditions. The main results can be summarized as follow:

• The increase in the second-grade fluid parameter reduced fluid velocity in both aiding and opposing flows, with the opposing flow instance showing a more dramatic decrease. reasoning.

• The viscoelastic properties of the fluid are more effective on the flow retardation under opposing flows conditions.

• Due to the decrease in pore size, the increase of the porous medium parameter causes a reduction in fluid velocity for both flow regimes.

• Due the increased drag and reduced porosity, an increase in Forchheimer Number decrease the fluid velocity for both flow types.

• Considering radiation in the energy equation enhanced the temperature, and thus improved the het transfer.

• higher Soret numbers enhanced the mass concentration for both flow regimes, due to enhanced temperature gradients.

• The increase of Dufour number also increased the temperatures for in both flows.

• The skin friction rises with increasing second-grade fluid parameter and porosity parameter.

• The Nusselt number rises with second-grade fluid parameter but reduces with porosity parameter increasing values.

• The Sherwood number increases with second-grade fluid parameter but delimitates with porosity parameter increasing values.

• The comparison of the currents results with already published is performed and concluded that there is an excellent agreement between both them indicating the validity and accuracy of the present model.

Future recommendations

• In future, this study can be extended to highlight the hybrid nanofluid, and ternary hybrid nanofluid flow on different geometries.

• This study is limited to one non-Newtonian model it can be extended to extend other non-Newtonian models.

• This study can be extended to include the reduce gravity effects and non-linear buoyancy forces.

Ethical approval and consent to participate

The study does not involve any ethical problem.

Consent for publication

All the authors have agreed to publish this manuscript.