Introduction

Chirality is a fundamental feature of nature, referring to the geometric properties of objects lacking mirror reflection symmetry1. The interaction of light with these geometries can cause chiral optical effects. During this process, the chiral features of the structures can be measured. A typical technique based on optical method is circular dichroism (CD), which measures the difference in intensity and phase response between left and right circularly polarized (LCP/RCP) light illumination2. Although chirality plays a key role in various research fields such as drug synthesis, chiral sensing3 and optical communication4, CD in natural optical materials is extremely weak due to the mismatch between light wavelength and the size of chiral molecule, which limits the applications of chiral optical techniques5.

Meticulously designed artificial chiral structures can exhibit exceptionally strong chiral optical signals6,7,8. A key parameter to enhance the intensity of chiral light-matter interaction is the quality (Q) factor of the associated resonance. Importantly, bound states in continuous domains (BICs) provide a feasible solution to design the chiral narrow-band structure. BICs are identified as local states coexisting with extended modes within the light cone, which have attracted significant attention due to the infinite Q-factor9. In recent years, bound states in the Continuum (BICs) have made significant research advancements in the realms of wavefront phase control10 and polarization conversion11. By utilizing the decoupling between BICs and continuum states, a research team has successfully designed and fabricated the metasurface with the extreme chirality (i.e. chiral BIC) for the first time, addressing the challenge of achieving chiral metasurfaces with huge CD signal12.

In recently years, the evolution from passive to actively tunable chiral metasurfaces has been emphasized13. Actively tunable chiral metasurfaces are ideal for dynamically controlling the interaction between chiral wave-matter and circularly polarized light14. General GST (GST-225) is a nonvolatile phase change material, which exhibits excellent dielectric constant contrast during the phase transition from amorphous to crystalline state15. Meanwhile, GST-based metasurfaces can be regulated by phase transition without changing the geometric parameters of the cell structure, showing great potential in applications such as biosensing16, thermal imaging17 and thermal camouflage18.

Chiral BIC metasurfaces have the characteristics of high CD and high Q-factor. We introduce phase change materials into the chiral BIC metasurface, and design the structure which achieves wavelength tunability of chiral resonance with high CD and high Q-factor simultaneously. This paper adopts a dual perturbation structure design and introduces the phase-change material GST as the structural medium. The out-of-plane mirror symmetry of the metasurface is broken by the method of structural tilt, and the in-plane mirror symmetry is broken by adding a trapezoidal nanopore. The key parameters of the designed structure are optimized. In addition, the optical constant of GST during the phase change process are measured experimentally in the mid-infrared range. By utilizing the variable optical properties of phase change material GST, the infrared chiral metasurface with high CD absorption and tunable resonance with narrow bandwidth is realized. The demonstrated results of tunable infrared chiral metasurfaces will pave the way for the development of dynamically controlled chiral photonic devices to advance applications such as chiral thermal switches, infrared imaging, and tunable chiral photonics.

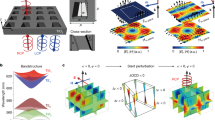
The schematic diagram presented in Fig. 1(a) illustrates the design of a chiral meta-surface based on the phase change material Ge2Sb2Te5. This metasurface consists of a skewed trapezoidal nano-hole array in GST film, with its upper and lower regions filled with silicon to match the refractive index. The structure evolved from vertical square hole, as shown in Fig. 1(b). It is worth noting that this structure is characterized by introducing two types of perturbations: a deformation angle α for in-plane symmetry breaking and a tilt angle β for out-of-plane symmetry breaking. The combination of these two perturbations transforms the hole into a chiral structure. Implementing a chiral metasurface utilizing tilted perturbations in trapezoidal nanoholes is relatively straightforward. The structural design dimensions lie within the micrometer scale, and the structural design is relatively uncomplicated. It can be accomplished through a series of processes, including thin film depositions, focused ion beam processing, and etching techniques. The trapezoidal nanoholes break the in-plane symmetry of the structure, while the structural tilt breaks the out-of-plane symmetry, leading to alterations in the local field distribution and the generation of chirality. The shape and structural tilt angle of the trapezoidal nanoholes are key factors affecting the intensity of the chiral optical response; different shapes and different tilt angles will produce different chiral optical response intensities. Compared to other geometric shapes, such as square or circular holes, trapezoidal nanoholes, due to their unique shape, can more effectively break symmetry with the assistance of structural tilt, thus providing superior performance in optical chiral response12.

Fig. 1
figure 1

(a) Schematic of the slant-perturbation metasurface with GST-225 phase-change material. (b) Disturbance diagram of in-plane deformation Angle α and out-of-plane inclination Angle β. The geometric parameters are: a = 1300 nm, b = 1000 nm, h = 500 nm. (c) The illustration of the phase transition of GST-225 from the amorphous state to the crystalline state.

Full size image

When no disturbances are involved (α = 0 and β = 0), this structure supports a continuous domain in the momentum space, with a symmetry-protected bound state. However, when the in-plane disturbance (α ≠ 0 and β = 0) is introduced, the bound states in the continuum (BICs) are broken and evolve into quasi-BIC (Q-BIC). This Q-BIC exhibits far-field radiation in the form of linear polarization. When both in-plane deformation and out-of-plane tilt disturbances (α ≠ 0 and β ≠ 0) are introduced, the eigenstate at Γ point produces chiral far-field radiation.

Figure 1(c) elucidates the phase transition process of GST from amorphous to crystalline states and vice versa. When the temperature of the amorphous GST exceeds its melting point, which is approximately 160 °C, the amorphous phase transforms into an unstable cubic crystal structure, akin to sodium chloride (NaCl)19. If the temperature is further increased, the unstable crystal structure will evolve into a stable hexagonal structure. This phase transition from amorphous to crystalline can be achieved by subjecting GST to a heating plate, using laser pulses, or applying an external voltage20. Conversely, by heating crystalline GST above its melting point of about 640 °C, liquefying it, and then rapid cooling, amorphous GST can be formed14. The skewed trapezoidal nanohole arrays in GST film is designed to achieve the tunability of chiral metasurfaces and to optimize other geometric parameter for the desired operating wavelength range. The dynamic tuning of the chiral resonance wavelength can be achieved by the variable optical constant of GST during the phase transition process.

Results and discussion

We conduct numerical simulation analysis on the structure to understand the chiral optical response mechanism of the metasurface based on the finite element method (FEM). Figure 2(a) shows the band structure diagram and corresponding Q-factor of the structure without perturbation (α = 0, β = 0), demonstrating that the eigenmode at the Γ point in momentum space supports a symmetry-protected bound state in the continuum. The theoretical basis for the relationship between the Q-factor and the perturbation angles α and β originates from the micro-disturbance theory of quasi-BIC structures21. Any operation that disrupts the C2 symmetry of the structure is considered a micro-disturbance to the original structure, which leads to the coupling of BIC with the radiative continuum, thereby obtaining a quasi-BIC. (C2 symmetry denotes the property of a molecule or crystal wherein the structure is superposable upon its original configuration upon a 180-degree rotation about the C2 axis.) The quality factor of symmetry-protected quasi-BICs is closely related to the degree of disruption of the structural C2 symmetry. Research has found that this correlation can be expressed as Q = Q0·α−2, where Q0 is a constant determined by the structure, and α represents the asymmetry coefficient, which is a parameter that measures the degree of disruption of the structure’s C2 symmetry21. It is evident that the quality factor decreases with increasing asymmetry, and when the asymmetry is enhanced to a certain extent, the quality factor of the quasi-BIC resonance will degrade to the level of ordinary resonance. In this paper, two perturbation angles are introduced to affect the Q-factor. Upon deriving the relevant equations, it is found that when the perturbations α and β are small, the Q-factor of the quasi-BIC is approximately proportional to the square of all perturbations: Q ~ 1/ (α2 + Aβ2), where A represents the different sensitivities of Q to α and β12. Figure 2(b) illustrates the Q-factor under different tilt angle β when the in-plane deformation angle α is fixed at 0.052. One can see that when both in-plane and out-of-plane perturbations (α ≠ 0, β ≠ 0) are introduced, the BIC state is broken and evolves into a Q-BIC, with the Q-factor experiencing a significant drop during the increase of β perturbation, However, even after the deformation with large β angle, the Q-BIC mode still maintain a relative high Q-factor compared with other modes. Figure 2(c) demonstrate the simulated transmission rates for LCP and RCP incidence and the CD spectrum of the metasurface after introducing both in-plane and out-of-plane perturbation angles. The inset shows the momentum-space characteristic polarization diagram of the mode. It can be observed that after breaking both in-plane and out-of-plane symmetries of the structure, the metasurface exhibits totally different response for LCP and RCP incident states, resulting in extremely high CD values. Here CD is defined as CD = (TL-TR)/(TL+TR), where TL(R) is the normalized transmission spectra under LCP(RCP) illumination. The polarization state in reciprocal space is shown in the inset of Fig. 2(c). Near the Γ point, the eigenmode with LCP state can be solved, which is the origin of high CD. In Fig. 2(d), we illustrated the relationship between the in-plane disturbance angle β and the CD amplitude with α = 0.052. It is evident that there exists an optimal combination of in-plane and out-of-plane perturbation angles that maximizes the optical chirality of the perturbed metasurface. Subsequent investigations into other parameters of the metasurface are conducted based on this perturbation angle configuration.

Fig. 2
figure 2

(a) Simulated Q-factor of characteristic modes near the Г point, with the inset showing the mode band structure. (b) Function curve of the Q-factor of characteristic modes after perturbation as the perturbation angle β varies. (c) Transmission spectra and corresponding CD response of the metasurface under LCP and RCP incidence with α = β = 0.052. The inset displays the characteristic polarization map of the first Brillouin zone, where the polarization states are represented by ellipses and the blue and red ones representing left-handed and right-handed states, respectively. (d) Function curve of the maximum CD response of the metasurface with α = 0.052 as the perturbation angle β varies.

Full size image

Beside the eigenmode analysis, the chirality of BIC in the metasurface can also be explained by the interaction between electric dipole and magnetic dipole. The theoretical foundation for enhancing chiral optical response by breaking symmetry stems from the generalized theory of chiral optics22 and the theoretical basis of BIC9. The electric field of a quasi-BIC is predominantly out-of-plane, while the magnetic field is primarily polarized along the x-axis. In the dipole approximation, the optical chirality of an object is governed by the dot product ( p⊥·m⊥), where p⊥ and m⊥ are the projections of electric dipole p and magnetic dipole m onto the plane perpendicular to the incident wave vector k22. For the metasurface in this work, in the absence of any perturbations (α = β = 0), the metasurface supports symmetry-protected bound states in the continuum (BICs) at the Γ point of Brillouin zone. When the metasurface is subjected to in-plane perturbations (α ≠ 0, β = 0), the in-plane symmetry is broken, and the BIC evolves into a quasi-BIC, the magnetic fields of quasi-BICs are predominantly directed along the x axis whereas the electric fields are out-of-plane (along z direction). In this case, p⊥·m⊥ is zero. However, when the metasurface experiences both in-plane and out-of-plane perturbations (α ≠ 0, β ≠ 0), the nanohole is slanted towards the x direction, resulting in an electric field component aligned with this direction. Meanwhile, the magnetic field components are predominantly maintained along x-axis, leading to non-zero value of p⊥·m⊥ and optical chirality12.

Fig. 3
figure 3

(a) Simulated transmission Jones matrix spectra of Tll, Trr, Trl and Tlr. (b) The scattering power of the multi-level components derived from the Cartesian multi-level expansion under RCP incidence. (c) The scattering power of the multi-level components derived from the Cartesian multi-level expansion under LCP incidence.

Full size image

To further validate the physical mechanisms underlying the chiroptical response of metasurfaces. We calculated the simulated transmission Jones matrix spectra for Tll, Trr, Trl, and Tlr (Fig. 3a). It is evident that the chiral optical response is due to a significant decrease in Trr at 4654.8 nm while Tll remains at a relatively high value. In addition, the transmission spectra of Trl and Tlr are approximately equal and less than 0.05, indicating that the transmission spectra for left circularly polarized (LCP) and right circularly polarized (RCP) light are co-polarized and do not include cross-polarized components. Moreover, the chiroptical response can also originate from the electric quadrupole moment, toroidal dipole and magnetic quadrupole moment23,24. To verify that the chiroptical optical response of the system is predominantly attributed to the coupling between electric and magnetic dipoles. We conducted a more in-depth analysis, calculating the decomposition of far-field scattered power for each multipolar resonance in the Cartesian coordinate system. The scattered power from the chiral q-BIC’s multipolar components, including electric dipole (ED), magnetic dipole (MD), electric quadrupole (EQ), magnetic quadrupole (MQ), and toroidal dipole (TD), is illustrated in Fig. 3. Figure 3(b) and 3(c) represent the scattered power of the multipolar components derived from the Cartesian multipolar expansion under RCP and LCP incidence, respectively. In both scenarios, the MD component is dominant, while the ED contributes a secondary portion to the scattered power, with other multipolar contributions being negligible. It is noteworthy that the total scattered power for RCP is approximately two orders of magnitude greater than that for LCP. This result is consistent with the significantly higher transmission rate for LCP compared to RCP.

Fig. 4
figure 4

The chiral resonance wavelength and CD value of chiral metasurface as functions of the main geometric parameters.

Full size image

In order to investigate the influence of structural geometric parameters on the chiral optical response of metasurfaces, we perform parameter scanning calculations for the period a, the size b of the trapezoidal nanoholes, and the thickness h of the GST film in this structure. Figure 4(a) shows the chiral optical response of the metasurface when the period is varied from 1200 nm to 1400 nm with b = 1000 nm and h = 500 nm. It can be observed that wavelength of the chiral resonance is tuned from 4200 nm to 5200 nm by increasing the period of metasurface. During the tuning process, the peak CD value remains above 0.8. The influence of hole size is shown in Fig. 4(b), when a = 1300 nm and h = 500 nm. When the parameter b varies from 850 nm to 1100 nm, the chiral optical response of the metasurface exhibits significant fluctuations, with a wavelength span of the peak CD ranging from 5000 nm to 4500 nm. Therefore, considering the fabrication of this structure, it is necessary to ensure size accuracy of the trapezoidal holes to achieve a higher chiral optical response of the metasurface. In addition, the thickness of the GST film is considered in the simulation in Fig. 4(c). The wavelength of the chiral resonance can also be tuned by the film thickness, but the peak value of the CD spectrum is significantly affected by it. According to the simulation result, the optimized value of the GST film thickness is in the range of 450–550 nm. Therefore, to fabricate the chiral metasurface, film thickness is key parameter to obtain high CD signal.

Fig. 5
figure 5

(a) The real and imaginary parts of the refractive index of GST-225 at different phase transition temperatures. (b) The influence of the refractive index of GST near the phase transition temperature of 170 °C on the chiral resonance wavelength and CD value.

Full size image

The dynamic adjustment of metasurfaces is primarily achieved by applying heat, light, or voltage to the structural material GST, inducing a phase transition14. GST exhibits different refractive indices at various temperatures, and changes in the structural refractive index led to shifts in the wavelength of chiral resonance, thereby enabling tunability of the wavelength. The response speed of the metasurface to the phase state changes of GST depends on the rate of temperature change, such as using laser pulses to induce phase transitions in GST. The dynamic modulation and switching speeds of the metasurface can range from picoseconds to nanoseconds, depending on the duration and intensity of the laser pulse14. This paper considers GST-225, the most classical GST material, which exhibits significant refractive index changes between the crystalline and amorphous states, making it highly suitable for the design of tunable chiral metasurface structures. Different GST materials and modified varieties can accommodate a variety of technological and application requirements. Each GST material possesses unique physical and chemical properties, which can be optimized by adjusting the chemical composition ratios or doping techniques. For instance, Ge1Sb2Te4 (GST-124): altering the Ge/Sb/Te ratio allows for the adjustment of the material’s phase change temperature, latent heat, and stability; GST-Se (selenium-doped): replacing a portion of tellurium (Te) with selenium (Se) enhances the phase change speed and material stability while reducing power consumption25. By utilizing the phase change property of GST material, it is possible to modify the chiral resonance of the metasurface based on the BIC effect. Unlike the volatile phase change material VO2, GST does not require continuous energy to maintain the crystalline state, and can retain this state when it returns to room temperature after reaching the phase change temperature26,27. The typical phase transition temperature of GST-225 phase change material from amorphous to crystalline state is about 160 °C25. In order to study the dynamic tuning of chiral metasurface resonance wavelength by phase change material GST, we experimentally measured the refractive index of GST at different heating temperatures, as shown in Fig. 5(a). It can be seen that within the wavelength range from 4 μm to 5 μm, the real and imaginary parts of the refractive index of GST gradually increase with the increase of the heating temperature. If the imaginary part of refractive index is too large, it means that the energy loss of the metasurface is greater caused by GST film absorption, and the corresponding chiral dispersion (CD) response is smaller. To avoid this problem, we confine our analysis of the tunable chiral metasurface in the low loss cases, which corresponding to the heating temperature of GST film within the range from 20℃ to 200℃. As shown in Fig. 5(b), when the refractive index of GST is in the range of 4.8 to 5.0, the CD response of the designed chiral metasurface is above 0.8, and the corresponding chiral resonance wavelength is tunable within the range of 50 nm. Therefore, it can be seen that the metasurface with phase change material can dynamically tune the chiral resonance wavelength by controlling the heating temperature of GST.

Conclusion

In conclusion, a wavelength-tunable infrared chiral metasurface based on phase-change material GST-225 with chiral perturbation has been proposed and analyzed. This metasurface introduces the out of plane tilt angle as a degree of freedom to build chiral structure, avoiding the use of a complex bilayer structure design. Combined with the phase-change material GST-225, it is able to achieve a CD value of above 0.8, and the wavelength bandwidth of the chiral resonance is only about 1 nm. Moreover, the working wavelength can be tuned by varying the heating temperature, instead of the structural parameters. This work not only promotes the development of adaptive and active metasurfaces using phase-change materials but also provides an opportunity for dynamic modulation of circular polarization control in switchable metasurfaces with narrow working bandwidth. Additionally, the dynamic modulation of chiral metasurfaces induced by opto-thermally triggered GST phase transitions can reach timescales ranging from picoseconds to nanoseconds, depending on the duration and intensity of the laser pulses for heating process, as well as the thermal conductivity of the material28,29. Advancements in phase-change chiral metasurfaces will drive research in the infrared band for filter devices30, optical switches31, thermal imaging, and chiral sensing32.

Methods

All the simulations in this work are conducted by a finite-element-method solver in COMSOL Multiphysics. Bloch boundary conditions are applied in the x and y directions, whereas perfectly matched layers are used in the z direction. The circularly polarized light incident along the z-axis direction was used to calculate the optical absorption spectra. The refractive index Si of the substrate is set as 3.4. Ge2Sb2Te5 (GST) thin films of varying thicknesses are grown on silicon substrates via magnetron sputtering. Following the growth, the as-deposited GST films are subjected to electrical heating to induce phase transitions of varying degrees. The optical constants of the phase-transformed GST are then measured using an ellipsometer. Subsequently, data fitting is performed to extract the refractive index (n) and the absorption coefficient (k) of the GST films.