Introduction

Brain-Computer Interface (BCI) integrates the brain with different actuators using a computer. This captures the minds of various researchers to make it practically feasible. Several non-invasive brain-reading techniques like EEG, functional Magnetic Resonance Imaging (fMRI), and fNIRS are used commonly for this application1,2. Amongst most mental activities Motor Imagery (MI) is an interesting candidate for investigation and hence feature extraction and classification of MI signals have gained much importance3,4. Classification of Motor Imagery (MI) signals using EEG were commonly investigated using various machine learning algorithms5,6. Common machine learning classifiers like Tree classifiers, K-Nearest Neighbor (KNN), Linear Discriminant Analysis (LDA) and Support Vector Machines (SVM) have shown an accuracy of up to 95% for 2 class MI tasks7,8,9. Optimizations have also helped to improve the accuracy10. Furthermore, intelligent algorithms have also been investigated for single modalities for improving accuracy in two class classifications11. These improvements have led to multi-class classification of MI or MI with other mental activities like mental arithmetic12. Nevertheless, beyond the best techniques used for classification, a single modality has its own merits and demerits which introduces the use of Hybrid BCI that can be achieved by combining two modalities. This can complement each other’s limitations13. It was also found that the hybrid system showed improved performance for motor imagery hand clenching in terms of speed and force14. Such a system can also be applied for multi-class applications like four class classification of Alzheimer’s disease15, mental arithmetic, motor imagery, and motor executions, which are further converted into command signals to be used for clinical and non-clinical applications like quadcopter and wheelchair controls16,17. The initial limitations in hybrid BCI setup were overcome by upgrading the acquisition devices18.

Processing both motor imagery and motor execution tasks acquired from EEG and fNIRS modalities are seen in some of the recent work to investigate the performance of multi-class motor imagery and execution19,20. EEG is known to have a good temporal resolution while spatial resolution is good in fNIRS. However, fNIRS has a slow response due to hemodynamic activity. In addition, fNIRS is preferred to fMRI for being cost-effective and reducing acquisition complexity21,22. Hybrid BCI with EEG and fNIRS is a good combination for classifying motor imagery and motor tasks. Many feature extraction techniques and classifiers have been used to achieve good classification accuracy. Common machine learning classifiers that were employed for the classification of two-class motor imagery or motor tasks were also used initially with EEG or fNIRS modalities12,23. The same has been applied to Hybrid datasets either as a single model or a combination of 2 models or applying feature selections24,25. However, good accuracy could not be achieved since the complexity also increases with the number of modalities and the amount of data that has to be handled by the machine learning algorithms. Increasing dimensionality and computational cost can be handled better by deep neural networks26. A deep neural network was also used by fully connected layers, but achieved a lesser accuracy27,28. Aiming to increase the performance of machine learning algorithms for multi-class hybrid datasets, channel selection methods were employed before extracting features29,30,31. This additional pre-processing improved the machine learning model accuracy from approximately 92% to 98%32, however, this would compensate for the spatial information especially if the dataset is small. The performance of the models can also vary with the feature extraction methods. In order to preserve the spatial information, techniques like Common Spatial Pattern (CSP), Regularized Common Spatial Pattern (RCSP), and Principal Component Analysis (PCA)33,34were commonly employed33,34. Linear and non-linear features were also considered35,36,37to investigate the linear and non-linear relationship in the signals35,36,37. However, these feature extraction models along with machine learning classifiers have given a classification accuracy ranging from 92 to 98%. An increase in accuracy has always been met with complex methods. Channel selections can increase the accuracy but compensate for spatial information. Machine learning models without channel selection yield less than 98% accuracy. This reduction in accuracy is seen especially for multi-class classification of limb movements since their spatial distribution along the scalp is more adjacent which makes the classification more challenging. This challenge may be resolved by additional processing layers which can extract more complex features as in Deep Neural Networks (DNN)26. DNN and combinations of two DNN models – commonly called hybrid DNN have been used for single modality like EEG. The most common model is combining Convolutional Neural Network (CNN) and Recurrent Neural Network (RNN). This is because CNN can improve spatial features while RNN works well for temporal features. This combination can be used to improve spatio-temporal features38. However, it is seen that the deep learning models are not explicitly investigated for these hybrid BCI systems where spatio-temporal features co-exist.

The proposed work investigates a hybrid deep learning approach on a limited dataset for contralateral and ipsilateral limb movements to know if a good accuracy can be attained without compensating for the spatial information. The data would be more spatially localized signals which may lead to generalization and misclassification problems39,40. Since both hand movements are performed, the number of trials and the time taken to perform the task is also limited. The objectives of this study are – to classify ipsilateral (spatially localized)/contralateral (spatially distinct) hand movements and to investigate deep learning algorithms for improving classification accuracy with reduced pre-processing steps thereby reducing the computational load. The dataset used for this study consists of Motor Imagery (MI) and Motor Execution for the Right arm, Left arm, Right hand, and Left hand. Since the cortical locations for these movements lie adjacent to each other, it increases the chances of misclassification. The proposed Hybrid CNN model uses more filters to simplify the classification problem. The Hybrid CNN was developed and trained using Python Version 3.11. The paper is further divided into a methodology which consists of dataset description with its preparation, pre-processing, feature extraction and classification. The results and discussions section presents the performance comparisons with another proposed model. The comparison of the proposed model performance with previous works is also presented.

Methodology

Dataset description data augmentation and preprocessing

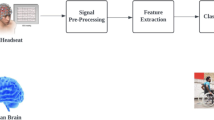
The overall work done is shown in Fig. 1. The dataset provided by Buccino et al.20 has a simultaneous recording of both EEG and fNIRS taken during motor execution. 15 healthy male subjects aged from 22 to 54 years participated in the experiment and were given 4 different upper limb tasks.

Fig. 1
figure 1

Block diagram of methodology.

Full size image

The motor tasks assigned were flexion of Left/Right Arm/Hand. The acquisition system had 21 channels for EEG and 34 channels for fNIRS with a sampling frequency of 250 Hz and 10.42 Hz respectively. Each trial of tasks lasts for 12 s with 6 s of rest and 6 s of movement with 25 such trials for one class. The 6 s of movement performance is augmented for further processing.

Data Augmentation is done to increase the input data to the model since the dataset is limited. This was done using time-slicing and overlapping methods. The first second after the cue was skipped due to delay in hemodynamic response and the first second of rest was taken due to sustenance of the response. The time slicing was done for 3 s at three intervals as seen in Fig. 2. Data redundancy was also induced to increase the quantity of input data.

Fig. 2
figure 2

Schematic block diagram of data augmentation.

Full size image

The EEG data was filtered in the mu (8–13 Hz) and beta band (13–30 Hz) for motor imagery and motor execution signals with a filter order of 5 due to its constant group delay and improved Signal-to-Noise Ratio. A Gaussian transformation was used for normalization as in Eq. (1)

$${x}_{norm}\left(t\right)= \frac{x\left(t\right)- \mu }{\sigma }$$
(1)

The optical wavelengths acquired from fNIRS were converted to changes in optical densities showing oxygen concentration in blood using Modified Beer-Lambert Law (MBLL) at two wavelengths, W1 = 760 nm (red) and W2 = 850 nm (infrared). These were filtered from 0.01 Hz to 0.1 Hz to extract motor imagery and motor execution data.

Feature extraction

The common features used in previous studies are mean, peak, standard deviation, skewness kurtosis and slope indicators20,32. Spatial filtering is another common method of feature extraction which preserves the spatial information. This is done by using a variety of Common Spatial Pattern (CSP) algorithms which are more prominently used in two class problems. This was introduced as a feature extraction method by41. The objective of the algorithm is to maximize the ratio of variance of the two classes present in the signal.

Multi-class CSP

The four classes were converted into two-class problems – Right Hand/Left Hand and Right Arm/Left Arm. The CSP filters were derived for these two class problems by solving Rayleigh’s eigen value problem using Eq. (2),

$$J\left(b\right)= \frac{{b}^{T}{\Sigma }_{1}b}{{b}^{T}{\Sigma }_{2}b}$$
(2)

where \({\Sigma }_{1}\) and \({\Sigma }_{2}\) denote the covariance matrix of classes 1 and 2 while b is the spatial filter that can be obtained by solving the generalized Eigenvalue decomposition. In this work, we have considered 2 filters for 4 classes hence, N = 8.

Thin-ICA CSP

In order to use CSP more effectively in four class, this is combined with Thin-ICA method which computes the second and fourth-order of statistics and extracts the independent components37. ICA belongs to the Blind Source Separation methods, which detect the source amongst many sources. This method can extract motor movement features given a proper initialization. CSP aids in giving the appropriate initialization for ICA to extract the independent components that belong to motor movements. The independent components to be extracted can be modified as required. Since this is applied only to EEG data, the binary problem is considered as Right hand, Left hand, Right Arm and Left arm. The EEG signal can be represented as x(t) with a linear equation Eq. (3)

$$x\left(t\right)=As\left(t\right)+ w(t)$$
(3)

where, \(A \epsilon {R}^{m \times n}\) is the mixing matrix, \(w(t) \epsilon {R}^{m}\) is the zero mean gaussian noise and \(s(t) \epsilon {R}^{n}\) is the independent source vector. The estimated output is given as in Eq. (4)

$$y\left(t\right)= {U}^{T}z(t)$$
(4)

where U (U = WA) is considered as the orthogonal matrix, which was obtained after the pre-whitening process and z(t) represents the pre-whitened observations, which is given as \(z\left(t\right)=Us\left(t\right)+Wn\left(t\right) \epsilon {R}^{N}\)

Equation 5 gives the contrast function to estimate the second order and higher-order statistics,

$${\varphi }_{\Theta }\left(U\right)= {\gamma }_{4}\sum_{n=1}^{N}\sum_{i=1}^{P}{|Cum\left({y}_{i}{(t}_{n}\right),\dots ,{y}_{i}\left({t}_{n}\right)|}^{2 }+ {\gamma }_{2 }\sum_{n=1}^{N}\sum_{i=1}^{P}\sum_{\tau \epsilon {\rm T}}{|Cum({y}_{i}\left({t}_{n}+ \tau \right), {y}_{i}({t}_{n})|}^{2}$$
(5)

where, N signifies the number of splits and P signifies the number of independent components to extract. Here we set N = 3 (three splits in data), P = 20 and T = {1,…..,6}(delays).

The underlying condition here is that the independent components that would be extracted should belong to Motor Imagery and motor execution tasks. This can be assured by using the CSP matrix to initialize the unmixing matrix in the Thin ICA algorithm. The EEG signals were then spatially filtered using the computed spatial filters. The Thin-ICA parameters were tuned, to get 8 and 20 independent components with splits = 3. The log variances of these filtered signals gave the features which were applied to train the classifier as in Eq. (6)

$${Feature}_{i}=log(var\left({u}_{i}^{T}z\right))$$
(6)

These extracted EEG features were input to Hybrid CNN for classification. However, optical densities for changes in hemoglobin concentration were fed to Hybrid CNN for feature extraction and classification.

Hybrid-CNN with bidirectional long short-term memory (Bi-LSTM)

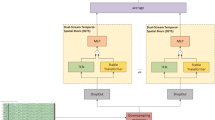
The Bi-LSTM model is a combination of forward and backward LSTM which is useful for collecting front and back information42. Sequence models can collect temporal information but lacks capability for collecting spatial information43. However, CNN had good performance for fNIRS since they are spatial features. Combining these two models can improve the extracting and classifying process for both temporal and spatial features of EEG and fNIRS. CNN is added as the first two layers since they can extract localized patterns and also reduce sequence length and this processed data is then sent to Bi-LSTM layers, which can send both positive and inverted sequence of data to be trained. Placing CNN first can extract spatio-temporal features in time series data, and also detect important information from various positions with a good accuracy. In addition, univariate data can be converted to multi-dimentional data, leading to multiple feature extraction from the dataset44.

The model architecture is given in Fig. 3. The architecture is called hybrid since the convolutional layers are included along with the Bi-LSTM layers. The input data (EEG and fNIRS) is prepared to be presented to the model. The EEG data is zero padded to match the columns of fNIRS. The input data was first passed into two layers (layer 1 and layer 2) of convolutional neural networks with 128 filters and a 1 × 3 kernel of filter coefficients. Rectified Linear Unit (ReLU)/Exponential Linear Unit (ELU) activation functions were experimented with appropriate dropouts along with Max/Average pooling. This was followed by the classifier – Bi-LSTM with , 128 and 64 filters (layer 3 and layer 4). Two dense layers were followed by Softmax activation for final classification. The model was run for 100 epochs and a fivefold cross-validation was performed.

Fig. 3
figure 3

Hybrid—CNN model architecture.

Full size image

Results and discussion

The dataset used for the current study is taken from CORE dataset. This consists of EEG and fNIRS scalp recording taken simultaneously while performing Left Hand, Right Hand, Left Arm and Right Arm motor tasks. The concentration changes of oxygenated and deoxygenated blood are considered features for fNIRS which is taken from MBLL. Thin–ICA applied to EEG gives independent components as features for EEG data. However, feature extractions like CSP were not applied to fNIRS data since it led to over fitting as compared with raw HbO and HbR. Applying feature extractions to fNIRS reduced the effect of CNN, which also extracts patterns, leading to poor performance with 60% accuracy. The performance was significantly increased to 90% while the fNIRS data was presented as changes in optical densities of HbO and HbR using MBLL. The data pre-processing done for both EEG and fNIRS is band-pass filtering.

A 60:40 ratio is considered for splitting data for training and testing respectively. However, as seen in Fig. 4, the performance is poor in the Hybrid CNN model with an accuracy of 84.3.

Fig. 4
figure 4

Hybrid CNN Performance for original input data—Accuracy (Left), Confusion matrix (Right).

Full size image

Since the batch size of the hybrid model is 200, and the input shape is (1054,1), for every epoch 20 batches were trained. The poor performance may be due to insufficient input data; therefore, a redundancy is created 3 times to increase the data size. Feature redundancy can improve performance even if some features are not learned or absent in an instance. A fivefold cross-validation was used. 60 batches were trained for each epoch. This shows an improved model performance as seen in Fig. 5 with an accuracy of 99% and loss of 0.045 using hybrid CNN model with max pooling and ReLU activation function. However, a 40% drop in accuracy for the data used without redundancy as seen in Fig. 4 since the amount of data for training is less while this is reduced to 10% when the training input is increased by introducing redundancy (as seen in Fig. 5). It is also seen that the generalization of training and testing is achieved as the number of epochs is increased. In Fig. 4, due to insufficient data, the test data is underfitting even after 200 epochs. This is improved by increasing the input data, the generalization is achieved at 100 epochs of training although there is initial overfitting due to similarities in data. The number of CNN, BiLSTM and dense layers were restricted to only two layers since complexity and execution time increases with layers.

Fig. 5
figure 5

Hybrid CNN Performance for original input data with redundancy – Accuracy (a), Confusion matrix (b) (ReLU activation with Max pooling) [class 0 – right hand, class 1 – left hand, class 2 – right arm, class 3 – left arm].

Full size image

To ensure faster convergence, ELU activation was also experimented with both average and max pooling as in Fig. 6. It is observed that ELU activation provides a faster convergence than ReLU (shown in Fig. 5). This is because the number of negative values in the input data are more than the number of positive values and ELU provides a non-zero value to a negative input, which is unlike ReLU which gives zero output for negative values. Also, in order to get a smooth generalization, the zero masking was also done, since EEG data were zero-padded. The drop in around 20–30 epochs is continuously witnessed due to a drop in fold 2 and fold 4 of the five-fold cross-validation. This can be attributed to the zero values in the data or the shuffling of data during the fold separation in cross-validation and also due to the variations in the batch of data taken during the training. However, the stabilization occur as the upcoming epochs train a better combination of data. Nevertheless, it is observed that the drop is significantly reduced when zero-masking is done since it has further reduced the decrease in performance due to the zero-padding done. The max pooling along with ELU activation has given a smooth generalization curve. The test accuracy and loss were, 99.5% and 0.045 respectively. Some more conclusions can be drawn from the confusion matrix of Fig. 5b and 6c as seen in Table 1.

Fig. 6
figure 6

Performance of Hybrid CNN with ELU activation and zero masking for average pooling (a) and Max pooling (b), Confusion matrix of ELU activation with max pooling and zero masking [class 0 – right hand, class 1 – left hand, class 2 – right arm, class 3 – left arm] (c).

Full size image
Table 1 Comparison of metrics for confusion matrix obtained from model without and with zero masking.
Full size table

From the observations in Table 1, it can be seen that, true positives remain the same. However, the false positive and false negatives are greatly reduced while applying zero masking. It is also noted that, the true negatives are also slightly lower when zero masking is done. Hence it is clear, that the misclassifications are reduced especially on class 0 (right hand) and class 2 (right arm) on zero masking and the drop in the epoch is reduced as seen in Fig. 6b. This is important since both contralateral and ipsilateral movements are classified accurately.

The current model was compared with a 5-layer CNN model whose accuracy was 98% and Hybrid CNN which uses CNN and Bi-LSTM layers shows better accuracy of classification and better performance as compared with CNN as seen in Table 2. In addition to the accuracy, F1 score, Precision. Recall and AUC parameters prove that the Hybrid CNN model is extracting the spatio-temporal features more efficiently and classifying multi-class motor movement as seen in Fig. 7It can also be seen that the time taken to train one epoch is lower in the Hybrid CNN model. This is because the number of CNN layers and the number of filters used are comparatively lesser (only 2 layers) than using only CNN which used 5 CNN layers.

Table 2 Performance metrices and computational time for CNN and Hybrid CNN models.
Full size table
Fig. 7
figure 7

ROC curve for Hybrid CNN performance with redundancy.

Full size image

Besides the 5-layer CNN model, the current work performs better than CNN + LSTM models which was experimented in our previous work. This also includes experimentation with lesser CNN layers and how 5-layer CNN was chosen45. Machine learning methods like LDA and SVM were also experimented for the same dataset and feature extraction methods, which gave lower accuracy46.

As seen in Fig. 8, the obtained accuracy of 99% is higher compared to the previous works on the classification, especially the classification of contralateral and ipsilateral limb movements, which in previous works gave 94%20and 98%32.

Fig. 8
figure 8

Comparison of accuracy with previous works.

Full size image

Conclusion

The proposed work aims to address the challenging classification of contralateral and ipsilateral data which can be achieved by properly extracting spatial and temporal patterns. A deep learning model is developed to investigate this challenge by combining CNN and Bi-LSTM which can identify spatial patterns and temporal patterns respectively. The investigation shows that the Hybrid CNN model with 2 CNN and 2 Bidirectional LSTM layers showed better classification compared with CNN models alone. Also, zero padding the input data with ELU activation and Max pooling provided a smooth generalization of the model and a faster convergence. The achieved classification accuracy is 99% for the Hybrid CNN model with minimal pre-processing, feature extraction and 2 CNN layers to detect the complex patterns in the signal.