Impact of exterior envelope thermal performance on energy demand and optimization strategies for university teaching-office buildings

Abstract

It is very different from that of ordinary buildings due to the unique operational characteristics of university teaching-office buildings, and the energy-saving potential is huge, among them, the building’s exterior envelope is an important factor in its energy loss. It is an important basis for building energy conservation to explore the influence of the thermal parameter of the building exterior envelope on energy consumption from the perspective of thermal theory. Meanwhile, most of the buildings are old in university, limited by the actual conditions, studying the energy-saving optimization scheme from the main influencing factors and actual characteristics is a prerequisite for achieving high efficiency and energy saving. Therefore, based on the actual characteristics of university buildings, the influence law of the thermal performance of the exterior envelopes on energy demands is explored in this study through numerical simulation, and an energy-saving optimization scheme is proposed based on the existing materials. The results show that: (1) For university buildings in Chengdu, the energy-saving effect of the interior thermal insulation in exterior wall is the best; (2) the effect of insulation material type on total annual load tends to be the same as the insulation thickness is increased and stabilizes after the energy savings rate reaches 20%; (3) the selection of facing materials with low solar radiation absorption coefficients for exterior wall and roof has a much higher impact on cooling loads than on heating loads; (4) the suitable range of the heat transfer coefficient of the exterior window is 2.5 ~ 3.5, and the solar heat gain coefficient is 0.1 ~ 0.5; (5) using the optimization scheme can be saved by 18% of the heating load, 33% of the cooling load, and 28% of the total load compared to the status quo. The research results can provide a theoretical basis and data reference for energy-saving renovation of educational buildings.

Introduction

With the continuous development of higher education in China, the volume of university buildings is increasing, and the energy consumption of buildings is also increasing rapidly. Currently, energy consumption in universities accounts for 31% of the total social energy consumption, while energy used in university buildings comprises 84.1% of this total¹. Liu et al.² conducted a study analyzing energy consumption data from 16 universities in Shanghai. Their findings indicated that the potential energy savings for the total building energy consumption across these universities could reach up to 58%, with a minimum saving rate of 16%. However, in the higher energy consumption of university buildings, the energy consumption of air conditioning and heating caused by the heat transfer loss of the building envelope accounts for more than 70% of the total life cycle energy consumption of buildings^3,4. As a result, it has become our main research direction to reduce building energy consumption by selecting appropriate energy-saving measures for the building envelope. At present, many scholars have studied the reduction of building energy consumption in building technology mainly by adding air layer⁵, phase-change material^6,7, changing door and window type^8,9,10, adding retro-reflective material to the exterior wall¹¹, changing the thermal insulation layer attributes and locations on wall^12,13, building a green roof^14,15 and enhanced roof ventilation unit (ERU)¹⁶ to improve indoor thermal environment and building energy efficiency.

Alexandra et al.¹⁷ simulated the effect of different exterior walls, roofs, windows, doors, and airtightness on the building energy consumption by using SIMEB, and concluded that increasing wall insulation and replacing windows and doors could reduce the total annual energy consumption by 45%. Ma et al.¹⁸ examined the energy consumption of 119 public buildings in North China and used eQUEST to analyze the main factors affecting the energy consumption. They found that air conditioning system, lighting intensity, and building envelope are significant influencing factors. Zhou et al.¹⁹ studied four office buildings located in Beijing, Taiwan, Hong Kong, and Berkeley. By simulating energy consumption with different combinations of the three key factors (climate, building envelope, and occupant behavior), and discovered that the difference in cooling energy consumption due to the different climatic conditions was nearly two times, while the largest difference (up to three times) was due to occupant behavior. In addition, Mirrahimi et al.²⁰ reviewed the selection of suitable parameters for high-rise building envelopes, including climatic conditions, form, width, length and height, external walls, roofs, glass area, shading equipment, natural ventilation, and occupant thermal comfort. Ren et al.²¹ investigated factors such as building form factor, window-to-wall ratio, building orientation, and heat transfer coefficient of the building envelope utilizing Weather Tool and DesignBuilder software, and established an energy consumption optimization model. As a result, it is not difficult to find out the huge energy-saving potential in buildings through the above research, and there are more factors affecting the energy consumption of buildings. This mainly includes building structure design parameters, indoor equipment, outdoor thermal environment, human thermal comfort demand, energy management, and others.

In the context of today’s energy shortage, as a special public building, the high energy consumption of university buildings has made the construction of a conservation-minded campus the focus of contemporary scholars’ research, and it is also an inevitable requirement for countries to achieve sustainable development. Rewthong et al.²² found that the total electricity consumption increased by an average of 10% per year by counting the total electricity consumption, unit energy consumption, and energy utilization index in the total energy consumption of the Royal University of Hesunantha in Thailand from 2012 to 2014. Semprini et al.²³ measured the microclimate environment of different classrooms in typical historical buildings of the University of Bologna, Italy, and observed that the indoor thermal environment was uncontrollable due to the poorly insulated envelope, resulting in higher energy consumption. However, the potential energy savings of 32% could be achieved by retrofitting the building with less impactful building materials. Delvaeye et al.²⁴ compared the energy-saving potential of different daylighting control systems by counting the one-year test data of a typical university in Belgium and showed that it ranged from 18 to 46%. Liu et al.²⁵ carried out energy consumption data statistics on 16 universities in Shanghai and analyzed the energy-saving potential using weights. The results demonstrated that the total building energy saving rate of 16 universities could reach 58%, at least 16%. Moreover, by analyzing the actual operation data of universities throughout the year, Gao et al.²⁶ concluded that air-conditioning and lighting accounted for 85% of the energy consumption of the whole teaching building, which is the key area of energy saving in university buildings. Sun et al.²⁷ analyzed the energy saving of university buildings in severe cold regions of China and found that strict control of the building shape coefficient, strengthening the thermal performance of the building envelope, and using renewable energy could achieve good energy saving.

Based on the above research results, it is clear that studying the factors influencing building energy consumption is crucial for achieving energy savings in buildings, which can provide theoretical support for high-efficiency energy saving. Furthermore, many university buildings are older, limited by the actual conditions, studying the energy-saving optimization scheme from the main influencing factors and actual characteristics is a prerequisite for achieving high efficiency and energy saving. Meanwhile, the energy consumption characteristics of university buildings differ significantly from those of ordinary office and residential buildings. Universities tend to have lower energy consumption in January, February, July, and August, which are peak energy consumption months for other types of buildings. Another point is that there are big distinctions between the use function of university buildings and other buildings. Generally, university buildings not only bear the function of office but also teaching, and those room sizes and personnel density will also be quite different. Therefore, on the basis of previous scholars’ research, this study analyzes the thermal performance of the envelope of the teaching office building from the actual characteristics of the teaching office building and studies the relationship between the thermal performance of the envelope of the building energy consumption by using the numerical simulation method combined with the climatic conditions in Chengdu. On this basis, combined with the economy, existing materials, and construction characteristics, an optimization strategy is proposed for the building envelope. The research methods and conclusions can provide theoretical support and technical reference for the energy-saving design of educational public buildings and the energy-saving renovation of existing buildings.

Research flow

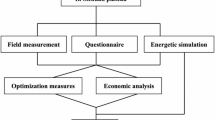
This study investigates how the thermal properties of exterior building envelopes influence energy demand and aims to develop an optimization strategy for university teaching-office buildings. First, a case study building in Chengdu is selected, and its structural and thermal characteristics are analyzed. A numerical simulation model is then created using EnergyPlus incorporating real-world climatic conditions, building materials, and operational schedules. To ensure accuracy, the model is validated through experimental measurements. Next, parametric analyses are performed to evaluate the impact of key thermal parameters, including insulation type and thickness, window properties, and solar radiation absorption coefficients, on heating and cooling loads. Based on the findings, an energy-saving optimization strategy is proposed, which considers practical constraints such as material availability and cost-effectiveness. Finally, the effectiveness of the optimized scheme is quantified, demonstrating its potential for reducing energy demands. The whole research flow is illustrated in Fig. 1.

Fig. 1

Flow diagram of the study.

Description of case building

Location overview of case building

The selected case building is located in Chengdu, China, positioned between 102°54’~104°53’E and 30°05 ~ 31°26’N, which territory is flat with an altitude ranging from 400 to 750 m above sea level, extending from northwest to southeast (see Fig. 2). Chengdu is a typical area with hot summers and cold winters in China. The annual temperature varies from − 2℃ to 28℃, with mild overall conditions. Summer temperatures can reach up to around 30 °C, while winter temperatures generally remain above 0 °C, but the relative humidity is high throughout the year¹². Considering the thermal comfort of the human body, there is still a high demand for heating and cooling in winter and summer, which also leads to relatively high energy consumption of air conditioning.

Fig. 2

Location of case building.

Functional layout and structural characteristics of case building

This case building is a typical university teaching-office building with a five-story frame structure and a standard layer of 3.9 m. It is divided into three relatively independent areas: A, B, and C with a total building area of 12340m² (see Fig. 3). Among them, area A is used as classrooms, floors 1–3 of area B are offices and laboratories, and floors 4–5 are drawing classrooms and teachers’ lounge. In Area C, the 1–2 floors are conference rooms, the 3rd floors are offices, and the 4–5 floors are offices and classrooms. The thermophysical properties of the materials related to the building envelopes are given in Table 1, and the construction methods and heat transfer coefficients of the main exterior envelope are shown in Table 2.

Fig. 3

Architectural plan (standard layer)²⁸.

It can be seen from Table 2 that the heat transfer coefficients of exterior walls and roofs meet the limits of K ≤ 1 and K ≤ 0.7 specified in the “Design Standard for Energy Efficiency of Public Buildings"²⁹, but they are almost close to the limit standards. In terms of high-energy consumption buildings, improving their thermal performance is still the focus of continuous research by related scholars.

Table 1 Thermophysical parameters of the Building envelopes.

Table 2 The construction method and heat transfer coefficient of main external envelope.

Methodology

EnergyPlus

Currently, representative building energy simulation software includes DOE-2, BLAST, EnergyPlus, ESP-r, and TRNSYS. Among them, EnergyPlus was jointly developed by the U.S. Department of Energy (DOE) and Lawrence Berkeley National Laboratory (LBNL) based on BLAST and DOE-2. It integrates the advantages of both and serves as a building energy consumption simulation engine that performs hourly load/system/equipment simulations in a synchronized manner. EnergyPlus provides higher computational accuracy compared to other software, and its simulation results have been validated in numerous analytical, comparative, and empirical cases³⁰. The computational process of EnergyPlus is based on the integrated processing of multi-program modules^31,32. The envelope heat transfer is determined by the conduction transfer functions (CTF)³³ and the airflow between zones is simulated by defining the flow rate and time or COMIS modules³⁴. Moreover, the WINDOWS program³¹ is used to calculate the heat transfer from exterior windows and the solar heat gain from the glazing. Whose core is the basic heat balance principle^13,35, and the calculation methods and characteristics are also described in the literature^28,31,32.

Determination of the numerical model

The numerical simulation is carried out in this study by EnergyPlus. The numerical model is shown in Fig. 4(b), and the specific geometry and thermal performance of the envelopes are described in Sect. 3.2. Furthermore, considering that Zone-C embodies all the characteristic features of a typical teaching-office building (including occupancy patterns, internal load dynamics, and HVAC operational behavior), it is selected as the research object for analysis and discussion. In the meantime, to simulate the actual characteristics of air-conditioning loads in university teaching-office buildings (Chinese universities have winter and summer vacations), the air-conditioning operation periods are set to be May 15th-July 15th in summer, and November 15th-January 25th of the second year in winter, every day from 08:00–12:00,14:00–18:00,19:30 − 22:00. The CSWD (Chinese Standard Weather Data) is used as the outdoor thermal boundary, which can be downloaded from EnergyPlus Weather Data³⁶. These data are more authoritative and reliable as the base data derived from the measured data of Chinese weather stations. Meanwhile, to simulate the air-conditioning load of university teaching-office buildings, an ideal HVAC system was set up in the offices and classrooms. Its heating thermostat is 18℃ while the cooling thermostat is 26℃³⁷. That is, the HVAC system is enabled to run when the indoor air temperature is below 18℃ in winter or above 26℃ in summer. Besides, considering the high personnel density of university teaching-office buildings, the office and classroom were set to 0.15 person/m² and 0.5 person/m², respectively, the power used for indoor lighting was set to 4 W/m² and the personnel activity (sitting and slight movement) was set at 72 W/person^28,38,39.

Model validation

In order to ensure the accuracy of the numerical model and the reliability of the simulation results, two representative rooms of the case building were selected for testing and validation in this paper, namely, B-5FC (zone B-5th Floor Classroom) and C-5FO (zone C-5th Floor Office), and the specific geometry and thermal performance of the envelopes were described in Sect. 3.2. The test parameters mainly include indoor and outdoor air temperature, relative humidity, solar radiation intensity, outdoor wind speed, and so on. The measurement of temperature and relative humidity were located at 1.5 m high above the floor (the middle of the test room), and the outdoor parameters were arranged on the roof (no shade). Among them, the indoor air temperature and relative humidity were measured using Testo-174 H-Mini with a temperature range of -20-70℃ and an error of ± 0.5℃ and relative humidity: 0–100%RH (error: ±3%). The outdoor ambient parameters were measured by using JTR05 within a range of temperature: − 50℃-50℃ (error: ±0.5℃), solar radiation intensity: 0–2000 W/m² (error: ±2%), and wind speed using TM404 with 0–25 m/s (error: ±2%+0.2). All tests were done according to the relevant standards⁴⁰ and data were recorded at 15-minute intervals. The experimental instruments were calibrated before the tests, and the tests were carried out from Jul. 12 to Jul. 22 (summer). In addition, to prevent the influence of thermal disturbances on the experimental results, doors and windows were closed during the tests. Detailed experimental arrangement is represented in Fig. 4a.

Fig. 4

(a) Experimental test arrangement, (b) numerical modeling, and (c) validation results.

Based on the above results, considering the stability of the experimental instruments, the continuous 72 h measured data during the summer experimental period from July 16 to July 18 for validation, and the experimental and numerical results are shown in Fig. 4c. It can be seen that the numerical results are in good agreement with the experimental results. However, to ensure the validation accuracy, two metrics: root mean square error (RMSE) and coefficient of variation (CV_(RMSE)) were employed and expressed by Eqs. (1) and (2)^28,41, respectively, as follows:

$${\text{RMSE=}}\sqrt {\frac{1}{{\text{n}}}\sum\limits_{{t=1}}^{n} {{{\left( {{M_t} - {S_t}} \right)}^2}} }$$

(1)

$${\text{C}}{{\text{V}}_{\left( {{\text{RMSE}}} \right)}}{\text{=}}\frac{{RMSE}}{{\overline {{{M_t}}} }} \times 100\%$$

(2)

It is found by calculation that the RMSE of the present numerical results is only 0.38℃ and 0.37℃ respectively for B-5FC and C-5FO, compared to experimental results, and the CV_(RMSE) are same only 1.37%. These results meet the simulation requirements with the ASHRAE criterion of CV_(RMSE) less than 30%⁴² and indicate the ability of EnergyPlus to predict the targets in this study.

Results and discussion

Impact of the different wall insulation properties on energy demands

Insulation forms

To investigate the impact of different insulation forms on energy demands, five commonly used wall insulation configurations were selected based on standard construction practices and existing literature^28,43,44,45. As shown in Fig. 5a, all configurations are designed with the same heat transfer coefficient of 1.0 [W/(m²·K)]⁴⁵. Among them, three insulation configurations (Exterior (wall-1), Sandwich (wall-2), and Interior thermal insulation (wall-3)) are commonly adopted in building energy-saving designs⁴⁴. Expanded polystyrene board (EPS) is selected in this study as the thermal insulation materials (TIM) due to its favorable thermal properties and cost-effectiveness. The other two are self-insulation walls with different weights. Apart from the insulation forms of the external wall to be studied, other boundary conditions are set according to the actual situation. The thermophysical parameters of the wall materials are listed in Table 3.

Fig. 5

(a) Typical wall insulation forms and (b) annual air-conditioning loads for five typical insulated walls.

Table 3 Thermo-physical parameters of wall materials⁴⁵.

Figure 5b shows the annual energy demands of the above five typical walls. It can be seen by comparison that the five walls have little effect on the annual cooling load and a relatively high impact on the annual heat load. Compared with other walls, the wall of interior thermal insulation (wall-3) has the lowest annual heat load and the highest annual cooling load. The main reason is that the lower thermal conductivity of the second layer material in the interior insulation wall blocks the transfer of indoor heat to the outdoors, which leads to energy saving in winter and wastage in summer. In terms of the heating load energy-saving, the wall-3 is 10.19% and the lowest is 2.1% compared with other walls. Furthermore, compared with wall-3, the lightweight self-insulation wall (wall-4) is greatly affected by the outdoor environment due to its high thermal response rate, which requires more heat in winter to maintain indoor warmth and dissipates heat faster in summer, resulting in higher annual heating load and lower cooling load. However, it can further be observed that the heavyweight self-insulation wall (wall-5) has the highest annual heat load and the lowest cooling load. Primarily because of the high thermal inertia of wall-5 can slowly absorb and release heat, which makes the indoor temperature fluctuation smaller. This characteristic causes it to require more heat in winter to maintain room temperature. Conversely, it can effectively isolate outdoor heat and reduce the rate of indoor temperature rise in summer, which leads to considerably higher energy-saving than other walls. In addition, from the perspective of the total annual load, wall-5 consumes the most energy, wall-3 is the most energy-saving, and wall-3 can save by 0.5%~2.3% compared with other walls. It also means that wall-3 is more suitable for building energy-saving in Chengdu than the other forms of insulation walls. Therefore, based on the above results, it can be easily concluded that for areas with different heating and cooling needs, a reasonable choice of wall insulation form is one of the more effective ways to achieve building energy savings.

Insulation material types and thicknesses

Based on the analysis above, it is evident that wall insulation can significantly enhance building energy saving However, as the performance of the TIM improves, the variety of available materials has also increased, and at the same time, different properties of TIM also affect building energy-saving. Thus, this study use a wall without insulation as a reference to explore the impact of adding different types and thicknesses of insulation layers to the exterior wall on the energy demands. Among them, it is necessary to point out that, although the above results have indicated that the interior insulation form is superior, considering the practical application, construction convenience, and the relatively small differences in energy-saving effects for five walls, the subsequent analysis and discussion are carried out using the exterior insulation wall. Table 4 provides the thermophysical parameters of several commonly used insulation materials.

Table 4 Thermophysical parameters of thermal insulation materials (TIM)⁴⁶.

Figure 6 presents the variation of energy demands after adding insulation layers of different types and thicknesses to the exterior walls. Figure 6a,b reveal that the impact of the TIM on cooling load is minimal, whereas on heating load is more significant. As the thickness of the TIM increases, the heating load is reduced and the cooling load is increased, but the magnitude of the increase in cooling load is basically negligible compared to the reduction in heating load, which is also consistent with previous research findings¹². The primary reason for this is that Chengdu is a hot summer and cold winter zone, with an average temperature of 25.4 °C during the hottest month, and the temperature difference between indoors and outdoors is relatively small, in contrast, the larger temperature difference in winter. It means that adding insulation effectively reduces the heat transfer coefficient of the building envelope, preventing indoor heat from escaping and improving insulation performance. However, in summer, the inability of indoor heat to dissipate effectively to the outside increases the cooling demand.

Fig. 6

Variation of annual air-conditioning load with insulation thickness for different insulation material types: (a) cooling load, (b) heating load, (c) total load, and (d) total load energy-saving rate.

Additionally, the energy-saving effects on energy demand vary depending on the type of insulation material, even at the same thickness. Taking the heating load energy saving of adding 30 mm TIM as an example, the percentage reduction in annual heating load is reduced by 54.59, 50.94, 45.29, 39.87, and 37.10%, respectively under the exterior wall is integrated with five different TIM (A, B, C, D, E). This indicates that adding TIM to the exterior walls significantly improves the energy-saving rate of the heating load. In the meantime, it can be observed from Fig. 6b that the impact of further increasing the insulation thickness on the heating load diminishes gradually. Furthermore, the thickness of different insulation materials is also different when the same energy-saving rate is reached. For example, to achieve a 50% reduction in the heating load, a thickness of ≥ 25 mm of polyurethane foam is sufficient, whereas expanded perlite requires a thickness of ≥ 60 mm to meet the same target, representing a 58% difference in thickness. Considering the cost of materials, it is essential to select the appropriate insulation material based on the specific conditions in engineering construction.

In terms of the annual total load (Fig. 6c,d), it can be noticed that the total load continues to decrease as the thickness of the TIM increases. However, when the thickness exceeds 100 mm, the energy-saving rate is basically stable at 20% (see Fig. 6d). and further increases in thickness result in similar total load reductions across different insulation materials. Continue to increase the thickness, the influence of the type of TIM on the total load tends to be the same. Moreover, it is discovered that as the thickness of the best performance of TIM (polyurethane foam) is increased from 0 mm to 100 mm, the incremental change in the annual total load energy-saving rate with each additional 10 mm is 11.27, 4.46, 2.23, 0.58, 0.41, 0.18, 0.06, -0.05, -0.05, and − 0.12%, respectively. This indicates that blindly increasing the insulation thickness can lead to diminishing returns and even negative growth in the energy-saving rate, ultimately producing counterproductive results, which further underscores the importance of selecting appropriate insulation materials based on factors such as climate characteristics, building type, and energy use requirements.

Impact of solar radiation absorption coefficients of wall outer-facing materials on energy demands

For building exterior walls, the outer facing layer is the first medium through which the outdoor thermal environment influences the indoor thermal environment, its solar radiation absorption coefficient (ρ_s) directly affects the outer surface temperature of the wall, and then the heat transfer through the entire wall, thereby influencing the indoor air conditioning load. For this reason, Fig. 7 illustrates the relationship between the ρ_s of outer facing materials and the heating load. It can be found from Fig. 7a that the heating load shows a linear decrease with the enhancement of the ρ_s. The higher the ρ_s, the more significant the energy-saving effect on the heating load. From 0.1 to 1, the energy-saving rate of the heating load for each 0.1 increment is 3.1, 6.3, 9.3, 12.2, 15, 17.6, 20.2, 22.7, and 25.2%, respectively. The result is produced mainly due to the fact that higher ρ_s raise the outer wall surface temperature, allowing the heat transferred through the wall to the interior to compensate for the energy consumption in heating the wall, thereby promoting the reduction of the heating load. On the contrary (see Fig. 7b), as the ρ_s increases from 0.1 to 1, the growth rate of the cooling load is 6.78, 13.55, 20.33, 26.66, 32.98, 39.46, 45.78, 52.26, 58.58% in order for each increase of 0.1. As seen from the data, it is evident that although increasing the ρ_s can effectively reduce the heating load, the resulting increase in cooling load far outweighs the reduction in heating load, so the annual total load shows a linear increase (see Fig. 7c). Indicating that while increasing the ρ_s may contribute to energy savings during the winter season, it does not lead to overall energy savings throughout the year. Hence, it can be drawn that for the higher cooling demand in Chengdu, selecting outer-facing materials with a lower ρ_s is more conducive to building energy-saving considering that the material is not replaced intermittently due to seasonal changes.

Fig. 7

Variation of annual air-conditioning load with solar radiation absorption coefficients of wall exterior facing materials: (a) cooling load (b) heating load (c) total load index.

Impact of different thermal properties of exterior windows on energy demands

As a special type of public building, teaching-office buildings typically have a larger window-to-wall ratio, which leads to a relatively higher proportion of energy consumption for the window. Therefore, the effect of different window heat transfer coefficients (K_win) and Solar Heat Gain Coefficient (SHGC)⁴⁵ on the energy demand is explored in this study on the basis of consideration of the heat transfer from window frames. Figure 8 shows the relationship between energy demand and the K_win and SHGC. It should be pointed out that when quantitatively analyzing the SHGC, the K_win and the visible light transmittance (τ_v), the thermal parameters were set according to the commonly used double-hollow-glazing (6 mm + 12 A + 6 mm), which are taken as 0.75, 3.4, and 0.81, separately⁴⁶.

As seen in Fig. 8a, the heating load rises linearly as the K_win increases, while the cooling load decreases linearly, but the impact on the heating load is greater than on the cooling load. The primary reason for this is that in Chengdu, during the summer, the time when the outdoor temperature is higher than the indoor temperature (T_out-T_in > 0) is shorter than the time when the outdoor temperature is lower than the indoor temperature (T_out-T_in < 0). A higher K_win allows more indoor heat to be transferred to the outdoors through the windows, thereby reducing the cooling load. However, the situation is reversed in winter. The time when T_out-T_in > 0 is less than the time when T_out-T_in < 0, resulting in the heat transfer from indoors to outdoors being enhanced under a higher K_win so that the heating load is enlarged. From the perspective of the impact on the total load, the total load first decreases and then increases during the process of K_win changing from 1 to 5.5, showing a certain inverted parabolic, the lowest load index being observed between 2.5 and 3.5 (optimal value). Additionally, it can be seen from Fig. 8b that the heating load is decreased as SHGC is raised, while the cooling load is increased, the total load shows an overall upward trend. Nevertheless, the change trend can be observed to be relatively small (△1) when SHGC is changed from 0.1 to 0.5. Once SHGC exceeds 0.5, the change rate of the total load is getting higher and higher (△2), which means a faster growth in total load. As a result, considering the energy-saving effect, it can be concluded that the optimal range of SHGC for exterior windows of teaching-office buildings in Chengdu is between 0.1 and 0.5.

Fig. 8

Variation of air-conditioning load with (a) heat transfer coefficient and (b) solar heat gain coefficient of exterior windows.

Impact of roof thermal performance on energy demands

As an important part of the building envelope, the roof receives long-wave radiation larger than any vertically facing wall. Its thermal performance significantly affects building energy consumption, especially for top-floor rooms. The relevant standard²⁹ stipulates that the heat transfer coefficient of building roofs (K_roof) in hot summer and cold winter areas should be ≤ 0.7. Accordingly, Fig. 9 gives the effects of different K_roof and outer surface solar radiation absorption coefficients (ρ_s) of the roof on the energy demands. It can be seen from Fig. 9a that as the K_roof increases, the heating load gradually increases, while the cooling load gradually decreases, and the annual total load shows an upward trend. It shows that the changes in the K_roof have a much greater impact on the heating load than on the cooling load. Meanwhile, the change rate of the total load is basically between 0.3% and 0.5% as the increase of K_roof from 0.1 to 0.7, with a total growth rate of 4.9%. So, it can be concluded based on the above results that for Chengdu, selecting a roof structure with a lower K_roof is more beneficial for building energy efficiency when considering the annual total load.

Fig. 9

Variation of air-conditioning load with (a) roof heat transfer coefficient and (b) solar radiation absorption coefficient on the outer surface of the roof.

In addition, to further investigate the impact of the roof’s solar radiation absorption coefficient (ρ_s) on energy demands, the K_roof is set at 0.7 [W/(m²·K)]. Figure 9b shows that the heating load decreases linearly when the roof ρ_s is large, which has a similar conclusion with the above-mentioned wall outer facing materials. As ρ_s increases from 0.1 to 1.0, up to 11.22% of the heating load can be saved, indicating that improving the ρ_s of roofing materials can effectively reduce heating load, which will have a more pronounced energy-saving effect in northern regions of China with higher heating demands. In comparison, although the heating load in winter can be reduced with the increase of roof ρ_s, the higher wall temperature significantly increases the cooling load for summer, leading to t a continuous growth in the annual total load. For this reason, from the perspective of year-round energy savings, choosing roofing materials with a lower K_roof and ρ_s is more suitable for energy-saving in educational buildings in Chengdu. However, for buildings in the cold climate zone of China with higher heating demand, increasing the ρ_s of the roof is also an effective way to reduce the annual total energy demand.

Analysis of optimization strategies

Selection of optimum thickness of TIM

Through the above analysis, it is evident that the TIM is the primary factor influencing its thermal performance for the non-transparent building exterior envelopes, which also directly affects energy demand. However, when the type of TIM is fixed, the thickness of the insulation layer becomes the main parameter influencing the thermal performance of the envelope structure. For this reason, considering the cost and energy saving effect of TIM, the relationship between the thickness of five types of TIM (A, B, C, D, and E) and the energy cost, material cost, and total cost was calculated in this study through Life Cycle Economic Evaluation (LCEE) model, and the results are shown in Fig. 10. The LCEE is described as shown in Eqs. (3) and (4). Moreover, the detailed process of calculating the LCEE can be also found in our previous studies^2,12,13.

$$C=\frac{{0.0052 \times PWF}}{{{R_{wt}}+\frac{{{\delta _{ins}}}}{{{\lambda _{ins}}}}}} \times \left( {\frac{{HDD18}}{{EER}}+\frac{{CDD26}}{{COP}}} \right)+{C_i}{\delta _{ins}}$$

(3)

When $\frac{{dC}}{{d\delta }}$= 0, C takes the minimum value, and the economic thickness δ of the insulating layer can be calculated by Eq. (4).

$${\delta _{op}}=\sqrt {\frac{{0.0052 \times PWF \times \left( {\frac{{HDD18}}{{EER}}+\frac{{CDD26}}{{COP}}} \right) \times {\lambda _{ins}}}}{{{C_i}}}} - {R_{wt}}{\lambda _{ins}}$$

(4)

Where, C—the total operating cost per unit area, RMB/(m²·a); HDD18, CDD26—the heating and cooling degree days; EER, COP—the energy efficiency ratios for air conditioning systems operating in winter and summer work, which are taken as 2.6 and 3.0 respectively. δ_ins—the thickness of insulation material, m; λ_ins—the thermal conductivity coefficient of material, W/(m·K); C_i—the cost per unit volume of insulation material, RMB/(m³·a); the 0.52 number represents the electricity price in Chengdu, RMB/kW·h; PWF—the present worth factor in the life cycle is expressed as the future value of funds converted to present value and is determined by Table 5; R_wt—the total thermal resistance of the base wall (excluding the insulation thermal layer), (m²·K)/W.

Table 5 The calculating method of present worth factor.

Based on the above results, using XPS installed on walls as an example, it can be seen from Fig. 10a that as the insulation thickness increases, the material cost rises linearly, while the energy-saving effect (energy cost) follows an inversely proportional function shape (first quadrant). The total cost curve forms an inverted parabola, with the minimum point occurring at a thickness of 20 mm. This indicates that thicker insulation does not necessarily result in better energy efficiency, instead, an optimal thickness must be chosen to achieve practical building energy savings. Otherwise, increasing the thickness beyond this point (optimal value) could lead to diminishing returns or even counterproductive outcomes. The above results have also been proved in previous studies¹².

Fig. 10

(a) The relationship between the thickness of different TIMs and the costs (XPS installed on the wall as an example), (b) for wall, and (c) roof.

Moreover, as seen in Fig. 10b, c, there are optimal values for different TIMs installed on the exterior wall and roof, but the optimal values (extreme points) for these five TIMs differ when applied to roofs compared to walls. The main reason for this difference is that the construction measures for walls and roofs vary although using the same TIM, leading to differences in their thermal performance. Consequently, the baseline heat transfer coefficient of walls and roofs differ, which further causes distinct optimal insulation thicknesses for each TIM application. Based on these results, Table 6 provides the optimal economic thickness and unit total cost for five typical TIMs installed on the exterior wall and roof. It reveals that although polyurethane foam has superior thermal performance compared to the other TIM, its optimal economic thickness does not yield the lowest unit total cost when both material costs and building operational costs are considered. For example, on the exterior wall, the corresponding unit total cost is 82.75 RMB/m², which is 21.17, 20.47, 27.82, and 35.77% higher than the other four commonly used TIM when each is applied at its optimal economic thickness. Meanwhile, compared to uninsulated walls, the unit area can be saved from 22.95 to 42.95% for the total cost of building operation. It shows that the materials with good thermal insulation performance are not necessarily the most energy-saving when considering both material investment and operational costs. Selecting the appropriate TIM and economic thickness is crucial for optimizing building energy efficiency.

Table 6 Economic thickness and total costs for different TIM installed in exterior wall and roof.

Comprehensive optimization model for exterior envelopes

Considering the impact of the aforementioned single factor on energy demands, construction difficulty, material costs, energy-saving rates, and other factors, this study has developed optimized solutions for energy-saving design or retrofits suitable for teaching-office buildings in Chengdu by selecting existing materials⁴⁶, which is shown in Table 7.

Table 7 Comprehensive optimization model for the exterior envelopes.

Figure 11 presents the energy demand and energy-saving rate under the present situation and optimized solutions. As shown in the figure, by implementing the comprehensive optimization of the building envelope, the heating load can be reduced by 17.72%, the cooling load by 33.34%, and the total load by 28.13% compared to the present situation, demonstrating a significant energy-saving effect. Therefore, it is clear based on the above results that for teaching-office buildings or even residential buildings in Chengdu, the impact of various factors should be considered comprehensively when carrying out energy-saving renovation or design so as to achieve maximum building energy-saving. Besides, optimization parameters for the building exterior envelopes will also vary depending on the energy demands of different climate zones. At the same time, building components are not replaced intermittently due to changes in climate or season, energy-saving design and retrofitting of teaching-office buildings should focus on the side with the highest energy demands, or set the annual total load as the energy-saving target, which is more conducive to realizing the maximum benefits of building energy-saving.

Fig. 11

Present situation of energy demand and optimization results.

Conclusions

This study has explored the relationship between the thermal performance of exterior envelopes and energy demands in a typical university teaching-office building in Chengdu through numerical simulation and experimental validation. Results indicate that the design and material properties of the building envelope are key factors influencing overall energy performance, particularly in terms of heating loads. The analysis reveals that the configuration and placement of insulation significantly affect the building’s energy efficiency, with interior insulation configurations showing a distinct advantage in minimizing heat loss during colder periods. Moreover, while enhanced insulation can effectively reduce heating loads, an optimal balance must be maintained to avoid diminishing returns or counterproductive increases in cooling demand.

Furthermore, it is further highlighted in this study that the importance of selecting exterior materials with lower solar radiation absorption coefficients. Although a higher absorption coefficient can reduce heating demands, it may also lead to increased cooling loads, particularly in hot climates like Chengdu. This finding underscores the need for a balanced approach to material selection and envelope design, which should be tailored to the specific climatic conditions and functional requirements of the building.

Overall, optimal building performance is achieved not by solely maximizing insulation or material performance, but by harmonizing multiple factors (insulation type, placement, and material properties) with the building’s specific operational and climatic context. In general, this research provides a comprehensive, qualitative understanding of how various envelope components interact to affect energy performance. The integrated optimization strategy proposed not only offers practical guidelines for improving energy efficiency in educational buildings but also contributes valuable insights for sustainable building design in climates similar to Chengdu.