Enhancing the accuracy of seismic velocity in near-surface layers through Laplacian spectra analysis of weighted graphs

Abstract

Shallow seismic surveys can play an important role in sustainable urban planning as well as monitoring of geological changes, contributing to climate resilience and the sustainable management of terrestrial ecosystems. A typical seismic layout involves devices (essentially senders and receivers) that transmit signals among themselves. Such layouts can be modeled by a graph using the notions of vertices and edges. In this paper, we propose a regression model to estimate seismic velocity in common near surface settings from spectra data of the normalized Laplacian matrix of the graph representing the seismic layout. The method is validated through tests on both synthetic and real seismic datasets, demonstrating exceptional accuracy. For the synthetic dataset, our model achieved about 99 % accuracy in velocity estimation. Remarkably, when applied to a real dataset acquired over a sabkha (salty soil) in eastern Saudi Arabia, it estimated the second layer’s velocity within 0.3% of the value determined by traditional methods, performed by an experienced geophysicist. In comparison to conventional velocity analysis approaches, the proposed method requires only one or few traces. In addition, it does not require picking of first arrivals, which can be costly and often inaccurate.

Introduction

Humans depend greatly on near-surface layers as these layers are used for agriculture, water resources, urban development, and industrial activities. That is why several UN Sustainable Development Goals (SDGs) have targets that interact with near-surface layers including SDG 2, 6, 9, 11, and 15¹. For example, SDG 2 targets food security through sustainable agriculture while SDG 15 targets halting and reversal of desertification. Both of these targets depend on a better characterization of near-surface layers. One of the main methods to characterize near-surface layers is through seismic surveys that provide velocities of compressional waves that depend in turn on the properties of the solid and fluid constituents of these layers.

The integration of graph theory into seismic modeling has significantly evolved since the mid-1970s, marked by the innovative work of Beitzel and Davis², who utilized it to refine velocity picking from velocity spectrum data, achieving results that rivaled those of experienced seismic data processors with greater efficiency. Nakanishi and Yamaguchi,³ introduced a compelling analogy, comparing the minimum-time path of a seismic ray to the route optimization challenges faced by a traveling salesperson. This conceptual groundwork was further explored by Moser^4,5, who demonstrated the utility of graph theory in seismic modeling by representing the subsurface with vertices and edges weighted by travel times, and employing Dijkstra’s algorithm to predict minimum-time paths with remarkable accuracy.

This approach was extended by Yang et al.⁶ through the development of a nonlinear iterative back projection algorithm aimed at enhancing travel-time tomography. Fischer and Lees⁷ optimized this algorithm by generating sparse graphs that adhere to Snell’s Law, thus significantly reducing processing times. Avendonk et al.⁸ proposed a hybrid method that allowed for more flexible ray bending, which, when applied to crustal models, significantly improved efficiency. Hu et al.⁹ further refined this approach to accurately calculate seismic event amplitudes due to geometrical spreading.

The extension of Moser’s method to 3D data by Cheng and House¹⁰ maintained the efficiency of the original method, while Bai et al.¹¹ introduced secondary nodes on 3D cell boundaries to better handle real-world models. Molodtsov and Roslov¹² as well as Anton and Weir-Jones¹³ advanced these methods to accommodate highly heterogeneous media and optimize travel-time calculations without derivatives, respectively.

Graph theory’s application has also spanned seismic migration, microseismic event location, and earthquake seismology, with notable contributions from Moser^14,15, Franklin¹⁶, and Eisner et al.¹⁷, demonstrating its versatility and accuracy in diverse seismic contexts. Zhang et al.¹⁸ utilized parallel GPUs to significantly accelerate pre-stack depth migration, while McBrearty et al.¹⁹ and Bogiatzis et al.²⁰ applied graph theory to earthquake seismology and the calculation of sensitivity kernels, respectively, showcasing the method’s robustness and precision.

In a recent study, Alfuraidan et al.²¹ employed spectral graph theory to innovatively approximate seismic velocities from the largest eigenvalues of weighted graph models, demonstrating promising accuracy with synthetic data. This work highlighted the potential for further enhancements in model accuracy and the interpretation of model parameters through the application on both synthetic and real data.

Our research aims to precisely estimate seismic velocities of subsurface layers through the analysis of graph models, focusing on the eigenvalues of the symmetrically normalized Laplacian matrix of a weighted graph which are known reveal important properties of the graph, as highlighted by Chung²². Graph’s topology and edge weights directly influence the Laplacian matrix, providing insights into the graph’s spectral properties. The eigenvalues derived from the normalized Laplacian matrices typically reflect the graph’s connectivity and structure, offering a spectral perspective that is pivotal for analyzing and interpreting the underlying physical systems modeled by the graph. The approach presented in this paper not only facilitates the incorporation of distances between seismic objects of interest but also provides a framework for intuitive physical interpretation. Our proposed linear regression model, leveraging the second largest eigenvalue of the symmetrically normalized Laplacian matrix, addresses previous challenges and demonstrates improvements in estimating seismic velocities with minimal residual errors.

The proposed method shows significant advantages in providing a more physically intuitive framework by directly incorporating distances between seismic sources and receivers into the graph model. In addition, the method demonstrates enhanced accuracy, significantly reducing velocity estimation errors compared to previous spectral graph-based methods. Furthermore, the method eliminates the need for extensive first-arrival picking, making it particularly useful for noisy datasets where conventional picking-based techniques struggle since only a smaller number of traces are picked. It is worth mentioning that conventional techniques in seismic velocity estimation require extensive work either in traveltime picking or velocity picking on the velocity-semblance images, while the proposed method requires picking of only three traces and the estimated velocity values show a very high accuracy. This method improves the efficiency and accuracy of seismic velocity estimation, which has significant implications for geophysical exploration and environmental applications. Additionally, it aligns with several UN SDGs that require accurate characterization of near-surface layers for sustainable resource management.

This paper is structured to introduce graph-theoretical preliminaries 3, define key matrices 4, and detail the seismic graph model and regression analysis 5 and 6. A sensitivity analysis of the model is presented in Section 8. We compare our model with existing approaches 7, validate it with field data 9, and discuss the advantages of graph-theory-based methods over traditional seismic velocity analysis techniques, highlighting their efficiency and the elimination of the need for extensive trace picking, as critiqued by Yilmaz²³.

Through this comprehensive study, we aim to advance the application of graph theory in seismic velocity analysis, offering a novel, efficient, and accurate method for understanding subsurface seismic velocities.

A flowchart describing the organization of this manuscript is presented in Fig. 1.

Fig. 1

A flowchart representation of the manuscript structure, illustrating the sequential organization of sections and their interconnections.

Preliminaries

This section outlines foundational concepts of graph theory pivotal to our analysis. The reader is encouraged to consult key sources for a deeper understanding, including^22,24, and²⁵.

Definition 2.1

A graph G is a structure comprising a set of vertices V(G), a set of edges E(G), and a mapping associating each edge with a pair of vertices, known as its endpoints. These vertices may be identical or distinct.

Vertices are adjacent if connected by an edge, and such pairs are considered neighbors. Adjacency between vertices a and b is denoted by $a \sim b$. The edge connecting a and b is denoted as $a \sim b$, implying that $a \sim b$ is incident to both vertices. Graphs are classified as directed if their edges possess orientation, else they are undirected if lacking such directionality.

Definition 2.2

A weighted graph assigns a numerical value, or weight, to each edge, quantifying some characteristic of the connection between vertices.

The weight between vertices a and b is expressed as w(a, b); if a and b share no edge, $w(a,b) = 0$.

Definition 2.3

An edge loop is an edge that connects a vertex to itself, while multiple edges refer to multiple connections between the same pair of vertices.

A simple graph lacks loops and multiple edges. Our study focuses on simple, undirected weighted graphs, simplifying terminology by referring to our models as weighted graphs.

Definition 2.4

The degree of a vertex v in a weighted graph, denoted as $d_v^\text {w}$, is the sum weight of all edges incident to v.

Formally,

$$\begin{aligned} d_v^\text {w} = \sum _{u \sim v} w(u,v), \end{aligned}$$

(1)

where the degree in unweighted graphs equals the count of incident edges. Throughout, we utilize the subscript w to distinguish between entities defined for both weighted and unweighted contexts.

This primer sets the stage for our subsequent exploration of graph models and their application to seismic velocity analysis.

Exploring graph structures with the weighted spectral Laplacian

The study of graph spectra through Laplacian matrices is fundamental in understanding the structure and properties of graphs. Let us consider a graph G with n vertices, denoted as $v_1, v_2, \ldots , v_n$. For the purpose of matrix representation, we align the $i^\text {th}$ row of any matrix with the vertex $v_i$ in the graph.

The adjacency matrix A(G), an essential construct, is an $n \times n$ symmetric matrix defined by:

$$\begin{aligned} a_{ij} = {\left\{ \begin{array}{ll} 1, & \text {if } v_i \sim v_j, \\ 0, & \text {otherwise}, \end{array}\right. } \end{aligned}$$

(2)

whereas the weighted adjacency matrix W(G) incorporates edge weights:

$$\begin{aligned} w_{ij} = {\left\{ \begin{array}{ll} w(i,j), & \text {if } v_i \sim v_j, \\ 0, & \text {otherwise}, \end{array}\right. } \end{aligned}$$

(3)

with w(i, j) representing the weight of the edge between $v_i$ and $v_j$.

The concept of the symmetrically normalized Laplacian, particularly relevant for weighted graphs, is introduced as:

$$\begin{aligned} L_{\text {sym}}^\text {w} (G) = I - D_\text {w}^{-\frac{1}{2}} W D_\text {w}^{-\frac{1}{2}}, \end{aligned}$$

(4)

where I is the identity matrix, and $D_\text {w}$ is the degree matrix for weighted graphs, a diagonal matrix with $d_{ii} = d_{v_i}^\text {w}$, the sum of weights of all edges incident to vertex $v_i$, as in (1). This formulation ensures that the matrix captures the connectivity and weight distribution of the graph, reflecting distances between connected vertices.

The entries of $L_{\text {sym}}^\text {w}(G)$, representing the symmetrically normalized Laplacian for weighted graphs, are given by:

$$\begin{aligned} l_{ij}^\text {w} = {\left\{ \begin{array}{ll} 1, & \text {if } i = j, \\ -\frac{w_{ij}}{\sqrt{d_{v_i}^\text {w} d_{v_j}^\text {w}}}, & \text {if } i \ne j \text { and } v_i \sim v_j, \\ 0, & \text {otherwise}, \end{array}\right. } \end{aligned}$$

(5)

emphasizing the importance of edge weights in modulating the graph’s Laplacian properties. This approach is restricted to connected graphs to ensure the invertibility of $D_\text {w}$, thereby guaranteeing that every vertex has a positive degree and that the matrix definition is sound.

For graphs where every edge weight represents the same physical quantity, the degrees of vertices (weighted) share the unit with the edge weights, leading to dimensionless entries and eigenvalues for $L_{\text {sym}}^\text {w}(G)$, as noted in the following remark:

Remark 1

The entries and eigenvalues of the normalized weighted Laplacian matrix are dimensionless, offering a universal metric for comparing graph structures regardless of the physical units of edge weights.

An illustrative example of a simple undirected weighted graph is shown in Fig. 2. The graph has vertex set and edge set $V(G) = \{a,b,c,d\}$ and $E(G) = \{ab,bc,bd,cd\}$, respectively, and the numerical value on each edge indicates its weight.

Fig. 2

An illustration of simple undirected weighted graph, demonstrating the adjacency and weight relationships between vertices.

Synthetic data modelling and seismic velocity estimation via graph theory

To validate our proposed graph theory-based technique for estimating seismic velocities, synthetic seismic data was generated using a three-layer velocity model. This model simulates layers with velocities of 500 m/s, 1500 m/s, and 2200 m/s, respectively, with the first and second layers having thicknesses of 30 m and 50 m. We simulated three shot gathers at offsets of 0 m, 100 m, and 200 m along the ground surface, and organized this data into a common mid-point (CMP) format as depicted in Fig. 3. This synthetic model was designed to demonstrate the accuracy and feasibility of the proposed graph theory technique; therefore, no random or coherent noise was added to the data.

The conversion of this seismic model into a graph format required defining sources, receivers, transmission points, and a midpoint as vertices. The edges were then established based on the ray paths connecting these points. The model includes source and receiver points ($\text {S}_1$ to $\text {S}_3$ and $\text {R}_1$ to $\text {R}_3$, respectively), transmission points ($\text {r}_1$ to $\text {r}_6$), and midpoint M. The positions of $\text {S}_1$ to $\text {S}_3$, $\text {R}_1$ to $\text {R}_3$, and M were fixed, while the locations of transmission points $\text {r}_1$ to $\text {r}_6$ varied based on the velocity and thickness values ($\text {V}_1, \text {V}_2, \text {H}_1,$ and $\text {H}_2$).

Fig. 3

Synthetic model validating the technique. Source points at $\text {S}_1$, $\text {S}_2$, $\text {S}_3$, receiver points at $\text {R}_1$, $\text {R}_2$, $\text {R}_3$, and reflection point at M. $\text {r}_1$ exemplifies a vertex, with $\text {S}_1-\text {r}_1$ illustrating an edge. Edge and vertex weights are also depicted.

An adjacency matrix of size $13 \times 13$ was constructed to represent the 13 points in our model (3 sources + 3 receivers + 6 transmission points + 1 midpoint). The weights for the edges, such as the edge $\text {S}_1 - \text {r}_1$, were determined by measuring distances between points and their projections along the layer boundaries, as illustrated in Fig. 3. These weights were then used to populate the adjacency matrix, assigning zero where no direct connection existed.

The graph theory problem was approached by considering all possible locations for the transmission points within the constraints outlined in Fig. 3:

(1):

$\text {r}_1, \text {r}_2,$ and $\text {r}_3$ are positioned with offsets smaller than that of M,

(2):

$\text {r}_4, \text {r}_5,$ and $\text {r}_6$ are positioned with offsets larger than that of M,

(3):

transmission points $\text {r}_1$ to $\text {r}_6$ are sequentially arranged.

A more detailed description is given using a case study presented in subsection 5.2.

Figure 4a and b showcase one of the synthetic shot gathers generated and the CMP gather extracted from the data, respectively.

Fig. 4

(a) A synthetic shot gather sample, with a small red arrow marking the trace used in the CMP gather (b). Key seismic events (direct and reflected waves) are identified. (b) CMP gather derived from synthetic data, with traces 1, 2, and 3 corresponding to source-receiver pairs ($\text {S}_3$-$\text {R}_3$), ($\text {S}_2$-$\text {R}_2$), and ($\text {S}_1$-$\text {R}_1$), respectively. The red arrow atop trace 2 links to the trace highlighted in (a).

Extension to the multi-layer

A sequential approach is proposed to generalize the procedure outlined above for models with multiple layers. To provide further clarity on this approach, we will explain it using the 3-reflector model depicted in Fig. 5. Initially, both V1 and V2 values are estimated following the procedure described earlier. Once these values are obtained, we can proceed to analyze the common midpoint gather from the third reflector, as illustrated in Fig. 5. This gather comprises 19 vertices and 18 edges, resulting in a $19 \times 19$ adjacency matrix. As the model complexity increases, we adopt a two-index notation $\text {r}_{ij}$ to label the vertices. Here, the index i represents the reflector number, while the index j denotes the vertex sequence number, as depicted in Fig. 5. It is important to note that the weights assigned to the edges $\text {S}_1-\text {r}_{11}$ and $\text {S}_1-\text {r}_1$ differ. Subsequently, an appropriate range of $\text {V}_3$ velocities needs to be selected. Once this range is determined, we can generate a $19 \times 19$ adjacency matrix for each attempted $\text {V}_3$ value using the approach described earlier in this section. By following this sequential approach, we can effectively extend the procedure to models with a greater number of layers. The systematic analysis of each reflector and the corresponding selection of velocity ranges allow for a comprehensive evaluation of the model’s properties. Overall, this sequential approach provides a structured methodology for handling models with increased complexity. It ensures that each layer is analyzed individually, leading to a more thorough understanding of the overall model.

Fig. 5

Synthetic model extending the proposed technique to a four-layer model. Source points at $\text {S}_1$, $\text {S}_2$, $\text {S}_3$, receiver points at $\text {R}_1$, $\text {R}_2$, $\text {R}_3$, and reflection point at M (on the reflector 3). $\text {r}_{21}$ exemplifies the first vertex on the second reflector. $\text {i}_1$, $\text {i}_2$, and $\text {i}_3$ are incidence angles of the ray from $\text {S}_1$ to M through reflectors 1, 2, and 3, respectively. Weighted are also depicted.

Synthetic data generation for two-layer seismic layout

This section presents a case study to describe the generation of the synthetic data used in this study. We generated synthetic seismic data using a three-layer velocity model to validate our proposed graph theory-based technique for estimating seismic velocities. This model consists of layers with velocities of 500 m/s, 1500 m/s, and 2200 m/s, with the first and second layers having thicknesses of 30 m and 50 m, respectively (Fig. 2). For our graph theory approach, we required only three shots. Consequently, we simulated three noise-free shot gathers at offsets of 0 m, 100 m, and 200 m along the ground surface. The generated data was then organized into a common mid-point (CMP) gather, from which we extracted and utilized three traces for our analysis (Fig. 2).

To represent the seismic model in a graph-theory format, we defined the sources, receivers, transmission points, and midpoint as vertices. The edges were established based on the ray paths connecting these points. The model included source and receiver points ($\text {S}_1$ to $\text {S}_3$ and $\text {R}_1$ to $\text {R}_3$, respectively), transmission points ($\text {r}_1$ to $\text {r}_6$), and midpoint M, resulting in a total of 13 vertices. It is important to note that the positions of the sources, receivers, and midpoint remained fixed regardless of the velocity or thickness values. However, the locations of the transmission points ($\text {r}_1$ to $\text {r}_6$) varied based on the specific velocity and thickness values ($V_1$, $V_2$, $H_1$, and $H_2$).

To represent the relationships between the points in our model, we constructed an adjacency matrix of size $13 \times 13$. This matrix accounted for the thirteen points in our model, including the sources, receivers, transmission points, and midpoint. The weights for the edges, such as the edge between $\text {S}_1$ and $\text {r}_1$, were determined by measuring the distances between the transmission point and the projection of the vertex along the layer boundary, as illustrated in Fig. 3. These weights were subsequently used to populate the adjacency matrix, with zero assigned where no direct connection existed.

Forming the adjacency matrix is a key step in applying the graph theory. To provide a clear understanding of this process, we explain how to form the adjacency matrix in the following steps:

• 1. The velocity of the first layer ($V_1$) is calculated from the original shot gathers using the standard Intercept Time Method (ITM)^26,27. In this method, the velocity of the first layer is determined as the inverse of the slope of the first arrival travel times associated with that layer.

• 2. The data is then rearranged into a common mid-point (CMP) configuration, and only three traces are extracted from the CMP gather. It is recommended to choose traces at near, intermediate, and far offsets that exhibit a high signal-to-noise ratio, minimizing errors caused by background noise.

• 3. The expected range of the velocity for the second layer ($V_2$) is determined based on two factors: knowledge of the geology in the study area. In this synthetic example, we assumed an extreme range for the velocity of the second layer, spanning from 1.10 to 4.0 times the velocity of the first layer. This broad range is used to demonstrate the efficiency of the proposed technique.

• 4. Since $V_1$ is equal to 500 m/s, we consider a range for $V_2$ from 540 m/s to 2000 m/s with a step of 5 m/s, i.e. $550, 555, 560, \dots , 2000$. This results in a set of 291 possible values for $V_2$. The range and step of the $V_2$ are typically determined by the user based on the general geology of the study area.

• 5. We generate one adjacency matrix for each of the 291 possibilities. As we have a total of 13 vertices, each adjacency matrix will have a size of $13 \times 13$. The order of the vertices is as follows: vertices 1 to 3 correspond to $\text {S}_1$ to $\text {S}_3$, respectively; vertices 4 to 6 correspond to $\text {R}_3$ to $\text {R}_1$, respectively; vertices 7 to 12 correspond to $\text {r}_1$ to $\text {r}_6$, respectively; and vertex 13 corresponds to the midpoint M. The following rules are used to determine the edges connecting the vertices:

  • There are no edges between any vertex and itself. The corresponding value in the adjacency matrix will always be 0.

  • Edges exist only between vertices connected by seismic ray paths, as depicted in Fig. 2. In this model, we have 12 edges in total.

  • Only these 12 edges will have values in the adjacency matrix, while all other elements in the matrix will be equal to 0.

  • We begin with a $13 \times 13$ matrix initialized to 0 in all entries, as shown in the matrix below

    $$\begin{aligned} \left( \begin{array}{cccccccccccccc} 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{array}\right) \end{aligned}$$

• 6. We illustrate the formation of the adjacency matrix when $V_2$ is assumed to be 1220 m/s as an example:

  • Given the positions of the three sources as $\text {S}_1$ (0,0), $\text {S}_2$ (100,0), and $\text {S}_3$ (200,0), the positions of the three receivers as $\text {R}_1$ (300,0), $\text {R}_2$ (400,0), and $\text {R}_3$ (500,0), and the position of the midpoint (point M) at (250,0).

  • Knowing the velocity of the first layer (500 m/s)

  • Assuming the velocity of the second layer (1220 m/s)

  • Find the locations of the six transmission points ($\text {r}_1$ to $\text {r}_6$) that satisfy Snell’s law, $\left( \frac{\sin i}{\sin r} = \frac{V_1}{V_2}\right)$, where i and r are the incident and refraction angles, respectively.

  • Calculate the weight of each edge by calculating the distances between the vertex projection and the transmission point along the layer boundaries. For example, the weight for the edge $\text {S}_1$-$\text {r}_1$ is equal to the distance between the projection of $\text {S}_1$ and the position of $\text {r}_1$ along the first boundary; in our case, it is 13.133 m. Since we are considering vertex 1 (point $\text {S}_1$) and vertex 7 (point $\text {r}_1$) in this edge, this value will be assigned in the adjacent matrix in positions (1,7) and (7,1), where the first number refers to the row and the second to the column value in the adjacency matrix.

  • To increase the accuracy of the adjacency matrix, we convert all distances into millimeters. Hence, the adjacency matrix after inserting the weight of the first edge is shown below

    $$\begin{aligned} \left( \begin{array}{cccccccccccccc} 0 & 0 & 0 & 0 & 0 & 0 & 13133 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 13133 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{array}\right) \end{aligned}$$

  • This process is repeated for all other edges ($\text {r}_1$-M, M-$\text {r}_6$, $\text {r}_6$-$\text {R}_1$, $\text {S}_2$-$\text {r}_2$, etc.) to form a $13 \times 13$ matrix

    $$\begin{aligned} \left( \begin{array}{cccccccccccccc} 0 & 0 & 0 & 0 & 0 & 0 & 13133 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 12521 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 8177 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 8177 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 12521 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 12521 & 0 \\ 13133 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 236567 \\ 0 & 12521 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 137479 \\ 0 & 0 & 8177 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 41823 \\ 0 & 0 & 0 & 8177 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 41823 \\ 0 & 0 & 0 & 0 & 12521 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 137479 \\ 0 & 0 & 0 & 0 & 0 & 12521 & 0 & 0 & 0 & 0 & 0 & 0 & 236867 \\ 0 & 0 & 0 & 0 & 0 & 0 & 236567 & 137479 & 41823 & 41823 & 137479 & 236867 & 0 \end{array}\right) \end{aligned}$$

• 7. The resulting matrix in step ($\textrm{vi}$) above can be interpreted as the adjacency matrix of the weighted graph abstraction of the seismic layout in Fig. 3. A particular representation of such weighted graph is shown in Fig. 6. The normalized Laplacian of the graph model is then computed as discussed in Section 3.

  For this case study, the eigenvalues of the resulting normalized Laplacian are:

  $$\begin{aligned}&[2, 1.4044, 1.3921, 1.2889, 1.2673, 1.2267, 1.0, 0.7327, 0.7111, 0.6079, 0.5956, 0]. \end{aligned}$$

  The eigenspectrum is then explored to find a suitable predictor variable for our target $V_2$ (see discussion in Section 6). In the rest of this paper, we denote the eigenvalues of the normalized Laplacian by $\lambda$, with the convention that $\lambda _1 \ge \lambda _2 \ge \cdots \ge \lambda _{13}$.

• 8. The process is now repeated for other adjacency matrices, assuming different possible values for $V_2$. We always honor the following three conditions when applying the proposed technique:

  • $\text {r}_1$, $\text {r}_2$, and $\text {r}_3$ are positioned with offsets smaller than that of M,

  • $\text {r}_4$, $\text {r}_5$, and $\text {r}_6$ are positioned with offsets larger than that of M,

  • Transmission points $\text {r}_1$ to $\text {r}_6$ are sequentially arranged.

• 9. Finally, we find the optimal $V_2$ value among all possible $V_2$ values (291 in this case), which minimizes the root mean square error (RMSE) between the calculated and observed travel times for all source-receiver pairs.

Fig. 6

A graph abstraction of the seismic layout in Fig. 3 for a particular case whose adjacency matrix is described in subsection 5.2.

Figure 3a and b showcase one of the synthetic shot gathers generated and the CMP gather extracted from the data, respectively. The graph theory approach yielded a $V_2$ value of 1500.18 m/s, closely matching the true value of 1500 m/s and demonstrating an error of only 0.012%. This result underscores the high accuracy of the proposed method in determining seismic velocities.

Data-driven model for seismic velocity prediction

This section outlines the development of a data-driven model to approximate seismic velocities using graph theoretical approaches. The analysis begins with an exploration of potential predictor variables derived from the seismic layout’s graph model, specifically focusing on the spectrum of the normalized Laplacian matrix.

Data exploration

Exploration of the spectrum of the normalized Laplacian of each seismic model was conducted to identify suitable predictor variables for the seismic velocity, $V_2$. In many applications, the spectrum of graphs typically contains valuable information about the physical model they represent. Such applications include use of graph spectra in graph signal processing²⁸, study of conjugated molecules via the spectra of their graph representation^29,30. Quantities such as spectral radius, smallest eigenvalue, mean of the eigenvalues, sum of eigenvalues, among others, are often of interest.

In this study, we first observe that the graph in Fig. 6 is bipartite with $\{M, \text {S}_1, \text {S}_2, \text {S}_3, \text {R}_1, \text {R}_2, \text {R}_3\}$ in one partition and $\{\text {r}_1, \text {r}_2, \text {r}_3, \text {r}_4, \text {r}_5, \text {r}_6\}$ in the other. For such graphs, it is known that the spectral radius ($\lambda _1$) of the normalized Laplacian always equals 2, see Lemma 1.7 in Ref.²². Moreover, all the graph models obtained from the seismic layout of Fig. 3 have the same bipartite structure and, as such, the spectral radius always equals 2. Consequently, the spectral radius proves unsuitable for prediction purposes.

Additionally, for any eigenvalue $\lambda _i$, $i = 1, 2, \dots , 6$, $2 - \lambda _i$ is also an eigenvalue, see Lemma 1.8 of the aforementioned reference. Thus, for each model, the smallest eigenvalue equals 0, making it an unsuitable predictor as well. A similar issue is observed with the sum of eigenvalues and their mean, as it is immediate to see that the trace of the normalized Laplacian for the model with thirteen nodes is always 13.

To this end, other quantities in the spectrum of the graph model were investigated. A detailed exploration revealed a suitable pattern between the second largest eigenvalue, $\lambda _2$ (and by extension $2 - \lambda _2$), and the target variable $V_2$. The plots in top row of Fig. 7 provide a visualization of the relationship between the second largest eigenvalue $\lambda _2$ and the target $V_2$ (left) as well as the relationship between $2 - \lambda _2$ and the target $V_2$ (right).

Other quantities in the spectrum were also investigated. It was observed that all eigenvalues $\lambda _2, \dots , \lambda _6$ exhibit a similar relationship with $V_2$, while eigenvalues $\lambda _8, \dots , \lambda _{12}$ also exhibit a similar relationship. For completeness, the cases of $\lambda _3$ and $\lambda _{11}$ are presented in the bottom row of Fig.  7. Consequently, each element in the spectrum, other than $\lambda _1 = 2$, $\lambda _7 = 1$, and $\lambda _{13} = 0$ (for all models), proves to be a suitable predictor variable. This further highlights the significant potential of the normalized Laplacian over the weighted adjacency matrix for our application of interest.

Fig. 7

Exploration of the relationship between eigenvalues of the normalized Laplacian and the seismic velocity $V_2$.

A linear regression model

Given the observation from the data exploration, and the numerical nature of both the predictor (second largest eigenvalues) and the target (seismic velocities), a regression approach is deemed appropriate. Empirical evidences suggest that a quartic polynomial model strikes an optimal balance between fitting accuracy and avoidance of overfitting, thus ensuring model generalization. Explicitly, the regression model considered is given by

$$\begin{aligned} V_2 = \sum _{i = 0}^{4} \beta _i x^i + \epsilon _i, \end{aligned}$$

(6)

where $\epsilon _i$ is some error term, and x represents the second largest eigenvalue of the normalized Laplacian of the graph model abstraction of the seismic layout. The coefficients $\beta _i$ are determined from the data using regression tools from the scikit-learn library in Python, facilitating efficient data splitting for training and testing. Given the dimensionless nature of the predictor variable x, the regression coefficients $\beta _i$ carry units of velocity ($\text {m/s}$), allowing for direct interpretation in terms of seismic velocities.

The model’s efficacy is validated using data partitioned into a 70% training set and a 30% testing set. The data splitting is performed using the train_test_split function in Python, which shuffles the entire dataset randomly before partitioning it according to the specified criteria (70% training and 30% testing in our case). This method largely ensures that neither the training nor the testing dataset is biased towards any particular parameter value. Splitting the data this way results in 203 training data points and 88 testing data points, out of the total 291 data points.

Applying the training data to Eq. (6), we formulate a linear system as follows:

$$\begin{aligned} A\textbf{b} = \textbf{V}_{tr} + \mathbf {\mathcal {E}}, \end{aligned}$$

(7)

where

$$\begin{aligned} A = \begin{pmatrix} 1 & x_1 & x_1^2 & x_1^3 & x_1^4 \\ 1 & x_2 & x_2^2 & x_2^3 & x_2^4 \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ 1 & x_{203} & x_{203}^2 & x_{203}^3 & x_{203}^4 \end{pmatrix}, \qquad \textbf{b} = \begin{pmatrix} \beta _0 \\ \beta _1 \\ \beta _2 \\ \beta _3 \\ \beta _4 \end{pmatrix}, \\ \textbf{V}_{tr} = \begin{pmatrix} V_2^{(1)} \\ V_2^{(2)} \\ \vdots \\ V_2^{(203)} \end{pmatrix}, \qquad \mathbf {\mathcal {E}} = \begin{pmatrix} \epsilon _1 \\ \epsilon _2 \\ \vdots \\ \epsilon _{203} \end{pmatrix}, \end{aligned}$$

where $x_i^j$ is the jth power of the ith second largest eigenvalue in the training set, and $V_2^{(i)}$ is the ith velocity in the training set.

Dropping the error term $\mathbf {\mathcal {E}}$, the parameter vector $\hat{\textbf{b}} \approx \textbf{b}$ (in a componentwise sense) can be learnt by solving the least square problem:

$$\begin{aligned} \hat{\textbf{b}} = \mathop {\textrm{argmin}}\limits _\textbf{b} ||\textbf{V}_{tr} - A\textbf{b}||_2^2, \end{aligned}$$

(8)

where the vector $\textbf{V}_{tr}$, contains the values of the seismic velocity $V_2$ in the train data and $||.||_2$ denotes the usual number on the $\ell ^2$-norm. The learned parameters, $\hat{\beta }_i \approx \beta _i$, are as follows (with some truncated decimals):

$$\begin{aligned} \hat{\beta }_0&= 892690.28,&\hat{\beta }_1&= -2287817.14, \\ \hat{\beta }_2&= 2213169.32,&\hat{\beta }_3&= -956057.72, \\ \hat{\beta }_4&= 155433.07, \end{aligned}$$

from which we have the estimate $\hat{V}_2 \approx V_2$:

$$\begin{aligned} \hat{V}_2 = \sum _{i = 0}^{4} \hat{\beta }_i x^i. \end{aligned}$$

(9)

Accuracy is assessed using the percentage error metric $P_e = \frac{|V_2 - \hat{V}_2|}{|V_2|}$, which quantifies the model’s pointwise prediction accuracy. In addition, the root mean square error (RMSE), mean absolute error (MAE), mean absolute percentage error (MAPE), and the $R^2$, score are computed as metrics to further assess the model performance.

The plots in Fig. 8 showcase the model’s performance on training as well as testing datasets. The model demonstrates good predictive accuracy, with most data points exhibiting a percentage error of 0.1% or less, indicating a maximum absolute error in predicting $V_2$ from the second largest eigenvalues of less than $0.001 \times V_2$ for the test data.

Fig. 8

Data predictions: Plot of Data matching (left), percentage error (right). Top row: training data, bottom row: testing data.

The oscillating patterns observed in the plots of the percentage error in Fig. 8 indicate that the residuals do not exhibit a normality pattern. This may be attributed to the fact that the synthetic data was generated without noise. Further investigation is conducted in Subsection 8, where some noise is injected into the data. Additionally, in the left plots of Fig. 8, it can be seen that the values of the target variable, $V_2$, do not exhibit sporadic random changes but rather lie almost completely on a smooth curve with respect to the independent variables. In particular, the zoomed regions $550 \le V_2 \le 615$ for the training data and $575 \le V_2 \le 770$ for the test data show a typical pattern, where it can be seen that the true values of $V_2$ drift mildly around the curve of the predicted values.

Comparative analysis of seismic velocity prediction models

This section presents a comparison between the current study’s model and the approach introduced in our previous work²¹. Both studies employ quartic regression models to estimate seismic velocity $V_2$, albeit with different predictor variables. Our earlier research utilized the spectral radius of the weighted adjacency matrix from the graph model of the seismic layout as the predictor, contrasting with the current model’s use of the second largest eigenvalues of the normalized Laplacian matrix.

More specifically, Alfuraidan et al.,²¹ used another graph theory approach to estimate the seismic wave velocities. However, in their work, they demonstrated their approach using only a synthetic model; whereas, in this work, we used a different approach of the graph theory, which produced more accurate results, and we also demonstrated the method using synthetic and field examples. To compare Alfuraidan et al. 2023 synthetic results and the current results; in Alfuraidan et al. 2023, the true value of the velocity was 1500 m/s, and the estimated value was 1509 m/s with an error equal to 0.6%. Using the current approach, the estimated velocity value was 1500.18 m/s, with an error of 0.012%, which indicate a significant improvement.

To facilitate a fair comparison, we construct datasets incorporating the weighted adjacency matrix and the normalized Laplacian for each seismic model, alongside the actual seismic velocities. Each dataset is then divided, allocating 70% for the identification of model parameters (training) and the remaining 30% for model validation (testing).

Graphical comparison of the prediction accuracy of the two models are presented in Fig. 9 with plot of the percentage error in predicting the training data on the left and that of the test data on the right. The analysis reveals that the model based on the spectral radius of the weighted adjacency matrix yields residuals approximately an order of magnitude larger than those obtained with the current study’s approach. This observation underscores the enhanced precision afforded by leveraging the spectrum of the normalized Laplacian matrix within weighted graph models for predicting seismic velocities.

Further comparisons are presented Table 1 via the RMSE, MAE, MAPE, and $R^2$-score. Values of the first three metrics highlight accuracy of the models. Moreover, comparing the values of these metrics for predictions from the normalized Laplacian, presented in this paper, to those of the weighted adjacency matrix,²¹, highlight the improved accuracy attained in this paper. The high $R^2$ score achieved by the two models suggests both of them well explain variability in the data.

Fig. 9

Model performance comparison: A comparison of the prediction residuals in using second largest eigenvalues of the normalized Laplacian (red dots) versus spectral radius of the weighted adjacency matrix (blue dots) to approximate the seismic velocity $V_2$. Training data (left), testing data (right).

Table 1 A comparison of some metric values for the normalized Laplacian based model and the weighted adjacency matrix.

Sensitivity analysis

We present here some numerical results related to learning the regression parameters in (6) from a noisy dataset. Two separate cases are considered, one case to simulate data with noisy velocity readings and the other for noisy values in the location of the sensor and/or transmission points.

Noisy velocity readings

To generate a noisy data set, random numbers generated from a normal distribution are added to the target variable $V_2$. For the training data, a noise vector, denoted $\varepsilon _{tr}$, consisting of 203 random numbers is generated from a normal distribution with mean 0 and standard deviation 10. This noise vector is then added to the vector $\textbf{V}_{tr}$, which contains the values of the seismic velocity $V_2$ in the training data, resulting in the noisy training data vector:

$$\begin{aligned} \textbf{V}^n_{tr} = \textbf{V}_{tr} + \varepsilon _{tr}. \end{aligned}$$

(10)

Similarly, for the test data, another noise vector, denoted $\varepsilon _{te}$, consisting of 88 random numbers is generated from the same normal distribution (mean 0 and standard deviation 10), to obtain:

$$\begin{aligned} \textbf{V}^n_{te} = \textbf{V}_{te} + \varepsilon _{te}, \end{aligned}$$

(11)

where $\textbf{V}_{te}$ is a vector containing the values of the seismic velocity $V_2$ in the test data.

The resulting noisy data for training the model is presented in Fig. 10 (top plot), showing the true and noisy values of $V_2$, while the plot on the bottom shows the noise against the velocity values, $V_2$, indicating how much noise is added to each $V_2$ as well as the randomness in the noise. Similar scenarios are presented in Fig. 11 for the test data.

Fig. 10

Profiles of the velocity $V^n_2$ from the noise and noiseless training data (left), associated noise in the data (right).

Fig. 11

Profiles of the velocity $V^n_2$ from the noise and noiseless test data (left), associated noise in the data (right).

Applying the noisy training data to the regression model (6), we solve the least squares problem:

$$\begin{aligned} \hat{\textbf{b}}^n = \mathop {\textrm{argmin}}\limits _{\textbf{b}^n} ||\textbf{V}_n^{tr} - A\textbf{b}^n||, \end{aligned}$$

(12)

where A is the same as in (8) (since no noise is added to the eigenvalues), to learn the corresponding parameters:

$$\begin{aligned} \hat{\beta }_0^n&= 940886.77,&\hat{\beta }_1^n&= -2425751.63, \\ \hat{\beta }_2^n&= 2360980.59,&\hat{\beta }_3^n&= -1026349.04, \\ \hat{\beta }_4^n&= 167949.21. \end{aligned}$$

The velocity estimated from the noisy data, $\hat{V}^n_2 \approx V^n_2$, is given as:

$$\begin{aligned} \hat{V}^n_2 = \sum _{i = 0}^{4} \hat{\beta }^n_i x^i. \end{aligned}$$

(13)

Unlike the clean data, Fig. 12 shows that the residuals from the noisy data do exhibit true randomness, validating the normality assumption as a result of the normally distributed noise in the data. This also indicates that the nonnormality in the residuals observed in the noiseless is likely due to the absence of noise in the target variable and not due to overfitting in the model. Plots of the percentage error in the approximation are presented in Fig. 13, and it is observed that in the presence of artificial noise, the model is able to cope reasonably.

Fig. 12

Residuals in predicting $V_2^n$ in the noisy data by (13): training data (left), test data (right).

Fig. 13

Percentage error in predicting $V_2^n$ in the noisy data by (13): training data (left), test data (right).

Noisy position readings

The effect of possible noisy measurements in the positions of the sensor nodes $\text {R}_i$, $\text {R}_i$, $\text {r}_i$ and $\text {M}$ are examined here. These measurements affect the weights on the edges of our graph models and consequently, eigenvalues of the matrices. To simulate this noisy system, randomly generated numbers from three normal distributions each having mean 0 and different values of standard deviation $0.1, 0.5, \text { and } 1$ are added to the weights on edges of the graph model. A particular case is presented in Table 2 showing changes to the weights for different standard deviation values.

Table 2 Edge-weights of a particular model, showing the clean data and the noisy counterpart.

The plots in Fig. 14 show the percentage change in the second largest eigenvalues at different noise levels $\sigma = 0.01$ on the left and $\sigma = 0.1$ on the right. These errors are computed for each of the two-hundred and ninety one models in our dataset. It is observed that the percentage change in the eigenvalues is relative to the noise level introduced in the input data (the weights), with rise in (maximum) percentage error from 0.03 to 0.3 (about ten folds) corresponding to rise in the noise level standard deviation 0.01 to 0.1 (about ten folds). From these eigenvalues (arising from noisy inputs), sensitivity of the regression model to noisy values of the weights on edges in the graph model is analyzed. Figure 15 shows the percentage error in estimating the seismic velocity at different noise levels $\sigma = 0.01$ on the left and $\sigma = 0.1$. It observed that the maximum percentage error grows from in about nine folds (similar to the change in values of the eigenvalues) as $\sigma$ increases ten folds. Similar observation is made on the training data in Fig. 16.

Fig. 14

Percentage change in the second largest eigenvalues of the normalized Laplacian matrix for noise levels $\sigma = 0.01$ (left) and $\sigma = 0.1$ (right).

Fig. 15

Percentage error in estimating the velocity of the test data from noisy values $\lambda _2$ for noise levels $\sigma = 0.01$ (left) and $\sigma = 0.1$ (right).

Fig. 16

Percentage error in estimating the velocity of the training data from noisy values $\lambda _2$ for noise levels $\sigma = 0.01$ (left) and $\sigma = 0.1$ (right).

Some error metrics presented in Table 3 are computed to further analyze the sensitivity of the model to noisy inputs in the edge weights. In particular, it can be is seen here that the RMSE, in particular, scales similar to $\sigma$ (which measure the magnitude of added noise). The change in values of these metrics indicate that the model can be sensitive to noise. This issues suggest that model could further benefit from noise reduction strategies such has regularization. On the bright side, resilience of the $R^2$ score in presence of the noise highlights that the model retains a good explanatory power.

Table 3 Values of the root mean square error, mean absolute error, mean absolute percentage error and the $\text {R}^2$, metrics for the predictions from data with noisy edge-weight.

Field data validation of the proposed model

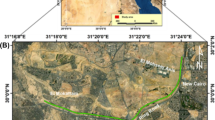
The field data used to test the proposed method is recorded on a barchan dune located at northwest of Dammam, Eastern Province of Saudi Arabia (Hanafy et al. 2020). The seismic source used here is a 200-lb accelerated weightdrop hitting the same spot 10 times to enhance the signal-to-noise ratio (SNR) of the recorded data. Total number of recorded shot gathers is 96 with 3 m intervals, each shot gather has 96 receivers at 3 m intervals and 40-Hz dominant frequency. Hanafy et al.³¹ picked the first arrival traveltimes of the recorded data and inverted it to generate a 2D velocity tomogram of the subsurface.

To have a ground truth at the test site, we drilled a 10 m deep vertical borehole at the midslope of the dune. In order not to disturb the sand while drilling we used a dry percussion-drilling method. As a result, we extracted an 0.7 m core sample from each 1.5 m drilling interval. The well penetrated the entire dune, as well as the top 3 m of the underlying sabkha. Based on analysis shown on Hanafy et al. (2020) quartz was the main mineral in the dune with smaller amounts of feldspar and traces of calcite, while the underline sabkha contained quartz, feldspar, calcite, and significant amounts of halite and gypsum.

To apply the proposed method to the selected field example, we rearranged the seismic data into common mid-point (CMP) gathers for analysis. Figure 17a illustrates an example of such a gather, CMP no. 36, which showcases identifiable direct(DA), refraction(Rr), reflection(Rl), and surface waves.

The velocity of the surface layer was determined to be 360 m/s from the direct-wave arrivals. For the application of graph theory to the seismic data, we selected three specific traces from the CMP gather (traces no. 1, 7, and 13), highlighted in Fig. 17a with red arrows and further detailed in Fig. 17b.

In the field example, the positions of the sources, receivers, and midpoint remain consistent with the configuration shown in Fig. 3. However, the transmission points ($\text {r}_1$ to $\text {r}_6$) exhibit slight variations depending on the assigned $V_2$ value. This adjustment allows for a total of 21 potential transmission locations, each corresponding to a different $V_2$ value. Consequently, 21 adjacency matrices were calculated to correspond with each possible ray-path geometry. From these, a range of seismic velocity values ($V_2$) between 640 m/s and 780 m/s, with 7 m/s interval, were derived. The reflection times for these $V_2$ values were calculated, followed by an RMSE analysis between these computed and the observed reflection travel times (as shown in Fig. 17b). The $V_2$ value with the minimum RMSE was selected as the most accurate.

Verification of our model’s results was performed using conventional velocity analysis methods, including the fitting of a hyperbolic curve to the CMP gather. The conventional methods yielded a $V_2$ estimate of 712 m/s, closely aligning with the 710 m/s estimate derived from our graph theory-based model, resulting in an error margin of approximately 0.28%. This negligible discrepancy demonstrates the high accuracy of the proposed model in determining seismic velocities.

Fig. 17

Field example CMP gather and trace selection for graph theory analysis. (a) CMP no. 36 showing direct (DA, blue lines), refraction (Rr, red lines), reflection (Rl, green curve) arrivals, and surface waves (yellow-shaded zone). (b) Extracted traces (no. 1, 7, and 13) highlighted with red arrows, indicate the data used for graph theory application.

The success demonstrated in the field example presented here serves as an example of the model’s versatility. Based on several other synthetic and field tests, not shown here, the proposed method shows success in finding the seismic propagation velocities for different geological scenarios. The close alignment between the $\hbox {V}_2$ estimate obtained through our graph theory approach and the conventional velocity analysis methods further underscores the reliability and accuracy of our model across varying terrains. The key factor for a successful velocity estimation is working with traces with a good signal-to-noise ratio. One of the advantages of the proposed technique is we need only three traces, and since the CMP gathers usually have many more than three traces, then we can easily select three traces with a high signal-to-noise ratio to guarantee the success of the velocity estimation. This consistency in results across methodologies not only validates the efficacy of our approach but also suggests its potential applicability in a range of geological contexts, emphasizing its generalizability and effectiveness in seismic velocity determination.

Conclusion

In this study, we introduced a novel approach for estimating the seismic velocity of the second subsurface layer using the second largest eigenvalue of the normalized Laplacian matrix derived from the graph representation of seismic layouts. Our investigation uncovered a polynomial relationship between this eigenvalue and the seismic velocity, leading to the development of a quartic regression model for velocity prediction. This model outperforms the method presented in²¹, which relied on the spectral radius of the weighted adjacency matrix as the predictor.

When applied to a synthetic dataset, our proposed method achieved a relative error predominantly below 0.1%, compared to errors below 4% for the earlier approach. This marks a substantial improvement in accuracy, approximately 40 times. Furthermore, validation of the model using field data from a site near Dammam City, Saudi Arabia, confirmed its effectiveness, estimating seismic velocity with a relative error of about 0.28%.

The findings of this study underscore the potential of graph theory-based models, specifically those leveraging the normalized Laplacian matrix, in enhancing the accuracy of seismic velocity predictions. More importantly, this research serves several UN SDGs that depend on a proper characterization of near-surface layers.

The main limitation of this method is the picking of noisy traces. As mentioned earlier, only three traces would be enough to estimate an accurate velocity value. However, picking of reflection time is required to estimate the velocity value. In the case of noisy traces, picking reflection time could be challenging, which leads to errors in velocity calculations. The fact that only three traces are required to apply the proposed graph theory approach gives the user the freedom to select three traces with a high signal-to-noise ratio and avoid traces with a low signal-to-noise ratio. Another point that should be considered when selecting the three traces is to avoid selecting nearby traces; the selected traces should be distributed across the CMP gather.