Performance and energy optimization of ternary optical computers based on tandem queuing system

Abstract

As an emerging computer technology with numerous bits, bit-wise allocation, and extensive parallelism, the ternary optical computer (TOC) will play an important role in platforms such as cloud computing and big data. Previous studies on TOC in handling computational request tasks have mainly focused on performance enhancement while ignoring the impact of performance enhancement on power consumption. The main objective of this study is to investigate the optimization trade-off between performance and energy consumption in TOC systems. To this end, the service model of the TOC is constructed by introducing the M/M/1 and M/M/c models in queuing theory, combined with the framework of the tandem queueing system, and the optimization problem is studied by adjusting the processor partitioning strategy and the number of small TOC (STOC) in the service process. The results show that the value of increasing active STOCs is prominent when system performance significantly depends on response time. However, marginal gains decrease as the number of STOCs grows, accompanied by rising energy costs. Based on these findings, this paper constructs a bi-objective optimization model using response time and energy consumption. It proposes an optimization strategy to achieve bi-objective optimization of performance and energy consumption for TOC by identifying the optimal partitioning strategy and the number of active small optical processors for different load conditions.

Introduction

Since the initiated exploration in 2003, the research on TOC^1,2 has made remarkable progress after years of unremitting efforts. For example, the theory of the Decrease-Radix Design Principle³ proposed in 2005 simplified the design of ternary logic operators and laid the theoretical foundation for the development of TOC. Under the guidance of this theory, optical computing devices such as SD11⁴ and SD16⁵ (an optical computer developed by Shanghai University in 2016, with “SD” representing the abbreviation of its Chinese name Shangda) have been designed and manufactured. In addition, TOC has successfully implemented the operation of typical algorithms such as cellular automata⁶, the jacobi iterative algorithm⁷, genetic algorithm⁸, and the particle swarm algorithm⁹. Although certain results have been achieved in improving computational speed and optimizing task processing efficiency, existing research still mainly focuses on performance improvement, while systematic research on the trade-offs between performance and energy consumption is scarce. This is particularly critical for TOC, where energy consumption cannot be overlooked. The relevant theoretical framework has not yet formed a unified system, and the discussion of energy consumption in the existing literature is mostly simplistic or secondary, while the trade-off relationship between performance and energy consumption lacks in-depth analysis, which needs to be further explored and improved.

However, to solve these problems and achieve the bi-objective optimization of performance and energy consumption, the existing research paradigm alone is insufficient. At this point, it is especially important to provide new perspectives and tools for TOC research with the help of theoretical approaches from other disciplines. Queuing theory, as a mature and widely used mathematical model, provides strong support to solve the performance optimization problem of complex systems.

Queuing theory, initially developed for optimizing early telephone networks¹⁰, has become a fundamental tool for system performance analysis across various domains, including computing^11,12. In traditional electronic computing systems, queuing models such as M/M/c have been extensively applied to optimize resource allocation and improve system efficiency¹³.

As an emerging computer technology, the TOC can realize efficient processing of large-scale data by the parallel processing capability and high-speed transmission characteristics of optical components. This makes TOC have important application potential in areas such as large-scale data processing^14,15,16, artificial intelligence, and cloud computing. Compared to traditional electronic components, the low energy consumption and high transmission efficiency of optical components are the keys to achieving high performance and low energy consumption in TOC. However, in the current context of explosive growth in data volume, even TOCs, known for their low energy consumption, inevitably face the challenge of high energy consumption in the face of massive data processing¹⁷. Therefore, effective control of TOC energy consumption becomes the core issue of system optimization and targeted energy-saving. The measures are urgently needed.

To this end, based on the theory of the queueing system, this paper combines the technical characteristics of TOC, mathematically models its service pattern, and proposes a strategy for synergistic optimization of performance and energy consumption.

Related works

The TOC architecture

The emergence of the TOC originates from humanity’s persistent exploration of computational tools. Throughout history from ancient counting rods and abacuses to modern electronic computers the essence of computation has relied on manipulating physical states to represent and process information. With technological advancements, optical computing emerged as a novel paradigm, utilizing light’s physical properties (intensity, wavelength, phase, propagation direction, and polarization) for information encoding. However, studies revealed critical limitations: intensity, wavelength, and phase suffer from signal attenuation or complex control requirements, whereas propagation direction and polarization orientation demonstrate superior stability and controllability¹⁸.

As shown in Fig. 1, this is the main structure in a TOC unit consisting of two polarizers sandwiching a rotator, but the polarizers of each primitive are oriented differently or the control signals of the rotator are different. This characteristic led to the definition of three stable states: absence of light and two orthogonally polarized light states¹⁹. Such a tri-state framework not only simplifies physical implementation but also enables efficient parallel operations.

Fig. 1

Main structure of TOC.

During the foundational research phase of the TOC, researchers recognized that its processor supports a vast set of 19683¹⁸ ternary logic operations. Direct implementation of all operators was impractical due to prohibitive hardware complexity. This challenge motivated the Decrease-Radix Design Principle (DRDP)³, which synthesizes arbitrary x-valued logic operations through a minimal set of primitive units. Specifically, the DRDP demonstrates that only $x * x * (x - 1)$ primitives are required to construct all possible x-valued logic operators. For TOC ($x = 3$), merely 18 primitives can combinatorially generate all 19683 ternary operators³.

MSD adder

In TOC, the modified signed-digit (MSD) number system is employed for data encoding and computation, enabling fully parallel carry-free addition. The MSD number system was first proposed by Avizienis et al. in 1961 and represents a signed-digit ternary binary system²⁰. For any real number A, its MSD representation is given by:

$$\begin{aligned} A = \sum _{i} a_i \cdot 2^i \end{aligned}$$

(1)

where $a_i \in \{\text {u},0,1\}$, with u representing $-1$. Any number (except zero) can have multiple MSD representations. For example:

$$\begin{aligned} (6)_{10}&= (110)_2 = (1\text {u}10)_{\text {MSD}} = (1\text {uu}10)_{\text {MSD}}, \\ (-6)_{10}&= (\text {u}1\text {u}0)_{\text {MSD}} = (\text {u}11\text {u}0)_{\text {MSD}}. \end{aligned}$$

From Eq. (1), the following characteristics of the MSD number system can be observed:

• The bitwise negation of an MSD number, following the rules $u \rightarrow 1$, $1 \rightarrow u$, and $0 \rightarrow 0$, yields its additive inverse.

• If the most significant digit is positive, the number is positive; otherwise, it is negative. Thus, the MSD representation does not require a separate sign bit.

• The MSD system exhibits redundancy.

• Positive and negative numbers share the same representation, eliminating the need for one’s complement or two’s complement representations.

Due to its redundancy, MSD addition and subtraction operations do not involve carry propagation or borrow propagation. To enable fully parallel execution of MSD addition in an optical computing system, four types of transformations are utilized, as shown in Table 1. The following example in Table 2 illustrates the MSD addition process in TOC²¹.

Table 1 Four transformations.

Table 2 Calculation Example: 14 + 112.

Through the following three steps, the sum of 14 and 112 can be calculated in the MSD number form:

• 1. Perform both $\text {T}$ and $\text {W}$ transforms simultaneously. The result of the $\text {T}$ transform at the $i$th position is taken as the carry and should be written at the $(i+1)$th position, with the 0th position padded with $\phi$.

• 2. Apply both $\text {T}'$ and $\text {W}'$ transforms simultaneously to the result of Step 2. The result of the $\text {T}'$ transform at the $i$th position is taken as the carry and should be written at the $(i+1)$th position, with the 0th position padded with $\phi$.

• 3. Perform the $\text {T}$ transform on the result of Step 2 to obtain the sum of the two MSD numbers.

Converting the third step’s result using Eq. (1) yields the decimal number 126.

Performance study on TOC

Previous studies on TOC have primarily focused on performance optimization, aiming to enhance processing speed, reduce response time, and improve computational efficiency. For instance, in order to improve QoS, Zhang Sulan et al. combined the M/M/1 queuing system and used the average response time to analyze and evaluate the performance of TOC²². A simulation model was employed to demonstrate the impact of various indicators on response time. The results indicate that computational and network transmission speeds are the bottlenecks of system response time.

Furthermore, Wang Xianchao et al. constructed a service model for TOC by integrating it with M/M/1, $\hbox {M}_X$/M/1, and $\hbox {M/M}_B$/1 queuing systems²³. They proposed a computation completion scheduling strategy and its corresponding algorithm. The study discussed the computation methods for request reception time, preprocessing time, execution time, and transmission time based on various queuing systems. The total response time was obtained by summing these time components. Finally, numerical simulation models were utilized to evaluate response times under two scheduling strategies. The results demonstrate that the proposed computation completion scheduling strategy outperforms the immediate scheduling strategy.

These studies focus on performance optimization, the trade-off between performance and energy consumption remains underexplored^24,25.

TOC service model

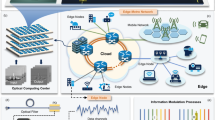
The TOC employs a service model similar to that of cloud computing²⁶, delivering services to users through a network. The paradigm of TOC service delivery is illustrated in Fig. 2. Like cloud computing, TOC enables users to submit computation-data files through terminals to obtain desired computational services, process the data, and return the results. However, unlike cloud computing, TOC is designed based on the Decrease-Radix Design Principle, granting it exceptional flexibility and scalability. Specifically, TOC primarily handles binary and ternary logic operations, either directly or indirectly²¹. Moreover, it features massive-bit parallelism¹⁸, enabling efficient large-scale computations²⁷. Additionally, TOC service requests exhibit significant diversity, and its processors can be dynamically reconfigured to adapt to varying computational demands^28,29. This architecture differs fundamentally from traditional electronic computers, which are often limited by fixed hardware structures that constrain efficient parallel processing. As a result, TOC provides users with a more flexible, efficient, and adaptable computing environment.

Fig. 2

Service paradigm of TOC.

When a user submits a service request to the TOC, the user’s tasks are initially encapsulated into a specialized format, referred to as the SZG file³⁰, where “SZG” originates from the Chinese pinyin SanZhiGuang, which means ternary optical. The system scheduler then manages these requests. The TOC’s dynamic bit-wise reconfigurability and allocation enable exceptional parallel processing capabilities. Each optical processor can be further subdivided into multiple independent small optical processors, enabling the system to execute multiple tasks simultaneously in parallel³¹.

Fig. 3

Four-stage service model.

The Tandem Queuing model is particularly suitable for TOC because it mirrors the multi-stage, sequential nature of the computation and data processing processes in TOC. Specifically, the stages of task processing in TOC are closely linked, with each STOC in the system performing a distinct computation task before passing it on to the next. The Tandem Queuing system effectively captures this flow of tasks between stages, which allows for a more accurate representation of the service process in TOC.

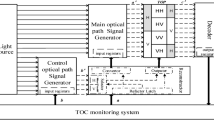
By incorporating queueing theory, a four-stage tandem queueing system is developed. As depicted in Fig. 3, this service model consists of four sequential stages. The platform employed in this study is an extension of the SD16 architecture, offering a total capacity of 1152 data bits³². By using optical processor reconfigurable technology, the platform is evenly divided into n independent optical processors (OPs), resulting in the creation of n Small ternary optical computers (STOCs) available for user access.

In the first stage of the service process, users submit requests to the server using high-level language text. These requests may involve various computational tasks, such as data analysis, algorithmic processing, or other complex operations. The Receiving Service (RS) is the dedicated module responsible for handling these tasks, following the First Come, First Served (FCFS) rule. This approach ensures that tasks are queued and processed strictly in the order they arrive, promoting fairness and systematic management for all users. Upon receiving a request, the RS validates and organizes the tasks into an internal service queue, where they are securely stored and prepared for further processing. At this stage, the TOC server accurately records and manages incoming user requests, ensuring they are appropriately prioritized and maintained.

In the second stage, user requests are sent to the data Pre-Processing Server (PPS) following the FCFS principle. During this stage, each task within the requests is converted into a ternary data format³⁰ to ensure compatibility with optical processing. This conversion is a critical step, as it aligns the tasks with the processing capabilities of the optical computers, thereby enhancing the efficiency of ternary data handling by the optical processors. Simultaneously, the TOC service system calculates the computational workload of each task, providing essential insights into its complexity and estimated processing time. This workload analysis is crucial for optimizing resource allocation and improving overall system processing efficiency. The main objectives of this stage are to accurately and promptly transform user requests into data suitable for optical processing and to prepare for subsequent task allocation and execution.

In the third stage, all tasks are sequentially dispatched to the Calculation Server (CS) based on their arrival order as recorded by the scheduler. Upon detecting an idle small optical processor within the system, the scheduler assigns a task to the available processor, allowing computation to commence promptly. This task allocation mechanism strictly adheres to the FCFS principle, ensuring fairness and maintaining the sequential order of task processing. Conversely, if the scheduler determines that no tasks remain pending for processing, the scheduling algorithm automatically ceases operation. This approach not only guarantees efficient utilization of computational resources but also minimizes redundant system activities, thereby enhancing overall processing efficiency.

In the fourth stage, the TOC service system transmits the processed data to users via the Sending Service Server (SS), adhering to the FCFS rule. This step concludes the service process, ensuring that all computational results are delivered in the order of task submission. This approach upholds fairness and completes the cycle of handling user requests.

Performance model

This study uses system response time (T) as the performance metric, where T is defined as the time required for the system to receive the computational results after a user submits a request. The formula for T is given by:

$$\begin{aligned} T = T_{\textrm{RS}} + T_{\textrm{PPS}} + T_{\textrm{CS}} + T_{\textrm{SS}} \end{aligned}$$

(2)

$T_i(i=\textrm{RS}, \textrm{PPS}, \textrm{CS}, \textrm{SS})$ represents the time required for each stage of the model shown in Fig. 3. Specifically, $T_{\textrm{RS}}$ denotes the queue reception time, $T_{\textrm{PPS}}$ indicates the time required for data pre-processing, $T_{\textrm{CS}}$ represents the total time spent on data computation and decoding, and $T_{\textrm{SS}}$ refers to the data transmission time.

Task reception stage

The requests submitted by users are random and each request is independent of others, with no mutual influence³³. In this stage, the M/M/1 queuing model³⁴ can be applied for modeling. It is assumed that user requests arrive at a rate $\lambda$, meaning the inter-arrival times follow an exponential distribution with parameter $\lambda$. Additionally, it is assumed that the service rate of the receiving server RS follows an exponential distribution with parameter $\mu _{\textrm{RS}}$. Based on the M/M/1 queuing model, the service of the RS in the first stage is modeled, and the corresponding Continuous-Time Markov Chain (CTMC) state transition diagram is shown below as Fig. 4.

Fig. 4

State transition diagram of the M/M/1 queuing model.

At this point, the utilization of the task reception server can be expressed as:

$$\begin{aligned} \rho _{\textrm{RS}}=\frac{\lambda }{\mu _{\textrm{RS}}} \end{aligned}$$

(3)

Assuming that the arrival probability of tasks and the service rate of the receiving server remain stable, both follow exponential distributions. When the average service rate exceeds the average arrival rate, it indicates that the system has sufficient time to process requests. In this case, the system will be in a steady state. In other words, when $\lambda /\mu _{\textrm{RS}}<1$, the system will achieve stability, and this process conforms to the Markov queuing model. According to the state transition diagram of the M/M/1 queuing model, in the steady state, for any state n, the “inflow” equals the “outflow,” leading to the following equation:

$$\begin{aligned} \left\{ \begin{aligned} p_1\mu _{\textrm{RS}}&= p_0\lambda \\ p_0\lambda + p_2\mu _{\textrm{RS}}&= p_1\mu _{\textrm{RS}} + p_1\lambda \\ p_1\lambda + p_3\mu _{\textrm{RS}}&= p_2\mu _{\textrm{RS}} + p_2\lambda \\&\vdots \\ p_{n-1}\lambda + p_{n+1}\mu _{\textrm{RS}}&= p_n\mu _{\textrm{RS}} + p_n\lambda \end{aligned} \right. \end{aligned}$$

(4)

From the first set of equations, it is evident that the balance conditions for each state are established through the transition rates between neighboring states. By observing these recursive relationships, we can progressively derive the probability distribution for each state. Next, by applying the recursive formula, we express the probabilities of each state in terms $p_0$, yielding the following results:

$$\begin{aligned} \left\{ \begin{aligned} p_1&=\frac{\lambda }{\mu _{\textrm{RS}}}p_0\\ p_2&=\frac{\lambda ^2}{\mu _{\textrm{RS}}^2}p_0\\ p_3&=\frac{\lambda ^3}{\mu _{\textrm{RS}}^3}p_0\\&\vdots \\ p_n&=\frac{\lambda ^n}{\mu _{\textrm{RS}}^n}p_0 \end{aligned} \right. \end{aligned}$$

(5)

$p_0$ represents the probability of having zero tasks in the system, and $p_2$ represents the probability of having two tasks in the system. Let $p_m$(m = 0,1,2,...) denote the probability of having m tasks in the system. The probability $p_{m}=\frac{\lambda ^{m}}{\mu _{\textrm{RS}}^{m}}p_{0}$.Summing the probabilities of all possible states in the task reception system yields $p_0+p_1+p_2+\cdots +p_n=1$, or $\sum _{i=0}^np_i=1$. Assuming the average number of requests in the system is $N_{RS}$:

$$\begin{aligned} N_{\textrm{RS}}=\sum _{m=0}^\infty mp_m=\rho _{\textrm{RS}}(1-\rho _{\textrm{RS}})\sum _{m=0}^\infty m\rho _{\textrm{RS}}^{m-1}=\frac{\lambda }{\mu _{\textrm{RS}}-\lambda } \end{aligned}$$

(6)

According to Little’s Law³⁵, the average time for receiving a task is:

$$\begin{aligned} T_{\textrm{RS}}=\frac{N_{RS}}{\lambda }=\frac{1}{\mu _{\textrm{RS}}-\lambda } \end{aligned}$$

(7)

Data pre-processing stage

The time for a user request to enter the second stage follows an exponential distribution with parameter $\lambda$. During this stage, the primary task of the Pre-processing Service Server is to convert the operands into MSD format, with a service rate of $\mu _{\textrm{PPS}}$. The modeling of PPS response time $T_{\textrm{PPS}}$ can be referenced from the first stage. In this queuing process, the average queue length of tasks in the pre-processing queue is given by $N_{\textrm{PPS}}$, where $T_{\textrm{PPS}}=W+W_{q}$, with W being the time spent by the system servicing the task and $W_{q}$ representing the waiting time of the task in the system. The total number of tasks in the system, $N_{\textrm{PPS}}$ includes both the tasks currently being processed and those in the queue. The average response time $T_{\textrm{PPS}}=\frac{N_{\textrm{PPS}}}{\lambda }$

$$\begin{aligned} \left\{ \begin{aligned} W&=\frac{1}{\mu _{\textrm{RS}}}\\ W_{q}&=\frac{\lambda }{\mu _{\textrm{RS}}(\mu _{\textrm{RS}}-\lambda )} \end{aligned} \right. \end{aligned}$$

(8)

We begin by considering the service time W and the queuing time $W_{q}$, which represent the average time spent servicing a single request and the average time spent waiting in the queue, respectively. Using these parameters, we can further derive the total response time of the system, $T_{\textrm{PPS}}$. By definition, $T_{\textrm{PPS}}$ is the sum of the service time and the queuing time. Applying this relationship, we arrive at the following expression for the total response time:

$$\begin{aligned} T_{\textrm{PPS}}=W+W_q=\frac{N_{\textrm{PPS}}}{\lambda }=\frac{1}{\mu _{\textrm{PPS}}-\lambda } \end{aligned}$$

(9)

Data computation stage

The features of TOC lie in its numerous bits and bit-wise allocation, allowing different logic operators to be constructed on the computing units and enabling parallel processing of multiple requests. As the number of divisions increases, parallelism improves, but the service capacity of each STOC decreases. Conversely, when the number of divisions decreases, parallelism reduces, but the service capacity of each STOC increases. Therefore, the choice of division strategy directly affects both the computation time and system energy consumption.

When the processors of TOC are divided into n STOCs, the modeling of the third stage can be referenced from the M/M/c queueing system, where n represents the division number of TOC and c denotes the number of active STOCs, with $c\le n$. It is assumed that each STOC is identical in specifications with the same software and hardware configurations and that the probability of task assignment by the scheduler is equal for each STOC. The corresponding state transition diagram of the M/M/c queuing model is depicted in Fig. 5.

Fig. 5

State transition diagram of the M/M/c queuing model.

The service rate of the entire OP is $\mu$, so the service rate of each STOC is $\mu _c=\frac{\mu }{n}$. When the arrival rate of computation requests is also $\lambda$, n represents the number of TOC divided equally into STOCs and c represents the number of activated STOCs. In this stage, the utilization rate of each STOC is $\rho _c=\frac{\lambda }{\mu _c}$. When $\rho _{c}<1$, the system reaches a steady state. The probability that there are no tasks in the system, $p_{0}$, can be expressed as:

$$\begin{aligned} p_0=\left[ \sum _{i=0}^{c-1}\frac{1}{i!}\left( \frac{\lambda }{\mu _c}\right) ^i+\frac{1}{1-\rho _c}\frac{1}{c!}\left( \frac{\lambda }{\mu _c}\right) ^c\right] ^{-1} \end{aligned}$$

(10)

The probability $p_{m}$ of having m tasks in the system for $m=0,1,2,\cdots$ is given by:

$$\begin{aligned} p_m=\left\{ \begin{array}{ll}\frac{1}{m!}\left( \frac{\lambda }{\mu _c}\right) ^mp_0,& \quad 0<m\le c\\ \frac{1}{c! c^{m-c}}\left( \frac{\lambda }{\mu _c}\right) ^mp_0,& \quad m>c \end{array}\right. \end{aligned}$$

(11)

At this point, the queue length of the system,$L_{q}$, can be expressed as $L_q=\frac{1}{c!}\left( \frac{\lambda }{\mu _c}\right) ^c\frac{\rho _c}{(1-\rho _c)^2}p_0$, The total system length $L_{c}$, is $L_c=L_q+\frac{\lambda }{\mu _c}$, The total time $T_{c}$ that a task spends in the computation stage is determined by the average number of tasks in the system, $L_{c}$:

$$\begin{aligned} L_c=\frac{1}{c!}\left( \frac{\lambda }{\mu _c}\right) ^c\frac{\rho _c}{(1-\rho _c)^2}p_0+\frac{\lambda }{\mu _c} \end{aligned}$$

(12)

The response time during the computation phase can be expressed as: $T_c=\frac{L_c}{\lambda }$.

Data transmission stage

In the final stage of service, the results computed by the upper-level system are aggregated and subsequently packaged by the data transmission server before being sent to the user terminal. During this period, the process can be modeled as a simple M/M/1 queuing system. The average service rate of the Sending Server (SS) is denoted by $\mu _{\textrm{ss}}$. Based on the modeling of the task reception phase and pre-processing phase, the time expenditure for the data transmission phase is given by:

$$\begin{aligned} T_{\textrm{ss}}=\frac{1}{\mu _{\textrm{ss}}-\lambda } \end{aligned}$$

(13)

By solving the equations for $T_{\textrm{RS}}$, $T_{\textrm{PPS}}$, $T_{\textrm{CS}}$, and $T_{\textrm{SS}}$, the overall response time T can be obtained.

Energy consumption model

In this study, the TOC service platform, an expansion of the SD16 architecture, comprises a total of 1152 data trits³². This platform can be partitioned into multiple smaller processors, thereby generating several STOC. While TOC processors are known for their low energy consumption, the increasing number of trits in these processors in recent years points to their potential evolution into cloud servers, data centers, or even supercomputers. However, this expansion presents significant challenges in managing large-scale data processing tasks, inevitably leading to higher energy consumption and substantial economic costs.

To explore the potential for reducing energy consumption while enhancing performance, this study proposes uniformly dividing the optical processors of the platform into n independent STOCs. Specifically, to achieve the dual objective of minimizing energy consumption and maintaining system performance, the TOC service platform integrates a sleep mode for inactive STOCs, thereby significantly reducing power usage. Meanwhile, particular attention is given to analyzing the energy consumption of active STOCs during this process. This approach ensures a balanced trade-off between performance optimization and energy efficiency, providing a feasible solution for sustainable computing.

Let E denote the total energy consumption of the TOC system. Let $E_{\textrm{work}}$ and $E_{\textrm{sleep}}$ represent the power consumption of the STOCs during active and sleep modes, respectively. The total energy consumption E is then given by:

$$\begin{aligned} E=cE_{\textrm{work}}+(n-c)E_{\textrm{sleep}} \end{aligned}$$

(14)

where c is the number of active STOCs, and n is the total number of STOCs. The power consumption of the backlight for each SD16 unit is approximately 150 mA$\times$5 V=750 mW. Since the TOC service platform is expanded from 6 SD16 units, the total backlight power consumption is approximately 4.5 W.

Simulation experiment of the TOC service model

Impact of STOC partitioning and activation numbers on response time

This section aims to investigate the effects of different partitioning strategies and the number of activated STOCs on system response time under various load conditions. Special emphasis is placed on the role of the number of active STOCs. Based on the reconfigurability of TOC, the system can be partitioned into different numbers of STOCs, and the choice of partitioning strategy directly affects response time. By analyzing the relationship between these variables, this study seeks to elucidate how the quantity of STOCs influences system performance across different load scenarios, thereby providing a theoretical basis for optimizing response time.

To analyze the system response time under varying load conditions, task arrival rates were set according to 20%, 40%, 60%, 80%, and 90% of the system’s service capacity, representing low, medium-low, medium, medium-high, and high load conditions, respectively. The measured response times for each load condition are summarized in Tables 1, 2, 3, 4, 5, with Table 3 corresponding to the low load condition, Table 4 to the medium-low load condition, Table 5 to the medium load condition, Table 6 to the medium-high load condition, and Table 7 to the high load condition.

Table 3 System response time under low load with $\rho =0.2$ (s).

Table 4 System response time under medium-low load with $\rho =0.4$ (s).

Table 5 System response time under medium load with $\rho =0.6$ (s).

Table 6 System response time under medium-high load with $\rho =0.8$ (s).

Table 7 System response time under high load with $\rho =0.9$ (s).

In queuing systems, the system load factor ($\rho$) is defined as the ratio of the arrival rate ($\lambda$) to the service rate ($\mu$), represented as:

$$\rho = \frac{\lambda }{\mu }$$

In the third stage, the switching of STOCs can be controlled to enhance system service capacity, enabling it to meet demands under varying load conditions. Consequently,

$$\begin{aligned} \rho = \frac{\lambda }{\mu }< \frac{\lambda }{c \mu _c} < 1 \end{aligned}$$

(15)

where c denotes the number of servers. For a stable system, $\rho$ should remain less than 1 (i.e., $\rho < 1$), which implies that the average arrival rate will not exceed the service capacity. This ensures that, over the extended operation, the system will not accumulate an infinite queue length, thereby maintaining stability and avoiding potential collapse. When the “Number of Active STOCs” in the table is less than the “Partitions of STOCs,” certain data entries are left blank because, in these cases, the arrival rate exceeds the service capacity (i.e., $c \mu _c < \lambda$). This indicates that the arrival rate (demand) surpasses the system’s capacity to serve. In such instances, the system, on average, cannot fully process all incoming requests per time unit, resulting in persistent occupation of resources and leaving new requests with minimal chance of timely processing. Consequently, the system trends toward saturation or even collapse. Therefore, scenarios where the arrival rate exceeds service capacity are excluded from consideration.

Fig. 6

Response time under different load conditions.

From Fig. 6, it is evident that under the same partitioning conditions, as the number of STOCs increases, the system’s response time gradually decreases, although the rate of reduction becomes increasingly gradual. In an M/M/c queuing model, an increase in the number of servers typically leads to a reduction in system response time. More servers allow for the parallel processing of a greater number of tasks, thereby reducing the waiting time of tasks in the queue. Hence, increasing c generally enhances the overall system efficiency, reflected by a decrease in response time. However, this improvement is not linear. Once c reaches a certain critical point, the performance enhancement becomes less pronounced as the waiting time approaches its minimum value.

Additionally, in Fig. 6a–c, there are instances where the response time is significantly higher than others. This occurs when the system service rate is slightly higher than the task arrival rate. In an M/M/c queuing model, when the task arrival rate approaches the service rate, the system is nearly saturated. Under such conditions, the server utilization is very high, with nearly all servers continuously handling tasks. This leads to a backlog of tasks in the queue, causing the queue length to increase rapidly and requiring new tasks to wait longer for processing. Consequently, the average waiting time of the system is markedly extended. Therefore, when the arrival rate is close to the service rate, the system’s performance deteriorates significantly, resulting in a considerable increase in response time.

Furthermore, an interesting phenomenon is observed: with a fixed task arrival rate and total system service rate, increasing the number of partitions leads to a longer system response time. This phenomenon is intuitively illustrated in Fig. 6d,e. To investigate this phenomenon, a verification experiment was conducted using an M/M/c queuing system, as summarized in Table 8. The parameters were set as follows: task arrival rate is $\lambda = 80$ tasks per hour, and the service rate is $\mu = 120$ tasks per hour. The parameter c represents the number of active STOCs, with the condition that $c \cdot \mu _c = \mu$, where $\mu _c$ denotes the service rate of a single STOC. $W_q$ represents the average queueing time of a task, while $\frac{1}{\mu _c}$ is the service time per task handled by an individual STOC. T denotes the system’s response time.

Table 8 Verification experiment.

From the table, it is clearly observed that the system response time T, the average queueing time $W_q$, and the task service time $\frac{1}{\mu _c}$ all vary with the number of partitioning STOCs (which is also the number of all active STOCs c). Specifically, when all STOCs are activated, as the number of partitioning STOCs increases, the average queueing time $W_q$ significantly decreases from 60 seconds to approximately 25 seconds. This indicates that increasing the number of service stations helps to effectively reduce queueing delays and improve the overall system service capacity. However, increasing the number of STOCs also brings a noticeable side effect: the performance of each individual STOC declines, leading to an increase in the time required to process each task, $\frac{1}{\mu _c}$.

Furthermore, the system response time T is the sum of the average queueing time $W_q$ and the task service time $\frac{1}{\mu _c}$. It can be intuitively seen from the table that the system response time T is largely influenced by the task service time $\frac{1}{\mu _c}$. Although increasing the number of evenly distributed STOCs significantly reduces the average queueing time, the increase in task service time greatly offsets this advantage, resulting in an increase in the system response time.

Therefore, the analysis indicates that a higher number of evenly partitioning STOCs is not always better. In practical applications, it is necessary to find a balance between the number of service stations and the performance of each individual server to achieve optimal system response time.

Impact of STOC partitioning and activation on system energy consumption

Based on the relationship between system energy consumption, the number of partitions, and the number of active processors, $E=cE_{\textrm{work}}+(n-c)E_{\textrm{sleep}}$, an energy consumption graph is plotted as Fig. 7.

When the number of service stations c increases, the opportunity for each task to wait for service decreases, leading to a reduction in the average waiting queue length $L_{q}$. This is because more service stations mean that more tasks can be handled concurrently, reducing the time tasks spend waiting in the queue. However, as the number of service stations increases, the total number of busy service stations $L_{\textrm{busy}}=\rho _1=\frac{\lambda }{\mu _c}$ also rises. The total number of tasks in the system $L_{s}$, which equals the number of tasks in the queue $L_{q}$ plus the number of tasks being served $L_{\textrm{busy}}$ increases because although $L_{q}$ decreases with the increase in c, the increase in $L_{\textrm{busy}}$ is more significant. Consequently, the total number of tasks $L_{s}$ in the system increases with the number of service stations c.

Fig. 7

Relationship between energy consumption E, number of partitions n, and active processors c.

It is evident from the Fig. 7 that the greater the number of TOC partitions, the more precise the control over power consumption. When the system load is approximately 10%, a server divided into two STOCs must keep one STOC active, resulting in noticeably higher power consumption compared to a server divided into 10 STOCs, where only one STOC is active and nine are in sleep mode. Similarly, when the system load is around 60%, a server divided into two STOCs needs both STOCs to remain active, whereas a server divided into six STOCs only requires five to be active, with one in sleep mode. In this case, the power consumption is lower than when the system is divided into two STOCs. Thus, the greater the number of partitions, the more beneficial it is for fine-tuned control over energy consumption.

Bi-objective optimization of performance and energy consumption

In studying the relationship between the performance and energy consumption of the TOC service system, it was observed that as the number of active STOCs (denoted as c) increases, the system’s response time decreases, indicating an enhancement in performance. This suggests that with the increase in the number of processors, task execution times are relatively shortened, leading to an overall improvement in system performance. However, this performance gain is accompanied by an increase in total energy consumption, as the activation of more processors results in higher energy usage, thereby driving up the overall energy cost.

Evidently, there exists a trade-off between system performance and energy consumption. Increasing the number of processors can enhance parallel processing capabilities and improve execution efficiency, thereby reducing task completion time. However, this also results in greater energy consumption. Thus, when designing and optimizing the system, it is crucial to account for this performance-energy trade-off and determine the optimal number of processors to meet specific performance goals while adhering to energy constraints.

Both response time and energy consumption should be regarded as distinct objective functions, where improving one often negatively impacts the other. Consequently, a balance between these competing objectives must be achieved. For instance, increasing the number of processors to reduce overall execution time may lead to higher total energy consumption, whereas lowering energy usage might prolong task execution time. Therefore, identifying the optimal number of processors necessitates a comprehensive consideration of these factors to achieve an optimal balance between performance and energy consumption.

For simplicity, the optimization of the TOC service model focuses on the M/M/c model for the third stage. By controlling the number of STOCs and their operational status, the goal is to achieve multi-objective optimization of both response time and energy consumption.

Let h represent the energy consumption per unit time for each STOC, and $\omega$ denote the energy consumed per unit time that each task spends in the system. The objective function can be defined as:

$$\begin{aligned} f(c_n)=hc_n+\omega L_s \end{aligned}$$

(16)

where $c_{n}$ represents the state of the system with the optical processor divided into n parts and c STOCs. Both c and n are discrete, and it must hold that $\lambda /c\mu _n<1$. To determine the optimal $c_{n}$, marginal analysis can be employed, where the optimal ${C_{n}}^{*}$ must satisfy:

$$\begin{aligned} {\left\{ \begin{array}{ll} f({c_n}^*)<f({c_n}^*-1)\\ f({c_n}^*)<f({c_n}^*+1)& \end{array}\right. } \end{aligned}$$

(17)

Substituting Eq. (16) into Eq. (17), we obtain:

$$\begin{aligned} {\left\{ \begin{array}{ll} h{c_n}^*+\omega L_s({c_n}^*)<h({c_n}^*-1)+\omega L_s({c_n}^*-1)\\ h{c_n}^*+\omega L_s({c_n}^*)<h({c_n}^*+1)+\omega L_s({c_n}^*+1) \end{array}\right. } \end{aligned}$$

(18)

Simplifying, we get:

$$\begin{aligned} L_s(c_n^*)-L_s(c_n^*+1)<\frac{h}{\omega }<L_s(c_n^*-1)-L_s(c_n^*) \end{aligned}$$

(19)

For the third stage M/M/c model, calculations will be performed to find the optimal ${c_n}^*$, such that the response time is minimized while maintaining the system energy consumption at a lower level. The queue length under low load conditions and with a partition number of 10, calculated using Eqs. (16) and (19), is presented in Table 9.

Table 9 Queue lengths with different numbers of active STOCs when the partition quantity is 10 under low load. Significant values are in bold.

Under low load, when the partition quantity is 10, each additional small optical processor incurs an extra power consumption of 350 mW. The energy cost per unit time for each task remaining in the system, denoted as $\omega$, is approximately 500 mW. With $\frac{h}{\omega }=0.7$, which falls within the interval (0.1341, 0.7150), the optimal number of active STOCs ${c_n}^* = 4$.

Similarly, the optimal value of ${c_n}^*$ for other partition scenarios under different loads can be calculated accordingly, as shown in Tables 10, 11, 12, 13 and 14, corresponding to low, medium-low, medium, medium-high, and high load conditions, respectively.

Table 10 Low Load($\lambda =\mu *20\%$). Significant values are in bold.

Table 11 Medium-low Load($\lambda =\mu *40\%$). Significant values are in bold.

Table 12 Medium Load($\lambda =\mu *60\%$). Significant values are in bold.

Table 13 Medium-high Load($\lambda =\mu *80\%$). Significant values are in bold.

Table 14 High Load($\lambda =\mu *90\%$). Significant values are in bold.

From Table 10, it can be observed that under a low load the system does not require extensive parallel processing capabilities. The impact of the partition number and the number of activated STOCs on the response time is much more significant than on energy consumption; in fact, activating too many STOCs leads to unnecessary power usage. Dividing the TOC into 3 parts and activating only 1 STOC can effectively reduce energy consumption while maintaining a moderate response time.

When the load increases to a medium-low level, as shown in Table 11, the system’s demand for processing capacity rises slightly. Under these conditions, activating only 1 STOC is no longer sufficient to meet the required response speed, so the number of activated STOCs needs to be increased. The data indicate that partitioning the system into 3 STOCs and activating 2 of them can better handle the increased load, resulting in a significant improvement in response time. Although the energy consumption increases somewhat, the overall performance remains optimal, demonstrating that activating additional STOCs under these conditions can better balance performance and energy consumption.

As the load further increases to medium levels, as evidenced by Tables 12 and 13, the system requires a higher degree of parallel processing capability. Reducing the partition number by dividing the system into 2 STOCs and activating both fully utilizes the available resources, thereby better controlling both response time and energy consumption.

In high-load scenarios, as shown in Table 14, the system’s demand for processing capacity surges dramatically. Regardless of the partition number, all STOCs must be activated to maintain stable system operation, resulting in maximum energy consumption when all STOCs are active. Moreover, increasing the partition number leads to a rapid rise in response time. Therefore, under high-load conditions, the system cannot further reduce the response time and energy consumption simply by increasing the partition number.

Overall, as the load increases, the optimal configuration shifts from “more partitions with fewer activations” to “fewer partitions with full activation.” In addition, merely increasing the number of partitions does not necessarily improve the response time; it may instead introduce additional coordination overhead. The data from these five tables clearly demonstrate how to adjust the strategy of combining the STOC partition number $n$ and the number of activated STOCs $c_n$ under different load conditions to achieve the best balance between response time and energy consumption.

In previous studies, researchers mainly focused on enhancing the parallel processing capability of optical processors through reconfiguration and partitioning techniques, thereby improving system performance. In contrast, our study not only focuses on performance but also places significant emphasis on the energy consumption issues that arise with performance improvements in today’s era of ever-increasing data volumes. This trade-off between performance and energy consumption enables the system to boost computational capacity while effectively controlling energy usage, in line with the demands for green computing in the big data era.

In our research, we considered the impact of both the partition number and the number of activated STOCs on the system’s energy consumption. By jointly tuning these two parameters, we can achieve a better balance between response time and energy consumption, potentially reducing the system’s energy usage significantly without sacrificing performance. Consequently, our optimization of performance and energy consumption in TOC exhibits superior results compared to previous studies.

Summary

As TOC technology advances toward large-scale practical applications, balancing performance optimization with energy consumption control becomes a critical step in realizing its widespread adoption. Based on M/M/1 and M/M/n models, this study conducts an in-depth analysis of the service response times at various stages of ternary optical computing and the energy consumption characteristics of different system components. By establishing an optimization model between execution time and energy consumption, the study aims to reduce energy usage while ensuring high system performance, thus optimizing system configurations to achieve a dual-objective optimization of both performance and energy efficiency. Specifically, through rational adjustment of system resource allocation, the analysis explores how to strike the optimal balance between performance and energy efficiency under different load conditions.

The proposed research mechanism aims to optimize both performance and energy consumption in TOC systems, but several limitations should be noted. First, the underlying model relies on simplified assumptions regarding arrival processes, service time distributions, and queueing behavior. Such assumptions, while beneficial for analytical tractability, may not fully capture the complexities and variability encountered in real-world scenarios. Moreover, the optimization results depend heavily on the specific configuration of the STOC partition number and the number of activated STOCs. This sensitivity means that the optimal settings derived under controlled conditions might not hold in environments with dynamic or unpredictable workloads. In our future research, we will work to address this limitation.

Throughout the research, this study not only conducts detailed analysis and calculations for various model parameters but also validates the effectiveness of the optimization model through experiments. The resulting strategy significantly reduces system energy consumption under certain load conditions, while maintaining or even enhancing overall system performance. Furthermore, we discovered that the ARM9 control unit in the SD16 supports Dynamic Voltage and Frequency Scaling (DVFS)³⁶. This technology allows real-time adjustment of the chip’s operating frequency and voltage to adapt to varying workload conditions, effectively reducing the chip’s energy consumption while delivering the required performance. Future research will continue to explore the performance and energy consumption of TOC based on more complex models such as tandem queuing models and DVFS.