Introduction

Power electronic devices account for a large proportion of industrial and residential applications, such as car battery chargers, and their high efficiency makes them not only one of the key components of but also a powerful energy conversion device. However, these devices operate as nonlinear loads that can greatly affect the quality of electrical power in transmission systems1,2.

Reactive power plays a crucial role in maintaining a stable and efficient electrical grid. When there’s not enough of it, voltage levels can fluctuate or even collapse, which can disrupt sensitive equipment and impact the entire system’s stability. In contrast, excessive reactive power leads to wasted energy and higher transmission losses. It also puts extra strain on transformers and generators, causing them to overheat, wear out faster, and require more maintenance. Furthermore, reactive power can contribute to harmonic distortion, which interferes with electronic devices and reduces overall power quality3.

In this context, the literature explains a variety of solutions for improving grid power quality and ensuring its stable operating conditions. Certainly, what has contributed most to this development is the development of controllable power electronic devices like Insulated Gate Bipolar Transistors (IGBTs) and Silicon Carbide devices (SiC) that are incorporated into sophisticated power-generation management systems. If managed properly, these systems can mitigate harmonic distortions and compensate for the reactive power caused by nonlinear loads, thus increasing the efficiency and stability of the whole power network.

The shunt active power filter is widely employed to enhance the quality of the grid. It comprises a voltage source inverter connected in parallel with the grid allowing the injection of real-time compensating currents for harmonic distortions and reactive power. Such a VSI is interfaced with the grid via a filter at its output; this smoothes the injected current. This process contributes greatly to the mitigation of the side effects of harmonic currents and offers stabilized voltage levels. Their effectiveness greatly relies on the speed and effectiveness of their algorithms, along with the design consideration of the output filters. In the system of SAPF, there exists a control unit that contains three important algorithms. The first is harmonic detection and extraction, which is classified into time-domain, frequency-domain, and combined methods4,5,6,7,8,9,10,11,12,13,14,15,16. The second algorithm is the DC-link voltage regulation algorithm, which is generally based on a PI controller in order to keep the DC link voltage at its desired value17,18,19. While the last is the current controller algorithm, it’s the most important part in any SAPF system for accurate current reference tracking.

Much attention has gone to research activities aimed at proposing advanced controllers, hence ensuring maximal possible speed of approach, high precision, and the required stability of a given system. For instance, the deadbeat controller has been widely exploited due to its high precision, robustness, and fast response, but its dependence on the model of the system results in large tracking errors when it is driven to operate under suboptimal conditions20,21. On the other hand, the hysteresis controller is valued for its simplicity and ease of implementation but suffers from the drawback of variable switching frequency22,23. Moreover, the sliding mode controllers (SMC) have a high level of robustness against disturbances and system uncertainties but may suffer from stability problems in some cases24,25,26,27. Fuzzy Logic Control (FLC) is potent in dealing with vague and imprecise inputs, but it strongly relies on the knowledge of experts and demands updates of the rule base in many instances26,27. Additionally, repetitive control is featured with poor dynamic response and is thereby constrained to perform under fast-changing conditions28,29. The controller based on the Lyapunov function has high tracking accuracy but suffers from some drawbacks like variable switching frequency, the necessity of high sampling rates, and high computational burden30,31. Table 1 presents a summary of different controllers used in past works.

Table 1 Comparison of control strategies for SAPF systems.
Full size table

Generally, controller tuning and parameter design strategies are classified into three major approaches. The first one includes classical tuning methods, which involve both analytical and numerical techniques32. The second approach is the self-tuning methods, which are based on adaptive control principles, such as Model Reference Adaptive Control (MRAC), whereby parameters are automatically updated according to a reference model33. Lastly, smart tuning methods make full use of modern optimization and intelligent techniques to carry out precise and optimal adjustments in parameters. These methods dramatically improve the system performance; hence, they are the most effective solution for the difficulties posed by today’s applications1,34. Most of the studies carried out so far indicate that most of the SAPF systems are dependent on conventional approaches, which have some limitations. Consequently, this can lead to improper control adjustments, probable instability and poor performance under critical conditions.

In the wake of these limitations and developments in control and optimization, better controllers through precise design and optimal tuning are an urgent need, especially for an improvement in compensation performances. The integration of metaheuristic approaches has indeed revolutionized power quality enhancement strategies by changing the design and control approaches of the SAPFs. This integration has shown promising potential in achieving optimizations for essential factors such as proportional-integral (PI) controller gains via metaheuristic techniques1,32,34,35,36,37. However, most of these methods have difficulties finding a balance between exploration and exploitation, which is necessary to prevent the algorithms from falling into early convergence and not reaching global optimization. In this respect, ongoing research is developing new algorithms for such a problem. In summary, Table 2 provides an overview of the existing literature regarding the controller design and parameter tuning strategies.

Table 2 Comparison of controller tuning and parameter design strategies.
Full size table

Accordingly, in this paper we introduce a methodology to determine the optimal design of SAPF system with an anti-windup PI controller and a hysteresis controller for effective overall power quality improvement. This design combines a hysteresis controller within the internal current control loop, leveraging its fast response and flexibility to rapidly track current reference signals, an optimized DC link PI controller to improve the performance of the inverter, and an optimized output filter to enhance the quality of the injected current.

As pointed before, one of the main difficulties in SAPF design is the tuning of control parameter, which has a significant influence on system performance. Thus, our design relies on the Golden Jackal Optimizer (GJO) to obtain the PI controller and output filter optimal parameters. The GJO achieves a good balance between exploration and exploitation during optimization and avoids local optima to maximize overall system efficiency. The objective function is formulated in a way that it compromises on reducing harmonic distortion, improves the dynamic response, and maximizes power quality. Simulation studies confirm that the new method effectively suppresses harmonic intrusions in the grid current and effective reactive power compensation compared to conventional tuning methods.

Fig. 1
figure 1

System Configuration of the Three-Phase Shunt Active Power Filter.

Full size image

System description

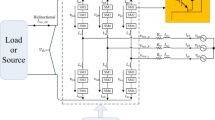
The configuration scheme of the three-phase SAPF system is represented in Fig. 1. This SAPF is connected between the grid and the harmonic-generating nonlinear load to mitigate all harmonic-generated power quality issues. The main parts contained in this system are:

  • DC link capacitor.

Added to the DC side of the inverter is a capacitor. This is an energy storage element for providing the required energy for harmonic compensation. It is a very critical component and plays a very important role in order to maintain a stable DC-link voltage and to keep the inverter operational.

  • Voltage Source Inverter (VSI).

VSI is the heart of the SAPF. The VSI converts the DC energy from the capacitor into AC currents opposing the harmonic and reactive components in the grid. VSI operates on the basis of PWM techniques for precise compensation.

  • Output filter.

Inductors are connected between the VSI and the grid. They are the transmission elements which smooth the output currents of the inverter and provide a good synchronization with the grid. Moreover, they operate as filters to damp the high-frequency noise produced during the switching process.

  • Control Unit.

The control unit performs real-time monitoring and control of the SAPF. It uses advanced algorithms in the detection of harmonic distortions, among other power quality issues on the grid. The control system produces accurate reference signals for the VSI to inject compensating currents effectively. Most modern applications use either instantaneous reactive power theory or synchronous reference frame methods for better performance, which ensures reliable operation under dynamic conditions.

Control unit description

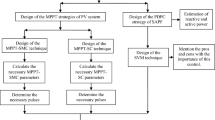
The control unit constitutes the heart of the three-phase SAPF. The essence of the operating principle of this control unit includes real-time control and monitoring, so that one can effectively have harmonic mitigation that ensures improvement of power quality. It consists of three sections: harmonic extraction, DC-link voltage regulation, and current control.

In this study, we selected a PI controller for DC-link voltage regulation, the Synchronous Reference Frame (SRF) method for harmonic extraction14,37,38, and a hysteresis controller for the current control loop. The schematics of these sections are presented in Figs. 2 and 3, and 4, respectively.

Fig. 2
figure 2

PI controller with windup handling.

Full size image
Fig. 3
figure 3

Reference Current Extraction Using the SRF.

Full size image
Fig. 4
figure 4

Hysteresis current controller.

Full size image

Optimal design of the PI controller and RL output filter

The PI controller parameters (K_p, K_i, and K_a) are tuned to achieve rapid response and minimal steady-state error. Similarly, the RL output filter is designed to reduce interactions between the inverter and the grid, ensuring stable operation and efficient harmonic compensation. The optimization process considers system dynamics and power quality standards.

Optimization problem formulation

The optimization process aims at improving the performance of the three-phase SAPF by minimizing three key factors: the DC-link voltage error, the current error, and the Total Harmonic Distortion (THD) of the grid currents. These factors are combined into one fitness function that will be used for the evaluation of the system performance.

The fitness function is defined as the weighted sum of the three components:

$$\:F=\:{w}_{1}{\times\:E}_{DC}+\:{w}_{2}{\times\:E}_{I}+\:{w}_{3}\times\:THD$$
(1)

IAE will be the performance index that will be used to judge the deviations of both DC-link voltage and current errors over time. It gives the accumulated absolute error to ensure a comprehensive evaluation of system stability and dynamic response.

$$\:{E}_{DC}=\:{\int\:}_{t-T}^{t}\left|{V}_{dc\:ref}-\:{V}_{dc}\right|$$
(2)
$$\:{E}_{I}=\:{\int\:}_{t-T}^{t}\left|{i}_{ref}-\:{i}_{F}\right|$$
(3)

Golden Jackal optimizer

The GJO is a new nature-inspired metaheuristic proposed by Chopra and Ansari to solve optimization problems; it is inspired from the social and hunting behaviors of golden jackals. GJO has been developed on the basis of building balanced exploration and exploitation between the male and female jackals in the search space. This optimizer is more suited for finding the solutions to complex engineering optimization problems39.

This algorithm utilizes the two most important agents, namely, the male jackal and the female jackal, which are the best and the second-best solutions, respectively. Dynamic positions of these two jackals are used to drive the population of the search agents toward the optimal solutions. Taking inspiration from the evading behavior of the jackals, an energy factor E is introduced that can be dynamically updated depending on the number of iterations. Depending on the factor, either the exploration or exploitation of the algorithm will be considered. Another novelty introduces the algorithm by means of the distribution of Levy flights to improve exploration by randomizing step size. The flow chart of the GJO is represented in Fig. 5 as summary of its steps.

The movement of the jackals in the search space can be modeled by the following equations:

$$\:\overrightarrow{X}\left(t+1\right)=\:{\overrightarrow{X}}_{P}\:\:-\:\:\:E\:\:\times\:\:\overrightarrow{D}$$
(4)
$$\:{\overrightarrow{D}}_{1}=\:\left|{\overrightarrow{X}}_{P}\:\:-\:\:\:{\overrightarrow{R}}_{L}\:\:\times\:\:\overrightarrow{X}\left(t\right)\right|$$
(5)
$$\:{\overrightarrow{D}}_{2}=\:\left|{\overrightarrow{R}}_{L}\:\:\times\:\:\:{\overrightarrow{X}}_{P}\:\:-\:\:\:\overrightarrow{X}\left(t\right)\right|$$
(6)
$$\:{\overrightarrow{X}}_{new}=\:\frac{\overrightarrow{X}{\left(t+1\right)}_{male}+\:\overrightarrow{X}{\left(t+1\right)}_{female}}{2}$$
(7)

With.

\(\:\overrightarrow{X}\left(t\right)\) is the current position of the jackal.

\(\:\overrightarrow{X}\left(t+1\right)\) is the new position according to the position female or the male jackal.

\(\:{\overrightarrow{X}}_{P}\) is the position of the male and female jackals.

\(\:E\:\:\)is the evading energy.

\(\:\overrightarrow{D}\) is the distance between the current position and the prey.

\(\:{\overrightarrow{R}}_{L}\) is a random factor derived from Levy flight distribution.

$$\:E=\:\left(\:1.5\:\times\:\:\frac{1.5\:\times\:iteration}{Max\:iteration}\right)\:\times\:\:\left(2\times\:{r}_{1}-1\right)$$
(8)
$$\:{\overrightarrow{R}}_{L}=\:0.05\:\times\:levy$$
(9)

Where.

\(\:{r}_{1}\) is a random number between 0 and 1.

\(\:iteration\) is the current iteration.

\(\:Max\:iteration\) is the maximum iteration number.

\(\:levy\) is a random factor derived from Levy flight distribution.

The update mechanism is divided into two phases based on \(\:\mid\:E\mid\:\). When \(\:\mid\:E\mid\:>1\) (exploration phase), search agents update their positions relative to the male and female jackals using Eqs. (4), (5), and (7). Conversely, when \(\:\mid\:E\mid\:<1\) (exploitation phase), the position updates are governed by Eqs. (4), (6), and (7).

Fig. 5
figure 5

Flow chart of GJO.

Full size image

Results and discussion

A sophisticated simulation was developed using the MATLAB/Simulink programming environment to thoroughly investigate the dynamic response and behavior of the SAPF when exposed to an assortment of rigorous usage profiles. The tests put the SAPF through a series of demanding situations, such as rapidly changing loads producing transient load currents, unbalanced source voltage levels, and dramatically fluctuating reactive power demands.

GJO evaluation against PSO, GWO, and ACO

The performance of the GJO was compared with three well-known optimizers: Particles Swarm Optimizer (PSO), Grey Wolf Optimizer (GWO), and Sine Cosine Algorithm (SCA), based on their convergence behavior. The optimization parameters for each algorithm are given in Table 3.

Table 3 Parameters of the optimization.
Full size table

Figure 6 shows the convergence curves of the algorithms, from which the superiority of GJO can be clearly observed. The GJO has a fast convergence rate in the initial iterations and keeps a stable upward trend toward the global optimum. This means that the algorithm has a very good balance between exploration and exploitation, enabling it to outperform PSO, GWO, and SCA in terms of better avoidance of local optima for more optimal solutions. Further, the following Table 4 presents the obtained fitness values and the parameters optimized by each method.

Table 4 Optimization results.
Full size table
Fig. 6
figure 6

Convergence curves.

Full size image
Fig. 7
figure 7

Performance of the optimized SAPF system with load 3 under balanced grid conditions.

Full size image

Optimized SAPF evaluation

The performance of the designed Shunt Active Power Filter (SAPF) was evaluated using simulation parameters detailed in Table 5, with Load 3 as the test condition. The SAPF was activated at \(\:t=0.2s\), and the results are illustrated in Fig. 7, which contains five subplots describing key aspects of the system’s operation.

Table 5 Parameters of the system.
Full size table

Figure 7-a presents the DC link voltage and its reference, demonstrating that the optimized controller effectively tracks the reference voltage with no overshoot and achieves a settling time of just \(\:0.35\hspace{0.17em}s\). This reflects the controller’s precision and stability in regulating the DC link voltage. Figure 7-b shows the grid voltage, where a minor voltage drop is observed after the SAPF is connected, and indicating minimal impact on grid voltage stability.

Figure 7-c illustrates the currents of the grid, load, and SAPF. The optimized system successfully generates the required compensation current to eliminate harmonics and reactive power, resulting in a sinusoidal grid current. This is further validated in Fig. 7-d, which provides an FFT analysis of the grid current (\(\:{i}_{sa}\) ​), showing a significant reduction in Total Harmonic Distortion (THD) from \(\:14.64\%\) to \(\:0.8\%\). Additionally, the magnitude of the current was reduced from \(\:23.9\:A\) to \(\:15.71\:A\), demonstrating the SAPF’s effectiveness in improving current quality.

Finally, Fig. 7-e presents the reactive power analysis of the grid and the load. Before SAPF activation, the reactive power from the grid was approximately \(\:2000\:VAR\). After activation, the SAPF successfully compensated for the reactive power, reducing it to nearly zero, thereby ensuring optimal power factor correction.

Fig. 8
figure 8

Comparison between the optimized SAPF system and the system in1: (a) Performance of the optimized SAPF with load 1 under balanced grid conditions, (b) Results from1.

Full size image

The next evaluation is to compare the performance of the proposed SAPF with the results presented in1. According to Fig. 8b which represent the FFT analysis of the grid current captured from1, the optimized proportional-resonant (PR) controller, designed using the Genetic Algorithm (GA), achieved a Total Harmonic Distortion (THD) of 3.86%. In contrast, as shown in Fig. 8.a the proposed SAPF, utilizing the optimized controller, achieved a significantly lower THD of 0.86%. The test was conducted under the same load and grid conditions as described in1, which are detailed in Table 5 of our paper, where the load corresponds to load 1. Additionally, a comparison of the DC link voltage performance reveals that the proposed controller demonstrates superior regulation characteristics.

Specifically, the overshoot of the proposed controller is only 6 V, whereas the controller in1 exhibits a significantly higher overshoot of 12 V.

Fig. 9
figure 9

Performance of the optimized SAPF with dynamic load and unbalanced grid voltage.

Full size image

The final evaluation of the proposed SAPF was conducted under unbalanced grid voltage conditions, where the voltage \(\:{V}_{sc}\) was reduced by 20%. Initially, the system was tested with Load 1 under the unbalanced grid, and at \(\:t=1\hspace{0.17em}s\), the load was switched to Load 2. Despite this dynamic and challenging scenario, the optimized SAPF demonstrated its robustness and effectiveness by significantly reducing the THD and compensating for reactive power.

The results, illustrated in Fig. 9, confirm the SAPF’s excellent performance. Figure 9-a shows the DC link voltage and its reference, where the SAPF successfully maintains stability and tracks the reference throughout the load transition. Figure 9-b shows the grid voltage under the unbalanced condition in which the system keeps working effectively though the voltage goes down. Figure 9-c illustrates grid, load, and SAPF currents the results confirm also that although the voltage is unbalanced and the dynamic load change also occurs, SAPF can maintain the sinusoidal grid current. Figure 9-d shows the FFT analysis of grid current, which is showing a significant reduction in THD. Figure 9-e shows the reactive power compensation result, and here, the SAPF is able to reduce the reactive power to nearly zero in the grid.

Conclusion

This paper presented an optimization approach for the PI controller and the output filter in a Shunt Active Power Filter (SAPF) system. The design of both the controller and the filter was formulated as an optimization problem, which was then solved using the Golden Jackal Optimizer (GJO). GJO has been selected after comparing its convergence performance with the convergence performance of three well-known optimizers, namely Grey Wolf Optimizer, Sine Cosine Algorithm, and Particle Swarm Optimization. The outcome of this comparison proved that GJO had superior convergence performance and is the best suitable optimizer for the said application.

The optimized SAPF system has been tested under nominal grid conditions, unbalanced grid, and dynamic load variations. Tests yielded much better results in THD reduction, harmonic elimination, and reactive power compensation. The optimized PI controller ensured that the DC link voltage was regulated in a fast and stable way, while the optimized output filter minimized grid distortion by improving the quality of the injected current. Both enhancements are critical in maintaining the overall performance and reliability of the SAPF system. Moreover, the extended comparative analysis with the state-of-the-art studies confirmed that the proposed optimization approach outperforms the existing methods, especially regarding THD reduction, DC link voltage overshoot, and overall system stability.

In conclusion, the main contributions of this paper are as follows:

  • Development of an optimized PI anti-windup regulator for DC link voltage regulation.

  • Optimization of the output filter in SAPF systems to enhance the quality of the injected current.

  • Comprehensive evaluation of the proposed method under normal, unbalanced, and dynamic load scenarios.

  • A comparative analysis with recent works, demonstrating superior performance in harmonic compensation and dynamic response.