Introduction and preliminaries

Quantum entanglement1,2 is an essential resource in the fields of quantum computing3 and quantum communications4,5. Entangled qubits cannot have their properties expressed individually in a way that fully characterizes the shared state; instead, the entire entangled state is intrinsically linked. This effect can be observed regardless of distance6,7 between the entangled qubits. This correlation between the qubits, which is a purely quantum effect, with no analogue in classical computing or communications, can be leveraged in ways that are at the foundation of the majority of quantum protocols and algorithms.

Introduction to entanglement distribution

An example of a protocol that particularly benefits from the non-local correlation of entanglement is the quantum teleportation protocol8,9,10. This protocol is used to transfer quantum information between two nodes, which share an entangled pair (ebit). As the quantum information is transferred without a physical exchange of matter, there is no possibility of eavesdropping. However, the speed of this transfer is not superluminal as the name of the protocol suggests, as, even though the transfer of quantum information appears to be near instantaneous11, there is a need to apply corrections upon the received quantum state, for which two classical bits need to be transferred. In this process of quantum teleportation, the pre-shared entanglement between the parties is consumed. Thus, for sustained communications using the teleportation protocol, a way to resupply the communicating parties with entanglement is needed. The teleportation protocol is not the only protocol which uses entanglement. The E91 protocol12 for quantum key distribution13,14 also uses entanglement as a resource in order to distribute keys. In this protocol, entanglement between the parties is used to verify against potential eavesdroppers on the quantum channels where the keys are transferred.

In quantum computing, alongside the concept of superposition, entanglement is the cornerstone of quantum algorithms15,16,17. Through the use of these two effects, one can perform parallel computations using multiple entangled qubits, which is the equivalent of sifting through all possible configurations of these qubits at the same time. Since quantum states are fragile and prone to decoherence due to environmental factors, with the highest coherence times for photonic qubits in the range of tens of milliseconds18, scaling entanglement distribution networks proves to be a difficult task. A way to limit the adverse effects of transmitting photons through very long channels and, implicitly, long transmission times, is through the entanglement swapping protocol19,20.

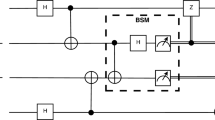
The entanglement swapping protocol involves three parties, Alice, Bob, and Charlie. With the goal being to share an entangled pair between Alice and Bob, both of them create an entangled pair and transmit one of the two particles towards Charlie, a node between them. If Charlie is at half of the distance between Alice and Bob, the exponential attenuation experienced by the particles during this exchange would be minimized globally. When the two particles reach Charlie, a Bell State Measurement (BSM) is performed on them, and the entanglement is transferred between the two particles that never left Alice and Bob. Therefore, Alice and Bob become entangled without actually having to transmit a physical particle all the way between themselves. This protocol stands at the foundation of a global Quantum Internet21,22,23.

The Quantum Internet is envisioned to be the global network through which quantum information is transferred. Proposed quantum network stacks22,24 include a layer where entanglement distribution25 is handled, such that higher level functions of the Quantum Internet may be performed, such as the quantum teleportation protocol. In order to efficiently ensure the functionality of this layer of the Quantum Internet, the physical nodes of this network need to be able to perform two functions, namely BSMs and entangled pair generation26. In this work we will consider a homogeneous network where all nodes are able to perform these operations.

Quantum network topologies

There have been various studies that have focused on entanglement distribution applied for different specific network topologies27,28. In the following, we will succinctly present a couple of such studies which are related to the scope of this work.

In a 2011 study29, van Meter et al. proposed the concept of Quantum Recursive Network Architecture (QRNA). The framework proposed in this work abstracts complex subnetworks as individual nodes, paving the way towards a modular approach for sharing entanglement between remote nodes. The architecture introduces a recursive request structure, where entanglement distribution tasks are broken down into smaller requests that can be processed independently by different layers in the network. This approach facilitates the use of various entanglement management techniques, such as purification, entanglement swapping, and quantum error correction, to maintain high-fidelity states across the network. We may consider any specific topology with a known optimal entanglement routing protocol as a subnetwork within a larger recursive quantum network, that may receive specific requests which aid in establishing a shared state between nodes of the larger network.

In a study by Chakraborty et al.30, the authors propose a linear programming (LP) formulation to find the maximum rate of distributing entanglement in a general network graph, which is based on the length-constrained multi-commodity flow problem31. The path-length constraint (i.e. the number of consecutive edges connecting two end nodes that request entanglement) takes into consideration a minimum entanglement fidelity, as well as the probabilistic nature of the entanglement swapping, crucial for distribution of entangled pairs over long distances. The number of LP variables and constraints in the algorithm scales polynomially (\(|D| \times |E| \times |V|\) for variables, and \(|V|^2|E||D|+|V||E|+|V|^2|D|\) for constraints), where |V| represents the number of nodes in the network graph, |E| the number of edges, and |D| the number of requests. However, as the LP formulation gives the maximum rate only, an additional algorithm is proposed to retrieve the set of edges used for achieving that rate, in polynomial O(\(|D| \times |V|^4 \times |E|\)) time.

Azuma et al.32 explores advancements in quantum repeater networks, focusing on protocols for entanglement generation, purification, and distribution over long distances. Key findings include the optimization of entanglement rates through hybrid architectures (e.g., combining discrete and continuous-variable methods), the role of quantum error correction in fault-tolerant repeaters, and strategies to mitigate photon loss in lossy channels. These findings can directly inform entanglement distribution in multi-ring topologies, where interconnected rings require robust, low-loss protocols to ensure redundancy and efficient resource allocation across nodes. In the current study, we adopt a system-level perspective on entanglement distribution networks, analyzing routing strategies while abstracting node-specific purification operations to focus on higher-level network behavior.

A recent study of optimal entanglement distribution in star-shaped quantum network topologies33 was performed by introducing two modes of distributing entanglement through an intersection between chains, asymmetrical and symmetrical. In the symmetrical approach, nodes at even indices along intersecting routes generate entangled pairs and distribute qubits bidirectionally, minimizing interference but limiting success to resolving one request per time slot if all transmissions and BSMs succeed. This strategy’s performance depends on transmission success probability and BSM success rate. The asymmetrical scheme, however, assigns alternating node generations (e.g., even vs. odd nodes) to routes, enabling simultaneous success for multiple requests if operations succeed. While this increases throughput in high success rate environments, it requires additional BSMs, reducing overall success probability. In the current manuscript, we apply the results of this analysis to an idealized network with 100% transmission and BSM success rates, exploring how these foundational principles of intersecting routes scale under optimal conditions.

Building on the foundation of optimal entanglement distribution within intersecting routes, the study of optimal entanglement distribution through crossbar quantum networks34 extends the principles of even/odd distribution to a grid-like topology, where nodes are interconnected in a non-blocking crossbar architecture. Here, the even/odd parity constraints are adapted to manage intersections between routes in a two-dimensional grid, ensuring no node performs more than one BSM per cycle. The crossbar’s scalability is analyzed via an algorithmic framework that formulates parity constraints as a MAX-2SAT problem, optimizing the distribution of BSMs across nodes. However, unlike star-shaped networks, which inherently avoid intersection conflicts due to their radial structure, the crossbar’s grid architecture has critical limitations: certain input-output configurations cannot be resolved without blocking.

The novelty of the current work compared to the crossbar quantum networks analysis, beyond the particular topology analyzed, lies in its extended scope. While earlier studies focused on developing an algorithm to schedule entanglement distribution requests within a single time slot, this manuscript extends this framework by addressing two critical dimensions: quantifying the resources required to fulfill all requests in a single time slot, and determining the number of time slots needed to distribute entanglement given fixed resource constraints. This dual focus transcends the narrow scope of prior work, offering a comprehensive framework for both resource optimization and temporal scalability in quantum networks.

In a 2025 study Meng et al.35 examines how quantum communication networks behave when they experience ”path percolation,” a process where communication between nodes consumes the links along the shortest path, effectively breaking those connections. Over time, this can fragment the network into smaller disconnected clusters. A critical threshold was found: if entanglement generation outpaces communication-driven loss (scaling with the square root of network size), the network remains connected; otherwise, it fragments into tree-like clusters. This fragmentation is mitigated by strategically prioritizing cross-component link replenishment. In the case of an entanglement resupply network, being able to determine the rate of replenishment as a function of entanglement resupply requests satisfied per time slot can be crucial in order to assess whether the network exceeds the fragmentation threshold.

Fig. 1
figure 1

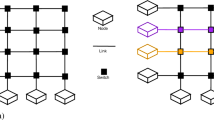
The multi-ring network topology. (a) Highlights that each node is the same for all the layered rings. (b) Shows the Ring to Ring (R2R) topology, where each ring acts as a separate network, with no path between rings, as the nodes do not allow switching between ring layers. (c) Shows the any Ring to any Ring (aR2aR) topology, where each node allows switching between ring layers.

Full size image

Ring quantum network topology

A topology that has not yet been formally analyzed in the realm of entanglement distribution is the multi-ring topology. Ring topologies have many use cases in classical networking, due to their built-in redundancy and routing simplicity. A ring quantum network topology is one where the quantum nodes are connected in a circular manner, forming a single closed loop. Each node has a cardinality of 2, and is able to communicate bidirectionally on both links. To describe a ring quantum network, we consider two key parameters: the number of links connecting nodes, each link layer forming a ring in the multi-ring topology, as in Fig. 1, and the number of BSM devices per node. Our analysis considers a homogeneous network, where all nodes have the same capabilities and parameters. We consider this to be a more realistic scenario, as the analogues in classical networks rarely exhibit varying capabilities along the ring.

Multi-ring networks offer enhanced security and flexibility. Their layered architecture enables dynamic path selection, ensuring secure rerouting of entangled pairs if segments are compromised, while also allowing prioritization of critical requests on dedicated rings. This adaptability supports heterogeneous workloads, such as high-priority quantum computing tasks alongside routine communication, without overloading the system. These features make multi-ring topologies indispensable for next-generation quantum systems, which demand robustness, efficiency, and scalability.

Despite these clear benefits, multi-ring networks remain underexplored in entanglement distribution optimization due to the complexity of scheduling concurrent requests across multiple rings without path overlaps. This gap motivates our work, which introduces novel linear programming formulation and algorithms. By addressing these challenges, our framework paves the way for scalable and efficient quantum networks capable of supporting sustained quantum communication and distributed quantum computing at scale.

We are addressing a ring topology with many layers, as the particular problem of entanglement distribution poses some unique problems, not found in classical networking. For example, as the quantum states are very sensitive and prone to decoherence, two photons should not travel along a link at the same time, as there is a possibility of interference. Therefore, it is easy to imagine many situations where a single ring network, with multiple concurrent entanglement resupply requests, may have overlapping distribution routes and, therefore, some resupplies will need to be delayed. With a multi-layer topology, the congestion may be avoided or minimized.

The central question addressed in this work is: how can we minimize the time slots, and resources (rings and BSM devices), required for concurrent entanglement distribution in multi-ring quantum networks ensuring scalability? To formulate this problem, we consider a multi-ring network, where entanglement distribution requests must adhere to three constraints: requests on the same ring must have non-overlapping paths, there must be minimal resource usage, and the solution must scale with network size.

While addressing these questions, our methodology focuses on two possible scenarios for routing entanglement within a multi-ring topology. The Ring to Ring (R2R) scheme, where a pair of nodes requesting entanglement may route their entanglement within a single layer of the network, that being that all the ebits transmitted in order to generate entanglement between them will only be routed on link number x between all intermediary nodes. The other scenario we are considering, any Ring to any Ring (aR2aR), as the name suggests, means that between intermediary nodes transmissions of ebits may be routed on different link numbers. This also means that if a half of an ebit comes on link x, and the other part comes on link y, they can be routed to the same BSM device in order to perform the entanglement swapping. It should be noted that the different links do not necessarily need to be physical links between nodes, but it can be a single physical link that multiplexes multiple channels. While the network is functioning, we denote a unit of time within its runtime as a time slot. We define a time slot as the time it takes to transmit a half of an ebit along the longest link within the network, and the time it takes to make the BSM of it and its corresponding half of another ebit. We consider the transmission time along the longest link in order to avoid timing drifts of the network, and ensure that all operations along the network happen synchronously.

Our methodology includes novel Linear Programming (LP) constraints to enforce ring-layer uniqueness for intersecting paths and track BSM placement, extending the linear programming framework for entanglement distribution in crossbar quantum networks34. LP is a mathematical optimization framework used to model and solve problems where the objective is to maximize or minimize a linear function subject to linear constraints. In LP variables can be continuous, while for Integer Linear Programming (ILP) problems all variables within the problem statement need to be integers (or booleans, represented as either 0 or 1). The algorithms presented in this work solve for minimal resources and time slots, balancing scalability and redundancy. The key findings from these algorithms reveal that, except in specific edge cases, there is no substantial difference in time slots or resource requirements between the aR2aR and R2R schemes. These results indicate that the higher complexity of an aR2aR deployment might not be justified unless optimizing for peak performance is critical.

This work is structured as follows. In Section “Ring to ring (R2R) entanglement distribution” we analyze optimal entanglement distribution and resource allocation for the R2R scenario. In Section “Any ring to any ring (aR2aR) entanglement distribution”, we analyze the optimal entanglement distribution and resource allocation for the aR2aR scenario. In Section “Simulation results” simulation results and comparisons between the two scenarios are provided. This work ends with conclusions and future outlooks.

Fig. 2
figure 2

The R2R multi ring topology. An entanglement resupply request may only be routed within a single ring, as the nodes do not allow switching between ring layers.

Full size image

Ring to ring (R2R) entanglement distribution

We consider the following scenario. Each request can only be routed within a single layer of the network. Effectively, this means that the entire network acts as a collection of independent ring networks that connect the same physical nodes. A visual example can be seen in Fig. 2. This kind of a network requires less complex hardware, therefore would have a reduced cost in a real world application. The node used in this scenario can be envisioned either as a single physical unit that has multiple quantum links connected to it, with each input pair leading to a single Bell State Measurement device assigned to it. Alternatively, the nodes may be multiple such units that are in the same physical location.

In this section, we will focus on finding the optimal entanglement distribution strategy in order to minimize the number of time slots required to satisfy an array of requests, and the optimal network resources—number of independent rings and BSM devices per node that are needed to satisfy an array of requests in a single time slot. Alongside the algorithms, a complexity analysis for each is provided.

Optimal time entanglement distribution, with given resources, in a R2R topology

We denote the number of pairs requesting entanglement as M, the number of nodes of the network as N, the set of all requests as J, the number of rings as R, and the number of maximum BSMs allowed per node in a time slot as B. A route in a ring graph may be defined by a tuple (\(J_j\), k, l), with \(k,l \in \{0, 1\}\), where \(J_j\) defines the request, represented as a tuple (a, b), with \(a,b \in \{0, 1, \ldots , N-1\}\) denoting the nodes that request to be entangled; k represents the path between a and b on the ring graph, with k=0 indicating the clockwise path from a to b, and k=1 indicating the counterclockwise path from a to b; and l specifies the distribution scheme, defining the role of each node included in the path: l=0 for an even scheme (nodes at even positions generate entangled pairs, while nodes at odd positions perform BSM) and l=1 for an odd scheme (nodes at odd positions generate entangled pairs, while nodes at even positions perform BSM). Since the R2R topology does not allow movement from one ring to another at each node hop, it is necessary to assign to each request the ring layer that will be used by a given route to distribute the entangled pairs to the two nodes.

The optimal time for entanglement distribution can be achieved by minimizing the number of time slots required to fulfill all requests, while adhering to the constraints of the maximum BSMs allowed in a time slot, and the number of rings. The problem of entanglement distribution in an optimal time can be expressed in an ILP framework that includes an integer variable \(i_{max}\), with \(0 \le i_{max} \le M-1\), as the objective function used to determine the minimum number of time slots, and a scheduling boolean variable \(s_{ijklm}\) to indicate the satisfiability of allocating the request j in the time slot i, using the route defined by \((J_j, k, l)\), and the ring m. It is presented as follows:

$$\begin{aligned} \begin{aligned} \text {Let } \mathbf {i_{max}} \text { be an integer variable and }&\mathbf {s_{ijklm}} \text { a boolean defined for all } i,j \in \{0, 1, \ldots , M-1\}\text {, }\\&k,l \in \{0, 1\} \text {, }\; m \in \{0, 1, \ldots , R-1\} \\ \text {find } \mathbf {s_{ijkl}} \text { that minimizes }&\mathbf {i_{max}}&\\ \text {subject to }&i_{max} \ge i * s_{ijklm}, \forall i,j \in \{0, 1, \ldots , M-1\}, \forall k,l \in \{0, 1\}, \forall m \in \{0, 1, \ldots , R-1\}&\\ &\sum _{i=0}^{M-1} \sum _{m=0}^{R-1} \sum _{\begin{array}{c} k=0,1 \\ l=0,1 \end{array}} {s_{ijklm}} = 1, \forall j \in \{0, 1, \ldots , M-1\}&\\&\sum _{j=0}^{M-1} \sum _{m=0}^{R-1} \sum _{\begin{array}{c} k=0,1 \\ l=0,1 \end{array}} {s_{ijklm}} \le B, \text { if node } a \text { performs BSM on route } (J_j,k,l), \\&\forall a \in \{0, 1, \ldots , N-1\}, \forall i \in \{0, 1, \ldots , M-1\}&\\&\sum _{j=0}^{M-1} \sum _{\begin{array}{c} k=0,1 \\ l=0,1 \end{array}} {s_{ijklm}} \le 1, \text { if node } a \text { generates entanglement to right, or node } \\&a+1 \text { generates to} \\&\text {left, on route } (J_j,k,l), \forall a \in \{0, 1, \ldots , N-1\}, \forall m \in \{0, 1, \ldots , R-1\},\\&\forall i \in \{0, 1, \ldots , M-1\}&\end{aligned} \end{aligned}$$
(1)

In Algorithm 1 we present the constraint building process for the ILP problem 1 which provides the optimal timing for distributing entanglement in a R2R network with a given number of rings and BSMs per time slot. We consider a solver that can efficiently solve the ILP problem and provide an accurate result for it. The optimality of the solution may depend on the solver used, and not on the constraints imposed. As such, the hereby presented algorithm is generally applicable.

Algorithm 1
figure a

Optimal Time Entanglement Distribution in a R2R Topology

Full size image

Optimal resources for entanglement distribution, in a time slot, for a R2R topology

In order to determine the optimal resources to distribute entanglement between an array of requesting pairs within a single time slot we define our objective function. We want to minimize the sum of the number of rings required, and the maximum amount of BSM performed within a single node. We will not be assigning a different weight to these two measures, as the cost difference between these is not quantifiable currently. We will use the same notations as before, the number of rings required as R, and the maximum number of BSMs performed as B. Therefore, we want to minimize \(R + B\).

We will start from a basic observation. If two routes intersect, they cannot be resolved within the same ring layer. As we have stated before, however, each request has 4 possibilities of being routed. Clockwise (CW), counterclockwise (CCW), and for each of these it may perform the BSMs in an even or odd parity. The choice of even or odd does not affect whether or not two routes intersect, only if they are CW or CCW.

We introduce a few other variables that will aid with solving this problem. \(B_i \in \mathbb {Z}\) will be the number of BSMs performed in node i. \(R[i] \in \mathbb {Z}\) will be the rings on which request i is routed. \(X_{i, parity, direction}\) is a boolean that signifies that route i has or has not chosen a certain parity (even or odd), and direction (CW or CCW). We will also denote \(C_{i,j_{direction_i,direction_j}}\) a boolean that is true when both route i and route j have chosen the directions specified.

The problem can be expressed in an ILP framework as follows

$$\begin{aligned} \begin{aligned} \text {Let } \textbf{d} = [R, B] \text { be a an integer vector}&\text { where } R, B \in \{0, 1, \ldots , M\}&\\ \text {find } \textbf{d} \text { that minimizes }&\textbf{d}^\top \textbf{d} & \\ \text {subject to }&X_{i, odd, cw} + X_{i, even, cw} + X_{i, odd, ccw} + X_{i, even, ccw} = 1, \forall i \in [1, M] & \\&C_{i,j_{cw-cw}} = X_{i, cw} \wedge X_{j, cw}, \forall i,j \in [1, M], i \ne j&\\&C_{i,j_{cw-ccw}} = X_{i, cw} \wedge X_{j, ccw}, \forall i,j \in [1, M], i \ne j&\\&C_{i,j_{ccw-cw}} = X_{i, ccw} \wedge X_{j, cw}, \forall i,j \in [1, M], i \ne j&\\&C_{i,j_{ccw-ccw}} = X_{i, ccw} \wedge X_{j, ccw}, \forall i,j \in [1, M], i \ne j&\\&R[i] \ne R[j], \forall i,j \in [1, M] \text { where route i intersects j}&\\&R>= R[i], \forall i \in [1, M]&\\&B[i] = \sum _j X_j \text {if route j performs a measurement in node i}&\\&B >= B[i], \forall i \in [1, N]&\end{aligned} \end{aligned}$$
(2)

The above constraints are further implemented in Algorithm 2.

In order to impose the constraint that \(R[i] \ne R[j]\), in a ILP context, we will need to use two constraints, which introduce an additional free boolean variable \(D_{i,j}\). The purpose of \(D_{i,j}\) is to act as a binary selector for the two possibilities where either R[j] is larger or smaller than R[i]. By toggling between 0 and 1, \(D_{i,j}\) ensures that one of these strict inequalities is enforced while avoiding the equality. This variable is essential for modeling discrete logical relationships between variables in optimization problems where direct non-equality constraints are not permitted. The two constraints are the following.

$$\begin{aligned} R[j] \le R[i] - 1 + M * (1 + D_{i, j} - C_{i,j}) \end{aligned}$$
$$\begin{aligned} R[j] \ge R[i] + 1 - M * (2 - D_{i, j} - C_{i,j}) \end{aligned}$$

This pair of constraints effectively reduces to \(R[j] \ge R[i] + 1\) or \(R[j] \le R[i] - 1\), meaning that it can have any value other than R[i].

Algorithm 2
figure b

Optimal Resources for Entanglement Distribution within a Time slot in A R2R topology

Full size image

Complexity analysis of entanglement distribution schemes in a R2R topology

The complexity class of ILP optimization problems is generally NP-hard36. Consequently, the worst-case time complexity is exponential relative to the input size (that being the number of constraints and the number of variables), making ILP problems computationally challenging to solve optimally, especially as the problem size grows. As we can observe, the inputs here, even though they increase polynomially, may become unfeasible for large network sizes.

Regarding the ILP problem proposed for obtaining the optimal entanglement distribution with respect to the number of time slots, it can be easily computed that the number of variables in the problem statement is equal to \(4\times M^2\times R + 1\) accounting for all s variables and the additional \(i_{max}\) variable, and the number of constraints is \(M + 4\times M^2\times R + M \times N + M \times N \times R\)] With M constraints for route uniqueness, \(4 \times M^2 \times R\) constraints for pairwise interactions and the rest for BSM limits and entanglement generation. For the problem of obtaining the optimal resources, the number of variables is \(2 + 4 \times N^2 + 6 \times M\), since each request has 4 options for the pairwise ring constraints, along with pairwise direction constraints, added with two global variables, the number of rings and maximum number of BSMs. The number of conditions is \(4 \times M^2 + M + 2 \times N\), with \(4 \times M^2\) coming from the pairwise direction contraints, M route selection constraints and \(2 \times N\) global constraints on B.

The worst case complexity for ILP problems, if the solver uses Branch and Bound techniques37,38, is \(\mathcal {O}(2^n)\), where n is the tree depth. In our case, the tree depth is at most the number of variables (\(4\times M^2\times R + 1\) for optimal time problem and \(2 + 4 \times N^2 + 6 \times M\) for the optimal resources problem). It should be however noted that most ILP solvers make use of advanced heuristics to further improve practical efficiency and reduce runtime for real-world applications.

Any ring to any ring (aR2aR) entanglement distribution

Fig. 3
figure 3

The aR2aR multi ring network topology. Requests may be routed on segments of different rings, as each node allows switching between ring layers through an interconnection between all of their direct links.

Full size image

In the previous section we have focused on a scenario where a request may only be routed through a single layer of the multi-ring topology. Intuitively, by eliminating this restriction and allowing the request to change the layer of the network when passing through a node, we expect to minimize the number of unused resources when solving an array of entanglement distribution requests. This kind of topology is very similar to a torus topology. It is apparent that a network that would permit layer-switching may need more complex hardware, therefore more expensive, and more difficult to acquire. A visual example of such a network can be observed in Figure 3.

In this section we will focus on the same objectives. First, finding the optimal entanglement distribution strategy in order to minimize the number of time slots required to satisfy an array of requests, and secondly, the optimal network resources - number of independent rings and BSM devices per node, needed to satisfy an array of requests in a single time slot. Along with the algorithms, a complexity analysis for each is provided.

Optimal time entanglement distribution, with given resources, in an aR2aR topology

While the objective function, the minimum number of time slots constraint, the requests fulfillment constraint, and maximum BSMs in a time slot constraint remain the same, the ring constraint is more relaxed. This is because the aR2aR topology allows movement from one ring to another at each node hop. As a result, there is no need to assign a ring layer to each request; instead, we only need to consider how many entangled pairs are forwarded between two adjacent nodes in each time slot.

The problem can be formulated in an ILP framework as outlined below:

$$\begin{aligned} \begin{aligned} \text {Let } \mathbf {i_{max}} \text { be an integer variable and }&\mathbf {s_{ijkl}} \text { a boolean defined for all } i,j \in \{0, 1, \ldots , M-1\}\text {, }\; k,l \in \{0, 1\} \\ \text {find } \mathbf {s_{ijkl}} \text { that minimizes }&\mathbf {i_{max}}&\\ \text {subject to }&i_{max} \ge i * s_{ijkl}, \forall i,j \in \{0, 1, \ldots , M-1\}, \forall k,l \in \{0, 1\}&\\&\sum _{i=0}^{M-1} \sum _{\begin{array}{c} k=0,1 \\ l=0,1 \end{array}} {s_{ijkl}} = 1, \forall j \in \{0, 1, \ldots , M-1\}&\\&\sum _{j=0}^{M-1} \sum _{\begin{array}{c} k=0,1 \\ l=0,1 \end{array}} {s_{ijkl}} \le B, \text { if node } a \text { performs BSM on route } (J_j,k,l), \\&\forall a \in \{0, 1, \ldots , N-1\}, \forall i \in \{0, 1, \ldots , M-1\}&\\&\sum _{j=0}^{M-1} \sum _{\begin{array}{c} k=0,1 \\ l=0,1 \end{array}} {s_{ijkl}} \le R, \text { if node } a \\&\text { generates entanglement to right, or node } a+1 \text { generates to} \\&\text {left, on route } (J_j,k,l), \forall a \in \{0, 1, \ldots , N-1\}, \forall i \in \{0, 1, \ldots , M-1\}&\end{aligned} \end{aligned}$$
(3)

These constraints are further specified in the ILP Algorithm 3.

Optimal resources for entanglement distribution, in a time slot, for an aR2aR topology

In order to determine the optimal resources for entanglement distribution within an aR2aR topology, we will make use of an observation. The number of BSM devices is always less or equal to the number of rings of the network. Intuitively, this stems from the fact that we cannot make more BSMs than entangled pairs may arrive at the node at a given time. Given this fact, we can greatly reduce our search surface for the optimal resources for entanglement distribution as we know that there is no point in searching for configurations where \(B > R\), and, furthermore, if we find a configuration \(B_k, R_k\) that can serve the requests within a single time slot, there is no point in searching for configurations l, where \(B_l + R_l >= B_k + R_k\).

Algorithm 3
figure c

Optimal Time Entanglement Distribution in an aR2aR Topology

Full size image

As such, we can perform a linear search for the number of rings R and then, for each R that can serve all requests within a time slot, given \(B = R\), perform a binary search of the minimum B value with which we can perform the entanglement distribution within a single time slot. To perform the check, we make use of Algorithm 3 with a given R, B and J set of values, which we will denote as a subroutine get_timeslots in the following. In Algorithm 4 we showcase how to efficiently find the optimal resources for entanglement distribution within an aR2aR topology.

Complexity analysis of entanglement distribution in an aR2aR topology

As the aR2aR topology does not impose a restriction on preserving the same ring layer while fulfilling an entanglement request on a route, the ILP problem of optimal time distribution of entangled pairs in this topology consists of fewer variables and conditions - \(4\times M^2 + 1\) variables, this figure is reached in a similar manner to the R2R algorithm, since there are \(4 \times M^2\) s constraints, and an additional global variable, and \(M + 4\times M^2 + 2 \times M \times N\) constraints stemming from the fact that the first constraint applies to all i, j, k, l, yielding \(4 \times M^2\) constraints. The second constraint applies to each j, yielding M constraints. The third and fourth constraints involve sums over j and node-specific conditions (involving N nodes and M time slots), contributing \(2\times M \times N\) constraints. This reduces the worst case complexity of the branch and bound technique to \(\mathcal {O}(2^{4\times M^2})\).

The optimal resources problem uses a linear and a binary search on the optimal time problem, in order to calculate both the number of rings and number of BSMs in a time slot, thus giving a complexity of \(\mathcal {O}( 2^{4\times M^2} \times M \log _2 M)\).

Algorithm 4
figure d

Optimal Resources for Entanglement Distribution within a Time Slot in an aR2aR Topology

Full size image

Simulation results

In order to analyze the distribution of entanglement over the two proposed scenarios, R2R and aR2aR, we have performed thorough simulations using the proposed algorithms in order to extract qualitative data regarding the possible resource efficiency of an aR2aR topology, and performance outlook for ring topology quantum networks.

Fig. 4
figure 4

Mean number of time slots required as a function of number of requests for both R2R and aR2aR network topologies and the slopes of these functions. The aR2aR network topology has at most an advantage of one time slot compared to the R2R configuration in all the tests performed. There are very slight differences between the mean time slot values, on a few scenarios, typically when more resources are used, due to the small range of values that the tests yielded. The small discrepancies are explained in the following.

Full size image

The simulations were performed on a machine equipped with an AMD Threadripper 5975WX with 32 cores and with 256GB RAM, with the solvers using much of the available compute power due to the complexity of the ILP problems. For each datapoint, we have averaged 30 different, randomly generated arrays of requests J. We have used the same array of requests for both the R2R and aR2aR configuration simulations.

Since in a ring topology both clockwise and counterclockwise routes are available, the minimum path length between the two route alternatives (in terms of number of nodes), that can be used to fulfill a request, has a maximum value of N/2. For a better statistic, we generated 50% of the 30 requests as distant (which means the minimum path length between the two route alternatives is greater than N/4), and the other 50% as close (which means the minimum path length between the two route alternatives is smaller than N/4).

Optimal time entanglement distribution simulations

Figure 4 shows the relationship between the number of requests and the mean number of time slots required to fulfill all those requests, using different amount of network resources, in both R2R and aR2aR configurations. It can be seen that in almost all cases, the same number of time slots are required for both topologies, while for some tests that employ more network resources, the aR2aR topology performs better, by 1 time slot, explaining the small distances that can be seen between several R2R and aR2aR points.

We mention that we have only considered resource configurations where the number of BSM devices is always less or equal to the number of links, as there would be no purpose for the surplus BSM devices, as there would be no possibility of getting enough entangled particles to measure. Regardless of the amount of resources available, all results mostly indicate a linear relationship between the number of requests and the optimal time slots to fulfill these thus, the observed linear relationship scales predictably with entanglement demand. The variation in the slope of this linear function, dictated by the resources allocated for this entanglement resupply network, highlights that insufficient resources lead to disproportionately higher time slot requirements to fulfill all the requests. This underscores the importance of adequate resource provisioning to maintain efficiency as demand increases. It can be observed that, naturally, the slope of the function quantifying the relationship between the number of requests and mean time slots becomes gentler with more resources allocated to the network. However, there seems to be an inverse logarithmic relationship between the resources and the slope, as the difference between 1 ring and 1 BSM and 5 rings and 5 BSMs is far greater than going from 5 rings and 5 BSMs to 10 rings and 10 BSMs - 0.24 compared to 0.02.

The tests in which the aR2aR topology resolves faster by a time slot have an important common characteristic—one or more requests need to change the ring layer in the route traversal, in order to be included in a lower time slot number, as there are no more new available rings to reserve. As this is possible only for the aR2aR topology, in the R2R one these requests are rescheduled for the next time slots. A simple example of this behavior is a scenario in which there are 3 requests in a topology with 2 rings. Each request intersects with the other two individually, but there is no mutual intersection among the three, i.e. \(R_1 \cap R_2 \ne \emptyset , R_2 \cap R_3 \ne \emptyset , R_3 \cap R_1 \ne \emptyset , R_1 \cap R_2 \cap R_3 = \emptyset\). In this case, the aR2aR topology can fulfill all three requests in only one time slot, because the maximum overlap on any link between two adjacent nodes is 2. However, the R2R topology will require two time slots, since any two requests can not be served by the same ring in the same time slot, and since we have three requests, one will need to be fulfilled in the second time slot.

Optimal resources for entanglement distribution simulations

Regarding the simulations of the algorithms for optimal resources for entanglement distribution, we have considered the same simulation environment. The main goal is to observe the relationship between the number of requests and the optimal resources needed to fulfill that set of requests.

Fig. 5
figure 5

The relationship between the number of requests and the median number of rings and the median number of BSM devices for the R2R scenario is presented in (a), and the mean values for these metrics is presented in (b).

Full size image

In Fig. 5 it can be observed that, naturally, the resources needed to satisfy a set of requests for the R2R scenario increases linearly with the number of requests, having a high correlation coefficient. It can be observed that there are outliner configurations that require much fewer resources to be satisfied within a time slot, but the vast majority fall within a relatively tight window of resource requirements. We can once again observe the linear relationship between the number of requests and the average number of resources, with the number of BSM devices being approximately half of the number of rings.

Also in figure 5 the aR2aR configuration is analyzed side by side, and we observe a higher correlation coefficient, although for the number of BSM devices the correlation remains the same. However, across the board, the optimal resource requirements are lower when compared to the R2R configuration. The aR2aR scenario generally needs less resources than the R2R scenario, and the vast majority of request configurations have a much lower dispersion of resources needed.

In Figure 6 the average of the optimal resources required for both scenarios are presented, with respect to the number of requests. It should be noted that in both the results for the R2R configuration, as well as in the ones for aR2aR the mean number of BSM devices is close to half the number of rings required. This can be intuitively explained by the fact that each request route, regardless of whether or not it uses an even or odd distribution or its ability of switching layers, will use roughly half of the BSM devices along its route. This means that if two routes intersect, there is a 1/2 chance that the nodes where the routes overlap would need to perform two BSMs.

Fig. 6
figure 6

The relationship between the number of requests and the median number of rings and the median number of BSM devices for the aR2aR scenario is presented in (a), and the mean values for these metrics is presented in (b).

Full size image

Comparisons between optimal resources in R2R and aR2aR topologies

Given the fact that in the aR2aR topology there are less restrictions regarding the routing of an entanglement resupply request compared to the R2R topology, intuitively we would expect that resources are used more efficiently in an aR2aR topology. We believe that an apt comparison between these configurations is with the discrete and the continuous knapsack problem39. In the R2R topology, the request will either ”fit” entirely within a ring layer, similar to the discrete knapsack problem, while the aR2aR topology is more akin to the continuous knapsack problem, where you can fit a section of the request within a ring and resolve the rest elsewhere.

Fig. 7
figure 7

Relationship between the unused percentage of network resources and the number of requests and the number of request overlaps. In (a) these values are presented for the R2R scenario, and in (b) the same relationships are analyzed for the aR2aR scenario.

Full size image

We define the percentage of unused resources in a multi ring network as the sum of nodes that are not used for any request in any way (regardless of whether these perform BSM or not) divided by the total number of nodes in the network. These nodes serve no purpose in the entanglement resupply operation, as they do not generate entanglement, nor perform BSMs. In Fig. 7 we can observe the relationship and correlation between the number of requests and the percentage of unused resources in the network, for both the R2R and aR2aR topologies. As indicated by the low negative correlation coefficient in both plots, the number of requests does not seem to have any bearing on the number of unused nodes, which is very high for both the R2R and aR2aR configurations.

The non-zero correlation coefficient of the unused resources percentage with respect to the number of requests observed in Figs. 7a and b might in fact emerge from a metric that correlates with the number of requests, as we will discuss further. We would in fact expect that there is no relationship between these figures, as what resources are used depends solely on the configuration of requests given.

With regards to the percentange of unused resources with respect to the number of request overlaps, in the R2R scenario there seems to be a low correlation coefficient between these values, however, in the aR2aR scenario there seems to be a stronger correlation. As such, these results may be inconclusive and need higher volumes of data to reach a meaningful result with regards to this metric.

In Fig. 7a and b the relationship between the number of intersections between request paths and the percentage of unused resources is also shown. Through these plots, we can first see that, in the R2R scenario, the unused resources of the network do not in fact depend on either the number of requests or the number of request routes overlaps. In the aR2aR scenario, a stronger correlation can be observed only between the number of requests overlaps and the number of unused resources in the network. Furthermore, it can be observed that for the same set of requests, the median percentage of unused resources in the aR2aR configuration is generally lower than the R2R configuration, with the average percentage of unused resources lower than half in most tests.

The relationship between the number of requests and the number of request intersections can be observed in Fig. 8. We have used the same set of requests, so that we are able to infer the cause of the non-zero correlation coefficient between the number of requests and unused resource percentage, as in both the R2R and aR2aR scenario we see stronger correlations between the number of request routes overlaps and the number of unused resources. The number of request routes overlaps is a metric that can qualitatively describe the request configuration, as it dictates which routes need to be on separate rings or ring segments.

Conclusions and future work

In this work we have analyzed the previously unexplored problem of entanglement distribution along a multiple ring topology quantum network. Although the potential cost and complexity of maintaining a single ring topology network should be lower, it is apparent that concurrent entanglement distribution within such a network comes with tight restrictions regarding the nodes that can request entanglement simultaneously. Therefore, we have proposed optimal entanglement distribution schemes for two configurations of multi-ring networks that are able to scale to support any entanglement resupply request configuration.

The first considered configuration of the multiple ring topology is that where each ring within the network is isolated (R2R). That wouldn’t mean that the layers cannot communicate with each other, since the nodes are shared. More explicitly, a request is served only through a single layer of the multiple ring topology. In a real world application, this configuration would be the easiest to deploy, as it effectively would mean that the nodes may have multiple independent transceivers for each ring of the network.

The second considered configuration (aR2aR) is one where the requests may be served through multiple rings throughout the route between the requesting nodes. Although this configuration would be harder to achieve physically, since it would effectively mean that each node is equipped with an interconnection between all the rings, and is able to perform BSMs between any ring and any ring, as well as generate an entangled pair and route each particle on separate rings. However, intuitively, such a configuration should utilize the resources of the network more efficiently.

For each of these configurations we have proposed an algorithm for distributing entanglement optimally in terms of the time slots required to serve the request, given the resources available (number of rings, BSM devices per node and nodes). Additionally, we have presented an algorithm for computing the optimal number of resources to serve a configuration of entanglement requests between nodes, in a single time slot.

Fig. 8
figure 8

Relationship between the number of requests and the number of overlaps between requests with a ring of size 100. The high correlation coefficient indicates that with more requests, there will be more overlaps between the paths these requests have.

Full size image

We have validated the algorithms experimentally, and showed that the aR2aR topology utilizes the resources of the network more efficiently than the R2R topology, having a lower percentage of unused resources when requests overlap. Our results also suggest that the percentage of unused resources does not in fact depend on the number of requests, but rather on how many of these requests overlap.

The results regarding optimal time entanglement distribution indicate an almost linear relationship between number of requests and time slots needed to fulfill all requests. The slope of the resulting function depends on the resources provided, with less resources allocated to the network resulting in a higher slope, i.e. more time needed to fulfill the requests. The more important finding is that the additional complexity brought by the aR2aR network implementation might not be worthwhile, as there are few specific request configurations where the aR2aR network would resolve the requests faster than the R2R network. Furthermore, throughout our tests, the aR2aR network had at most an advantage of one single time slot in resolving these requests.

As future work, we propose an analysis using a higher amount of resources in the multi-ring topology in order to obtain broader results regarding these networks. Another analysis proposed is one of a more generalized topology which contains multi-ring network components.