Introduction

In recent years, China has witnessed the extensive construction of offshore wind farms. The safe running of offshore wind turbines in the northern sea is affected by intermittent floating ice and turbulent winds, which are unique working conditions they must confront. The intermittent impact of floating ice presents a distinctive marine environment challenge for offshore wind power development, as it induces long-lasting and relatively stable vibrations on the overall structure due to ice load coupled with ocean current movement1,2. Such vibrations can lead to fatigue damage and continuous structural strain accumulation under sustained exposure to ice load. Additionally, the wind load exerts significant vibrational effects on both the tower foundation and mud surface line position of the unit’s platform structure. These loads and their coupling effects alter aeroelasticity and structural dynamic response of wind turbines, making it crucial to investigate their influence on operational status under different marine environmental conditions. Since the wind is of turbulent nature, the dynamic behavior of wind turbines is highly affected by the turbulence intensity value. The study of dynamic loads and behavior of wind turbine components is of crucial importance to making decisions regarding a wind turbine’s operation3,4. Considering various installed capacities and structural types of wind turbines nowadays, it becomes evident that annual ice formation characteristics in the northern Gulf of China pose a substantial threat to operational safety in this region5. Therefore, studying wind load, ice load, wave load along with their interactions holds great engineering significance for advancing offshore wind power development in China.

Shi Wei et al.6 employed ANSYS/AQWA to establish a hydrodynamic numerical model for a semi-submersible floating foundation and conducted dynamic response analysis of a 10 MW offshore floating wind turbine under the influence of wind and waves. Hu Xuan et al.7 developed the Kane multi-body dynamic model for wind turbines, utilized the asynchronous Matlock model to simulate ice-induced vibration, and investigated the tower’s dynamic response to turbulent wind loads and asynchronous ice-induced vibrations.

Zhang Minghua et al.8 used the harmonic superposition method (WAWS) to calculate the ice load of large diameter single pile foundation of offshore wind power, simulated the time history of random ice load on single pile foundation in a specified environment, and compared the simulated power spectrum with the target spectrum to verify the feasibility of the harmonic superposition method. Based on the cohesive element method (CEM) -finite element method (FEM) coupling method, Liu Yingzhou et al.9 considered the interaction between pile and soil by using the nonlinear distributed projectile. A nonlinear finite element model of the integrated coupled ice induced vibration of a single pile offshore wind turbine structure under the combined action of wind and ice is established. The interaction process of ice with side-side structure and foundation structure with anti-ice cone is simulated, and the accuracy of the simulation of dynamic ice load is verified by comparing with the existing extrusion and bending ice force models. The change law of dynamic ice load under two ice failure modes is discussed. Wang Bin et al.10 simulated the pile-soil interaction with PSI curve suitable for large diameter single pile structure, and established the dynamic analysis model of the support structure with SACS software. Based on the semi-coupled time-domain method, SACS software was used to analyze the ice induced vibration of the support structure. The sensitivity of ice induced vibration of the support structure is analyzed according to ice parameters such as ice thickness, ice velocity and sea ice strength. Aiming at the design rationality of ice cones for offshore wind power foundation in cold areas, Wang Gang et al.11 established an on-site monitoring system for ice cones for offshore wind power foundation based on the analysis of monitoring elements for design rationality verification, clarified the crushing behavior of ice and cone structure of wind power foundation, and verified the structure’s ice resistance performance and ice design rationality. Liu Hongjian et al.12 determined the ice force time history of the foundation structure under different ice velocity and ice attack Angle by physical model test. By analyzing the measured data on cones of different sizes such as offshore wind power structures and oil and gas platforms, Wang Guojun et al.13 established the relationship between the average ice force period, ice thickness and ice velocity parameters, and studied the applicability of the maneuvering ice load model on wind power infrastructure. Chen Li et al.14 used indoor model tests to study the failure mode of sea ice and the vibration characteristics of the structure when a single pile interacts with sea ice, and verified the effect of the anti-ice cone structure. The numerical model of ANSYS and SACS is established to compare and analyze the dynamic response of single pile foundation under typical ice-induced vibration conditions. Wang Shuaifei et al.15 made a comparative analysis of the ice resistance performance of the offshore wind power foundation before and after installing the cone structure, and the research results provided insights into the ice resistance design and performance of the engineering structure in the offshore ice area environment. Based on IEA’s 15 MW ultra-large single pile offshore wind turbine, Zhang Lixian et al.16 adopted the integrated analysis software OpenFAST v2.3.0 to establish the coupling numerical model of large single pile under the combined action of wind and ice, and carried out the dynamic response analysis of ultra-large single pile offshore wind turbine under the combined action of wind and ice. The dynamic response of large single-pile offshore wind turbine with different loading time, ice-induced vibration model and fatigue damage combination method was investigated.

Yang Dongbao et al.17 employed a discrete element model with bond-crushing capability to characterize the damage and failure behavior of level sea ice, while utilizing the DEM-FEM (Digital Elevation Model and Finite Element Method) coupling approach to simulate the interaction process between single-pile wind turbines and level ice under varying ice velocities and thicknesses. Wang Guojun et al.18 conducted a statistical analysis on the relationship between sea ice fracture length and sea ice thickness, and utilized a modified deterministic ice force function to calculate the structural response of the ice under measured conditions. Huang Yan et al.5 simulated the dynamic characteristics of winopebd power structures with significant differences in their master-slave structure, and performed transient dynamic analysis throughout the entire time domain. Zhang Lixian et al.19 carried out dynamic response analysis on single-pile offshore wind turbines subjected to floating ice using FAST coupling numerical analysis. Ba Yueqiao20 conducted fatigue analysis on offshore wind turbines in icy areas, and proposed a discrete element analysis method for determining ice loads on offshore wind turbines.

Based on ABAQUS finite element numerical analysis software and FAST numerical analysis software, Heinonen et al.21 conducted a dynamic characteristic analysis of single-pile wind turbines under the action of floating ice. The results showed that joint mathematical model analysis could improve the reliability of offshore wind turbine structural design. Wang et al.22 analyzed the fatigue characteristics influencing factors (ice load and wind load) of offshore wind turbines using Kärnä ice force spectrum model. Wei Shi et al.23 combined with semi-empirical structural action model of sea ice to analyze the dynamic response of single-pile wind turbine structures under different ice velocities and thicknesses’ actions by ice cones. Matlock et al.24 added spring damping during loading process modeling analysis for floating ice, while Kärnä et al.25 proposed self-excited vibration response calculation method for marine structures based on actual measurement data from sea ice, which was calculated with sawtooth-shaped ice force function.

Currently, there is a limited number of studies investigating the impact of multi-load and ice load coupling on the fatigue life and safe running of offshore wind turbines. Considering the presence of floating ice in the northern seas of China and the national economic development’s demand for offshore wind power, it is imperative to examine the dynamic response of offshore wind turbines under the combined influence of multi-load and ice load. In this study, numerical analysis using discrete element method and turbulent spatial coherence model was conducted to investigate the dynamic response of NREL 5 MW offshore wind turbines subjected to wind-wave-ice load coupling. The effects of different durations, ice excitation, and coupled load excitation on ultimate dynamic response and fatigue life were explored. Additionally, frequency domain response analysis was performed for large-scale offshore wind turbines under single action from ice load as well as coupled excitation from multiple loads. Cumulative effect on structural fatigue response due to various combinations of fatigue damage was considered, while relative errors in fatigue loading caused by individual actions (wind-wave-ice) versus coupling effects were calculated. These findings aim to provide valuable insights for future construction projects involving offshore wind power in cold regions within China.

In this paper, based on the hydrological characteristics and wind resource characteristic data of the cold sea area in northern China, the calculated load spectrum was established by using OpenFAST v2.3.0 and EDEM 2024.1 software respectively, and combined with the characteristics of offshore wind power engineering, the calculation domain was divided into blocks and the multi-direction coupling method of ice-wave-wind load was used to study the structural response characteristics of offshore wind turbines.

Load calculation

Calculation theory of openfast wind load

The aerodynamic load calculation of wind turbines primarily relies on the blade element momentum theory and the generalized dynamic inflow theory to accurately describe wind loads.

The leaf element momentum theory is based on the leaf element of wind turbine to solve the problem of rotating wake under the condition of airflow resistance. For a wind turbine with blade number N, blade radius R, chord length c and blade element pitch Angle β, both chord length and pitch Angle vary along the blade axis. If the rotational angular velocity of the wind wheel is Ω, the wind speed is v∞. The sum of the tangential velocity Ωr of leaf element and the tangential velocity a’ωr of the air flow in the middle of the wind wheel thickness is the relative tangential flow velocity of the two, and its value is (1 + a’)Ωr (a’ is the tangential induction factor).

The relative velocity of the air flow on the blade is

$$w = \sqrt {v_{\infty }^{2} \left( {1 - a} \right)^{2} + \Omega^{2} r^{2} \left( {1 + a^{\prime}} \right)^{2} }$$
(1)

The Angle between the relative flow velocity and the rotating surface (known as the flow inclination) is \(\phi\), then

$$\sin \phi = \frac{{v_{\infty } \left( {1 - a} \right)}}{w}$$
(2)
$$\cos \phi = \frac{{\Omega r\left( {1 + a^{\prime}} \right)}}{w}$$
(3)

The relative air velocity w acting on the length dr leaf element aerodynamic dR can be broken down into the normal force dFn and the tangential force dFt, dFn can be expressed as

$$dF_{n} = \frac{1}{2}\rho w^{2} cC_{n} dr$$
(4)
$$dF_{t} = \frac{1}{2}\rho w^{2} cC_{t} dr$$
(5)

Where, Cn is the normal force coefficient, Ct is the tangential force coefficient.

The axial force (thrust) dF and torque dT acting on the Leaf element dr of the wind wheel plane can be expressed as

$$dF = \frac{1}{2}\rho w^{2} NcC_{n} dr$$
(6)
$$dT = \frac{1}{2}\rho w^{2} NcC_{t} rdr$$
(7)

Therefore, according to the specific technical parameters of wind turbine blades, such as blade number, blade length and airfoil characteristics, the power output and aerodynamic characteristics of this type of wind turbine under different working conditions can be calculated according to the airfoil experimental data.

In this study, we employ the blade element momentum theory to discretize wind turbine blades during load calculations. By iteratively calculating stress and moment acting on each blade element along the span, a closed-loop solution is established between lift and resistance coefficients and the induction factor. This approach ensures both engineering applicability and calculation accuracy.

  1. (1)

    Kaimal turbulent wind spectrum model.

The turbulent wind spectrum mathematical model is established using the Sandia method in TurbSim26, and is generated based on the time series of Kaimal wind spectrum. According to the wind condition in northern sea areas of China belongs to medium turbulence characteristics, so the turbulence intensity is class B, that is, Iref (-) = 0.1427. The fore-aft (u), lateral (v), and side-side (w) directions of the fluid domain are defined with respect to the tower top coordinate system of the wind turbine, as illustrated in Fig. 1.

Fig. 1
figure 1

Coordinate system at the top of the wind turbine tower28.

Full size image

The mathematical formulation of the fluctuating wind velocity spectrum is presented29.

$${S_K}\left( f \right)=\frac{{{{4\sigma _{K}^{2}{L_K}} \mathord{\left/ {\vphantom {{4\sigma _{K}^{2}{L_K}} {{{\overline {u} }_{hub}}}}} \right. \kern-0pt} {{{\overline {u} }_{hub}}}}}}{{{{\left( {{{1+6f{L_K}} \mathord{\left/ {\vphantom {{1+6f{L_K}} {{{\overline {u} }_{hub}}}}} \right. \kern-0pt} {{{\overline {u} }_{hub}}}}} \right)}^{\frac{{\text{5}}}{{\text{3}}}}}}}$$
(8)

Where, K represents the directions of the fluid domain, namely u, v, and w; f denotes the circulation frequency; LK is defined as the integral scale parameter.

\({L_K}=\left\{ {\begin{array}{*{20}{c}} {8.10{\Lambda _U},}&{K=u} \\ {2.70{\Lambda _U},}&{K=v} \\ {0.66{\Lambda _U},}&{K=w} \end{array}} \right.\), \({\Lambda _U}\)is turbulence scale parameter, \({\Lambda _U}\)= 0.7 min (60 m, HubHt), HubHt is the hub height. The standard deviation of different directions is defined as \({\sigma _v}=0.8{\sigma _u}\),\({\sigma _w}=10.5{\sigma _u}\), and the turbulent wind load spectrum at the wheel hub of the wind turbine is formed, as shown in Fig. 2.

Fig. 2
figure 2

Turbulent wind load spectrum at hub (Kaimal wind spectrum).

Full size image

In practical working conditions, the standard deviation of the u component in the Kaimal wind spectrum model undergoes certain variations due to spatial coherence influences, the wind condition data of the wind farm for this analysis are shown in Table 1.

Table 1 Wind farm wind condition data.
Full size table
  1. (2)

    Spatial Coherence Model.

To ensure consistency between calculation and actual conditions in establishing a three-dimensional pulsating fluid field, the wind speed distribution across the entire swept area of the wind turbine cannot be calculated using a single-point wind load spectrum alone. Moreover, consideration must be given to the mutual relationship between various streamlines in space, which can be expressed through a spatial coherence model. The IEC defines this relationship as the flow direction component fluid field coherence function30.

$$Co{h_{i,j}}=\exp \left( { - a\sqrt {{{\left( {\frac{{{f_r}}}{{{{\overline {u} }_{hub}}}}} \right)}^2}+{{\left( {0.12\frac{r}{{{L_C}}}} \right)}^2}} } \right)$$
(9)

Where, r is the distance between any point i and j on the grid; f is the frequency; LC is the coherent scale parameter; \({\overline {u} _{hub}}\) is the average wind speed at the wheel hub. The wind speed distribution in the fluid domain was calculated31, the published random wind speed data and the calculation results of formula 3 were used as data sources to form wind load spectrum through OpenFAST simulation, as shown in Fig. 3.

Fig. 3
figure 3

Wind speed distribution in the computational fluid domain.

Full size image

The OpenFAST of open source software was used to simulate and calculate the random wind speed of the wind turbine, and extract the wind load spectrum of the 5 MW wind turbine, which was coupled to the wind wave load and the ice load as the boundary condition, so as to provide wind load data for the next coupling analysis.

Calculation theory of EDEM ice load

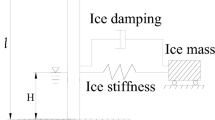
In contrast to other marine engineering structures, offshore wind turbines are characterized by their tall and flexible design. When floating ice interacts with the tower in the presence of ocean currents and when the frequency of ice loads matches the natural frequency of the overall wind turbine structure, it can lead to severe structural response. This study employs the discrete element method along with Matlock single-tooth model and asynchronous failure model to describe the interaction process between ice loads and wind turbine structures. The Matlock single-tooth numerical calculation model assumes that each ice tooth undergoes linear elastic deformation upon contact with the structure until reaching maximum deformation, after which point either no longer contacting or breaking results in zero ice force. Thus, the expression for ice force is as follows

$$F=\left\{ {\begin{array}{*{20}{c}} {{K_{ice}}{\Delta _i},}&{0<{\Delta _i}<{\Delta _{\hbox{max} }}} \\ {0,}&{{\Delta _i} \leqslant 0,{\Delta _i}={\Delta _{\hbox{max} }}} \end{array}} \right.$$
(10)

Where, Kice is ice tooth stiffness, N; Δi is the deformation of the ith ice tooth, m; Δmax is the maximum deformation of ice teeth, m. The floating ice calculation domain is shown in Fig. 4.

In this paper, the joint simulation of FAST and EDEM is carried out. The data show that the average wind speed in the northern cold area is 18 m/s, the wave spectrum peak period is 8s, the ocean current velocity ranges from 0.01 to 0.05 m/s, and the sea water density ρ = 1030 kg/m3, Taking the NREL 5 MW wind turbine as a case study, its key parameters are presented in Table 232,33,34.

Table 2 Main parameters of NREL 5 MW wind turbine.
Full size table
Fig. 4
figure 4

Calculation domain of floating ice impact of wind turbine tower.

Full size image

In the asynchronous failure model, the ice tooth stiffness is determined based on the uniaxial compressive strength of ice. Once the quasi-static ice force acting on the failure zone i reaches its limit, failure of the corresponding ice element occurs. The total ice load at time t can be calculated as the summation of local ice loads and can be expressed as follows

$$F=\left\{ {\begin{array}{*{20}{c}} {{K_{ice}}\left[ {y+{V_{ice}}t - L\left( {n - 1} \right)} \right],}&{0<\Delta \leq {\Delta _L}} \\ {0,}&{\Delta \leq 0} \end{array}} \right.$$
(11)

To enhance the precision of load calculation on wind turbine tower post floating ice impact, it is crucial to emphasize the bonding bond (i.e., connection bond) among particles while establishing an ice model. The bonding strength in the bonding bond is determined by the physical and chemical compositions of ice, ultimately determining its structural type as depicted in Fig. 5. By referring to the relevant literature of Marine science35,36,37,38, the floating ice types that appear more frequently in the freezing period in the cold area are obtained and taken as the object of analysis. This study only discusses the analysis method of the dynamic response of offshore wind turbines under multi-load coupling. If it is widely recognized by the wind power engineering, it can be applied to the actual offshore wind power projects. The specific floating ice analysis model can be adjusted by DEM according to the actual ice type data to make it conform to the specific actual characteristics of offshore wind power projects.

Fig. 5
figure 5

Ice floe model.

Full size image

Working condition simulation

Wind turbines running in cold regions are subjected to a complex working environment, where wind load, wave load, and ice load act together on the tower of wind turbines. The schematic diagram illustrating the coupling of these loads is presented in Fig. 6. In the calculation of wind load, a turbulent fluid domain is established based on the Kaimal wind speed spectrum, and the momentum-leaf element theory is employed to determine the wind load acting on offshore wind turbines.

Fig. 6
figure 6

Schematic diagram of loading of offshore wind turbines.

Full size image

Turbulent fluid domain

In the natural environment, air flow exhibits spatial non-uniformity and temporal unsteadiness. To capture the statistical characteristics of wind speed time series in three directions, this study employs TurbSim, an open-source turbulent wind stochastic simulator developed by NREL. The wind speed power spectrum in the frequency domain is transformed into the time domain using inverse Fourier transform, enabling generation of three-dimensional turbulent wind data for multiple points within the flow field domain based on spatial coherence function. The structural dynamic response analysis and calculation of wind turbines are facilitated by calling the wind data file during computation.

In the calculation process of OpenFAST, the fluid calculation domain’s coverage area encompasses the entire range of the wind turbine and tower. Therefore, the fluid calculation domain is divided into regions based on the hub point. Considering the structural size data of the wind turbine and ensuring accurate calculations for maximum tower deformation, a calculation interval within a 145 m×145 m range at hub center height is determined. This interval is further divided into 15 grid regions for individual calculations. The flow field calculation area’s grid division can be seen in Fig. 7, while maintaining the wind turbine’s tower top coordinate system as the basis for calculating coordinates.

Fig. 7
figure 7

Regional division of flow field.

Full size image

With the hub center as the reference point, based on relevant offshore wind resource data39, the time-domain average wind speed at the reference calculation point was determined to be 12 m/s, with a calculation time of 600s and a time step of 0.05s. By applying an inverse FFT transform to the NWTCUP wind spectrum model40 and considering spatial coherence, we obtained the wind speed variation characteristics at each grid node, which are depicted in Fig. 8 showcasing the wind speed distribution within the turbulent flow field calculation domain. The load diagram of offshore wind turbines after multi-load (wind, wave, ice) coupling is used as the boundary condition for subsequent multi-load coupling analysis, as illustrated in Fig. 8. It is evident that the wind speed within this flow field undergoes iterative changes over time, exhibiting noticeable variations in side-side direction due to wind shear.

Fig. 8
figure 8

Three-dimensional wind velocity distribution in the turbulent flow field calculation domain.

Full size image

Selection of working conditions

The effect of ice load on the tower foundation of wind turbines is primarily determined by various factors, including ice speed, ice thickness, ice drift direction, and the movement of floating ice with ocean currents. Therefore, the calculation of ice load involves considering wave load in a coupled superposition analysis. In line with the research objectives of this study, we initially assume that wind load and ice load are independent from each other. Additionally, we assume that the wind flow direction aligns with the drift direction of the ice and that the running speed of ocean currents carrying ice is a key influencing factor for failure modes related to loads. The failure modes associated with ice load can be categorized into three forms: intermittent extrusion fracture, frequency self-locking fracture, and continuous extrusion fracture failure. Typically, when the ocean velocity in an area covered by floating ice is less than or equal to 0.02 m s–1, intermittent extrusion fractures occur. When the velocity falls within (0.02 m s–1, 0.04 m s–1), frequency self-locking extrusion fractures are observed in floating ice conditions; whereas velocities exceeding 0.04 m s–1 result in continuous extrusion fractures in floating ice scenarios. The calculation conditions for wind turbines under coupling effects between wind and ice loads are presented in Table 3, it shows the analysis results of multi-load coupled offshore wind turbines calculated by OpenFAST and EDEM.

The setting conditions are set according to the average meteorological and hydrological conditions from January to March in the cold sea area of north China, which is representative and general in the description of the hydrological characteristics of the north sea area of China. Note: Data provided by Huaneng Liaoning Qingneng Dalian Offshore Wind Farm.

Table 3 Calculation conditions of offshore wind turbines.
Full size table

According to the conditions in the northern sea area of China41, an ice thickness of h = 0.0125 m was specified in the ice load boundary file. For different operational scenarios, values of vice = 0.01 ms–1, 0.021 ms–1, and 0.05 ms–1 were assigned for ice and ocean current velocities respectively. The structure diameter D was set at 6 m, indentation coefficient Ikm at 2.7, ice brittleness strength σ = 5 MPa, ice teeth spacing P = 1 m, and maximum elastic deflection Δmax = 1 m. Figure 9 illustrates the time history curve depicting the variation in ice load under these three distinct working conditions.

Fig. 9
figure 9

The time history curve of ice loading.

Full size image

Engineering example calculation

Coupling effect of wave-ice load

This paper focuses on investigating the impact load and unit load of wind turbine towers subjected to floating ice, while analyzing the influence of different running speeds and thicknesses of floating ice on these towers42. The impact load calculation area is the contact area between wind turbine tower and the sea level, and also the contact area between the floating ice and wind turbine tower. Figure 10 illustrates the occurrence of broken ice when the floating ice thickness is 12.5 mm and the ice speed is respectively 0.01 m/s and 0.05 m/s. Figure 11 presents the impact load and unit load of wind turbine towers for varying floating ice running speeds, namely, 0.01 m/s, 0.021 m/s, and 0.05 m/s.

Fig. 10
figure 10

Fragmentation of floating ice with ice thickness of 12.5 mm at different flow rates.

Full size image
Fig. 11
figure 11

Impact load of wind turbine tower (Ice thickness of 12.5 mm, ice of speed 0.01 m/s, 0.021 m/s, 0.05 m/s) and unit load.

Full size image

Coupling effect of wind-wave-ice load

Through the coupling algorithm of EDEM, FLUENT and OpenFAST, the data of fluid module (wave) and solid/discrete element module (ice) are exchanged. The effect of waves on ice changes the position, speed and breaking pattern of ice through wave motion, and updates the boundary conditions of ice load. The effect of ice on waves, changes the flow field distribution through ice cover, and ice modifies the wave propagation equation. In terms of time, sub-cycle technology is adopted, and a smaller time step is adopted for the high-frequency ice load, which is iterated synchronously with the low-frequency wave load, and multiple iterations are made in each time step until the response of the wave, ice and structure converges, ensuring the conservation of energy and momentum. The fore-aft displacement of the wind turbine tower top under the coupling effect of wind-wave-ice load, as shown in Fig. 12a, is significantly greater than that under the coupling effect of wave-ice load alone. Moreover, the amplitude (displacement) of the tower top under the combined effect of all three loads is larger and more intense. Notably, when subjected to ice load alone, the vibration at the tower top fluctuates around its centerline with a rapid decay in amplitude from maximum to minimum after 80s. Conversely, under wind load alone or coupled with all three loads, the vibration equilibrium point at the tower top shifts approximately 0.3 m along its fore-aft direction (i.e., x-direction in terms of tower top coordinate system). This indicates that when exposed to wind load, bending occurs along the flow direction and cannot be effectively recovered within this period. Additionally, when ice and wave loads are combined, there is an offset between their respective bending directions and resulting vibration equilibrium points at the tower. As depicted in Fig. 12b regardless of variations in magnitude or direction for wind load conditions observed here, the vibration equilibrium point for fore-aft bending moment remains consistent with geometric shape center across different scenarios. Moreover, coupling effects among wind-wave-ice loads result in significantly greater vibrations compared to individual loading conditions. Furthermore, the shape and trend exhibited by fore-aft loading curves at foundation level remain consistent across these three working conditions, and it’s worth noting that vibrational amplitude changes are considerably higher when all three loads are coupled compared to individual loading effects.

Fig. 12
figure 12

Fore-aft physical quantities of offshore wind turbines under load.

Full size image

The fore-aft load and side-side load at the tower top of the wind turbine under the three-load coupling effect are shown in Fig. 13a, while Fig. 13b illustrates the lateral bending moment and fore-aft bending moment at the tower foundation under the same effect. Since the direction of bending moment is perpendicular to that of load, i.e., side-side vector direction of tower load aligns with fore-aft vector direction of bending moment, it can be observed from figure that both load and bending moment exhibit vibrations around the geometric center of the tower as their equilibrium point in its fore-aft direction. However, along the side-side direction, both load and bending moment experience varying degrees of displacement from their respective equilibrium points due to loads applied. Moreover, it is noteworthy that while there exists higher amplitude variation in fore-aft direction compared to side-side direction with more random patterns. For bending moments, higher amplitude variations occur fore-aft direction than side-side direction with greater randomness as well. Nevertheless, overall randomness degree is found to be higher for loads than for bending moments. The randomness of the fore-aft and side-side loads of wind turbines is verified by the autocorrelation function (ACF), that is, the autocorrelation coefficient of the load calculation time series with a lag of 1 order. If the coefficient of more than 95% of the lag order falls \(\frac{{ \pm 1.96}}{{\sqrt n }}\) within the confidence interval (n is the load sample size), then the load is assumed to be random. The monthly mean series ACF analysis of wind speed data in the northern cold sea area shows that the lag first-order correlation coefficient is less than 0.68, that is, there is a random assumption, and the smaller the lag first-order phase relationship value, the greater the randomness43.

Fig. 13
figure 13

Load changes of offshore wind turbines.

Full size image

The lateral vibration amplitude of the support platform of wind turbines is generally greater than the fore-aft vibration amplitude under various working conditions, as depicted in Fig. 14. Moreover, the fore-aft vibration amplitude remains small and exhibits overall stability, while the lateral vibration displacement shows significant variability. Considering the impact of individual wind loads or ice loads, it is observed that ice load has a higher effect compared to wind load. Furthermore, when considering coupling loads, their effect surpasses that of any single load in terms of both tower amplitude after ice load and tower amplitude attenuation frequency.

Fig. 14
figure 14

Amplitude of offshore wind turbine platform under load.

Full size image

The findings in Fig. 15 demonstrate that, regardless of the running conditions of offshore wind turbines, the vibration pattern and trend of the tower support platform align with those observed for tower vibration displacement. Moreover, both in terms of amplitude and frequency, lateral load vibrations surpass fore-aft vibrations.

Fig. 15
figure 15

Comprehensive vibration displacement changes of the platform under load.

Full size image

Conclusion

The present study investigates the dynamic response of offshore wind turbines subjected to wind load, wave load, ice load, and their coupled effects. Additionally, an estimation of fatigue damage is conducted. The obtained results demonstrate that:

  1. (1)

    Under the separate action of wind load and ice load, the fore-aft bending moments at the tower foundation of wind turbines are essentially identical. When wind-wave-ice load is coupled, the fore-aft bending moments at the tower foundation of wind turbines exceed those under individual loads. Additionally, due to wind load participation, the equilibrium point for tower vibration in wind turbines shifts along the direction of the wind load vector, with a linear translation corresponding to the calculated wind speed. Under isolated ice load conditions, both horizontal and fore-aft amplitudes at the top of wind turbines are smaller compared to those under isolated wind load conditions. This can be attributed to a longer duration of action for wind loads despite their lower instantaneous impact force when compared to ice loads; thus resulting in more pronounced cumulative effects. When considering coupled wind-wave-ice loading scenarios, although similar trends are observed as seen under individual actions from winds and ice alone, there exist significant differences in amplitude and attenuation rate. The displacement offset experienced by support platforms in response to combined loading is greater than that caused by either winds or ice alone. Moreover, lateral displacement significantly exceeds fore-aft displacement on these platforms. Furthermore, it should be noted that compared with its influence on tower foundations from winds alone, ice loads have a more noticeable effect on displacements.

  2. (2)

    When analyzing the impact of ice load on standalone wind turbines, the discrete element method is employed to investigate the characteristics of floating ice impacting offshore wind turbine towers. To enhance the accuracy in calculating the tower’s impact load caused by ice, the mutual influence resulting from changes in floating ice composition is achieved through designing numerical values for bonding bonds between particles. This approach helps narrow the gap between simulation calculations and actual working conditions. The analysis and calculation results reveal that the velocity at which floating ice moves significantly affects wind turbine towers. Therefore, in practical projects, a well-designed tower foundation platform structure can be implemented to reduce the speed at which floating ice moves, thereby mitigating damage caused by both floating ice and other objects to supporting platforms of wind turbines while enhancing their structural stability and reliability.

  3. (3)

    The fatigue damage value of wind load and ice load on wind turbines under separate action is greater than the effect of coupling load, as the direction and magnitude of wind load are uncertain. This uncertainty helps to balance the fatigue damage caused by ice load and wave load on wind turbines to some extent. In the calculation process, the DNV method yields a higher damage value through superposition calculation compared to the calculation result considering load coupling effects. From an engineering design and evaluation perspective, this indicates a higher safety factor for the DNV method. Therefore, it is recommended to utilize the DNV method in practical engineering applications for evaluating the fatigue life of offshore wind turbines under coupling loads.