V3DQutrit a volumetric medical image segmentation based on 3D qutrit optimized modified tensor ring model

Abstract

This paper introduces 3D-QTRNet, a novel quantum-inspired neural network for volumetric medical image segmentation. Unlike conventional CNNs, which suffer from slow convergence and high complexity, and QINNs, which are limited to grayscale segmentation, our approach leverages qutrit encoding and tensor ring decomposition. These techniques improve segmentation accuracy, optimize memory usage, and accelerate model convergence. The proposed model demonstrates superior performance on the BRATS19 and Spleen datasets, outperforming state-of-the-art CNN and quantum models in terms of Dice similarity and segmentation precision. This work bridges the gap between quantum computing and medical imaging, offering a scalable solution for real-world applications.

Introduction

Volumetric Segmentation of Medical Images¹ is in trends from the recent few years in the field of Medical Research and Health Care. It involves dividing a 3D Medical Image into distinct regions based on characteristics like intensity, texture or shape. This is a vital function of the model as it helps in rationalizing the structures, organs, tissues as well as other details that are abnormal in the images. But the process of Manually segmenting volumetric images is quite challenging and demanding for large databases and it needs expertise which can’t be available in all cases and even if they are available there is no assurance that the results will be free from mistakes. For that, automated image segmentation techniques were introduced to minimize human intervention and reducing errors. Region Based Segmentation Edge Based Segmentation are the traditional methods used in medical image segmentation, but these methods are not efficient in providing full accuracy due to their complexity and they are also sensitive to noise.

With recent advancements in Deep Learning, traditional techniques are introduced in integration with Deep Learning Models for higher accuracy. Supervised CNN² was introduced and achieved high accuracy in 2D image segmentation³ but due the limitation that it segments the images in slice by slice manner, which limits the processing of the segmented images, With some minor changes 2D-CNNs⁴ are introduced to overcome the limitation of the classical CNNs, 2D-CNNs are able to segment the image in 2D slices, which directly increases their accuracy but it are only limited to 2D data and can’t capture 3D information present in the volumetric data, So 3D-CNNs⁵were introduced that outperforms on limitations of 2D-CNNs with comparatively high convergence and are able to segment the images and to provide a 3D view. It is highly capable of extracting extensive features from the volumetric 3D images and segmenting them more accurately. Researchers developed specialized architectures and training methodologies to handle the various challenges which are proposed by 3D volumetric data such as the problem of memory consumption and complexity of the data, it have 3D convolution and pooling layers to analyze complex patterns across multiple frames and have improved efficiency and performance over the 2D CNNs, but 3D-CNNs also suffer with various limitations, such as lack of interpret ability, problem of vanishing gradients and over fitting with slow convergence.

Currently Quantum Inspired Networks⁶ (QINNs) have been introduced and its simply integration of Deep Learning Models and Quantum Computing which overcomes the limitations of traditional Networks, it adds faster information processing and solve complex problems in volumetric segmentation with expert-level accuracy. Researchers started to explore and develop new quantum neuron models, which directly enhance the power of traditional networks. New and advanced quantum inspired algorithms are introduced, which increases efficiency through quantum back-propagation algorithms and quantum encoding algorithms⁷, which gives the model more resources, uses qubits to represent the data in multiple states simultaneously due to the superposition property of qubits, and use weight vectors to represent the relationships between the different layers of the model, Quantum gates are used to manipulate qubits to extract information from them, and are used in the training process of the QINNs. However, QINNs suffer from slow convergence, mainly because they utilize a complex quantum back-propagation algorithm in training’s of their model, and also due to the use of fixed activation axes. QINN models are limited to gray-scale image segmentation. With recent advancements in technology, optimized QINNs are going to be introduced.

The proposed model, is tailored and tested on the given benchmark datasets such as the BRATS 2019 dataset namely the (Multi modal Brain Tumor Image Segmentation)⁸ and the Spleen dataset.

The BRATS19 dataset⁸ mainly consists of the MRI volumes of brain focusing on brain tumor images. It totally includes 315 MRI volumes with 240 volumes of high-grade gliomas and also 75 volumes of low-grade Gliomas with multiple modalities including the T1-weighted, T1-weighted with contrast-enhanced, T2-weighted and FLAIR images with a resolution of 240 × 240 pixels per slice. Whereas the Spleen dataset mainly consists of 61 CT Scans 41 for training and 20 for testing of the patients undergoing chemotherapy treatment for liver. Each of the CT Scan volume contains variable number of slices of 512 × 512 resolutions.

The scope of the proposed model is helping in extending domain of semantic segmentation for volumetric medical data, mainly focusing on voxel-wise processing and analysis of complex data which helps in providing expert level accuracy in comparison to the traditional models. The models architecture comprises of the following layers: first input layer, secondly the intermediate or the hidden layer and at last output layer which is connected through III order neighborhood-oriented design to gather complex relationship between the voxels. By incorporating the quantum inspired techniques and the cross mutation tensor ring decomposition, the model aims to enhance the convergence and segmentation accuracy. Proposed model addresses main challenges such as slow convergence, gradient instability and lack of interpret-ability faced by classical networks and aim to accelerate the segmentation process with high precision and reduces the problem of distorted segments.

The model includes qutrit encoding, cross mutated tensor ring decomposition voxelwise information processing These techniques enable the model to process high-dimensional data efficiently, which is helpful for feature extraction the weight vectors are represented using tensor ring representation structure the input neurons that have pixel information are portrayed as qutrits as well as the quantum gates are utilized to express their inter-connected weights, which are used to manipulate qutrits the 3d-QTR Net model is centered on counter-propagation which is bi-directional for more rapid convergence, Adaptive hyper-parameters are linked with gray scale image segmentation and information sensitive to voxel is demonstrated in quantum form The proposed model demonstrates superior performance compared to traditional models, showcasing its potential for advancement in segmentation tasks The primary contributions of this purposed model are highlighted below:

(1) In this work, the authors has come up with a qutrit inspired self-supervised pixel-wise cross-mutated tensor ring network for segmentation of volumetric data.

(2) To overcome correlation and the entanglements between model parameters, a cross mutated tensor ring structure is used for regularization of data, which helps in gathering more complex relationship information from data.

(3) For faster convergence bi-directional counter propagation is used.

(4) Qutrit’s extra states allow the quantum model in encoding the quantum neurons with higher dimensions and offer better representation which enables faster counter propagation between these states.

(5) An adaptive voxel-wise Q-sigmoid (Vox-QSig)⁹ activation function is used.

(6) In this work we used a advanced 3rd order S shaped neighborhood neuron architecture for pixel-wise handling of three dimensional image data.

The arrangement of the next sections is structured as follows: overall review of deep learning and quantum based segmentation methods with overview of challenges faced by them is showcased in “Prior literature review”. “Quantum computing and it’s fundamentals” describes main fundamentals of quantum computing and introduces the architecture of the QTR-Net, in “The architecture”. Experimental analysis, which includes dataset experimental setups and outcomes, is provided in “Experimental analysis” the advantages and the shortcoming’s of the author’s model is presented in Section VI. At last, the results and the conclusion are provided in “Conclusion”.

Prior literature review

In this section we will trace the development from the beginnings of volumetric image segmentation¹ to the changes it has undergone. This section is divided into three main topics: traditional methods for volumetric medical image segmentation and their limitations, advancements in deep learning models and integration with traditional models, integration of deep learning models and quantum computing.

Originally, image segmentation was performed manually by humans. This task requires an expert to continuously monitor the work until the segmentation is complete, which is very time-consuming if the data set is very large. To minimize errors and human intervention, automated methods are therefore proposed, such as region-based segmentation. In this method, the images are segmented based on the features of a region and each region is classified differently. In the second method, edge-based segmentation, the segmentation is proposed based on the edges of the different regions and these are classified.

In recent years, deep learning has made various advances, and then traditional deep learning models, which are a combined version of both traditional models and deep learning models, and deeply supervised Convolutional Neural Networks (CNN)², which have higher segmentation accuracy, but segment the images in slice by slice manner, which limits the processing of the segmented images, with some minor modifications, we then proposed 2D CNNs⁴that can segment the images into 2D slices, which helps in faster processing of the data but still lags behind in many factors as we are not able to utilize the 3D features of MRI and CT scans, hence a powerful model was introduced, the 3D CNNs⁵ that are able to segment the images and provide a 3D view and help in understanding. It is highly capable of extracting extensive features from the volumetric 3D images and segmenting them more accurately, but suffers from slow convergence¹⁰, that distorts the image segments and makes it difficult to distinguish features such as shape, size and location, and as the feature levels are increased it starts to suffers with vanishing gradient problem.

Currently, quantum-inspired neural networks (QINNs) as an integrated idea is in trends, which adds faster information processing to the capabilities of conventional neural networks. QINNs¹¹ have gained acceptance in solving complex problems in volumetric image segmentation with expert-level accuracy. It has addressed all the challenges that were presented by the earlier models by employing quantum inspired algorithms that help in presenting simplicity of the model along with enhanced convergence rate, along with introducing the abstraction of learning processes as implemented in quantum computers. High computing costs, error rates in quantum processes, and a lack of quantum hardware are some of the obstacles to scaling quantum-inspired models for practical implementation. The scalability of existing hybrid quantum-classical systems is hindered by energy consumption, memory constraints, and noisy qubits. For real-world applications, developments in error correction methods and quantum computers are essential⁶. It provides more capability to the model, encoding the data in qubits leads to encoding in several states at once because of the superposition of qubits, weight vectors that represent the connections of one layer to another layer in the model, quantum gates for manipulations on qubits to get information out of them, and in the training process of the quantum inspired model named QNN in Fig. 3. However, QINNs suffer from slow convergence¹⁰, mainly due to the complex quantum back propagation algorithm¹² used to train the model, and due to the use of fixed activation axes, QINN models are limited to gray scale image segmentation. To overcome the traditional models, new models have recently been developed.

Despite the great success of newly developed models, the motivation for the proposed 3D quantum-inspired self supervised tensor mesh is as follows:

(1) Additional efforts are required to optimize the hyperparameters of the conventional neural networks for deep learning.

(2) The inability of conventional CNN models to capture complex patterns and structures within images for accurate segmentation.

(3) The major drawbacks of the QINN models include slow convergence and the employment of fixed activation functions that restrict the usage of these models only up to the segmentation of gray-scale image data.

(4) QINN models characterized by high complexity and low interpret ability resulted in low accuracy of volumetric image segmentation.

Addressing them authors have offered a Tensor Shallow Neural Network architecture inspired by quantum which is self supervised for the segmenting volumes of medical data for overcoming problems associated with complex 3D CNNs.

Quantum computing and it’s fundamentals

The fundamental idea of quantum computing offers the features such as superposition, decoherence, coherence and quantum entanglement which helps in implementation of quantum algorithms¹³. Early classical systems are based on binary logic, Now most of the quantum systems are based on multiple levels. States of these systems are called as qudits (d-level system).

(a) Qubits and qutrits.

The latest quantum d-level system can be represented as combination of d basis states.

$$\:\begin{array}{c}\left|{\Psi\:}>=\sum\:_{s=0}^{d-1}\:\:{\alpha\:}_{s}\right|s> \end{array}$$

(1)

Here, every coefficient represents the likelihood that the system will be in the matching basis state. When we use s = 2, it’s the traditional quantum two-state system, which is described as a qubit

$$\:\begin{array}{c}|0>=\left(\begin{array}{l}1\\\:0\\\:0\end{array}\right),|1>=\left(\begin{array}{l}0\\\:1\\\:0\end{array}\right),|2>=\left(\begin{array}{l}0\\\:0\\\:1\end{array}\right).\end{array}$$

(2)

Here, the authors used a three-level quantum system with s = 3. Three states described as states 0〉,1〉 and 2〉are used for every qutrit. The superposition of all three states constitutes the pure state of a qutrit, which is represented as:

$$\:\begin{array}{c}\left|{\Psi\:}>={\alpha\:}_{0}\right|0>+{\alpha\:}_{1}\left|1>+{\alpha\:}_{2}\right|2>\end{array}$$

(3)

(b) Quantum Operations.

To execute qutrit quantum computation, we mainly require the set of unitary operations and perform measurements. GellMann¹⁴ observable are used, it naturally generalizes the qubit Pauli operations and it describes a measurement on qutrits.

$$\:\begin{array}{c}{X}_{p}=\sum\:_{s=0}^{d-1}\:\:|s+1(mod3)><s|,{Z}_{p}=\sum\:_{s=0}^{d-1}\:\:{\theta\:}^{s}|s >< s|\end{array}$$

(4)

here $\:\theta\:={e}^{j\frac{2{\Pi\:}}{d}}$ represents dth root of unity. Here X and Z generalized Pauli group performs shifting of one state to the next and multiplies the states with a phase. To create superposition in the states Hadamard gate is used on qutrits.

$$\:\begin{array}{c}H=\frac{1}{\sqrt{3}}\left[\begin{array}{ccc}1&\:1&\:1\\\:1&\:{e}^{j\frac{2\pi\:}{3}}&\:{e}^{-j\frac{2\pi\:}{3}}\\\:1&\:{e}^{-j\frac{2\pi\:}{3}}&\:{e}^{j\frac{2\pi\:}{3}}\end{array}\right] \end{array}$$

(5)

The observables we are going to measure are the GellMann¹⁴ observable. there are 3 × 3 × 3 for one candidate voxel hermitian observables which we generalize qubit Pauli group.

$$\:\begin{array}{rr}{\lambda\:}_{1}&\:=\left(\left(\begin{array}{lll}0&\:1&\:0\\\:1&\:0&\:0\\\:0&\:0&\:0\end{array}\right)+\left(\begin{array}{lll}0&\:0&\:0\\\:0&\:0&\:1\\\:0&\:1&\:0\end{array}\right)\right)\\\:{\lambda\:}_{2}&\:=-i\left(\left(\begin{array}{ccc}0&\:1&\:0\\\:-1&\:0&\:0\\\:0&\:0&\:0\end{array}\right)-\left(\begin{array}{lll}0&\:0&\:0\\\:0&\:0&\:1\\\:0&\:&\:1\end{array}\right)\right.\end{array}$$

$$\:\begin{array}{rr}{\lambda\:}_{3}&\:=\left(\left(\begin{array}{lll}1&\:0&\:0\\\:0&\:-1&\:0\\\:0&\:0&\:0\end{array}\right)+\left(\begin{array}{lll}0&\:0&\:0\\\:0&\:0&\:1\\\:0&\:1&\:0\end{array}\right)\right)\dots\:.\\\:{\lambda\:}_{26}&\:=-i\left(\left(\begin{array}{ccc}0&\:1&\:0\\\:-1&\:0&\:0\\\:0&\:0&\:0\end{array}\right)-\left(\begin{array}{lll}0&\:0&\:0\\\:0&\:0&\:1\\\:0&\:1&\:0\end{array}\right).\right.\end{array}$$

Algorithm 1

Initialize neighboring qutrits neurons and there corresponding central qutrit neuron.

The architecture

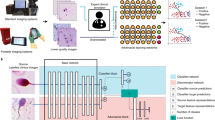
Here a 3D qutrit based model which is shown in Fig. 1, self-supervised with a tensor ring network is suggested to perform automatic pixel based segmentation of the medial data. The three-dimensional QTRNet architecture consists of three layers of volumetric qutrit neurons arranged throughout the architecture layers. The volumetric input (H x W x D) is first normalized using the min - max normalization before transforming into qutrits as:

$$\:\begin{array}{c}{\alpha\:}_{m,n}^{d}=\frac{{\alpha\:}_{m,n}^{d}-\text{m}\text{i}\text{n}\left({\alpha\:}_{m,n}^{d}\right)}{\text{m}\text{a}\text{x}\left({\alpha\:}_{m,n}^{d}-\text{m}\text{i}\text{n}\left({\alpha\:}_{m,n}^{d}\right)\right)} \end{array}$$

(6)

Fig. 1

3D Qutrit Model. For all Central quantum neurons, which is in the middle of all neighboring qutrits, It form the S neighborhood-oriented architecture with inter-layer connections, Information from volumetric data is mapped to qutrits with the help of angle encoding. The weights interconnected between input and the hidden or the intermediate layers are represented as $\:\mid\:Op{t}_{b,a}^{lyr,dpt}>$, then for the output between hidden layer and the output layer is represented as $\:\mid\:Op{t}_{a,c}^{lyr,dpt}>$,similarly for the output and the intermediate layer $\:\mid\:Op{t}_{c,a}^{lyr,dpt}>$ at a layer lyr with depth dpt. Then the interconnected weights are transformed in quantum formalism with rotation gates with as rotational angle, which is determined by utilizing the fuzzy relative difference¹⁵of intensities between central pixel and neighbor hood pixels in the S shaped architecture with quantum neurons inside a $\:3\text{*}3\text{*}3$ structured voxel, here there are multiple such blocks of S-connected neighborhood neurons so fuzzy¹⁵ intensities form all the blocks are taken through the outcome of there respective central qutrit neuron L1,L2,L3.Ln.

Then propagated through the three-dimensional input qutrit layer to subsequent intermediate layer and output layer of the architecture and then processing takes place in S-structured voxels. Inter layer connections between the layers is formed using a 3rd order S-connected pixel wise neighborhood architecture.

$$\:\begin{array}{c}v=voxel\left( {\nu} \:\right) \end{array}$$

(7)

Here the spatial feature from the qutrit neurons as neighborhood pixels are extracted and transmitted as inputs which are guided by a voxel multilevel sigmoid function (Vox-Sig)⁹ and the accumulation at the next layer’s candidate central neuron with slope as λ and activation as ϑ.

$$\:\begin{array}{c}{\sigma\:}_{Vox-Sig}\left(x\right)=\frac{1}{{\kappa\:}_{\varphi\:}+{e}^{-\lambda\:(z-\vartheta\:)}} \\ \:0\le\:{\kappa\:}_{\varphi\:}\le\:\frac{{\Pi\:}}{2}\end{array}$$

(8)

here $\:{\kappa\:}_{\varphi\:}$ is described as the multi-response exhibited by S shaped III order neighbor hood voxels and it is expressed as:

$$\:\begin{array}{c}{\kappa\:}_{\varphi\:}=\frac{{\chi\:}_{s}}{{\beta\:}_{\varphi\:}-{\beta\:}_{\varphi\:-1}} \end{array}$$

(9)

here the $\:{\beta\:}_{\varphi\:},{\beta\:}_{\varphi\:-1}$ are the $\:\varphi\:th,\varphi\:-1$ response outcomes of the neighborhood architecture and the $\:{\chi\:}_{s}$ is the contribution of the gray-scale pixels, which is defined as:

$$\:\begin{array}{c}\left|{\chi\:}_{s}\right.>=\left[\begin{array}{l}\text{c}\text{o}\text{s}\left(2\pi\:\times\:\left(\sum\:_{n=1}^{S}\:\:{\alpha\:}_{m,n}\right)\right)\\\:\text{s}\text{i}\text{n}\left(2\pi\:\times\:\left(\sum\:_{n=1}^{S}\:\:{\alpha\:}_{m,n}\right)\right)\end{array}\right]\end{array}$$

(10)

Then the information by voxels is counter propagated by the output layer and transmitted to the intermediate layer for further processing of the data. Qutrit based neurons from every layer and then reassigned through transformation gate, the weights between the layers are being mapped by Phased Hadamard gates which are described as:

$$\:\begin{array}{c}{\bf H }\left(\left|{\theta\:}_{\mathbf{m}\mathbf{k}}\right.> \right)=cos\left(\frac{2\pi\:}{3}{\omega\:}_{m,k}\right)+\iota\:sin\left(\frac{2\pi\:}{3}{\omega\:}_{m,k}\right)\end{array}$$

(11)

the quantum fuzzy thresholding¹⁶ is employed to ascertain how the information is propagating both forward and backward between layers by self-organizing weight matrices. Now the product between the quantum states

$$\:\left|{\psi\:}_{d}\right.>={\left(\left|{\alpha\:}_{1}\right.>,\left|{\alpha\:}_{2}\right.>,\left|{\alpha\:}_{3}\right.>,\dots\:,\left|{\alpha\:}_{d}\right.>\right)}^{k}$$

and quantum weights

$$\:\left|{W}_{d}\right.>={\left(\left|{\theta\:}_{1}\right.>,\left|{\theta\:}_{1}\right.>,\left|{\theta\:}_{1}\right.>,\dots\:,\left|{\theta\:}_{1}\right.>\right)}^{k}$$

is given as:

$$\:\begin{array}{c}<{\psi\:}_{d}\mid\:{W}_{d}>=\sum\:_{s=1}^{d}\:\:<{\alpha\:}_{s}\mid\:{\theta\:}_{s}>={\tau\:}_{d}\left|{\alpha\:}_{s}\right.>H\left|{\theta\:}_{s}\right.> \end{array}$$

(12)

where $\:{\tau\:}_{d}$ and $\:{H}_{d}$ are transformation and Hadamard gate.

The dimensions are reduced using the tensor ring decomposition¹⁷ which is one of the best data compression techniques which enhances the representation of weight matrices, the loss function applied in the architecture is expressed in terms of weight matrices’ root mean squared error. with the depth as dt in a given uth epoch which is determined by the phase angles specified and with the help of all these components, the whole 3D-QTRNet model is designed for volumetric segmentation.

Algorithm 2

Propagating Relationships in Qutrit Model with Cross-Mutated Tensor Ring Network.

Experimental analysis

A. Dataset descriptions

In this proposed 3D QTR-NET all the experiments have been performed using the Multi modal brain tumor segmentation dataset⁸) and the Spleen dataset. The dataset mainly consists 315 MRI volumes. Each pf the volumes mainly consists of 155 slices having a resolution 240 × 240 along with the original ground truth (mask labels) as well as 4 distinct MRI modalities t1, having FLAIR, t1 with enhanced contrast (t1-ce) and t2. Three primary classes of annotation are applied to the segmented labels: non-enhancing tumor region, tumor-enhancing tumor region, and tumor core (TC). The Decathlon Medical Segmentation is a free for all challenge mainly for testing of various ML algorithms generally utilized for tasks involving segmentation. The segmentation of the Spleen images is a task of MSD which mainly consists of 61 CT scans: 41 for training and 20 for the purpose of testing the individuals getting liver chemotherapy. A varied number of slices with 512 × 512 resolutions are present in each CT Scan volume.

B. Experimental setup

In this given work, experiments were conducted by employing 3D QTR-Net on MR brain images taken from the BRATS⁸ of size 240 × 240 and the Spleen dataset of size 512 × 512 with super computer with GPU integration. The proposed 3D-QTR-Net architecture is implemented using multi-class levels of the voxel sigmoid activation function⁹. The main steepness varied between the ranges from 0.24 to 0.25, with the learning rate of 0.001 and the S = 26 (3 × 3 × 3) neighborhood pixels providing optimal performance. Mainly to identify a whole tumor, the image segments are then resized in order to correspond with the mask’s dimensions, with result 1 showcasing the tumor region and result 0 showcasing the background. Dice Similarity: A standard assessment technique is used to evaluate segmented images voxel-to-voxel in comparison with the original image mask. Each of the 2D pixels is then predicted as true positive, true negative, false positive, and false negative. The goodness measure (predictive positive value) (PPV), accuracy (AC), dice similarity (DS), and sensitivity (SS) are used to evaluate results.

Here we are looking at the metrics used to evaluate the results provided by the models it comprises of the following:

• True Positive (TP): The condition when the actual result is 1(True) and the model truly predicts it to be 1(True).

• True Negative (TN): The condition when the actual result is 0(False) and the model truly predicts it to be 0(False).

• False Positive (FP): The condition when the actual result is 0(False) and the model truly predicts it to be 1(True).

• False Negative (FN): The condition when the actual result is 1(True) and the model truly predicts it to be 0(False).

• Precision: It is the measure of positively true predictions out of all positive predictions. It’s the ratio of true positives to sum of true positives and false positives.

$$\:\begin{array}{c}\text{}\text{P}\text{r}\text{e}\text{c}\text{i}\text{s}\text{i}\text{o}\text{n}\text{}=\frac{TP}{TP+FP}\end{array}$$

(13)

-Accuracy: It is a measure of instances that are classified correctly to total instances and is calculated as the ratio correct predictions to total predictions.

$$\:\begin{array}{c}\text{}\text{A}\text{c}\text{c}\text{u}\text{r}\text{a}\text{c}\text{y}\text{}=\frac{TP+TN}{TP+TN+FP+FN}\end{array}$$

(14)

-Recall (Sensitivity): Recall, also known as sensitivity. measures the proportion of predictions which are truly positive out of total positive predictions in the dataset. It’s simply ratio of true positives to the sum of true positives and false negatives.

$$\:\begin{array}{c}\text{}\text{S}\text{e}\text{n}\text{s}\text{i}\text{t}\text{i}\text{v}\text{i}\text{t}\text{y}\text{}=\frac{TP}{TP+FN}\end{array}$$

(15)

-Specificity: It mainly measures of the ratio of true negative prediction over all the actual negative instances. It can be calculated by taking the ratio of true negatives to addition of false positive and true negative values.

$$\:\begin{array}{c}\text{}\text{S}\text{p}\text{e}\text{c}\text{i}\text{f}\text{i}\text{c}\text{i}\text{t}\text{y}\text{}=\frac{TN}{TN+FP}\end{array}$$

(16)

-Dice Similarity Coefficient (F1 Score): It is frequently used to compare the similarity of predicted image and segmentation masks in tasks such as segmentation. It mainly tries to measure the overlap between two image masks which are mostly the predicted image and the segmentation mask (ground truth). It is the ratio of twice the intersection of the two sets to the sum of the cardinalities of the sets, with 1 indicating perfect overlap and 0 indicating no overlap.

$$\:\begin{array}{c} F1- \text{Sc}\text{o}\text{r}\text{e} =\frac{2\times\:\text{Precision} \times \:\text{Sensitivity}} {\text{Precision}+\text{Sensitivity}} \end{array}$$

(17)

C. Experimental results

In this configuration, the experiments are conducted, and the outcomes are reported with numerical analysis utilizing all these models 3D-QTRNet, DRINet¹⁸, 3D-UNet¹⁹,3DQNet⁶, and VoxResNet²⁰ using the Spleen and BraTS2021 datasets shown in Fig. 2. The provided Tables 1, 2, 3, 4 and 5 presents complete Spleen segmentation and also in the Fig. 5. This proves that the proposed model, 3D-QTRNet, performs optimally for spleen segmentation of CT volumes using the activation method guided by the 26 neighboring voxel intensities over following evaluation matrices: (AC, PV, SS, DC)^21,22,23.

Fig. 2

Results on the BraTS2021 dataset.

Table 1 Performance matrix accuracy scores.

Table 2 Performance matrix dice similarity.

Table 3 Performance matrix sensitivity.

Table 5 provides us the quantitative results which are obtained by using the proposed 3D-QTRNet, DRINet¹⁸, 3D-UNet¹⁹,3D-QNet⁶, and VoxResNet²⁰ on evaluating the AC, DS, SS and PV on all modalities if the BraTS dataset.

Table 4 Performance matrix positive value.

It has been observed that the proposed model, 3D-QTRNet, outperforms the convolutional models (DRINet¹⁸, 3D-QNet⁶, 3D-UNet¹⁹, and VoxResNet²⁰) in the prediction of the complete brain tumor. 3D-QTRNet is experimented on classical systems; as higher quantum computing tasks such as Q-parallelism¹³ and many more are not yet been fully explored. Comparing the developed quantum model to the classical CNN models, requires fewer trainable parameters.

Table 5 Overall comparison of all models with evaluation metrics on brats different modalities.

Conclusion

The 3D qutrit inspired network is fully self-supervised and it’s architecture comprises of a S-connected neighbour hood topology for processing the voxel to voxel information in segmentation of brain tumor volumes (MR) and the Spleen CT volumes are showcased in above sections (Figs. 3, 4, 5). In order to display the efficiency of proposed 3D-QTRNet model it is validated against the BraTS-2021 and the Spleen dataset (Fig. 4) which promotes automatic segmentation of volumetric images well in comparison to other recent cutting-edge techniques. The proposed model is capable of being used immediately in any application, whereas the other models for deep learning encounter various challenges. However, the model is unable to yield extremely optimal outcomes in the segmentation of multi-level data due to hardware limitations and the undiscovered domain of quantum computing. The authors are working in extend and up-scale the 3D-QTRNet model to yield more optimal segmentation outcomes.

Fig. 3

Training and validation loss with dice coeff value for BraTS dataset.

Fig. 4

Results on the spleen dataset.

Fig. 5

Validation loss with dice coeff value for spleen dataset.