Deep Learning Image Compression Method Based On Efficient Channel-Time Attention Module

Abstract

Remote monitoring of transmission lines plays a vital role in ensuring the stable operation of power systems, especially in regions with weak or unstable network signals, where efficient data transmission and storage are essential. However, traditional image compression methods face significant limitations in both quality and efficiency when applied to high-resolution imagery in such scenarios.To address these challenges, this paper proposes a deep learning–based image compression approach incorporating an Efficient Channel-Temporal Attention Module (ETAM). The ETAM module integrates Efficient Channel Attention (ECA-Net) and a Temporal Attention Module (TAM) to jointly enhance the extraction of spatial and temporal features, thereby improving compression efficiency and reconstruction quality.Experimental results demonstrate that the proposed method consistently outperforms both traditional and state-of-the-art deep learning–based compression techniques across multiple evaluation metrics, including PSNR, SSIM, and LPIPS. Notably, evaluations on the STN PLAD dataset show that ETAM better preserves fine-grained details and textures, even under high compression ratios, resulting in reconstructions that closely resemble the original images.These findings underscore the practical potential of the ETAM method for efficient, high-quality image compression in real-world applications such as transmission line monitoring under constrained network conditions.

Introduction

The stable operation of transmission lines is critical to the security and reliability of power systems, particularly in remote regions where signal coverage is weak or unavailable¹, making real-time monitoring significantly more difficult. Traditional approaches to monitoring primarily rely on manual ground inspections or UAV-based image and video acquisition for equipment status assessment. However, with the growing number of transmission components and the continuous expansion of monitoring coverage, the efficient transmission and processing of collected data—especially in signal-limited or disconnected environments—has emerged as a major challenge.

In this context, the application of image compression technology in remote monitoring is crucial. While traditional image compression methods (e.g., JPEG and JPEG2000) have achieved some success in reducing data transmission, the growing resolution and volume of surveillance images have led to the dual challenges of limited transmission bandwidth and storage capacity². Therefore, improving compression efficiency without compromising image quality has become a key challenge to ensure the effectiveness and safety of transmission line monitoring.

This paper proposes a deep learning-based image compression method utilizing the Efficient Channel-Temporal Attention Module (ETAM). The method integrates Efficient Channel-Net and the Temporal Attention Module (TAM) to optimize both spatial and temporal representations of images, significantly improving compression efficiency while maintaining high-quality reconstruction. The ETAM method is particularly suited for monitoring areas with weak signals, as it reduces both transmission bandwidth and storage costs by minimizing data volume, while ensuring high-quality image recovery under constrained conditions.

With the rapid development of deep learning, image compression methods are evolving beyond traditional algorithms toward more intelligent and efficient approaches³. This paper explores the potential application of the ETAM method in transmission line monitoring, evaluates its advantages in data transmission efficiency, image quality retention, and feature extraction, and demonstrates its practical value in real-world monitoring scenarios through experimental results.

Related work

Image compression technology is a key research area in computer vision, with the goal of reducing data size while maintaining image quality. In recent years, the rapid advancement of deep learning has sparked increasing interest in integrating traditional image compression techniques with learning-based approaches to improve both compression efficiency and perceptual quality. Previous research has primarily focused on traditional compression techniques, deep learning-based methods, and the application of attention mechanisms in image processing.

Traditional image compression methods

Traditional image compression methods—such as JPEG, JPEG2000, BPG, and WebP—achieve data reduction through a combination of transformation, quantization, and entropy coding, all governed by hand-crafted and fixed coding rules. At lower compression ratios, these methods can maintain relatively satisfactory image quality; however, as the compression ratio increases, detail loss and blocking artifacts become more pronounced. For instance, JPEG and JPEG2000 are prone to significant artifacts when processing edges and high-frequency regions.

To address these issues, Yee et al. proposed an enhanced method based on BPG⁴. This method divides the image into regions of interest (ROI) and non-ROI areas: lossless BPG encoding is applied to the ROI, while lossy BPG encoding is used for the non-ROI areas, and the two parts are then merged to reconstruct the final image. While such approaches offer moderate compression efficiency, their performance degrades significantly when applied to high-resolution images or visually complex scenes, often resulting in suboptimal rate-distortion trade-offs and noticeable visual artifacts.

To further mitigate these limitations, Tu et al. introduced an adaptive block transform image coding algorithm⁵. This algorithm improves the efficiency of block transform coefficients through pre-filtering, post-filtering, and higher-order null-frequency context modeling, thereby enhancing coding performance and reconstruction quality. Although this method improves distortion control at high compression ratios, its adaptability and flexibility for complex and diverse image data are still limited, as it is based on fixed rules.

Deep learning based image compression method

In recent years, deep learning has made remarkable advancements in the field of image compression⁶. Compared to traditional methods, deep learning models based on autoencoders (AE) achieve a superior balance between compression efficiency and reconstruction quality by learning nonlinear feature representations of images. For instance, Cheng et al. proposed a lossy image compression architecture⁷ leveraging the properties of convolutional autoencoders (CAE) to enable efficient coding, while Ben et al. utilized convolutional neural networks (CNNs) to extract compact structured features, combining them with Lempel-Ziv Markov Chain (LZMC) coding for high-quality compression and reconstruction results⁸.

Despite the strong performance of these methods in still image compression, challenges remain regarding computational resource demands and the processing of temporal data (e.g., video). To address these limitations, Cheng et al. developed a follow-up method employing discretized Gaussian mixture likelihoods to parameterize the latent code distribution, constructing a more accurate and flexible entropy model⁹. Similarly, Mentzer et al. systematically optimized components such as normalization layers, generator and discriminator architectures, training strategies, and perceptual loss functions to achieve a better balance between perceptual quality, compression rate, and distortion. Their approach can be extended to high-resolution images, offering technical support for integrating rate-distortion-perception theory into practice¹⁰.

To accommodate varying compression rate requirements during deployment, Toderici et al. introduced a neural network-based method for full-resolution lossy image compression¹¹. This method is notable for requiring a single training process, enabling the network to dynamically adjust compression rates in real-world applications without retraining separate models for different bit rates. This feature significantly reduces operational and maintenance costs, paving the way for the broader application of deep learning in image compression.

Although autoencoders perform well in static image compression, they struggle to effectively handle temporal data. To address this limitation, this paper incorporates the Efficient Channel-Temporal Attention Module (ETAM) into deep learning-based image compression. The channel attention mechanism optimizes feature extraction along the channel dimension, while the temporal attention module captures temporal variations and emphasizes critical information by adjusting the weights of key time points. These mechanisms enable joint optimization of spatio-temporal features, enhancing the model’s feature representation and its applicability to video and dynamic image processing.

Attentional mechanisms in image processing

Attention mechanisms are extensively utilized in deep learning for feature extraction and enhancement, playing a critical role in remote monitoring of transmission lines without stable signals¹². The channel attention mechanism improves the feature representation of key components in surveillance images by capturing dependencies between channels, thereby enhancing the accuracy of transmission line state identification. The temporal attention mechanism (e.g., TAM) focuses on identifying critical change points in temporal signals, which is crucial for detecting line anomalies (e.g., line breaks or overloads) in dynamic environments. In areas with no or unstable signal, an attention mechanism that effectively integrates spatial and temporal features can optimize image compression and reconstruction, significantly reducing the data volume and ensuring the stable operation of the remote monitoring system.

Methods

Efficient channel attention module (ECA-Net)

The Efficient Channel Attention Module (ECA-Net), proposed by Wang et al.¹³, is a lightweight attention mechanism designed to enhance feature representation in image processing tasks. Unlike traditional channel attention mechanisms, ECA-Net improves computational efficiency by using an adaptive one-dimensional convolutional approach to learn inter-channel correlations, thereby avoiding the dimensional compression problem common in conventional methods.

In ECA-Net, the input feature maps undergo Global Average Pooling (GAP) to capture global statistical information for each channel. Then, by adaptively selecting the convolutional kernel size (k), a weighting operation is applied to the channel dimensions, allowing the model to learn the importance of each channel. There is a direct relationship between the convolutional kernel size (k) and the number of channels (C) in the input feature map, which enables ECA-Net to flexibly adjust the importance of each channel, thereby emphasizing critical information relevant to the task. Finally, the weights for each channel are transformed into normalized coefficients through a sigmoid activation function, which are then used to adjust the intensity of each channel feature in the original feature map, resulting in a weighted feature map.

The key advantages of ECA-Net include its low computational complexity, high efficiency, and the absence of channel dimensionality reduction, addressing the common parameter redundancy issue in traditional channel attention mechanisms¹⁴. This mechanism enables ECA-Net to effectively capture important features in images and improve the model’s representational power, all while avoiding unnecessary computational overheads, making it suitable for image tasks that require real-time processing. The specific flow of ECA-Net is illustrated in Fig. 1.

Fig. 1

Efficient channel attention module.

Let x denote the input feature map, C represent the number of channels in x, and x ̂ the output feature map. GAP stands for Global Average Pooling, and σ denotes the activation function (sigmoid). k refers to the coverage for local cross-channel interactions, and there exists a mapping relationship between k and C:

$$\:k=\varphi\:\left(C\right)={\left|\frac{{\text{l}\text{o}\text{g}}_{2}C}{\gamma\:}+\frac{b}{\gamma\:}\right|}_{\text{o}\text{d}\text{d}},\gamma\:=2,b=1$$

The corner symbol ⊙ denotes the closest odd number to the value inside∣⋅∣The main process of the ECA attention mechanism is as follows: After the input feature map enters the ECA attention mechanism, the Global Average Pooling (GAP) operation is first applied to average pool the feature values of each channel, producing the global average value for each channel. Subsequently, this pooled value is passed through a channel-wise Fully Connected Layer (FC), which outputs the weight coefficients for each channel. These coefficients are then used to adjust the feature weights of different channels. Finally, the ECA attention mechanism applies these weight coefficients to rescale the original feature map, thereby weighting the features of different channels and obtaining the weighted feature map.

Temporal attention module (TAM)

The Temporal Attention Module (TAM), proposed by Wu et al.¹⁵, aims to capture important features in signals over time and highlight critical signal changes through a weighting mechanism. Unlike traditional spatial attention modules, TAM focuses on signal variations in the time dimension, allowing it to effectively extract time-related information.

The application of the Temporal Attention Module (TAM) is particularly crucial in remote monitoring scenarios of transmission lines, especially in regions with no signal coverage. TAM operates on the feature maps generated by the preceding Efficient Channel Attention Module (ECA-Net), applying both max pooling and average pooling to produce two complementary temporal descriptors. These maps represent the global importance of line monitoring data in the time dimension and the local critical features. These feature maps are then merged and converted into a single-channel feature map via convolution, which is subsequently combined with a sigmoid activation function to generate temporal attention weights that highlight critical changes at different time points.

The key role of this temporal attention mechanism in transmission line monitoring lies in its ability to adaptively adjust the focus of the model’s attention on temporal features based on the dynamics of the input signals.

Finally, TAM multiplies the temporal attention-weighted feature map element-wise with the original feature map to obtain a weighted feature map, which significantly enhances the signal feature performance during abnormal states. Through this process, TAM not only improves the model’s sensitivity to dynamic changes in transmission lines, but also enhances the efficiency and accuracy of data compression and processing in signal-free regions. This mechanism is particularly well-suited for scenarios requiring fast transmission and high-quality reconstruction, providing vital technical support for remote monitoring of transmission lines. The specific flow of the Temporal Attention Module is shown in Fig. 2.

Fig. 2

Temporal attention module.

TAM generates two feature maps through maximum pooling and average pooling from the output of the channel attention module. These two feature maps are then merged into a single-channel feature map via a convolution operation. The temporal attention feature map is obtained using a sigmoid function. Finally, the output is element-wise multiplied with the original feature map. The formula for temporal attention is as follows:

$$\:{M}_{s}\left(Y\right)=\sigma\:\left(f\left(\left[AvgPool\left(Y\right);MaxPool\left(Y\right)\right]\right)\right)=\sigma\:\left(f\left(\left[{Y}_{avg}^{s};{Y}_{max}^{s}\right]\right)\right)$$

Where Ms(Y) denotes the convolution result of TAM, f denotes active convolution, and $\:{Y}_{avg}^{s}$ and $\:{Y}_{max}^{s}$ denote the output features of different pooling layers under the time-attentive module.

Efficient channel-time attention module (ETAM)

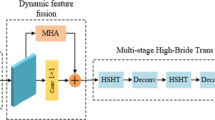
As shown in Fig. 3, the Efficient Channel-Temporal Attention Module (ETAM) is a dual-attention mechanism proposed in this paper for the image compression task. Its goal is to address the challenge of optimizing both spatial and temporal dynamic features of an image, thereby achieving more efficient feature representation and better reconstruction quality in compression and reconstruction tasks. The ETAM module integrates the Efficient Channel Attention Module (ECA-Net) and the Temporal Attention Module (TAM), which not only identifies spatially important features in an image but also captures key temporal dynamics, injecting new vitality into deep learning-based image compression methods.

In the design of ETAM, the ECA-Net optimizes the spatial features of images. Traditional channel attention mechanisms typically learn inter-channel weights through a fully connected layer. While this can capture important channel relationships, it is computationally expensive and prone to redundant parameters¹⁶. ECA-Net addresses this limitation by first applying Global Average Pooling (GAP) to capture global contextual information across each channel, followed by an adaptive one-dimensional convolution that directly models local cross-channel interactions and generates channel-wise attention weights. This approach avoids dimensional compression and redundant parameters, enabling the model to flexibly capture key spatial features and highlight the most relevant information for the task. Ultimately, the weights of each channel are normalized using a sigmoid activation function, achieving precise optimization of the spatial features of the input image. Compared with traditional methods, ECA-Net’s lightweight design improves computational efficiency while effectively enhancing the spatial feature representation of the image.

The TAM, on the other hand, focuses on capturing temporal features of the signal to enhance the model’s sensitivity to dynamic changes over time¹⁷. TAM first performs maximum pooling and average pooling operations on the feature maps output by ECA-Net, extracting globally significant and locally critical features in the time dimension. These two feature maps are then merged, and a single-channel time-weighted feature map is generated through a convolution operation. The temporal attention weights, generated by the sigmoid activation function, apply different weights to the temporal signals, highlighting critical changes while reducing attention to irrelevant or redundant temporal information. Ultimately, the temporal attention module multiplies the temporally weighted feature map with the original feature map element-wise to obtain a time-optimized feature representation, significantly improving the model’s ability to capture temporal dynamics.

In order to accurately model the key information in an image, this paper proposes an Efficient Channel-Temporal Attention Module (ETAM) to simultaneously extract spatially salient features and temporally dynamic features of an image.The ETAM module improves the model’s ability to pay attention to important features through the tandem integration of the ECA-Net and TAM, thus improving the quality of the reconstructed image by retaining a more discriminative representation during the compression process. -The ETAM module improves the model’s ability to focus on important features by integrating the channel attention mechanism (ECA) and temporal attention mechanism (TAM) in tandem, so as to retain more discriminative representations during the compression process and improve the quality of the reconstructed image.

Firstly, the input feature maps will be modeled by channel attention through the ECA-Net module.ECA-Net (Efficient Channel Attention Network) is a lightweight channel attention mechanism, whose core idea is to extract the statistical features of each channel by using Global Average Pooling. The core idea is to use Global Average Pooling to extract the statistical features of each channel, and then capture the inter-channel dependencies through local one-dimensional convolution to generate the attention weights of each channel. These weights are activated by Sigmoid to weight each channel of the original feature map, to strengthen meaningful spatial features and suppress redundant channel information. Compared with the traditional SE module, ECA-Net does not require channel dimensionality reduction operation, has less parameter overhead, and can realize more detailed spatial attention capability while maintaining efficiency.

Next, the feature maps weighted by ECA-Net are fed into the TAM module to further mine their key information in the temporal dimension (or the dimension of feature dynamics change).TAM (Temporal Attention Module), which is initially used to process temporal signals, is introduced in this study to simulate the importance of the change of image features in context. The process includes: performing maximum pooling and average pooling operations on the input feature maps to obtain the statistical distributions of the feature maps on the global and local scales, respectively; then fusing the two and extracting a unified attention map through convolutional operations, and then activating it by Sigmoid to form the final temporal attention weight map. The weight map reflects the importance of the features in the “time” dimension, and is used to adjust the intensity of expression of the feature map at different locations. In this way, TAM can improve the model’s ability to perceive dynamic information such as local changes and detail evolution in the image.

The ETAM module is embedded in both the encoder and decoder stages of the compression network, making it useful in both feature extraction and reconstruction recovery processes. In the encoder, ETAM helps to extract more compact and semantically rich latent representations, which contributes to the subsequent entropy coding; in the decoder, ETAM enhances the ability to restore important details and structures in the image reconstruction process. Experimental results show that the introduction of ETAM module significantly improves the performance of the image compression model, especially at high compression ratios, it can still retain clear edges and texture features, and outperforms the traditional and existing deep learning compression methods in a number of metrics, such as PSNR, MS-SSIM, and LPIPS, and demonstrates a strong feature representation and generalization ability.

Fig. 3

Efficient channel-temporal attention module.

Residual module

The residual module, shown in Fig. 4, optimizes information flow and enhances the learning capability of the model by introducing skip connections¹⁸ in deep neural networks. This module allows information to pass directly across multiple layers, helping to overcome the common problem of gradient vanishing in traditional deep networks and accelerating the training process. In the model proposed in this paper, the residual module enables the network to retain feature information learned in the shallow layers without adding additional computational burden by simply adding the input features to the convolved features.

In the residual module, the input is first passed through a series of convolutional layers followed by nonlinear activation functions to extract enhanced feature representations. These new features are then added to the input signals through skip connections to form the final output. This “additive” operation allows the model to learn the relative “residuals,” or the differences between the inputs and outputs, at each layer, rather than learning the complete mapping from scratch. This design enables the network to better capture the core information of the original data and refine it in subsequent layers.

The introduction of residual connections is particularly important for training deep networks¹⁹, as it effectively prevents performance degradation as the number of layers increases. In traditional deep networks without residual structures, information can gradually be lost as the network deepens, resulting in poorer performance compared to shallow networks. The residual module addresses this issue by enabling the direct transmission of informative features from shallow to deeper layers, thereby preserving information integrity throughout the network. Moreover, the residual connections help mitigate the vanishing gradient problem by providing an alternative gradient flow path, which facilitates more stable and consistent weight updates during training.

The residual module is particularly effective in image compression tasks. Images contain a large amount of multi-scale detail, and the residual module enhances the model’s ability to capture and represent these details by reinforcing the connections between different levels of features in the image. By combining low-level detail information with high-level abstract features, the residual module helps the model retain key details and reduce information loss during compression, ultimately improving the quality of the compressed image. Thus, the residual module not only enhances the expressive power of the network but also significantly improves the efficiency and effectiveness of image compression. The definition of this module can be expressed as follows.

$$\:Y={X}_{out}+X$$

Where X and X_out represent the input and output of the residual module, respectively, and Y denotes the total output. The features learned by the shallow network can be passed to the deeper layers through the residual connection module, thus preventing network degradation.

Fig. 4

Residuals module.

Loss function

The target loss of the proposed framework in this paper consists of four components: bit rate loss, distortion loss, perceptual loss and adversarial loss.For distortion loss, we use mean square error (MSE) loss.The calculation formula is:

$$\:{\mathcal{L}}_{MSE}=\frac{1}{N}\sum\:_{i=1}^{N}({y}_{i}-\hat{y}_{i}{)}^{2}$$

where y_i represents the ground truth pixel values, ŷ_i represents the predicted pixel values, and N is the number of pixels in the image.

For perceptual loss, this paper employs LPIPS (Learned Perceptual Image Patch Similarity) loss. LPIPS²⁰ is a method for calculating perceptual similarity between images using deep neural networks. It assesses visual differences by extracting features from images through a pre-trained network and computing the differences between these features, which more closely aligns with human visual perception. LPIPS loss is widely used in tasks such as image generation, restoration, and super-resolution, as it enhances the visual quality of generated images and captures more detailed structural and semantic differences. The calculation formula is as follows:

$$\:LPIPS(x,\widehat{x})={\sum\:}_{l}\frac{1}{{H}_{l}{W}_{l}}\sum\:_{h=1}^{{H}_{l}}\sum\:_{w=1}^{{W}_{l}}\left|\right|{w}_{l}\bullet\:({\varnothing\:}_{l}\left(x\right)-{\varnothing\:}_{l}(\widehat{x})\left)\right|{|}_{2}^{2}$$

Where $\:{{\varnothing}}_{l}\left(x\right)$ and $\:{{\varnothing}}_{l}\left(\widehat{x}\right)$ represent the feature maps extracted by the l-th layer of the neural network, Hl and Wl denote the height and width of the feature maps, respectively, and wl represents the weighting coefficient for each layer, which adjusts the importance of features from different layers.

The overall objective function is calculated as follows:$\:{L}_{total}=\alpha\:{L}_{r}+{\lambda\:}_{1}{L}_{d}+{\lambda\:}_{2}{L}_{per}$

where Lr refers to the code rate loss, Ld refers to the distortion loss, and Lper refers to the perceptual loss. α and λ1,2 are hyperparameters.

Network structure

The image compression framework proposed in this paper comprises two primary components: a core autoencoder sub-network and an entropy coding sub-network. These two modules work in tandem to efficiently perform image compression and reconstruction.

First, the core autoencoder sub-network compresses the input image into a latent representation, which is subsequently quantized to produce a quantized latent representation. Specifically, the input image x is transformed into a latent representation y by the encoder g_a:

$$\:y={g}_{a}\left(x\right)$$

Next, the potential representation y undergoes a quantisation operation to obtain the quantised representation ŷ:

$$\:\hat{y}=Quantize\left(y\right)$$

The sub-network incorporates a Residual Block (RB) to expand the receptive field and enhance the learning capability, thereby optimizing compression efficiency. The Residual Block helps mitigate the gradient vanishing problem in deep networks, enabling smooth information flow across multiple layers.

Additionally, an Efficient Channel-Time Attention Module (ETAM) is introduced in the encoder. This module combines the Efficient Channel Attention Module (ECA-Net) and the Temporal Attention Module (TAM), aiming to optimize both spatial and temporal feature extraction. ECA-Net improves channel correlations by adaptively selecting convolution kernel sizes to efficiently weight spatial features, while TAM leverages maximum and average pooling to capture temporal dynamics, thus enhancing the model’s performance in processing temporal signals.

The latent representation processed by the encoder is passed to the decoder (gs), which shares a similar structure to the encoder, utilizing both a residual module and an efficient channel-time attention module. The decoder’s task is to decode the quantized latent representation $\:\hat{y}$ into a reconstructed image $\:\widehat{x}$:

$$\:\widehat{x}={g}_{s}\left(\hat{y}\right)$$

By incorporating ETAM, the decoder can not only extract spatial features but also address temporal variations in the image, thereby enhancing the quality and accuracy of image reconstruction.

The entropy coding sub-network is a critical component of the proposed image compression framework. It enables efficient storage and transmission of latent representations by leveraging a context model, which operates in conjunction with a hyperprior network to accurately estimate the probability distribution of encoded features. The context model extracts dependencies among latent variables using 5 × 5 convolutional masks to provide accurate contextual information for predicting probability distributions. Meanwhile, the hypernetwork dynamically generates the distribution parameters (mean µ and standard deviation σ) of the latent variables through multiple convolutional layers, constructing a Gaussian distribution model to precisely capture the statistical properties of the latent representations²¹. Building on this, entropy coding leverages the Gaussian distribution to encode latent variables, effectively reducing the bit rate and optimizing data compression efficiency. By integrating this module, the model achieves substantial performance improvements in experiments, excelling in metrics such as PSNR and MS-SSIM, while also demonstrating excellent reconstruction quality in LPIPS perceptual similarity, thus fully validating its practical value in efficient image compression tasks.

The entropy encoding process is:

$$\:p\left({\widehat{y}}_{i}|{z}_{i}\right)=\frac{1}{\sqrt{2\pi\:{\sigma\:}^{2}}}\text{e}\text{x}\text{p}(-\frac{({\hat y}_{i}-\mu\:{)}^{2}}{2{\sigma\:}^{2}})$$

Here, µ and σ are the mean and standard deviation obtained from hypernetwork learning, representing the probability distribution of the potential representation. By entropy coding the potential representation, information loss can be minimized while ensuring compression efficiency.

The training objective of the entire network is to optimize compression performance by minimizing the trade-off between distortion and bit rate:

$$\:\mathcal{L}={\mathcal{L}}_{distortion}+\lambda\:{\mathcal{L}}_{rate}$$

Where $\:{\mathcal{L}}_{distortion}$ measures the distortion between the compressed image and the original image, $\:{\mathcal{L}}_{rate}$ measures the number of bits used in entropy coding, and λ is a hyperparameter that controls the balance between distortion and the number of compressed bits.

The proposed network enhances spatial and temporal feature extraction during compression by integrating both the Residual Module and the Efficient Channel-Temporal Attention Module (ETAM), thereby facilitating efficient feature learning and accurate information reconstruction. In parallel, the entropy coding sub-network improves compression performance by refining the probability distribution of the quantized latent representations through context modeling.

This architecture achieves a well-balanced trade-off between compression efficiency and reconstruction quality. The overall network structure is depicted in Fig. 5.

Fig. 5

Network structure.

Evaluation indicators

PSNR

PSNR (Peak Signal-to-Noise Ratio) is a crucial metric for image quality assessment²², used to evaluate the similarity between the reconstructed and the original images. A higher PSNR value indicates that the quality of the reconstructed image is closer to that of the original. The formula for PSNR is defined as follows:

$$\:PSNR=10\bullet\:{log}_{10}\left(\frac{{R}^{2}}{MSE}\right)$$

Where R is the maximum possible pixel value of the image (255 for an 8-bit image) and MSE is the Mean Square Error, calculated as:

$$\:MSE=\frac{1}{H\bullet\:W}\sum\:_{i=1}^{H}\sum\:_{j=1}^{W}({x}_{i,j}-{\widehat{x}}_{i,j}{)}^{2}$$

Where H and W are the height and width of the image respectively, $\:{x}_{i,j}$ and $\:{\widehat{x}}_{i,j}$ denote the pixel values of the original and reconstructed images at position (i, j) respectively.

PSNR is mainly used to quantify the quality of signal reproduction in reconstructed images and can reflect the performance of images in tasks such as noise processing, compression and reconstruction.Higher PSNR values usually indicate lower distortion and better visual quality of the compressed image.

MS-SSIM

SSIM (Structural Similarity Index) is used to evaluate the similarity of an image in terms of brightness, contrast, and structure. The closer the SSIM value is to 1, the more structurally similar the image is to the original. The formula for SSIM is as follows:

$$\:SSIM\left(x,y\right)=\frac{(2{\mu\:}_{x}{\mu\:}_{y}+{c}_{1})({2\sigma\:}_{xy}+{c}_{2})}{({\mu\:}_{x}^{2}+{\mu\:}_{y}^{2}+{c}_{1})({\sigma\:}_{x}^{2}+{\sigma\:}_{y}^{2}+{c}_{2})}$$

Where µ_x and µ_γ represent the mean values of the two images, σ_x and σ_γ are the standard deviations, σ_xγ is the covariance, and c₁ and c₂ are constants. MS-SSIM computes SSIM values at multiple scales²³ and aggregates these values to generate a final metric score. The MS-SSIM metric aligns more closely with subjective quality assessments, with values ranging from 0 to 1, where higher values indicate better image quality. To better visualize the variability of MS-SSIM across different results, MS-SSIM-dB represents the MS-SSIM metric in decibels and is calculated as follows:

$$\:MS-SSIM-db=-10{log}_{10}(1-MS-SSIM)$$

LPIPS

LPIPS (Learned Perceptual Image Patch Similarity) is an important metric for assessing the perceptual similarity between images, as it more closely aligns with human visual perception. Unlike traditional pixel-level metrics (e.g., MSE), LPIPS evaluates perceptual differences by extracting multi-layer features from an image using a neural network and calculating the weighted distances in the feature space. The formula is defined as follows:

$$\:LPIPS(x,\widehat{x})={\sum\:}_{l}\frac{1}{{H}_{l}{W}_{l}}\sum\:_{h=1}^{{H}_{l}}\sum\:_{w=1}^{{W}_{l}}\left|\right|{w}_{l}\bullet\:({{\varnothing}}_{l}\left(x\right)-{{\varnothing}}_{l}(\widehat{x})\left)\right|{|}_{2}^{2}$$

In the formula, ∅₁(x) and ∅₁(x̂) represent the feature maps extracted by the l-th layer of the neural network, respectively. H₁ and W₁ denote the height and width of the feature maps, while w₁ refers to the weighting coefficients of each layer, used to adjust the importance of features from different layers.

The advantage of LPIPS lies in its ability to capture perceptual differences by focusing on semantic content and visual quality, rather than low-level pixel-wise discrepancies. Unlike traditional distortion metrics, LPIPS measures the distance between original and reconstructed images in a deep neural network feature space, allowing it to more accurately assess detail preservation and semantic consistency. Notably, in scenarios where pixel-level differences are high but visual appearance remains similar, LPIPS better reflects the subtle variations that are perceptually significant to the human eye.

Data sets and parameter settings

The training set used in this paper comprises approximately 30,000 high-resolution images collected from the Internet. These images were resized to a random size between 500 and 1000 pixels and then randomly cropped to 256 × 256. After training, the model’s performance is evaluated and compared using the STN PLAD dataset, which is independent of the training set, to validate the model’s effectiveness.

Hardware environment

All experiments were conducted on workstations equipped with NVIDIA Tesla V100 GPUs to ensure efficiency and stability. The specific hardware environment is as follows: Processor: Intel Xeon Gold 6248R; GPU: NVIDIA Tesla V100 32GB; Memory: 256GB DDR4; OS: Ubuntu 18.04; Deep Learning Framework: PyTorch 1.12; CUDA version: 11.2. The training and testing durations were 24 h in total, with the training phase lasting approximately 16 h and the testing phase lasting about 8 h.

Experimental configuration

For specific training, the Adam optimiser is used to train the network, and the batch size is set to 8. The initial learning rate is set to $\:1\times\:{e}^{-4}$, which is halved at 500k iterations. In this paper, λ1 is set to $\:2\times\:{e}^{-3}$ and λ2 is set to 1. For different target code rates, the approach used in this paper is to keep each λ relatively fixed and adjust α. The α-list is set to [2.2, 2.8] for constraining the low code rate at around 0.1, [1.2, 1.6] for constraining the medium code rate at around 0.25, and [0.5, 0.8] for constraining the high code rate at around 0.4.

Training process

In the data preprocessing stage, all input images are normalized by scaling the pixel values to the [0, 1] range and uniformly resized to 256 × 256 pixels. During each training cycle, the model batches the input images and performs forward propagation through the ETAM model to compute the error between the reconstructed and original images. Backpropagation is then used to update the gradients during training and optimize the network weights, with a learning rate scheduler adjusting the learning rate every 5000 steps. To prevent overfitting and accelerate convergence, L2 regularization²⁴ and dropout techniques²⁵ are applied during training.

During the testing phase, the trained ETAM model is evaluated on the designated test set. For each image, compression is performed and corresponding evaluation metrics—including PSNR, SSIM, bitrate, and bits per pixel (BPP)—are calculated. To assess the effectiveness of the proposed method, its performance is compared against both traditional and state-of-the-art deep learning–based compression methods across all metrics.

The overall experimental design aims to comprehensively assess the superior performance of ETAM in image compression tasks through a variety of experimental configurations and a wide range of evaluation metrics.

Experimental results

Comparison experiment

As shown in Fig. 6, to verify the superiority of the Efficient Channel-Time Attention Module (ETAM) proposed in this paper, comparative experiments were conducted with mainstream image compression methods, including JPEG, JPEG2000, BPG, and WebP²⁶. These experiments were performed using the STN PLAD dataset, which consists of high-resolution color images captured by UAVs.

The STN PLAD dataset is designed to support intelligent inspection and maintenance of power lines, with important applications in identifying line assets and detecting potential defects. It is particularly suitable for fault detection on transmission lines in signal-free areas.

The model was trained by adjusting parameters to produce several models at different code rates, and the Rate-Distortion Curve and Rate-Perception Curve were plotted.

Fig. 6

Bit rate-distortion curves for different compression models.

As shown in Fig. 6, the PSNR and MS-SSIM metrics of the proposed method on the STN PLAD dataset are significantly higher than those of traditional compression methods. The PSNR curve demonstrates that the proposed method provides higher quality reconstructed images at the same bit rate, further confirming the advantages of ETAM in efficiently extracting image features and minimizing information loss. The MS-SSIM curve indicates a significant improvement in structural similarity with the proposed method.

As shown in Fig. 7, the proposed method outperforms traditional and other deep learning methods in terms of the perceptual similarity metric (LPIPS). LPIPS measures the perceptual similarity of images, and the inclusion of a perceptual loss function in the proposed model leads to a substantial improvement in this metric. The experimental results show that the proposed method is better at capturing image details and semantic information, making it more aligned with human subjective perception in terms of visual quality.

Fig. 7

Bit rate-perception curves for different compression models.

The experimental results show that the ETAM method proposed in this paper significantly outperforms mainstream compression methods in terms of both bit rate-distortion performance and perceptual performance. This confirms the effectiveness of the ETAM module in optimizing spatial and temporal feature extraction through the dual attention mechanism and highlights its potential for application in image compression tasks.

As shown in Table 1, to validate the generalization of the proposed method, the average PSNR, MS-SSIM, and LPIPS metrics are tested around 0.1 Bpp using the Kodak dataset.

Table 1 Performance of different compression methods on Kodak dataset.

As shown in Table 1, it can be observed that the experimental results follow the same pattern as those obtained on the STN PLAD dataset.

Traditional compression methods, such as JPEG and JPEG2000, lack the ability to adaptively model image content, and are prone to significant block effects, edge blurring, and loss of texture details, especially at high compression ratios. Modern image compression standards such as BPG and WebP, while improving compression efficiency, still rely on rule-driven coding frameworks and are unable to optimize feature extraction strategies through learning mechanisms, thus presenting bottlenecks in preserving the structural integrity and perceptual quality of images. Some deep learning-based compression methods introduce nonlinear modeling capabilities, but their feature extraction modules usually focus on modeling spatial information only, ignoring the contextual evolution and dynamic relationships of features, which can easily lead to insufficient detail recovery, especially when dealing with complex image scenes. In addition, some of the deep attention mechanisms improve the expression ability, but the high computational complexity and large number of parameters are not favorable to be deployed in practical applications.

Aiming at the above problems, ETAM module realizes the joint optimization of spatial and dynamic features by introducing the cascade mechanism of channel attention and temporal attention.ECA-Net can accurately mine the salient features of the image in the channel dimension at a very low parameter cost, so as to enhance the model’s ability to pay attention to the spatial structure; and the TAM module simulates the change rule of the features in the temporal or contextual dimension, so that the model has the ability to model dynamically. The TAM module simulates the change pattern of features in time or context dimension, so that the model has the ability of dynamic modeling, which can effectively make up for the shortcomings of the traditional model in semantic expression. Thanks to this dual-attention mechanism, ETAM can greatly improve the expression efficiency and information density of compressed features while keeping the network structure lightweight, thus improving the overall compression rate and reconstruction quality. In addition, the introduction of perceptual loss further optimizes the model’s ability to restore texture and details, which makes the reconstructed image closer to the subjective experience of the human eye in terms of visual effect. Comprehensive experimental results show that the ETAM method outperforms the comparison methods on several typical datasets and exhibits good generalization ability, which proves that it not only has advantages at the index level, but also effectively overcomes the key limitations of the existing image compression techniques in the method design.

Ablation experiment

In the ablation experiment design, we begin with a simple base model and progressively add different modules from the ETAM model, observing the impact of each module on overall performance. This approach helps to clearly understand the contribution of each module and validate its role in improving model performance. All experiments are evaluated using three metrics: PSNR, MS-SSIM, and LPIPS, to assess the image reconstruction quality. The experimental results are presented in Table 2.

Table 2 Results of ablation experiments by sequentially stacking different modules.

The experimental results demonstrate that ETAM significantly enhances both image reconstruction quality and compression efficiency. Specifically, after incorporating ETAM, the PSNR improves from 27.0 to 28.5, SSIM increases from 0.78 to 0.81, and perceptual quality (LPIPS) decreases from 0.52 to 0.42. Adding the residual module further boosts PSNR to 29.2, SSIM to 0.83, and perceptual quality (LPIPS) improves with a reduction to 0.37. Finally, with the inclusion of the entropy coding sub-network, PSNR reaches 31.5, SSIM rises to 0.85, and perceptual quality achieves its highest level, with LPIPS dropping to 0.26. These results indicate that the dual-attention mechanism in ETAM effectively enhances image compression performance by optimizing the extraction of both spatial and temporal features. Moreover, the addition of the residual module and entropy coding sub-network further refines both compression efficiency and image quality, ultimately achieving an optimal performance balance.

Comparison of visualisation results

As illustrated in Fig. 8, each group of images demonstrates the reconstruction performance and visual characteristics of different image compression methods applied to the STN PLAD dataset at a target bitrate of 0.1 bpp.Specifically, images a1–a5 are the original uncompressed references, preserving full detail and color, and serve as the ground truth for comparison. Images b1–b5 show the results of JPEG compression at approximately a 20:1 compression ratio. These reconstructions exhibit prominent blocking artifacts and noticeable loss of detail, particularly around edges and in high-frequency regions.Images c1–c5 are compressed using JPEG2000, also at around 20:1. While JPEG2000 retains more detail than JPEG, it suffers from significant quality degradation in complex regions under high compression, often resulting in blur and loss of fine structures.Images d1–d5 are WebP-compressed with a ratio of approximately 25:1. WebP achieves better compression efficiency compared to JPEG and JPEG2000, but still loses high-frequency content at lower bitrates, affecting visual quality.Images e1–e5 depict the results of BPG compression, operating at a ratio of around 50:1. Although BPG outperforms earlier methods in preserving image quality at low bitrates, it introduces minor artifacts and blurring in areas with complex textures.Finally, images f1–f5 are reconstructed using the proposed ETAM method, achieving an ultra-high compression ratio of approximately 235:1. Despite this aggressive compression, ETAM effectively preserves edge sharpness and fine textures, with minimal blocking or visible artifacts. The reconstructed results are visually close to the original images, highlighting the superiority of ETAM in maintaining perceptual quality under extreme compression conditions.

The ETAM method proposed in this paper significantly improves image quality at high compression ratios, especially in preserving details and edges, with almost no artifacts or block effects. By introducing a perceptual loss function and optimizing LPIPS, the reconstructed images produced by ETAM align more closely with human visual perception. The experimental results demonstrate that ETAM outperforms traditional and modern compression methods across several metrics, including PSNR, SSIM, and LPIPS. This confirms its balanced approach, combining efficient compression with high-quality reconstruction, making it especially well-suited for practical applications, such as monitoring transmission lines in signal-free areas.

Fig. 8

Comparison of image reconstruction effect under different compression methods.

To further verify the superiority of the ETAM method proposed in this paper, we calculated the PSNR, MS-SSIM, and LPIPS metrics for various compression methods (JPEG, JPEG2000, WebP, BPG, and ETAM) on the images shown in Fig. 8. The results are presented in Table 3.

Table 3 Comparison of metrics of different compression methods on each image.

The results demonstrate that ETAM outperforms all other methods across all images. For image a1, ETAM achieves a PSNR of 30.5 dB, which is significantly higher than JPEG (27.3 dB), JPEG2000 (29.1 dB), WebP (28.5 dB), and BPG (29.6 dB). In terms of the MS-SSIM metric, ETAM scores 0.87, while JPEG, JPEG2000, WebP, and BPG score 0.78, 0.82, 0.80, and 0.84, respectively. For LPIPS, ETAM achieves the lowest score of 0.27, compared to 0.60, 0.58, 0.54, and 0.56 for JPEG, JPEG2000, WebP, and BPG, respectively. Similarly, for image a2, ETAM achieves a PSNR of 30.7 dB, outperforming JPEG (26.9 dB), JPEG2000 (29.0 dB), WebP (28.4 dB), and BPG (29.5 dB). For MS-SSIM, ETAM scores 0.88, significantly higher than the other methods, and for LPIPS, ETAM scores 0.28, much lower than the other methods. These results indicate that the ETAM method significantly improves image quality in terms of both PSNR and MS-SSIM, while further reducing perceptual differences as measured by LPIPS, aligning more closely with human subjective perception. Overall, ETAM not only effectively minimizes information loss at high compression ratios but also greatly enhances the visual quality of image reconstruction, confirming its superior performance in image compression tasks and offering an efficient and reliable solution for real-world applications, such as remote monitoring of transmission lines.

Limitations of the ETAM method

Although the ETAM method proposed in this paper performs well in most of the test images, its compression fails to significantly outperform the existing methods in some image categories, and even slightly degrades in perceived quality. In order to present the performance boundaries of the model more comprehensively, three representative images in the Kodak24 dataset are selected as examples, including a brick wall, a lighthouse, and a close-up of a human face, as shown in Figure. 9.

Fig. 9

Visual example of the limitations of the ETAM approach.

It is worth stating that the main application scenario of the method in this paper is remote monitoring and inspection image compression of transmission lines, rather than generalized image compression. In typical transmission datasets such as STN PLAD, most of the images have clear structural boundaries, high-contrast features (e.g., conductors, insulators, tower contours, etc.), and have a relatively homogeneous background, which does not involve complex faces, repetitive textures, or extreme low-contrast.

Therefore, while there are individual images in some of the Kodak24 datasets where ETAM performance gains are not evident, these failures do not represent a performance deficiency in the actual target domain. On the contrary, ETAM has consistently demonstrated good detail reproduction and perceptual consistency on transmission monitoring images, which is especially valuable in weak signal, high compression ratio transmission conditions.

Discussion

Scalability for high-resolution images

The ETAM image compression method proposed in this paper adopts an end-to-end fully convolutional design in the model structure, which does not rely on fixed-size inputs and thus has good input size adaptation capability. Although a 256 × 256 image patch is mainly used in the training phase of the model to improve the training efficiency and enhance the feature diversity, the model is able to seamlessly process higher resolution image data without any structural adjustments or additional modules in the testing phase. This design makes the model not only suitable for image compression experiments at conventional resolutions, but also has the potential to be extended to high-resolution images in real-world application scenarios.

In order to verify its scalability, we apply the trained model to image compression tasks at 1024 × 1024 and 1920 × 1080 resolutions without modifying the model parameters or structure, and the test samples include industrial scene images, natural landscape images, and UAV images, etc. The experimental results show that the ETAM model is suitable for image compression experiments at conventional resolutions. The experimental results show that the ETAM model still maintains good compression and reconstruction performance under high-resolution inputs: the image structure sharpness (PSNR), perceptual similarity (LPIPS), and multi-scale structural similarity (MS-SSIM) are all consistent with those of the low-resolution test, and the reconstructed image has clear edges, intact texture, and good subjective visual quality.

In addition, since both ECA-Net and TAM adopt a lightweight local convolutional attention mechanism and do not introduce complex global self-attention or redundant fully-connected structures, the growth in computational resource consumption remains linear when the image size is enlarged, and no obvious inference bottleneck occurs. On the NVIDIA RTX 3090 graphics card, the average inference time for the model to process a 1080p image is no more than 300ms, showing good inference efficiency and practical deployability.

From the practical application point of view, high-resolution image compression has a wide range of needs in the fields of telemedicine, city monitoring, electric power inspection, and geographic information systems. Traditional methods are often ineffective in high-resolution scenes due to high information density and limited compression ratio, and the recovered images are prone to artifacts or blurring. The method in this paper has strong expressive ability in structure and maintains high efficiency in design, so it is more suitable to be deployed in this kind of edge equipment with high requirements on image quality and limited processing resources, and provides a feasible solution for practical scenarios.

Adaptability to video sequences and expansion prospects

Although this study mainly focuses on the compression of still images, the proposed ETAM module has been conceptually designed to extend to video compression, and the Temporal Attention Module (TAM) in ETAM is essentially used to capture key information of the feature map in the “temporal dimension” or “feature dynamics”, which is the “time dimension” or “feature dynamics” of the feature map. The temporal attention module (TAM) in ETAM is essentially used to capture the key information of the feature map in the “time dimension” or “feature dynamics”. In the image compression task of this study, this temporal attention is more about modeling the context or internal trend of the features, i.e., modeling the “dynamic” information by fusing the maximum pooling with the average pooling, so as to enhance the model’s ability to perceive the feature changes.

This “pseudo-temporal modeling” mechanism does not involve explicit time series modeling between real video frames, but it provides structural compatibility for subsequent extensions. If ETAM is applied to a video compression task, the TAM module can further utilize its ability to handle dynamic changes between frames. For example, in a sequence of video frames, TAM can capture temporal consistency and trends by aggregating the intermediate representations of the current frame with the preceding and following frames, thus generating a more discriminative temporal attention map that enhances the critical frame regions, which can help to reduce redundant coding and improve compression efficiency.

Conclusion

In this paper, we propose a deep learning-based image compression method using the Efficient Channel-Temporal Attention Module (ETAM), designed to address the challenges of data transmission and storage efficiency in transmission line monitoring scenarios, especially in regions with unstable or no signals. The ETAM module jointly optimizes image spatial features and temporal dynamic features. Specifically, ECA-Net efficiently captures inter-channel correlations through adaptive one-dimensional convolution to improve spatial information representation, while TAM captures key temporal dynamics through a combination of maximum and average pooling, thereby enhancing the modeling capability of temporal features. Coupled with the residual module and entropy coding sub-network, this method further boosts the model’s ability to represent data and enhances compression efficiency, significantly reducing information loss under high compression ratios.

The experimental results comprehensively validate the superiority of the ETAM method. Tests on the STN PLAD and Kodak datasets show that our method outperforms traditional compression methods (e.g., JPEG, JPEG2000) and other modern techniques (e.g., BPG, WebP) across multiple metrics (e.g., PSNR, MS-SSIM, LPIPS). Specifically, ETAM effectively preserves edge details and texture features under high compression ratios, with the reconstructed images closely resembling the original ones. Additionally, the ablation experiments provide valuable insights into the contributions of the ETAM module, the residual module, and the entropy coding sub-network to the overall performance. By jointly optimizing context modeling and super-network generation, the entropy coding sub-network accurately models the distributional characteristics of latent variables, further improving compression efficiency and reconstruction quality. Furthermore, the significant improvement in the perceptual similarity (LPIPS) metric demonstrates that the reconstructed images generated by our method align closely with human visual perception, achieving high subjective quality.